Confidence intervals for the common coefficient of variation of rainfall in Thailand

Fiducial generalized confidence interval

The FGCI uses the FGPQs. The FGPQs are a subclass of the GPQs. The FGCI has correct frequentist coverage probability. For i = 1, 2, …, k, let ${\bar{X}}_i$ and $S_i^2$ be the sample mean and the sample variance for log-transformed data and let ${\bar{x}}_i$ and $s_i^2$ be the observed sample mean and the observed sample variance respectively. Let ${\bar{X}}_i^{\ast }$ and $S_i^{2\ast }$ be independent copies of ${\bar{X}}_i$ and $S_i^2$, respectively. Let ${\bar{X}}_i$ and ${\bar{X}}_i^{\ast }$ be independent and identically distributed with mean μ_i and variance ${\sigma }_i^2∕n_i$. It is well known that (8)${\displaystyle {\bar{X}}_i\sim N\left({\mu }_i,\frac{{\sigma }_i^2}{n_i}\right)\text{and}{\bar{X}}_i^{\ast }\sim N\left({\mu }_i,\frac{{\sigma }_i^2}{n_i}\right).}$

Furthermore, let $S_i^2$ and $S_i^{2\ast }$ be independent and identically distributed. Then (9)${\displaystyle \frac{\left(n_i-1\right)S_i^2}{{\sigma }_i^2}\sim {\chi }_{n_i-1}^2\text{and}\frac{\left(n_i-1\right)S_i^{2\ast }}{{\sigma }_i^2}\sim {\chi }_{n_i-1}^2,}$ where ${\chi }_{n_i-1}^2$ is chi-squared distribution with n_i − 1 degree of freedom.

According to Hannig, Iyer & Patterson (2006a) and Hannig et al. (2006b), the FGPQs of μ_i and ${\sigma }_i^2$ are defined by (10)${\displaystyle R_{{\mu }_i}={\bar{X}}_i-\frac{S_i}{S_i^{\ast }}\left({\bar{X}}_i^{\ast }-{\mu }_i\right)}$ and (11)${\displaystyle R_{{\sigma }_i^2}=\frac{S_i^2}{S_i^{2\ast }}{\sigma }_i^2.}$

Therefore, the FGPQ for θ_i based on the FGPQ for ${\sigma }_i^2$ is given by (12)${\displaystyle R_{{\theta }_i}=\sqrt{exp\left(R_{{\sigma }_i^2}\right)-1}.}$

The FGPQ of θ_i in Eq. (12) satisfies two conditions defined in Definition of Hannig, Iyer & Patterson (2006a) and Hannig et al. (2006b). The definition of Hannig, Iyer & Patterson (2006a) and Hannig et al. (2006b) has two conditions such as the distribution of the GPQ is free of all unknown parameters and the observed value of the GPQ is the parameter of interest. From Eq. (4), the variance of ${\hat{\theta }}_i$ is provided by (13)${\displaystyle Var\left({\hat{\theta }}_i\right)\approx \frac{{\sigma }_i^{4}exp\left(2{\sigma }_i^2\right)}{2\left(n_i-1\right)\cdot \left(exp\left({\sigma }_i^2\right)-1\right)}.}$

The FGPQ of $Var\left({\hat{\theta }}_i\right)$ is given by (14)${\displaystyle R_{Var\left({\hat{\theta }}_i\right)}=\frac{R_{{\sigma }_i^2}^{2}exp\left(2R_{{\sigma }_i^2}\right)}{2\left(n_i-1\right)\cdot \left(exp\left(R_{{\sigma }_i^2}\right)-1\right)}.}$

The FGPQ for the common coefficient of variation θ is a weighted average of the FGPQ R_θi based on k individual sample. Therefore, the FGPQ is given by (15)${\displaystyle R_{\theta }=\sum _{i=1}^k\frac{R_{{\theta }_i}}{R_{Var\left({\hat{\theta }}_i\right)}}/\sum _{i=1}^k\frac{1}{R_{Var\left({\hat{\theta }}_i\right)}},}$ where R_θi is defined in Eq. (12) and $R_{Var\left({\hat{\theta }}_i\right)}$ is defined in Eq. (14).

The FGPQ in Eq. (12) satisfies two conditions of the definition given above. The FGCI is constructed using the quantiles of FGPQ defined in Eq. (15). Therefore, the $100\left(1-\alpha \right)\text{\%}$ two-sided confidence interval for the common coefficient of variation θ based on the FGCI approach is (16)${\displaystyle C{I}_{FGCI}=\left[L_{FGCI},U_{FGCI}\right]=\left[R_{\theta }\left(\alpha ∕2\right),R_{\theta }\left(1-\alpha ∕2\right)\right],}$ where $R_{\theta }\left(\alpha ∕2\right)$ and $R_{\theta }\left(1-\alpha ∕2\right)$ denote the $100\left(\alpha ∕2\right)$-th and $100\left(1-\alpha ∕2\right)$-th percentiles of R_θ, respectively.

The following algorithm is used to construct the FGCI:

 
 
 Algorithm 1 
For a given ¯ xi  and s2i, where i = 1,2,...,k 
For g =  1 to m, where m is number of generalized computation 
Generate X∗ and then compute ¯ x∗i  and s2∗i 
Generate χ2ni−1  from chi-squared distribution with ni − 1  degrees of 
freedom 
Compute Rσ2 
i  from Eq.  (11) 
Compute Rθi  from Eq.  (12) 
Compute RV ar(ˆθ 
i)  from Eq.  (14) 
Compute Rθ  from Eq.  (15) 
End g loop 
Compute Rθ (α∕2)  and Rθ (1 − α∕2)  from Eq.  (16)    

Method of variance estimates recovery confidence interval

Zou & Donner (2008) and Zou, Taleban & Hao (2009) proposed the MOVER approach to construct the confidence interval for the sum of two parameters. For i = 1, 2, let θ₁ and θ₂ be the parameters of interest. Let L and U be the lower limit and upper limit of the confidence interval for θ₁ + θ₂. Moreover, let ${\hat{\theta }}_1$ and ${\hat{\theta }}_2$ be the estimators of θ₁ and θ₂, respectively. The central limit theorem and the assumption of independence between the point estimates ${\hat{\theta }}_1$ and ${\hat{\theta }}_2$ are used. Therefore, the lower limit L is (17)${\displaystyle L={\hat{\theta }}_1+{\hat{\theta }}_2-z_{\alpha ∕2}\sqrt{\widehat{Var}\left({\hat{\theta }}_1\right)+\widehat{Var}\left({\hat{\theta }}_2\right)},}$ where z_α∕2 is the $100\left(\alpha ∕2\right)$-th percentile of the standard normal distribution.

Let l_i and u_i be the lower limit and upper limit of the confidence interval for θ_i, where i = 1, 2. The lower limit L must be closer to l₁ + l₂ than to ${\hat{\theta }}_1+{\hat{\theta }}_2$. The variance estimate for ${\hat{\theta }}_i$ at θ_i = l_i is defined by (18)${\displaystyle \widehat{Var}\left({\hat{\theta }}_{l_i}\right)=\frac{{\left({\hat{\theta }}_i-l_i\right)}^2}{z_{\alpha ∕2}^2}.}$

Substituting back into Eq. (17) as follows (19)${\displaystyle L={\hat{\theta }}_1+{\hat{\theta }}_2-\sqrt{{\left({\hat{\theta }}_1-l_1\right)}^2+{\left({\hat{\theta }}_2-l_2\right)}^2}.}$

Similarly, the variance estimate for ${\hat{\theta }}_i$ at θ_i = u_i is defined by (20)${\displaystyle \widehat{Var}\left({\hat{\theta }}_{u_i}\right)=\frac{{\left(u_i-{\hat{\theta }}_i\right)}^2}{z_{\alpha ∕2}^2}.}$

The upper limit U is (21)${\displaystyle U={\hat{\theta }}_1+{\hat{\theta }}_2+\sqrt{{\left(u_1-{\hat{\theta }}_1\right)}^2+{\left(u_2-{\hat{\theta }}_2\right)}^2}.}$

Therefore, the variance estimate for ${\hat{\theta }}_i$ at θ_i = l_i and θ_i = u_i is defined by (22)${\displaystyle \widehat{Var}\left({\hat{\theta }}_i\right)=\frac{1}{2}\left(\frac{{\left({\hat{\theta }}_i-l_i\right)}^2}{z_{\alpha ∕2}^2}+\frac{{\left(u_i-{\hat{\theta }}_i\right)}^2}{z_{\alpha ∕2}^2}\right),}$ where i = 1, 2.

In this paper, the k parameters of interest are θ₁, θ₂, …, θ_k. The concepts of Zou & Donner (2008) and Zou, Taleban & Hao (2009) are motivated for constructing the confidence interval for θ₁ + θ₂ + … + θ_k are (23)${\displaystyle L={\hat{\theta }}_1+{\hat{\theta }}_2+\dots +{\hat{\theta }}_k-\sqrt{{\left({\hat{\theta }}_1-l_1\right)}^2+{\left({\hat{\theta }}_2-l_2\right)}^2+\dots +{\left({\hat{\theta }}_k-l_k\right)}^2}}$ and (24)${\displaystyle U={\hat{\theta }}_1+{\hat{\theta }}_2+\dots +{\hat{\theta }}_k+\sqrt{{\left(u_1-{\hat{\theta }}_1\right)}^2+{\left(u_2-{\hat{\theta }}_2\right)}^2+\dots +{\left(u_k-{\hat{\theta }}_k\right)}^2},}$ where (l₁, u₁), (l₂, u₂), …, (l_k, u_k) contain the parameter values for θ₁, θ₂, …, θ_k, respectively.

According to Graybill & Deal (1959), the common coefficient of variation θ is weighted average of the coefficient of variation ${\hat{\theta }}_i$ based on k individual samples. Therefore, the common coefficient of variation is defined by (25)${\displaystyle \hat{\theta }=\sum _{i=1}^k\frac{{\hat{\theta }}_i}{\widehat{Var}\left({\hat{\theta }}_i\right)}/\sum _{i=1}^k\frac{1}{\widehat{Var}\left({\hat{\theta }}_i\right)},}$ where ${\hat{\theta }}_i=\sqrt{exp\left(S_i^2\right)-1}$ and $\widehat{Var}\left({\hat{\theta }}_i\right)$ is defined in Eq. (22).

Applying Krishnamoorthy & Oral (2017), the lower limit and upper limit of the confidence interval for the common coefficient of variation θ are defined by (26)${\displaystyle L_{MOVER}=\hat{\theta }-\sqrt{\sum _{i=1}^k\frac{{\left({\hat{\theta }}_i-l_i\right)}^2}{{\left(\widehat{Var}\left({\hat{\theta }}_{l_i}\right)\right)}^2}/\sum _{i=1}^k\frac{1}{{\left(\widehat{Var}\left({\hat{\theta }}_{l_i}\right)\right)}^2}}}$ and (27)${\displaystyle U_{MOVER}=\hat{\theta }+\sqrt{\sum _{i=1}^k\frac{{\left(u_i-{\hat{\theta }}_i\right)}^2}{{\left(\widehat{Var}\left({\hat{\theta }}_{u_i}\right)\right)}^2}/\sum _{i=1}^k\frac{1}{{\left(\widehat{Var}\left({\hat{\theta }}_{u_i}\right)\right)}^2}},}$ where $\hat{\theta }$ is defined in Eq. (25).

According to Niwitpong (2013), for i = 1, 2, …, k, the confidence interval for coefficient of variation of log-normal distribution based on the ith sample is given by (28)${\displaystyle \left[l_i,u_i\right]=\left[\right.\sqrt{exp\left(\frac{\left(n_i-1\right)S_i^2}{{\chi }_{\left(n_i-1\right),\left(1-\alpha ∕2\right)}^2}\right)-1},\sqrt{exp\left(\frac{\left(n_i-1\right)S_i^2}{{\chi }_{\left(n_i-1\right),\left(\alpha ∕2\right)}^2}\right)-1}\left]\right.,}$ where ${\chi }_{\left(n_i-1\right),\left(1-\alpha ∕2\right)}^2$ and ${\chi }_{\left(n_i-1\right),\left(\alpha ∕2\right)}^2$ denote the $100\left(1-\alpha ∕2\right)$-th and $100\left(\alpha ∕2\right)$-th percentiles of the chi-squared distribution with n_i − 1 degrees of freedom.

Therefore, the $100\left(1-\alpha \right)\text{\%}$ two-sided confidence interval for the common coefficient of variation θ based on MOVER approach is (29)${\displaystyle C{I}_{MOVER}=\left[L_{MOVER},U_{MOVER}\right],}$

where L_MOVER is defined in Eq. (26), U_MOVER is defined in Eq. (27), and l_i and u_i are defined in Eq. (28).

Computational confidence interval

Theorem 1: Let $Y_i=\left(Y_{i1},Y_{i2},\dots ,Y_{i{n}_i}\right)$ be a log-normal population with parameters μ_i and ${\sigma }_i^2$, where i = 1, 2, …, k. For i = 1, 2, …, k and j = 1, 2, …, n_i, let $X_{ij}=log\left(Y_{ij}\right)$ be the normal distribution with mean μ_i and variance ${\sigma }_i^2$. The maximum likelihood estimators of μ_i and θ given by Eq. (3) under θ₁ = θ₂ = … = θ_k = θ are given by (30)${\displaystyle {\hat{\mu }}_i={\bar{X}}_i}$ and (31)${\displaystyle \sum _{i=1}^k\frac{n_i{\hat{\sigma }}_i^2}{log\left({\theta }^2+1\right)}-\sum _{i=1}^k{n}_i=0.}$

Proof: The log-likelihood function of normal distribution with parameters μ_i and θ is given by ${\displaystyle lnL=-\frac{1}{2}\sum _{i=1}^k{n}_{i}log\left(2\pi log\left({\theta }^2+1\right)\right)-\sum _{i=1}^k{n}_{i}log\left(Y_{ij}\right)-\sum _{i=1}^k\sum _{j=1}^{n_i}\frac{{\left(log\left(Y_{ij}\right)-{\mu }_i\right)}^2}{2log\left({\theta }^2+1\right)}.}$

Differentiating the lnL with respect to μ_i and θ, respectively, the maximum likelihood estimators of μ_i and θ are given by

${\hat{\mu }}_i={\bar{X}}_i$

and

${\displaystyle \sum _{i=1}^k\frac{n_i{\hat{\sigma }}_i^2}{log\left({\theta }^2+1\right)}-\sum _{i=1}^k{n}_i=0.}$

Hence, Theorem 1 is proved.

According to Pal, Lim & Ling (2007), the computational approach uses the maximum likelihood estimates (MLEs). The common coefficient of variation based on maximum likelihood estimator is defined by (32)${\displaystyle {\hat{\theta }}_{ML}=\sum _{i=1}^k\frac{{\hat{\theta }}_i}{\widehat{Var}\left({\hat{\theta }}_i\right)}/\sum _{i=1}^k\frac{1}{\widehat{Var}\left({\hat{\theta }}_i\right)},}$

where ${\hat{\theta }}_i=\sqrt{exp\left(S_i^2\right)-1}$ and $\widehat{Var}\left({\hat{\theta }}_i\right)$ is defined in Eq. (4) with σ_i replaced by s_i.

The computational approach is to obtain the restricted maximum likelihood estimates (RMLEs) of parameters. The maximum likelihood estimators of μ_i and θ under θ₁ = θ₂ = … = θ_k = θ provide the RMLEs of these parameters.

Then the RMLE of μ_i is defined by ${\hat{\mu }}_{i\left(RML\right)}={\bar{X}}_i$. The RMLE of θ obtained iteratively from Eq. (31) by using bisection method. The θ converge to the RMLE denoted as ${\hat{\theta }}_{RML}$.

Data replication from $f\left(x|{\hat{\mu }}_{i\left(RML\right)},{\hat{\theta }}_{RML}\right)$ is used to construct the confidence interval based on computational approach. Let artificial sample $X_{i\left(RML\right)}=\left(X_{i1\left(RML\right)},X_{i2\left(RML\right)},\dots ,X_{i{n}_i\left(RML\right)}\right)$ be the normal distribution with mean ${\hat{\mu }}_{i\left(RML\right)}$ and variance ${\hat{\sigma }}_{i\left(RML\right)}^2$. Let ${\bar{X}}_{i\left(RML\right)}$ and $S_{i\left(RML\right)}^2$ be the mean and variance of the log-transformed sample from a log-normal distribution for the ith artificial sample and let ${\bar{x}}_{i\left(RML\right)}$ and $s_{i\left(RML\right)}^2$ be observed sample mean and observed sample variance, respectively.

Therefore, the common coefficient of variation based on k individual samples is defined by (33)${\displaystyle {\hat{\theta }}_{RML}=\sum _{i=1}^k\frac{{\hat{\theta }}_{i\left(RML\right)}}{\widehat{Var}\left({\hat{\theta }}_{i\left(RML\right)}\right)}/\sum _{i=1}^k\frac{1}{\widehat{Var}\left({\hat{\theta }}_{i\left(RML\right)}\right)},}$

where ${\hat{\theta }}_{i\left(RML\right)}=\sqrt{exp\left(S_{i\left(RML\right)}^2\right)-1}$.

Therefore, the $100\left(1-\alpha \right)\text{\%}$ two-sided confidence interval for the common coefficient of variation θ based on computational approach is (34)${\displaystyle C{I}_{CA}=\left[L_{CA},U_{CA}\right]=\left[{\hat{\theta }}_{RML}\left(\alpha ∕2\right),{\hat{\theta }}_{RML}\left(1-\alpha ∕2\right)\right],}$

where ${\hat{\theta }}_{RML}\left(\alpha ∕2\right)$ and ${\hat{\theta }}_{RML}\left(1-\alpha ∕2\right)$ denote the $\left(\alpha ∕2\right)$-th and $\left(1-\alpha ∕2\right)$-th percentiles of ${\hat{\theta }}_{RML}$, respectively.

The following algorithm is used to construct the computational confidence interval:

 
 
   Algorithm 2 
For a given ¯ xi, s2i, and θ, where i = 1,2,...,k 
Compute ˆ μi(RML)  and ˆ θRML  from Eqs.  (30)--31 
For g =  1 to m 
Generate xij(RML)  from N ( 
  ˆ μi(RML),∘ 
  __________log ( 
   ˆ θ2 
RML + 1) 
            ) 
Compute ¯ xi(RML)  and s2i(RML) 
Compute ˆ θRML  from Eq.  (33) 
End g loop 
Compute ˆ θRML (α∕2)  and ˆ θRML (1 − α∕2)  from Eq.  (34)    

Bayesian confidence interval

The FGCI approach, MOVER approach, and computational approach are the classical approach. The classical approach and the Bayesian approach are fundamentally different. In the classical approach, the parameter of interest θ is unknown, but it is fixed. In the Bayesian approach, the parameter is considered to be a quantity. The variation of the quantity is described by the prior distribution. Bayes (1763) introduced that Bayesian approach uses Bayes’ theorem to update probabilities. Bayes’ theorem describes the conditional probability of an event based on data. The data is prior information or beliefs about the event. The posterior distribution is combination of the likelihood function and the prior distribution. The Bayesian confidence interval is constructed based on the posterior distribution. The posterior distribution is a conditional distribution which is based on the observed values of the sample. The posterior distribution is used to make statements about the parameter. The parameter is considered a random quantity. The conditional posterior distribution for μ_i given ${\sigma }_i^2$ and x_i is the normal distribution with mean ${\hat{\mu }}_i$ and variance ${\sigma }_i^2∕n_i$. The distribution is defined by (35)${\displaystyle {\mu }_i|{\sigma }_i^2,x_i\sim N\left({\hat{\mu }}_i,{\sigma }_i^2∕n_i\right).}$

The posterior distribution for ${\sigma }_i^2$ is inverse gamma distribution. It is defined by (36)${\displaystyle {\sigma }_i^2|x_i\sim IG\left(\left(n_i-1\right)∕2,\left(n_i-1\right)s_i^2∕2\right).}$

The posterior distribution of coefficient of variation of log-normal distribution is (37)${\displaystyle {\hat{\theta }}_i=\sqrt{exp\left({\sigma }_i^2\right)-1},}$ where ${\sigma }_i^2$ is defined in Eq. (36).

The variance of ${\hat{\theta }}_i$ is (38)${\displaystyle Var\left({\hat{\theta }}_i\right)\approx \frac{{\sigma }_i^4\left(exp\left(2{\sigma }_i^2\right)\right)}{2\left(n_i-1\right)\left(exp\left({\sigma }_i^2\right)-1\right)},}$ where ${\sigma }_i^2$ is defined in Eq. (36).

The common coefficient of variation of log-normal distribution based on k individual samples which the parameter of interest defined by (39)${\displaystyle {\hat{\theta }}_{BS}=\sum _{i=1}^k\frac{{\hat{\theta }}_i}{Var\left({\hat{\theta }}_i\right)}/\sum _{i=1}^k\frac{1}{Var\left({\hat{\theta }}_i\right)},}$

where $\left({\hat{\theta }}_i\right)$ is defined in Eq. (37) and $Var\left({\hat{\theta }}_i\right)$ is defined in Eq. (38).

Gelman et al. (2013) introduced the highest posterior density interval to construct the Bayesian confidence interval. Therefore, the $100\left(1-\alpha \right)\text{\%}$ two-sided confidence interval for the common coefficient of variation θ based on Bayesian approach is (40)${\displaystyle C{I}_{BS}=\left[L_{BS},U_{BS}\right],}$ where L_BS and U_BS are the lower limit and the upper limit of the shortest $100\left(1-\alpha \right)\text{\%}$ highest posterior density interval of ${\hat{\theta }}_{BS}$, respectively.

The following algorithm is used to construct the Bayesian confidence interval:

 
 
   Algorithm 3 
For a given ¯ xi  and s2i, where i = 1,2,...,k 
For g =  1 to m 
Generate μi|σ2i,xi ∼ N(ˆμi,σ2i∕ni) 
Generate σ2i|xi ∼ IG((ni − 1)∕2,(ni − 1)s2i∕2) 
Compute θi  from Eq.  (37) 
Compute V ar(ˆθi)  from Eq.  (38) 
Compute θBS  from Eq.  (39) 
End g loop 
Compute LBS  and UBS    

An empirical application

The rainfall has been the seasonal problem in Thailand. Rainy season in Thailand is between May and October. The daily rainfall appears on 17 June 2020. Real data example of rainfall data is used to illustrate the FGCI, MOVER, computational, and Bayesian approaches. All data were reported by the Thai Meteorological Department (https://www.tmd.go.th/climate/climate.php).

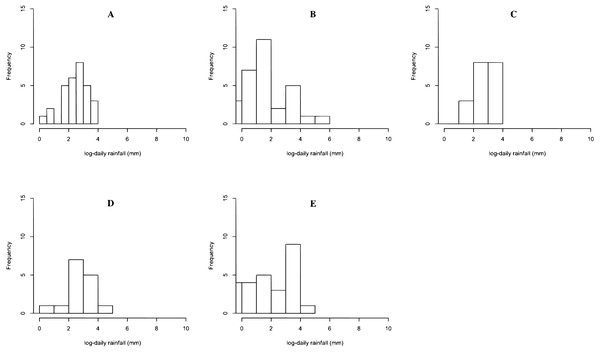
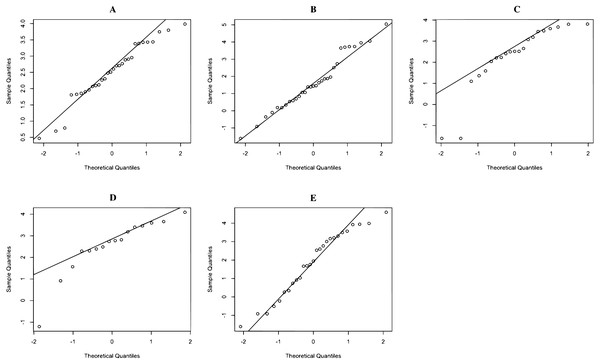
The rainfall data on 17 June 2020 in Northern, Northeastern, Central, Eastern, and Southern regions are reported in Dataset 1, and histogram and normal QQ-plots are presented in Figs. 1 and 2, respectively. The data sets consist of 30 measurements in Northern region, 31 measurements in Northeastern region, 21 measurements in Central region, 16 measurements in Eastern region, and 27 measurements in Southern region. The statistics is summarized in Table 3. The Shapiro–Wilk normality test is used to check the assumption that the log-data is normal distribution. The Shapiro–Wilk normality test with p-values 0.2176, 0.4981, 0.0009, 0.0128, and 0.2127 for Northern, Northeastern, Central, Eastern, and Southern regions, respectively. From p-values, the results show that the rainfall of the three regions follow log-normal distributions such as Northern, Northeastern, and Southern regions. The data of Northern, Northeastern, and Southern regions were used to construct the confidence interval for the common coefficient of variation based on the four approaches. The true common coefficient of variation was 1.2084. The point estimators of the common coefficient of variation based on the FGCI, MOVER, CA, and Bayesian approaches were 1.2776, 1.1486, 1.2273, and 1.2669. The FGCI, MOVER, computational, and Bayesian confidence intervals were [0.8380, 2.0301] with an interval length of 1.1921, [0.8460, 1.8481] with an interval length of 1.0021, [0.7745, 1.8663] with an interval length of 1.0918, and [0.7991, 1.7704] with an interval length of 0.9713, respectively. Hence, the length of the Bayesian confidence interval was shorter than those of the others, and so was more accurate.