Angle information assisting skeleton-based actions recognition
Author and article information
Abstract
In human skeleton-based action recognition, graph convolutional networks (GCN) have shown significant success. However, existing state-of-the-art methods struggle with complex actions, such as figure skating, where performance is often unsatisfactory. This issue arises from two main factors: the lack of shift, scale, and rotation invariance in GCN, making them especially vulnerable to perspective distortions in 2D coordinates, and the high variability in displacement velocity, which depends more on the athlete’s individual capabilities than the actions themselves, reducing the effectiveness of motion information. To address these challenges, we propose a novel cosine stream to enhance the robustness of spatial features and introduce a Keyframe Sampling algorithm for more effective temporal feature extraction, eliminating the need for motion information. Our methods do not require modifications to the backbone. Experiments on the FSD-10, FineGYM, and NTU RGB+D datasets demonstrate a 2.6% improvement in Top-1 accuracy on the FSD-10 figure skating dataset compared to current state-of-the-art methods. The code has been made available at: https://github.com/Jiahao-Guan/pyskl_cosine.
Cite this as
2024. Angle information assisting skeleton-based actions recognition. PeerJ Computer Science 10:e2523 https://doi.org/10.7717/peerj-cs.2523Main article text
Introduction
Action recognition has become an active research area in recent years, as it plays a significant role in video understanding. Prior investigations have explored various modalities for feature representation, such as RGB frames, optical flows, audio waves, and human skeletons. Among these modalities, skeleton-based action recognition has garnered heightened interest in recent years due to its action-focusing nature and robustness against complicated background. Early pioneering efforts primarily relied on recurrent neural networks (RNN) (Du, Wang & Wang, 2015; Song et al., 2017) and convolutional neural networks (CNN) (Ke et al., 2017; Liu, Liu & Chen, 2017) to extract features or generate pseudo-images from human joint data for action recognition. While these methods achieved reasonable performance, they were fundamentally limited in their ability to model the complex inter-dependencies between joints, a crucial aspect for fine-grained action recognition.
Graph convolutional networks (GCN) have become a popular approach for skeleton-based action recognition. Yan, Xiong & Lin (2018) were among the first to apply GCN with temporal convolution for this task. However, their model uses a fixed, pre-defined topology based on the physical structure of the human skeleton, which limits its expressive power across different network layers.
To bolster the capabilities of GCN, recent approaches (Shi et al., 2019, 2020; Liu et al., 2020b; Chen et al., 2021) have aimed to acquire more fitting topologies. They successfully transformed the skeleton topology into a learnable structure by introducing a learnable weight matrix and combining it with the skeleton topology, enabling the model to learn the dependency relationship between two physically unrelated joint points, such as two hands. However, GCN-based approaches struggle with shift and scale invariance. Specifically, when working with 2D data, projecting from 3D to 2D can change the apparent size of the characters in the image, with objects closer appearing larger and those farther away appearing smaller, as illustrated in Fig. 1 right side. Additionally, horizontal movement can alter positions, and these changes in scale and position may not reflect the actual movement, especially for sports with large displacements, like figure skating. When the model lacks shift, scale invariance, these coordinate changes can interfere with the model’s recognition.
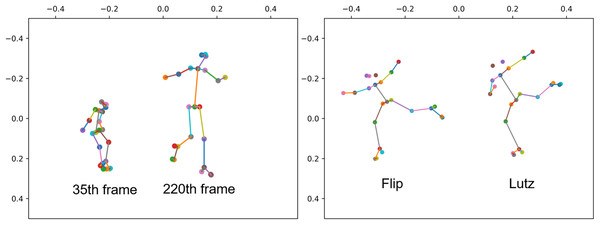
Figure 1: The two people in the left image correspond to the 35th and 220th frames of the same sample human skeleton, respectively.
The two people in the image on the right correspond to the take off stage of Flip jump and the take off stage of Lutz jump in figure skating, respectively.To solve above problems, In this work, We introduce a new angle feature that complements existing joint and bone features. Additionally, we present an improved keyframe Sampling algorithm that accounts for sample randomness and better preserves important semantic information in keyframes.
Drawing inspiration from leveraging high-order information, we leverage novel high-order information extracted from skeleton data to quantify the joint range of motion between two bones. The joint range of motion, typically measured in degrees, provides a valuable metric for assessing joint flexibility and mobility. Inherently linked to posture and movement, it emerges as an inherently discriminative feature for action recognition tasks. We represent the joint range of motion through cosine similarities between pairs of bone vectors, forming the foundation of our cosine stream. By feeding these cosine similarities into a graph convolutional network, we make predictions for action labels. Simultaneously, the cosine stream integrates with the joint-bone two-stream network, giving rise to the development of a comprehensive three-stream network.
In sampling, a recent work by Duan et al. (2022a) introduces a uniform sampling technique, evenly dividing sequences into N non-overlapping segments with an equal number of frames. One frame is then randomly selected from each segment and aggregated to form a new sub-sequence. While effective, this method overlooks considerations for keyframes. Building upon ideas from Liu et al. (2020b) and Wang et al. (2019), we enhance the approach by simplifying the keyframe selection strategy and integrating it with the original uniform sampling. Various combination strategies have been explored, resulting in particularly significant improvements in the joint stream and bone stream.
Our contribution are summarized as follows:
We propose a cosine stream, which quantifies the joint range of motion between two bones in degrees, to assist in action recognition with significant displacement.
We have enhanced the existing downsampling algorithm by integrating the keyframe concept. This enhancement yields substantial improvements in both the joint and bone streams.
The experimental results indicate that our method can enhance the accuracy performance of the model without necessitating modifications to the network structure itself.
Method
Cosine stream
In figure skating, athletes often maintain a consistent skating speed during the execution of actions, leading to significant displacement and variations in position features. The angle of the ice skate blade relative to the ice surface, distinguishing between the inside and outside edges, is a crucial factor in action classification. Figure 1 left side showcases two similar jumps in figure skating: the Flip and the Lutz. In the Flip jump on the left, the skater positions the left foot on the inner edge of the skate blade, shifting the overall body weight towards the inside of the blade, while extending the left arm naturally. In contrast, for the Lutz jump on the right, the only difference lies in the skater placing the left foot on the outer edge of the skate blade, resulting in a relatively outward shift of the body weight. To achieve stability and enhance takeoff power, skaters typically opt to naturally curve their left hand towards the right side. To preserve blade clarity, slight differences in body joint angles occur, which tend to remain relatively stable during displacement compared to coordinates. Joint angle changes are typically induced by specific actions, making them more discriminative.
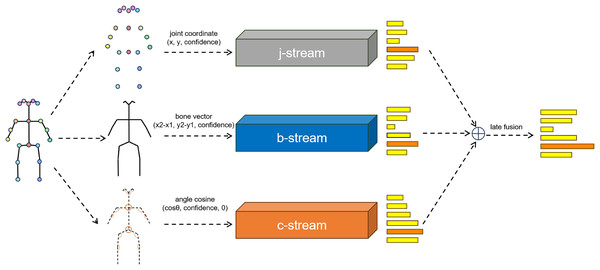
We aim to input human body joint angles as raw features into the network in the form of cosine similarities. The cosine similarity cosvi for vertex vi is calculated using Eq. 1, where N(vi) is the neighborhood of vi, A2|N(vi)| is the number of permutations, and →eij is the vector from vi to vj. Values for vertices in the cosine stream graph are generated, and an empty cosine similarity with a value of 0 is added to the outermost vertices, ensuring consistency in the design of the graph and network of cosine with that of joints and bones. Due to consistency in data format, our network can be easily integrated with mainstream joint bone two stream networks, as shown in the Fig. 2.
(1)
cosvi=1A2|N(vi)|∑j∈N(vi)∑k∈{N(vi)−j}→eij||→eij||→eik||→eik||.
Figure 2: Illustration of the overall archtecture of the network.
The softmax scores of the three streams are fused using weighted summation to obtain the final prediction. j denoted the joint information. b denotes the bone information. c denotes the angle information.Regarding other calculation methods for joint angles, further exploration has been conducted in Qin et al. (2022), and we will not provide too much repetitive introduction here.
Keyframe sampling algorithm
Sampling keyframes is a crucial aspect of video analysis in figure skating, ensuring that selected frames encapsulate the most discriminative information within a video. In the figure skating task, the fast changing motion frames are distinctly important for jump action. Through Eq. (1), we transformed the original joint stream into a cosine stream, with attribute values stored in the vertices ranging from −1 to 1. This reflects the joint’s range of motion from 180 degrees to 0 degrees, eliminating the need for normalization. We then sum the angles for all joints in the body to obtain the downsampling indicator, representing the extent of limb extension in each frame. A smaller value indicates a larger sum of angles for various joints in the entire body, implying greater limb extension. Hence, it is immensely beneficial in identifying keyframes within sequences. For instance, in a jumping sequence, the indicator during the takeoff phase is stronger than that during the mid-air spinning phase. This suggests that recognizing the takeoff is more crucial than identifying the posture during mid-air action, aligning with the focus on judging actions in figure skating sports.
We decided to incorporate uniform sampling, as introduced by Duan et al. (2022c, 2022b, 2022a), into our proposed keyframe sampling approach, leading to various fusion strategies:
-
(0)
Create a sequence of N+M frames using uniform sampling as the control sequence.
-
(1)
Sort video frames based on the keyframe selection indicator. Choose frames with the smallest indicator to create a new subsequence of M frames, appending it to the N-frame subsequence from Uniform Sampling.
-
(2)
Divide the sequence into M non-overlapping substrings. Select the frame with the smallest indicator from each substring to form a new M-frame subsequence. Connect it to the N-frame subsequence from Uniform Sampling.
-
(3)
Building upon (1), rearrange the generated N+M frames chronologically to create a new downsampling sequence.
-
(4)
Building upon (2), rearrange the generated N+M frames chronologically to create a new downsampling sequence.
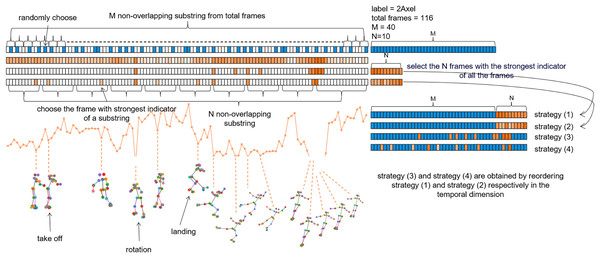
As illustrated in the Fig. 3, the blue section represents the uniform sampling process, which evenly divides the total frames into M non-overlapping segments, randomly samples frames within each segment, and combines the M selected frames into a subsequence. The orange section represents the process of downsampling keyframes, where the depth of the orange color indicates the intensity of the indicator: the darker the color, the smaller the indicator, signifying a greater degree of joint opening. The difference between Strategy (1) and Strategy (2) lies in the keyframe selection method. Strategy (1) directly selects N frames to form a subsequence based on the intensity of the indicator, while Strategy (2) evenly divides the total frames into N non-overlapping segments in the time dimension, selects the frame with the highest indicator intensity within each segment, and forms these N frames into a subsequence. The main distinction between Strategies (1) and (2) vs. Strategies (3) and (4) is in how the M-frame and N-frame subsequences are combined. Strategies (1) and (2) simply append the N frames after the M frames, while Strategies (3) and (4) add a reordering step, aiming to maintain the temporal continuity of the samples. We will further analyze these different strategies in the ablation study section.
Figure 3: Illustration of Uniform Sampling and Keyframe Sampling.
The blue grids represents uniform sampling, while the orange grids depicts keyframe sampling. In this sample, the total number of frames is 116, with an assumed M of 40 and N of 10.Experiments
Datasets
FSD-10. The Figure Skating Dataset (FSD-10) (Liu et al., 2020a) is a challenging dataset in competitive sports, featuring 1,484 figure skating videos labeled with 10 actions. It includes 989 training and 495 testing videos, segmented from around 80 h of global figure skating championships (2017–2018).
FineGYM. FineGYM (Shao et al., 2020) is a high-quality action recognition dataset with 29 k videos and 99 fine-grained gymnastic action classes. Human poses are extracted using GT bounding boxes (provided by Duan et al. (2022c)).
NTU RGB+D. The NTU RGB+D dataset (Shahroudy et al., 2016) is a human action recognition dataset with 56,880 skeleton sequences from 40 volunteers, categorized into 60 classes. It suggests two evaluation setups: (1) Cross-subject (X-sub), with training from 20 subjects and testing from the remaining 20; (2) Cross-view (X-view), training from views 2 and 3, and testing exclusively from view 1. In our experiments, 2D human poses are estimated using HRNet (Sun et al., 2019) (provided by Duan et al. (2022b)).
Implementation details
All experiments are conducted on one RTX 3090 GPU with PYSKL (Duan et al., 2022b) and MMaction2 (Contributors, 2020). Additionally, keyframe sampling was used to sample 25 frames in both datasets. By default, all models are trained with SGD with momentum 0.9, weight decay 5e−4. We set the batch size to 16, set the initial learning rate to 0.1. For the FSD-10 dataset, we repeated it 50 times, train the models for 64 epochs with CosineAnnealing learning rate scheduler. We use uniform sampling to sample 100 frames and keyframe sampling to sample 25 frames from skeleton data to form training samples. Previously, bone vectors were calculated by subtracting key point coordinates in the pipeline. Our proposed method uses cosine similarity based on these bone vectors. To improve efficiency, we suggest precomputing and storing both the bone vectors and cosine similarities.
Experiment result
We conducted experiments on the FSD-10 dataset using CTRGCN as the baseline, and reported in Table 1 the improvements in various categories and mean accuracy after adding cosine stream and Keyframe Sampling.
| ChComboSpin4 | 2Axel | ChoreoSequence1 | 3Loop | StepSequence3 | |
|---|---|---|---|---|---|
| CTRGCN_jb_uni | 100.0 | 93.6 | 75.8 | 95.4 | 88.9 |
| CTRGCN_jbc_uni | 100.0 | 93.6 | 80.7↑ | 97.7↑ | 88.9 |
| CTRGCN_jbc_key | 100.0 | 95.7↑ | 83.9↑ | 95.4 | 91.7↑ |
| 3Flip | FlyCamelSpin4 | 3Axel | 3Lutz | 3Lutz_3Toeloop | Mean accuracy | |
|---|---|---|---|---|---|---|
| CTRGCN_jb_uni | 90.9 | 97.5 | 90.9 | 94.1 | 96.4 | 92.5 |
| CTRGCN_jbc_uni | 95.2↑ | 97.5 | 90.9 | 94.1 | 96.4 | 93.5↑ |
| CTRGCN_jbc_key | 97.6↑ | 97.5 | 90.9 | 97.1↑ | 96.4 | 94.6↑ |
FSD-10 is a fine-grained figure skating dataset where movements are categorized into spins, sequences, and jumps. Spins are further classified based on rotation posture, such as FlyCamelSpin4 and ChComboSpin4, which are both level four spins (though levels are not distinguished in this dataset). Sequences include two types of footwork: StepSequence, which combines several defined movements and can be divided into four levels, and ChoreSequence, which is more flexible and not graded. For jumps, there are six basic types—Axel, Toeloop, Flip, Lutz, Salchow, and Loop—categorized by the entry action. Jumps are further classified by the number of rotations, and combinations to form combinations jumps or sequence jump. In FSD-10, examples include 2Axel, 3Loop, 3Flip, 3Axel, 3Lutz, and 3Lutz_3Toeloop, with the latter being a combinations jump.
As shown in Table 1, the main categories with improved accuracy after introducing the cosine stream and Keyframe Sampling are ChoreSequence1, StepSequence3, 3Flip, and 3Lutz. The improvement in sequence accuracy aligns with our expectations, as sequences are composed of a series of sub-actions. Compared to other types of actions, sequences often have longer durations and noticeable displacement effects. Introducing angle features helps mitigate the impact of displacement. The improvements in Flip and Lutz accuracy are also expected. As shown in Fig. 1 right side, these two actions have very high similarity and are often the most controversial in referee decisions. The introduction of angle features effectively helps the model distinguish the subtle differences between these fine-grained actions. The improvement in 3Loop accuracy may be due to training errors, and returned to normal values when Keyframe Sampling was introduced.
Ablation study
In this section, we analyze the proposed cosine stream and Keyframe Sampling algorithm on the FSD-10 dataset. For the cosine stream, we selected three latest and widely recognized skeleton-based action recognition models—AGCN (Shi et al., 2019), MSG3D (Liu et al., 2020b), and CTRGCN (Chen et al., 2021)—as baselines. No modifications are required to the network structure for the cosine stream. For the Keyframe Sampling algorithm, we chose the current state-of-the-art model CTRGCN (Chen et al., 2021) as the baseline and demonstrated its effectiveness on the joint, bone, and cosine streams. As publicly available results for these methods on the FSD-10 dataset were not found, we conducted our experiments on this dataset using networks successfully reproduced from the PYSKL (Duan et al., 2022b) toolbox. The experiments were conducted with the same hyper-parameter settings to ensure fairness and consistency in the evaluation.
Effectiveness of cosine stream. We also evaluated the cosine stream on three widely used skeleton-based methods (Table 2). Despite slightly lower performance compared to joint and bone streams, the cosine stream employs 1D cosine similarity data, while the others use 2D coordinate data. However, the aggregated three-stream model consistently outperforms two-stream methods in Mean Class Accuracy and Top1 Accuracy. The addition of cosine stream improves Mean Class Accuracy by 0.9%, and Top1 Accuracy by 0.7% in AGCN, by 0.8% and 0.2% in MSG3D, and by 1.0% and 1.2% in CTRGCN, respectively. This proves the effectiveness of cosine stream.
| Acc (%) | AGCN | ||||
|---|---|---|---|---|---|
| j | b | c | j&b | j&b&c | |
| Mean class | 90.2% | 91.5% | 87.7% | 91.7% | 92.6%↑ |
| Top1 | 88.9% | 90.4% | 87.1% | 90.8% | 91.5%↑ |
| Acc (%) | MSG3D | ||||
|---|---|---|---|---|---|
| j | b | c | j&b | j&b&c | |
| Mean class | 90.1% | 90.5% | 89.4% | 90.9% | 91.7%↑ |
| Top1 | 90.1% | 89.2% | 88.5% | 90.6% | 90.8%↑ |
| Acc (%) | CTRGCN | ||||
|---|---|---|---|---|---|
| j | b | c | j&b | j&b&c | |
| Mean class | 90.9% | 91.5% | 90.1% | 92.5% | 93.5%↑ |
| Top1 | 90.1% | 90.8% | 90.4% | 92.0% | 93.2%↑ |
In addition, we conducted supplementary experiments on the latest InfoGCN and HD-GCN, with results presented in Table 3. Since both models are enhanced versions of AGCN and CTRGCN, they include numerous attention modules, leading to increased model complexity. Given the limited amount of FSD-10 data, this complexity resulted in overfitting, even though we employed more data augmentation techniques than in the original work. Nevertheless, the introduction of cosine flow still yielded a 1.2% to 1.4% accuracy improvement, demonstrating its effectiveness.
| Model | InfoGCN | ||||
|---|---|---|---|---|---|
| Stream | j | b | c | j&b | j&b&c |
| Top1 acc (%) | 82.4 | 82.8 | 81.8 | 85.4 | 86.6↑ |
| Model | HD-GCN | |||||||
|---|---|---|---|---|---|---|---|---|
| Stream | j_com_1 | b_com_1 | c_com_1 | j_com_8 | b_com_8 | c_com_8 | j&b | j&b&c |
| Top1 acc (%) | 83.3 | 82.1 | 80.8 | 82.4 | 83.1 | 81.1 | 88.5 | 89.9↑ |
Due to the prevalent use of motion features in current state-of-the-art methods, we incorporated experiments involving joint motion, bone motion, and our proposed cosine stream extended to include cosine motion in the temporal dimension in our experiments with CTRGCN. As shown in Table 4, we observed that both joint motion and bone motion, as well as cosine motion, performed worse than the spatial dimension feature streams. This indicates that the motion information performs poorly when faced with situations where the correlation between speed and action itself is not significant, which is consistent with our expectations. Furthermore, the fusion of joint motion and bone motion with the original joint-bone dual-stream model (j&b) only resulted in a modest increase of 0.7% in Mean Class accuracy and 0.5% in Top1 accuracy, while the inclusion of cosine motion brought about negligible improvement. We hypothesize that this may be due to the fact that the actions in the dataset generally involve certain speeds during execution, which are not significantly correlated with the actions themselves, thereby resulting in unsatisfactory performance of the motion features. Therefore, we did not utilize motion features in subsequent experiments.
| Acc (%) | CTRGCN | |||||
|---|---|---|---|---|---|---|
| j | jm | b | bm | c | cm | |
| Mean class | 90.9 | 89.5 | 91.5 | 89.6 | 90.1 | 88.6 |
| Top1 | 90.1 | 88.2 | 90.8 | 88.7 | 90.4 | 87.3 |
| Acc (%) | CTRGCN | |||
|---|---|---|---|---|
| j&b | j&b&jm&bm | j&b&c | j&b&jm&bm&c&cm | |
| Mean class | 92.5 | 93.2 | 93.5↑ | 93.6↑ |
| Top1 | 92.0 | 92.5 | 93.2↑ | 93.2 |
Effectiveness of keyframe sampling. We explored various keyframe sampling and uniform sampling strategies 3, with results shown in Table 5. Strategy analysis reveals that merely increasing downsampled frames (Origin and Strategy (0) columns in the prior three sub tables) may lead to a slight improvement in model performance. Strategies (1) through (4) share the same frame rate as Strategy (0), with the exception that the M frames are obtained through keyframe sampling. As depicted in the chart, the performance differences stem from how these frames are processed.
| Acc (%) | Strategies for joint stream | |||||
|---|---|---|---|---|---|---|
| j_origin | j0 | j1 | j2 | j3 | j4 | |
| Mean class | 90.9 | 91.4 | 89.4 | 90.7 | 91.6↑ | 92.4↑ |
| Top1 | 90.1 | 90.1 | 88.2 | 90.6↑ | 90.4↑ | 91.5↑ |
| Acc (%) | Strategies for bone stream | |||||
|---|---|---|---|---|---|---|
| b_origin | b0 | b1 | b2 | b3 | b4 | |
| Mean class | 91.5 | 92.1 | 89.8 | 91.7 | 92.9↑ | 94.3↑ |
| Top1 | 90.8 | 91.3 | 89.9 | 91.1 | 92.7↑ | 93.2↑ |
| Acc (%) | Strategies for cosine stream | |||||
|---|---|---|---|---|---|---|
| c_origin | c0 | c1 | c2 | c3 | c4 | |
| Mean class | 90.1 | 89.4 | 89.5 | 90.9↑ | 90.1 | 90.6↑ |
| Top1 | 90.4 | 88.7 | 88.7 | 90.4 | 88.7 | 89.4 |
| Acc (%) | multi-stream | |||
|---|---|---|---|---|
| j0&b0 | j4&b4 | j4&b4&c4 | j4&b4&c_origin | |
| Mean class | 92.5 | 94.3↑ | 94.3↑ | 94.6↑ |
| Top1 | 91.8 | 93.2↑ | 93.2↑ | 94.4↑ |
Strategy (1): Simply concatenates the strongest M frames based on an indicator after the N-frame subsequences. However, this disrupts the temporal continuity of the actions since the strongest frames may not be sequential, resulting in a slight decrease in accuracy.
Strategy (3): After selecting the M keyframe frames, it immediately downsamples and reorders both the keyframes and N-frame subsequences in the temporal dimension to ensure continuity. This approach significantly improves accuracy.
Strategy (2): Demonstrates another method of keyframe selection by dividing the video into M non-overlapping temporal segments and selecting the frame with the strongest indicator from each segment to form a new subsequence. This method naturally maintains temporal continuity and has a more even distribution, leading to better performance compared to Strategy (1).
Strategy (4): Goes a step further by rearranging the entire M+N frame samples. This finer adjustment enhances the assistance provided to the model, resulting in further improvements.
In summary, the key lies in effectively selecting and utilizing keyframes while maintaining temporal continuity and even distribution. Strategies (3) and (4) achieve this through more sophisticated processing, thereby boosting the model’s accuracy. Compared with origin strategy, Strategy (4) notably improves mean class accuracy by 1.5% and Top1 Accuracy by 1.4% in the joint stream, and by 2.8% and 2.4% in the bone stream, respectively. If compared with Strategy (1), the improvements in the joint stream are 1.0% and 1.4%, and the improvements in the bone stream are 2.2% and 1.9%. This proves the effectiveness of Keyframe Sampling and can help improve the performance of the model under appropriate combination strategies.
Analyzing the third sub-table reveals keyframe sampling does not improve the cosine stream. This is attributed to the indicator using raw data from the cosine stream, causing redundancy and a slight performance decrease. This confirms that improvements in the first two sub-tables are due to keyframes rather than increased downsampled frames.
Fusing the streams with keyframe sampling (fourth sub-table) involves Strategy (4) for joint and bone streams. Compared to the original joint-bone two-stream model, there is a 1.8% improvement in mean class accuracy and 1.2% in Top1 Accuracy. However, keyframe sampling does not enhance the performance of the cosine stream. On the other hand, when fused with the cosine stream using the original strategy, it results in a 2.1% increase in mean class accuracy and 2.4% in Top1 Accuracy. This proves that keyframe sampling does not conflict with the introduction of cosine stream in improving model performance.
Cross-dataset validations
To validate the applicability of our method, we conducted cross-dataset validation on the FineGYM and NTU RGB+D datasets, in addition to the experiments conducted on FSD-10 as mentioned above.
Table 6 presents the results of introducing the cosine stream on the FineGYM dataset, showcasing a 0.5% improvement in mean class accuracy and a 0.2% improvement in Top-1 Accuracy for the original joint-bone two-stream model. When employing keyframe sampling strategy four for both the joint stream and bone stream, the three-stream model exhibited a 1.0% increase in mean class accuracy and a 0.6% increase in Top-1 Accuracy compared to the original joint-bone two-stream model. The observed smaller enhancement is attributed to dataset differences, where the categorization of action classes in the FineGYM dataset may have less correlation with the angular relationships of joints within the body.
| Acc (%) | CTRGCN | ||||
|---|---|---|---|---|---|
| j | b | c | j&b | j&b&c | |
| Mean class | 88.7 | 91.4 | 85.0 | 92.0 | 92.5↑ |
| Top1 | 91.9 | 93.7 | 89.0 | 94.5 | 94.7↑ |
| Acc (%) | CTRGCN & Keyframe Sampling | ||||
|---|---|---|---|---|---|
| j4 | b4 | c4 | j4&b4 | j4&b4&c | |
| Mean class | 89.5↑ | 91.5↑ | 84.1 | 92.6↑ | 93.0↑ |
| Top1 | 92.6↑ | 93.9↑ | 88.4 | 94.8↑ | 95.1↑ |
In Table 7, the results indicate that the enhancements of the model with the cosine stream and Keyframe Sampling on the NTU RGB+D dataset are not as promising. This holds true for both our experimental results and the data results cited in other works. We attribute this observation to two factors: (1) In terms of the inherent categorization of the dataset, NTU RGB+D places less emphasis on human joint angles. (2) The dataset is collected in a controlled lab environment where subjects do not exhibit significant displacement relative to the camera, leading to a loss of the advantageous shift, scale, and rotation invariance of angle features.
| Acc (%) | CTRGCN on X-sub | ||||
|---|---|---|---|---|---|
| j | b | c | j&b | j&b&c | |
| Top1 | 89.3 | 91.6 | 87.8 | 92.3 | 92.9↑ |
| Acc (%) | CTRGCN & Keyframe Sampling on X-sub | ||||
|---|---|---|---|---|---|
| j | b | c | j&b | j&b&c | |
| Top1 | 89.9 | 91.4 | 87.3 | 92.5 | 92.8 |
| Acc (%) | CTRGCN on X-view | ||||
|---|---|---|---|---|---|
| j | b | c | j&b | j&b&c | |
| Top1 | 96.2 | 96.1 | 87.0 | 97.3 | 97.4↑ |
| Acc (%) | CTRGCN & Keyframe Sampling on X-view | ||||
|---|---|---|---|---|---|
| j | b | c | j&b | j&b&c | |
| Top1 | 95.7 | 95.7 | 87.5 | 97.2 | 97.2 |
Limitations
Our method excels at handling the ‘near large, far small’ phenomenon that occurs during 3D-to-2D projection, as well as actions involving significant character displacement within an image. However, it has a limitation: the cosine features we use are limited to two dimensions—cosine similarity and confidence—which may not be as expressive as the three-dimensional keypoint coordinates and skeleton vectors in a single stream.
Although we achieved good results on the FSD-10 dataset, this success stems from a careful balancing of our method’s strengths and weaknesses. In scenarios where actions involve minimal displacement or where the raw data is inherently 3D, our method may be less effective. For instance, in the X-view of the NTU RGB+D dataset (Table 7), the cross-view enhancements of the original data or the data’s inherent 3D nature (Table 8) mean that depth information is not lost during 3D-to-2D projection. Consequently, the advantages of the cosine stream are not fully realized, while its limitations persist, resulting in significantly lower performance compared to the other two streams.
| Acc (%) | CTRGCN on X-sub-3d | ||||
|---|---|---|---|---|---|
| j | b | c | j&b | j&b&c | |
| Top1 | 89.6 | 90.0 | 80.9 | 91.5 | 91.5 |
| KS Top1 | 89.9 | 90.0 | 80.5 | 91.8 | 91.9 |
| Acc (%) | CTRGCN on X-view-3d | ||||
|---|---|---|---|---|---|
| j | b | c | j&b | j&b&c | |
| Top1 | 95.6 | 95.4 | 84.4 | 96.6 | 96.6 |
| KS Top1 | 95.5 | 95.5 | 84.6 | 96.7 | 96.7 |
Addressing the challenge of expanding cosine representation to mitigate its two-dimensional limitation is an important direction for future research.
Conclusion
In this work, we propose a cosine stream that leverages joint angles and the cosine similarity of bone vectors for accurate action prediction. Additionally, we introduce a keyframe sampling method based on joint cosine values to quantify body extension. Our approach excels in handling 2D data by mitigating the loss of depth information during 3D-to-2D projection, particularly for movements involving significant displacement.
The main contribution of this research lies in providing an effective method for action recognition, especially in preserving spatial information during the projection from 3D to 2D. Our method demonstrates strong robustness in handling complex actions with large displacements. This achievement not only extends the current body of knowledge in skeleton-based action recognition but also lays the foundation for future studies.
However, the work also has limitations. The cosine features are confined to two dimensions—cosine similarity and confidence—making them less expressive than three-dimensional keypoint coordinates and skeleton vectors. Future research could explore ways to expand the representation capabilities of the cosine stream to overcome its two-dimensional limitation. Additionally, improving the keyframe sampling method to enhance adaptability and generalization is another important direction for further investigation.
Overall, this work provides a novel perspective and technical approach to action recognition, with practical implications particularly in the context of 3D-to-2D projection. Future work can focus on extending cosine representation, refining the sampling method, and exploring broader applications across other datasets, thereby advancing the field further.
Supplemental Information
Additional Information and Declarations
Competing Interests
Yidan Chen is employed by Shangu Cyber Security Technology Company Limited.
Author Contributions
Chengming Liu conceived and designed the experiments, analyzed the data, performed the computation work, authored or reviewed drafts of the article, and approved the final draft.
Jiahao Guan conceived and designed the experiments, performed the experiments, analyzed the data, performed the computation work, prepared figures and/or tables, authored or reviewed drafts of the article, and approved the final draft.
Haibo Pang analyzed the data, authored or reviewed drafts of the article, and approved the final draft.
Lei Shi analyzed the data, authored or reviewed drafts of the article, and approved the final draft.
Yidan Chen analyzed the data, authored or reviewed drafts of the article, and approved the final draft.
Data Availability
The following information was supplied regarding data availability:
The code and data are available at GitHub and Zenodo:
- https://github.com/Jiahao-Guan/pyskl_cosine
- Jiahao Guan. (2024). Jiahao-Guan/pyskl_cosine: v0.1 (first). Zenodo. https://doi.org/10.5281/zenodo.13679682.
The FSD-10 dataset is available at GitHub: https://shenglanliu.github.io/fsd10.
The FineGym and NTU RGBD 60 datasets are available at Zenodo: Guan. (2024). gym_nturgbd60 [Data set]. Zenodo. https://doi.org/10.5281/zenodo.14049728.
Funding
This work was supported by the National Key R&D program of China (2020YFB1712401), the Nature Science Foundation of China (62006210, 62206252), the Key science and technology project of Henan province (221100211200, 221100210100), the technological research projects in Henan province (232102210090). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
