Research on three-state reliability evaluation method of high reliability system based on multi-source prior information

Bayes hypothesis of non-information prior distribution

The Bayes method puts forward that the unknown parameter is assumed to have equal probability within its possible range of values, that is when the unknown parameter is a continuous random variable, it is assumed to obey the uniform distribution in a certain interval (Marichal, Mathonet & Paroissin, 2017; Ashrafi & Asadi, 2014). If the unknown parameter is a discrete random variable with only a limited numerical value, it is assumed that the probability of taking these values is equal.

Criterion 1: for the success rate R in binomial distribution:

According to the Bayes hypothesis and maximum entropy method, the prior distribution density is Beta(1, 1). On the basis of Jeffreys’ criterion, its prior distribution density is Beta(1/2, 1/2). According to the method of Reformulation and ALI, the prior distribution density is Beta(0, 0).

In the above three kinds of non-information prior distributions, Beta(0, 0) = R⁻¹(1 − R)⁻¹ is not a normal density function, but a generalized prior distribution, and named prior distribution 1. Beta(1/2, 1/2) and Beta(1, 1) are normal density functions, named prior distribution 2 and prior distribution 3 respectively.

Determination method of non-information prior distribution

The non-failure data source is a synthesis of machine data, information data and cross-border data of the industrial chain from all aspects of the equipment life cycle. In principle, the attributes of non-failure data sources belong to uncertain data, and their significant characterization feature is non-stationary. It is well known that the sharp changes of non-stationary signals are the most critical points in analyzing signals (Le Guen & Thome, 2023). For example, during the operation of precision electronic module, due to the erosion of insulation layer, acid, alkali, moisture and the role of cyclic stress, etc. It is very easy to catalyze the initiation and evolution of potential failure, thus leading to open circuit, short circuit, electric leakage, arc fault and other functional failures.

For the whole population (binomial distribution) of success or failure type test, the prior distribution of its distribution parameter R (success rate) usually uses its conjugate prior distribution Beta(a, b), so the problem becomes: how to determine the super parameters a and bwithout prior information. The usual practice is to take the prior distribution as Beta(0, 0), Beta(1/2, 1/2) or Beta(1, 1) (Chien et al., 2023; Xu, Liu & Xiao, 2023; Stefan et al., 2022). When solving specific engineering problems, how to determine which of them should be taken as a prior distribution is an important scientific problem.

Priori information fusion method

For the traditional reliability theory (normal or failure), the prior distribution in the engineering application usually uses its conjugate prior Beta(a, b), the prior density is: (4)${\displaystyle {\pi }_1\left(R;a,b\right)=Beta\left(a,b\right)=\frac{1}{\beta \left(a,b\right)}{R}^{a-1}{\left(1-R\right)}^{b-1}0\le R\le 1}$

Where a, b is super parameters respectively, so there are two corresponding second prior distributions, which are the uniform distributions on [a^L, a^U] and [b^L, b^U] respectively, and the density is: (5)${\displaystyle {\pi }_{21}\left(a\right)=\left\{\begin{array}{c}1/\left(a^U-a^L\right),a^L<a<a^U\hfill \\ 0,\begin{array}{cc}other\hfill & \hfill \end{array}\hfill \end{array}\right.}$ (6)${\displaystyle {\pi }_{22}\left(a\right)=\left\{\begin{array}{c}1/\left(b^U-b^L\right),b^L<b<b^U\hfill \\ \begin{array}{cc}0,other\hfill & \hfill \end{array}\hfill \end{array}\right.}$

According to the multi-layer Bayes method of binomial distribution, the multi-layer prior density of R is: (7)${\displaystyle \pi \left(R\right)={\int }_{b^L}^{b^U}{\int }_{a^L}^{a^U}{\pi }_1\left(R;a,b\right).{\pi }_{21}\left(a\right){\pi }_{22}\left(b\right)dadb=\frac{{\int }_{b^L}^{b^U}{\int }_{a^L}^{a^U}\frac{1}{\beta \left(a,b\right)}{R}^{a-1}{\left(1-R\right)}^{b-1}dadb}{\left(a^U-a^L\right)\left(b^U-b^L\right)}.}$

Considering that estimation and inspection are all based on posterior distribution, when a prior distribution is available and on-site data (n, s) is achieved, n is the total number of tests and s is the number of successful tests, the posterior density can be achieved as follows: (8)${\displaystyle \pi \left(R\mid n,s\right)=\frac{R^s{\left(1-R\right)}^{n-s}\pi \left(R\right)}{{\int }_0^1{R}^s{\left(1-R\right)}^{n-s}\pi \left(R\right)dR}=\frac{{\int }_{b^L}^{b^U}{\int }_{a^L}^{a^U}\frac{1}{\beta \left(a,b\right)}{R}^{a+s-1}{\left(1-R\right)}^{b+n-s-1}dadb}{{\int }_{b^L}^{b^U}{\int }_{a^L}^{a^U}\frac{\beta \left(a+s,b+n-s-1\right)}{\beta \left(a,b\right)}dadb}}$

When the test data is failure, a > 1 and 0 < b < 1 are determined according to the principle that R is more likely when there is no failure, but R is less likely when there is less , and the second prior is the uniform distribution on (1, c) and (0, 1) (Shen et al., 2023; Levitin, 2001), that is (9)${\displaystyle a^L=1,a^U=c,b^L=0,b^U=1.}$

If the first prior distribution is Beta(a, b), the significance of the super parameter a, b will be weakened, the multi-layer prior density formula Eq. (7) and the posterior density formula Eq. (8) are no longer conjugate, thus losing the advantages of the beta distribution. Therefore, the first prior distribution is the uniform distribution on (a, 1), and the super parameter a is the lower bound of the possible value of reliability R.

When the on-site data and historical batch data are respectively from two different populations X and Y, we proposed most of the historical batch data, a mixed prior is introduced. The mixed prior of the success or the failure population is: (10)${\displaystyle {\pi }_{\rho }\left(R\right)=\rho Beta\left(a,b\right)+\left(1-\rho \right)0\le \rho \le 1}$

When evaluating the reliability of high reliability system, given the confidence degree γ, R_L will be solved from Eq. (11): (11)${\displaystyle {\int }_{R_L}^1{\pi }_{\rho }\left(R|s\right)=\gamma }$

Reliability evaluation model of three-state system

For a high reliability module, assume that the module is composed of n components from the functional logic, which is recorded as N = (1, 2, …, n); the i component has multiple states, which is recorded as M = (1, 2, …, m); the occurrence probability of each state is recorded as p_ij(i = 1, 2, …, n; j = 0, 1, …, m), and ${\sum }_{i=0}^m{p}_{ij}\left(i=1,2,\dots ,n\right)$. There are two possibilities for each state: occurrence and non-occurrence, and the probabilities are p_ij and 1 − p_ij.

For the i component, the historical data is recorded as X = (x₀, x₁, …, x_m), and x_j is the numerical value of historical data in j state. On-site data is recorded as $X^{{}^{\prime }}=\left(x_0^{{}^{\prime }},x_1^{{}^{\prime }},\dots ,x_m^{{}^{\prime }}\right)$, and $x_j^{{}^{\prime }}$ is the numerical value of on-site data in j state.

The on-site data and historical data are from two categories, decrease the effect of historical data and on-site data on reliability evaluation (Zhan & Niu, 2013; Liu, Paulino & Gardoni, 2016; Bai et al., 2021). At the same time, make the most of the information in historical data, a mixed prior is introduced: (12)${\displaystyle {\pi }_{\rho }\left(p_{ij}\right)=\rho Beta\left(x_j,\sum _{k=0,k\ne j}^m{x}_k\right)+\left(1-\rho \right)0\le \rho \le 1}$

After obtaining the on-site data $Y^{{}^{\prime }}=\left(x_j^{{}^{\prime }},{\sum }_{k=0,k\ne j}^m{x}_k^{{}^{\prime }}\right)$, the posterior density can be derived as: (13)${\displaystyle {\pi }_{\rho }\left(p_{ij}|x\right)=\frac{MBeta\left(x_j^{{}^{\prime }}+1,\sum _{k=0,k\ne j}^m{x}_k^{{}^{\prime }}+1\right)+NBeta\left(x_j^{{}^{\prime }}+x_j,\sum _{k=0,k\ne j}^m\left(x_k^{{}^{\prime }}+x_k\right)\right)}{M+N}}$

Where, $M=\left(1-\rho \right)\beta \left(x_j,{\sum }_{k=0,k\ne j}^m{x}_k\right)\beta \left(x_j^{{}^{\prime }}+1,{\sum }_{k=0,k\ne j}^m{x}_k^{{}^{\prime }}+1\right)$ ${\displaystyle N=\rho \beta \left(x_j^{{}^{\prime }}+x_j,\sum _{k=0,k\ne j}^m\left(x_k^{{}^{\prime }}+x_k\right)\right)}$

According to Eq. (11), for reliability evaluation of high reliability system, p_ijL is solved from the following equation after the confidence γ is given: (14)${\displaystyle {\int }_{p_{ijL}}^1{\pi }_{\rho }\left(p_{ij}|x\right)=\gamma }$

Reliability analysis process of three-state system

In order to effectively evaluate the reliability of the three-state system, a typical module with progressive development trend must be reasonably selected (Xu & Chen, 2014; Kwon, 2014). There are three states for a typical module: functional failure, potential failure and safety, which are recorded as M = (0, 1, 2); the probabilities of occurrence and non-occurrence of each state are p_ij and $1-p_{ij}\left(j=0,1,2\right)$ respectively. For the i component, the historical data is recorded as X = (x₀, x₁, x₂), and x₀, x₁, x₂ represent the numerical value of functional failures, the numerical value of potential failures and the numerical value of safety of the historical data respectively. On-site data are recorded as $X^{{}^{\prime }}=\left(x_0^{{}^{\prime }},x_1^{{}^{\prime }},x_2^{{}^{\prime }}\right)$, $x_0^{{}^{\prime }},x_1^{{}^{\prime }}$ and $x_2^{{}^{\prime }}$ represent the numerical value of functional failures, the numerical value of potential failures and the numerical value of safety of on-site data, respectively. If the occurrence and non-occurrence of the failure of the i component obeys the binomial distribution, the historical data X = (x₀, x₁, x₂) is marked as Y = (x₀, x₁ + x₂), x₀ and (x₁ + x₂) represent the fault numerical value and the fault-free numerical value in the historical data respectively. On-site data $X^{{}^{\prime }}=\left(x_0^{{}^{\prime }},x_1^{{}^{\prime }},x_2^{{}^{\prime }}\right)$ can be recorded as $Y^{{}^{\prime }}=\left(x_0^{{}^{\prime }},x_1^{{}^{\prime }}+x_2^{{}^{\prime }}\right)$, $x_0^{{}^{\prime }}$ and $\left(x_1^{{}^{\prime }}+x_2^{{}^{\prime }}\right)$ represent the fault numerical value and the fault-free numerical value in the on-site data respectively .

According to formula Eqs. (12)–(14): (15)${\displaystyle {\pi }_{\rho }\left(p_{i0}\right)=\rho Beta\left(x_0,x_1+x_2\right)+\left(1-\rho \right)0\le \rho \le 1}$ (16)${\displaystyle {\pi }_{\rho }\left(p_{i0}|x\right)=\frac{MBeta\left(x_0^{{}^{\prime }}+1,x_1^{{}^{\prime }}+x_2^{{}^{\prime }}+1\right)+NBeta\left(x_0^{{}^{\prime }}+x_0,x_1^{{}^{\prime }}+x_2^{{}^{\prime }}+x_1+x_2\right)}{M+N}}$

Where, $M=\left(1-\rho \right)\beta \left(x_0,x_1+x_2\right)\beta \left(x_0^{{}^{\prime }}+1,x_1^{{}^{\prime }}+x_2^{{}^{\prime }}+1\right)$ ${\displaystyle N=\rho \beta \left(x_0^{{}^{\prime }}+x_0,x_1^{{}^{\prime }}+x_2^{{}^{\prime }}+x_1+x_2\right).}$

Therefore, the reliability calculation formula is as follows: (17)${\displaystyle {\int }_{p_{i0L}}^1{\pi }_{\rho }\left(p_{i0}|x\right)=\gamma }$

State probability of potential failure unit

In the high reliability system, it is efficient to determine the reliability of the unit structure by using n_i − 1 test items. Assuming that the unit reliability index without considering j test items is R_Li,j(j = 1, 2, …, n_i), then rearrange R_Li,j: (18)${\displaystyle R_{Li,1}^{\ast }\le R_{Li,2}^{\ast }\le \dots R_{Li,j}^{\ast }\le R_{Li,n_i}^{\ast }}$

And (19)${\displaystyle R_{Li}\le R_{Li,1}^{\ast }\le R_{Li,2}^{\ast }\le \dots R_{Li,j}^{\ast }\le R_{Li,n_i}^{\ast }.}$

From the formula above, the reliability index is R_Li,ni, the corresponding test items have the biggest impact to the evaluation of unit reliability. Hence, the test items which correspond to R_Li,ni are the key tracking test links.

For high reliability system, if the unit has the ‘Safety-Potential failure-Functional failure’ work mode, then the following steps can be considered:

The state probability of unit safety is the unit reliability by all test items.

The state probability of unit functional failure is the lose efficiency which not considering the tracking items.

The difference numerical value between the reliability without considering the tracking items and the reliability with considering all test items is the state probability of unit potential failure.

Then (20)${\displaystyle \left\{\begin{array}{c}P\left(x_i=1\right)=R_{Li}\hfill \\ P\left(x_i=0.5\right)=R_{Li,n_i}^{\ast }-R_{Li}\hfill \\ P\left(x_i=0\right)=1-R_{Li,n_i}^{\ast }\hfill \end{array}\right.}$

Result comparison and analysis

The reliability of the equipment is evaluated according to the conjugate prior and mixed prior methods, respectively. This paper adopts data from open literature (Huang, Duan & Hao, 2010; Wang, Cai & Jiao, 2007). In the process of multi-source data fusion, firstly, the detection items (performance indicators) are considered as a series system, and their reliability is calculated separately; secondly, it comprehensively evaluates the three state reliability of each module based on the Bayesian reliability evaluation method.

Method 1: according to Bayes hypothesis, the distribution interval of R is $\left(0,1\right)$.

Method 2: the distribution interval of R is $\left(a,1\right)$.

Method 3: the distribution interval of R is $\left(a,1\right)$, the expert gives the estimation interval (interval number) of a, and gives the confidence level of this interval number. The results of expert opinions are shown in Table 5.

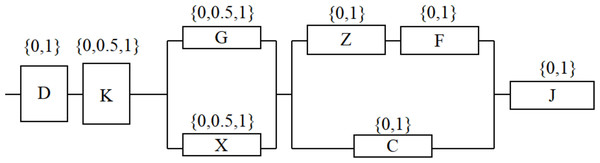
A typical module is composed of power supply (D), control circuit (K), photoelectric converter (G), shaping amplifier (X), rotor (Z), amplifier (F), trigger circuit (C), counter (J) and other modules.

The photoelectric converter and the shaping amplifier are mutually compensated and backed up; the rotor, amplifier and trigger circuit form a compensation backup system. The control circuit, photoelectric converter and shaping amplifier in the system have three states respectively: 1 (safe), 0.5 (potential failure) and 0 (functional failure); The other units are in two states: 1 (safe) and 0 (functional failure). The multi-state electronic system structure with potential failure units effectively reflects the actual operation of the system, the system reliability block diagram is shown in Fig. 1.

The field test conditions of the typical module are: 8 tests, 6 failures. That is n = 8, s = 2. The reliability evaluation is carried out according to the above different methods. When we set the confidence to 0.9, the comparison of reliability evaluation results are shown in Table 6.

The first group of experts has a detailed understanding of the development process of the virtual prototype. They know that most of the components and subsystems of the virtual prototype have been fully tested and should have high reliability. However, because of virtual prototype, they are not very confident about the design scheme of the virtual prototype and the assembly process of the system, the first group of experts gave a high estimate of a, but only 60% to 70% confidence. The second group of experts, based on the experience gained from the development of similar or similar products, believe that the reliability of the virtual prototype was generally 30 to 70 percent of that of the formal product, and have a high degree of confidence in this judgment.

Since it is difficult to distinguish the importance of the two groups of experts, equal weights are used in method 2. As can be seen in Table 4, the opinions of the two groups’ experts are quite different. Therefore, it is difficult for the experts to agree with the reliability evaluation results achieved by averaging the experts’ experience directly. In method 3, due to the use of interval numbers, the trust of experts is used as the weight to reduce the difference among the opinions of the two groups of experts. At the same time, due to the robustness of the method, the evaluation results are easily accepted by all aspects.

On the basis of the above reliability evaluation results, we adopted the method 3 to estimate the state probability of the eight constituent units of the typical module, fully integrating the historical test data and field test data of each unit, and the conditional probability results of each unit are shown in Table 7. The data in the Table 7 is consistent with the actual work of this typical module.

It can be seen from the above table that when considering the potential failure state, the conditional probability of the control circuit K in the potential failure is the highest, so it is necessary to strengthen the detection of the control circuit K.