The reconstruction of equivalent underlying model based on direct causality for multivariate time series

Entropy

Within the domain of information theory, Shannon entropy characterizes the average degree of “information,” “surprise,” or “uncertainty” associated with the potential outcomes of a random variable (Shannon, 1948). When considering a discrete random variable X, this variable assumes values from the alphabet χ and is distributed according to p:X → [0, 1], such that probability density functions (PDFs) p(x): = ℙ[X = x]: (1)${\displaystyle \mathrm{H}\left(X\right)=\mathbb{E}\left\{-logp\left(X\right)\right\}=-\sum _{x\in \chi }p\left(x\right)logp\left(x\right)}$ where 𝔼 is the expected value operator. In the context of multivariate scenarios (q-dimensional), the estimation of PDFs $\hat{p}\left(x_1,x_2,\dots {,x}_q\right)$, which is commonly used to approximate $p\left(x_1,x_2,\dots {,x}_q\right)$, is: (2)${\displaystyle p\left(x_1,x_2,\dots ,x_q\right)\approx \hat{p}\left(x_1,x_2,\dots {,x}_q\right)=\frac{1}{N{h}_1\cdots h_q}\sum _{i=1}^{N}K\left(\frac{x_1-x_{i1}}{h_1}\right)\left(\frac{x_q-x_{iq}}{h_q}\right)}$ where N is the number of samples $h_s=c\cdot \sigma {\left(x_{\text{is}}\right)}_{i=1}^N\cdot N^{\frac{-1}{\left(4+q\right)}}$ for s = 1, …, q. Conditional entropy can be defined with respect to two variables X and Y, which assume values from sets $\mathcal{X}$ and $\mathcal{Y}$, respectively, as: (3)${\displaystyle \mathrm{H}\left(X|Y\right)=-\sum _{x,y\in \mathcal{X\times Y}}^{}{p}_{X,Y}\left(x,y\right)log\frac{p_{X,Y}\left(x,y\right)}{p_Y\left(y\right)}}$ where $p_{X,Y}\left(x,y\right)$ is the joint PDFs of random variables X and Y. $p_Y\left(y\right)$ is the marginal PDFs of Y.

Mutual information

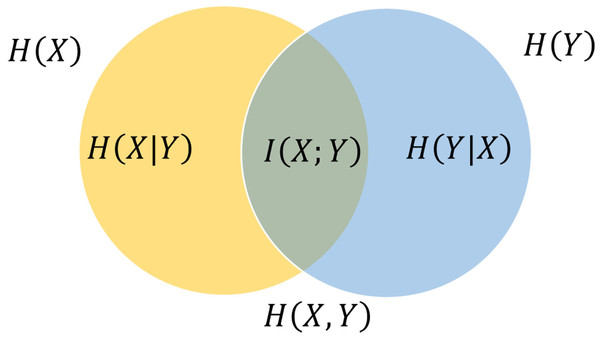
Mutual information quantifies the interdependence shared between the two variables (Cover, 1999), as shown in Fig. 1. In the case of two jointly discrete random variables, X and Y, the definition of mutual information (MI) is as follows: (4)${\displaystyle I\left(X;Y\right)=\mathrm{H}\left(X\right)-\mathrm{H}\left(X|Y\right).}$

Substituting Eqs. (1) and (3) into (4) yield: (5)${\displaystyle I\left(X;Y\right)=\sum _{y\in \mathcal{Y}}^{}\sum _{x\in \mathcal{X}}^{}{p}_{X,Y}\left(x,y\right)log\frac{p_{X,Y}\left(x,y\right)}{p_X\left(x\right)p_Y\left(y\right)}}$ where $p_{X,Y}\left(x,y\right)$ is the joint PDFs of X and $Y.p_X\left(x\right)$ and $p_Y\left(y\right)$ are the PDFs of X and Y, respectively.

Conditional mutual information

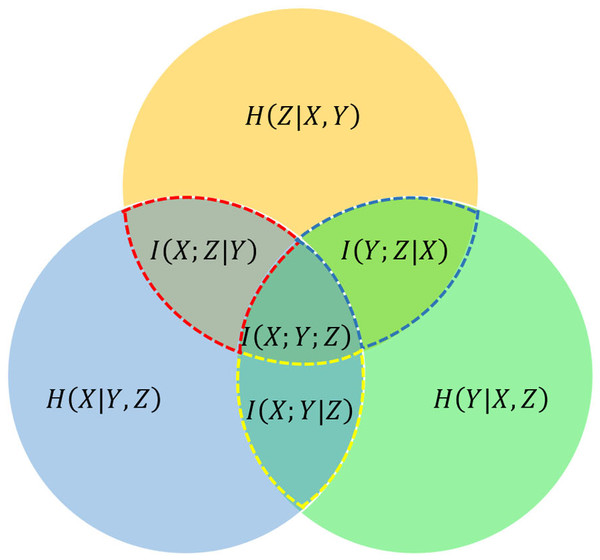
Conditional mutual information is the formal definition of the mutual information between two random variables when conditioned on a third variable, as illustrated in Fig. 2. For jointly discrete random variables, this definition can be expressed as follows: (6)${\displaystyle I\left(X;Y|Z\right)=\mathrm{H}\left(X,Z\right)+\mathrm{H}\left(Y,Z\right)-\mathrm{H}\left(X,Y,Z\right)-\mathrm{H}\left(Z\right)=\mathrm{H}\left(X\left|Z\right.\right)-\mathrm{H}\left(X\left|Y,Z\right.\right)=\mathrm{H}\left(X\left|Z\right.\right)+\mathrm{H}\left(Y\left|Z\right.\right)-\mathrm{H}\left(X,Y\left|Z\right.\right)=I\left(X;Y,Z\right)-I\left(X;Z\right).}$

Substituting Eqs. (5) into (6) yield: (7)${\displaystyle I\left(X;Y|Z\right)=\sum _{z\in \mathcal{Z}}^{}\sum _{y\in \mathcal{Y}}^{}\sum _{x\in \mathcal{X}}^{}{p}_{X,Y,Z}\left(x,y,z\right)log\frac{p_{X,Y,Z}\left(x,y,z\right)p_Z\left(z\right)}{p_{X,Z}\left(x,z\right)p_{Y,Z}\left(y,z\right)}.}$

In the context of discrete variables, Eq. (7) has been employed as a fundamental building block for establishing various equalities within the field of information theory.

Transfer entropy

Transfer entropy serves as a non-parametric statistical metric designed to quantify the extent of directed (time-asymmetric) information transfer between two stochastic processes (Schreiber, 2000; Seth, 2007). TE provides an information-theoretic methodology for evaluating causality by quantifying uncertainty reduction. According to Schreiber (2000), the TE from a stationary time series X to Y is defined as: (8)${\displaystyle T{E}_{X\to Y}=I\left(Y;\mathbf{X}|\mathbf{Y}\right)}$ where, X and Y denotes the historical information of X and Y. It indicates that Eq. (8) is a special CMI (Wyner, 1978; Dobrushin, 1963) in Eq. (6) with the history of the influenced variable Y in the condition, which is used widely in practice.

Substituting Eqs. (7) into (8) yield: (9)${\displaystyle T{E}_{X\to Y}=\sum _{}^{}p\left(y_{i+h},{\mathbf{y}}_i^{\left(k\right)},{\mathbf{x}}_j^{\left(d\right)}\right)\cdot log\frac{p\left(y_{i+h}|{\mathbf{y}}_i^{\left(k\right)},{\mathbf{x}}_j^{\left(d\right)}\right)}{p\left(y_{i+h}|{\mathbf{y}}_i^{\left(k\right)}\right)}}$ where p means the PDFs, ${\mathbf{x}}_j=\left\{x_j,x_{j-\tau },\cdots ,x_{j-\left(d-1\right)\tau }\right\},{\mathbf{y}}_i=\left\{y_i,y_{i-\tau },\cdots ,y_{i-\left(k-1\right)\tau }\right\}$, τ represents the sampling period, and h denotes the prediction horizon. k signifies the embedding dimension for variable y_i and d represents the embedding dimension for variable x_j.TE_X→Y from X to Y can be conceptualized as the improvement gained by using the historical data of both X and Y to forecast the future of Y, as opposed to solely relying on the historical data of Y alone. Essentially, it measures the information regarding an upcoming observation of variable Y obtained from the simultaneous observations of past values of both X and Y, while subtracting the information solely derived from Y’s past values concerning its future.

In a more detailed context, given two random processes and gauge the quantity of information using Shannon entropy (Shannon, 1948), the TE_X→Y can be expressed as: (10)${\displaystyle T{E}_{X\to Y}=\mathrm{H}\left(y_{i+h}|{\mathbf{y}}_i^{\left(k\right)}\right)-\mathrm{H}\left(y_{i+h}|{\mathbf{y}}_i^{\left(k\right)},{\mathbf{x}}_j^{\left(d\right)}\right)}$ where H is the Shannon entropy of X.

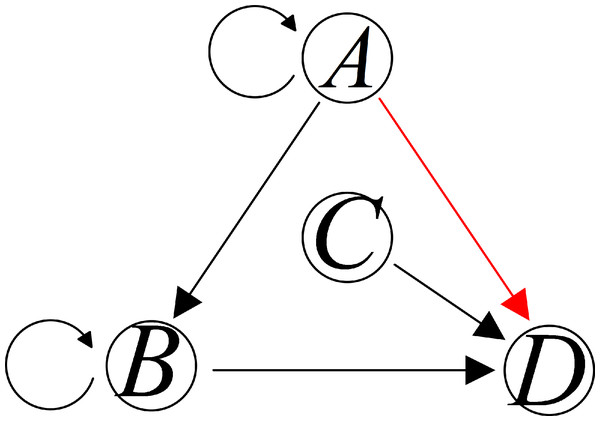
Derived from Eqs. (9) or (10), an indirect causality topology based on multivariate time series can be obtained, as shown in Fig. 3.

Consider four processes denoted as A, B, C, and D, as illustrated in Fig. 3. Suppose the TE method uncovers a causal influence from A to D. Within this context, two distinct causal patterns exist from A to D. However, it is essential to note that the TE, as described in Eqs. (9) or (10), is unable to distinguish whether this impact is direct or if it is transmitted through B. In other words, the TE lacks the capability to differentiate between a direct causality relationship and an indirect one. Additional methods must be incorporated to address the need for an equivalent underlying model to capture direct causality.

Conditional transfer entropy

In a complex system, it is not always guaranteed that TE exclusively represents the directed causal influence from X to Y. Information shared between X and Y may be conveyed through an intermediary third process, denoted as Z. In such scenarios, the presence of this shared information can lead to an augmentation in TE, potentially confounding the causal interpretation. One possible approach is conditional transfer entropy, which reduces the influence of shared information through alternative processes. CTE from a single source X to the target Y, while excluding information from Z, is then defined as follows: (11)${\displaystyle CT{E}_{X\to Y|Z}=I\left(y_{i+h};{\mathbf{x}}_j^{\left(d\right)}|{\mathbf{y}}_i^{\left(k\right)},{\mathbf{z}}_l^{\left(n\right)}\right)}$ where n represents the embedding dimension for variable z_l.

In the case mentioned in Fig. 3, the direct causality relationship can be distinguished from the indirect one via the CTE method to capture the direct causal topology. When the causal impact from A to D is entirely conveyed through B, CTE_A→D|B is uniformly zeros theoretically, which means that the addition of past measurements of A, contingent on B, will not enhance the prediction of D any further. Conversely, when there exists a direct influence from A to D, incorporating past measurements of A alongside those of B and D leads to enhanced predictions of D, resulting in a causal effect CTE_A→D|B > 0.

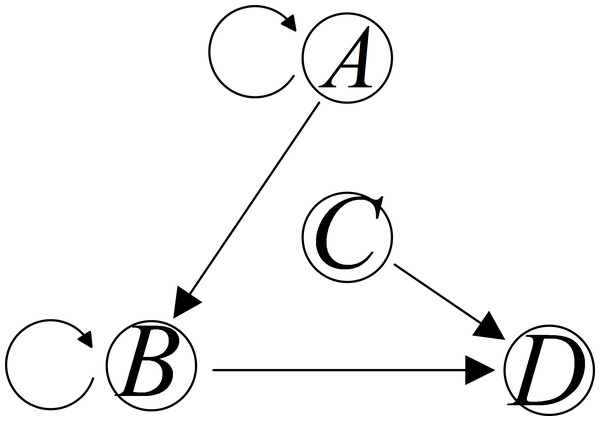
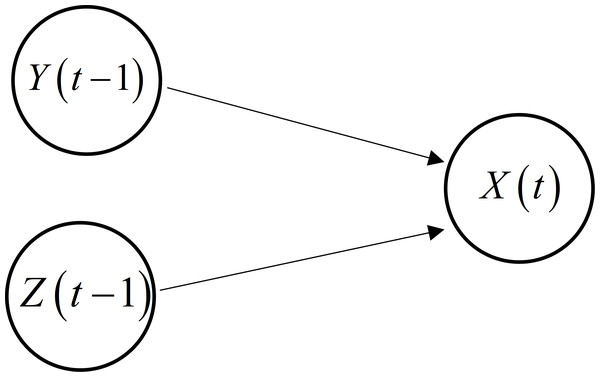
Utilizing MI in Eq. (5), CMI in Eq. (7), TE in Eq. (9), and CTE in Eq. (11), a set of foundational elements derived from the direct causality topology. Given four variables A, B, C, and D, suppose that the direct causal inference can be obtained, as shown in Fig. 4.

Derived from the direct causality topology depicted in Fig. 4, we can ascertain the sets of fundamental elements associated with each variable. The equivalent foundational model can be articulated as follows: (12)${\displaystyle A\left(t\right)=f_A\left(A_{\mathcal{A}}\right)+{ϵ}_{A}B\left(t\right)=f_B\left(A_{\mathcal{B}},B_{\mathcal{B}}\right)+{ϵ}_{B}C\left(t\right)={ϵ}_{C}D\left(t\right)=f_D\left({B_{\mathcal{D}},C}_{\mathcal{D}}\right)+{ϵ}_D}$ where each $f_i\left(x\right)$ represents the equivalent underlying model of variable i, i = A,  B,  C,  D. x signifies a collection of fundamental elements corresponding to variable i. For instance, consider the case where $C_{\mathcal{D}}=\left\{C\left(t-1\right),C\left(t-2\right)\right\}$. Here, $C_{\mathcal{D}}$ presents the measurements of C at sampling stamp t − 1 and t − 2, directly contributing to the causal relationship to D. It is worth noting that x can be determined through MI, TE, CMI, and CTE methods. In the subsequent section, the parameters and order of the functions f_i will be determined using a polynomial fitting approach.

Significance test

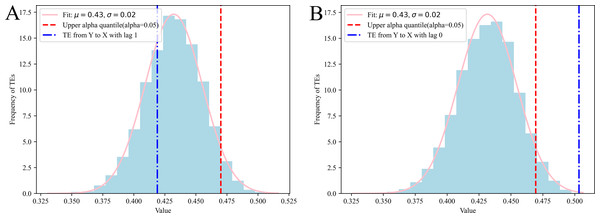
By conducting N-trial Monte Carlo simulations (Kantz & Schreiber, 2004), we compute the MIs, TEs, CMIs and CTEs for various surrogate time series, following Eqs. (5), (9), (7) and (11). These surrogate time series are randomly generated, and any potential causality between the time series is intentionally removed. In Fig. 5, the TEs for 10,000 pairs of uncorrelated random series are presented (partial results are presented here, with all results displayed in Supplemental Information). The results suggest that the MIs, TEs, CMIs and CTEs derived from the surrogate data demonstrate a Gaussian distribution, represented as $\mathcal{N}\left(\mu ,{\sigma }^2\right)$. If we denote the MIs, TEs, CMIs and CTEs as random variables X, the PDF can generally be expressed as follows: (13)${\displaystyle f\left(x\right)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{1}{2}{\left(\frac{x-\mu }{\sigma }\right)}^2}}$ where the parameter µrepresents the expected value of the distribution, while the parameter σ denotes its standard deviation. The variance of the distribution is expressed as σ². Let $Z=\frac{\left(X-u\right)}{\sigma }\sim \mathcal{N}\left(0,1\right)$, the PDF of Z can be written as: (14)${\displaystyle \phi \left(z\right)=f\left(\frac{x-\mu }{\sigma }\right)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{1}{2}{z}^2}.}$

The cumulative distribution function (CDF) of the standard normal distribution, typically denoted by the capital Φ, is defined as the integral: (15)${\displaystyle \Phi \left(z\right)=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^z{e}^{\frac{-t^2}{2}}\text{dt}.}$

There exists α > 0 such that: (16)${\displaystyle P\left(z>z_{\alpha }\right)=1-\Phi \left(z_{\alpha }\right)=\alpha .}$

The quantile ${\Phi }^{-1}\left(1-\alpha \right)$ of the standard normal distribution is frequently symbolized as z_α. A normal standard random variable will lie beyond the bounds of the confidence interval $\left(-\infty ,z_{\alpha }\right]$ with probability α, which is a small positive number, often 0.05, denoting as z_0.05. It means that 95% of the MIs, TEs, CMIs and CTEs derived from uncorrelated random series should be included in $\left(-\infty ,z_{0.05}\right]$. We could also say that with 95% confidence, we reject the null hypothesis that the MIs, TEs, CMIs and CTEs are insignificant. Therefore, if $I\left(X;Y\right)>z_{0.05}$ or $P\left(\frac{I\left(X;Y\right)-\mu }{\sigma }>z_{0.05}\right)<\alpha$, it implies a noteworthy connection between variable X and Y. Moreover, if TE_X→Y > z_0.05 or $P\left(\frac{T{E}_{X\to Y}-\mu }{\sigma }>z_{0.05}\right)<\alpha$, it implies a noteworthy causal connection from variable X to Y. Meanwhile, TE_X→Y|Z > z_0.05 or $P\left(\frac{T{E}_{X\to Y|Z}-\mu }{\sigma }>z_{0.05}\right)<\alpha$ , it indicates a significant causality from variable X to Y,  excluding information from Z. Additionally, if $I\left(X;Y|Z\right)>z_{0.05}$ or $P\left(\frac{I\left(X;Y|Z\right)-\mu }{\sigma }>z_{0.05}\right)<\alpha$, it indicates a significant connection between variable X and Y,  excluding information from Z. It should be noted that the value of z_0.05 depends on the specific distribution.

Polynomial fitting

The polynomial fitting method, employing a maximum exponent of k for each input feature, utilizes $\mathbf{X}=\left\{X_1,X_2,\dots ,X_n\right\}$ to create a polynomial features matrix A. This matrix comprises $C_{k+n}^n$ features, consequently leading to the establishment of a linear system: (17)${\displaystyle Y\left(t\right)=ABA=\left\{\underset{C_{k+n}^n}{\underbrace{1,X_1,X_2,\dots ,X_n,X_1^2,X_2^2\cdots ,X_n^k}}\right\}}$ where B is the coefficients and intercept. The Eq. (17) can be effectively solved using the “preprocessing.PolynomialFeatures” and “linear_model.LinearRegression” classes within the Python package “sklearn”.

Case 1: simulation case

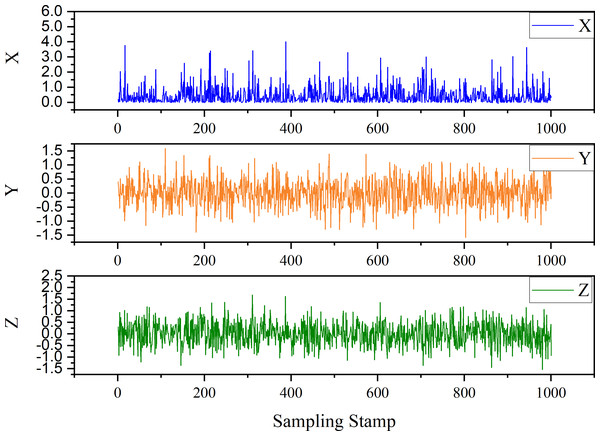
In the first instance, we have a discrete-time dynamical system. The expression is as follows: (18)${\displaystyle X\left(t\right)=\left[\sigma Y\left(t-1\right)-\rho Z\left(t-1\right)\right]\left[Y\left(t-1\right)-\beta Z\left(t-1\right)\right]+0.01\ast {ϵ}_{1}Y\left(t\right)=0.5\ast {ϵ}_{2}Z\left(t\right)=0.5\ast {ϵ}_3}$ where the two parameters are σ = 0.9, ρ = 0.7, and $\beta =\frac{4}{3}$. The initial conditions are X(0) = 0.2, Y(0) = 0.4, and Z(0) = 0.3. The ${ϵ}_i\mathcal{\sim \; N}\left(0,1\right)$, where i = 1, 2, 3, represent the White Gaussian Noise. The trend generated by the time series derived from Eq. (18) is shown in Fig. 6.

Table 1 presents a comprehensive overview of TEs between each pair of variables with their respective time lags. In this table, p denotes the probability and the z_0.05, upper α quantile (α = 0.05), serves as the upper boundary of the confidence interval.

The causality topology, derived from Tables 1 and 2 through TE and MI analysis, is visually depicted in Fig. 7. Notably, it becomes evident that there is only one unique pattern of causality between each pair of variables, each associated with their respective time lags. In other words, there is no presence of indirect causal influence. Consequently, the equivalent underlying model can be succinctly expressed as follows: (19)${\displaystyle X\left(t\right)=f_X\left(Y\left(t-1\right),Z\left(t-1\right)\right)+{ϵ}_{X}Y\left(t\right)={ϵ}_{Y}Z\left(t\right)={ϵ}_Z.}$

In the subsequent step, we employ polynomial approximation to estimate the genuine underlying model. The parameters and order of the equivalent f_X are determined through the polynomial fitting approach as outlined in Eq. (18). In this process, we opt for a higher order k for f_X: (20)${\displaystyle X\left(t\right)=f_X\left(Y\left(t-1\right),Z\left(t-1\right)\right)+{ϵ}_X=AB}$ where $A=\left[1,Y{\left(t-1\right)}^1,Z{\left(t-1\right)}^1,Y{\left(t-1\right)}^2,Y{\left(t-1\right)}^{1}Z{\left(t-1\right)}^1,Z{\left(t-1\right)}^2,\dots ,Z{\left(t-1\right)}^k\right]$, B = [b_0,0], [b_1,0, b_0,1, b_2,0, b_1,1, b_0,2⋯, b_1,k−1, b_0,k]^T. When selecting k = 4, these parameters can be obtained by fitting, b_0,4 = 3.2∗10⁻³, b_1,3 = 3.2∗10⁻³, b_2,2 =  − 3.2∗10⁻³, b_3,1 =  − 4.8∗10⁻³, b_4,0 = 2.1∗10⁻³, b_0,3 =  − 3.4∗10⁻³, b_1,2 =  − 6.8∗10⁻³, b_2,1 =  − 2.9∗10⁻³, b_3,0 = 7.7∗10⁻⁴, b_0,2 = 0.93, b_1,1 = 1.9, b_2,0 = 0.9, b_0,1 = 2.4∗10⁻³, b_1,0 = 1.5∗10⁻³, b_0,0 = 1.9∗10⁻⁴. Disregarding coefficients that are insignificantly close to zero, the expression in Eq. (20) can be redefined as follows: (21)${\displaystyle X\left(t\right)\approx b_{0,2}{Z\left(t-1\right)}^2+b_{1,1}Y\left(t-1\right)Z\left(t-1\right)+b_{2,0}{Y\left(t-1\right)}^2+{ϵ}_X=0.93\ast {Z\left(t-1\right)}^2-1.89\ast Y\left(t-1\right)Z\left(t-1\right)+0.9\ast {Y\left(t-1\right)}^2+{ϵ}_X}$

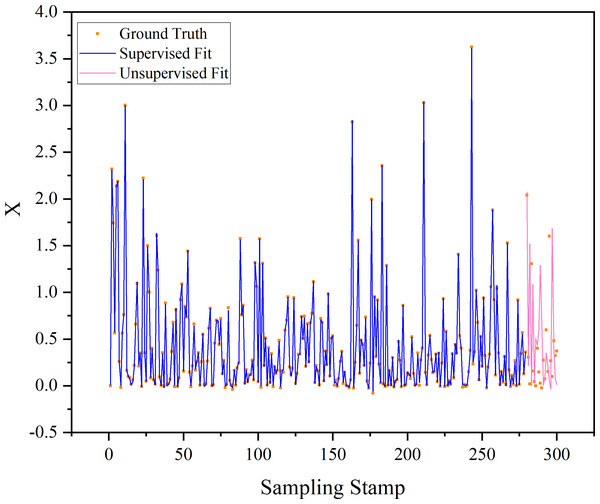
It is evident that the underlying model in Eq. (18) can be concisely represented by Eq. (21). The training dataset consists of 700 samples in our experimental configuration, while the testing dataset comprises 300 samples. Figure 8 elegantly showcases the fitting curves of the time series achieved through the proposed method. Remarkably, when supervised, the original series and the polynomial fit data (derived from the equivalent underlying model) exhibit an exceptionally close alignment. In contrast, without supervision, the performance is significantly reduced. This reduction in performance is likely attributed to $Y\left(t\right)$ and $Z\left(t\right)$ relying solely on white Gaussian noise, which exhibits a considerable degree of randomness.

Case 2: Henon map chaotic time series

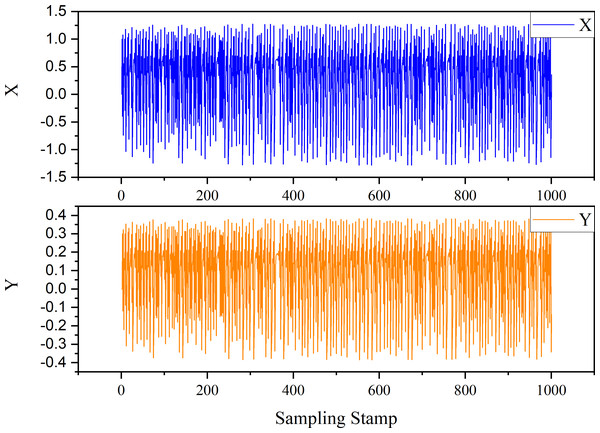
The Henon map constitutes a discrete-time dynamical system characterized by chaotic behavior. Here is the expression of the Henon map system: (22)${\displaystyle X\left(t+1\right)={1-\alpha X}^2\left(t\right)+Y\left(t\right)+0.0001\ast {ϵ}_{X}Y\left(t+1\right)=\beta X\left(t\right)+0.0001\ast {ϵ}_Y}$ where the parameters α and β are set to α = 1.4 and β = 0.3, respectively, while the initial states are X(0) = 0 and Y(0) = 0. The trend generated by the time series derived from Eq. (22) is shown as Fig. 9.

Table 3 presents a comprehensive overview of TEs between each pair of variables with their respective time lags. Notably, the TE method has detected the causal influences from $Y\left(t-1\right)$ to $X\left(t\right)$, $Y\left(t-2\right)$ to $X\left(t\right)$, $X\left(t-1\right)$ to $Y\left(t\right)$.

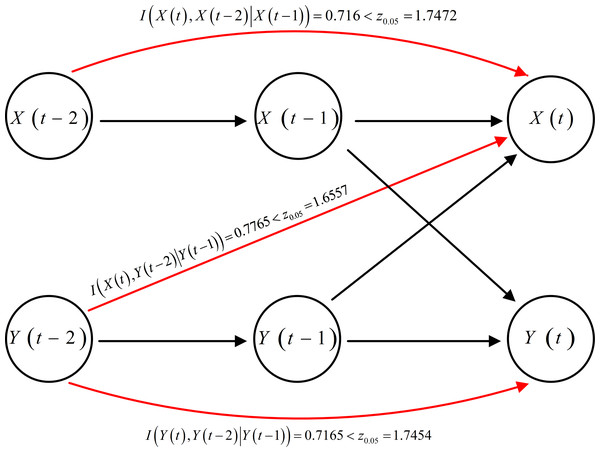
The causality topology, derived from Tables 3 and 4 through both TE and MI analyses, is visually represented in Fig. 10. Notably, there exist two types causal influences, direct and indirectly, among the following three pairs of variables: $X\left(t-2\right)$ to $X\left(t\right)$, $Y\left(t-2\right)$ to $X\left(t\right)$, and $Y\left(t-2\right)$ to $Y\left(t\right)$. To further investigate these causal relationships and distinguish whether the influence is direct or mediated by three, we employ CMI or CTE to capture direct causality.

Each of these three undetermined causal relationships involves its historical measurements. Consequently, the CMI is more suitable for distinguishing whether a third variable’s influence is direct or mediated. The outcomes of the analysis using CMI are outlined in Table 5. The results indicate that these causal relationships are indeed direct rather than indirect. This implies that the red arrows should be removed, and the rest of the diagram reflects the direct causal topology (shown in Fig. 10).

Consequently, the equivalent underlying model can be succinctly expressed as follows: (23)${\displaystyle X\left(t\right)=f_X\left(X\left(t-1\right),Y\left(t-1\right)\right)+{ϵ}_{X}Y\left(t\right)={f_Y\left(X\left(t-1\right),Y\left(t-1\right)\right)+ϵ}_Y}$

In the subsequent step, we employ polynomial approximation to estimate the genuine underlying model. When choosing k = 4, these parameters of f_X can be obtained by fitting. b_0,0 = 1, b_0,1 = 1, b_2,0 =  − 1.4, and the rest of the coefficients are insignificantly close to zero, one expression in Eq. (23) can be redefined as follows: (24)${\displaystyle X\left(t\right)\approx 1+Y\left(t-1\right)-1.4\ast {X\left(t-1\right)}^2+{ϵ}_X.}$

Similarly, another the expression in Eq. (23) can be redefined as follows: (25)${\displaystyle Y\left(t\right)\approx 0.3\ast X\left(t-1\right)+{ϵ}_Y.}$

The underlying model of the Henon map can be concisely represented by Eqs. (24) and (25). Within our experimental configuration, the training dataset consists of 700 samples, while the testing dataset comprises 300 samples. Figure 11 elegantly portrays the fitting curves of the time series achieved through the proposed method. Both supervised and unsupervised cases exhibit an exceptionally close alignment between the original series and the polynomial fit data derived from the equivalent underlying model. This outcome is likely due to $X\left(t\right)$ and $Y\left(t\right)$ not relying on White Gaussian Noise, thereby reducing the influence of randomness.