Dynamic coefficient symmetric polynomial-based secure key management scheme for Internet of Things (IoT) networks

Introduction

In the network architecture of the Internet of Things (IoT), some new distributed models (Bouarourou, Boulaalam & Nfaoui, 2021; Labib et al., 2021) and multi-hop clustering scheme (Muthukkumar et al., 2022) for heterogeneous wireless sensor networks (WSNs) to efficiently deal with heterogeneous sensors in a dynamic IoT environment, it greatly increases the service life and communication efficiency of node networkst. In the security architecture of the IoT, (Alansari et al., 2023) presents a novel lightweight system for anomaly detection of grayhole, blackhole, and selective forwarding attacks, and a survey (Osamy et al., 2022) reviews and analyzes the research trends related to the utilized artificial intelligence (AI) methods for IoT and the potential enhancement of IoT. In terms of key management, due to the complexity of the structure and high mobility of the IoT structure, the key management strategy based on static implementation cannot be directly applied to the IoT environment. In order to deal with the drawbacks of security and efficiency of the Internet of Things, the design of key management scheme has become one of the key breakthroughs to provide a secure and efficient IoT environment for key negotiation and secure communication between users. At the same time, compared with the common computer network key management model, the key management model oriented to IoT must meet the integrity, reliability, privacy and anonymity, non-repudiation and other characteristics, security and efficiency become the basic standards to measure its availability. Therefore, the IoT needs to design a more appropriate security key management technical solution to solve the security problem.

In order to reduce the energy overhead of wireless sensor networks in the IoT environment and improve network security, several security solutions have been proposed in the literature. Blundo et al. (1998) proposed a scheme in which all nodes use a common polynomial to establish a pairwise key. This simplifies the process of establishing a shared key and has a high connectivity rate between sensor nodes. In Liu, Ning & Li (2003), the authors presented a protocol using grid-based key predistribution and random subset assignment. This scheme further extends the idea of a polynomial to establish pairwise keys. In random subset assignment, nodes select a set of polynomials from a pool and use the same polynomials in selected polynomials to establish pairwise keys. Das & Sengupta (2008) proposed a deterministic group-based key pre-distribution scheme based on a hierarchical wireless sensor network using bivariate polynomials over a finite field. Zhang, Li & Li (2018) developed another key predistribution for pairwise key establishment, which fuses polynomial pool-based and random key predistribution.

Reegan & Baburaj (2017) have proposed a triple key distribution scheme based on polynomial and multivariate mapping, aiming at the problem that the security performance of previous schemes decreases with the increase of the number of damaged nodes. And an improved energy-saving key distribution and management scheme has been proposed by Chakavarika, Gupta & Chaurasia (2017). This scheme is scalable in terms of storage cost and computation cost. The security of network is improved by introducing encrypted random numbers in the key updating stage. In order to solve the memory overhead problem of q-composite scheme, Gandino, Ferrero & Rebaudengo (2017) proposed a new protocol q-s-composite to improve the efficiency of memory management. Albakri & Harn (2019) proposed a group key pre-distribution scheme based on probabilistic polynomials. Which significantly reduces the probability of sensor being attacked by node capture, and improves the security of wireless sensor networks. Li et al. (2020) proposed a secure random key distribution scheme aiming at the shortcomings of q-s-composite scheme in literature (Gandino, Ferrero & Rebaudengo, 2017), which could not resist node replication attacks, combining localization algorithm with voting mechanism. To support the detection and cancellation of malicious nodes, and further modify parameters to resist node replication attacks. In order to solve the security of key management and IoT security performance index optimization problems, Harn, Hsu & Xia (2021) proposed a novel key distribution scheme. The key distribution protocol only needs logical XOR operation, which is much faster than other schemes. Wang et al. (2020) proposed a WSN layer-cluster key management scheme based on quadratic polynomial and Lagrange interpolation polynomial is proposed. Nafi, Bouzefrane & Omar (2020) proposed a new lightweight matrix-based key management protocol for IoT network. Sharma & Purushothama (2022) proposed a new and efficient scheme (BP-MGKM) for secure multi-group key management based on bivariate polynomial. Najafi & Babaie (2023) proposed approach, a lightweight hierarchical key management approach, generating shorter and more secure keys due to the use of a hierarchical structure based on the position and remaining energy of nodes. Msolli et al. (2023) proposed the key management scheme with pool-hash for the establishment, which exposes a new key pool contains original keys and other hashed admit the same identities thus new session keys transmitted in sensors nodes are established during the discovery and path key phases. Taurshia et al. (2022) presented a novel Group Key Management scheme for Low-Resource Devices (GKM-LRD) to offer key management service to groups in IoT applications. Nafi et al. (2022) proposed a new key management protocol aiming to secure communications before and after key establishment, used hash and one–one functions to achieve security during the key establishment process. Rezaeipour & Barati (2022) presented a key management protocol that delivers services such as message confidentiality, integrity, and authenticity to wireless sensor networks by handling keys generation, distribution, and maintenance. Kandi et al. (2022) proposed a novel decentralized blockchain-based protocol for the IoT, balanceing the loads between nodes according to their capabilities. Wei et al. (2021) proposed two space-efficient Bitcoin-compatible key management schemes for the lighting network, based on the hash function and trapdoor one-way function, respectively.

However, for all these solutions, there are shortcomings in the overall performance of connectivity, energy consumption, and security. Especially, a small number of compromised nodes may affect the majority of pairwise keys. This greatly restricts the maximum number (nodes’ limitation number) of nodes the sensor network can hold if the polynomial is unconditionally secure. While increasing the safety threshold λ of the polynomial f(x,y), these schemes are able to make the nodes’ limitation number λ a little enlarged. But it will make nodes suffer from some more serious problem, such that polynomials can extremely enhance the computation and storage overhead at the same time.

Making node communication of these schemes more secure requires a new mechanism to address the λ-secure problem. In addition, we should also consider the following questions: as some nodes are captured, the communication security of other nodes will be directly affected, and all nodes could even be compromised. It should be noted that the energy, storage and communication overhead of sensor nodes are limited. The proposed scheme should maintain high node connectivity and low energy consumption.

Our scheme has better resilience to node capture attacks, a high connectivity rate between nodes, and can considerably reduce the communication and storage overhead. The contributions of this article are summarized as follows:

• Offers more effective resilience to node capture attacks for the λ-secure problem and has better resistance than other key management schemes.

• The wireless sensor network has a high connectivity rate. Our scheme uses an identity mapping algorithm to map a series of coefficients of $P(x,y)$, and each pair of communication nodes is able to establish a pairwise key.

• Low computational overhead. Even though the phase of pairwise key establishment consumes more energy than the other key management schemes, the node’s chip is sufficient to deal with polynomial and hash algorithms.

• Low communication overhead. All communication nodes exchange identity information with each other, and the sensor network directly implements the identity mapping algorithm with the identity information of sensor nodes to get pairwise keys. There are no extra communication streams, except for identity information, during the process of pairwise key establishment, which can greatly reduce communication overhead.

• Low storage overhead. With a value of λ = 7, our scheme in pairwise key establishment generates quite a small amount of code. The shared matrix M can generate a series of coefficients of $P(x,y)$ according to the sensor node’s ID, and the sensor network of a head-cluster node is able to hold 1.75 × 10⁵ nodes, which meets the requirements of many scenarios.

The structure of the article is as follows. “Preliminaries” describes the preliminaries. “Overview of Proposed Scheme” proposes our scheme with dynamic coefficient symmetric polynomials including key pre-distribution and key agreement phase. In “Theoretical Analysis”, we analyze some classical security. “Performance Analysis” presents a comparative study and simulation results. “Conclusions” presents the conclusion of this article.

Preliminaries

In this section, we introduce the network model and background, as well as explain the symbols used and their descriptions in this article.

Network model

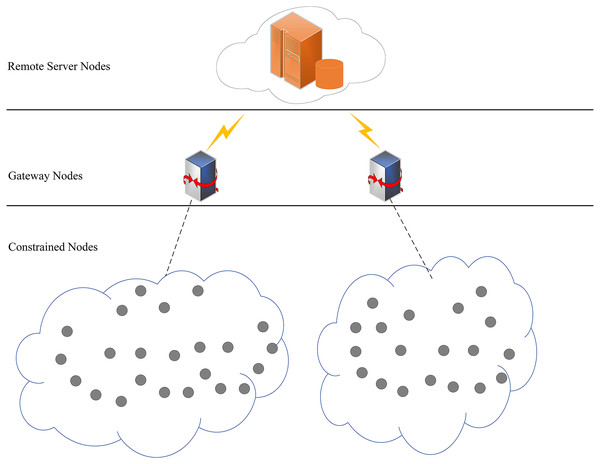
Our scheme is suitable for a distributed network architecture, which consists of remote server nodes, gateway nodes and sensor nodes. All sensor nodes in the network have the same resources with the functions of sensing, collecting and transmitting data. Moreover, these sensor nodes are able to communicate with each other. Figure 1 shows the network model we have assumed.

Overview of proposed scheme

In this section, we describe the key management scheme of dynamic coefficient symmetric polynomial for IoT networks, which has two phases: pairwise predistribution phase and pairwise key agreement phase. In the following, we describe the details of each phase.

Key agreement phase

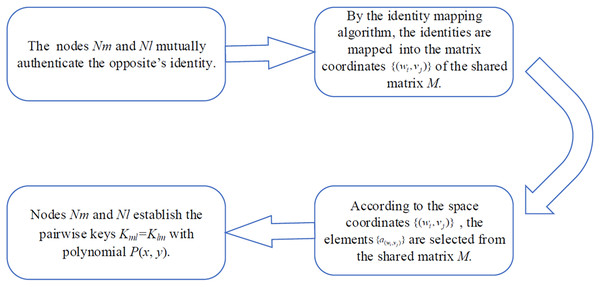
The pairwise key is used for end-to-end unicast communication. Communicating nodes authenticate each other’s identity, construct the matrix coordinates $\{(w_i,v_j)|i,j=0,1,2,\cdots ,\lambda \}$ and coefficient set $\{a_{(w_i,v_j)}|i,j=0,1,2,\cdots ,\lambda \}$ of $P(x,y)$, and establish a pairwise key, as shown in Fig. 2.

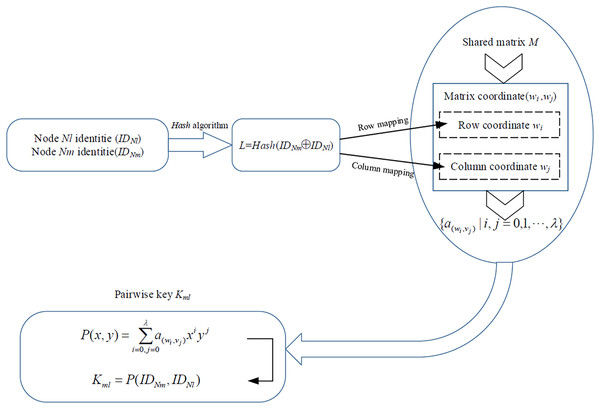
Construct matrix coordinate set C_ml and coefficient set A_ml. Nodes Nl and Nm map their identities to matrix coordinates (w_i,v_j) of M and obtained the element $a_{(w_i,v_j)}$ from M by the matrix coordinates (w_i,v_j). Figure 3 shows the identity mapping algorithm.

(1) Nodes Nl and Nm obtain the mapped identity,

(2) $$I{D}_{ml}=I{D}_{Nm}\oplus I{D}_{Nl}.$$

(2) Nodes Nl and Nm output more than 2t (λ + 1) bits of fixed-length data.

(3) $$L=H\mathrm{a}sh(I{D}_{ml})=w_0,w_1,\dots ,w_{\lambda },v_0,v_1,\dots ,v_{\lambda },\dots$$

(3) The first t(λ + 1) bits in L are mapped to the row coordinate w_i of M as

(4) $$W=w{}_0,w{}_1,...,w{}_{\lambda }$$

The length of w_i (0 ≤ i ≤ λ) is fixed at t $(t=1,2,\dots )$ bits with $\lambda =2^0+2^1+\dots +2^{(t-1)}$, indicating the row coordinates of M. The output L of the hash function is binary and must be converted to decimal form. For instance, $w_1=01011$ can be expressed in decimal form as w₁ = 0 × 2⁴ + 1 × 2³ + 0 × 2² + 1 × 2¹ + 1 × 2⁰ = 11.

(4) The next t(λ + 1) bits in L are mapped to column coordinate v_j of M as

(5) $$V=v{}_0,v{}_1,....,v{}_{\lambda }.$$

The length of v_j (0 ≤ j ≤ λ) is fixed at t $(t=1,2,\dots )$ bits with $\lambda =2^0+2^1+\dots +2^{(t-1)}$, indicating the column coordinates of M. Like w_i, v_j is binary and must be converted to decimal form.

(5) Nodes Nl and Nm generate the matrix coordinate set C_ml of symmetric polynomial P(x,y), with row coordinates w_i and column coordinates v_j,

(6) $$C_{ml}=\{(w_i,v_j)|i,j=0,1,\dots ,\lambda {\}}_{ml}.$$

The coefficient set A_ml of P(x,y) is established by C_ml, and then used as coefficients of P(x,y),

(7) $$A_{ml}=\{a_{(w_i,v_j)}|i,j=0,1,\dots ,\lambda {\}}_{ml}.$$

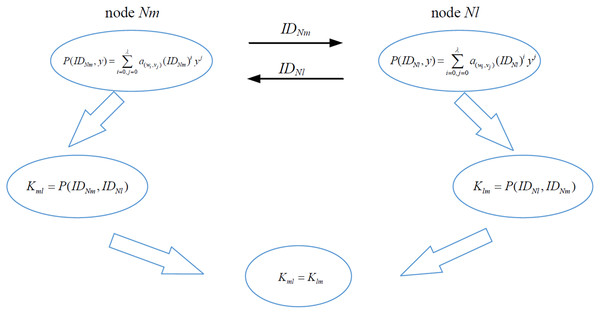
The communication nodes establish pairwise keys with P(x,y). Nodes Nm and Nl respectively construct the pairwise keys K_ml and K_lm, as shown in Fig. 4, according to the elements $a_{(w_i,v_j)}$ of M, as

(8) $$P(x,y)=\sum _{i=0,j=0}^{\lambda }{a}_{(w_i,v_j)}{x}^i{y}^j.$$

(1) When node Nm executes P(x,y), the input terms of the variable x and y are x = ID_Nm, y = ID_Nl,

(9) $$\begin{array}{rl}{K}_{ml}& =P(I{D}_{Nm},I{D}_{Nl})\\ & =\sum _{i=0,j=0}^{\lambda }{a}_{(w_i,v_j)}(I{D}_{Nm}{)}^i(I{D}_{Nl}{)}^j\end{array}.$$

(2) When node Nl executes $P(x,y)$, we input x = ID_Nl, y = ID_Nm, and

(10) $$\begin{array}{rl}{K}_{lm}& =P(I{D}_{Nl},I{D}_{Nm})\\ & =\sum _{i=0,j=0}^{\lambda }{a}_{(w_i,v_j)}(I{D}_{Nl}{)}^i(I{D}_{Nm}{)}^j\end{array}.$$

(3) Since the polynomial P(x,y) is symmetric, K_ml is equal to K_lm, and

(11) $$P(I{D}_{Nm},I{D}_{Nl})=P(I{D}_{Nl},I{D}_{Nm}).$$

So that nodes Nl and Nm have established a pairwise key, i.e., when node Nm communicates with node Nl, they have a common coefficient set A_ml for P(x,y). The coefficient sets A of P(x,y) are different in distinguishing pairs of communicating nodes. For example, when communicating, two pairs of nodes (Nm, Nl) and (Nm, Nd) in sensor network have different coefficient sets A_ml and A_md, i.e., the attacker cannot use Lagrange interpolation to reconstruct P(x,y).

Theoretical analysis

In this section, we evaluate the λ-secure of symmetric polynomial and size of polynomial pool. Theoretical analysis shows that the proposed scheme can effectively address the λ-secure, and also has a large enough size of polynomial pool to resist brute force attacks.

Size of polynomial pool with different λ

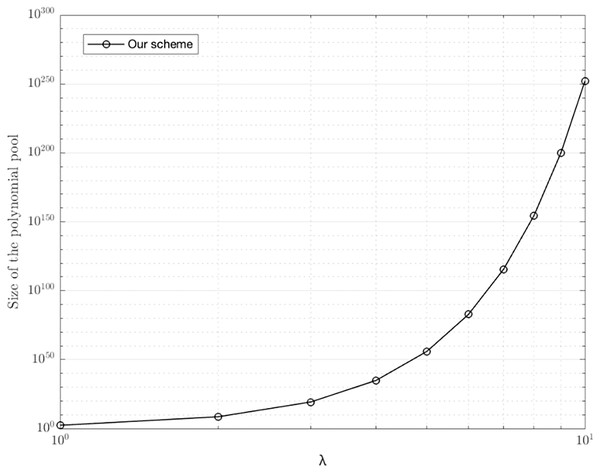
Due to the limitation of λ and t, our scheme uses the hash function of length is 2t(λ +1) bits, which makes coefficients to be combined $[(\lambda +1{)}^2{]}^{{(\lambda +1)}^2}$polynomials. That is, our key management scheme generates a polynomial pool ω containing large $|\omega |=[(\lambda +1{)}^2{]}^{{(\lambda +1)}^2}$polynomials, and each node selects a polynomial from the polynomial pool. In other words, every node in the network has the probability $1/|\omega |$ to carry a polynomial from the polynomial pool. Given the security, our scheme should put a limit on the maximum $|\omega |(\lambda +1{)}^2$ nodes. Figure 5 shows the size of polynomial pool |ω| with different λ. When λ = 3, our scheme can generate a polynomial pool holding 1.84 × 10¹⁹ polynomials, allowing our scheme to be used in most scenarios. In addition, our scheme is able to well resist brute force attacks. If someone wants to obtain a pairwise key, they should obtain the coefficients $a_{(w_i,v_j)}$ of P(x,y) from the shared matrix M. There are a total of $[(\lambda +1{)}^2{]}^{{(\lambda +1)}^2}$possibilities for an attacker to repeat. When λ = 3, our scheme can generate a polynomial pool holding 1.84 × 10¹⁹ polynomials, where it's hard for an attacker to repeat so many times.

Performance analysis

We have conducted a comparative study of a number of related schemes, carried out scientific research, collected data through compliant methods, and evaluated the performance of our scheme through realistic simulations, including the resilience of node capture, connectivity, and resource overhead (energy, memory, and computation) in the pairwise key establishment process.

Resilience against node capture

A proper key management scheme should resist attacks while the network continues its normal operation. The main security threat to the proposed solution is the λ-secure. The security analysis of the new scheme proposed in this section mainly analyzes its resilience to node capture. Resilience is computed as the fraction of links compromised in non-compromised nodes. When the number of nodes is large enough in the network, the output values of hash functions will collide, and communication nodes will hold the same output value L of the hash function and P(x,y). Security analysis shows that our scheme not only offers more effective resilience to node capture attacks for the λ-secure, but has better resistance to node capture attacks compared with the other key management scheme.

Probability of at least one matrix being broken

Denote that S_i is an event in the ith polynomial P(x,y) is cracked $(i\in \{1,2,\dots ,|\omega |\})$. All coefficients a_ij (i, j = 0, 1, $\dots$, λ) selected from M can be combined into |ω| different kinds of polynomials. The probability that one of these polynomial P(x,y) $(P\in \{P_1,P_2,\dots ,P_{|\omega |}\})$occurrence in a node is $\theta ={\displaystyle \frac{1}{|\omega |}}$. Cx is an event that x nodes are compromised in a network.

(17) $$|\omega |=[(\lambda +1{)}^2{]}^{{(\lambda +1)}^2}.$$

We have,

(18) $$P_r(\mathrm{a}\mathrm{t}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{n}\mathrm{e}P(x,y)\mathrm{i}\mathrm{s}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}|C_x)=P_r(S_1\cup S_2\cup \dots \cup S_{|\omega |}|C_x).$$

It is obtained by union bound,

(19) $$P_r(S_1\cup S_2\cup \dots \cup S_{|\omega |}|C_x)\le \sum _{i=1}^{|\omega |}{P}_r(S_i|C_x).$$

It is equal probability for each P(x, y) to be broken. That is,

(20) $$\sum _{i=1}^{|\omega |}{P}_r(S_i|C_x)=|\omega |\cdot P_r(S_i|C_x).$$

Therefore,

(21) $$P_r(\mathrm{a}\mathrm{t}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{n}\mathrm{e}P(x,y)\mathrm{i}\mathrm{s}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}|C_x)\le \sum _{i=1}^{|\omega |}{P}_r(S_i|C_x)=|\omega |\cdot P_r(S_i|C_x)$$

The total number of terms in P(x,y) is $n=(\lambda +1{)}^2=(2^0+2^1+\dots +2^{(t-1)}+1{)}^2$. Because every coefficient a_ij (i, j = 0, 1, $\dots$, λ) in P(x,y) is different, the safety threshold of the proposed scheme is ${\lambda }^{\mathrm{\prime }}=n-1=(\lambda +1{)}^2-1$. We have,

(22) $$P_r(S_i|C_x)=\sum _{i={\lambda }^{\prime }+1}^x\left(\begin{array}{c}x\\ i\end{array}\right){\theta }^i{\left(1-\theta \right)}^{x-i}.$$

Therefore we get the following upper bound:

(23) $$\begin{array}{rl}{P}_r(\mathrm{a}\mathrm{t}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{o}\mathrm{n}\mathrm{e}P(x,y)\mathrm{i}\mathrm{s}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}|C_x)& \le \sum _{i={\lambda }^{\prime }+1}^x\left(\begin{array}{c}x\\ i\end{array}\right){\theta }^i{\left(1-\theta \right)}^{x-i}\\ & =\sum _{i={\lambda }^{\prime }+1}^x\left(\begin{array}{c}x\\ i\end{array}\right){\left({\displaystyle \frac{1}{|\omega |}}\right)}^i{\left(1-{\displaystyle \frac{1}{|\omega |}}\right)}^{x-i}\end{array}.$$

The fraction of compromised network communication

c is a link that two uncompromised nodes establish a communication with a common key K. Bi is a event that one common key K of two nodes is derived by compromised key space S_i.

(24) $$P_r(c\mathrm{i}\mathrm{s}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}|C_x)=P_r(B_1\cup B_2\cup \dots \cup B_{|\omega |}|C_x).$$

Since the link c is built securely by one common key K that derived by a key space S_i. Due to events $B_1,B_2,\dots ,B_{|\omega |}$ are mutually exclusive and probability of occurrence in Bi is equally, therefore,

(25) $$P_r(\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}|C_x)=\sum _{i=1}^{|\omega |}{P}_r(B_i|C_x)=|\omega |\cdot P_r(B_1|C_x).$$

Note that $(K\in S_1)$ represents an event that “key K was derived by S_i.”

(26) $$P_r(B_1|C_x)={\displaystyle \frac{P_r((K\in S_1)\cap (S_1\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}\mathrm{d})\cap C_x)}{P_r(C_x)}.}$$

Event $(K\in S_1)$ is independent of the events Cx and (S₁ is compromised).

(27) $$\begin{array}{rl}{P}_r(B_1|C_x)& ={\displaystyle \frac{P_r(K\in S_1)\cdot P_r(S_1\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}\mathrm{d})\cap C_x)}{P(C_x)}}\\ & =P_r(K\in S_1)\cdot P_r(S_1\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}\mathrm{d}|C_x)\end{array}.$$

The probability of event $(K\in S_1)$ is equal to the probability of event “the link c established by space S_i”. Each key space appears randomly and uniformly in a node.

(28) $$P_r(K\in S_1)=P_r(\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{k}c\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{s}\mathrm{h}\mathrm{e}\mathrm{d}\mathrm{b}\mathrm{y}\mathrm{s}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{e}{S}_i)={\displaystyle \frac{1}{|\omega |}.}$$

Therefore, the probability of event that one link is compromised when x nodes captured show as

(29) $$\begin{array}{rl}{P}_r(c\mathrm{i}\mathrm{s}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}|C_x)& =|\omega |\cdot P_r(B_1|C_x)\\ & =|\omega |\cdot {\displaystyle \frac{1}{|\omega |}\cdot P_r(S_1\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{e}\mathrm{d}|C_x)}\\ & =\sum _{i={\lambda }^{\prime }+1}^x\left(\begin{array}{c}x\\ i\end{array}\right){\left({\displaystyle \frac{1}{|\omega |}}\right)}^i{\left(1-{\displaystyle \frac{1}{|\omega |}}\right)}^{x-i}\end{array}.$$

Assume that w secure communication links do not involve any of the x compromised nodes. Denote R as the event “the rest of w secure communication links except x compromised nodes participating in”. That is,

(30) $$\begin{array}{rl}{P}_r(R)& ={\displaystyle \frac{w\cdot P_r(c\mathrm{i}\mathrm{s}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}|C_x)}{w}}\\ & =P_r(c\mathrm{i}\mathrm{s}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}|C_x)\end{array}.$$

The above equation indicates that, given that x nodes are compromised, the fraction of the compromised secure communication links outside of those x compromised nodes is the same as the probability of one P(x, y) being compromised.

Comparison to previous work

Although many key managements based on Blundo’s scheme can ensure that all nodes are able to be connected, they are faced with λ-secure. Security analysis shows that our scheme not only offers more effective resilience to node capture attacks for the λ-secure, but has better resistance to node capture attacks compared with other key management schemes. Table 2 lists some different schemes of comparison used in this article.

Table 2:

Some different schemes of comparison.

Scheme	Liu, Ning & Li (2003)	q-composite scheme (Chan, Perrig & Song, 2003)		Our scheme	Zhang, Li & Li (2018)
s	−	20		−	12
|S|	−	340	200	−	−
q	−	2	3	−	−
τ (2 ≤ τ < |ω|)	2	−		−	2
|ω|	11	−		−	18
t	−	−		1	−
λ	18	−		1	18
N	−	−		−	200

DOI: 10.7717/peerj-cs.1726/table-2

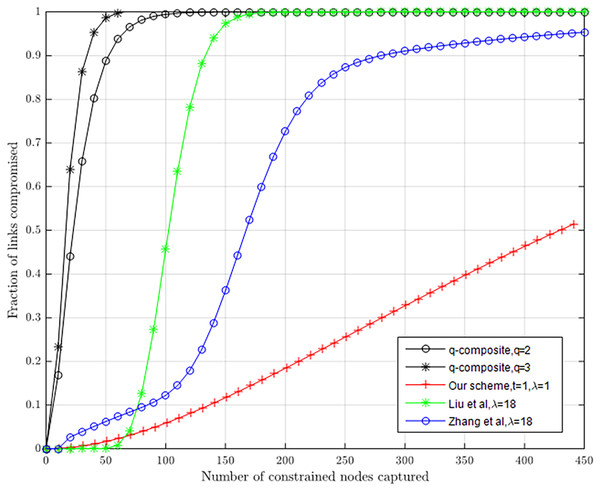
Our scheme offers better resilience to node capture attacks than q-composite, Liu, Ning & Li (2003) and Zhang, Li & Li (2018) in Fig. 6. If attackers capture 231 sensor nodes, about 22.8% of the pairwise keys, in our scheme with λ = 1 and t = 1, between non-compromised nodes will be compromised. If an attacker captures 401 nodes, about 46.5% of the pairwise keys between non-compromised nodes will be compromised. In Blundo et al. (1998), when captured nodes remain at 410, all pairwise keys between non-compromised nodes will be compromised. In Liu, Ning & Li (2003), when captured nodes remain at 500, all pairwise keys between non-compromised nodes will be compromised. In Zhang, Li & Li (2018), when captured nodes remain at 500, about 91.0% of pairwise keys between non-compromised nodes will be compromised. In q-composite (q = 2) and q-composite (q = 3), when captured nodes remain at 800, almost all pairwise keys between non-compromised nodes will be compromised.

Resilience to node capture in our scheme

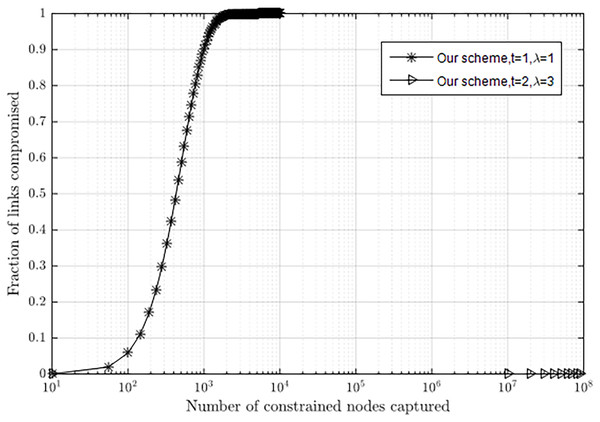
The relationship between λ and t can be described as $\lambda =2^0+2^1+\dots +2^{(t-1)}$ in our scheme, i.e., λ and t affect the fraction of compromised links. Figure 7 shows the relationship between the fraction of compromised links for non-compromised sensors and the number of compromised nodes with different values of λ and t. If attackers capture 1,000 sensor nodes, about 90.2% of the pairwise keys between non-compromised nodes will be compromised when λ = 1 and t = 1. If attackers capture 1.0 × 10⁸ sensor nodes, nearly no pairwise keys between non-compromised nodes will be compromised when λ = 3 and t = 2. Actually, with λ = 3 and t = 2, the sensor network can hold at least 1.0 × 10⁸ nodes, which is enough to meet the requirements of many scenarios.

Connectivity rate

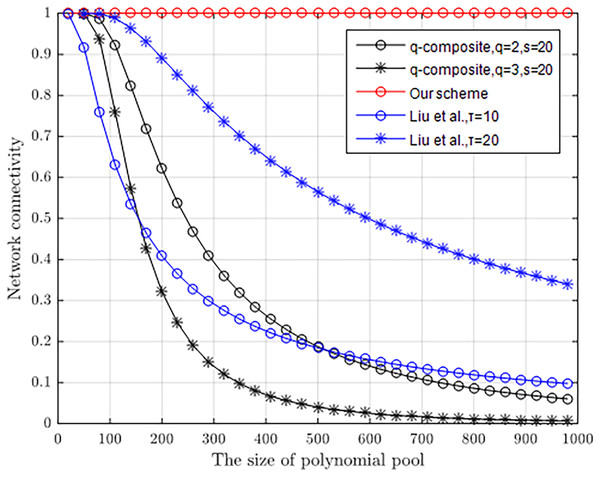
A higher connectivity rate of the node network can increase the communication efficiency of the node and reduce the loss of communication energy. Figure 8 compares the network connectivity of the proposed scheme with that of Liu, Ning & Li (2003) and q-composite (Chan, Perrig & Song, 2003). In the simulation, we assume that the q-composite preloaded s = 50 keys in each sensor, and τ = 10 and τ = 20 polynomials in Liu, Ning & Li (2003) are preloaded in each node. The result illustrates that the proposed scheme has 100% connectivity regardless of the size of polynomial pool.

Table 3 in more detail shows that our scheme offers a better connectivity rate of nodes than the other three schemes, and inherits that every node in a sensor network is able to establish a connection in Blundo et al. (1998). When three polynomials are selected from one polynomial pool holding 25 polynomials, about 33.0% of nodes in Liu, Ning & Li (2003) are connected. However, when still remaining 34.6% of nodes are connected, Liu, Ning & Li (2003) should select two polynomials from a polynomial pool with 11 polynomials. In q-composite (q = 2) (Chan, Perrig & Song, 2003), when 20 keys are selected from one key pool holding 340 keys, about 33.2% of nodes are connected. However, when still remaining 32.0% of nodes are connected, the q-composite (q = 3) scheme (Chan, Perrig & Song, 2003) should scale down the key pool size to 200. When three polynomials are selected from one polynomial pool holding 18 polynomials, about 57.8% of nodes in Zhang, Li & Li (2018) are connected. However, when two polynomials are selected from the same polynomial pool, only about 31.8% of nodes in Zhang, Li & Li (2018) are connected.

Table 3:

Comparison of connectivity among various schemes.

Scheme	Connectivity P
q-composite (Chan, Perrig & Song, 2003) (q = 2, s = 20, |S| = 340)	0.332
q-composite (Chan, Perrig & Song, 2003) (q = 3, s = 20, |S| = 200)	0.320
Blundo et al. (1998) (λ = 18)	1
Blundo et al. (1998) (λ = 19)	1
Li et al. (2020) (λ = 18, τ = 2, |ω| = 11)	0.346
Li et al. (2020) (λ = 18, τ = 3, |ω| = 25)	0.330
Zhang, Li & Li (2018) (λ = 18, τ = 2, s =12, |ω| = 18, N = 200)	0.318
Zhang, Li & Li (2018) (λ = 18, τ = 3, s = 23, |ω| = 18, N = 200)	0.578
Our scheme (t = 2, λ = 3)	1
Our scheme (t = 3, λ = 7)	1

DOI: 10.7717/peerj-cs.1726/table-3

Resource overhead

We selected several classic key management solutions for comparative study from the aspects of communication, computation, and storage overhead. For convenience, we only consider the polynomial P(x,y) cost. The l_k represents the length of key. we assume that each generated key takes the same storage as the coefficient of a λ-degree polynomial. l_ID is the length of a node or key identifier. We assume that the node and key identifiers have the same length. τ are the number of polynomials selected for each node in Liu, Ning & Li (2003) and Zhang, Li & Li (2018). s is the number of keys preloaded in each sensor.

We estimate the computation, communication, and storage energy consumed by constrained nodes during pairwise key establishment. Owing to selecting a set of polynomials from a polynomial pool, we use the same amount of polynomials for Liu, Ning & Li (2003) and Zhang, Li & Li (2018) per node. There are the same λ-degree for a polynomial for the four schemes. Table 4 lists the comparative study in resource overheads.

Table 4:

Comparative study in resource overheads.

Scheme	Storage overhead	Communication overhead	Computational overhead
Blundo et al. (1998)	(λ+1)lk + lID	lID	λ+1
Liu, Ning & Li (2003)	[τ(λ+1)]lk + (τ+1)lID	(τ+1)lID	λ+1
Zhang, Li & Li (2018)	[s+τ(λ+1)]lk + (2s+τ+1)lID	(2s+τ+1)lID	λ+1
Our scheme	(λ+1)2 lk + lID	lID	λ+1

DOI: 10.7717/peerj-cs.1726/table-4

Computational overhead

The key management schemes with polynomials rely on the existence of the same polynomial between two nodes. In other words, the polynomial has an important impact on the computation cost in nodes, when the pairwise key is established. To evaluate the computational cost, we mainly consider the number of calculations in polynomial. Table 5 lists the computational overhead of the comparative study, which shows that these four schemes have the same consumption in computation. In fact, although these schemes owe the same computational overhead, our scheme has better advantages in applying to some field environments compared with the other three schemes, with better resilience against node capture and lower storage overhead.

Table 5:

Computational overhead of comparative study.

Scheme	Blundo et al. (1998)	Liu, Ning & Li (2003)	Zhang, Li & Li (2018)	Our scheme
Computational overhead	λ+1	λ+1	λ+1	λ+1

DOI: 10.7717/peerj-cs.1726/table-5

Communication overhead

The information exchange of wireless sensor networks relies on the emission of electromagnetic waves, which depletes much energy carried by nodes. In other words, energy cost in communication is significantly impacted by the length of communication message and the number of data packets. The longer the data length, the more energy in communication is consumed. These schemes mainly send the identities of the node, the identities of the secret key and the identities of the polynomial when the pairwise key is established. τ is the number of polynomials selected for each node. Table 6 lists the communication overhead of the comparative study, where $s={\displaystyle \frac{1}{2}\tau }$.

Table 6:

Communication overhead of comparative study.

Scheme	Blundo et al. (1998)	Liu, Ning & Li (2003)	Zhang, Li & Li (2018)	Our scheme
Communication overhead	lID	(τ+1)lID	(2τ+1)lID	lID

DOI: 10.7717/peerj-cs.1726/table-6

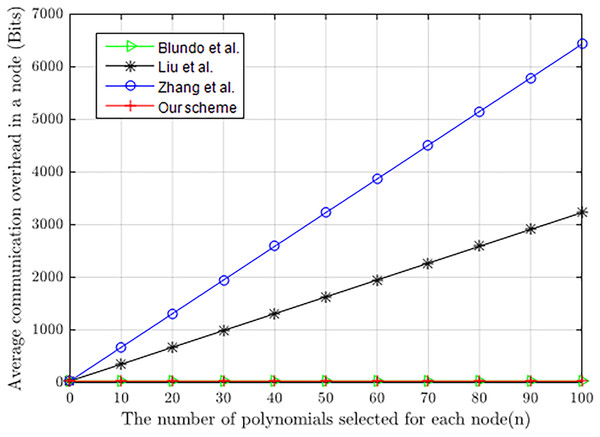
Note that both l_k and l_ID are 32 bits. Figure 9 shows the comparison in communication consumption of our scheme with Blundo et al. (1998), Liu, Ning & Li (2003) and Zhang, Li & Li (2018), where the loss of energy in communication is represented by the length of information (bits). The figure clearly illustrates that the communication cost of our scheme is significantly lower than in Zhang, Li & Li (2018) and Liu, Ning & Li (2003), and equal to Blundo et al. (1998) during pairwise key establishment. As we know, our scheme, similar to Blundo et al. (1998), only needs nodes to pass their own identities to each other, which improves communication efficiency and reduces the energy consumption of nodes in communication.

Storage overhead

Sensor nodes are highly constrained in terms of memory resources. When designing a key management scheme, we should reduce the memory overhead of nodes as much as possible. The storage overhead this scheme depends on the cost of the nodes’ dentities, the coefficients of the λ-degree polynomials and the dentities of polynomials, where l_k = log₂ q. Table 7 lists the storage overhead of the comparative study, in which τ = 50, s = 25.

Table 7:

Storage overhead of comparative study.

Scheme	Blundo et al. (1998)	Liu, Ning & Li (2003)	Zhang, Li & Li (2018)	Our scheme
Storage overhead	(λ+1)lk +lID	50(λ+1)lk+51lID	[25+50(λ+1)]lk+101lID	(λ+1)2 lk +lID

DOI: 10.7717/peerj-cs.1726/table-7

Note:

s = 25

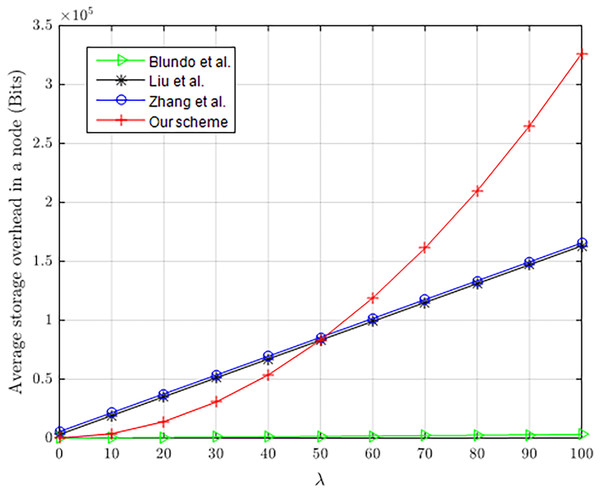
Assume that both l_k and l_ID are 32 bits. Figure 10 shows the comparison in memory consumption (bits) of our scheme with Blundo et al. (1998), Liu, Ning & Li (2003) and Zhang, Li & Li (2018), which clearly shows the advantage of our scheme to some extent. As the λ no more than 50, the storage cost in our scheme is much smaller than in Zhang, Li & Li (2018) and Liu, Ning & Li (2003) during pairwise key establishment. The storage overhead in our scheme remains stable, not changing with the number of nodes. In fact, with a small λ, our scheme can still hold a large number of nodes and maintain better resilience to node capture. Our scheme, when λ = 3, can hold 5.53 × 10¹⁹ nodes in a network. However, Liu, Ning & Li (2003) (λ = 18, τ = 3, |ω| = 25) is only able to hold 158 nodes in a network. When 1.0 × 10⁸ nodes are captured in a network, the capture rate of communication links in non-compromised nodes is still nearly close to 0. Therefore, our scheme has greater advantages in applying to large-scale networks, not only with lower storage overhead but also resilience to node capture attacks.

Conclusions

We proposed a key management scheme with a dynamic coefficient symmetric polynomial. The scheme allows every pair of communicating nodes to use their own IDs to map into the elements of the shared matrix M and assigns these elements to polynomial $P(x,y)$ to establish pairwise keys. Different from other schemes, ours deterministically configures a different polynomial for each pair of communicating nodes by an identity mapping algorithm. This enables a high connectivity rate and solves the λ-secure problem of key management, when no hash collision occurs. Security analysis shows that the proposed scheme has stronger resilience to node capture from various types of attacks. It consumes less energy in storage and communication than other protocols.

Supplemental Information