Selection of suitable wheat genotypes under thermal stress and complex genotype-environment interaction using stability analyses and selection indices

Experiment description

Experimental material: Twenty wheat genotypes were chosen (DHL12 (G01), DHL02 (G02), DHL25 (G03), DHL07 (G04), DHL26 (G05), Gemmeiza-9 (G06), DHL11 (G07), KSU106 (G08), Gemmeiza-12 (G09), DHL01 (G10), DHL14 (G11), DHL29 (G12), DHL15 (G13), DHL06 (G14), Misr1 (G15), DHL05 (G16), DHL23 (G17), Sakha-93 (G18), Pavone-76 (G19) and DHL08 (G20)), the pedigree for these genotypes is listed in Table S1. Environment description: The experiment was conducted for three seasons from 2018/19 to 2020/21 at the King Saud University Agricultural Research Station (24°42’N, 44°46’E, 400 m asl), with a total of six experiments/environments (ENVs), the environments (optimal conditions (OC) and thermal stress conditions (TSC)) were separated (Table 1). Each environment for twenty genotypes was three-repeated in a randomized complete block design. Plot area, texture soil type, seedling rate, fertilizer rates and the timing of their application, and meteorological conditions (Table S2) as detailed in earlier studies (Al-Ashkar et al., 2022; Al-Ashkar et al., 2023c).

Measurements

To measure differences between the 20 genotypes used under (OC and TSC), the grain yield (GY, ton ha⁻¹) trait was valuated after harvest from yield three rows two m long. The GY data had been used to assess heat tolerance indices according to the subsequent mathematical formulas presented by Bennani et al. (2017) and Lamba et al. (2023). TOL_{stress tolerance} = GY_oc − GY_tsc, STI${}_{\mathrm{stress tolerance index}}=\left({\mathrm{GY}}_{\mathrm{oc}}\times \mathrm{G}{\mathrm{Y}}_{\mathrm{tsc}}\right)/{\overline{x}}_{\mathrm{tsc}}^2$, STI${}_{\mathrm{m}\mathrm{modified stress tolerance index}}=\left[\left(\Sigma G{\mathrm{Y}}_{\mathrm{tsc}}^2/\Sigma {\overline{\mathrm{GY}}}_{\mathrm{tsc}}^2\right)\times \mathrm{STI}\right]$, SSI${}_{\mathrm{stress susceptibility index}}=\left[\left(1-\left({\mathrm{GY}}_{\mathrm{tsc}}/\mathrm{G}{\mathrm{Y}}_{\mathrm{tsc}}\right)\right)/\left(1-\left({\overline{x}}_{\mathrm{tsc}}/{\overline{x}}_{\mathrm{oc}}\right)\right)\right]$, SSPI${}_{\mathrm{stress susceptibility percentage index}}=\left[\left({\mathrm{GY}}_{\mathrm{oc}}-{\mathrm{GY}}_{\mathrm{tsc}}/2{\overline{x}}_{\mathrm{oc}}\right)\times 100\right]$, YI${}_{\mathrm{yield index}}=\left[G{\mathrm{Y}}_{\mathrm{tsc}}/{\overline{x}}_{oc}\right]$, YSI_{yield stability index} = [GY_tsc/GY_oc], RDI${}_{\mathrm{relative drought index}}=\left[\left({\mathrm{GY}}_{\mathrm{tsc}}/\mathrm{G}{\mathrm{Y}}_{\mathrm{oc}}\right)/\left({\overline{x}}_{\mathrm{tsc}}/{\overline{x}}_{\mathrm{oc}}\right)\right]$, MP_{mean productivity} = [(GY_oc + GY_tsc)/2], GMP${}_{\mathrm{geometric mean productivity}}=\left[\sqrt{}\left({\mathrm{GY}}_{\mathrm{oc}}\times {\mathrm{GY}}_{\mathrm{tsc}}\right)\right]$, HM_{harmonic mean} = 2[(GY_oc × GY_tsc)/(GY_oc + GY_tsc)], MRP${}_{\mathrm{mean relative performance}}=\left[\left({\mathrm{GY}}_{\mathrm{tsc}}/{\overline{x}}_{\mathrm{tsc}}\right)+\left(\mathrm{G}{\mathrm{Y}}_{\mathrm{tsc}}/{\overline{x}}_{\mathrm{oc}}\right)\right]$, PYR_{percent yield reduction} = [((GY_oc − GY_tsc)/GY_oc) × 100], REI${}_{\mathrm{relative efficiency index}}=\left({\mathrm{GY}}_{\mathrm{tsc}}/{\overline{x}}_{\mathrm{tsc}}\right)\times \left(\mathrm{G}{\mathrm{Y}}_{\mathrm{oc}}/{\overline{x}}_{\mathrm{oc}}\right)$, ATI${}_{\mathrm{abiotic tolerance index}}=\left({\mathrm{GY}}_{\mathrm{oc}}-{\mathrm{GY}}_{\mathrm{tsc}}\right)/\left({\overline{x}}_{\mathrm{oc}}/{\overline{x}}_{\mathrm{tsc}}\right)\times \sqrt{\left(\text{(}{\mathrm{GY}}_{\mathrm{oc}}\times {\mathrm{GY}}_{\mathrm{tsc}}\right)}$, SNPI${}_{\mathrm{stress/non-stress production index}}=\left[\sqrt[3]{\left({\mathrm{GY}}_{\mathrm{oc}}+{\mathrm{GY}}_{\mathrm{tsc}}\right)/\left({\mathrm{GY}}_{\mathrm{oc}}-{\mathrm{GY}}_{\mathrm{tsc}}\right)}\right]\times \left[\sqrt[3]{\left({\mathrm{GY}}_{\mathrm{oc}}\times {\mathrm{GY}}_{\mathrm{tsc}}\times \mathrm{G}{\mathrm{Y}}_{\mathrm{tsc}}\right)}\right]$, SWPI${}_{\mathrm{stress-weighted performance index}}=\sqrt{{\mathrm{GY}}_{\mathrm{oc}}}/{\mathrm{GY}}_{\mathrm{tsc}}$ and RSC_{relative stress change} = ((GY_oc − GY_tsc)/GY_oc) × 100, where GY_oc and GY_tsc are the GY of genotypes, while ${\overline{x}}_{\mathrm{oc}}$ and ${\overline{x}}_{\mathrm{tsc}}$ are the overall mean GY under optimal conditions (oc) and thermal stress conditions (tsc), respectively.

Statistical analyses

The variance components were appreciated by restricted maximum likelihood (REML) as described by Dempster, Laird & Rubin (1977). To evaluate the significance of the random effects, a likelihood ratio test (LRT) was performed involving comparing two models (one that included all random terms and another that excluded one of these terms), utilizing a chi-square (χ²) test for the comparison. Eight parameters were calculated as described by Sampaio Filho et al. (2023):

• Heritability_{expected mean square} (h²_ems)$=\left({\sigma }_{\mathrm{gen}}^2\right)/\left({\sigma }_{\mathrm{gen}}^2+\frac{{\sigma }_{\mathrm{gen}:\mathrm{env}}^2}{\mathrm{b}}+{\sigma }_{\mathrm{res}}^2\right)$

• Heritability_plot mean (h²_pm) $=\left({\sigma }_{\mathrm{gen}}^2\right)/\left({\sigma }_{\mathrm{gen}}^2+\frac{{\sigma }_{\mathrm{gen}:\mathrm{env}}^2}{\mathrm{b}\times \mathrm{env}}+\frac{{\sigma }_{\mathrm{res}}^2}{\mathrm{b}\times \mathrm{env}}\right)$

• Accuracy = $\sqrt{h_{pm}^2}$

• Coefficient of determination_{GEN:ENV effects} (R²) = $\left({\sigma }_{\mathrm{gen}:\mathrm{env}}^2\right)/\left({\sigma }_{\mathrm{gen}}^2+{\sigma }_{\mathrm{gen}:\mathrm{env}}^2+{\sigma }_{\mathrm{res}}^2\right)$

• Coefficient of variation_genotypic (CV_gen) = $\sqrt{{\sigma }_{gen}^2/\overline{\mathrm{x}}}\times$ 100

• Coefficient of variation_residual (CV_res) = $\sqrt{{\sigma }_{res}^2/\overline{\mathrm{x}}}\times$ 100

• CV ratio = Cv_gen/Cv_res

• Correlation_{genotype−environment} (r_gen:env) $=\left({\sigma }_{\mathrm{gen}}^2\right)/\left({\sigma }_{\mathrm{gen}}^2+{\sigma }_{\mathrm{gen}:\mathrm{env}}^2\right)$

where ${\sigma }_{\mathrm{gen}}^2$, ${\sigma }_{\mathrm{gen}:\mathrm{env}}^2$ and ${\sigma }_{\mathrm{res}}^2$ signify the variances of genotypic, genotype × environment, and residual (error), respectively; b and env signify the blocks number and environments respectively $\overline{\mathrm{x}}$ is the overall mean.

Data of GY trait from six ENVs underwent a variety of analyses for estimating genetic stability—AMMI analysis (AMMI-ANOVA and AMMI biplots; AMMI’s model was employed to assess multiplicative effects and identify stable genotypes), Joint regression model, stability indexes, and WAAS biplot). Data of selection indices generated by GY under optimal and thermal stress conditions underwent a variety of analyses for estimating relationships between the various indices, including genetic (rg) and phenotypic (rp) correlations, genetic parameters, and MGIDI index. All statistics analyses and biplots were created by RStudio packages (R version 4.3.3; R Core Team, 2023). The metan R package was used as per Olivoto, Lúcio & Jarman (2020). Selection indices were computed to the mathematical formulas by Microsoft Excel 2019.

The variance in wheat grain yield

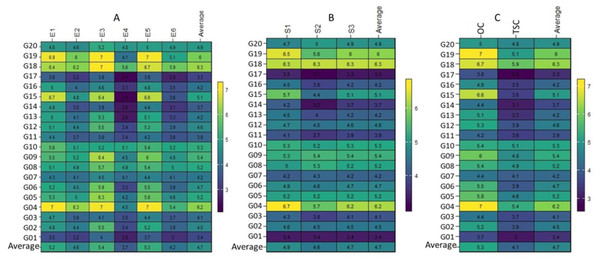
This conclusion was strengthened by the range in the performance of the genotypes assessed, which varied for optimum conditions from 3.5 (t ha⁻¹) (G01 in E1) to 7.0 (t ha⁻¹) (G04 in E1), (G04, G18 and G19 in E3) and (G04, and G19 in E5). The G01 genotype showed the minimum performance at one place (E1). In contrast, the G04 genotype showed the maximum performance at the three ENVs (E1, E3, and E5). In every optimum condition, genotype G04 performed best (Fig. 1A). Under thermal stress values, they varied from 2.4 (t ha⁻¹) (G15 and G17 in E4) to 6.3 (t ha⁻¹) (G04 in E2). The G15 and G17 genotypes showed the lowest performance at one place (E4), whereas the G04 genotype showed the highest performance at one place (E2) (Fig. 1A). The performance of the genotypes in the three seasons varied from 3.1 (t ha⁻¹) (G17 in S2) to 6.7 (t ha⁻¹) (G04 in S1), and genotypes G04 or G18 performed best in the three seasons and the average (Fig. 1B). In the case of treatments, the values ranged from 3.7 (t ha⁻¹) in (G04) to 7.0 (t ha⁻¹) in (G04 and G17) under OC, and ranged from 2.8 (t ha⁻¹) in (G17) to 5.9 (t ha⁻¹) in (G18) under TSC. In the two cases, genotypes G04 and G18 grossed the most (Fig. 1C).

Joint ANOVA and AMMI model analyses for grain yield

The joint analysis of variance (ANOVA) and AMMI model for the six environments is shown in Table 2. The joint ANOVA determined that the GEN, ENV, and GEN: ENV were highly significant (Table 2), given that GEN: ENV significantly impacts GY. IPCA [1] and IPCA [2] were determined to be significant, and there was an inequality between ENVs for genotype classifications. The best-predicted AMMI model was with two IPCs, the first two components were significant and accounted for 84.90% and 14.10% of the GEN: ENV, respectively, for six ENVs at the 0.001 probability level.

Joint regression model of stability analysis

The joint regression model (Eberhart & Russell, 1966) detected highly significant differences by a pooled ANOVA for all model effects (Table 3). The mean GY ranged between 3.30 (G17) to 6.31 (G18), with an average of 4.72 t ha⁻¹. The stability analysis parameter (bi) noted no genotype had bi = 1 and S²di = 0. The genotypes G05 and G09 had b_i values close to 1 indicating that they are more stable under every six ENVs (Table 3). Genotypes G04 (µ= 6.20, bi = 1.51***, S²di = 0.042***), G06 (µ= 4.74, bi = 1.420***, S²di = 0.011), G12 (µ= 4.59, bi = 1.240***, S²di = −0.008), G13 (µ= 4.24, bi = 1.610***, S²di = −0.014), G15 (µ= 5.07, bi = 2.650***, S²di = 0.053***) and G19 (µ= 6.04, bi = 1.750***, S²di = 0.020) were observed to be stable in optimal (ENV1, ENV3 and ENV5) conditions (Table 3), whereas for genotypes G08 (µ= 5.20, bi = 0.393**, S²di = 0.031*), G10 (µ= 5.25, bi = 0.161**, S²di = 0.017), and G18 (µ= 6.31, bi = 0.735**, S²di = 0.019), high means with bi values less than 1 indicate that these genotypes show more resilience to unfavorable environments as thermal stress (ENV2, ENV4 and ENV6) were observed. The root mean square error (RMSE) is used to evaluate the prediction quality, which ranged between 0.021 (G17) and 0.327 (G14), while R² values ranged between 0.265 (G20) and 0.999 (G13 and G17).

Stability indexes of evaluated genotypes

The Annicchiarico method measures genotypic stability, which received the top rank for genotypes G19, G04, G18, and G15 of analysis favorable environment, genotypes G18, G04, G10, and G19 of analysis unfavorable environment, and genotypes G18, G04, G19, and G09 of general analysis (Table 4). Shukla’s rank-sum method integrates mean performance and stability into a unified selection criterion, which revealed that the top four ranks were for genotypes (G17, G12, G02, and G16), which matched in ranking with Wricke’s (1962) ecovalence. The AMMI-based stability parameter (ASTAB) computes by significant interaction principal components (IPCs) in the AMMI model, which revealed that the top four ranks were genotypes G17, G12, G01, and G02. AMMI Stability Index (ASI), AMMI-stability value (ASV), modified AMMI Stability Index (MASI), modified AMMI Stability value (MASV), and weighted average of absolute scores (WAAS) were matched in ranking genotypes, which received the top four genotypes G17, G05, G09, and G16. Annicchiarico’s D parameter values (DA) and stability measure based on fitted AMMI model (FA) were matched in ranking genotypes, which received the top four genotypes G17, G12, G02, and G16. Zhang’s D parameter (DZ) and sums of the averages of the squared eigenvector values (EV) were matched in ranking genotypes, which received the top four genotypes G17, G12, G01, and G18. Sums of the absolute value of the IPC Scores (SIPC), which received the top four genotypes G17, G12, G02, and G05. WAASY (the index that considers the weights for stability and productivity in the genotype ranking) received the top four genotypes G18, G09, G04, and G05 (Table 4).

Analyses biplots

AMMI biplot

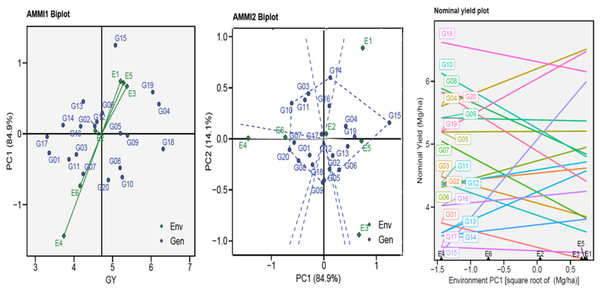
The AMMI biplots (GGE biplots) were used to visually the yield potential (GY) of the twenty genotypes in six environments by describing the relationship between the genotypes and six environments vs. IPC1 (Fig. 2). The AMMI1 biplot indicated that the one ENV4 (E4) was beyond their sources and had a longer vector, pointing to a higher interaction, while the five other ENVs had a shorter vector and were closer to their source point to a lower interaction. The non-stressful environments (E1, E3, and E5) had an angle between the vectors mostly less than 90°, pointing to positive correlations, and the heat-stress environments (E2, E4, and E6) gave themselves similar results. This suggests that when applied under comparable conditions, the genotype–environment interactions (GEI) effects are often given within the same range. The AMMI2 biplot indicated that IPCA1 and IPCA2 described a combined variance of 99.00%. Figure 2 shows the GEI volume with the ENV type by the vertical projection from the GEN to the ENV vector. Accordingly, the genotypes might be viewed (G03, G05, G06, G08, G09, G10, G14, G15, and G20) as unstable in environments used. Using the AMMI biplot (generic genotypic adaptation) map (nominal plot) for genotypes. The adaptation map showed that G05, G09, and G17 were more suited, and exhibited identical performance in all environments. Although they vary from environment to environment, G15 performed best in E1, unlike G10 and G20 performance of the least in E1. The G02, G11, and G16 exhibited reduced GEI.

WAAS biplot

To gain a more thorough and improved yield characterization (genotypes/environment), the WAASB analyses were utilized in selecting genotypes based on performance and stability (Fig. 3). Sector-I contains unstable genotypes with significant contributions to GEI and high distinction capacity, Sector-II contains unstable but highly productive genotypes where environments significantly influence GEI, Sector-III contains genotypes adopted on a larger scale with lower performance than average, indicating stable genotype performance across environments due to reduced WAASB values and Sector-IV contains genotypes with high performance and stability. For this, the G04, G05, G06, G09, and G18 genotypes were chosen for GY as perfect genotypes (Fig. 3). The genotype ranking (WAASBY) based on the weights of the stability (WAASB) and mean performance (Y) considering weights of 50 and 50 for GY, for the mean performance trait and WAASB (Fig. 3). Building on the number of IPCAs used in the WAASB assessment, the heatmap was used to show the genotype ranking of stable individuals (Fig. 3). The genotype’s relative ranking is demonstrated by the color (intensity or hue), where higher ranks are represented by darker hues and lower rankings by lighter hues. Three IPCAs for traits were particularly noticeable, and the genotype ranking was modified by the IPCAs utilized in the WAASB assessment. Using genotype colors, it is easy to identify the groups with the same performance levels and stability (Fig. 3). The genotypes G01, G02, G03, G04, G05, G06, and G09 showed the lowest WAASB values (so were more stable), genotypes gathered in the same cluster (based on one or more IPCAs).

Heat tolerance indices in GY trait

Variance components of indices traits

The LRT exhibited highly significant (p < 0.001) for all indices for both GEN and GEN: ENV, except for the SNPI index (Table 6). The variance components exhibited great variation between indices, the genotypic variance exhibited the highest value for the MP index and the lowest value for the SNPI index. The GEN: ENV exhibited the highest value for the RDI index and the lowest value for the SNPI index, and the residual exhibited the highest value for the SNPI index and the lowest value for the YI index. h²_ems showed mixed heritability values, in which most indices were more than 0.60, except for the RDI index (0.53), and the SNPI index is very low (0.18). The h²mg exhibited more value compared to h²_ems for all indices. The accuracy exhibited a high value for all indices (>81.00%). The coefficient of variation (CVs) (g/r) ratio was greater than 1, except for the SNPI index. The r_gen:env showed high values for all indices, which shows that the genotypic effect plays a major role in their inheritance, except for GY_oc and SNPI indices.

Factor identifying and selection of heat-tolerant genotypes

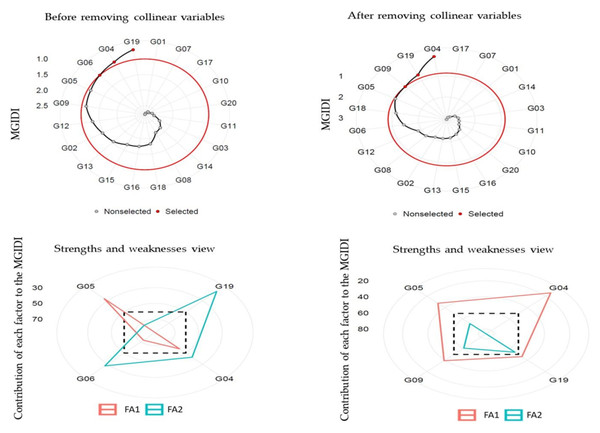
Principal component analysis (PCA) stated that the first two components (eigenvalue >1) illustrated 94.30% (before removing) and 87.80% (after removing) collinear variables of the cumulative variation among the 20 and 7 studied variables, respectively (Table 7). Before removing, FA illustrated that ten variables GY_oc, GY_tsc, STI, STI_m, YI, MP, GMP, HM, MRP, and REI were settling in FA1; and the remaining ten variables stress tolerance (TOL), SSPI, SSI, yield stability index (YSI), RDI, PYR, SWP, RSC, ATI and SNPI were settling in FA2. After removing variables, FA illustrated that four variables YSI, PYR, RSC, and SNPI were settling in FA1, and three variables STI, STI_m and GMP were settling in FA2. The MGIDI index was used to identify the ideotype heat-tolerant after and before removing collinear. The selection gains (MGIDI index) before removing revealed that 13 out of 20 variables were desired gains, and four out of seven after removing collinear variables. The results illustrated that MGIDI showed higher total gains of 345.96 and 106.54 for variables that increased and −5.78 and −1.757 for variables that decreased before and after removing variables, respectively (Table 8). The abiotic tolerance index (ATI), REI, and SSPI illustrated the highest genetic gains (43.90%, 33.00%, and 26.10%, respectively) before removing variables, but after removing variables were STI_m (40.100) and GMP (19.50). The MGIDI index of the original population (Xo) before and after removing variables varied from 0.229 and 0.846 (the lowest one), for the ATI and STI to 339.00 (the highest one) for the STI_m, respectively (Table 8). The genotypes selected using the MGIDI were G04, G05, G06, and G19 before removing variables and they were G04, G05, G09, and G19 after removing variables (Fig. 4). The G05 was very close to the cutting point before and after removing variables. The strengths and weaknesses illustrated that before removing variables, FA1 had the highest contribution for G04, G06 and G19. FA2 had the highest contribution for G05 (Fig. 4). But after removing variables, FA2 had the highest contribution for the four genotypes, while FA1 didn’t have any contributions.