Applying stacking ensemble method to predict chronic kidney disease progression in Chinese population based on laboratory information system: a retrospective study
Author and article information
Abstract
Background and Objective
Chronic kidney disease (CKD) is a major public health issue, and accurate prediction of the progression of kidney failure is critical for clinical decision-making and helps improve patient outcomes. As such, we aimed to develop and externally validate a machine-learned model to predict the progression of CKD using common laboratory variables, demographic characteristics, and an electronic health records database.
Methods
We developed a predictive model using longitudinal clinical data from a single center for Chinese CKD patients. The cohort included 987 patients who were followed up for more than 24 months. Fifty-three laboratory features were considered for inclusion in the model. The primary outcome in our study was an estimated glomerular filtration rate ≤15 mL/min/1.73 m2 or kidney failure. Machine learning algorithms were applied to the modeling dataset (n = 296), and an external dataset (n = 71) was used for model validation. We assessed model discrimination via area under the curve (AUC) values, accuracy, sensitivity, specificity, positive predictive value, negative predictive value, and F1 score.
Results
Over a median follow-up period of 3.75 years, 148 patients experienced kidney failure. The optimal model was based on stacking different classifier algorithms with six laboratory features, including 24-h urine protein, potassium, glucose, urea, prealbumin and total protein. The model had considerable predictive power, with AUC values of 0.896 and 0.771 in the validation and external datasets, respectively. This model also accurately predicted the progression of renal function in patients over different follow-up periods after their initial assessment.
Conclusions
A prediction model that leverages routinely collected laboratory features in the Chinese population can accurately identify patients with CKD at high risk of progressing to kidney failure. An online version of the model can be easily and quickly applied in clinical management and treatment.
Cite this as
2024. Applying stacking ensemble method to predict chronic kidney disease progression in Chinese population based on laboratory information system: a retrospective study. PeerJ 12:e18436 https://doi.org/10.7717/peerj.18436Main article text
Introduction
Chronic kidney disease (CKD) is a worldwide clinical and public health problem that is associated with major adverse health events, including kidney failure, cardiovascular disease, and mortality. It leads to poor quality of life and high costs of treatment (Luyckx et al., 2023). In China, CKD is integrated into the national public health surveillance program. The subgroups with a greater incidence of CKD included older age, female, sex, non-Han ethnic background, and living in rural areas or in the northern and central regions of China (Wang et al., 2023). Over the past 20 years, the number of CKD-related deaths has increased by 82.3% worldwide, especially for CKD stages 4 and 5 (Bello et al., 2017). Early identification of patients who may develop renal dysfunction in the future and proper management of CKD and its risk factors are crucial for slowing the progression of the disease. It can effectively reduce progression to end-stage renal disease (ESRD) and cardiovascular mortality and reduce the economic burden of CKD.
Currently, several clinically reliable biomarkers are available to predict progressive CKD. Traditional kidney biomarkers, such as serum creatinine and proteinuria, have many well-recognized limitations, including a lack of specificity and sensitivity in predicting a decline in renal function and delayed detection of kidney injury. Studies employing new technologies have focused on identifying structural markers of kidney tubular and glomerular injury in urine or blood, but these biomarkers are not available or affordable in clinical practice (Owens et al., 2022). Multiple risk factors for CKD have been identified, including older age, diabetes mellitus, hypertension, proteinuria, hyperuricemia and hyperphosphatemia (Kawasoe et al., 2023; Samanta, Bandyopadhyay & Samanta, 2023). Establishing renal prognostic prediction models based on the evaluations of these variables is a hot and difficult issue in current research. It may be helpful and convenient to identify those at high risk who may benefit from more intensive management, reduce progression to ESKD and cardiovascular mortality, and, eventually, improve health system efficiency. Several studies have developed models for predicting worse clinical outcomes in CKD patients. Tangri et al. (2011) developed kidney failure risk equations (KFREs) that can accurately predict the progression to kidney failure. Kawasoe et al. (2023) performed multivariable logistic regression analysis and assigned scores to each clinical factor to predict CKD. However, this equation differs in the target population’s ethnicity and CKD risk factors, and the factors associated with CKD development vary by race (Harada et al., 2022; Nelson et al., 2019). We need a unique Chinese predictive model for CKD progression to identify high-risk patients in the Chinese population. Additionally, CKD is generally managed by primary care physicians in China. The development of convenient and clinically useful tools for identifying high-risk CKD patients and providing appropriate counseling where clinical resources are limited is vital.
More recently, machine learning (ML) approaches have shown excellent ability to identify variables relevant to clinical outcomes, predict better performance, model complex relationships better, and overcome the limitations of expert systems. A strong growth of diagnostic equations for which ML algorithms are designed. Xiao et al. (2019) developed diagnostic models by deep neural networks to quickly predict the severity of CKD based on more easily available demographic and blood biochemical features instead of urinary protein and showed good predictive ability. For the prediction and risk stratification of kidney outcomes, Chen et al. (2019) used the extreme gradient boosting (XGBoost) algorithm to select the 10 most important variables and established a prediction model that can stratify the risk for kidney disease progression in the setting of IgAN. However, the risk stratification system is specific to IgA and cannot be generalized or applied to other types of kidney disease (Chen et al., 2019). Ferguson et al. (2022) reported that random forest algorithms can predict estimated glomerular filtration rate (eGFR) decline or kidney failure accurately. Nevertheless, the model involves 22 variables; from a clinical point of view, although a complex scoring system may provide accurate predictions, it is inconvenient in daily clinical practice. Furthermore, it was targeted at CKD stages G1 to G5, which is generally too wide, and it is too early to plan possible dialysis sessions since the G1 stage (Ferguson et al., 2022). Recently, researchers have focused more on the performance of ensemble learning in medicine than on the performance of a single ML algorithm (Li et al., 2024). Stacking is a powerful method for integrating different types of base learners and is rarely used in CKD prediction.
In this study, we developed an accurate but simple online prediction model based on stacking methods using a new dataset from the Chinese CKD population with long-term follow-up and evaluated its validity in an external validation set. The aim was to use variables routinely measured in patients with CKD to create an online calculator to predict progression to kidney failure that could be easily and quickly applied in clinical diagnosis and treatment. The model can be generalized to assist clinicians in managing CKD in primary hospitals in China.
Materials and Methods
Study population
We conducted a single-center, retrospective study using the laboratory information systems (LIS) database and electronic health records (EHR) database from Peking University First Hospital. Development and validation of prediction models using demographic, clinical, and laboratory data from patients with CKD stages 3 to 5 (eGFR between 30 and 60 ml min−1 (1.73 m)2) who were referred to nephrologists between January 1, 2018, and December 31, 2021, and had at least 24 months of follow-up. The outcome of ESRD was defined as an eGFR < 15 mL/min/1.73 m2 for more than two times or the initiation of dialysis or transplantation. The eGFR was calculated via the CKD-EPI creatinine equation. Participants were excluded if they (1) were younger than 18 years old, (2) were pregnant, (3) had a history of kidney failure (dialysis or transplant), or (4) had missing data. Finally, according to the above inclusion and exclusion criteria, the data of 987 participants were analyzed, among which 148 patients reached the endpoint. A total of 148 progressive CKD patients and 148 nonprogressive CKD patients were ultimately included via propensity score matching (PSM) based on age and sex. The ML model was further evaluated on an external test dataset. An external test dataset was also collected from Peking University First Hospital from January 1, 2018, to December 31, 2021; this dataset had at least 12 months of follow-up and followed the same inclusion and exclusion criteria as the internal dataset. Our study was reviewed and approved by the Clinical Ethics Review Committee of Peking University First Hospital (Ethical Application Ref: 2024Yan237-002). All participants consented to use their de-identified data and access to electronic health records and laboratory information systems. The participants signed the informed consent form.
Data collection
The clinical parameters extracted from the LIS and EHR databases included demographic information, primary renal disease, and laboratory tests. The included patients were required to have complete demographic information on age, sex, body mass index (BMI), systolic pressure, diastolic pressure and comorbid conditions, such as diabetes, hypertension, anemia and cardiovascular disease. These parameters were collected on the date of the first eGFR. Based on the LIS system, we identified common follow-up indicators for CKD patients. Through an extensive literature search and discussion with experts in this area, 53 potential features were ultimately identified, which are as follows: (1) hematologic indices, such as white blood cell count, mean corpuscular hemoglobin concentration, lymphocyte count, and blood platelet count; (2) biochemical indices, such as uric acid (UA), urea, glucose, and total protein (TP); and the urine index, 24-h urine protein (24 hrUpr). These biomarker measurements were taken at the time of the patient’s baseline eGFR measurement or ≤7 days before or after the baseline eGFR measurement in an individual patient.
Statistical analysis
PSM is a commonly used statistical method that eliminates confounding bias from observational cohorts where the benefit of randomization is impossible owing to a smaller sample size. It attempts to balance covariates and reduce bias by matching exposure subjects with control subjects who exhibit a similar propensity based on preexisting covariates. A new control group was established by removing outlier control subjects, thus reducing the unwanted effects of covariates and allowing for proper measurement of the expected variable (Kane et al., 2020). Therefore, PSM was applied to balance the distribution of covariates (age and sex) between the progressive and non-progressive CKD groups.
Continuous variables are expressed as the means ± standard deviations (SDs) for normally distributed variables or medians with interquartile ranges (IQRs) for nonnormally distributed variables, and categorical variables are expressed as the number of events and the percentage of events to total events. Demographic and laboratory tests were compared via t-tests or Mann–Whitney U tests for continuous variables and chi-square tests for categorical variables. We applied the Kolmogorov‒Smirnov normality test and Levene’s test to assess the distribution of variables across the entire patient cohort. Then, normally distributed variables were compared via Student’s t-test, and nonnormally distributed variables were compared via the Mann‒Whitney U test. In this study, all the statistical tests were two-sided and p < 0.05 was considered significant. R (version 3.6.1; R Core Team, 2019), Python (version 3.4.3), and SPSS (version 25.0) were systematically used for statistical analysis. The Deepwise & Beckman Coulter DxAI platform (https://dxonline.deepwise.com/) was used to construct CKD prediction models.
Machine learning-based model development and evaluation
Feature selection over the initial set of included variables is needed to reduce the probability of overfitting and improve the generalization capabilities of predictive models. In the training cohort, least absolute shrinkage and selection operator (LASSO) logistic regression analysis was used to select laboratory variables that best-identified high-risk patients. The LASSO regression reduces the β coefficient of variables not strongly associated with the outcome to 0 and eventually removes these variables from the model. Two different λ optimization criteria, lambda with the standard error of the minimum distance (λ-1SE) and lambda with the minimum mean square error de (λ-min), were selected in this study to construct the prediction model.
(2) Stacking ensemble technique
The stacking ensemble model is an ML technique that combines multiple base models to improve predictive performance. In stacking, meta-models are trained to learn how to best combine the predictions of the base models. The stacking models include base models and meta-models. The base-model classifier is trained using the initial training dataset. The output of the base model is used as the input feature of the meta-learner. A new dataset is then formed using the corresponding original labels as new labels to train the meta-learner. First, we use three algorithms, XGBoost, LightGBM and Random Forest, as the base models. The meta-model included a logistic regression model, which combined the predictions from the aforementioned three base-learners, analogous to the propensity score method (Li, Stein & Nallasamy, 2023). In this study, the aim of using an integrated ML model is to take full advantage of different classes of ML algorithms and improve the overall performance of the prediction model. K-fold cross-validation (k = 5) was applied to the modeling dataset, and various parameter combinations were exhausted via grid search.
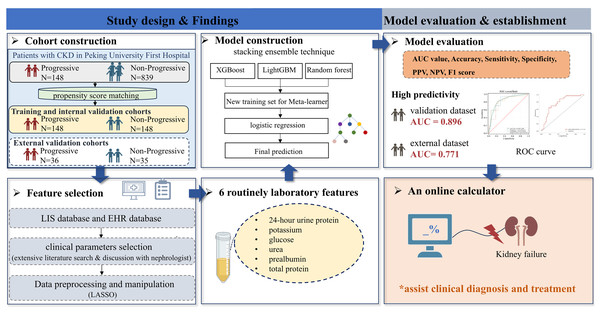
Models were evaluated for accuracy via the area under the receiver operating characteristic curve (AUC) with 95% confidence, F1 score, sensitivity, specificity, positive prediction value (PPV), and negative prediction value (NPV). The calibration curve was assessed for the prediction of the outcome at 1 to 4 years in 1-year intervals, and decision curve analysis (DCA) assessed the clinical benefit of the model. SHAP is used to interpret models, which calculates the contribution and influence of each feature toward the final prediction precisely. The SHAP values describe how each predictor enhances or detracts from the outcome variable. The workflow to develop the prediction model of CKD progression is shown in Fig. 1.
Figure 1: A workflow to develop the prediction model of CKD progression.
Abbreviations: AUC, area under curve; EHR, electronic health records; LIS, laboratory information systems; LASSO, least absolute shrinkage and selection operator; NPV, negative predictive value; PPV, positive predictive value; ROC, receiver operating characteristic.Results
General characteristics
A significant difference in age and sex was observed between the CKD progression and nonprogression groups (p < 0.001, p < 0.001; Table S1). After PSM, 148 progressive and 148 nonprogressive patients were selected for further analysis, where age and sex were well balanced between the two groups. An overview of the baseline descriptive statistics is provided in Table 1. The median ages of the patients in the progressive and nonprogressive cohorts were 48 (34, 62) and 49 (36, 61) years, respectively. The percentage of males in the two cohorts was almost two times greater than that of females. Compared with those in the CKD nonprogressive cohort, patients in the CKD progression cohort had higher rates of diabetes, hypertension and anemia (p < 0.05) and higher laboratory indicators, including Cr, 24hrUpr, potassium, P, CL, urea, UA, glucose (GLU), total cholesterol, and red blood cell distribution width (p < 0.05). However, lower levels of eGFR, albumin (Alb), total bilirubin, direct bilirubin, indirect bilirubin, total bile acid, and TP were observed in patients with progressive CKD (p < 0.05).
| Clinical characteristics | Progressive cohort (N = 148) | Non-progressive cohort (N = 148) | p value |
|---|---|---|---|
| Age (years), median (IQR) | 48 (34, 62) | 49 (36, 61) | 0.756 |
| Gender | |||
| Male | 99 (66.892) | 100 (67.568) | 0.901 |
| Female | 49 (33.108) | 48 (32.432) | |
| BMI | 25.495 ± 4.407 | 24.976 ± 3.773 | 0.298 |
| Systolic BP (mm Hg), median (IQR) | 136.000 (124.000, 149.000) | 130.000 (120.000, 141.000) | 0.009** |
| Diastolic BP (mm Hg), median (IQR) | 80.000 (75.000, 89.000) | 80.000 (74.000, 89.000) | 0.6 |
| Diabetes | 47 (31.76%) | 25 (16.89%) | 0.002** |
| Hypertension | 112 (75.68%) | 94 (63.51%) | 0.018* |
| Anemia | 44(29.73%) | 28 (18.92%) | 0.023* |
| Cardiovascular disease | 34 (22.97%) | 19 (12.84%) | 0.099 |
| Follow-up (days), median (IQR) | 1,279 (958, 1,633) | 1,463 (1,046, 1,714) | 0.004** |
| Laboratory characteristics | |||
| Biochemical indexes | |||
| Cr (μmol/L), mean (±SD) | 160.081 ± 30.675 | 145.510 ± 29.236 | <0.001*** |
| eGFR, median (IQR) | 39.348 (34.137, 46.720) | 47.003 (38.090, 53.609) | <0.001*** |
| 24 hrUpr (g/24 h), median (IQR) | 2.380 (1.040, 4.900) | 0.870 (0.400, 2.160) | <0.001*** |
| Alb (g/L), median (IQR) | 39.600 (35.300, 42.300) | 41.500 (38.700, 43.200) | <0.001*** |
| CHE (IU/L), mean (±SD) | 8,693.581 ± 1,965.322 | 8,474.959 ± 1,939.200 | 0.338 |
| LDL (mmol/L), median (IQR) | 2.850 (2.090, 3.490) | 2.620 (2.090, 3.150) | 0.13 |
| HDL (mmol/L), median (IQR) | 1.090 (0.930, 1.400) | 1.090 (0.910, 1.410) | 0.889 |
| CO2 (mmol/L), median (IQR) | 24.440 (22.900, 26.600) | 24.970 (23.400, 26.800) | 0.292 |
| Ca (mmol/L), median (IQR) | 2.300 (2.190, 2.370) | 2.320 (2.240, 2.390) | 0.074 |
| TG (mmol/L), median (IQR) | 2.150 (1.340, 3.160) | 1.850 (1.340, 2.400) | 0.066 |
| GGT (IU/L), median (IQR) | 25.000 (18.000, 40.000) | 22.000 (16.000, 29.000) | 0.14 |
| ALT (IU/L), median (IQR) | 15.000 (12.000, 22.000) | 16.000 (12.000, 22.000) | 0.277 |
| AST (IU/L), median (IQR) | 17.000 (14.000, 20.000) | 18.000 (14.000, 21.000) | 0.425 |
| ALP (IU/L), median (IQR) | 66.000 (54.000, 79.000) | 62.000 (50.000, 74.000) | 0.062 |
| K (mmol/L), median (IQR) | 4.300 (4.000, 4.800) | 4.200 (3.900, 4.430) | 0.016* |
| P (mmol/L), median (IQR) | 1.140 (1.050, 1.300) | 1.100 (0.990, 1.230) | 0.005** |
| CL (mmol/L), median (IQR) | 107.000 (105.000, 109.000) | 107.000 (105.000, 108.000) | 0.038* |
| Mg (mmol/L), median (IQR) | 0.900 (0.840, 0.950) | 0.900 (0.850, 0.960) | 0.799 |
| Na (mmol/L), median (IQR) | 141.410 (139.070, 144.000) | 142.000 (140.000, 143.000) | 0.318 |
| Urea(mmol/L), median (IQR) | 10.700 (8.600, 12.950) | 8.700 (7.280, 10.790) | <0.001*** |
| UA (μmol/L), median (IQR) | 437.568 ± 102.594 | 412.649 ± 85.198 | 0.024* |
| GLU (mmol/L), median (IQR) | 5.430 (4.880, 6.430) | 5.250 (4.840, 5.720) | 0.041* |
| PA (mg/L), mean (±SD) | 313.331 ± 73.787 | 315.601 ± 65.434 | 0.78 |
| TBIL (μmol/L), median (IQR) | 8.000 (5.800, 10.400) | 9.300 (6.700, 13.500) | 0.002** |
| DBIL (μmol/L), median (IQR) | 0.600 (0.300, 1.320) | 0.910 (0.350, 2.100) | <0.001*** |
| IBIL (μmol/L), median (IQR) | 7.450 (5.330, 9.400) | 8.210 (5.900, 11.730) | 0.005** |
| TCHO (mmol/L), median (IQR) | 5.240 (4.050, 6.090) | 4.790 (4.000, 5.660) | 0.022* |
| TBA (μmol/L), median (IQR) | 2.200 (1.250, 3.160) | 2.420 (1.400, 4.200) | 0.03* |
| TP (g/L), median (IQR) | 70.800 (64.700, 74.400) | 73.200 (68.600, 77.200) | 0.001** |
| Hematologic indexes | |||
| WBC (109/L), median (IQR) | 7.430 (6.080, 9.450) | 7.040[5.870, 8.780) | 0.233 |
| Monocyte count (109/L), median (IQR) | 0.500 (0.400, 0.700) | 0.500 (0.400, 0.700) | 0.566 |
| Lymphocyte count (109/L), median (IQR) | 1.900 (1.500, 2.300) | 1.900 (1.500, 2.200) | 0.639 |
| RBC (109/L), mean (±SD) | 4.247 ± 0.717 | 4.357 ± 0.648 | 0.215 |
| RDW (%), median (IQR) | 13.400 (12.900, 14.000) | 13.200 (12.700, 13.700) | 0.041* |
| Neutrophil count (109/L), median (IQR) | 4.800 (3.600, 6.200) | 4.500 (3.600, 5.700) | 0.162 |
| MCH (pg), median (IQR) | 30.100 (29.000, 31.600) | 30.600 (29.400, 31.800) | 0.148 |
| MCHC (g/L), median (IQR) | 332.755 ± 8.001 | 333.514 ± 8.681 | 0.481 |
| MCV (fl), median (IQR) | 90.400 (88.400, 94.100) | 91.900 (88.800, 94.500) | 0.219 |
| MPV (fl), median (IQR) | 8.500 (7.800, 9.270) | 8.430 (7.800, 9.100) | 0.568 |
| HGB (g/L), mean (±SD) | 128.325 ± 20.164 | 132.624 ± 18.943 | 0.09 |
| HCT (%), mean (±SD) | 38.570 ± 6.074 | 39.796 ± 5.742 | 0.109 |
| PLT (109/L), median (IQR) | 225.000 (182.000, 262.000) | 212.000 (179.000, 249.000) | 0.265 |
| PCT (%), median (IQR) | 0.190 (0.160, 0.220) | 0.180 (0.160, 0.210) | 0.147 |
| PDW (%), median (IQR) | 17.000 (16.600, 17.300) | 16.800 16.600, 17.200) | 0.074 |
Notes:
Values are presented as median (IQR) for continuous variables or n (%) for binary variables.
BMI, body mass index; estimated glomerular filtration rate (eGFR); 24hrUpr, 24-hour urine protein; Alb, albumin; ChE, cholinesterase; LDL, low density lipoprotein; HDL, high-density lipoprotein; TG, triglyceride; GGT, gamma-glutamyl transpeptidase; ALT, alanine aminotransferase; AST, aspartate amino transferase; Ca, calcium; ALP, alkaline phosphatase; K, potassium; P, phosphorus; CL, chlorine; Mg, magnesium; Na, sodium; UA, Uric Acid; GLU, glucose; PA, prealbumin; TBIL, total bilirubin; DBIL, direct bilirubin; IBIL, indirect bilirubin; TCHO, total cholesterol; TBA, total bile acid; TP, total protein; WBC, white blood cell; RBC, red blood cell; RDW, red blood cell distribution width; MCH, Mean corpuscular hemoglobin content; MCHC, mean corpuscular hemoglobin concentration; MCV, mean corpuscular volume; MPC, mean platelet volume; HGB, hemoglobin; HCT, hematocrit; PCT, platelet hematocrit; PLT, blood platelet count; SD, standard deviation; IQR, interquartile range.
ML model establishment and evaluation
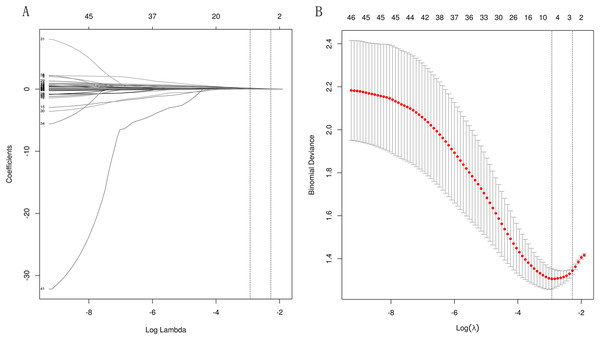
LASSO regularization was used to select laboratory variables that best identified patients at high risk for ESRD. Since the eGFR is used to define the outcome and is calculated from the serum creatinine level, the eGFR and creatinine level were not considered in the assessment. Based on the two different λ optimization criteria outlined in the “Methods” section (λ-1SE = 0.103, λ-min = 0.054), three and six out of 46 potential predictors yield the λ-min and λ-1SE models, respectively. The coefficient profile and the cross-validated error plot of the LASSO regression model are shown in Fig. 2. The derived laboratory variables included 24hrUpr, GLU, and urea. The second variable combination, derived from six laboratory variables, comprises potassium, prealbumin (PA), and TP, in addition to the aforementioned three laboratory variables.
Figure 2: Lasso regressions for candidate variables.
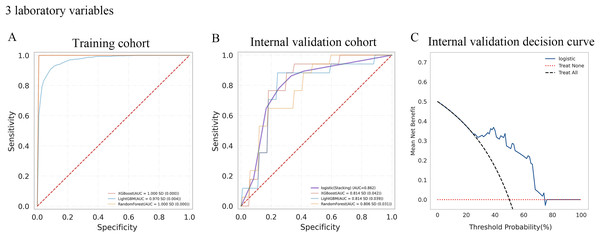
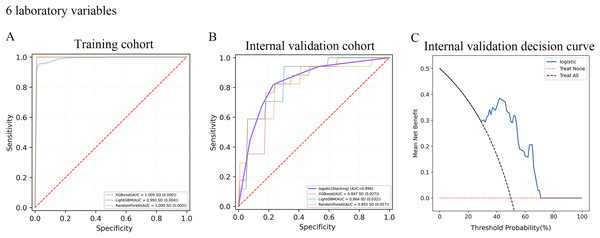
A total of 10-fold cross-validation was used to draw vertical lines and three variables were selected when the lambda with the standard error of the minimum distance (λ-1SE) = 0.103 and six variables were selected when the lambda with minimum mean square error de (λ-min) = 0.054.In the test set, the AUC for predicting CKD progression ranged from 0.806 to 0.896 when different learning methods and combinations of laboratory variables were used. Numerically, the stacking meta-classifier logistic regression with six variables achieved the best prediction performance, with an overall mean AUC of 0.896. Figures 3 and 4 show the ROC curves of each ML model. The accuracy, sensitivity, specificity, PPV, NPV, and F1 scores for this model in cross-validation were 0.824, 0.941, 0.765, 0.789, 0.867, and 0.859, respectively (Table 2). The results of the confusion matrices are summarized in Tables S2 and S3. In addition, the DCA curve showed that the model had high clinical benefits in the approximately 30% to 70% risk range, as shown in Figs. 3C and 4C. We finally chose those six laboratory variables to construct a prediction model of CKD progression.
Figure 3: Evaluation of the predictive models.
(A and B) ROC curve analysis of ML models based on three laboratory variables in training and internal validation cohort. (C) Decision curve analysis of the internal validation set.Figure 4: Evaluation of the predictive models.
(A and B) ROC curve analysis of ML models based on six laboratory variables in training and internal validation cohort. (C) Decision curve analysis of the internal validation set.| ML model | AUC | Accuracy | Sensitivity | Specificity | PPV | NPV | F1 score | ||
|---|---|---|---|---|---|---|---|---|---|
| Three Laboratory variables | Training cohort | XGBoost | 1 | 0.994 | 1 | 1 | 1 | 0.988 | 1 |
| LightGBM | 0.97 | 0.918 | 0.916 | 0.933 | 0.933 | 0.906 | 0.924 | ||
| RandomForest | 1 | 0.987 | 0.995 | 0.999 | 1 | 0.974 | 0.998 | ||
| Internal validation cohort | XGBoost | 0.814 | 0.712 | 0.865 | 0.759 | 0.769 | 0.676 | 0.812 | |
| LightGBM | 0.814 | 0.759 | 0.829 | 0.753 | 0.749 | 0.772 | 0.784 | ||
| RandomForest | 0.806 | 0.735 | 0.812 | 0.747 | 0.761 | 0.719 | 0.78 | ||
| Logistic (stacking) | 0.862 | 0.794 | 0.882 | 0.765 | 0.778 | 0.813 | 0.827 | ||
| Six Laboratory variables | Training cohort | XGBoost | 1 | 0.993 | 1 | 1 | 1 | 0.987 | 1 |
| LightGBM | 0.993 | 0.963 | 0.951 | 0.989 | 0.989 | 0.94 | 0.969 | ||
| RandomForest | 1 | 0.983 | 1 | 1 | 1 | 0.967 | 1 | ||
| Internal validation cohort | XGBoost | 0.847 | 0.712 | 0.847 | 0.788 | 0.865 | 0.651 | 0.855 | |
| LightGBM | 0.864 | 0.759 | 0.871 | 0.8 | 0.836 | 0.711 | 0.853 | ||
| RandomForest | 0.855 | 0.718 | 0.847 | 0.765 | 0.822 | 0.669 | 0.83 | ||
| Logistic (stacking) | 0.896 | 0.824 | 0.941 | 0.765 | 0.789 | 0.867 | 0.859 |
Note:
AUC, area under curve; ML, machine learning; NPV, negative predictive value; PPV, positive predictive value.
SHAP values were applied to determine the impact of the risk factors to detect the positive and negative relationships of the indicators with CKD progression. The importance of the features in the ensemble models, XGBoost, LightGBM and Random Forest are shown in Fig. S1. The attributions of all patients to the results are plotted with red dots indicating that the value of the feature is larger and blue dots indicating that the value of the feature is smaller. Compared with the nonprogressive cohort, increased 24hrUpr, GLU, urea and potassium, and decreased PA and TP contributed to the prediction of the risk of renal failure. The rankings of the six features were evaluated by the average absolute SHAP value.
Performance of the model with different follow-up periods
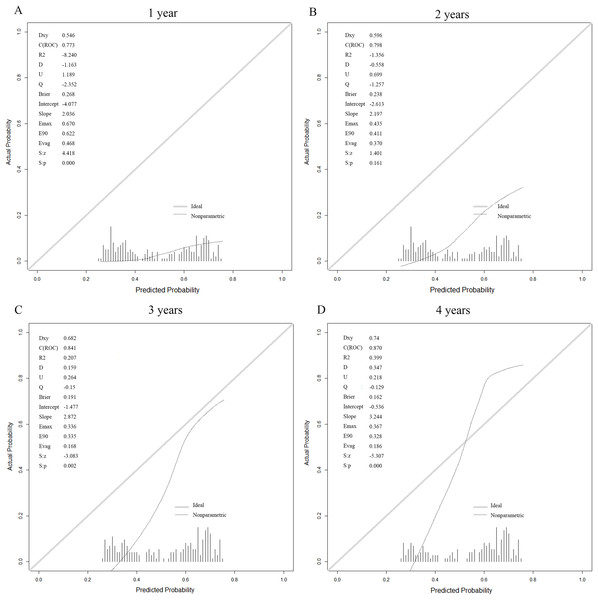
The prediction model based on the six laboratory variables yielded high ESRD AUCs of 0.773, 0.798, 0.841, and 0.87 for years 1, 2, 3, and 4 after the baseline visit, respectively (Table 3). The calibration curve showed good model prediction in terms of Brier scores evaluated on the test sets across all time points (Fig. 5). This demonstrated that the stacking model constructed in this study can predict the CKD status of patients across different periods. The visualization of the predictive model is implemented as an online web service tool available at http://www.xsmartanalysis.com/model/list/predict/model/html?mid=10255&symbol=817bW025614Bs59zK1sJ.
| Time frame, year | AUC | Sensitivity | Specificity |
|---|---|---|---|
| 1 | 0.773 | 1 | 0.574 |
| 2 | 0.798 | 0.867 | 0.706 |
| 3 | 0.841 | 0.971 | 0.685 |
| 4 | 0.87 | 0.947 | 0.76 |
Note:
AUC, area under curve.
Figure 5: Calibration for the six laboratory variables logistic (stacking) model for prediction of kidney failure.
At (A) 1 year, (B) 2 years, (C) 3 years and (D) 4 years.External validation study
We collected another 71 cases as an external test dataset to further evaluate the performance of the predictive model for CKD progression; 36 patients had CKD progression, and 35 patients had nonprogressive CKD. An overview of the baseline descriptive statistics is provided in Table S4. The performance was similar when evaluated in the external validation cohort, with an AUC of 0.771, a sensitivity of 0.639 and a specificity of 0.829 (Table 4). These results indicate that the constructed ML predictive model based on six laboratory variables had comparable predictive utility.
Discussion
Worldwide, experience indicates that the contribution of CKD to kidney dialysis, kidney transplantation and mortality is rapidly increasing (Ruiz-Ortega et al., 2020). Therefore, identifying risk factors for progression and obtaining accurate, individualized risk estimates to assist in clinical decisions on further management are important. Several studies have developed predictive scores for CKD, but these scores vary in terms of the target population’s ethnicity and the complexity of the scores, which are determined by the number and classification of factors involved. There is a need for a distinct Chinese predictive model for CKD progression to identify high-risk patients within the Chinese population. In this retrospective cohort study, we investigated possible predictive factors associated with the progression of CKD in a cohort of the Chinese population. The proposed stacking ensemble model that combines multiple base models achieves better performance in all respects and takes full advantage of different classes of ML algorithms. Furthermore, we developed an online risk prediction model based on only six easily available predictors for the occurrence of ESRD with good accuracy and satisfactory calibration that covers most patients in areas where there are only limited healthcare resources in China. The form of an online calculator should facilitate the long-term management of chronic diseases and the selection of patients most likely to benefit from innovative strategies to halt the progression of chronic kidney disease. In actual clinical practice, it can be easily and quickly applied in decision-making for treatment and lifestyle improvement and reduces the costs related to treatment.
Previous investigators have reported risk prediction models for predicting future renal dysfunction. Owens et al. (2020) developed a model for predicting progressive CKD based on a panel of biomarkers representing the pathophysiological processes of CKD and had an accuracy of 84.3%; however, deficiencies in the study included separate small sample sizes, and the included biomarkers, such as osteopontin and tryptase, are uncommon in clinical practice. Isaza-Ruget et al. (2024) studied a cohort from Colombia and developed a machine learning-based model for predicting the need for renal replacement therapy (RRT) and disease progression in patients with stage 3–5 CKD. However, the limitations of this study include its limited characteristics and uncertain data quality, which were extracted from private health insurers (Isaza-Ruget et al., 2024). Ventrella et al. (2021) applied machine learning to assess the advancement of CKD, but as many as 27 features were included in the model, which may have a high risk for overfitting and is not convenient for clinical application. Zhu et al. (2023) constructed recurrent neural network models to predict CKD progression from stages 2–3 to stages 4–5 based on time series records extracted from the EHR. However, the model was not validated in an external validation set.
As described above, appropriate adequate risk prediction models have shown high predictive power in predicting CKD risk, but they are not easy to calculate and do not translate into routine clinical practice to assist in clinical decision-making. Therefore, online calculators or others should be considered for practical application. The kidney failure risk equations proposed by Tangri et al. (2011) have shown good performance and are used to guide patient management. The model was established based on routinely obtained laboratory tests, and simple operation steps have driven its adoption (Tangri et al., 2011). It would be valuable to apply the prior risk model. However, the risk model could not be applied in this study because it requires an albumin-to-creatinine ratio, which was not used in our study, and the eGFR was used to determine outcomes. Furthermore, most studies based on a nationwide cohort of patients and risk prediction models have been constructed in various ethnic groups in different countries. For a predictive model of the progression of CKD, few studies have been conducted in the Chinese population. Since the prevalence of CKD and its risk factors vary among ethnic groups (Hsu et al., 2021), it is preferable to use Chinese data to predict CKD risk in the Chinese population.
The online prediction ML model we built showed high predictive ability for CKD progression and good discriminative ability in predicting patients with CKD in both the internal validation and external validation cohorts. Based on the LIS and EHR systems of Peking University First Hospital, our model includes various types of kidney diseases, such as IgA, membranous nephropathy, and focal segmental glomerulosclerosis, which can be widely used in clinical practice. Ensemble learning is a technique that trains to combine predictions from the base learner and has been widely used across multiple medical fields to improve predictive performance (Mahajan et al., 2023). Several diagnosis and prediction ensemble learning techniques have already been proposed for CKD. Chhabra, Juneja & Chutani (2023) used an ensemble learning approach based on the top three best-performing classifiers in terms of cross-validation results to identify patients at risk of CKD with an accuracy of 99.5%, but this high predictive power may be due to overfitting caused by the small dataset. Napa, Tulasi & Dhamodaran (2019) proposed an ensemble learning technique for predicting the occurrence of kidney disease by analyzing various medical factors that comprise a support vector machine, decision tree, C4.5, and particle swarm optimized multilayer perceptron, attaining an accuracy of 92.76%. Hasan & Hasan (2019) developed an ensemble method-based machine learning algorithm to improve the performance of classifiers for kidney disease. Five machine learning classifiers, namely, adaptive boosting, bootstrap aggregating, extra trees, gradient boosting, and random forest classifiers, were used to design the computer-aided diagnosis system, and the classification accuracy reached 99% (Hasan & Hasan, 2019). Ganie et al. (2023) used boosting techniques based on clinical parameters to predict the risk of developing CKD in at-risk populations with 98.47% accuracy in testing sets. However, most studies have focused on the detection and prediction of the incidence of CKD. Ensemble learning is less commonly used to predict the progression of renal function in CKD patients. Lu et al. (2023) developed an integrated algorithm (LR+XGBoost) to achieve good prediction performance on the CKD dataset, with AUCs of 0.856 and 17 features included in the model, whereas proteinuria was used as a standard for CKD in this study. As an extension of this work, we used ensemble learning techniques to take advantage of different classes of the ML algorithm (XGBoost, LightGBM and Random Forest) and improve the model’s overall performance. Compared with the single classifier-based model, the stacking model performs better. The model based on only six routine laboratory parameters performed well, with AUC values of 0.896 and 0.771 in the internal and external validation sets, respectively. Our risk prediction models have important implications for clinical practice, public health policy, and mechanism research. The models can be easily integrated into LISs and EHRs to aid clinical decisions. For community hospitals and healthcare centers in China, the testing equipment is limited, and clinicians are inexperienced. In daily clinical practice, our model can help physicians predict the progression of renal function based on accessibility and objective laboratory indicators and can contribute to guiding clinical treatment and patient lifestyle. For example, lower-risk CKD patients could be managed by healthcare centers and community hospitals without excessive medical treatment or testing, whereas higher-risk CKD patients could be managed by nephrologists and receive timely intervention and correct medication guidance. This method will decrease national healthcare costs, benefiting China, a developing country with a large population. In addition, developing an application that can calculate the risk prediction equation via portable laptops or mobile devices would be more convenient and clinically useful for assessing risk. CKD is a condition that requires long-term management and monitoring. Patients can use the online model to enhance their self-management capabilities, helping them better understand the progression of the disease and develop more effective management plans, thereby improving their adherence to treatment regimens. This model can also accurately predict the progression of renal function in patients with varying follow-up periods after their initial assessment. The poor performance of the calibration curve at 1 year may be because CKD is a chronic progressive disease, and fewer patients progress to ESRD within 1 year in our study, which needs to be verified in the future with a larger population. Furthermore, it needs to be aware that the developed model could serve as an initial decision-support tool for physicians, with further clinical examination needed to make more informed decisions.
By using the LASSO regularization method, six laboratory variables were selected that best identified patients at high risk for ESRD, namely, 24hrUpr, GLU, urea, potassium, PA and TP. Based on the feature importance of the ensemble models, 24hrUpr, GLU and urea were the top three indicators. Albuminuria has been studied extensively in the context of CKD and its progression. Albuminuria is a major risk factor for renal disease, and albuminuria testing is crucial for guiding evidence-based treatments to mitigate chronic kidney disease progression (Chu et al., 2023; Levey, Grams & Inker, 2022). The 24hrUpr was included in our ML model, thus confirming its importance as an independent factor in the progression of CKD. Makino et al. (2019) used big data machine learning to predict the progression of diabetic kidney disease (DKD), and blood glucose and HbA1c were selected in the model to reveal time series patterns related to 6-month DKD aggravation. Chen, Chen & Jiang (2022) reported that DKD patients have a greater risk of developing a 50% decrease in the eGFR and kidney transplantation replacement than non-DKD patients. Our study model also identified blood glucose as a risk factor for the progression of CKD. The modeling population included in this study was 38 patients with comorbid diabetes or DKD. Several studies have shown that urea is a marker of uremic retention in CKD patients and that elevated urea concentrations induce disintegration of the gut epithelial barrier and promote microhemorrhages. Urea toxicity leads to systemic inflammation and endothelial dysfunction, thus directly contributing to disorders of tubular function and the progression of kidney disease (Hobby et al., 2019; Lau et al., 2020; Rosner et al., 2022). In summary, urea is a key factor in CKD pathophysiology, and our study emphasized that minimizing urea accumulation is clinically beneficial for slowing the progression of CKD. Patients with chronic kidney disease often have abnormal serum potassium caused by a lower GFR and the administration of angiotensin-converting enzyme inhibitors, angiotensin-receptor blockers and other demographic factors (Clase et al., 2020; Kim, Valerio & Knobloch, 2023). Previous studies have suggested that hypokalemia is related to the accelerated progression of CKD. The possible reasons could be increased renal ammonia production and impaired renal angiogenesis (Gilligan & Raphael, 2017). For PAs, studies have shown that protein-energy wasting, which manifests as low serum levels of PAs, is one of the strongest predictors of mortality in patients with CKD (Barril et al., 2022). Studies have shown that higher intake of TP was associated with lower mortality in participants with CKD (Carballo-Casla et al., 2024). The reduced TP levels in our study contributed to an increased risk of CKD progression. Our study also emphasized that paying attention to the levels of PA and TP and proper nutritional support are essential for the prognosis and quality of life of patients with CKD. Although the laboratory markers mentioned above have also previously been associated with the progression of CKD and individual indicators inadequately explain the variability in the decrease in the glomerular filtration rate, our work integrates them into an online risk equation to predict the progress of kidney function and assist in clinical diagnosis and treatment.
The present study has several limitations. First, the retrospective study was restricted to Chinese patients from a single center with a relatively small sample size. Further studies including larger and multiple centers, are needed to improve and validate the risk prediction models. Second, model development was based on a retrospective cohort, which reduced the availability of complete data related to clinical characteristics, treatment-related information and laboratory indicators of interest for the final analysis. Therefore, prospective research based on full clinical information is needed to identify a better method for predicting CKD progression. Third, although we applied PSM designs to construct a balanced cohort, there may be potential bias in unmeasured or unknown factors. Fourth, the outcome of CKD progression can be subdivided, and monitoring the dynamic changes in clinical indicators during follow-up can be considered to improve the accuracy and timeliness of predicting the risk of kidney failure.
Conclusions
Overall, we applied the ML method to present an online portable model for accurately predicting the occurrence of ESRD in patients with CKD stages 3 to 5. The predictive ability of the model was confirmed through external validation. This model also accurately predicted the progression of renal function in patients with varying follow-up periods after their initial assessment. Only six easily accessible laboratory tests, which are easy to popularize in primary hospitals in China, were included in the model. The form of online calculators could be an easy and quick tool for detecting and recognizing high-risk CKD patients and for providing appropriate counseling and treatment. Moreover, the laboratory indices screened by the ML model provide a new idea and reference for managing CKD.
Supplemental Information
Critical characteristics in the unmatched and propensity-score matched cohorts.
Values are presented as median (IQR) for continuous variables or n (%) for binary variables, *p < 0.05; **p < 0.01; ***p < 0.001.
Confusion matrices in training and validation cohort based on three laboratory variables.
Confusion matrices in training and validation cohort based on six laboratory variables.
Baseline clinical and biochemical characteristics of patients in external validation cohort.
Values are presented as median (IQR) for continuous variables or n (%) for binary variables, *p < 0.05; **p < 0.01; ***p < 0.001. Abbreviations: BMI, body mass index; estimated glomerular filtration rate (eGFR); 24hrUpr, 24-hour urine protein; Alb, albumin; ChE, cholinesterase; LDL, low density lipoprotein; HDL, high-density lipoprotein; TG, triglyceride; GGT, gamma-glutamyl transpeptidase; ALT, alanine aminotransferase; AST, aspartate amino transferase; Ca, calcium; ALP, alkaline phosphatase; K, potassium; P, phosphorus; CL, chlorine; Mg, magnesium; Na, sodium; UA, Uric Acid; GLU, glucose; PA, prealbumin; TBIL, total bilirubin; DBIL, direct bilirubin; IBIL, indirect bilirubin; TCHO, total cholesterol; TBA, total bile acid; TP, total protein; WBC, white blood cell; RBC, red blood cell; RDW, red blood cell distribution width; MCH, Mean corpuscular hemoglobin content; MCHC, mean corpuscular hemoglobin concentration; MCV, mean corpuscular volume; MPC, mean platelet volume; HGB, hemoglobin; HCT, hematocrit; PCT, platelet hematocrit; PLT, blood platelet count; SD, standard deviation; IQR, interquartile range
SHAP summary plot of the 6 features of the ensemble models (XGBoost, LightGBM, RF).
(A,C,E) The SHapley Additive exPlanation (SHAP) values. Blue dots represent low risk values of the features and red dots represent high risk values of the features. (B,D,F) Feature importance of model, evaluated by the average absolute SHAP value. Abbreviations: RF, random forest; 24hrUpr, 24-hour urine protein
The cohort included 987 patients with more than 24 months of follow-up.
Database used for the development of the prediction model based on machine learning.
Additional Information and Declarations
Competing Interests
The authors declare that they have no competing interests.
Author Contributions
Jialin Du conceived and designed the experiments, performed the experiments, analyzed the data, prepared figures and/or tables, authored or reviewed drafts of the article, and approved the final draft.
Jie Gao conceived and designed the experiments, prepared figures and/or tables, and approved the final draft.
Jie Guan conceived and designed the experiments, prepared figures and/or tables, and approved the final draft.
Bo Jin conceived and designed the experiments, prepared figures and/or tables, and approved the final draft.
Nan Duan performed the experiments, authored or reviewed drafts of the article, and approved the final draft.
Lu Pang performed the experiments, authored or reviewed drafts of the article, and approved the final draft.
Haiming Huang analyzed the data, prepared figures and/or tables, and approved the final draft.
Qian Ma performed the experiments, prepared figures and/or tables, and approved the final draft.
Chenwei Huang performed the experiments, analyzed the data, authored or reviewed drafts of the article, and approved the final draft.
Haixia Li conceived and designed the experiments, performed the experiments, prepared figures and/or tables, authored or reviewed drafts of the article, and approved the final draft.
Human Ethics
The following information was supplied relating to ethical approvals (i.e., approving body and any reference numbers):
The Clinical Ethics Review Committee of the Peking University First Hospital (Ethical Application Ref: 2024Yan-237-002).
Data Availability
The following information was supplied regarding data availability:
The raw data and code are available in the Supplemental Files.
Funding
This study was supported by the National Natural Science Foundation of China (Grant No. 82072369), the “Sailing Plan” of Medical Youth Science and Technology Innovation of Peking University (Grant No. BMU2023YFJHPY003), the National High Level Hospital Clinical Research Funding (Scientific and Technological Achievements Transformation Incubation Guidance Fund Project of Peking University First Hospital) (Grant No. 2024CX12), and the National High Level Hospital Clinical Research Funding (Interdisciplinary Clinical Research Proiect of Peking University FirstHospital) (Grant No. 2022CR49). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.