Study on the relationship between net primary productivity and site quality in Japanese larch plantations in mountainous areas of eastern Liaoning

Study area

Dandong City was used as the study area (Fig. 1). Dandong City is located in the center of northeast Asia, with a geographical position of 123 23′–125 42′ east longitude and 39 44′–41 09′ north latitude. It is adjacent to the confluence of Yalu River and Yellow Sea and is an important area in the southeast of Liaodong Peninsula. It is the warmest and wettest place in Northeast China with a temperate sub-humid monsoon climate. The annual average rainfall is between 800–1,200 mm. Affected by monsoon, seasonal changes are obvious with four distinct seasons.

Sources of data

Sample plot

The data of this study comes from the forest resource inventory data for management in Liaoning Province in 2011. This study is a continuation and strengthening of the fixed-point survey and monitoring of forest area, forest species, and forest age in the Second National Land Survey. The contents of the survey include forest area, storage capacity, timber volume, stand structure, and ecological function. In the forest resource inventory data for management, 7,077 sample plots with an area greater than 2 hm² and a canopy density greater than 0.2 were selected for research. Figure 2 shows the shape of the woodland. Most of the growth in the 7,077 sample plots are young growths and half-mature forests. Among them, 6,811 sample plots have an average age of less than 40 years, accounting for 96.2% of the total. The average height of each age class ranges from 11.5 m to 24.7 m (see Table 1).

Table 1:

Statistics of age distribution of the sample plots.

Description of forest class characteristics based on forest survey data in 2011.

Age class/a	Sample plot number/N	Age/a	Average height/m
Young growth	3,590	0∼20	11.5
Half-mature forest	2,460	21∼30	14.8
Nearly mature forest	760	31∼40	17.2
Mature forest	215	41∼60	19.2
Overmature forest	52	>60	24.7

DOI: 10.7717/peerj.17820/table-1

To generate the family of H-AQ curves, pairs of observations of tree height and age of all plots with at least two measurements were fitted to four dynamic equations expressed under the GADA technique. We used the 2005 Liaoning Provincial Forest Resources Survey Data to match the 2011 Liaoning Provincial Forest Resources Survey Data to obtain 5,601 sets of data for modeling. Tree ages spanned from 0∼70 years and were divided into seven age intervals according to an age interval of 10 years. See Table 2 for stand characteristics of sample sites.

Table 2:

Statistics of age distribution of the sample plots.

The table summarizes the characteristics of the data used for modeling, including the average tree height, maximum tree height, minimum tree height, and the number of stands in each age group for the years 2005 and 2011.

Year	Age interval/a	Sample plot number/N	Standard deviation/m	Minimum value/m	Maximum value/m	Average tree height/m
2005	0∼10	1,199	2.2	0.9	13.0	5.5
2005	11∼20	2,754	2.4	3.0	19.5	10.1
2005	21∼30	1,285	2.7	4.5	24.0	14.0
2005	31∼40	246	2.8	7.4	25.3	17.1
2005	41∼50	64	3.3	11.5	25.0	18.2
2005	51∼60	23	4.6	10.0	29.5	21.5
2005	>60	35	3.0	18.3	29.9	24.9
2011	0∼10	66	1.2	2.4	7.3	3.7
2011	11∼20	2,518	3.0	3.1	22.7	12.2
2011	21∼30	2,102	3.0	6.8	24.3	14.9
2011	31∼40	669	3.3	5.1	27.2	17.0
2011	41∼50	164	3.1	8.4	27.5	19.26
2011	51∼60	30	3.0	12.9	26.4	18.85
2011	>60	52	4.1	10.2	31.1	24.9

DOI: 10.7717/peerj.17820/table-2

MODIS NPP

This study uses NPP remote sensing image provided by the NASA website (https://urs.earthdata.nasa.gov/). It is the product of MOD17A3HGF which is the MODIS image with spatial resolution of 500 m. NPP was calculated by determining the net photosynthesis (PSN), i.e., the difference between gross primary productivity and maintenance respiration costs (MR) every 8 days. The original format of the data is HDF, and the temporal resolution is annual. The data uses MODIS/TERRA satellite remote sensing parameters and simulates the NPP data set through the BIOME-BGC ecosystem model.

The downloaded data in HDF format were spliced, resampled, and reprojected in batches using the MRT tool. These data were multiplied by the scale factor of 0.1, and the attribute value representing non-vegetation pixels was assigned as a null value. Finally, based on the vector data of the study area, the remote sensing data of NPP time series of vegetation in Dandong City from 2013 to 2022 were obtained in batches.

Research methods

Derivation of the difference model

In 1974, Bailey and others put forward ADA. Based on this Cieszewski suggested GADA (Cieszewski & Bailey, 2000). GADA can be applied to several site-related parameters to derive polymorphic dynamic GADA formulation with variable horizontal asymptotic lines, so as to quickly and accurately predict site quality and build SI models (Cieszewski, 2001; Cieszewski, 2002).

Derivation of the differential SI model by GADA usually includes the following steps:

(1) Select a growth equation as the basic equation.

(2) Specify two or more parameters in the equation as parameters related to site.

(3) Propose a variable X₀ related to site quality. Assume that parameters related to site have various quantitative relationships with the variable (such as linear, inverse function, quadratic, exponential, etc.).

(4) Substitute the above functional into the basic equation and solve X₀, here defined as (t₀, h₀). Among them, t₀ is the specified forest age, h₀ is the tree height under the specified forest age. When t₀ is the benchmark forest age, h₀ is the SI.

(5) Substitute the solved X₀ into the basic equation, and the differential SI derived by GADA can be obtained.

The SI model constructed by this method can satisfy two attributes: multiple horizontal asymptotes and polymorphism. Taking Eq. (1) as an example, the parameters a and b in Eq. (1) are set as parameters related to site. Then set a linear relationship between parameter a and X₀, and an inverse proportional function relationship between parameter b and X₀. That means a = e^X₀, c = c₁ + c₂X₀. Equation (1) can be transformed into: (4)${\displaystyle \begin{array}{c}\hfill h=e^{X_0}{\left(1-e^{-bt}\right)}^{\left(c_1+c_2{X}_0\right)}.\hfill \end{array}}$

Then the following can be derived: (5)${\displaystyle \begin{array}{c}\hfill X_0=\frac{lnh-c_{1}ln\left(1-e^{-bt}\right)}{1+c_{2}ln\left(1-e^{-bt}\right)}.\hfill \end{array}}$

In Eq. (5), t = t₀, h = h₀, of which t₀ is the reference age and h₀ the tree height at the specified age. When t₀ is the reference age, h₀ will be the SI. Make Eq. (4) be t = t₁, h = h₁, of which t₁ is the predict age and h₁ the tree height under that age. Substitute Eq. (5) into Eq. (4), and the differential SI model based on Eq. (3) can be obtained by GADA. The representation is: (6)${\displaystyle \begin{array}{c}\hfill h_1=e^{X_0}{\left(1-e^{-b{t}_1}\right)}^{\left(c_1+c_2{X}_0\right)}.\hfill \end{array}}$

Among them, X₀: (7)${\displaystyle \begin{array}{c}\hfill X_0=\frac{ln{h}_0-c_{1}ln\left(1-e^{-b{t}_0}\right)}{1+c_{2}ln\left(1-e^{-b{t}_0}\right)}.\hfill \end{array}}$

In order to compare the difference between GADA and ADA, based on Richards equation, difference model E0 can be derived by ADA (Table 3).

The methods SI model was used, and the average tree height was used as the data. The final model was the mean height -age model.

Model fitting and validation

The model parameter estimation uses the nlsLM function in the minpack.lm package of R language. This function uses the Levenberg–Marquardt algorithm to solve the nonlinear least squares problem (Arias-Rodil et al., 2014). There are two main aspects for testing the goodness of the model: One is the biological meaning of the model and the parameters, and the other is the actual fitting effect of the model characterized by statistical indicators. This study uses three statistical indicators commonly used in regression analysis: the determination coefficient (R²), bias (BIAS), root mean square error (RMSE). Fitting samples are used to calculate the above three indicators; the closer the determination coefficient is to 1, the smaller the bias, the smaller the root mean square error and the smaller the mean absolute error, the better the prediction effect of the model. The formulas of indicators are as follows: (8)${\displaystyle \begin{array}{c}\hfill R^2=1-\frac{\sum _{i=1}^n{\left(h_i-{\hat{h}}_i\right)}^2}{\sum _{i=1}^n{\left(h_i-\overline{h}\right)}^2}\hfill \end{array}}$ (9)${\displaystyle \begin{array}{c}\hfill BIAS=\frac{\sum _{i=1}^n\left(h_i-{\hat{h}}_i\right)}{n}\hfill \end{array}}$ (10)${\displaystyle \begin{array}{c}\hfill RMSE=\sqrt{\frac{\sum _{i=1}^n{\left(h_i-{\hat{h}}_i\right)}^2}{n}}\hfill \end{array}}$

in which: h_i is the measured value of the tree height; ${\hat{h}}_i$ is the estimated value the tree height; $\overline{h}$ is the average of the measured values of tree height; n is the number of samples.

According to the above indicators, several models were evaluated and the best fitting model of the height-age curve cluster was chosen to verify whether the model met the properties of an ideal height-age model. All statistical analyses above were performed in R4.2.3 using R Studio (R Core Team, 2022; RStudio Team, 2002).

Selection of base age and H-AQ class interval

The tree heights of stands should be stable at the reference age and there should be obvious differences in the tree heights in different site conditions. There is no obvious influence of tree age on the site quality evaluation results of most tree species (Clutter, Fortson & Pienaar, 1983). Generally, the following aspects are considered: (1) the age class after the growth tends to be stable; (2) cutting age; (3) half of the natural maturity age; (4) the age when the average volume or tree height is maximum, etc. (Guo, Zhang & Zhang, 2007). However, China typically uses 1 m or 2 m as the SI interval and the number of index levels rarely exceeds 10 (Meng & Chen, 2001). Height-age grades also adopt this method. Therefore, combined with sample data, we set the reference age to 30 years (t_b), the H-AQ class interval 2 m, and the range of H-AQ from 10 m to 26 m.

NPP resolution of forest land under different site quality

Resolution (R) is an indicator to measure the degree of data separation. In this study, we use R to calculate whether the NPP value shows a separation trend under different site qualities and evaluate the influence of different site qualities on NPP value. If the result of R is positive, it indicates that the absolute data increases, and vice versa. The greater the absolute value, the higher the degree of data separation. Here, the influence of site quality on NPP of forest land was analyzed by calculating the NPP resolution of forest land with different site qualities. Its calculation formula is as follows: (11)${\displaystyle \begin{array}{c}\hfill R=2\ast \frac{T_2-T_1}{W_{B1}+W_{B2}}\hfill \end{array}}$

in which: T is the average NPP, and W_B is 2.354 times of NPP standard deviation. The numbers 1 and 2 represent different site qualities.

Correlation analysis between H-AQ and NPP

To explore the changes of NPP under different site categories, we drew a box diagram of the average NPP in the past ten years and made a linear regression analysis between the average NPP in the past ten years and H-AQ. Spearman correlation analysis and Kendall correlation analysis were used to deeply study the correlation between H-AQ and NPP. All the above tests and analyses were carried out in OriginLab, (2021).

The exponential order derived by GADA was divided into three levels to classify site quality. Specifically, lands with an exponential order of 10∼14 are classified as inferior sites, lands with 16∼20 as average-quality sites, and lands with 22∼26 as high-quality sites.

To explore the relationship between age class and NPP, we selected the data of 2013 for analysis, which was divided into an age class every ten years with 0–10 years as Grade I, 10–20 years as Grade II, and so on. Because there are few trees over 50 years old, trees over 50 years old were classified as Grade VI.

Model fitting results

Comparison of models derived from GADA and ADA

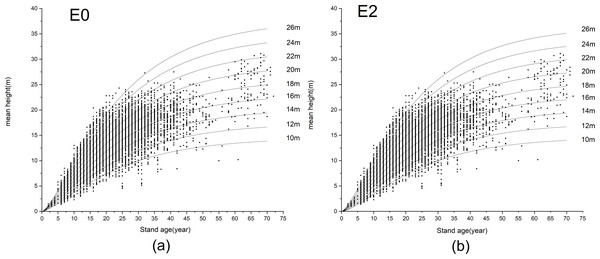
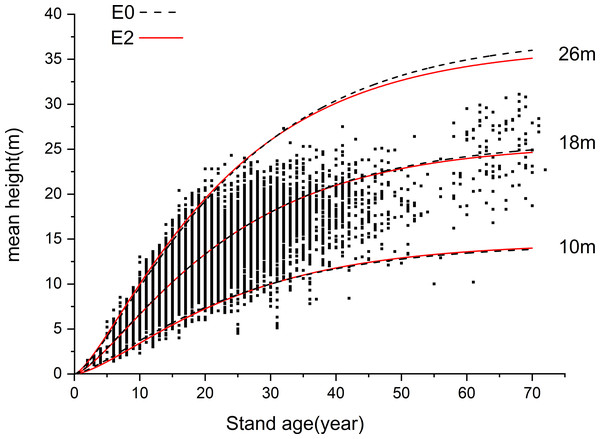
To reveal the advantages of GADA, we selected the E0 model based on the same Richards equation using ADA for subsequent comparative analysis. The H-AQ curve clusters of E0 and E2 were drawn (Fig. 3) and a comparative graph was created for the three site index curve clusters (10m, 18m, 26m) of the two models with good or bad performance (Fig. 4).

The growth processes of the trees in the two models are basically the same under average site conditions (18 m; Fig. 4). In trees over 35 years, the curve at the minimum H-AQ of model E2 was above model E0, while the curve at the maximum H-AQ was below model E0. From the scattergram, it can be observed that the height growth of Larix kaempferi plantations is slow when the age is less than 5. However, after the age of 5, the height growth showed an obvious upward trend. At this point, model E2 shows a slow upward trend first and then a rapid upward trend. In trees over 35 years, the curve at the minimum H-AQ of model E2 was below model E0, while the curve at the maximum H-AQ was above model E0; model E2 contains more data points. This indicates that in younger trees, model E2 better fits the growth process of Larix kaempferi in Dandong under different site conditions. Compared with ADA, the equations derived by GADA have two properties: multiple horizontal asymptotes and pleomorphism. To further verify this, we compared the inflection point position, the slope at the inflection point (the maximum annual growth) and the function value at the inflection point (the tree height at the inflection point) of the two curves to further illustrate the differences between the two methods after drawing the H-AQ curve clusters of E0 and E2. If a group of curves satisfies multiple horizontal asymptotes, the curves under different H-AQ will have different maxima, that is, different asymptotes; if a group of curves satisfies pleomorphism, the curves under different H-AQ will have different inflection points, and there should be no simple proportional relationship between curves. It can be seen in Table 5 that the differential H-AQ model E0 obtained by ADA only has a simple proportional relationship between the extreme values of curves under different H-AQ; their inflection points are exactly the same, while the slope at the inflection points is also proportional to the predicted values. This indicates that it satisfies the properties of multiple horizontal asymptotes but does not satisfy pleomorphism. In the differential H-AQ model E2 established by GADA, with the increase of H-AQ, the difference of extreme value between adjacent curves decreases gradually, the position of inflection points shifts obviously to the left, and the difference of slope at inflection point of adjacent curves increases gradually; at the same time, it satisfies the properties of multiple horizontal asymptotes and pleomorphism. Therefore, it can better predict the growth process of Larix kaempferi (Lamb.) plantation under different site conditions.

Table 5:

Comparison between model E0 and model E2 in terms of inflection, annual maximum height growth rate and dominant tree height at influence.

The inflection point of the curve is at the maximum slope.

H-AQ/m	E0			E2
	Inflection/ year	Annual maximum height growth rate/m	Dominant tree height at inflection/m	Inflection/ year	Annual maximum height  growth rate/m	Dominant tree height at inflection/m
10	7.4	0.4246	2.6238	9	0.4207	3.0196
12	7.4	0.5096	3.1486	8.6	0.5070	3.5093
14	7.4	0.5945	3.6734	8.3	0.5940	4.0045
16	7.4	0.6794	4.1982	8.0	0.6816	4.4609
18	7.4	0.7644	4.7229	7.7	0.7698	4.8764
20	7.4	0.8493	5.2477	7.5	0.8587	5.3354
22	7.4	0.9343	5.7725	7.2	0.9482	5.6737
24	7.4	1.0192	6.2973	7.0	1.0382	6.0709
26	7.4	1.1041	6.8220	6.8	1.1289	6.4402

DOI: 10.7717/peerj.17820/table-5

Site quality of a Larix kaempferi (Lamb.) Carrière (Lamb.) plantation in Dandong City

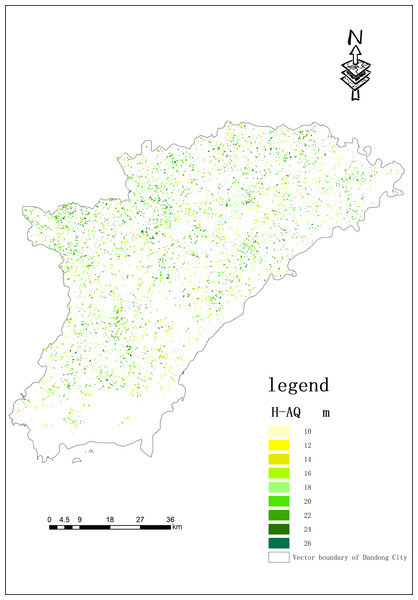
The area of forest land in each site was calculated and the results are shown in Fig. 5. The NPP values of sample plots in recent ten years was extracted by ArcMap 10.8 (the data comes from MOD17A3HGF-NPP data set), and its spatial distribution pattern is shown in Fig. 6. Forest land was divided into three site types according to status grade. This classification can evaluate ecological environment, resource utilization and productivity level according to site quality levels and provide reference for rational management and utilization of forest land resources. At the same time, this classification also meets the actual needs; it is simple, feasible, and has wide applicability. Among them, inferior sites account for 22%, average-quality site 58%, and high-quality sites 20%.

Figure 6 shows the spatial distribution of Larix kaempferi ’s site quality in Dandong City. It can be seen from the map that the compartments with better site qualities are mainly located in the west and north, showing a spatial distribution of regular dispersion and partial aggregation.

Different driving factors affecting NPP value

Correlation analysis between site class and NPP value

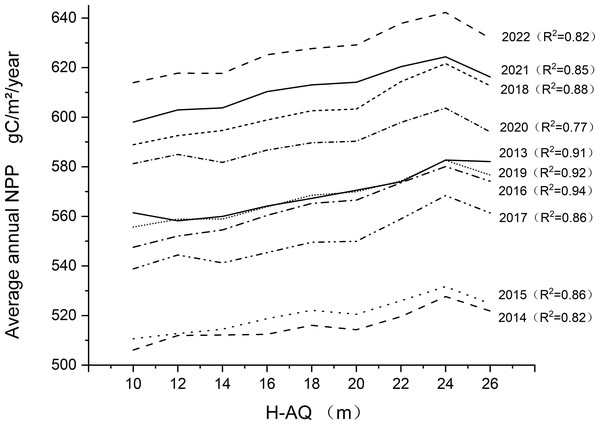
To verify the correlation between site class and NPP value, we drew a curve of the relationship between site class and average annual NPP value from 2013 to 2022 (Fig. 7). The results show that there is a good linear relationship between annual site classes and the average annual NPP value. Among them, the year with the highest determination coefficient (R²) is 2016, at 0.9401, while the lowest year is 2020, at 0.7657. Average determination coefficient (R²) is 0.86275. As can be seen from Table 6, there is a strong linear relationship between NPP and H-AQ, with the slope ranging from 10.5668 to 19.5745, with the highest slope in 2016 and the lowest in 2014. We also calculated the Spearman’s rank correlation coefficient and Kendall’s correlation coefficient for each year. The results are presented in Table 7. It can be observed from Table 7 that there was a positive correlation between NPP and H-AQ; the value of NPP increased with the promotion of H-AQ. The above results indicate that the NPP value of the Larix kaempferi plantation in Dandong City was significantly correlated with site class.

Table 6:

Table of parameters of the relationship between NPP and H-AQ for the year.

Prob > |t| indicates the significance of Pearson correlation coefficient.

Age	Parameter	Value	Prob >|t|
2013a	Intercept	5403.7360	1.63213E−13
2013a	Slope	15.8647	7.89518E−5
2014a	Intercept	4967.6172	2.34027E−13
2014a	Slope	10.5668	7.905E−4
2015a	Intercept	4994.4732	1.61517E−13
2015a	Slope	11.5183	3.54753E−4
2016a	Intercept	5285.6117	1.46458E−13
2016a	Slope	19.5745	1.56785E−5
2017a	Intercept	5205.7895	1.68817E−12
2017a	Slope	16.8432	3.47941E−4
2018a	Intercept	5693.6831	8.09517E−13
2018a	Slope	18.8428	1.57789E−4
2019a	Intercept	5388.7499	8.33928E−14
2019a	Slope	16.0164	3.92166E−5
2020a	Intercept	5685.6829	6.67134E−13
2020a	Slope	11.9316	0.00201
2021a	Intercept	5853.6045	2.76978E−13
2021a	Slope	14.5043	3.66374E−4
2022a	Intercept	5986.2488	9.29418E−13
2022a	Slope	15.7865	7.11769E−4

DOI: 10.7717/peerj.17820/table-6

Table 7:

Annual NPP and H-AQ correlation analysis.

	2013	2014	2015	2016	2017
Spearman	0.12099*	0.04030*	0.05904*	0.11995*	0.08439*
Kendall	0.08661*	0.02854*	0.04191*	0.08527*	0.05981*
	2018	2019	2020	2021	2022
Spearman	0.11895*	0.08701*	0.08545*	0.10476*	0.11079*
Kendall	0.08439*	0.06191*	0.06063*	0.07460*	0.07890*

DOI: 10.7717/peerj.17820/table-7

Notes:

Two-tailed significance test was used.

*The correlation is significant at the level of 0.05.

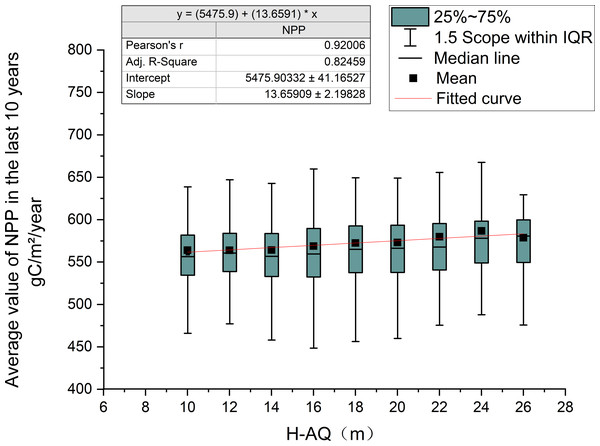
As can be seen from the linear fitting relationship between NPP and H-AQ in the last ten years (Fig. 8), the results show that its determination coefficient (R²) is 0.92006, indicating a highly significant linear correlation between NPP and H-AQ. When H-AQ increased by 2, the average NPP value in recent ten years increases by about 2.731 gC/m ²/year.

NPP resolution of under different site quality

The NPP quantity distribution of high-quality, average-quality, and inferior sites is shown in Fig. 9. The R of the NPP values for forest land with inferior quality and forest land with average quality, and forest land with average quality and high quality was calculated using Eq. (11).

According to the results in Table 8, there was a separation trend in the NPP value of forest land with different site qualities, but the separation trend was weak. Moreover, the forest land with better site quality showed an overall increasing trend compared with the forest land with poorer site quality.

Table 8:

Resolution.

Lands with an exponential order of 10∼14 are classified as inferior sites, lands with 16∼20 as average-quality sites, and lands with 22∼26 as high-quality sites.

R Inferior and average-quality	R average-quality and high-quality
0.057666	0.068485

DOI: 10.7717/peerj.17820/table-8

Effect of stand age on NPP value

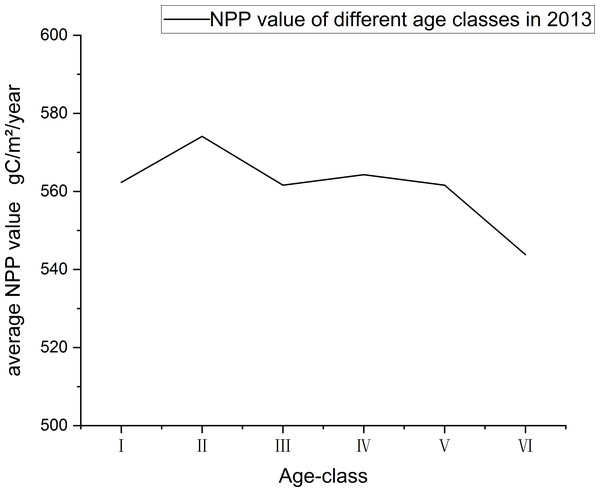
According to correlation analysis between the H-AQ and NPP values, there is a significant positive correlation between the NPP value and site classes in Dandong City. However, the variance of NPP value was relatively large under each site class, despite an overall growth trend (Fig. 8). According to Fig. 10 which shows the relationship between age class and average annual NPP, it can be observed that the maximum NPP values of Larix kaempferi in Dandong City, Liaoning Province in 2013 all appears in II (10-20 age class). By observing the age class-NPP curve of Larix kaempferi in Dandong City, Liaoning Province in Fig. 5, it can be seen that the rapid growth period occurs between 5 and 20 years. At this stage, the growth rate of Larix kaempferi is very fast. Therefore, the average NPP value of forest land of corresponding age class is the highest. This observation is also supported by Fig. 10. In addition, the age classes III and IV show low NPP values, which indicates that the growth of trees enters the mature stage and therefore the growth activity decreases (Fig. 10). Therefore, our observations were consistent with the growth characteristics of Larix kaempferi, showing that there is rapid growth between 5 and 20 years, after which trees grow slowly.