A data integration framework for spatial interpolation of temperature observations using climate model data

In situ data

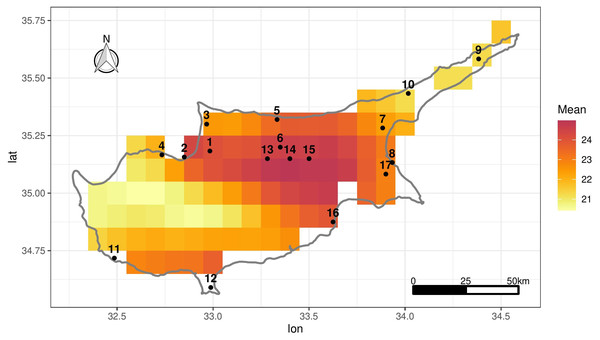
Daily measurements of maximum temperature (Tmax) at 2 m height were obtained from the Global Surface Summary of the Day (GSOD) which is derived from The Integrated Surface Hourly dataset (GSOD, 2022). There are 17 weather stations in Cyprus shown in Fig. 1 and 40 stations in Morocco (Fig. S5). For brevity we mostly focus on the Cyprus data, although we show some results relating to Morocco later on. Table 1 shows the temporal span of the data for each station, the elevation in meters and the proportion of missing values. Note that the stations are basically scattered around the coastline with little inland coverage particularly in terms of elevation (the middle and midwest of Cyprus where we have no data, have mountains reaching up to 2,000 m while the highest station in our data set is 217 m).

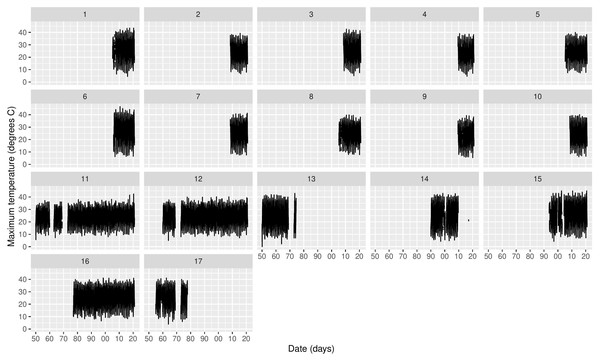
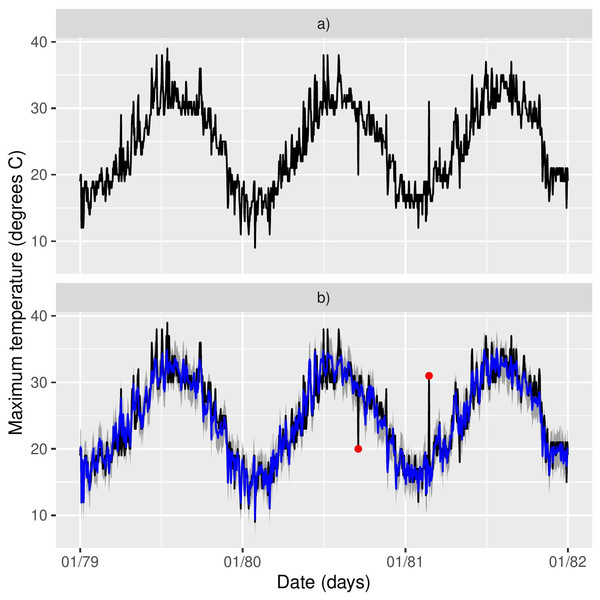
Figure 2 shows the time series of Tmax for the 17 stations, where missing values are clearly an issue both in terms of temporal span, but also in-between the sampling periods. The same table is provided for Morocco in the supplementary material. If we look at specific time snaps, for instance at station 16 between 1978 and 1982 shown in Fig. 3A, we can see that spurious outliers are apparent. Such outliers also appear in the Morocco time series (Fig. S6).

Reanalysis data

The data utilised here is the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis v5 or ERA5-Land (Muñoz Sabater, 2021; Muñoz Sabater et al., 2021). The ERA5-Land dataset has gridded hourly temperature at 2m height available from 1st January 1950 to 31st December 2020 at a 0.1° latitude × 0.1° longitude resolution (approximately 11 ×11 km). The reanalysis data set combines model data with observations from across the world and it is produced using 4D-Var data assimilation and model forecasts in CY41R2 of the ECMWF Integrated Forecast System (IFS). The maximum of the hourly temperature values in a given day was used as an estimate of the daily Tmax from ERA5-Land.

The ERA5-Land grid configuration over Cyprus is given in Fig. 1 which shows the mean daily Tmax in each grid cell over 1950–2020. Due to the coarseness of the grid, not all stations correspond to an ERA5-Land cell (e.g., stations 11 and 12). To match each station with an appropriate ERA5-Land grid cell, we associate a distance-weighted average of the ERA5-Land Tmax for the 10 nearest-neighbour cells of each station. For the remainder of the article, including the exploratory analysis that follows, the ERA5-Land values that are used are actually 10-cell weighted averages. This also alleviates the choice of a single “representative” grid cell for each station.

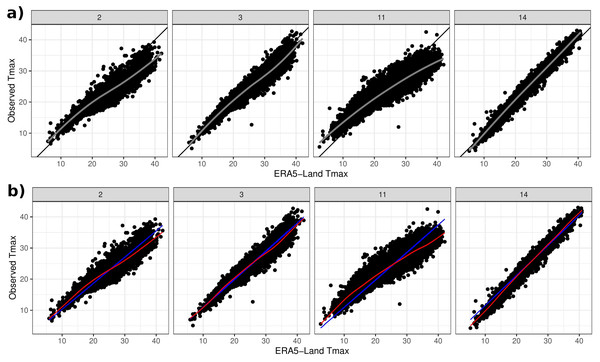
Figure 4A shows scatterplots of Tmax from four selected Cyprus stations plotted against the corresponding ERA5-Land Tmax. The plots were selected as a summary of the overall picture: a strong and approximately linear relationship. However, the slope of the apparent linear relationship varies, while some stations like 2 (Lefke) and 11 (Pafos) also exhibit non-linearity. Exploratory analysis (not shown) indicates that such non-linearities do not appear to be systematic e.g., they are not a function of coordinates or elevation or proximity to the coast. On the other hand, approximating the relationship with a linear (regression) fit indicates that stations in close proximity to each other exhibit a similar structure, as shown in Fig. S1 of the online supplementary material (e.g., stations 1–4 and also 6, 13–15). A qualitatively similar picture is also seen across the Morocco stations.

Bayesian penalised splines

A smooth function of some covariate x_i say, can be constructed using regression splines via a linear combination of basis function (Wood, 2017) e.g., (5)${\displaystyle f\left(x_i\right)=\sum _{k=1}^K{\beta }_k{b}_k\left(x_i\right)={\mathit{X}}_i\beta }$ where β = {β_k} are unknown coefficients (k = 1 conventionally aliased to an intercept) and b_k(⋅) are basis functions. Matrix X_i = {b_k(x_i)} with dimension n × K (n being the number of data points) is the model matrix. The value of K (conventionally the number of knots) determines the flexibility of f(⋅). Regression models involving such smooth functions can be estimated using penalised likelihood, where the penalty is in restricting the amount of flexibility in f(⋅) in order to avoid overfitting (Wood, 2011). Specifically, the log-likelihood to be maximised can be written as (6)${\displaystyle \ell \left(\beta ,\theta ;\mathit{y}\right)-{\lambda }_{\beta }{\beta }^{\prime }{\mathit{S}}_{\beta }\beta }$ where ℓ(⋅) is the log-likelihood, θ are other model parameters and λ_β is a penalty parameter. Moreover, S_β is a penalty matrix that relates to a quadratic penalty on β, and is basically a function of the particular basis functions chosen, as well as any constraints on the function. For instance, f(s) in equation Eq. (4) is centered on zero to identify the overall mean intercept α₀. The second term in Eq. (6) penalises the flexibility (wiggliness) of f(⋅) so the penalty increases with λ_β.

From a Bayesian perspective, the smoothness of f(⋅) can be viewed as a constraint on the values of β, which one can express in the form of an appropriate prior distribution (Wood, 2016; Wood, 2017). Specifically, (7)${\displaystyle \beta \sim N\left(0,{\Omega }_{\beta }^{-1}={\mathit{S}}_{\beta }^{-1}/{\lambda }_{\beta }\right).}$ This prior is improper since the precision matrix Ω_β = λ_βS_β is usually rank deficient (Wood, 2016). Instead, we can use the precision matrix ${\Omega }_{\beta }={\lambda }_{\beta }^{\left(0\right)}{\mathit{S}}_{\beta }^{\left(0\right)}+{\lambda }_{\beta }{\mathit{S}}_{\beta }$ where ${\mathit{S}}_{\beta }^{\left(0\right)}$ relates to the penalty of the null space of f(⋅) and ${\lambda }_{\beta }^{\left(0\right)}$ is the corresponding penalty parameter. This can be interpreted as separating the penalty matrix into penalised components S_β (e.g., wiggly behaviour) and unpenalised components ${\mathit{S}}_{\beta }^{\left(0\right)}$ (e.g., intercept and linear terms) (Pedersen et al., 2019; Wood, Scheipl & Faraway, 2013). This decomposition is exploited in defining function h_j(x) in Eq. (4), by not including the null space components. This way, the sum g(s)x + h_j(x) in Eq. (4) is a non-linear smooth function of x, decomposed into a linear part plus a non-linear “deviation”. Such penalty matrices and corresponding model matrices are readily provided by the R function jagam (Wood, 2016) from the R package mgcv.

Specification of the mean

Returning to the smooth functions f(⋅), g(⋅) and h(⋅) in Eq. (4), we choose thin-plate splines (Wood, 2017) as the basis functions for all of them. This particular basis can be used to define smooth functions of more that one variable whilst keeping the number of knots small. The slope term (dropping the station subscript j for clarity) is defined as: (8)${\displaystyle g\left(s\right)=g\left(lo{n}_s,la{t}_s\right)={\mathit{X}}^{\left(g\right)}\beta }$ (9)${\displaystyle \beta =\left({\beta }_1,\dots ,{\beta }_{N_{\beta }}\right)\sim N\left(\mathit{0},{\Omega }_{\beta }^{-1}\right)}$ (10)${\displaystyle {\Omega }_{\beta }=\sum _{i=1}^2{\lambda }_{\beta }^{\left(i\right)}{\mathit{S}}_{\beta }^{\left(i\right)}.}$ where X^(g) is the associated model matrix corresponding to the thin-plate splines of the coordinates. There are two penalty parameters, one for the null space and one for the wiggly part of g(⋅). We set N_β = J − 1, i.e., the total number of stations minus one (the maximum allowed given we only have J spatial locations), in order to a-priori give maximum flexibility should it be required.

The intercept term is defined in exactly the same way, except that we incorporate the overall mean α₀ in the vector of coefficients: (11)${\displaystyle \alpha =\left({\alpha }_0,{\alpha }_1,\dots ,{\alpha }_{N\alpha }\right)}$ (12)${\displaystyle f\left(s\right)=f\left(lo{n}_s,la{t}_s\right)={\mathit{X}}^{\left(f\right)}{\alpha }^{\left[-1\right]}}$ (13)${\displaystyle {\alpha }^{\left[-1\right]}\sim N\left(\mathit{0},{\Omega }_{\alpha }^{-1}\right)}$ (14)${\displaystyle {\Omega }_{\alpha }=\sum _{i=1}^2{\lambda }_{\alpha }^{\left(i\right)}{\mathit{S}}_{\alpha }^{\left(i\right)}}$ (15)${\displaystyle {\alpha }_0\sim N\left({\mu }_{{\alpha }_0,{\sigma }_{{\alpha }_0}^2}\right),}$ where the [ − 1] superscript denotes a vector without its first element and N_α = J − 1 as before. We set μ_α0 = 0 and ${\sigma }_{\alpha }^2=25$ to express a no prior beliefs about the value of the intercept but to also not allow it physically implausible values. (Recall that α₀ is the overall intercept when the value of ERA5-Land is zero, so it is reasonable to set the prior mean to zero given Fig. 4.) Note also that the full prior for α is (16)${\displaystyle \alpha \sim N\left({\mu }_{{\alpha }_0}=\left(\begin{array}{c}\hfill {\mu }_{{\alpha }_0}\hfill \\ \hfill \mathit{0}\hfill \end{array}\right),{\Omega }_{{\alpha }_f}^{-1}={\left(\begin{array}{cc}\hfill 1/{\sigma }_{{\alpha }_0}^2\hfill & \hfill \mathit{0}\hfill \\ \hfill \mathit{0}\hfill & \hfill {\Omega }_{\alpha }\hfill \end{array}\right)}^{-1}\right).}$

Finally, the non-linear effect of the ERA5-Land covariate is defined as (17)${\displaystyle h_j\left(x\right)={\mathit{X}}_j^{\left(h\right)}{\gamma }_j}$ (18)${\displaystyle {\gamma }_j=\left({\gamma }_{1,j},\dots ,{\gamma }_{N_{\gamma },j}\right)\sim N\left(\mathit{0},{\Omega }_{\gamma }^{-1}\right)}$ (19)${\displaystyle {\Omega }_{\gamma }={\lambda }_{\gamma }{\mathit{S}}_{\gamma }.}$ where ${\mathit{X}}_j^{\left(h\right)}$ is the model matrix of ERA5-Land values corresponding to station j and N_γ = 8, since exploratory analysis indicates that the non-linearity is not severe. There is only one penalty parameter as the function does not incorporate a linear term. Note also that while each station j has its own function h_j(x), they share a common penalty parameter λ_γ in order to pool information across the stations in this respect. Interpreting the function h_j(x) as a “random effect”, is also desirable in terms of being able to integrate it out when predicting at unseen locations.

Outlier mechanism

The outliers are modelled by a Uniform distribution, where station-specific parameter π_j determines the proportion of non-outliers. We model π_j hierarchically to further pool information across stations in this respect. Specifically, (20)${\displaystyle {\pi }_j\sim Beta\left({\alpha }_{\pi },{\beta }_{\pi }\right),}$ where we chose α_π = 5 and β_π = 2 so that the mean and standard deviation of π_j are 0.71 and 0.16. This way, more weight is given to values closer to 1, on the belief that most of the data points are not outliers.

Conditional variance

Each station is given its own conditional variance, to allow for station-specific variability about the mean (see Fig. 2). This is also done hierarchically: (21)${\displaystyle {\sigma }_j^2\sim InvGamma\left({\alpha }_{\sigma },{\beta }_{\sigma }\right).}$ so that again information is pooled across stations and one can integrate this parameter out when predicting in unseen locations. This prior is chosen to enable conditional conjugacy of ${\sigma }_j^2$ with the Gaussian likelihood. The hyperparameter α_σ is fixed to the value of 2, so that β_σ controls both the mean and variance of this distribution. Hyperparameter β_σ is given an Exp(0.1) prior with mean 10 and variance 100, to obtain a reasonably flat prior. Given α_σ and ${\sigma }_j^2$, β_σ is conjugate Gamma.

Penalty parameters

Lastly, for all penalty parameters ${\lambda }_{\alpha }^{\left(i\right)}$, ${\lambda }_{\beta }^{\left(i\right)}$ and λ_γ the half-Cauchy distribution (Gelman et al., 2013) with scale parameter 20 was chosen. Since larger values of λ imply more penalisation and therefore more smoothing, this heavy tailed prior was chosen to allow a wide range of values and therefore a wide range of wiggly behaviour of the smooth functions.

Sampling the outliers

Let Θ denote the list of all model unknowns and y denote the vector of all data points. The full conditional for z_j,t in Eq. (3) is (22)${\displaystyle p\left(z_{j,t}=1|\Theta ,\mathit{y}\right)\propto \frac{{\pi }_j}{\sqrt{2\pi }{\sigma }_j}exp\left\{2{\sigma }_j^{-2}{\left(y_{s_j,t}-{\mu }_{s_j,t}\right)}^2\right\}}$ (23)${\displaystyle p\left(z_{j,t}=0|\Theta ,\mathit{y}\right)\propto \frac{1-{\pi }_j}{U_{max}-U_{min}},}$ where we can reconcile proportionality by dividing Eqs. (22) and (23) by their sum.

Sampling the outlier proportions

Conditional on samples of z_j,t|Θ, y, the proportions π_j are sampled from their full conditional (24)${\displaystyle {\pi }_j|\mathit{z},\mathit{y},\Theta \sim Beta\left({\alpha }_{\pi }+\sum _t{z}_{j,t},{\beta }_{\pi }+n_j-\sum _t{z}_{j,t}\right)}$ using the fact that the Beta distribution is the conjugate prior of the Bernoulli proportion parameter (Fink, 1997).

Sampling the conditional variance

For the remainder of this section, we exploit conditional conjugacy when the likelihood is Gaussian, and therefore all results are presented conditionally on z_j,t = 1. Therefore, only data points corresponding to z_j,t = 1 contribute to the estimation of the non-outlier part of the model i.e., (1). As such, when vector y and model matrices such as X^(f) are used, they exclude indices or rows that correspond to z_j,t = 0.

Given z_j,t, the variances ${\sigma }_j^2$ can be sampled from their full conditional (Fink, 1997): (25)${\displaystyle {\sigma }_j^2|{\mathit{z}}_j,\mathit{y},\Theta \sim InvGamma\left({\alpha }_{\sigma }+n_j/2,{\beta }_{\sigma }+\sum _t{\left(y_{j,t}-{\mu }_{j,t}\right)}^2/2\right)}$ where n_j and the sum exclude any data points flagged as outliers by z_j,t|Θ, y.

Sampling the spline coefficients

For the coefficients, we use the following result. If θ ∼ N(Q⁻¹b, Q⁻¹) then θ ∼ N_C(b, Q) is the canonical parameterisation of the multivariate Normal. Now suppose that θ ∼ N_C(b, Q) (i.e., the prior) and also that y|θ ∼ N(θ, P⁻¹) (i.e., the conditional likelihood). Then, (26)${\displaystyle \theta |\mathit{y}\sim N_C\left(\mathit{b}+\mathit{P}\mathit{y},\mathit{Q}+\mathit{P}\right).}$ gives the full conditional for θ (Lemma 2.2 from Rue & Held (2005)).

We begin with the coefficients α of the intercept term. Let W|z = y − X^(g)β − X^(h)γ where γ = (γ₁, …, γ_J) and ${\mathit{X}}^{\left(h\right)}=\left({\mathit{X}}_1^{\left(h\right)},\dots ,{\mathit{X}}_J^{\left(h\right)}\right)$. Since y_sj,t|z_j,t = 1 is Gaussian, (27)${\displaystyle \mathit{W}|\mathit{z},\Theta \sim N\left({\mathit{X}}^{\left(f\right)}\alpha ,\Sigma \right)}$ where $\Sigma =\text{diag}\left({\sigma }_1^2,\dots ,{\sigma }_J^2\right)$ is a diagonal matrix such that each ${\sigma }_j^2$ is repeated n_j times. Pre-multiplying Eq. (27) by (X′^(f)X^(f))⁻¹X′^(f) gives (28)${\displaystyle {\left({{\mathit{X}}^{\prime }}^{\left(f\right)}{\mathit{X}}^{\left(f\right)}\right)}^{-1}{{\mathit{X}}^{\prime }}^{\left(f\right)}\mathit{W}|\alpha \sim N\left(\alpha ,\Sigma {\left({{\mathit{X}}^{\prime }}^{\left(f\right)}{\mathit{X}}^{\left(f\right)}\right)}^{-1}\right).}$ The prior on α is also Normal (see Eq. (16)) so using equation (26) its full conditional is (29)${\displaystyle \alpha |\mathit{W},\mathit{z},\Theta \sim N_C\left({\Omega }_{{\alpha }_f}{\mu }_{{\alpha }_0}+{{\mathit{X}}^{\prime }}^{\left(f\right)}{\Sigma }^{-1}\mathit{W},{{\mathit{X}}^{\prime }}^{\left(f\right)}{\Sigma }^{-1}{\mathit{X}}^{\left(f\right)}+{\Omega }_{{\alpha }_f}\right).}$

In the same way, we can sample the slope term coefficients β. Let A|z = y − X^(f)α − X^(h)γ. Then, (30)${\displaystyle \mathit{A}|\mathit{z},\Theta \sim N\left({\mathit{X}}^{\left(g\right)}\beta ,\Sigma \right)}$ (31)${\displaystyle ⟹{\left({{\mathit{X}}^{\prime }}^{\left(g\right)}{\mathit{X}}^{\left(g\right)}\right)}^{-1}{{\mathit{X}}^{\prime }}^{\left(g\right)}\mathit{A}|\beta \sim N\left(\beta ,\Sigma {\left({{\mathit{X}}^{\prime }}^{\left(g\right)}{\mathit{X}}^{\left(g\right)}\right)}^{-1}\right).}$ so that the full conditional is (32)${\displaystyle \beta |\mathit{A},\mathit{z},\Theta \sim N_C\left({{\mathit{X}}^{\prime }}^{\left(g\right)}{\Sigma }^{-1}\mathit{A},{{\mathit{X}}^{\prime }}^{\left(g\right)}{\Sigma }^{-1}{\mathit{X}}^{\left(g\right)}+{\Omega }_{\beta }\right).}$

Finally, the station specific coefficients γ_j are sampled similarly for each station j. Let ${\mathit{B}}_j|{\mathit{z}}_j={\mathit{y}}_j-{\mathit{X}}_j^{\left(f\right)}\alpha -{\mathit{X}}_j^{\left(g\right)}\beta$, where y_j are the response values in station j and ${\mathit{X}}_j^{\left(f\right)}$ and ${\mathit{X}}_j^{\left(g\right)}$ are the row-subsets corresponding to station j of X^(f) and X^(g) respectively. As before, (33)${\displaystyle {\mathit{B}}_j|{\mathit{z}}_j,\Theta \sim N\left({\mathit{X}}_j^{\left(h\right)}{\gamma }_j,{\Sigma }_j\right)}$ where ${\Sigma }_j=\text{diag}\left({\sigma }_j^2\right)$. Mirroring Eq. (29), equations Eqs. (26) and (18) give: (34)${\displaystyle {\gamma }_j|{\mathit{B}}_j,{\mathit{z}}_j,\Theta \sim N_C\left(\left(1/{\sigma }_j^2\right){{\mathit{X}}^{\prime }}_j^{\left(h\right)}{\mathit{B}}_j,\left(1/{\sigma }_j^2\right){{\mathit{X}}^{\prime }}_j^{\left(h\right)}{\mathit{X}}_j^{\left(h\right)}+{\Omega }_{\gamma }\right).}$

Sampling the hyperparameters

The hyperparameter β_σ of the conditional variance ${\sigma }_j^2$ is sampled from its full conditional: (35)${\displaystyle {\beta }_{\sigma }|{\sigma }^2,{\alpha }_{\sigma }\sim Gamma\left(c+J{\alpha }_{\sigma },d+\sum _{j=1}^{J}1/{\sigma }_j^2\right)}$ where recall that J is the number of stations. All penalty parameters(${\lambda }_{\alpha }^{\left(i\right)}$, ${\lambda }_{\beta }^{\left(i\right)}$ and λ_γ) are sampled using random walk Metropolis–Hastings (Gelman et al., 2013), with acceptance rate tuned to be in the region [0.2, 0.5].

Outliers

The first step of the analysis is to identify erroneous outliers using the model. It is important to do this before checking the model, since here the outliers are modelled by a Uniform distribution. This reflects the fact that there is no knowledge about the outlier-generating mechanism, but it also means that prediction of individual outliers will be poor (beyond their inclusion within a prediction interval). To identify outliers, we use the posterior distribution p(z_j,t|y). MCMC samples of z_j,t|y are used to compute the probability of a non-outlier i.e., p(z_j,t = 1|y), and here any data point y_j,t for which p(z_j,t = 1|y) < 0.5 is identified as an outlier. More strict choices than 0.5 are possible of course, such as only considering points as outliers if 1 − p(z_j,t = 1|y) > 0.9.

Figure 3B shows the outliers identified for the station 16 in red, illustrating that at least intuitively the model is identifying the correct points as outliers. (A similar plot is given in Fig. S6 for a station in Morocco.) The last column in Table 1 shows the posterior mean of (1 − π_j) i.e., an estimate of the proportion of outliers in each station. The proportion of outliers is overall quite small (and similar to Morocco, see Table S1) but it varies across stations.

A basic sensitivity analysis was conducted to assess the ability of the model to capture outliers. Specifically, 500 randomly chosen data points were artificially set as outliers (but not ones that were identified as such by the model). These outliers were produced by adding/subtracting (with probability 0.5) a random sample from a Unif(M − 5, M + 5) distribution, where M = max(|y_sj,t − mean(y_sj,t)|). Here, M = 25 °C. This choice ensured that the fictitious outliers are not too “obvious“, but rather close to what may be considered an extreme. In 10 trial runs, all 500 of these were correctly identified each time, providing confidence to the outlier-identification mechanism.

Model checking

To assess the performance of the model, we used posterior predictive model checking (Gelman et al., 2013). This involves obtaining samples from the posterior predictive distribution (PPD) $p\left({\tilde{y}}_{s_j,t}|\mathit{y},\mathit{z}\right)$ of the response value ${\tilde{y}}_{s_j,t}$ at any station j and day t. Conditioning on z implies that the predictions are only for data points not identified as outliers. The mean of samples from the PPD was used as the point estimate in Fig. 3, whereas the sample 2.5% and 97.5% quantiles were used to construct the associated prediction intervals.

We check the model both in terms of predicting the individual Tmax values, but also in terms of the overall distribution. Predictions were first compared with observations (for any non-outliers), and Fig. 5A shows this for a specific station, indicating a good fit with the exception of some under-estimation of the upper extremes. To assess whether the overall distribution is captured appropriately, we compare order statistics. Observations are sorted from smallest to largest, and compared with the corresponding ranked predictions in a plot that can be interpreted as a Q-Q plot. Figure 5B shows this for the same selected station, indicating an overall good fit albeit with some slight under-estimation of the extreme lower tail. The station in Fig. 5 was specifically chosen as the one with the least optimal model fit, while corresponding plots for the remainder of the stations are given in Figs. S3 and S4 respectively. On the whole the model fits quite well, although for some stations the predictions slightly underestimate the very high extremes. The overall distribution is captured well across stations, with no systematic discrepancies. A qualitatively similar picture is apparent for the Morocco stations (Figs. S7 and S8), for both the individual predictions but also the overall distribution.

Since we use the model for extrapolation to unobserved locations, it is also important to check the out-of-sample performance. For this reason we perform K-fold cross validation, where each station is left out in turn and then its values predicted. Figure 6 shows the associated predictions against observations for all 17 stations. Model performance is very good for all stations, even stations 11 and 12 that are isolated compared to the rest. As a summary, we define the posterior mean of the PPD for each data point as a point estimate, and in Table 2 we compare (a) the overall mean, (b) the 5% and (c) the 95% quantile of daily Tmax for each station, against the corresponding point estimates. The table indicates high accuracy in the predictions, with deviations generally smaller than 2 °C for the mean and lower quantile. However, deviations increase for the upper quantile, reflecting the in-sample results where high extremes are slightly underestimated.

Relationship with the reanalysis data

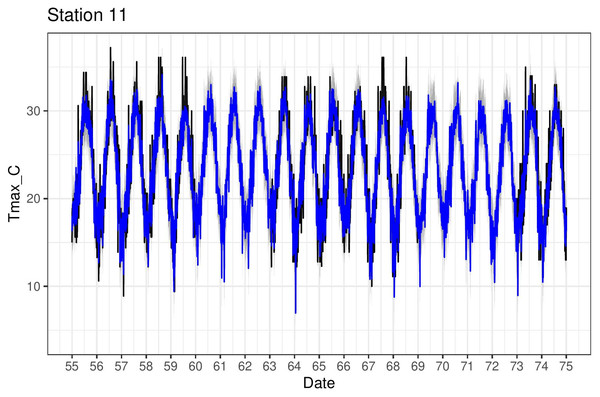
Figure 4B shows the estimates (posterior mean) of both the mean relationship Eq. (4) and also just the linear part f(s_j) + g(s_j)x_sj,t for the four chosen stations. The non-linear behaviour qualitatively matches the exploratory analysis in Fig. 4A. The model can also be used to impute missing values over the period 1950–2020 and Fig. 7 shows Tmax values for a particular station in the period 1955–1975. This station is missing values in 1960–1963 and also 1969–1973 so the model was used to impute these, along with quantifying the associated uncertainty.

Spatial extrapolation and aggregation

One of the aims of the framework is to allow for spatial extrapolation and aggregation to various spatial configurations (e.g., grids). To predict from the model at an unknown location, we must first integrate out the station-specific terms in the non-outliers part of the mode i.e., equation Eq. (1). These are: the non-linear part of the mean h_j(x) and the conditional variance ${\sigma }_j^2$. Mathematically, we simulate from the PPD of the response at location s: (36)${\displaystyle p\left({\tilde{y}}_{s,t}|\mathit{y}\right)={\int }_{{\sigma }_j^2,{\gamma }_j,\varphi }p\left({\tilde{y}}_{s,t}|{\sigma }_j^2,{\gamma }_j,\varphi \right)p\left({\sigma }_j^2|{\beta }_{\sigma }\right)p\left({\gamma }_j|{\lambda }_{\gamma }\right)p\left(\varphi |\mathit{y}\right)d{\sigma }_j^{2}d{\gamma }_{j}d\varphi }$ where ϕ denotes all parameters other than ${\sigma }_j^2$ and γ_j. Since h_j(x) is a function of γ_j, to integrate it out we need to simulate new γ_j’s from Eq. (18), where we use the R function jagam to set up the associated penalty matrix S_γ. Similarly we simulate “new” variances ${\sigma }_j^2$ for each unseen location using Eq. (25).

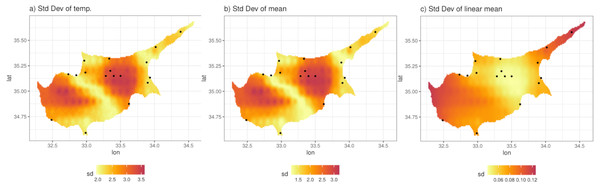
We illustrate this by predicting from the model at a grid of 0.01° ×0.01° (approximately 1 km ×1 km) resolution. Figure 8B shows the posterior predictive mean of the predictions for a particular day. Comparison with Fig. 8A, which shows the original ERA5-Land values for the same day, illustrates how the model can be used to downscale the reanalysis data, noting that the predictions from the model are also bias corrected (in a linear way). The non-linearity and station-specific variance have been integrated out and now are part of the prediction uncertainty. This uncertainty is quantified as the PPD standard deviation, shown in Fig. 9A. The contributing factors to the magnitude of this uncertainty are: station sparsity (i.e., more uncertainty when predicting in areas far from weather stations), the conditional variance ${\sigma }_j^2$, and the integration of the non-linear part of the relationship with ERA5-Land. Figure 9B shows the standard deviation of the mean temperature Tmax i.e., Eq. (4), which mirrors Fig. 9A indicating that the uncertainty due to the conditional variance is relatively small and spatially uniform. To understand the effect of non-linearity on the uncertainty, Fig. 9C shows the standard error of the mean, but without the non-linear term. This is clearly higher in regions with little data and vice versa. However, this uncertainty is small compared to when the non-linear terms is included, since the non-linear part adds uncertainty in regions where where ERA5-Land values are more extreme e.g., the central region with the highest temperature values (see Fig. 8B) that nonetheless contains four stations. This indicates that the non-linear term h_j(x) constitutes most of the prediction uncertainty.

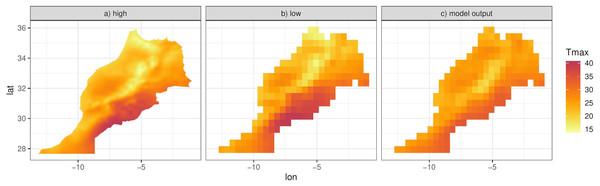
Since f(⋅), g(⋅) and h_j(x) are functions of random coefficients (α, β and γ), we can interpret the mean Eq. (4) and thus the predictions of the response as a random field. We can then integrate this random field over spatial regions, such as the six districts that make up the island of Cyprus (Fig. 8C). We can approximate this integral by simulating predictions at a high resolution grid (such as 0.01° ×0.01°) and then computing the mean of the simulations in each spatial unit. The higher the resolution, the better the approximation although for Cyprus we found virtually no difference in the results for resolutions higher than 0.01° ×0.01°. Figure 8C shows this approximation for the specific day, illustrating the ability of the model to predict at any spatial configuration. This also includes the ability to “upscale” the reanalysis to coarser resolutions for evaluating climate models. Figure 10 shows this for Morocco, where model predictions on a 0.01° ×0.01° grid are upscaled to 0.44° ×0.44° grid, the same grid corresponding to the output of a regional climate model (RCM) simulation. The RCM used to perform this simulation is the Weather Research and Forecasting (WRF) model (Skamarock & Klemp, 2008) driven by ERA-Interim reanalysis with a horizontal resolution of 0.44° (≈ 50 km) and 30 vertical levels, which was also used and evaluated in (Constantinidou et al., 2020). The model output is shown in Fig. 10C.