Benchmarking quantum mechanical methods for calculating reaction energies of reactions catalyzed by enzymes

Introduction

Quantum chemical calculations, including calculations with combined quantum mechanics/molecular mechanics (QM/MM) methods, are increasingly important in computational enzymology (Amaro & Mulholland, 2018; Blomberg et al., 2014; Huggins et al., 2019; Lonsdale, Ranaghan & Mulholland, 2010b; Senn & Thiel, 2009; Van der Kamp & Mulholland, 2013). It has recently become possible to apply high levels of quantum chemical theory to model enzyme-catalysed reactions (Bennie et al., 2016; Bistoni et al., 2018; Claeyssens et al., 2011; Daniels et al., 2014; Dieterich et al., 2010; Hermann et al., 2009; Ranaghan et al., 2019; Lawan et al., 2019; Mata et al., 2008; Van der Kamp, Perruccio & Mulholland, 2008; Van der Kamp et al., 2010), e.g., to model systems containing tens of atoms, i.e., of the size used in cluster models or as the QM region in a typical QM/MM calculation on an enzyme. Methods such as CCSD(T) offer the potential of ‘chemical accuracy’ (i.e., agreement with experiment to within ∼1 kcal mol⁻¹) in quantum chemical calculations (Bennie et al., 2016; Bistoni et al., 2018; Claeyssens et al., 2011; Daniels et al., 2014; Dieterich et al., 2010; Hermann et al., 2009; Lawan et al., 2019; Mata et al., 2008; Mulholland, 2007; Ranaghan et al., 2019; Van der Kamp, Perruccio & Mulholland, 2008; Van der Kamp et al., 2010; Zhang & Valeev, 2012). These methods provide a benchmark against which more approximate quantum chemical methods can be tested. This is important, because many applications to enzymes are likely (for reasons of computational requirements) to apply lower-level QM methods, e.g., for extensive reaction pathway or Hessian calculations (Lodola et al., 2005), or for biomolecular simulations (Khandogin, Musier-Forsyth & York, 2003; Khandogin & York, 2004), or for systems such as transition metal complexes. Here we compare and test a variety of quantum chemical methods that are commonly applied to model enzyme reaction mechanisms.

There are many levels of QM electronic structure calculations, falling into the broad categories of ab initio, semiempirical, and density-functional theory methods. Ab initio QM methods include Hartree-Fock (HF), coupled cluster singles and doubles and perturbative triples CCSD(T), second-order Møller Plesset perturbation theory (MP2) and its spin-component scaled variant (SCS-MP2) aim at the solution of the Schrödinger equation and hence focus on the wavefunction of the system. Semiempirical molecular orbital QM methods (Frisch et al., 2009; Thiel & Voityuk, 1992; Thiel & Voityuk, 1996), such as AM1 and PM3, neglect many of the terms that would arise in an ab initio calculation, and most of the remaining terms are represented by simpler functions, parameterized against theoretical or experimental data. These techniques have been modified to allow semiempirical electronic structure calculations on whole proteins (Khandogin, Musier-Forsyth & York, 2003; Khandogin & York, 2004; Van der Vaart et al., 2000). For density-functional theory methods (DFT), all properties are derived from the electron density. The computational effort required for DFT calculations is typically much smaller than that for correlated ab initio treatments, typically similar to HF theory, with a much higher accuracy than that of HF (Sousa, Fernandes & Ramos, 2007). There are many density functionals available for modeling enzyme reactions including BP86, BLYP, BPW91, B3LYP and B3PW91. Different functionals differ e.g., in their exchange-correlation functionals. A drawback of many density functionals is the lack of dispersion interaction (attractive Van der Waals forces), but empirical corrections can alleviate this problem (Grimme, 2004; Grimme, 2006; Jurečka et al., 2007; Wu & Yang, 2002). The resulting DFT-D3 methods (Grimme et al., 2010) are believed to be a promising method for calculations on biomolecular systems, where dispersion interactions are important (Schwabe & Grimme, 2008; Lonsdale, Harvey & Mulholland, 2012; Zhang & Chen, 2015).

Simplified DFT-based approaches which aim to retain DFT-type accuracy at reduced computational cost are also available (Foulkes & Haydock, 1989; Goringe, Bowler & Hernández, 1997; Porezag et al., 1995; Seifert, Eschrig & Bierger, 1986), such as the self-consistent charge density functional tight-binding (SCC-DFTB) method (Elstner et al., 1998). This method is a non-iterative DFTB implementation which introduces relaxation of the charge density at the level of Mulliken populations. This makes the method able to deal with in polar systems, in contrast to non-self-consistent tight binding approaches (Elstner et al., 2003). SCC-DFTB (and variants) is an increasingly widely used method in QM/MM studies of biomolecules (Capoferri et al., 2011; Elstner et al., 2000; Elstner, 2006; Lence et al., 2018; Liu et al., 2001).

In planning or judging QM/MM calculations, it is important to choose an appropriate quantum mechanical method. One must balance accuracy against feasibility of calculations, considering factors such as the size of the system, and how many calculations are needed. Several studies have reported the comparison of quantum mechanical methods for calculating reaction energy (Friedrich & Hänchen, 2013; Margraf, Ranasinghe & Bartlett, 2017) and for modelling enzyme-catalyzed reactions (Himo & Siegbahn, 2003; Kromann et al., 2016; Wappett & Goerigk, 2019).

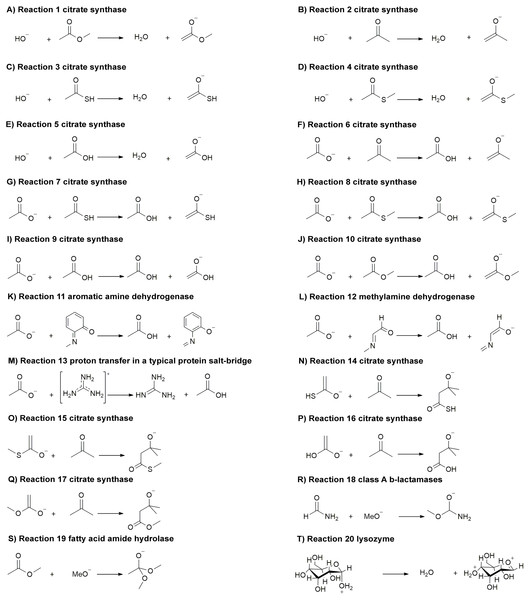
Here, we compare a range of quantum mechanical methods and basis sets that are often used for QM/MM calculations. We apply these methods for calculating 20 reaction energies of reactions (Fig. 1) related to the following enzymes (amongst others): citrate synthase (Bennie et al., 2016; Mulholland, Lyne & Karplus, 2000; Van der Kamp, Perruccio & Mulholland, 2007a; Van der Kamp, Perruccio & Mulholland, 2007b; Van der Kamp, Perruccio & Mulholland, 2008) (reaction 1–10, 14–17), aromatic amine dehydrogenase (AADH) (Johannissen, Scrutton & Sutcliffe, 2008; Masgrau et al., 2007; Pang et al., 2010; Ranaghan et al., 2017; Roujeinikova et al., 2007; Zelleke & Marx, 2017) (reaction 11), methylamine dehydrogenase (MADH) (Faulder et al., 2001; Nunez et al., 2006; Ranaghan et al., 2007; Tresadern et al., 2003; Zelleke & Marx, 2017) (reaction 12), proton transfer in a typical protein salt-bridge (reaction 13), class A β-lactamases (Chudyk et al., 2014; Hermann et al., 2003; Hermann et al., 2005; Hermann et al., 2006; Hermann et al., 2009; Langan et al., 2018; Meroueh et al., 2005) (reaction 18), fatty acid amide hydrolase (FAAH) (Lodola et al., 2005; Lodola et al., 2008; Lodola et al., 2010; Lodola et al., 2011; Palermo et al., 2014; Tubert-Brohman, Acevedo & Jorgensen, 2006) (reaction 19) and lysozyme (Bowman, Grant & Mulholland, 2008) (reaction 20), where reaction 1–13 and reaction 14–20 are proton transfer reactions and non-proton transfer reactions, respectively. These reactions represent widely different chemistry, and important classes of enzyme reactions: many of these enzyme reactions are model systems for testing and development of QM/MM methods. These ‘organic type’ reactions are also amenable to correlated ab initio calculations, for which transition metal systems are typically out of reach due to computational demands. The small models of these 20 reactions chosen here allow us to compare various quantum mechanical methods and basis sets with high level (CCSD(T)) calculations. Our aim is not to compare against experimental thermochemistry data (which is generally not available for complex reactions) but rather against high-level calculations, as a direct comparison of electronic structure methods.

Materials & Methods

The approach used in this work is comparable to procedures often applied in QM/MM calculations on enzyme reactions, for which reaction paths may be optimized with DFT methods, and then corrected with single point ab initio calculations (Claeyssens et al., 2006; Hermann et al., 2009; Lawan et al., 2019; Van der Kamp et al., 2010). The geometries of molecules from the 20 reactions were optimized in the gas phase at the B3LYP/6-311+G(d) level using the Gaussian03 (Frisch et al., 2004) program (see Table S1 and Supplemental Information 1 for coordinates). Energies of these structures were calculated using 24 combinations of quantum mechanical methods and basis sets: B3LYP/6-31+G(d), B3LYP-D3/6-31+G(d), B3LYP/6-311+G(d), B3LYP-D3/6-311+G(d), BP86/6-311+G(d), BP86-D3/6-311+G(d), BLYP/6-311+G(d), BLYP-D3/6-311+G(d), TPSS/6-311+G(d), TPSS-D3/6-311+G(d), BH&HLYP/6-311+G(d), HF/6-311+G(d), HF/aug-cc-pVDZ, HF/aug-cc-pVTZ, MP2/6-311+G(d), MP2/aug-cc-pVDZ, MP2/aug-cc-pVTZ, SCS-MP2/aug-cc-pVDZ, SCS-MP2/aug-cc-pVTZ, CCSD(T)/aug-cc-pVDZ, CCSD(T)/aug-cc-pVTZ, SCC-DFTB, AM1 and PM3 (Table S2). For all DFT, AM1, PM3, HF and MP2/6-311+G(d) calculations, the Gaussian03 program was used. For all other calculations, the Molpro92 program (Werner et al., 2012) was employed. CCSD(T)/aug-cc-pVTZ results were calculated as follows: CCSD(T)/aug-cc-pVTZ = CCSD(T)/aug-cc-pVDZ + [SCS-MP2/aug-cc-pVTZ –SCS-MP2/aug-cc-pVDZ]; this is an estimate of the results that would be obtained at the CCSD(T) level with the aug-cc-pVTZ basis set (Pitoňak et al., 2009; Sherrill, Takatani & Hohenstein, 2009; Smith & Gordon, 2011). For DFT-D3 energies, DFTD3 code (Grimme et al., 2010) with zero damping variant was employed to obtain the dispersion energy to add to the DFT energies. From the molecular energies, the reaction energies of each reaction were calculated and compared (Table S3). Zero-point and thermal contributions were not calculated as these cannot be calculated at the highest levels (e.g., CCSD(T)) and the aim here is to compare methods for calculating potential energy differences.

Results

Reactions energies of reaction 1–20 calculated with other methods are compared with those of CCSD(T)/aug-cc-pVTZ, which is, in principle, the most accurate of the approaches considered (Tables S4–Table S6). The mean absolute errors (MAEs) of reaction energies of reaction 1–20, MAEs of proton transfer reactions (PT reactions) and MAEs of non-proton transfer reactions (non-PT reactions) calculated by each method compared with those of CCSD(T)/aug-cc-pVTZ were calculated and shown in Fig. 2. These MAEs, standard deviations (SDs), large absolute errors (LAEs) along with their reaction number were also shown in Table S7. Moreover, coefficient of determinations (R²) between reaction energies calculated with other methods and reaction energies calculated with CCSD(T)/aug-cc-pVTZ were explored and shown in Table S7.

The results show that CCSD(T)/aug-cc-pVDZ has the lowest MAE (0.87 kcal mol⁻¹) followed by MP2/aug-cc-pVTZ, SCS-MP2/aug-cc-pVDZ and SCS-MP2/aug-cc-pVTZ which have MAEs of 1.16, 1.34 and 1.45 kcal mol⁻¹, respectively. It should be noted that, for some reactions (reaction 15–18), the absolute errors of 2.4 to 2.8 kcal mol⁻¹ are obtained from CCSD(T)/aug-cc-pVDZ. This indicates sensitivity to basis set for CCSD(T) calculations. Small basis sets are known to lead to inaccuracies for correlated wave-function methods. For CCSD(T) calculations, a large basis set (e.g. aug-cc-pVTZ) is required to achieve convergence (Helgaker, Klopper & Tew, 2008; Nagy & Jensen, 2017). Although the MAE of MP2/aug-cc-pVTZ is not significantly different from the MAE of SCS-MP2/aug-cc-pVDZ and SCS-MP2/aug-cc-pVTZ, the SD is much larger. This is due to a particularly poor performance of MP2/aug-cc-pVTZ in calculating the reaction energy of reaction 11 (absolute error of 6.39 kcal mol⁻¹ whereas its absolute errors from the other reactions was 2.22 kcal mol⁻¹ or less). For SCS-MP2/aug-cc-pVTZ, the largest absolute error and SD were only 2.48 kcal mol⁻¹ (reaction 14) and 0.78 kcal mol⁻¹, respectively, which are also lower than those of SCS-MP2/aug-cc-pVDZ (LAE = 3.48 kcal mol⁻¹ (reaction 20) and SD = 1.01 kcal mol⁻¹). These results indicate that SCS-MP2 is preferable to standard MP2 for calculations of reaction energies. In addition, the coefficient of determinations (R²) of SCS-MP2/aug-cc-pVDZ and MP2/aug-cc-pVTZ for 20 reactions (Table S7) (0.999 and 0.997, respectively) indicate that, compared to MP2, the SCS-MP2 method with a smaller basis set gives results close to accurate coupled-cluster calculations, at considerably less computational expense.

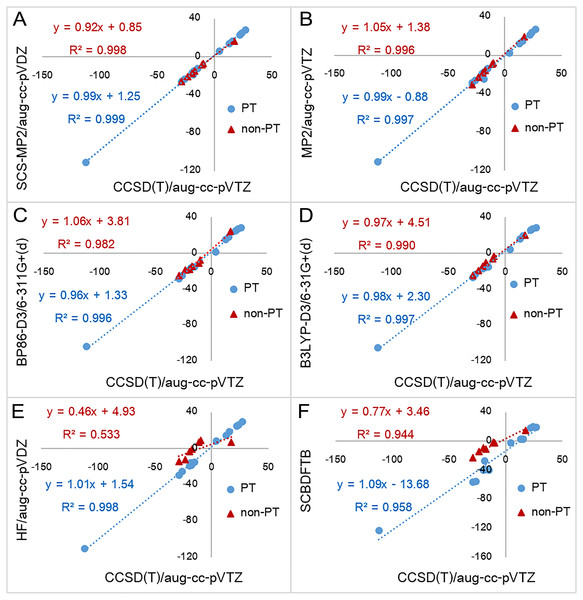
AM1 was found to have the largest MAE (14.58 kcal mol⁻¹) followed by PM3 (12.01 kcal mol⁻¹) and SCC-DFTB (11.56 kcal mol⁻¹). The largest absolute errors of AM1, PM3 and SCC-DFTB were 30.03 kcal mol⁻¹ (reaction 5), 21.32 kcal mol⁻¹ (reaction 3) and 29.44 kcal mol⁻¹ (reaction 3), respectively. This indicates that, in comparison of semi-empirical methods, SCC-DFTB is the best method for the calculation of reaction energies, especially for non-PT reactions. It can be noted that MAE of non-PT reactions obtained from SCC-DFTB (5.98 kcal mol⁻¹) is lower than those of B3LYP without dispersion correction (6.32 kcal mol⁻¹). The correlation plot between CCSD(T)/aug-cc-pVTZ reaction energies and SCC-DFTB reaction energies for non-PT reactions obtained has the linear regression line equation of y = 0.77x − 3.46 (R² = 0.944) (Fig. 3). However, semi-empirical methods perform particularly badly for PT reactions involving OH⁻ as the base (reaction 1–5) for which the MAEs of AM1, PM3 and SCC-DFTB are 26.92, 18.24 and 24.72 kcal mol⁻¹, respectively. When omitting reactions with OH⁻ as the base, the MAEs of AM1, PM3 and SCC-DFTB decrease to 10.60, 5.00 and 7.80 kcal mol⁻¹, respectively.

All DFT functionals without dispersion correction have similar MAEs at 3.56–5.10 kcal mol⁻¹, whereas the equivalent DFT-D3 functionals have somewhat smaller MAEs at 2.53–3.69 kcal mol⁻¹. BP86-D3/6-311+G(d) has the smallest MAE of 2.53 kcal mol⁻¹. For each DFT method, the MAE is slightly larger than that of the equivalent DFT-D3 method. This indicates that in inclusion of dispersion corrections improves the results. The largest absolute error obtained from DFT and DFT-D3 methods were 12.45 kcal mol⁻¹ (reaction 19 with BLYP/6-311+G(d)) and 9.28 kcal mol⁻¹ (reaction 19 with BLYP-D3/6-311+G(d)), respectively. Absolute errors for reaction 13 obtained from all DFT functionals are rather large (minimum of 6.72 kcal mol⁻¹ and 7.81 kcal mol⁻¹ in average). This indicates that all DFT functionals perform particularly badly for reaction 13, which involves a large change in conjugation. This error may be due to self-interaction error in DFT (Bao, Gagliardi & Truhlar, 2018; Gräfenstein & Cremer, 2009; Schmidt et al., 2014).

For HF, the MAEs (5.94–7.83 kcal mol⁻¹) are higher than those of DFT but much lower than those of AM1, PM3 and SCB-DFTB. Interestingly, MAEs of HF with Dunning basis set for PT are only 1.72–1.91 kcal mol⁻¹, which are lower than those of DFT functionals (2.20–3.44 kcal mol⁻¹). This indicates that HF performs particularly well for calculating reaction energies of PT.

MP2 and HF are clearly sensitive to basis set (MP2 with aug-cc-pVTZ and aug-cc-pVDZ, MAEs are 1.16 and 1.75 kcal mol ⁻¹, whereas with 6-311+G(d) the MAE is 3.92 kcal mol ⁻¹). The DFT results are less sensitive to the basis set. Increasing basis set size does not always improve the accuracy of the DFT functionals. For example, the MAE of B3LYP/6-311+G(d) is 0.11 kcal mol⁻¹ larger than that of B3LYP/6-31+G(d).

Discussion

AM1 and PM3 are found (as expected) to perform poorly in calculating reaction energy compared to all the other methods (MAEs of 14.58 and 12.01 kcal mol⁻¹, respectively). This is due to the fact that AM1 and PM3 include many approximations. Errors in reaction barriers from these methods are likely to be larger than the errors in reaction energies reported here. With a speed comparable to the semiempirical AM1 and PM3 methods and 2–3 orders of magnitude faster than ab initio and DFT methods, SCC-DFTB is found to perform similarly to PM3 and better than AM1 for the 20 reaction energies computed here (MAE of 11.56 kcal mol⁻¹). Additionally, our results demonstrate that SCC-DFTB performs very well for the calculation of reaction energies of non-PT reactions. Otte et al. found that the overall accuracy of SCC-DFTB was similar to popular semiempirical methods and its performance for geometries was very good, but the method appeared to be less suitable for radicals and excited states (Otte, Scholten & Thiel, 2007). Sattelmeyer, Tirado-Rives & Jorgensen (2006) compared the performance of SCC-DFTB and NDDO-based semiempirical methods and found that SCC-DFTB was typically intermediate between AM1 and PM3 for calculating isomerization energies and heats of formation, but less accurate for heats of formation of ions and radicals. Good performance of DFTB for the calculation of zero-point corrected reaction energies compared to BLYP and G2 methods was also observed by Krüger and Elstner (Kruger et al., 2005). SCC-DFTB is increasingly used successfully for QM/MM calculations (Capoferri et al., 2011; Elstner, 2006; Hou et al., 2012). Elstner et al. have also developed DFTB3 which are particularly useful for biomolecular systems because it improves the description of charged systems containing elements C, H, N, O, and P, especially regarding hydrogen binding energies and proton affinities (Gaus, Cui & Elstner, 2011).

For the biologically relevant reaction energies considered here, HF with a 6-311+G(d) basis set performs much better than the semi-empirical methods (a MAE less than half). However, HF results show relatively large errors compared with the other methods (MAE of 5.94–7.83 kcal mol⁻¹). HF also typically overestimates the activation energies and enthalpies, e.g., for a Claisen rearrangement in chorismate mutase (CM) and an electrophilic aromatic substitution in para-hydroxybenzoate hydroxylase (PHPH) by about factor of 3, compared with LCCSD(T0) (Claeyssens et al., 2006). However, the errors of HF tend to be systematic and may partly cancel out when comparing similar systems. Moreover, HF does well for predicting proton transfer reaction energies, because the proton carries no electrons with it and this type of reaction is therefore considerably less sensitive to the differential electron correlation in the reactants and the products (Cramer, 2004). QM/MM calculations on proton transfer in citrate synthase showed that this depends on the basis set used, however: QM/MM reaction energies with HF/6-31+G(d) and HF/aug-cc-pVDZ were 11.8 and 3.2 kcal mol⁻¹ higher than with LCCSD(T0)/aug-cc-pVDZ, respectively (Van der Kamp et al., 2010). Good HF results for reaction energies are obtained for some reaction types, such as isomerization reactions (Hehre, 1995; St.-Amant et al., 1995). Further, HF coupled with a dispersion correction has been found to be suitable for the optimization of small gas-phase peptide structures (Goerigk, Collyer & Reimers, 2014).

DFT methods are far superior to the AM1, PM3, SCC-DFTB and HF methods. The DFT MAEs are typically less than half of that of HF. Moreover, the results of different DFT functionals are similar. Although errors of DFT are about 50% larger than those of correlated ab initio calculations, their errors are still relatively small (2.53–5.10 kcal mol⁻¹). DFT is consequently a valuable tool for systems which do not need very high accuracy. Notably, the results reported in this work indicate that the accuracy of DFT can be improved by an empirical correction for dispersion (Grimme et al., 2010; Jurečka et al., 2007; Lonsdale, Harvey & Mulholland, 2010a; Lonsdale, Harvey & Mulholland, 2012), which requires very little additional computational effort. Although the (meta)-GGA functionals (BP86 and TPSS) do remarkably well once the dispersion correction is added, they are likely to perform much worse for transition states (and therefore reaction barriers), due to their semi-local nature. Additionally, because the computational effort required for DFT calculations is typically comparable with that required for HF, DFT and DFT-D3 are highly attractive, especially for medium to large systems for which the costs of correlated ab initio calculations are prohibitive (Himo & Siegbahn, 2003; Kromann et al., 2016; Lonsdale, Harvey & Mulholland, 2012; Zheng, Zhao & Truhlar, 2009). A good performance of DFT-D for geometries compared to DFT was also observed by Wappett and Goerigk (Wappett & Goerigk, 2019).

Prior to the advent of DFT, second-order Møller-Plesset perturbation theory (MP2) (Pople, Binkley & Seeger, 1976) was the simplest and the least expensive way of incorporating electron correlation effects in ab initio electronic structure calculations. MP2 is sometimes considered to be less accurate compared to density functionals such as B3LYP (Baker et al., 1996), though this lower accuracy is mainly encountered when using a basis set that is too small. It should however be noted that it is well known that convergence problems in the Møller-Plesset series appear primarily with extended basis sets (Olsen et al., 1996). The results presented here also demonstrate, as expected, that MP2 is very sensitive to the type of basis set used. In addition, for properties involving making or breaking of electron pairs, the performance of MP2 methods is substantially inferior to that of CCSD(T) and also not as good as the best DFT methods (Friesner, 2005). Hobza also demonstrated that MP2 overestimates dispersion interactions for non-covalent interactions (Hobza & Müller-Dethlefs, 2009). MP2 often gives surprisingly good results, especially if large basis sets are used (Helgaker et al., 1997; Jurecka et al., 2006).

For the calculation of reaction energies presented here, the simple modification of the MP2 approach termed SCS-MP2 (spin-component-scaled MP2) (Grimme, 2003) is found to be the best method compared to high-level coupled cluster theory. SCS-MP2 provides quite substantial corrections to the ground state energies, especially for molecules with complicated electronic structure, giving better performance than conventional MP2. Moreover, SCS-MP2 can give good predictions for energy barriers, hence SCS-MP2 is a good, reasonably affordable method for organic-type enzyme reactions (Bennie et al., 2016; Lawan et al., 2014; Lawan et al., 2019; Van der Kamp et al., 2010). Therefore, our benchmarking results here may help guide choices of QM methods for QM/MM calculations.

Overall the comparisons in this work show that MP2 and SCS-MP2 are in best agreement with CCSD(T)/aug-cc-pVTZ. Much larger errors are observed for AM1, PM3 and SCC-DFTB. Acceptable reaction energies are obtained from DFT and DFT-D3. DFT methods have also been found to give reasonable energy barriers for QM/MM calculations of potential energy barriers for enzyme-catalyzed reactions, compared with barriers derived from experiments and/or calculated with correlated ab initio methods (Kaiyawet et al., 2015; Lawan et al., 2019; Mlýnský et al., 2014; Rydberg et al., 2014; Van der Kamp, Perruccio & Mulholland, 2008).

Clearly, for modeling enzyme-catalyzed reaction, the accuracy of the results (such as the activation barrier, reaction energy and reaction pathway) depend not only on the QM method and basis set but also on other effects including the representation of surrounding amino acid residues and water environment, the size of QM regions etc (Boereboom, Fleurat-Lessard & Bulo, 2018; Jász et al., 2020 Mulholland, 2007; Ranaghan et al., 2019; Wappett & Goerigk, 2019). Hence, it would be of interest to (1) use larger model systems containing longer fragments or the nearest amino acid residues to test effects of system size, and (2) test more functionals and newer semiempirical methods. High level calculations such as CCSD(T)/aug-cc-pVQZ, which can be applied in QM/MM calculations on enzymes (Bennie et al., 2016; Bistoni et al., 2018; Claeyssens et al., 2011; Daniels et al., 2014; Dieterich et al., 2010; Hermann et al., 2009; Lawan et al., 2019; Mata et al., 2008; Ranaghan et al., 2019; Van der Kamp, Perruccio & Mulholland, 2008; Van der Kamp et al., 2010), can also be used to benchmark other methods.

Conclusions

The accuracy of several quantum mechanical methods for calculating reaction energies has been assessed for 20 small model reactions representing chemical steps catalyzed by enzymes. CCSD(T)/aug-cc-pVTZ results on a subset indicate that spin-component scaled MP2 (SCS-MP2) has similar accuracy. Comparison of methods for all reactions against CCSD(T)/aug-cc-pVTZ shows that several DFT functionals are also of good quality, especially with dispersion correction. Semi-empirical methods give much larger errors. The results should help with choosing and assessing QM methods for QM/MM calculations on enzyme-catalyzed reactions.

Supplemental Information