Composite learning tracking control for underactuated marine surface vessels with output constraints

Introduction

In recent years, with the development of the marine economy, marine transport vehicles have gained much attention (Shen et al., 2020; Yu, Guo & Yan, 2019). Marine surface vehicles (MSVs) have been widely used in marine exploration, marine transportation, marine survey and other fields (Liu et al., 2016; Shao et al., 2019). To accomplish these tasks, the trajectory tracking control of MSVs plays a significant role. Due to the influence of the external environment, the kinetics of MSVs inevitably have unknown dynamics and unknown time-varying environmental disturbances.

In view of this, a series of control approaches have been utilized for control of MSVs, including neural network (NN) control (Zhu et al., 2021; Li et al., 2015), fuzzy logic system (FLS) control (Peng, Wang & Wang, 2018; Wang, Sun & Er, 2018), disturbance observer-based (DOB) control (Guo & Zhang, 2020; Hu et al., 0000), and the finite-time control (Zhu, Ma & Hu, 2020; Wang, Pan & Su, 2019; Wang & Deng, 2020). In Zhu et al. (2021), Li et al. (2015), Peng, Wang & Wang (2018), Wang, Sun & Er (2018), NNs and FLSs are used to approximate the uncertain terms, such as unmodeled dynamics, unknown dynamics. In Guo & Zhang (2020), Hu et al. (0000), a DOB control approach was adopted to compensate compound uncertainty of parameter perturbations and unknown disturbances. In Do (2016) and Ghommam & Saad (2018), the dynamic uncertainties of MSVs were dealt with by parameter adaptive technique and a backstepping design tool.

To address the underactuation problem of MSVs, several control methods are introduced, such as additional control method (Do, 2010; Park, Kwon & Kim, 2017; Chen et al., 2020), output redefinition control (Shojaei & Arefi, 2015; Shojaei, 2017), line-of-sight (LOS) (Shojaei, 2015; Gao et al., 2016; Jia, Hu & Zhang, 2019; Liu, 2019), etc. Three additional control terms were adopted to address the underactuation problem of MSV in Do (2010), Park, Kwon & Kim (2017), Chen et al. (2020). To achieve the design of trajectory tracking control laws, the output redefinition control approach in Shojaei & Arefi (2015) and Shojaei (2017) was introduced to handle the underactuation problem, the combination of adaptive technique, NNs and saturation function to solve the unknown disturbances, unknown dynamic and input saturation, respectively. In Shojaei (2015), Gao et al. (2016), Jia, Hu & Zhang (2019) and Liu (2019), the LOS method was utilized to solve the underactuation problem of MSVs, the combination of parameter adaptive technology and NN approximation are used to successfully solve the time-varying external disturbance and parameter uncertainty.

For the sake of navigation safety, the output constraint problem is inevitably in practice. In practice, the navigable water areas are restricted, and then surface vessels should navigate in the navigable water areas. When the position error is too large, it may lead to collision accident of MSVs. When the yaw angle errors become excessive, the actuator will be damaged due to overload. Therefore, it is necessary to further study the MSVs trajectory tracking system with output constraints. Several methods have been presented to solve the output constraint problem, such as moving-horizon optimal control (Mayne & Michalska, 1990), artificial potential field (Sun & Ge, 2014), barrier Lyapunov function (BLF) (Tee et al., 2011) and output error transformation method (Zheng et al., 2020; Zhu, Du & Kao, 2020). In Zheng et al. (2020) and Zhu, Du & Kao (2020), the output constraint problem is transformed into a tracking error constraint problem by using the coordinate transformation. Coordinate transformation ensures that the tracking error always stays within predefined boundaries. Duo to the structure of Lyapunov function can be constructed by a barrier function, the BLF-based approach can solve the problem of trajectory tracking control for MSVs under the output constraint (Zhu, Du & Kao, 2020; Zhao, He & Ge, 2014). In simultaneous consideration of unknown dynamics and time-varying disturbances, Zhu, Du & Kao (2020) use a log-BLF method to solve the constant symmetric output constraint, Zhao, He & Ge (2014) utilize the asymmetric BLF method to deal with the asymmetric output constraints.

All the literature mentioned before have concentrated on the tracking and stability of the system. Most literature have not mentioned the precision accuracy of identifying models. In practice, the model uncertainty should be approximated as precisely as possible. In generally, the unknown dynamics of the system can be compensated by using adaptive control technique. In order to achieve better control performance, composite adaptive control scheme is developed in Patre & Bhasin (2010). It makes the system realize faster parameter convergence as well as smaller tracking error, and has been applied in various fields (Sun, Pan & Yang, 2017; Pan, Sun & Yu, 2016). By approximating the unknown dynamic items faster and more accurately to obtain better control performance, the prediction errors can be constructed by the serial-parallel estimation model (SPEM) (Peng, Wang & Wang, 2017). Then, the updating law of the neural network is designed by using the prediction error, which improves the transient performance effectively. To update the laws and optimize the system’s transient performance, Yucelen & Haddad (2013) presented an adaptive control modification. An error feedback term was included in the reference model in Pan, Sun & Yu (2016) and Stepanyan & Krishnakumar (2010) to improve the transient performance of the model. In Xu & Sun (2018), both the prediction errors and the tracking errors were applied to construct the updating law of NNs weights. The index of learning performance is introduced in the update rate, some literature focus on constructing composite learning laws by introducing auxiliary filter (Na et al., 2015; Huang et al., 2018) or using time interval data (Xu et al., 2019; Xu et al., 2018).

In this paper, we propose a composite learning control strategy for underactuated MSVs subject to unknown dynamics, ocean environmental disturbances, and output constraints based on the discussion above. The main contributions can be summarized as follows.

• Position error and yaw angle error constraints are addressed by employing the BLF-based method. The dynamic surface control approach is used to decrease the computation of the explosion problem that exists in the backstepping method.

• The composite NNs are employed to approximate the unknown dynamics of MSVs. Different from the traditional NN in which only the tracking errors are used to update the NN weights, both the tracking errors and prediction errors are used to update the NN weights. Therefore, the unknown dynamics can be approximated faster and more accurately.

• Using the approximation to the unknown dynamics of MSVs, the NDOs are constructed to estimate time-varying disturbances. By combining the dynamic surface control technique with disturbance observers and composite NNs, a trajectory tracking control system is developed. Compared with the control scheme based on neural networks, the proposed control scheme can effectively improve the transient and steady-state performance of MSVs trajectory tracking control.

The rest of this paper is arranged as follows. In Section 2, the mathematical model of MSVs and the problem formulation are introduced. In Section 3, the principle of intelligent approximation using NN is presented. In Section 4, proposes the details of controller design procedures. In Section 5, the simulation results are given to show the effectiveness of the controller. In Section 6, the entire work is summarized.

Problem formulation and preliminaries

Control Law Design

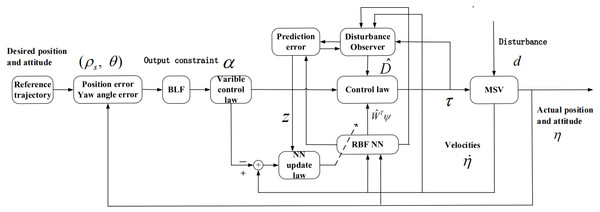
In this section, we can design the control law for the MSVs under Assumption 1–2. The block diagram of the trajectory tracking control system of MSVs is presented in Fig. 1. Combing Eqs. (5a) and (5b) with Eqs. (6a) and (6b), the time derivative of ρ_s can be written as (8)${\displaystyle {\dot{\rho }}_s=ucos\theta +vsin\theta +cos\theta {\zeta }_1+sin\theta {\zeta }_2}$ where ζ₁ and ζ₂ are defined as follows (9a)${\displaystyle {\zeta }_1=-{\dot{x}}_{d}cos\phi -{\dot{y}}_{d}sin\phi }$ (9b)${\displaystyle {\zeta }_2={\dot{x}}_{d}sin\phi -{\dot{y}}_{d}cos\phi }$

When MSV pass through a narrow passage, it is necessary to limit the position error ρ_s to prevent vehicle collisions. The BLF can be selected as the following form (10)${\displaystyle V_1=\frac{1}{2}log\frac{k_a^2}{k_a^2-{\rho }_s^2}}$

where log(∗) is the natural logarithm of (∗), k_a is the constraint of ρ_s, there exist $\left|{\rho }_s\right|<k_a$.

Taking time derivative of Eq. (10) , it can be further written as ${\displaystyle {\dot{V}}_1=\frac{{\rho }_s{\dot{\rho }}_s}{k_a^2-{\rho }_s^2}}$ (11)${\displaystyle =\frac{{\rho }_s}{k_a^2-{\rho }_s^2}\left(ucos\theta +vsin\theta +cos\theta {\zeta }_1+sin\theta {\zeta }_2\right)}$ The virtual control law can be designed as (12)${\displaystyle {\alpha }_u=sec\theta \left(-k_{\rho }{\rho }_s-vsin\theta -cos\theta {\zeta }_1-sin\theta {\zeta }_2\right)}$ where k_ρ is a positive constant.

In the surge direction, Let α_u pass through a first-order filter with a time constant T_u > 0 to get a new state variable β_u. (13)${\displaystyle T_u{\dot{\beta }}_u+{\beta }_u={\alpha }_u,{\beta }_u\left(0\right)={\alpha }_u\left(0\right)}$

Then, the filter error and velocity error can be defined as λ_u and u_e, respectively. So, it can be expressed as (14)${\displaystyle {\lambda }_u={\beta }_u-{\alpha }_u,u_e=u-{\beta }_u}$

The time derivative of λ_u can be calculated as ${\displaystyle {\dot{\lambda }}_u=-\frac{{\lambda }_u}{T_u}-{\dot{\alpha }}_u}$ (15)${\displaystyle =-\frac{{\lambda }_u}{T_u}+B_u}$ where B_u is a continuous function and has a maximum value H_u.

Then, V₂ can be further chosen as (16)${\displaystyle V_2=\frac{1}{2}log\frac{k_a^2}{k_a^2-{\rho }_s^2}+\frac{1}{2}{m}_{11}{u}_e^2}$

The time derivative of Eq. (16) can be written as ${\displaystyle {\dot{V}}_2=\frac{{\rho }_s{\dot{\rho }}_s}{k_a^2-{\rho }_s^2}+m_{11}{u}_e{\dot{u}}_e}$ (17)${\displaystyle =\frac{{\rho }_s}{k_a^2-{\rho }_s^2}\left(-u_{e}cos\theta -{\lambda }_{u}cos\theta -k_{\rho }{\rho }_s\right)+m_{11}{u}_e{\dot{u}}_e}$

According to Eqs. (2a) and (12), we can obtain the time derivative of as (18)${\displaystyle m_{11}{\dot{u}}_e=m_{22}vr-d_{11}u+{\tau }_u+\Delta f_u+d_u-m_{11}{\dot{\beta }}_u}$

The unknown term can be approximate using NN. We have m₂₂vr − d₁₁u + Δf_u = ω_u^Tψ_u + ξ_u. Here, let D_u = ξ_u + d_u. The ξ_u is the approximation error that satisfies the time derivative of ξ_u is bound. With Assumption 1, we can get (19)${\displaystyle \left|D_u\right|\le {\chi }_{u0},\left|{\dot{D}}_u\right|\le {\chi }_u}$ where χ_u0 and χ_u are unknown positive constants.

Therefore, the time derivative of V₂ can be further written as ${\displaystyle {\dot{V}}_2=\frac{{\rho }_s{\dot{\rho }}_s}{k_a^2-{\rho }_s^2}+m_{11}{u}_e{\dot{u}}_e}$ (20)${\displaystyle =\frac{{\rho }_s}{k_a^2-{\rho }_s^2}\left(u_{e}cos\theta +{\lambda }_{u}cos\theta -k_{\rho }{\rho }_s\right)+u_e\left({{\omega }_u}^T{\psi }_u+D_u+{\tau }_u-m_{11}{\dot{\beta }}_u\right)}$

Then, we can design the control law as (21)${\displaystyle {\tau }_u=-{\hat{\omega }}_u^T{\psi }_u-{\hat{D}}_u+m_{11}{\dot{\beta }}_u-k_u{u}_e-\frac{{\rho }_{s}cos\theta }{\left(k_a^2-{\rho }_s^2\right)}}$ where k_u is a positive constant. ${\hat{\omega }}_u$ is the estimation of the ${\omega }_u.{\hat{D}}_u$ is the estimation of the D_u. (22)${\displaystyle {\tilde{\omega }}_u={\omega }_u-{\hat{\omega }}_u,{\tilde{D}}_u=D_u-{\hat{D}}_u}$

From Eq. (21) along Eq. (20), we can get (23)${\displaystyle {\dot{V}}_2=\frac{{\rho }_s{\lambda }_{u}cos\theta -k_{\rho }{{\rho }_s}^2}{k_a^2-{\rho }_s^2}+u_e{\tilde{\omega }}_u^T{\psi }_u+u_e{\tilde{D}}_u-k_u{u_e}^2}$

Then, we can define z_u as prediction error (24)${\displaystyle z_u=u-\hat{u}}$

$\hat{u}$ can be defined with SPEM (25)${\displaystyle \dot{\stackrel{ˆ}{u}}=\frac{1}{m_{11}}\left({\tau }_u+{\hat{\omega }}_u^T{\psi }_u+{\hat{D}}_u+{\varphi }_u{z}_u\right)}$ where $\hat{u}\left(0\right)=u\left(0\right)$, ϕ_u is a positive constant.

The prediction error is employed to construct the weight updating (26)${\displaystyle {\dot{\stackrel{ˆ}{\omega }}}_u={\gamma }_u\left[\left(u_e+{\gamma }_{zu}{z}_u\right){\psi }_u-{\vartheta }_u{\hat{\omega }}_u\right]}$ where γ_u , γ_zu and ϑ_u are the positive constants to be designed.

The approximation information is employed to construct the NDO in the following form (27a)${\displaystyle {\hat{D}}_u=m_{11}u-{\sigma }_u}$ (27b)${\displaystyle {\dot{\sigma }}_u={\hat{\omega }}_u^T{\psi }_u+{\hat{D}}_u+{\tau }_u-\left(u_e+{\gamma }_{zu}{z}_u\right)}$

According to Eqs. (2a), (27a) and (27b), the derivative of ${\hat{D}}_u$ can be expressed as (28)${\displaystyle {\dot{\stackrel{ˆ}{D}}}_u={\tilde{\omega }}_u^T{\psi }_u+{\tilde{D}}_u+u_e+{\gamma }_{zu}{z}_u}$

Then, the ${\dot{\stackrel{̃}{D}}}_u$ can be calculated (29)${\displaystyle {\dot{\stackrel{̃}{D}}}_u={\dot{D}}_u-{\tilde{\omega }}_u^T{\psi }_u-{\tilde{D}}_u-u_e-{\gamma }_{zu}{z}_u}$

Combining Eqs. (5a)–(5b) with Eqs. (6a)–(6b), the time derivative of θ can be written as (30)${\displaystyle \dot{\theta }=-r+\frac{1}{{\rho }_e}\left(-usin\theta +vcos\theta -sin\theta {\zeta }_1+cos\theta {\zeta }_2\right)}$

It is also necessary to restrict θ in practice, there exist $\left|\theta \right|<k_b$. Similar to the above, we select the following BLF candidates as (31)${\displaystyle V_3=\frac{1}{2}log\frac{k_b^2}{k_b^2-{\theta }^2}}$

Taking time derivative of Eq. (31), it can be further written as (32)${\displaystyle {\dot{V}}_3=\frac{\theta }{k_b^2-{\theta }^2}\left(-r+\frac{1}{{\rho }_e}\left(-usin\theta +vcos\theta -sin\theta {\zeta }_1+cos\theta {\zeta }_2\right)\right)}$

According to Eq. (32), we can get virtual control law α_r for the yaw direction (33)${\displaystyle {\alpha }_r=k_{\theta }\theta +\frac{1}{{\rho }_e}\left(-usin\theta +vcos\theta -sin\theta {\zeta }_1+cos\theta {\zeta }_2\right)}$ where k_θ is a positive constant.

Remark 3: From Eq. (33), it can be seen α_r is undefined when ρ_e = 0. The positive constant ρ₀ is designed to make ρ_e − ρ₀ can converge to the neighbor of zero. It means that ρ_e can converge to the neighbor of ρ_e. Therefore, the singularity of α_r can be avoided.

Let α_r pass through a first-order filter with a time constant T_r > 0 to get a new state variable β_r. (34)${\displaystyle T_r{\dot{\beta }}_r+{\beta }_r={\alpha }_r,{\beta }_r\left(0\right)={\alpha }_r\left(0\right)}$

Then, the filter error and velocity error can be defined as λ_r and r_e, respectively. So, it can be expressed as (35)${\displaystyle {\lambda }_r={\beta }_r-{\alpha }_r,r_e=r-{\beta }_r}$

The time derivative of λ_r can be calculated as ${\displaystyle {\dot{\lambda }}_r=-\frac{{\lambda }_r}{T_r}-{\dot{\alpha }}_r}$ (36)${\displaystyle =-\frac{{\lambda }_r}{T_r}+B_r}$ where B_r is a continuous function and has a maximum value H_r.

Then, V₄ can be further chosen as (37)${\displaystyle V_4=\frac{1}{2}log\frac{k_b^2}{k_b^2-{\phi }_e^2}+\frac{1}{2}{m}_{33}{r}_e^2}$

The time derivative of Eq. (37) can be written as ${\displaystyle {\dot{V}}_4=\frac{\theta \dot{\theta }}{k_b^2-{\theta }^2}+m_{33}{r}_e{\dot{r}}_e}$ (38)${\displaystyle =\frac{\theta }{k_b^2-{\theta }^2}\left(-r_e-{\lambda }_r-k_{\theta }\theta \right)+m_{33}{r}_e{\dot{r}}_e}$

According to Eqs. (2c) and (35), we can obtain the derivative of r_e as (39)${\displaystyle m_{33}{\dot{r}}_e=\left(m_{11}-m_{22}\right)uv-d_{33}r+{\tau }_r+\Delta f_r+d_r-m_{33}{\dot{\beta }}_r}$

The unknown term can be approximate using NN. We have (m₁₁ − m₂₂)uv − d₃₃r + Δf_r = ω_r^Tψ_r + ξ_r . we can define D_r = ξ_r + d_r, The ξ_r is the approximation error that satisfies the time derivative of ξ_r is bound. With Assumption 1, we can get (40)${\displaystyle \left|D_r\right|\le {\chi }_{r0},\left|{\dot{D}}_r\right|\le {\chi }_u}$ where χ_r0 and χ_r are unknown positive constants.

Then, the time derivative of V₄ can be further written as (41)${\displaystyle {\dot{V}}_4=\frac{\theta }{k_b^2-{\theta }^2}\left(-r_e-{\lambda }_r-k_{\theta }\theta \right)+r_e\left({{\omega }_r}^T{\psi }_r+D_r+{\tau }_r-m_{33}{\dot{\beta }}_r\right)}$

Then, we can get (42)${\displaystyle {\tau }_r=-{\hat{\omega }}_r^T{\phi }_r-{\hat{D}}_r+m_{33}{\dot{\beta }}_r-k_r{r}_e+\frac{\theta }{k_b^2-{\theta }^2}}$ where k_r is a positive constant. ${\hat{\omega }}_r$ is the estimation of the ${\omega }_r.{\hat{D}}_r$ is the estimation of the D_r. (43)${\displaystyle {\tilde{\omega }}_r={\omega }_r-{\hat{\omega }}_r,{\tilde{D}}_r=D_r-{\hat{D}}_r}$

From Eqs. (41) along (40), we can get (44)${\displaystyle {\dot{V}}_4=\frac{\theta }{k_b^2-{\theta }^2}\left(-{\lambda }_r-k_{\theta }\theta \right)+r_e{\tilde{\omega }}_r^T{\psi }_r+r_e{\tilde{D}}_r-k_r{r_e}^2}$

Then, we can define z_r as prediction error (45)${\displaystyle z_r=r-\hat{r}}$

$\hat{r}$ can be defined with SPEM (46)${\displaystyle \dot{\stackrel{ˆ}{r}}=\frac{1}{m_{33}}\left({\tau }_r+{\hat{\omega }}_r^T{\psi }_r+{\hat{D}}_r+{\varphi }_r{z}_r\right)}$ where $\hat{r}\left(0\right)=r\left(0\right)$, ϕ_r is a positive constant.

The prediction error is employed to construct the weight updating (47)${\displaystyle {\dot{\stackrel{ˆ}{\omega }}}_r={\gamma }_r\left[\left(r_e+{\gamma }_{zr}{z}_r\right){\psi }_r-{\vartheta }_r{\hat{\omega }}_r\right]}$ where γ_r , γ_zr and ϑ_r are the positive constants to be designed.

The approximation information is employed to construct the NDO in the following form (48a)${\displaystyle {\hat{D}}_r=m_{33}r-{\sigma }_r}$ (48b)${\displaystyle {\dot{\sigma }}_r={\hat{\omega }}_r^T{\psi }_r+{\hat{D}}_r+{\tau }_r-\left(r_e+{\gamma }_{zr}{z}_r\right)}$

According to Eqs. (2a), (48a) and (48b), the derivative of ${\hat{D}}_r$ can be expressed as (49)${\displaystyle {\dot{\stackrel{ˆ}{D}}}_r={\tilde{\omega }}_r^T{\psi }_r+{\tilde{D}}_r+r_e+{\gamma }_{zr}{z}_r}$

Then, the ${\dot{\stackrel{̃}{D}}}_r$ can be calculated (50)${\displaystyle {\dot{\stackrel{̃}{D}}}_r={\dot{D}}_r-{\tilde{\omega }}_r^T{\psi }_r-{\tilde{D}}_r-r_e-{\gamma }_{zr}{z}_r}$

Remark 4: From Eqs. (26) and (47), it can easily obtain the weight updating of composite NN is designed by employing tracking error and prediction error. The prediction error can provide extra information for learning NN weight updating. Thus, better tracking performance can be achieved.

Remark 5: In Eqs. (26) and (47), γ_u and γ_r are positive constants used to optimize the learning rate. The ${\hat{\omega }}_u$ and ${\hat{\omega }}_r$ mainly tuned by the prediction errors if and are chosen larger, while if γ_zu and γ_zr are chosen smaller, the ${\hat{\omega }}_u$ and ${\hat{\omega }}_r$ mainly tuned by the tracking errors.

The compound unknown terms consist of unknown dynamics and time-varying disturbances are expressed as ∑_u and ∑_r. (51a)${\displaystyle m_{22}vr-d_{11}u+\Delta f_u+d_u={\Sigma }_u}$ (51b)${\displaystyle \left(m_{11}-m_{22}\right)uv-d_{33}r+\Delta f_r+{\tau }_{wr}={\Sigma }_r}$

Remark 6: The disturbance observer and neural network contain each other’s information. If compound unknown terms can be perfect follow by ${\hat{\omega }}_u^T{\psi }_u+{\hat{D}}_u$ and ${\hat{\omega }}_r^T{\psi }_r+{\hat{D}}_r$, the system’s estimation of unknown information can be more accurate. As a result, the objective of composite learning combining NN and NDO is accomplished.

Remark 7: Through trial and error, we first choose the appropriate design parameters k_ρ, k_θ, k_u, and k_r to ensure that the system is stable. Furthermore, we properly regulate the other design parameters γ_u, γ_zu, γ_r, γ_zr, ϑ_u, ϑ_r, ϕ_u and ϕ_r to get the satisfactory control performance. A large number of simulations in many cases show that the larger k_ρ, k_θ,, k_u, k_r , γ_zu, γ_zr, ϕ_u and ϕ_r are, the MSVs can obtain higher tracking accuracy.

Theorem 1: Considering the closed-loop system Eqs. (1a)–(1c) and Eqs.(2a)–(2c) with unknown dynamics, time-varying disturbances and output constraint under Assumption 1–Assumption 2, if virtual control law Eqs. (12), (33), control law Eqs. (21), (42), the NN updating laws Eqs. (26), (47) and NDOs Eqs. (27a)–(27b), Eqs. (48a)–(48b) are designed. It is guaranteed that all signals include in Eq. (52) are uniformly ultimately bounded (UUB).

Proof: Consider the following Lyapunov function (52)${\displaystyle V=V_2+V_4+\frac{1}{2}\left(\frac{1}{{\gamma }_u}{\tilde{\omega }}_u^T{\tilde{\omega }}_u+{\tilde{D}}_u^2+{{\lambda }_u}^2+m_{11}{\gamma }_{zu}{z}_u^2+\frac{1}{{\gamma }_r}{\tilde{\omega }}_r^T{\tilde{\omega }}_r+{\tilde{D}}_r^2+{{\lambda }_r}^2\mathrm{+}{m}_{33}{\gamma }_{zr}{z}_r^2\right)}$

The time derivative of Eq. (52) can be calculated as (53)${\displaystyle \dot{V}={\dot{V}}_2+{\dot{V}}_4+\frac{1}{{\gamma }_u}{{\tilde{\omega }}_u}^T\left(-{\dot{\stackrel{ˆ}{\omega }}}_u\right)+{\tilde{D}}_u\left(-{\dot{\stackrel{ˆ}{D}}}_u\right)+m_{11}{\gamma }_{zu}{z}_u{\dot{z}}_u+{\lambda }_u{\dot{\lambda }}_u+{\lambda }_r{\dot{\lambda }}_r+\frac{1}{{\gamma }_r}{{\tilde{\omega }}_r}^T\left(-{\dot{\stackrel{ˆ}{\omega }}}_r\right)+{\tilde{D}}_r\left(-{\dot{\stackrel{ˆ}{D}}}_r\right)+m_{33}{\gamma }_{zr}{z}_r{\dot{z}}_r}$

In the view of Eqs. (15), (36) and Young’s inequality, we can get (54)${\displaystyle {\lambda }_u{\dot{\lambda }}_u\le -\frac{{{\lambda }_u}^2}{T_u}+\frac{1}{2\iota }{{\lambda }_u}^2+2\iota {H_u}^2}$ (55)${\displaystyle {\lambda }_r{\dot{\lambda }}_r\le -\frac{{{\lambda }_r}^2}{T_r}+\frac{1}{2\iota }{{\lambda }_r}^2+2\iota {H_r}^2}$

Using Eqs. (26) and (47), we have (56)${\displaystyle \frac{1}{{\gamma }_u}{\tilde{\omega }}_u^T\left(-{\dot{\stackrel{ˆ}{\omega }}}_u\right)=-{\tilde{\omega }}_u^T\left[\left(u_e+{\gamma }_{zu}{z}_u\right){\psi }_u-{\vartheta }_u{\hat{\omega }}_u\right]}$ (57)${\displaystyle \frac{1}{{\gamma }_r}{\tilde{\omega }}_r^T\left(-{\dot{\stackrel{ˆ}{\omega }}}_r\right)=-{\tilde{\omega }}_r^T\left[\left(r_e+{\gamma }_{zr}{z}_r\right){\psi }_r-{\vartheta }_r{\hat{\omega }}_r\right]}$

From Eqs. (29) and (50), we have (58)${\displaystyle {\tilde{D}}_u{\dot{\stackrel{̃}{D}}}_u={\tilde{D}}_u\left({\dot{D}}_u-{\tilde{\omega }}_u^T{\psi }_u-{\tilde{D}}_u-u_e-{\gamma }_{zu}{z}_u\right)}$ (59)${\displaystyle {\tilde{D}}_r{\dot{\stackrel{̃}{D}}}_r={\tilde{D}}_r\left({\dot{D}}_r-{\tilde{\omega }}_r^T{\psi }_r-{\tilde{D}}_r-r_e-{\gamma }_{zr}{z}_r\right)}$

Combining Eqs. (2a)–(2c), (24), (25), (45) with Eq. (46), we can get (60)${\displaystyle m_{11}{\gamma }_{zu}{z}_u{\dot{z}}_u={\gamma }_{zu}{z}_u\left({\tilde{\omega }}_u^T{\psi }_u+{\tilde{D}}_u-{\varphi }_u{z}_u\right)}$ (61)${\displaystyle m_{33}{\gamma }_{zr}{z}_r{\dot{z}}_r={\gamma }_{zr}{z}_r\left({\tilde{\omega }}_r^T{\psi }_r+{\tilde{D}}_r-{\varphi }_r{z}_r\right)}$

Combining Eqs. (23), (44), (52)–(58) and Young’s inequality, Eq. (53) can be expressed as (62)${\displaystyle \dot{V}\le -\left(k_{\rho }-\frac{A}{2}\right)\frac{{{\rho }_s}^2}{k_a^2-{\rho }_s^2}-k_u{u_e}^2-{\gamma }_{zu}{\varphi }_u{z_u}^2-{\tilde{D}}_u^2-\left(\frac{1}{T_u}-\frac{1}{2A\left(k_a^2-{\rho }_s^2\right)}-\frac{1}{2\iota }\right){{\lambda }_u}^2+2\iota {H_u}^2+{\tilde{\omega }}_u^T{\vartheta }_u{\hat{\omega }}_u+{\tilde{D}}_u{\dot{D}}_u-{\tilde{D}}_u{\tilde{\omega }}_u^T{\psi }_u-\left(k_{\theta }-\frac{1}{2}\right)\frac{{\theta }^2}{k_b^2-{\theta }^2}-k_r{r_e}^2-{{\tilde{D}}_r}^2-\left(\frac{1}{T_r}-\frac{1}{2\left(k_b^2-{\theta }^2\right)}\right){{\lambda }_r}^2-{\gamma }_{zr}{\varphi }_r{z_r}^2+\frac{1}{2\iota }{{\lambda }_r}^2+2\iota {H_r}^2+{\tilde{\omega }}_r^T{\vartheta }_r{\hat{\omega }}_r+{\tilde{D}}_r{\dot{D}}_r-{\tilde{D}}_r{\tilde{\omega }}_r^T{\psi }_r}$

According to Young’s inequality, we can obtain (63)${\displaystyle -{\tilde{D}}_g{{\tilde{\omega }}_g}^T{\psi }_g\le \frac{1}{2}{\zeta }_g{\tilde{D}}_g^2{\varpi }_g^2+\frac{1}{2{\zeta }_g}{{\tilde{\omega }}_g}^T{\tilde{\omega }}_g}$ (64)${\displaystyle {\tilde{D}}_g{\dot{D}}_g\le \frac{1}{2}{\tilde{D}}_g^2+\frac{1}{2}{\chi }_g^2}$ (65)${\displaystyle {{\tilde{\omega }}_g}^T{\hat{\omega }}_g\le -\frac{1}{2}{{\tilde{\omega }}_g}^T{\tilde{\omega }}_g+\frac{1}{2}\parallel {{\omega }_g}^{\ast }{\parallel }^2}$ where ζ_g is positive user-defined parameter, ∥ψ_g ∥  ≤ ϖ_g, $\left|{\dot{D}}_g\right|\le {\chi }_g$, g = u, r.χ_g and ∥ω_g^∗ ∥ are positive constants.

From Eqs. (63)–(65), Eq. (62) can be expressed as

${\displaystyle \dot{V}\le -\left(k_{\rho }-\frac{A}{2}\right)\frac{{{\rho }_s}^2}{k_a^2-{\rho }_s^2}-k_u{u_e}^2-\left(\frac{1}{2}{\vartheta }_u-\frac{1}{2{\mu }_u}\right){\tilde{\omega }}_u^T{\omega }_u-\left(\frac{1}{T_u}-\frac{1}{2A\left(k_a^2-{\rho }_s^2\right)}-\frac{1}{2\iota }\right){{\lambda }_u}^2-\left(\frac{1}{2}-\frac{1}{2}{\mu }_u{\varpi }_u^2\right){\tilde{D}}_u^2-{\gamma }_{zu}{\varphi }_u{z_u}^2-\left(k_{\theta }-\frac{1}{2}\right)\frac{{\theta }^2}{k_b^2-{\theta }^2}-k_r{r_e}^2-{\gamma }_{zr}{\varphi }_r{z_r}^2-\left(\frac{1}{T_r}-\frac{1}{2\left(k_b^2-{\theta }^2\right)}-\frac{1}{2\iota }\right){{\lambda }_r}^2-\left(\frac{1}{2}{\vartheta }_r-\frac{1}{2{\mu }_r}\right){\tilde{\omega }}_r^T{\omega }_r-\left(\frac{1}{2}-\frac{1}{2}{\mu }_r{\varpi }_r^2\right){{\tilde{D}}_r}^2+2\iota {H_u}^2+\frac{1}{2}{\vartheta }_u\parallel {\omega }_u{\parallel }^2+\frac{1}{2}{\chi }_u^2+2\iota {H_r}^2+\frac{1}{2}{\vartheta }_r\parallel {\omega }_r{\parallel }^2+\frac{1}{2}{\chi }_r^2}$ (66)${\displaystyle \le -2aV+b}$ where $a=min\left(\left(k_{\rho }-\frac{A}{2}\right),k_u,\left(\frac{1}{T_u}-\frac{1}{2A\left(k_a^2-{\rho }_s^2\right)}-\frac{1}{2\iota }\right),{\gamma }_{zu}{\varphi }_u,\left(\frac{1}{2}{\vartheta }_u-\frac{1}{2{\mu }_u}\right),\left(\frac{1}{2}-\frac{1}{2}{\mu }_u{\varpi }_u^2\right),\left(k_{\theta }-\frac{1}{2}\right),k_r,\left(\frac{1}{T_r}-\frac{1}{2\left(k_b^2-{\theta }^2\right)}-\frac{1}{2\iota }\right),\left(\frac{1}{2}{\vartheta }_r-\frac{1}{2{\mu }_r}\right),\left(\frac{1}{2}-\frac{1}{2}{\mu }_r{\varpi }_r^2\right),{\gamma }_{zr}{\varphi }_r\right)$ , $b=2\iota {H_u}^2+\frac{1}{2}{\vartheta }_u\parallel {\omega }_u{\parallel }^2$ $+\frac{1}{2}{\chi }_u^2+2\iota {H_r}^2+\frac{1}{2}{\vartheta }_r\parallel {\omega }_r{\parallel }^2+\frac{1}{2}{\chi }_r^2.$

By choosing the appropriate design parameters to make $k_{\rho }>\frac{A}{2},k_u>0,\left(\frac{1}{T_u}-\frac{1}{2A\left(k_a^2-{\rho }_s^2\right)}-\frac{1}{2\iota }\right)>0,{\gamma }_{zu}{\varphi }_u>0,\left(\frac{1}{2}{\vartheta }_u-\frac{1}{2{\mu }_u}\right)>0,\left(\frac{1}{2}-\frac{1}{2}{\mu }_u{\varpi }_u^2\right)>0,k_{\theta }>\frac{1}{2},k_r>0,\left(\frac{1}{T_r}-\frac{1}{2\left(k_b^2-{\theta }^2\right)}-\frac{1}{2\iota }\right)>0,\left(\frac{1}{2}{\vartheta }_r-\frac{1}{2{\mu }_r}\right)>0,\left(\frac{1}{2}-\frac{1}{2}{\mu }_r{\varpi }_r^2\right)>0,{\gamma }_{zr}{\varphi }_r>0.$

By solving Eq. (66), we have (67)${\displaystyle 0\le V\le \frac{b}{2a}\mathrm{+\; [}V\mathrm{(0)}-\frac{b}{2a}\mathrm{]}{e}^{-2at}}$

From Eq. (67), we can obtain that $V\to \frac{b}{2a}$ as t → ∞. All signals in the Lyapunov function Eq. (52) are UUB. This concludes the proof.

Simulation Results

In this section, to demonstrate the effectiveness of the proposed control system, the dynamic model of an MSV in Do, Jiang & Pan (2004) is considered.

The model parameters of the MSV are presented as follows: m₁₁ =120 × 10³ kg, m₂₂ = 177.9 × 10³ kg, m₃₃ = 636 × 10⁵ kg m². d₁₁ =215 × 10² kg/s, d₂₂ = 147 × 10³ kg/s, d₃₃ = 802 × 10⁴ kg/m²s.

The proposed control scheme is marked as τ_CL. The control strategy without considering the prediction error is denoted as τ_NN.

Case 1: The reference trajectory is selected as x_d = 200sin(0.02t), y_d = 200cos(0.02t).

Unknown dynamics are selected as [Δf_u, Δf_v, Δf_r]^T = ${\left[\left(-0.2d_{11}\left|u\right|\right)u,\left(-0.2d_{22}\left|v\right|\right)v,\left(-0.2\left|r\right|\right)r\right]}^T.$ The external disturbances are given as [d_u, d_v, d_r]^T = [10⁴sin(0.3t − π/4) + 10⁴cos(0.2t + π/4) + 2 × 10⁴, 10³sin(0.2t − π/4)) + 10³cos(0.3t − π/4) + 3 × 10³, 10⁵sin(0.2t + π/6) + 10⁵cos(0.5t − π/4) (−3 × 10⁵]^T.

The initial condition is chosen as [x(0), y(0), φ(0), u(0), v(0), r(0)] =[20, 190,  − 0.02π,0,0,0]. The control laws design parameters are designed as ρ₀ = 10, k_ρ = 0.4, k_u = 6 × 10³, k_r = 3.18 × 10⁶, T_u = 0.8, T_r = 0.3, γ_u = 10000, γ_r = 100, γ_zu = 20, γ_zr = 3000, ϑ_u = 0.00001, ϑ_r = 0.0001, ϕ_u = 10, ϕ_r = 1.

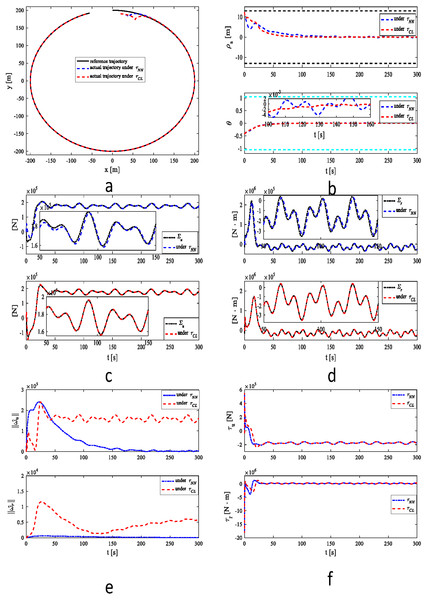
Figures 2A–2F illustrate the simulation results for the MSV under the two control strategies. Fig. 2A clearly illustrates that the MSV can track the reference trajectory in the presence of unknown dynamics, time-varying disturbances and output constraint under two control methods. The result in Fig. 2B shows that MSV can accomplish faster and more precise tracking under τ_CL. The results of approximation of unknown information in Figs. 2C and 2D further support this conclusion. The estimates of 2-norms weights are more sensitive under as illustrated in Fig. 2E. The control inputs τ_u and τ_r are plotted in Fig. 2F.

Case 2: The MSV’s unknown dynamics are raised 1.2 × Δf_n. The control law’s initial conditions and design parameters are the same as in Case 1, and the larger time-varying disturbances can be chosen as [d_u, d_v, d_r]^T = [1.5 × 10⁴sin(0.3t − π/4) + 1.5 × 10⁴cos(0.2t + π/4) + 3 × 10⁴, 1.5 × 10³sin(0.2t − π/4) + 1.5 × 10³cos(0.3t − π/4) + 3 × 10³, 1.5 × 10⁵sin(0.2t + π/6) + 1.5 × 10⁵cos(0.5t − π/4) − 4.5 × 10⁵]^T.

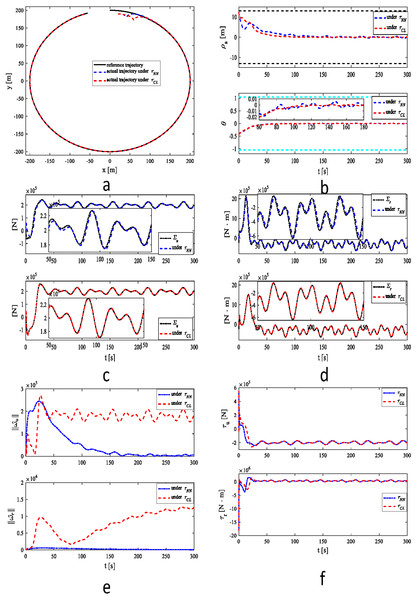
Under two control systems, MSV can track a reference trajectory in the presence of unknown dynamics, time-varying disturbances and output constraint as shown in Fig. 3A. As demonstrated in Fig. 3B, MSV can obtain higher tracking performance under τ_CL. The proposed control scheme has better robustness performance. As shown in Figs. 3C–3D, a similar result can be illustrated in case 1. The estimates of 2-norms weights are more sensitive under as illustrated in Fig. 3E. The control inputs are presented in Fig. 3F.

Case 3: The initial conditions and design parameters of the control law are the same as those in case 1. To further verify the superiority and effectiveness of the control scheme, another form of environmental disturbance are given as [d_u, d_v, d_r]^T = d + h. where d is d = [10⁴sin(0.3t − π/4) + 10⁴cos(0.2t + π/4) + 2 × 10⁴, 10³sin(0.2t − π/4) + 10³cos(0.3t − π/4) + 3 × 10³, 10⁵sin(0.2t + π/6) + 10⁵cos(0.5t − π/4) − 3 × 10⁵]^T. h is selected by the first-order Markov process. $\dot{\mathit{h}}$ = −Λh + Γ℘, where ℘ ∈ R³ is the zero-mean Gaussian white noise.

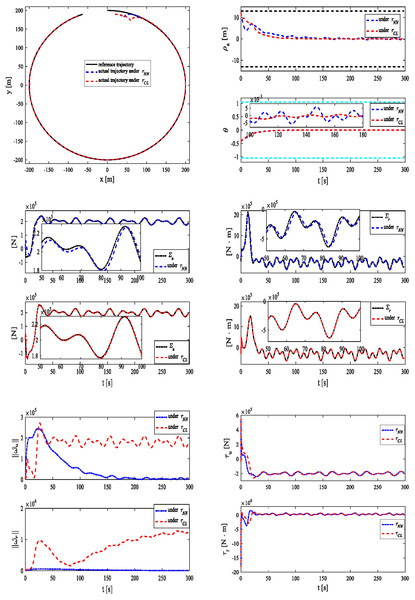
The simulation results are depicted in Figs. 4A–4F. Under two control systems, MSV can track a reference trajectory under unknown dynamics, time-varying disturbances and output constraint as shown in Fig. 4A. As demonstrated in Fig. 4B, MSV can achieve better tracking performance under τ_CL. As shown in Figs. 4C–4D, a similar result can be verified. The estimates of 2-norms weights are more sensitive under as shown in Fig. 4E. The control inputs are presented in Fig. 4F.

Conclusions

In this paper, a composite learning trajectory tracking control scheme is proposed for underactuated MSVs in the presence of unknown dynamics, time-varying disturbances and output constraints. The underactuation problem of the MSVs is addressed by the LOS approach. The barrier Lyapunov function is introduced to deal with the problem of output constraint. The composite learning control scheme is utilized to approximate unknown dynamics. The prediction errors and the tracking errors are adopted to construct the NN weight updating. Using approximation information, the disturbance observers are designed to estimates unknown time-varying disturbances. The Lyapunov method is used to demonstrate the stability of a closed-loop system. The simulation results demonstrate the effectiveness and superiority of the proposed control scheme.

Furthermore, the finite-time control can be further considered. The control scheme in this paper can be easily combined with event-triggered control.

Supplemental Information