An adaptive weighting mechanism for Reynolds rules-based flocking control scheme
- Published
- Accepted
- Received
- Academic Editor
- Tawfik Al-Hadhrami
- Subject Areas
- Adaptive and Self-Organizing Systems, Algorithms and Analysis of Algorithms, Autonomous Systems, Embedded Computing, Robotics
- Keywords
- Swarm behavior, Reynolds rules, Flocking control, Adaptive algorithm
- Copyright
- © 2021 Hoang et al.
- Licence
- This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, reproduction and adaptation in any medium and for any purpose provided that it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Computer Science) and either DOI or URL of the article must be cited.
- Cite this article
- 2021. An adaptive weighting mechanism for Reynolds rules-based flocking control scheme. PeerJ Computer Science 7:e388 https://doi.org/10.7717/peerj-cs.388
Abstract
Cooperative navigation for fleets of robots conventionally adopts algorithms based on Reynolds's flocking rules, which usually use a weighted sum of vectors for calculating the velocity from behavioral velocity vectors with corresponding fixed weights. Although optimal values of the weighting coefficients giving good performance can be found through many experiments for each particular scenario, the overall performance could not be guaranteed due to unexpected conditions not covered in experiments. This paper proposes a novel control scheme for a swarm of Unmanned Aerial Vehicles (UAVs) that also employs the original Reynolds rules but adopts an adaptive weight allocation mechanism based on the current context than being fixed at the beginning. The simulation results show that our proposed scheme has better performance than the conventional Reynolds-based ones in terms of the flock compactness and the reduction in the number of crashed swarm members due to collisions. The analytical results of behavioral rules’ impact also validate the proposed weighting mechanism's effectiveness leading to improved performance.
Introduction
Swarms of UAVs have recently achieved growing popularity in both industrial and research fields due to the development of UAV technology and reasonably priced models, namely drones or quadcopters (Bürkle, Segor & Kollmann, 2011). Compared with a single quadcopter, maneuvering a large group of these vehicles has many advantages (Seeja, Arockia Selvakumar & Berlin Hency, 2018; Tahir et al., 2019). For instance, fireworks are being replaced with light displays where manifold LED-equipped drones are controlled by an algorithm recreating objects from their flight patterns (Hörtner et al., 2012). Besides, UAV swarms can take soldiers’ place to sweep a large area in aerial reconnaissance missions (Wang et al., 2019). Since they are typically flown uninhabited, flocks of remotely piloted aircraft can be utilized in lethal situations such as gas leakage detection (Braga et al., 2017) or firefighting (Innocente & Grasso, 2019).
Although there are many benefits, multi-UAV systems still face certain challenges. Shakeri et al. (2019) demonstrated several architectures and design issues, including camera coverage of areas and objectives, control strategies for trajectory planning, image processing and vision-based methods, communication aspects, and low-level flight control. In practice, building a path planning scheme is one of the most fundamental yet crucial tasks as the basic activity of any swarms is to travel in groups before performing any particular tasks collectively. Besides, it requires that there is no collision not only among swarm members but also between an individual and its surroundings. Moreover, as wireless communication is usually deemed the backbone of a multi-UAV system, the problem arises when the aircraft have to keep a safe distance while maintaining adequate signal coverage among one another (Brust et al., 2012; Dai et al., 2019).
Possible solutions to swarm control methods are to adopt well-known clustering schemes. For example, Bannur et al. (2020) proposed a swarm control system responsible for obstacle avoidance and path planning based on Cohort Intelligence methodology (Kulkarni, Durugkar & Kumar, 2013), but refined for applications in dynamic environments. For UAV swarms using Flying ad-hoc Network (FANET), Khan, Aftab & Zhang (2019) implemented a self-organized flocking scheme by a behavioral study of Glowworm Swarm Optimization (GSO). The proposed system offered a wide range of functions such as route planning, cluster leader election, and cluster formation.
In addition, graph theory or topology can be studied to develop control schemes for multi-agent coordination systems. Olfati-Saber (2006) introduced a graph-theory-based framework to design and analyze three proposed algorithms for both distributed obstacle-free and constrained flocking. Shucker, Murphey & Bennett (2008) presented a cooperative control system that ensures the stability for network graphs, even in the graph topology switching. Likewise, Ning et al. (2018) investigated the dispersion and flocking behaviors by employing the acute angle test (AAT)-based rule for interactions with distant neighbors. Thanks to switching topology, this work has proved scalable, robust, and able to tackle the aforementioned signal coverage problem.
Other feasible and worth noting solutions are those based on the Reynolds rules (Reynolds, 1987). In such flocking schemes, each swarm member can perceive the surrounding environment, then makes its own movement decisions. A typical Reynolds-based flocking control scheme usually follows an iterative procedure adopted by every member in the entire swarm of N quadcopters to calculate the velocity vector and update its position. For example, quadcopter ith (i ∈ {1,2,…,N}) will determine its new position yi by yi = xi + vt where xi is the current position vector, v denotes the velocity vector affected by a set of swarm rules R, and t is the time traveled. Moreover, v is calculated by (1).
(1) where ui is the current velocity vector, wr and zr are the weight and the velocity vector for rule rth, respectively. That is to say, when cooperatively traveling in groups, quadcopters are directed by steering their current heading to the desired one, which is represented by the sum of all vectors zr generated by flocking behaviors. The act of calculating zr is also the feature of self-organizing flight schemes.
Conventionally, each rule’s weight w is fixed throughout the flight. The higher it is, the more its corresponding swarm rule affects the quadcopter’s behaviors. However, a problem arises as to how to determine an optimal set of rule weights, and thus it is essential to employ an adaptive weighting mechanism for the following reasons. Firstly, a set of rule weights not carefully chosen may lead to a considerable number of collisions between quadcopters due to excessive steering forces from swarm behaviors. Besides, optimal weights can usually be determined only after conducting a large number of experiments, which is time-consuming in general. Moreover, an adaptive weighting system will enable swarm members to be more robust against in-flight changes (e.g., an increasing number of swarm members).
However, developing an adaptive weighting scheme faces certain challenges. The scheme itself should adapt to different environments regardless of the length unit used in their coordinate system. Additionally, an effective weighting system should deal with the swarm’s common problems, such as reducing the swarm size or collision avoidance between UAVs. In this study, we propose an adaptive mechanism that allocates weights for each swarm rule’s velocity vector in every new step based on the current context rather than being fixed from the beginning. Meanwhile, our proposed method can also reduce the number of quadcopter crashes, compact the swarm shape, and work under various environment settings.
The Proposed Approach
Besides three traditional Reynolds rules, we also employ the Migration rule like Braga et al. (2018) to drive the UAV swarm to a specific location. In addition, the Avoidance rule is proposed and added to navigate the entire swarm away from stationary obstacles. Therefore, there are totally five behavioral rules adopted in our proposed control scheme, including Alignment, Avoidance, Cohesion, Migration, and Separation. As we examine the use of Reynolds rules for UAV swarm applications, it is required to consider which behaviors should be more particularly important based on real-world concerns. Therefore, we sort the swarm behaviors in priority order as partially suggested by Allen (2018), and then apply a novel adaptive weighting mechanism. However, in our proposed approach, the behaviors are grouped by their similarity in contextual significance instead of being separately prioritized. Hence, those behaviors in a group will share the same weighting function and the same value range of weight, ensuring that less important behaviors will not supersede those of greater importance.
Behavioral rule prioritization
The five above behavioral rules are divided into three groups of behaviors according to their contextual significance.
-
Both Separation and Avoidance should be given the highest priorities due to safety issues. In cases where they are both obstacles and neighbors violating the safety distance, the drone will attempt to avoid the nearest object.
-
The Migration rule is the second most crucial behavior since its role is to navigate the group of drones to destinations as planned.
-
The Alignment and Cohesion rules are used to make the drones travel in a swarm and maintain the compactness. They are the lowest priorities.
Adaptive weighting mechanism
The weights of the five behavioral rules, including wse (Separation), wav (Avoidance), wmi (Migration), wal (Alignment), and wco (Cohesion) are determined by (2)–(6), respectively.
(2)
(3)
(4)
(5)
(6) where
-
m denotes the number of nearby objects at a certain moment. An object within a quadcopter’s perception will be considered as its nearby neighbor in Separation, Cohesion, Alignment, and Migration rules or obstacles in Avoidance rule.
-
cs and ca are perception coefficients for the Separation and Avoidance rules, respectively.
-
dj,k is the distance between quadcopters ith and kth (in Separation); or between quadcopter ith and obstacle kth (in Avoidance), k ∈ {1,2,…,m}.
-
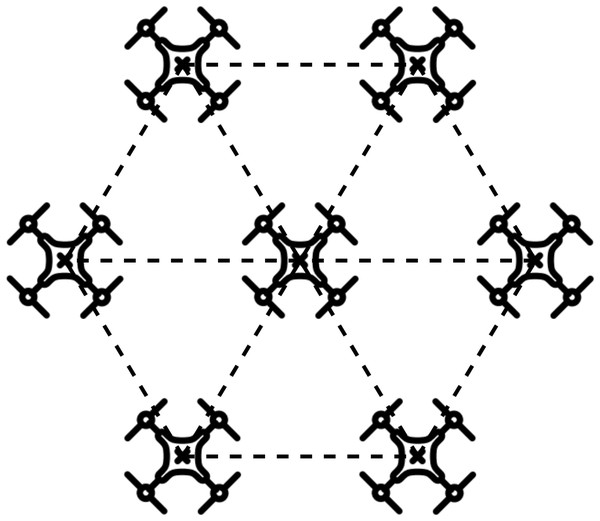
M is the optimal number of neighbors surrounding each quadcopter. In an ideal case, each of the six quadcopters will try to maintain the same relative distance with the one at the center and with two adjacent ones, consequently forming a hexagon with quadcopters at its center and vertices, as illustrated in Fig. 1. Therefore, for a swarm with a large enough number of members as in our implementation, M will be six (i.e., M = 6).
-
Ts and Ta are the transformation factors for Separation and Avoidance rules, respectively.
Figure 1: Ideal formation of a group of quadcopters.
Transformation factors
It is seen in (2) and (3), we introduce the transformation factors that are equal to the ratio of the desired maximum weight W to the corresponding perception coefficient (i.e., cs or ca). In detail, the solution of (cs − d2/cs) in (2) is a set of [0,cs] and that indicates the impact of distance based on the Separation rule perception, whose measurement unit may vary. For example, with cs = 5,000 m and maximum weight W = 30, the solution set [0,5000] is completely different from the weight range [0,30]. Therefore, Ts is used to keep the impact of Separation rule unaffected by the measurement unit, which makes our scheme able to adapt to different settings.
To calculate Ts, it is required to determine the maximum weight W and the distance dmin when Separation will become largely effective for safety issues. Since there is probably the situation where Migration, Alignment, and Cohesion vectors simultaneously point to the same direction, the Separation vector needs to point to the opposite direction to prevent any possible collisions. Therefore, the wse should satisfy (7).
(7)
As inferred from (4) to (6), the maximum values of wmi, wal, and wco are 2M, M, and M, respectively. Consequently, wse should be greater than 4M so as to take control of the drone. As a result, we have and 4M ∈ [0,W]. Additionally, since wse is proportional to (cs − d2/cs) according to (2), the maximum weight W can be computed by (8).
(8)
Then, Ts is obtained by (9).
(9)
In short, Ts can be computed based on particular preference for the shortest range dmin at which we want the drones begin to exponentially react to Separation rule. The act of choosing dmin can be done after M and cs are determined. For example, if dmin = 0.4cs then Ts ≈ 4.76M/cs. Similarly, the transformation factor Ta for Avoidance is determined by (10).
(10)
Rule implementation
The explanations for rules’ implementation will be given in prioritized groups. In both Separation and Avoidance, the drone travels away from nearby objects to avoid crashes, and a repulsion vector for each of them is formed. As we only consider the direction at this stage, these vectors are then normalized. Moreover, an impact called dist_impact is also calculated by (11).
(11) where c is the rule perception that can be cs or ca depending on either Separation or Avoidance, and d is the distance between two drones or between a drone and an obstacle. Subsequently, the normalized vectors are multiplied with dist_impact since we are expecting the smaller the distance is, the larger the magnitude of this repellent force is. Then, all resulting vectors are combined and the sum vector is scaled by (12).
(12)
where is the unit vector of v.
In addition, we need to find the nearest object among all detected ones with the most significant impact as max_impact inferred from (11) so that the drone will try to avoid the nearest object. Finally, the product of the scaled vector vs, max_impact, and T produces the return vector. Algorithm 1 describes the implementation of Separation and Avoidance rules, which are different by the transformation factor T (i.e., T can be Ts or Ta).
| Input: |
| d: The drone adopting the algorithm |
| ob: List of detected nearby objects, either neighbors or obstacles |
| T: The corresponding transformation factor Ts or Ta |
| Output: |
| vs: The scaled vector |
| 1: v ← (0,0) |
| 2: weight ← 0 |
| 3: max impact ← 0 |
| 4: for o in ob do |
| 5: dist ← distance between o and d |
| 6: if dist < c then |
| 7: dist_impact ← c − (dist * dist)/c |
| 8: vo ← o.position − d.position |
| 9: vo ← dist_impact * vo/dist |
| 10: v ← v − vo |
| 11: if max_impact < dist_impact then |
| 12: max_impact ← dist_impact |
| 13: end if |
| 14: end if |
| 15: end for |
| 16: vs ← scale(v) |
| 17: weight ← T * max_impact |
| 18: return vs * weight |
The Migration rule’s effect will attract the drones to the predefined target by forming a vector from the drone to the target point. The vector is then scaled using (12) and assigned a weight affected by the current number of nearby neighbors. If there are any detected neighbors, Migration weight will be M + M/m to get individuals in the group to the desired location rather than being stuck by the effects of Alignment and Cohesion. Otherwise, if there is no detected neighbor, the weight will be M. Both cases guarantee that Migration weight will always be equal or greater than the sum of Alignment and Cohesion weights. This weighting scheme ensures that even in case both Alignment and Cohesion velocity vectors point to the same direction but are opposite the target point, the drone will still be able to head towards its target. The implementation of the Migration rule is shown in Algorithm 2.
| Input: |
| d: The drone adopting the algorithm |
| m: The current number of detected neighbors |
| Output: |
| vs: The scaled vector |
| 1: v ← (0,0) |
| 2: weight ← 0 |
| 3: if checkpoint ≠ null then |
| 4: v ← checkpoint − d.position |
| 5: vs ← scale(v) |
| 6: if m ≠ 0 then |
| 7: weight ← (M + M/m) |
| 8: else |
| 9: weight ← M |
| 10: end if |
| 11: else |
| 12: vs ← (0,0) |
| 13: end if |
| 14: return vs * weight |
Alignment and Cohesion rules share the same weighting mechanism due to partial similarities in their effect. The implementation of these two rules is represented by Algorithm 3. In detail, the drone will fly in the same direction as its neighbors due to Alignment. The vector for this behavior is computed by calculating the average velocity of each drone’s nearby neighbors. Regarding Cohesion, the drone tries to fly towards the average location of its neighboring drones. The resulting vector is scaled and then multiplied with its weight.
| Input: |
| Neighbors: List of detected neighbors |
| m: The current number of detected neighbors |
| Output: |
| vs: The scaled vector |
| 1: v ← (0,0) |
| 2: weight ← 0 |
| 3: if m ≠ 0 then |
| 4: if Alignment then |
| 5: for each n in Neighbors do |
| 6: v ← v + n.velocity |
| 7: end for |
| 8: else |
| 9: for each n in Neighbors do |
| 10: v ← v + n.position |
| 11: end for |
| 12: end if |
| 13: v ← v/m |
| 14: vs ← scale(v) |
| 15: weight ← (M/m) |
| 16: else |
| 17: vs ← (0,0) |
| 18: end if |
| 19: return vs * weights |
Performance Evaluation
The proposed weighting mechanism’s performance has been evaluated in a flocking control scheme via the simulation developed using Pygame (https://www.pygame.org/wiki/about), a cross-platform and highly portable collection of modules in Python designed to make video games. Although Pygame does not support hardware acceleration and is not powerful in creating 3D graphics, it is well-known for being open-source and lightweight compared to other tools. Therefore, Pygame is an appropriate choice considering the scope of our implementation.
Evaluation metrics
Regarding the evaluation process, the proposed scheme is compared to the conventional one using the weighted sum of all rule vectors to assess their performance differences in terms of two metrics, including flock compactness and collision reduction represented by the number of crashed drones.
-
Flock compactness shows the drones’ capability in maintaining the optimal distances among one another by calculating the average distance of each pair of drones in the flock. The smaller the average distance is, the less space the flock uses. This is particularly useful for flights in confined environments or using wireless communication. This metric is represented by the average distance computed by (13).
(13) where Ns is the number of loops in the swarm algorithm, n is the number of drones, and di,j is the distance between drone i and j.
-
The number of crashed drones is counted if there are any other objects (i.e., obstacles or neighboring drones) within the collision distance around a drone.
Besides, the magnitude of each rule’s velocity vector before being combined into one final vector will be investigated over how each swarm behavior influences the drones’ movement trajectory during flights.
Methodology
In the simulation program, flight tests are conducted within 1,200 x 700 on a 2D plane measure by unit. The unit can be pixels or scalable to different measures since the proposed transformation factors keep the rules weighting computation unaffected by the measurement unit, as presented above.
For both conventional and proposed schemes, all common parameters that represent each drone’s characteristics are summarized in Table 1. Drones are assumed to fit in a circle with a diameter of 8 units, and the center coordinates are used as their position. Besides, a collision is determined once any objects within each drone’s safety zone are defined by a collision distance of 8 units (same as drone’s size). In addition, Alignment and Cohesion behaviors start taking effect when there are neighbors closer than their perceptions (50 units). Meanwhile, Separation and Avoidance will only become operative with a smaller perception (40 units) to prevent the unnecessary impact that may cause drones to be directed away from their group early. The speed of each drone will be scaled to 1.2 units/step if it exceeds this value.
| Parameter | Value |
|---|---|
| Drone size | 8 units |
| Collision distance | 8 units |
| Obstacle | 35 units × 35 units |
| Alignment perception | 50 units |
| Cohesion perception | 50 units |
| Separation perception | 40 units |
| Avoidance perception | 40 units |
| Maximum speed | 1.2 units/step |
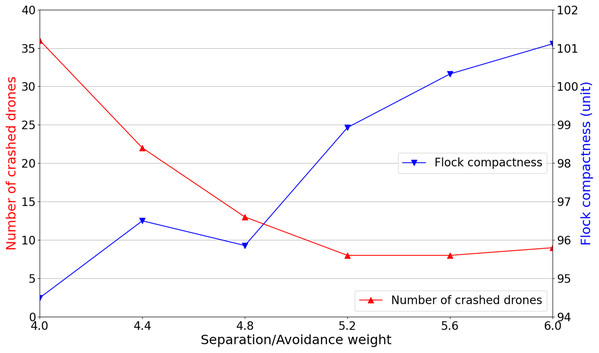
To evaluate our proposed scheme’s effectiveness compared with the conventional one adopting fixed weights, it is required to determine an optimal set of fixed rule weights that produce the conventional scheme’s best experimental results. Therefore, we conduct several simulations with Separation and Avoidance’s weight being gradually increased, whereas other rules’ weights are fixed. The reason is that with higher priorities, Separation and Avoidance rules have the most considerable influence on both the flock’s compactness and the number of crashed drones.
It is reasonable to start with the weight set of {wse:wav:wmi:wal:wco} as {4:4:2:1:1} based on the proposed rule prioritization and the rule’s weights computed by (2), (3), and (7). For every weight set, 100 simulations are executed with initial randomized positions of drones and obstacles. As can be seen in Fig. 2, the drones being too close leads to the large number of crashed drones. Thus, Separation and Avoidance weights are increased by 0.4 in each next experiment. It is seen that when the Separation and Avoidance weights begin to reach 5.2 and higher, the number of crashed drones remains steady at nearly 10. However, the flock compactness tends to rise along with the increase in weights of Separation and Avoidance. Regarding safety concerns and the flock compactness, Separation and Avoidance weights will be set as 5.2 (i.e., wse = wav = 5.2) for further performance comparison with our proposed scheme.
Figure 2: Separation and avoidance weights’ variation and their corresponding simulation results.
The optimal weight set of {5.2:5.2:2:1:1}, along with our adaptive weighting mechanism, are ready for further comparisons. For each simulation, ten drones are initially created with random positions near the upper left corner of the window, and then they proceed to move towards the target point at the lower right corner. There are two scenarios, as follows:
-
Flights without obstacles: this is the ideal environment for the deployment of any flocking control scheme. As there is no Avoidance behavior, the Separation velocity vectors keep being dominant during the entire flights, leading to no collision between drones. Therefore, flock compactness is the only metric for evaluation and comparison in this scenario.
-
Flights with obstacles: obstacles are randomly generated in an area of 800 × 300 in the middle of the window for each simulation, as depicted in Fig. 3. For this scenario, all two metrics are used.
Figure 3: (A–D) Initial positions of the swarm members and obstacle shapes being randomized for each simulation.
Simulation results
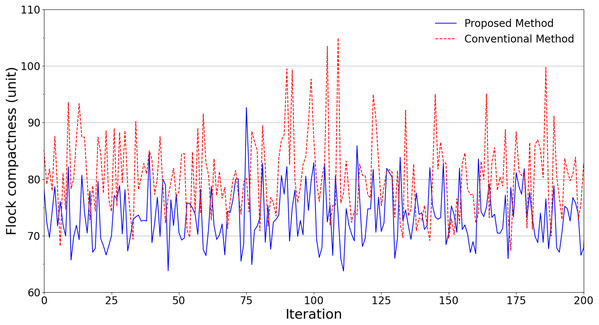
An ensemble of 200 simulations has been done for each scheme in all scenarios. Fig. 4 summarizes the simulation results regarding the flock compactness in the obstacle-free scenario. It can be noted that the drones have an average distance between each other of about 81 units with the conventional flocking control scheme. Meanwhile, our proposed approach produces approximately 73 units. This indicates that by leveraging our improved scheme, the flock is better at maintaining its compactness with roughly 10% smaller average distance.
Figure 4: Experimental results in terms of flock compactness obtained from scenarios without obstacles.
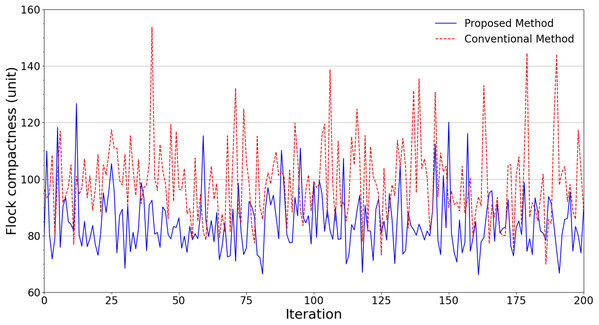
Figure 5 shows the average distance of each scheme when it comes to flying areas with obstacles. It can be noticed that in terms of the flock compactness, the proposed scheme continues to outperform its conventional counterpart. In fact, every pair of swarm members in the proposed scheme manages to maintain an average distance of 85 units, which is 14.14% lower than the conventional scheme’s result of 99 units.
Figure 5: Experimental results in terms of flock compactness obtained from scenarios with obstacles.
Besides maintaining a smaller relative distance with other neighbors, the drones maneuvered by the proposed scheme happen to encounter fewer crashes. In detail, the conflict of Separation and Avoidance rules in the conventional scheme leads to 15 crashed drones during 200 flight tests. Meanwhile, due to the flexibility in weight allocation, the proposed scheme keeps the flock free from collisions.
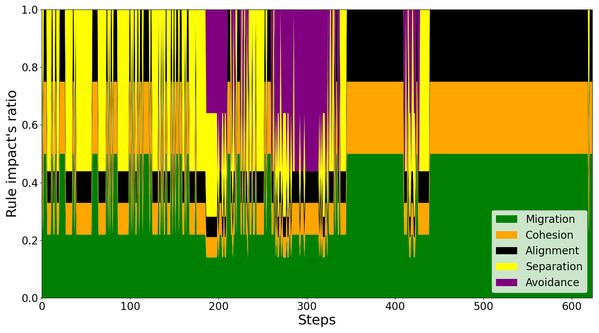
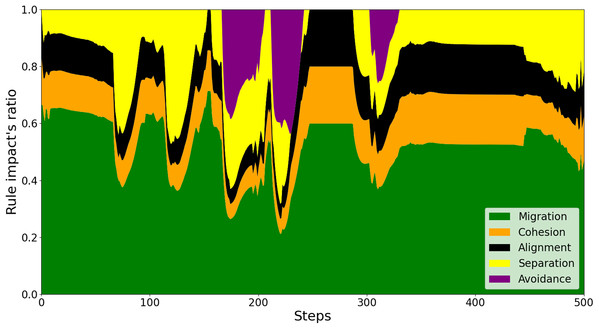
To explain the reason behind this better performance of the proposed scheme, we investigate every swarm rule’s impact on a drone’s behavior against the conventional control scheme. As shown in Fig. 6, it is observed that there are numerous times where the sudden detection of both nearby neighbors and obstacles leads to unexpected behaviors of the drone. For instance, at around simulation step 300, the sudden and considerably weighted appearance of Avoidance rule in purple leads the drone to be directed far from its neighbors. This is to the extent that Separation force is barely needed and Cohesion and Alignment forces are predominant to keep the drone closer. In contrast, regarding the proposed model, as investigated in Fig. 7, the adaptive weighting mechanism enables the drone to stay close in the swarm throughout the flight. This is indicated by all of the swarm behaviors’ presence during and after avoiding the obstacles (around steps 200, 300, and 410).
Figure 6: The effects of swarm rules on a drone’s behaviors by the conventional method.
Figure 7: The effects of swarm rules on a drone’s behaviors by the proposed method.
Conclusions
We propose an adaptive weighting mechanism to compute each behavioral velocity vector for a flocking control scheme adopting conventional Reynolds rules. The simulation results show that our proposed scheme has better performance than the conventional one in terms of flock compactness (smaller up to 14.14%), collision reduction (e.g., free from collisions under various scenarios), and how the swarm rules are retained during flights. In our proposed weighting mechanism, the transformation factors determined by (9) and (10) can keep the impact of the swarm rules unaffected by the measurement unit, which makes our scheme able to adapt to different settings. Therefore, our simulation results are reliable.
However, the current simulations are performed in an ideal environment where the flights occur without impact from external forces. For instance, in the real world, strong winds may affect the quadcopter flight stability. Combining our flocking control scheme with calculations of such forces will further prove our approach’s practical applicability. Moreover, our future study will develop more simulation scenarios in which the drones fly at different altitudes before deploying the proposed control scheme on physical drones for practical performance evaluation.