Towards optimal sparse CNNs: sparsity-friendly knowledge distillation through feature decoupling
- Published
- Accepted
- Received
- Academic Editor
- Consolato Sergi
- Subject Areas
- Artificial Intelligence, Computer Vision, Data Mining and Machine Learning, Neural Networks
- Keywords
- Sparse training, Knowledge distillation, Feature decoupling, Model compression, Machine learning
- Copyright
- © 2025 He et al.
- Licence
- This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits using, remixing, and building upon the work non-commercially, as long as it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Computer Science) and either DOI or URL of the article must be cited.
- Cite this article
- 2025. Towards optimal sparse CNNs: sparsity-friendly knowledge distillation through feature decoupling. PeerJ Computer Science 11:e3388 https://doi.org/10.7717/peerj-cs.3388
Abstract
Despite the efficacy of network sparsity in reducing the complexity of convolutional neural networks (CNNs), the performance of sparse networks often deteriorates significantly compared to their dense counterparts. Knowledge distillation is regarded as a potent strategy for utilizing large models to augment the performance of smaller counterparts; however, its advantages for sparse networks remain substantially constrained. We identify in this article that the underlying issue stems from sparse student models exhibiting disparate behaviors in processing foreground and background features, thereby hindering the uniform transfer of knowledge from dense models that address both feature types concurrently. Building on this insight, we introduce a novel sparsity-friendly knowledge distillation (SF-KD) method, which independently supervises the two feature types using feature decoupling to facilitate effective knowledge distillation for sparse networks. Specifically, we decouple the foreground and background features through unique pooling techniques and implement separate mean squared error (MSE) feature distillation. Furthermore, we dynamically adjust the weights of the two loss components to optimize performance. Experimental results on Canadian Institute For Advanced Research (CIFAR) datasets (including CIFAR-10 and CIFAR-100) and Mini-ImageNet benchmarks substantiate significant performance enhancements, underscoring the effectiveness of our proposed methodology.
Introduction
Convolutional neural networks (CNNs) have emerged as powerful tools for diverse computer vision applications (He et al., 2016; Shrivastava, Gupta & Girshick, 2016). However, the rapid advancements in CNNs are predominantly fueled by an increasing reliance on larger model parameters and heightened computational demands (Wei et al., 2022; Qin et al., 2022; Wei et al., 2023; Dong et al., 2023), which complicates their deployment on resource-limited devices. To overcome this limitation, the research community has developed various compression approaches include network sparsity (Han et al., 2015; Ding et al., 2019), parameter quantization (Hubara et al., 2016; Liu et al., 2020), tensor decomposition (Peng et al., 2018; Hayashi et al., 2019; Zeng et al., 2024), and knowledge distillation (Romero et al., 2014; Hinton, Vinyals & Dean, 2015). Among these methods, network sparsity has gained popularity as an effective means to eliminate redundant parameters, thereby achieving a sparse and more efficient model (LeCun, Denker & Solla, 1990; Zhu & Gupta, 2017; Tanaka et al., 2020).
While network sparsity effectively reduces model complexity, it often leads to substantial performance degradation, especially at extreme sparsity levels (e.g., 90%). Knowledge distillation offers a potential solution by transferring knowledge from dense to sparse networks through specialized loss functions (Hinton, Vinyals & Dean, 2015). While knowledge distillation proves to be highly effective in traditional downscaling from larger to smaller models, its effectiveness appears less pronounced within the realm of network sparsity i.e., employing the original dense network to distill into a sparse network often results in limited performance improvements.
To explore further, both teacher and student models typically employ dense architectures in conventional knowledge distillation scenarios. Such alignment in network structures promotes cohesive supervision, which in turn facilitates the precise transfer of knowledge from the teacher to the student network. However, we identify a distinctive challenge in training sparse networks, where there is a tendency for the model to disproportionately optimize background modeling capabilities at the cost of essential foreground features. This not only undermines the sparse model’s ability to effectively represent foreground components but also precipitates a shift in focus from that of its dense model. As a result, this shift introduces a bottleneck in the knowledge distillation process, preventing the sparse student model from fully assimilating the comprehensive knowledge transferred by the dense model.
Expanding on the above, we introduce a novel sparsity-friendly knowledge distillation (SF-KD) method to boost the performance of sparse networks. In response to the bottleneck induced by divergent behaviors of sparse models1 in processing foreground and background features, SF-KD deploys distinct pooling techniques to decouple these features in the student models (He, Fu & Xiang, 2024). This enables a more precise and targeted distillation policy, enhancing the utilization of the teacher’s knowledge for both feature types. Furthermore, we execute targeted mean squared error (MSE) feature distillation for both foreground and background features, customizing the distillation process to the unique needs of each feature type. Additionally, we implement adaptive weight adjustments for the loss components corresponding to these features. By dynamically balancing the weights, the contribution of both foreground and background features can be well optimized to the overall effectiveness of the student model.
To assess the performance of our proposed SF-KD, we undertook comprehensive experiments on established benchmarks, specifically the Canadian Institute For Advanced Research (CIFAR) datasets (including CIFAR-10 and CIFAR-100), and Mini-ImageNet datasets. Our experimental outcomes indicate that the sparsity-friendly distillation framework outperforms existing techniques in terms of classification accuracy. Our contributions in this article are as follows:
We examined the bottlenecks and limitations of knowledge distillation within sparse networks, identifying significant variances in emphasis on the foreground and background elements between sparse and dense networks. These discrepancies lead to differences in attention allocation, which in turn results in degradation of performance.
We introduce SF-KD for independently pooling and distilling features from the foreground versus background features between teacher and student models. This includes a configurable loss balancing to optimally integrate the distinct foreground and background distillation losses.
We provide comprehensive experimental validation of our framework on the extensively employed CIFAR-10, CIFAR-100, and Mini-ImageNet datasets, showing that our method achieves superior classification performance relative to current methods.
Background
Network sparsity
Network sparsity is an effective technique for reducing parameter counts in deep neural networks, offering significant improvements in computational efficiency and memory usage. By creating sparse models with smaller memory footprints and lower computational demands, this approach enables efficient deployment on resource-constrained devices. Current methods for inducing sparsity include pruning techniques including static pruning, layer-wise sparsity allocation, rand pruning at initialization approaches (Hu et al., 2021; Chen et al., 2022b), which we briefly introduce as follows.
Static sparse training with random pruning (Mariet & Sra, 2016; He, Zhang & Sun, 2017; Suau, Zappella & Apostoloff, 2019; Gale, Elsen & Hooker, 2019) employs layer-wise random masking based on predefined sparsity ratios. Liu et al. (2022) demonstrated that simple random pruning serves as an effective baseline. While uniform pruning applies identical sparsity ratios across all layers, more sophisticated approaches have emerged to enhance sparse model performance. For example, non-uniform and scale-free topologies have shown improved performance compared to dense counterparts when applied to restricted Boltzmann machines (RBMs). Expander graphs have also been used to construct sparse convolutional neural networks (CNNs) that achieve comparable performance to dense CNNs.
While not originally developed for static sparse training, advanced layer-wise sparsity methods like Erase Random (ER) (Mocanu et al., 2018) and Erase Random wrt Kernel (ERK) (Evci et al., 2020) from graph theory have demonstrated strong performance. These approaches differ from traditional methods that pre-specify layer sparsity ratios. Instead of pre-choosing a sparsity ratio for each layer, some approaches utilize saliency criteria to learn layer-wise sparsity ratios before training. This approach, known as pruning at initialization (PaI), selects structurally important connections at initialization based on various criteria. Several efficient criteria have been proposed to improve the performance of non-random pruning at initialization. These include criteria based on gradient flow, synaptic strengths, neural tangent kernel, and iterative approaches. However, recent studies have revealed that existing PaI methods hardly exploit information from the training data and are robust to mask shuffling. In fact, magnitude pruning after training has been shown to learn both layer-wise sparsities and achieve comparable or better performance compared to PaI methods. Several sanity-check experiments have demonstrated that methods like Gradient Signal Preservation (GraSP); (Wang, Zhang & Grosse, 2020), synaptic strengths (SynFlow; (Tanaka et al., 2020)), neural tangent kernel (Liu & Zenke, 2020), and iterative Single-shot Network Pruning based on Connection Sensitivity (SNIP) (de Jorge et al., 2021; Verdenius, Stol & Forré, 2020) hardly utilize information from the training data and are robust to mask shuffling.
Random pruning at initialization with hand-designed layer-wise sparsity ratios has been shown to outperform or achieve similar performance compared to PaI methods. These findings suggest that what pruning at initialization methods discover are the layer-wise sparsities themselves rather than specific weights or values. This highlights a broader challenge inherent to pruning at initialization and emphasizes the need for further exploration and improvement in sparse training techniques.
Knowledge distillation
Knowledge distillation (Hinton, Vinyals & Dean, 2015; Liu et al., 2023; Shao et al., 2023; Shen et al., 2022) enables efficient knowledge transfer from a large teacher network to a compact student network while reducing computational and memory requirements. This technique trains the student network to replicate both the final outputs and intermediate representations of the teacher network through carefully designed loss functions. Current approaches can be classified into three main categories based on knowledge transfer mechanisms: (1) response-based distillation, (2) feature-based distillation, and (3) relationship-based distillation.
Response-based knowledge distillation usually refers to the use of responses from the final output layer in a network to obtain knowledge and migrate it. Feature-based knowledge distillation primarily utilizes the characterization of feature maps in the middle of the teacher’s network to guide the training of the student’s network. The intermediate feature maps of a network contain rich spatial and structural information regarding image content. Therefore, feature distillation methods (Romero et al., 2015; Yim et al., 2017; Zagoruyko & Komodakis, 2017; Chung et al., 2020) are proposed to encourage the student model to mimic the feature representations learned by the teacher model, which shows improved knowledge transfer performance. Yang et al. (2024) introduced a student-centered distillation paradigm inspired by human educational principles, while Huang et al. (2022) specifically addressed feature map distillation for low-resolution recognition in the compressed networks. As the feature maps from different layers of the student and teacher networks usually have different dimensions (e.g., widths, heights, and channels), existing feature distillation methods adopt various transformations to match their dimensions and different distance metrics to measure feature differences. Relationship-based knowledge distillation (Park et al., 2019; Xie et al., 2019; Yang et al., 2024) further explores the relationships between different layers or data samples and utilizes such relationships as knowledge to be migrated, and as the study progressed, researchers found that relationships between features also play a large role in network performance.
Proposed methodology
Preliminary
We begin by outlining the fundamental preliminaries of knowledge distillation. The principal concept behind knowledge distillation involves the integration of soft targets derived from the teacher network into the overall loss function. This integration facilitates the training of student networks, thereby enhancing their performance via effective knowledge transfer. In classification tasks, the soft target represents the output from the teacher network’s final layer, indicating the probability that the input image is classified under a particular category. These soft targets are mathematically formulated as follows:
(1) Here, denotes the logits corresponding to class , and T is the temperature parameter used to modulate the relevance of each soft target.
The soft target encapsulates dark knowledge within the teacher’s network, which can be transferred to the student’s network by incorporating a knowledge migration loss, articulated as:
(2)
Here, KL represents the Kullback-Leibler divergence. By calculating the Kullback-Leibler divergence between the teacher and student outputs, we can facilitate the student network’s approximation of the teacher network’s logarithmic output. Beyond the transfer of knowledge, the student network also incurs a cross-entropy loss relative to the actual labels, culminating in a total loss function expressed as:
(3)
Background modeling of sparse networks
Sparse training entails the training of deep neural networks with sparse architectures, offering benefits such as enhanced computational efficiency and diminished memory demands. A significant challenge in sparse training, however, is the inadvertent neglect of critical foreground features, potentially diminishing the model’s overall effectiveness.
More particularly, there is a tendency for the sparse models during training to optimize background modeling capabilities at the expense of salient foreground features. This imbalanced focus may weaken the model’s ability to represent key foreground elements, thereby impairing performance. More critically, due to the absence of such foreground-background bias in dense models, employing the conventional distillation function, i.e., Eq. (3), introduces a bottleneck in the knowledge distillation process, which hinders the sparse student model from fully assimilating the comprehensive knowledge imparted by the dense model.
To mitigate this issue, it is imperative to maintain an equilibrium between sparsity and foreground feature modeling. This balance may be achieved through the implementation of distinct distillation processes tailored for both foreground and background features. By conscientiously distilling and integrating knowledge from both domains, the model can more accurately represent the comprehensive characteristics of the dataset, thereby enhancing its performance.
Sparsity-friendly knowledge distillation
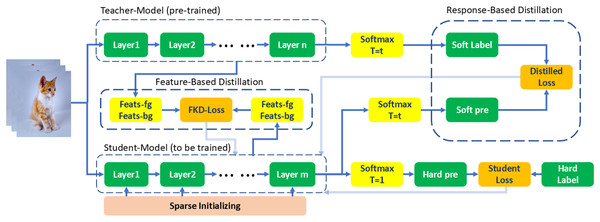
While sparse training provides benefits in computational efficiency and reduced memory requirements, it is imperative to address potential performance declines caused by the inadvertent omission of crucial foreground features. To counter this, we propose sparsity-friendly knowledge distillation (SF-KD), the overall framework of SF-KD is illustrated in Fig. 1, which deploys distinct distillation techniques to strike a balance between sparsity and accurate foreground feature representation, thereby achieving superior performance overall.
Figure 1: Framework overview: our proposed SF-KD leverages the unique behaviors of sparse student models in foreground and background features.
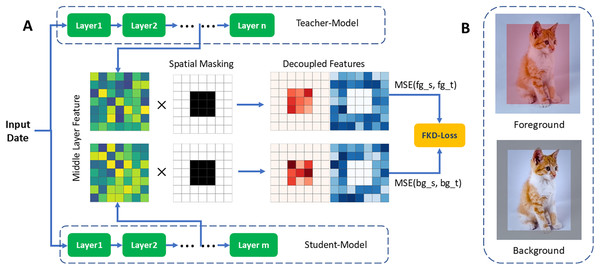
We separate these features using different pooling techniques and apply separate mean squared error (MSE) feature distillation. Additionally, we dynamically adjust the weights of the two loss components to optimize performance.In particular, we delineate foreground from background by extracting a central patch from the image, defining the central area as the foreground and treating the peripheral region as the background, foreground/background patches definition examples and feature decoupling schematic in Fig. 2. Such separate distillation of foreground and background features enables us to capture and preserve their distinctive qualities effectively. This approach not only allows for detailed comparison and analysis of these features within and across different classes but also facilitates the learning of decoupled, more informative, and discriminative features.
Figure 2: (A) Feature decoupling schematic. (B) Patch definition examples.
Instance with foreground (red) and background (gray) patches, we delineate foreground from background by extracting a central patch from the image, defining the central area as the foreground and treating the peripheral region as the background.We extract foreground and background features by applying a spatial mask. The mask matrix is defined as:
(4)
Here, is an empirically chosen value, which is further analyzed in our ablation studies. Using this mask, we obtain the foreground and background features as follows:
(5) where , denote the intermediate feature maps of the student model and the teacher model, respectively.
To orchestrate the knowledge distillation process, we introduce a loss function predicated on decoupling of middle layer features, articulated as follows:
(6)
Here, and denote the foreground and background features of the student network, respectively, while and represent those of the teacher network. The parameter , which is less than 1, moderates the focus on background features during distillation.
To enhance model efficacy further, we perform feature distillation on the decoupled features independently. This process involves training the student network to replicate the intermediate representations of the teacher network rather than merely its output. The incorporation of additional loss terms fosters learning from these intermediate representations, thereby improving the model’s performance while preserving its computational efficiency. The overall loss function for the student network is then defined as:
(7) In this equation, is a hyperparameter used to balance classification loss and distillation loss and is set to 1 by default; and serve as hyperparameters that adjust the weighting of the loss components related to response and feature decoupling.
Experiments
We evaluated our method on three popular datasets: CIFAR-10/CIFAR-100 and Mini-ImageNet. Our experiments consisted of training models with and without our method and comparing their performances. Additionally, we explored the impact of different distillation strategies on the decoupled features.
Datasets
(1) CIFAR-10 (Krizhevsky & Hinton, 2009) consists of 60,000 images of 32 32 pixels in color, which are divided into 10 different classes, with each class containing 6,000 images. These classes include: airplanes, automobiles, birds, cats, deer, dogs, frogs, horses, ships, and trucks. The dataset is split into 50,000 training images and 10,000 testing images. (2) CIFAR-100 (Krizhevsky & Hinton, 2009) contains 50 K training images with 0.5 K images per class and 10 K test images. (3) Mini-Imagenet (Deng et al., 2009) a subset of the ImageNet dataset, commonly referred to as Mini-ImageNet, which consists of 100 classes with 600 images per class.
Implementation
On CIFAR-100, we conduct experiments on various teacher-student models under same or different architecture style with Contrastive Representation Distillation’s (CRD’s) settings (Tian, Krishnan & Isola, 2020), whose training epochs are 240. We use a mini-batch size of 64 and a standard Stochastic Gradient Descent (SGD) optimizer with a weight decay of 0.0005. The multi-step learning rate is initialized to 0.05, decayed by 0.1 at 150, 180, and 210 epochs. For the comparison experiments with online KD methods, we adopt the same training settings with Online Knowledge Distillation with Diverse Peers (OKDDip) (Chen et al., 2020), whose training epochs are 300.
Main experiment
Results on CIFAR-10/CIFAR-100
Table 1 presents a comparison of the top-1 accuracies achieved by different training methods on the CIFAR10 dataset. Where Dense+KD denotes no sparse training model with baseline distillation method, ERK+KD and SNIP+KD denote sparse student model distillation experiments where no separation of foreground and background is done, and ERK+SF-KD and SNIP+SF-KD denote sparse student model distillation experiments where foreground and background features are decoupled. The comparison includes the no sparse training method as well as the addition of two sparse training methods: ERK and SNIP. The aim is to evaluate the impact of these sparse training methods in the distillation process. Starting with the no sparse training method, which represents a baseline approach, the accuracy obtained on the CIFAR10 dataset is not explicitly mentioned in the provided information. However, the subsequent results highlight the potential loss of accuracy incurred when applying sparse training strategies. When incorporating the ERK sparse training method, the accuracy of the model experiences a decline compared to the dense baseline. Similarly, the addition of the SNIP sparse training method also leads to a reduction in accuracy. These results suggest that sparse training strategies can result in a certain loss of accuracy compared to the dense approach. However, the provided information also mentions that our method, which is not explicitly described, can further enhance network performance. Specifically, our method achieves a higher test accuracy rate of 93.06% on the CIFAR10 dataset, surpassing the accuracy obtained by the dense baseline method. This improvement indicates that our method effectively mitigates the accuracy loss associated with sparse training strategies and leads to enhanced network performance.
| cifar10 | cifar100 | |||||||
|---|---|---|---|---|---|---|---|---|
| Density | 0.9 | 0.95 | 0.98 | 1.0 | 0.9 | 0.95 | 0.98 | 1.0 |
| Dense* | – | – | – | 92.37* | – | – | – | 68.76* |
| Dense+KD* | – | – | – | 93.06 | – | – | – | 70.67* |
| Dense+SF-KD | – | – | – | 93.13 | – | – | – | 71.60 |
| ERK | 92.43 | 91.54 | 91.78 | 69.5 | 69.5 | 69.27 | ||
| ERK+KD | 92.98 | 92.68 | 91.89 | 71.49 | 71.27 | 71.2 | ||
| ERK+SF-KD | 93 | 93.3 | 93.12 | 71.8 | 71.39 | 71.79 | ||
| SNIP | 92.39 | 92.39 | 92.89 | 69.26 | 69.44 | 69.7 | ||
| SNIP+KD | 92.99 | 92.69 | 92.67 | 70.97 | 71.36 | 71.73 | ||
| SNIP+SF-KD | 92.84 | 92.73 | 93.24 | 71.15 | 71.83 | 71.47 | ||
Results on Mini-ImageNet
We conducted our few-shot learning experiments on the Mini-ImageNet dataset. In Table 2 the top-1 and top-5 accuracies of the different models are compared, and the density set to 0.65. Our proposed method also achieves consistent improvements for all three models on Mini-Imagenet, a subset of large-scale datasets.
| Teacher/Student | ResNet110/ResNet20 | WRN-40-2/WRN-16-2 | VGG13/VGG8 | |||
|---|---|---|---|---|---|---|
| Accuracy | Top-1 | Top-5 | Top-1 | Top-5 | Top-1 | Top-5 |
| ERK+KD | 61.48 | 85.73 | 68.63 | 89.56 | 70.26 | 89.68 |
| ERK+SF-KD | 62.18 | 86.03 | 70.90 | 90.75 | 70.19 | 89.90 |
| SNIP+KD | 58.98 | 89.93 | 70.18 | 90.33 | 69.83 | 89.38 |
| SNIP+SF-KD | 61.10 | 85.80 | 70.40 | 90.64 | 70.12 | 89.29 |
It is interesting to note that SF-KD does not always outperform vanilla KD, e.g., in Table 1 sparse training is SNIP (SNIP+KD vs SNIP+SF-KD) at density = 0.9 in the cifar10 experiment and at density = 0.98 in the cifar100 experiment. Similar observations were made in subsequent experiments, such as in the Mini-Imagenet experiment (Table 2) and in the different teacher-student combination distillation experiments (Table 3).
| Teacher | ResNet110 | ResNet110 | ResNet56 | WRN-40-2 | VGG13 | VGG13 |
|---|---|---|---|---|---|---|
| Student | ResNet20 | ResNet32 | ResNet20 | WRN-16-2 | VGG11 | VGG8 |
| Dense* | 68.76* | 71.35 | 71.9 | 73.3 | 71.65 | 69.8 |
| Dense+KD* | 70.67* | 73.48 | 71.9 | 75.22 | 74.71 | 72.55 |
| Dense+ReviewKD* | 71.34* | 73.89* | 71.89* | 76.12* | – | 74.84* |
| Dense+SimKD* | 71.06* | 73.92* | 71.05* | 75.53* | – | 74.65* |
| Dense+CAT-KD* | 71.37* | 73.62* | 71.62* | 75.6* | – | 74.65* |
| Dense+SF-KD | 71.60 | 73.53 | 72.07 | 75.04 | 74.66 | 72.58 |
| ERK | 69.50 | 71.41 | 71.87 | 73.02 | 71.83 | 64.45 |
| ERK+KD | 71.49 | 73.83 | 71.87 | 75.27 | 73.58 | 72.61 |
| ERK+SF-KD | 71.80 | 73.67 | 71.43 | 75.55 | 74.86 | 72.90 |
| SNIP | 69.26 | 71.2 | 70.57 | 73.13 | 74.93 | 71.17 |
| SNIP+KD | 70.97 | 73.59 | 71.02 | 73.13 | 74.93 | 72.85 |
| SNIP+SF-KD | 71.15 | 73.59 | 72.00 | 74.92 | 74.54 | 73.20 |
The efficacy of SF-KD depends on two key assumptions: (1) that the teacher’s feature space contains semantically meaningful clusters and that the students have sufficient capacity to mimic the predictions and feature distributions; and (2) that the dataset is well characterized by the central region of the foreground. When these assumptions do not hold (e.g., overfitting with relatively weak teachers or extremely compact students), simpler logit matching with vanilla KD may be more robust, as observed in Table 3.
Different network structures
Table 3 shows the experimental results for different network architectures, including three backbones: standard resnet, vgg, wide resnet, with the dataset of CIFAR100 and the density uniformly set to 0.9. The experimental results show that the top-1 accuracy rate is improved after knowledge distillation, and the best result is achieved by our feature distillation method SF-KD. Compared to the state-of-the-art (SOTA) feature-based knowledge distillation methods, such as ReviewKD (Pengguang et al., 2021), SimKD (Chen et al., 2022a), and Class Attention Transfer (CAT)-KD (Guo et al., 2023), our method achieves competitive results even in models without sparsity.
The network sparsity experiments are shown in Table 4, the number of parameters of different structural models is halved after reducing the density from 1.0 to 0.5, and the sparsification process effectively reduces the model parameters. The inference time of a single image is reduced, and the sparsity effectively improves the computational efficiency of the model. However, the Top-1 accuracy generally decreases, ranging from −0.24% to −1.66%, indicating that sparsity has different degrees of negative impact on model performance.
| Model | Density | #Parameters (m) | Top-1 | Accuracy change | Runtime (ms) |
|---|---|---|---|---|---|
| ResNet20 | 1.0 0.5 | 0.28 0.14 | 68.84 67.68 | −1.16 | +0.006 |
| ResNet56 | 1.0 0.5 | 0.86 0.43 | 72.83 71.76 | −1.07 | −0.005 |
| ResNet110 | 1.0 0.5 | 1.74 0.87 | 70.58 70.77 | +0.19 | −0.006 |
| VGG8 | 1.0 0.5 | 3.96 1.98 | 70.21 70.3 | +0.09 | −0.001 |
| VGG11 | 1.0 0.5 | 9.27 4.63 | 71.77 71.53 | −0.24 | −0.005 |
| VGG13 | 1.0 0.5 | 9.46 4.73 | 74.79 74.25 | −0.54 | −0.012 |
| WRN-16-2 | 1.0 0.5 | 0.70 0.35 | 72.62 70.96 | −1.66 | +0.003 |
| WRN-40-2 | 1.0 0.5 | 2.26 1.13 | 76.21 75.32 | −0.89 | +0.003 |
Ablation
In the ablation experiments, following Gao et al. (2019), Zhang, Shu & Zhou (2018) we comparatively study the effects of different network densities, foreground v.s. background ratios, and different hyperparameter ratios on the performance of the network.
Different network densities
Table 5 demonstrates that reducing network density leads to a decrease in accuracy. The sparse training process necessitates finding the right balance between network density and accuracy, optimizing the trade-off to achieve the desired performance while leveraging the benefits of sparsity.
| Density | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|
| ResNet110-ResNet20 | 63.26 | 66.63 | 69.09 | 69.76 | 70.85 | 70.51 | 70.70 | 71.62 | 71.80 |
| VGG13-VGG11 | 73.25 | 74.38 | 74.37 | 74.67 | 74.89 | 75.09 | 74.78 | 75.10 | 74.86 |
Foreground-background ratios
Our experiments in Table 6 revealed that the Residual Network (ResNet) network performed optimally when the foreground-to-background ratio was 1:1 ( ). This finding emphasizes the importance of maintaining a balanced representation of foreground and background elements in the dataset for this particular network architecture. However, the impact of foreground-to-background ratios on other networks may vary, highlighting the need to consider the specific requirements of each architecture when determining the optimal ratio.
| feats_fg/feats_fg (l) | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|
| ResNet110-ResNet20 | 71.47 | 71.80 | 71.24 | 71.24 | 71.33 |
| VGG13-VGG8 | 72.59 | 72.27 | 73.00 | 73.00 | 73.00 |
Loss item study
We analyzed the effect of the distillation loss term of foreground/background separation on the network accuracy by setting different parameters of the hyperparameter . The data in Table 7 show that when the hyperparameter = , the best recognition accuracy can be obtained by taking to be 0.5; when is not equal to , equals to be 0.8 to obtain the best training results when the sparse initialization is set to ERK and density = 0.9. The data in Table 8 indicate that under both experimental conditions—dense+SF ( = 1, = 0, = 1, density = 1.0) and ERK+SF+KD ( = 0.5, = 0.5, = 0.5, density = 0.9)—optimal performance is achieved or approached at = 0.4, suggesting this value may represent a relatively ideal hyperparameter setting. These experiment proves that the foreground background-based the selection of distillation loss terms for separated features needs to be balanced between different loss terms.
| = 0.1 | = 0.2 | = 0.3 | = 0.4 | = 0.5 | = 0.6 | = 0.7 | = 0.8 | = 0.9 | = 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| = 0.5 = 0.5 | 71.33 | 71.80 | 71.10 | 71.73 | 71.83 | 71.41 | 69.20 | 71.62 | 71.38 | 71.74 |
| = 1.0 = 1.0 | 71.08 | 71.40 | 71.10 | 71.73 | 71.83 | 71.41 | 68.63 | 71.62 | 71.38 | 71.74 |
| = 1.0 = 0.5 | 71.47 | 71.13 | 71.40 | 71.70 | 69.54 | 71.41 | 69.20 | 71.62 | 71.38 | 71.71 |
| = 0.5 = 1.0 | 71.48 | 71.36 | 71.53 | 71.74 | 69.54 | 71.63 | 71.61 | 71.91 | 71.68 | 71.03 |
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
|---|---|---|---|---|---|---|---|---|---|
| Dense+SF | 69.53 | 68.59 | 69.68 | 70.01 | 69.92 | 69.39 | 69.79 | 69.98 | 69.85 |
| ERK+SF+KD | 71.53 | 71.53 | 71.98 | 72.10 | 71.76 | 71.64 | 72.27 | 71.64 | 71.73 |
Different sparse initialization
We have chosen various sparse methods ER, ERK, uniform, and SNIP, Gradient Signal Preservation (GraSP), and uniform+ for initialization, after which our proposed SF-KD is used for distillation training, and the experimental results are shown in Table 9. Among them, SNIP+SF-KD achieves higher accuracy in resnet architecture network and GraSP+SF-KD achieves higher accuracy in vgg architecture network, and the experiments prove that our proposed SF-KD scheme can adapt to different sparse initializations.
| sparse−init | ERK | SNIP | GraSP | uniformplus | Uniform | ER |
|---|---|---|---|---|---|---|
| ResNet110-ResNet20 | 71.80 | 71.83 | 71.28 | 71.36 | 71.57 | 71.28 |
| VGG13-VGG8 | 72.27 | 72.53 | 73.12 | 72.26 | 71.31 | 71.31 |
Visualization of feature map
We visualize the differences between the vanilla model, sparse model and distilled model by visualizing the feature maps, activation heatmaps as shown in Fig. 3. Relative to the dense resnet20 network, the sparsified resnet20+ERK model exhibits a focus on the background, thus weakening its ability to effectively represent foreground components. Our proposed SF-KD approach pulls attention back to foreground representation in sparse networks and outperforms dense vanilla resnet20.
Figure 3: Feature map visualization.
Activation heatmaps of the vanilla model, sparse model and distilled model.Conclusions
In summary, our proposed sparsity-friendly distillation approach offers several contributions to the field. Firstly, we have developed a novel distillation framework specifically designed for sparse students. This framework takes into account the unique challenges and constraints associated with compressing models under sparsity conditions. Secondly, we leverage the understanding that foreground and background representations hold distinct insights by incorporating separate distillation processes for these components. By treating foreground and background elements separately, we can capture and transfer knowledge more effectively, leading to improved performance in sparse models. Thirdly, we introduce an configurable loss balancing that intelligently integrates the separate losses from foreground and background distillation. This weighting approach enhances the overall distillation process and enables superior accuracy compared to baseline methods. Our approach addresses the limitations and difficulties encountered when compressing models under sparsity constraints through knowledge transfer. By leveraging foreground/background insights and employing configurable weighting, we provide a more effective solution for enhancing the performance of sparse models. Experimental results demonstrate the effectiveness of our proposed method, showcasing improved performance in the context of sparse models.
However, there still remain some unexplored limitations of our method: (1) performance depends significantly on accurate foreground/background delineation; (2) careful tuning of the boundary definition and weighting parameters is required; (3) current validation is primarily on classification tasks with spatial sparsity, necessitating further exploration for other sparsity patterns and vision tasks. Future work will address: (1) automatic techniques for defining foreground/background splits; (2) extending the framework to other tasks (e.g., detection, segmentation) and sparsity types; (3) enhancing compatibility with diverse model compression techniques beyond pruning. We believe that our work will be valuable to the knowledge distillation research community, offering insights and techniques that can contribute to advancements in compressing and improving the performance of sparse models.