Adaptive route optimization in tourism using ant colony graph neural networks with deep learning
- Published
- Accepted
- Received
- Academic Editor
- Siddhartha Bhattacharyya
- Subject Areas
- Agents and Multi-Agent Systems, Algorithms and Analysis of Algorithms, Data Mining and Machine Learning, Optimization Theory and Computation, Neural Networks
- Keywords
- ACO, GNN, Tourist route recommendation, Shortest path selection, Deep learning, Optimization
- Copyright
- © 2025 Ji and Shen
- Licence
- This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, reproduction and adaptation in any medium and for any purpose provided that it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Computer Science) and either DOI or URL of the article must be cited.
- Cite this article
- 2026. Adaptive route optimization in tourism using ant colony graph neural networks with deep learning. PeerJ Computer Science 12:e3366 https://doi.org/10.7717/peerj-cs.3366
Abstract
In a tourism recommendation system, adaptive route optimisation is an essential requirement for a cost-effective navigation system. When planning a tourism destination, contextual features are essential for creating a model that selects the most efficient route. The existing model fails to account for feature context when determining the path and calculating the shortest distance. The famous Dijkstra algorithm is static and cannot adapt to complex real-world factors such as climate, traffic, and road closures. To automate route optimisation, this research employs deep learning to identify patterns from existing datasets and adapt to the dynamic environment by learning new patterns. Adaptive route optimisation is conducted using an ant colony optimization (ACO) graph neural network (GNN) with a weight factor. ACO operates with pheromone updates for path selection, while GNN connects nodes based on pheromone and other weight factors. This model is less complex and requires less computation time to determine the nearest route. The performance of the model is evaluated, and the proposed model establishes the shortest path in 1.92 s with a cost of 2,141, compared to ACO and ACO with reinforcement learning (ACO-RL).
Introduction
Tourism continually plays a vital role in promoting global economic growth, evident in the increase in both inbound arrivals and revenue generation. India has shown resilient growth in the tourist sector, with figures indicating 18.89 million international tourists and 2.51 billion domestic visits recorded in 2023. There has been a significant recovery from the disruption caused by COVID-19. This expansion of tourism highlights the critical need for optimising travel experiences through effective route planning strategies, which not only enhance traveller satisfaction but also improve resource utilisation and support the development of a sustainable ecosystem.
To address the problem of tourism route optimisation, several computational models have been developed and deployed. Earlier methods developed smart recommendation systems that incorporated artificial intelligence and Internet of Things (IoT) frameworks, utilizing algorithms such as Apriori for association rule mining to capture tourist preferences (Song & He, 2023). To identify frequent itemsets, these methods are computationally intensive due to the exponential growth in candidate generation, which restricts their scalability for large and dynamic datasets. Subsequent efforts examined adaptive PSO methods targeting multi-objective trip planning, balancing factors such as cost, time, and satisfaction. Moreover, traditional PSO has limitations in terms of premature convergence and suboptimal exploration-exploitation trade-offs, which can decrease solution quality in complex, nonlinear search spaces. In previous work, enhancements in ant colony optimization (ACO) methods were proposed by integrating contextual awareness to dynamically adjust tourism routes (Liang et al., 2021). However, traditional ACO often experiences slow convergence and is sensitive to parameter tuning, which limits its capacity for real-time adaptability and responsiveness to rapidly changing tourist demands and environmental conditions. These methods face challenges, including limited scalability, inefficiency in computation, restricted dynamic adaptability, and inadequate personalized route customization, all of which are vital for practical deployment in smart tourism.
To overcome these challenges, this study proposes a robust and adaptive framework that integrates ACO and graph neural networks (GNN). This ACO-GNN model leverages GNN-generated node embeddings to incorporate both topological and connectivity features of the local tourism network. These embeddings facilitate as data-driven heuristics that inform pheromone updating dynamically, exceeding the static, distance-based heuristics of traditional methods. The framework integrates rigorous data normalisation and feature engineering to enhance the representation of city attributes, enabling efficient multi-criteria decision-making during route planning. Amongst end-to-end training pipelines, the GNN model consequently updates heuristic guidance, including both synthetic and real-world datasets, promoting accelerated and more effective path exploration and convergence. This approach ensures the model adapts to choose optimal routes in real-time, reporting on external dynamic attributes such as traffic conditions and user-specific preferences, thereby delivering a scalable, computationally effective, and highly personalised smart tourism route optimisation solution.
The increasing demand for smart and tailored tourism systems suitable for adapting to complex, dynamic environments support this research. The quick digital transformation in the tourism industry requires harnessing advanced computational methods, particularly the interaction of deep learning and swarm intelligence, to formulate optimised route planning methods. Such solutions must robustly address diverse user preferences and real-time environmental fluctuations to enhance the overall efficiency, adaptability, and user-centricity of tourism services.
Evolving smart technologies and increasing complexity in the tourism field necessitate the development and deployment of adaptive optimisation methods to manage diverse traveller requirements and varying conditions, including traffic and environmental fluctuations. The incorporation of deep learning methodologies, such as GNN and swarm intelligence algorithms, introduces dynamic learning of spatial relationships and enables real-time decision-making. This study proposes a hybrid ACO-GNN model which leverages learned node embeddings to ensure guidance for pheromone reinforcement and path choosing processes, ensuring a scalable, data-driven solution that continuously adapts to individualised traveller requirements and evolving contextual dynamics.
In this research, we define real-time environmental fluctuations as unpredictable alterations in traffic density, road availability, meteorological events, and user-specific route preferences, all of which jeopardise the stability of route optimisation. To counter these variations, we advance the ACO-GNN architecture through the following synergistic subsystems: (i) the GNN extracts high-dimensional embeddings that fuse the city’s static topological scaffold with live, streaming context-specific data, thereby producing heuristic signals directly responsive to real-time traffic and environmental states. Such embeddings allow consecutive refinements of the heuristics to mirror the most relevant operational reality. (ii) The ACO layer leverages the resultant heuristics to control the pheromone density and trajectory choices, sustaining the algorithm’s reactivity to live state perturbation by accentuating and propagating trails that continue to yield minimal congestion under the prevailing context. The effective cogeneration of these modules ensures that the framework trails and scales efficiently against emergent routing anomalies in operational environments. In the context of this study, “adaptive” optimization refers to the model’s ability to adjust the recommended routes in response to dynamic, real-world conditions. For instance, if a user begins a trip from Lucknow to Goa, and a sudden traffic jam is detected on the planned route near Delhi, the model can re-evaluate and recommend an alternative path through Jaipur and Pune that minimises delay and cost. This adaptivity is achieved by incorporating real-time data into the GNN embeddings, which continuously update the heuristics guiding the ant colony’s decisions. Such adaptability is crucial in practical tourism scenarios, where static, precomputed routes often fail to reflect current travel conditions or individual preferences accurately.
The main contributions of this proposed research are
-
1.
GNN-Node embeddings integrated with ACO for generating dynamic, context-aware embeddings that notify pheromone updates and decision-making that leverages learned node embeddings to ensure guidance for pheromone reinforcement and path choosing processes, resulting in processes of ant colony optimization that are more efficient and adaptable to changes in the environment.
-
2.
For optimizing route, we implemented a continuous learning method where GNN iteratively updates the heuristic predictions, improves routing efficiency and accuracy.
-
3.
We incorporate data-driven insights from GNN embeddings for enhancing the pheromone reinforcement.
-
4.
We introduced metaheuristic approaches to ensure the dynamic route adjustments to fluctuating conditions like traffic variations and user preference changes.
This research presents a new hybrid framework, ACO-GNN, that incorporates GNNs to enhance the heuristic guidance of traditional ACO. The model learns routing graphs with spatial and structural complexities, which facilitates quicker convergence, improved computational efficiency, and scalable optimisation for large complex networks. The study demonstrates that ACO-GNN exhibits comparable computational complexity and throughput, aligning with traditional benchmarks. The method shows a marked reduction in the time required for scalability while significantly accelerating convergence. Although there are certain instances where the routes are slightly less optimal, this approach offers a beneficial compromise that boosts the feasibility of real-time, large-scale route optimisation, far surpassing the capabilities of existing ACO and ACO-reinforcement learning (RL) frameworks.
Literature survey
Early research introduced knowledge-based hybrid ACO models, integrating hierarchical clustering and random sampling to optimize tourism routes by maximizing tourist satisfaction and attraction income (Li et al., 2022). These methods incorporated constraints such as tourist age, preferences, and route carrying capacity to reflect real-world conditions. The inclusion of a bacterial foraging algorithm mechanism enhanced the search process by reducing the risk of local optima and improving solution quality. However, reliance on predefined knowledge models limited adaptability in highly dynamic or large-scale tourism networks. To enhance adaptability and privacy, subsequent studies explored swarm intelligence (SI) and distributed learning techniques. Hawk Fire Optimization (HFO) with Federated Dropout Learning (FDL) was employed to enhance autonomous vehicle decision-making and adaptability, where HFO dynamically optimized parameters while FDL facilitated privacy-preserving distributed learning (Gupta et al., 2024). Despite the model’s enhanced performance in simulations, its complexity and challenges with federated synchronization hindered its real-time use under varying network conditions.
To optimise performance, strategies or initialization schemes from related tasks may be acquired through an optimisation strategy using meta learning, or learning to learn (Xia et al., 2022; Wang et al., 2025). In prediction, the application of multi-view learning enables the model to integrate different representations of molecules, thereby improving the model’s understanding of complex features (Zhang et al., 2024; Zuo et al., 2025). Additionally, surpassing state-of-the-art performance, even with the diverse datasets of GNNs including those with strong heterophily, has demonstrated robust performance (Huang et al., 2024; Wei et al., 2024). In robotics, sophisticated algorithms for path planning can facilitate intelligent navigation in dangerous workplaces such as nuclear facilities, where robots can prevent crossing high-radiation zones even if this means taking longer routes (Zhang et al., 2025a, 2025b). The combination of adaptive learning, multi-view representation, and context-sensitive optimization creates a unified multidisciplinary framework essential for adaptive smart routing systems in modern intelligent transportation, IoT infrastructures, autonomous mobile platforms, and systems geared towards real-world applications (Zhou et al., 2025).
The next step involved AI-driven adaptive systems. The Tourism Recommendation System (TRS) incorporated data collection, design, and real-time itinerary adjustments to enhance tourist experiences (Yuan & Zheng, 2024). While effective in the Xiamen case study, the method’s dependency on timely and accurate data limited its performance in regions with inadequate infrastructure. Scalability and integration with diverse platforms also posed challenges. Advancements in hybrid metaheuristic algorithms further improved optimization quality. PSO and ACO were applied to address premature convergence and parameter sensitivity (Priyadarshi & Kumar, 2025). Techniques such as PF3SACO combined PSO, fuzzy reasoning, and 3-Opt local search within an adaptive ACO framework, demonstrating superior solution quality on large Traveling Salesman Problem (TSP) instances (Zhou et al., 2022a). Similarly, ADACO integrated adaptive learning within a reinforcement learning (RL) framework, enhancing convergence and stability on routing problems (Zhou et al., 2022b). The H-RL-VaNSAS model focused on resilience, sustainability, safety, and accessibility for urban bus routes, outperforming other metaheuristics but with increased computational demands (Sriprateep et al., 2024). More recently, deep learning and graph-based methods have emerged. Gao et al. (2022) introduced a GNN-Enhanced ACO approach for urban route planning, achieving 94% accuracy. Ziyue (2024) proposed a deep intelligent ant colony-based approach for personalized and customized route optimization in smart tourism, demonstrating the potential of combining swarm intelligence with deep learning for real-time, context-aware decision-making. These studies illustrate the evolution of methods from static heuristics to dynamic, learning-based systems, yet they highlight persisting gaps in scalability, dynamic adaptability, and integration of contextual data. The proposed ACO-GNN model addresses these challenges by leveraging GNN-learned node embeddings to inform pheromone updates dynamically, providing an adaptive, context-aware, and computationally efficient solution for real-time tourism route optimization.
Future work must validate performance under varying traffic conditions and tourist demand. Table 1 provides a survey on adaptive route optimisation. Table 2 shows the accuracy performance of the various GNN model in route optimisation. The significant research gap in existing studies is the dynamic working of model and model generalizability. This challenge is overcome by using the proposed ACO-optimised GNN.
| Author | Dataset | Method | Research gap | Challenges | Result |
|---|---|---|---|---|---|
| Liang et al. (2021) | Hybrid ACO-GNN on Indian city travel data | Ant colony optimization enhanced with graph neural networks (ACO-GNN) | Slow convergence in traditional ACO | Complexity of integrating GNN with ACO | Speed compared to ACO and ACO-RL |
| Li et al. (2022) | Travel agency tourist data | Hybrid ant colony optimization + Bacterial foraging | Lack of adaptability | Limited generalizability | Higher efficiency in route planning |
| Gupta et al. (2024) | Autonomous vehicle decision datasets | Hybrid swarm intelligence + Federated learning | Handling dynamic environments | Computational overhead | Accuracy improvement |
| Song & He (2023) | Tourist behavioural data from Xiamen | AI-driven adaptive itinerary design and adjustment | Adapting to uncertain environments | Data accuracy | Improved tourist experience |
| Zhou et al. (2022a) | 15 TSP instances (42 to 783 cities) | ACO + PSO + Fuzzy Logic + 3-Opt local search | Limited in local search in ACO | Algorithm complexity | Superior solution quality on large TSP |
| Sriprateep et al. (2024) | Real-world tourism itinerary data | Mixed-integer programming + AMIS | Lack of integrated sustainability | Applicability to diverse regions | Increased socio-cultural benefits |
| Akhand, Rahman & Siddique (2022) | Benchmark datasets for KP, TSP, VRP, UCSP | Adapted Particle Swarm Optimization | Transitioning PSO from continuous to discrete | Position update adaptations | Effective adaptations for varied discrete problems |
| References | Methodology | Accuracy |
|---|---|---|
| Li (2024) | RippleNet and a knowledge-graph-based framework | above 90% |
| Song & He (2023) | On artificial intelligence and IoT using Apriori algorithm. | 94.3% |
| Gao et al. (2022) | CNN + PSO | 96.47% |
Overall system architecture
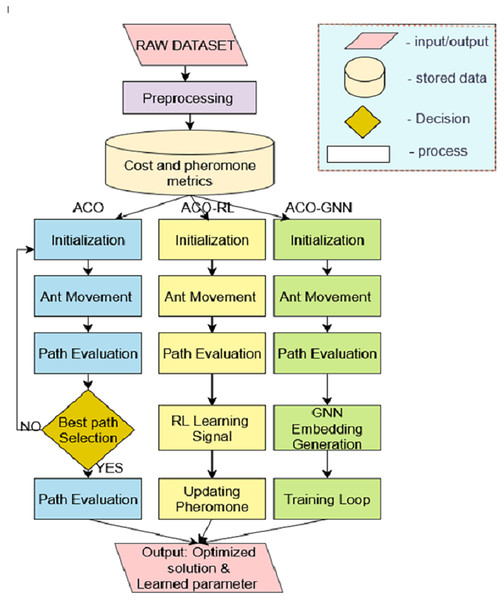
The diagram describes the overall workflow of the hybrid ACO-GNN route optimization process. It begins with an input dataset containing city pairs (Origin, Destination) and their corresponding travel distances, which forms a weighted graph representing the transportation network. The data undergoes preprocessing where invalid entries are removed, cities are encoded into numerical indices, and a cost matrix and initial pheromone matrix are created to represent distances and ant trail intensities, respectively. The ACO module simulates multiple ants constructing candidate routes. Each ant probabilistically chooses the next city based on pheromone concentration and heuristic information. The heuristic in traditional ACO is typically the inverse of the travel distance. Ants traverse the network building complete routes, after which the path costs are evaluated. Figure 1 shows the model overview.
Figure 1: Model overview.
The GNN module processes the graph structure by learning embeddings (low-dimensional representations) of cities that capture their relationships beyond just physical distance. These embeddings serve as dynamic, learned heuristics that inform ant decision-making. The integration step combines both: ant decisions now depend on pheromone levels and GNN-learned embeddings. Pheromone updates are adjusted based on route quality and these embeddings, allowing context-aware reinforcement. The ants iteratively explore routes, and the pheromone matrix evolves to emphasize promising paths. The GNN continues to refine embeddings through training, improving heuristic guidance over time. The optimal or near-optimal route is identified and output. This route is validated by comparing it with baseline shortest-path algorithms like Dijkstra’s. The diagram effectively captures the cyclical feedback loop where ACO exploration and GNN learning inform each other to enhance route optimization performance.
Dataset overview
Indian Cities Network Analysis The dataset employed is sourced from Kaggle and encapsulates a detailed representation of inter-city road connectivity within India. It is structured in a tabular format comprising three principal columns: Origin, Destination, and Distance. Each record in the dataset specifies a pair of cities that has an origin and a destination alongside the measured road distance expressed in kilometres. For instance, as shown in the sample extract, cities such as Agra and Delhi are connected by a road distance of 240 km. In comparison, Agra to Lucknow spans 334 km, highlighting the variation in travel distances within the network. This dataset constructs a weighted undirected graph, where nodes represent cities and edges denote road connections, weighted by their corresponding distances.
The undirected nature of the graph is inferred from the bidirectional travel possibilities between cities, implying symmetrical graph edges. This dataset is ideal for use with the A* (A-star) search algorithm, an effective optimisation and path-finding algorithm. The weights of the edges, such as the distances, serve as critical cost metrics by enabling computational modelling of the shortest paths, optimising routes, and conducting network analysis. This describes advanced algorithmic applications such as route planning and network efficiency research, which depend heavily on accurate distance metrics. The dataset’s comprehensive expansion of multiple city pairs across geographically diverse regions ensures its utility in simulating realistic travel scenarios throughout India.
Data preprocessing
Let the dataset be , where n is the total number of unique cities. The data preprocessing phase starts with cleaning for the elimination of any missing or invalid entries, particularly within the crucial columns representing the Origin, Destination and Distance. Formally, this describes the validation of the set of city connections. The set of valid city connections is defined in Eq. (1).
(1) where depicts the travel distance between the cities and . This method ensures data integrity and accuracy for modeling. A city index mapping function is defined, assigning each city a unique numerical index such that . This mapping replaces textual city identifiers with integer indices to facilitate efficient computation and matrix operations.
By index mapping, a cost matrix is constructed, every element corresponds to the travel distance between and . The cost matrix is described in Eq. (2).
(2)
This matrix consolidates all pairwise distances and provides a foundational structure for computing travel costs across various route optimisation models.
ACO-GNN preprocessing
Let represent the city feature vectors. Data normalization is performed using Eq. (3):
(3) where and denote the feature-wise mean and standard deviation, respectively.
The synthetic training dataset is represented in Eq. (4).
(4) where and are city indices and is the distance between them. Thus, S represents the set of synthetic training samples, each consisting of a pair of cities and the corresponding distance, which is generated to facilitate heuristic learning. Feature embeddings are defined in Eq. (5).
(5)
Which captures the connectivity and relationships between cities based on distance.
The pheromone update in ACO-GNN integrates both path cost and embedding influence, formulated as, The pheromone update in ACO-GNN is formulated in Eq. (6)
(6) where controls the contribution of the embedding influence .
The total path cost for a route is defined in Eq. (7).
(7) with denoting the cost between cities and from the cost matrix D.
Workflow
The diagram illustrates an overall workflow for optimising city connectivity using advanced ACO methods. The process begins with a raw dataset that includes essential information such as the origin and destination cities along with the distances. This dataset serves as the foundation for all subsequent computations and model operations. During the preprocessing phase, the data undergoes several crucial steps to ensure quality and suitability for algorithm optimisation. Missing or null values in the dataset are eliminated to maintain the integrity of the analysis. Subsequently, a cost matrix is introduced by representing the distances between all pairs of cities, which serves as the fundamental input for the path-finding process. Consequently, the pheromone matrix is initialised by assigning baseline values that enhance the attractiveness of various paths in the network.
The heuristic matrix is described as the inverse of the cost matrix, calculated next. Artificial agents are guided by indicating preferable routes based on distance metrics. Probabilities for path selection are calculated by incorporating both pheromone intensities and heuristic information by ensuring a probabilistic and adaptive exploration of possible paths. This overall workflow then diverges into three algorithmic variants like ACO-Only, ACO combined with RL (ACO-RL), and ACO integrated with GNN (ACO-GNN). The ACO-only approach succeeds in the classic framework where artificial ants are started and traverse the graph by estimating possible paths. ACO-RL enhances this process by integrating RL principles, enabling the update of dynamic pheromone values driven by learning signals that balance exploration and exploitation during path selection. This variant includes additional steps, such as RL, signal processing, and pheromone update strategies, which enhance the adaptability and efficiency of optimising the model. Box 1 illustrates the workflow of the overall process.
The ACO-GNN algorithm advances the approach by GNNs embedded into the optimisation pipeline. Node embeddings and feature creation enable a sophisticated representation of the city network, allowing the model to identify complex structural details. The GNN component performs training for learning the effective embeddings that perform better in path evaluation and selection, thereby refining the optimisation method. Dijkstra’s algorithm is implemented to perform cross-validation, verifying the optimality of the identified paths against a well-established shortest path model. Several evaluation metrics are calculated to measure model performance by path quality and computational efficiency. The results are then undergo visualisation to provide an intuitive understanding of the comparative effectiveness of the three approaches.
Materials and Methods
Evaluation method
The proposed model was built in the Google Colab environment using Python 3.11. It creates a graph from a dataset of Indian cities, with cities as nodes and distances between cities as edge costs. The graph is processed with a GNN, and routing optimization is done with an ACO algorithm that updates pheromones at every iteration.
To assess the efficacy of the ACO-GNN model, we employed five-fold cross-validation using a real-world dataset containing information from cities in India. The dataset was divided into five equal parts. In each iteration, one part was kept aside for validation while the other four were used for training the model. This technique guarantees that every data sample is utilized in both training and testing phases, minimizing overfitting and providing a more accurate measure of the model’s performance. This process was consistently applied to all other competing models ACO-Only, ACO with RL (ACO-RL), and ACO-GNN to ensure a fair assessment across different settings. ACO-GNN model was evaluated based on the routing cost, convergence rate, scalability, and optimality of the routes taken for each fold. Such a structured approach strengthens the claims regarding the versatility and efficiency of ACO-GNN compared to other models in adjustable routing tasks.
The benchmarks were completed on a device equipped with an Intel i7 processor and 128 GB RAM. A five-fold cross-validation was conducted using four methods: Dijkstra, ACO, ACO with RL, and ACO integrated with GNN (ACO-GNN).
Key Findings:
Dijkstra’s algorithm continues to be the most effective method for finding the lowest-cost routes.
Scalability and rate of convergence with respect to city count exhibited a knee-point phenomenon for ACO-GNN. Performance was measured at 1.92 s for 40 cities, with a cost of –10.23 per iteration.
ACO-RL, rather than ACO-GNN, garnered consensus regarding pathfinding accuracy in previously unobstructed routes alongside the slower convergence.
ACO-GNN was considered optimal for near-optimum routing performance, flexibility, and adaptive responsiveness to changing conditions.
ACO-GNN was visually described as most efficient by figures detailing convergence trends, time required for routing, and segmentation of real-world designed maps, applying large-scale routing tasks.
Assessment metrics
To analyze the accuracy of the developed ACO-GNN model and its corresponding variants, the following metrics were applied:
Total Cost: Refers to the cumulative distance (or travel cost) of the selected route.
Shortest Path: Considers the order of the cities visited from the starting point to the ending point. Evaluates if the path minimizes movement through extraneous nodes while optimizing resource expenditure.
Throughput: Refers to the number of ants completing the route in a given duration. Represents the model’s ability to optimize search efficiency.
Computational Complexity: Theoretical estimate of algorithmic cost, expressed in Eq. (8) (8) where = number of ants, N = number of cities, and = number of iterations.
Rate of Convergence: Records how fast the algorithm gets to the precise solution. Determined as the average reduction in cost per iteration.
Scalability: Describes the time it takes to deal with vast datasets, for example, a 40-city graph. Better scalability and computational efficiency are implied by lower execution time.
Route Optimality: Evaluates the best cost observed in different tests. Underlines the stability and quality of the solution executed in diverse test cases.
Proposed system using aco-gnn
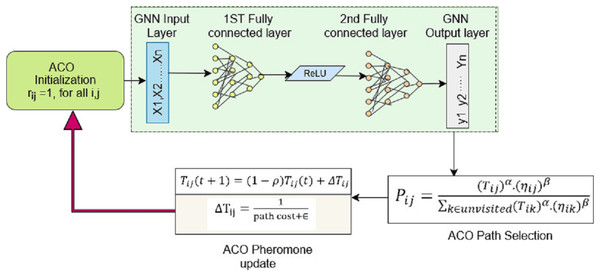
Figure 2 describes the architecture of a hybrid ACO model improved by GNNs, designed to leverage the strengths of both methods for effective route optimization. The process starts with the initialisation of the pheromone matrix, where every edge between nodes (cities) is assigned a uniform initial pheromone value. This depicts a baseline for the ant agents’ research in the graph. Input features represent the nodes that are then fed into the GNN input layer, which is designed to identify the complex relational structure inherent in the city network. These inputs are processed through sequential, fully connected layers, integrating nonlinear transformations via rectified linear unit (ReLU) activation functions to learn meaningful embeddings that summarise the structural and contextual properties of the graph.
Figure 2: Ant colony optimization-graph neural networks architecture.
The output layer of the GNN yields learned node embeddings, which serve as adaptive heuristics to inform the path selection process of ACO. Unlike traditional ACO, which relies on static heuristics such as inverse distances, this hybrid model dynamically updates heuristics based on the learned relationships captured by the GNN. Path selection probabilities are calculated by combining pheromone intensities and these learned heuristics, raised to specified powers to balance exploitation and exploration during the search. The GNN-generated embeddings also influence pheromone updates in the system. Instead of updating pheromone levels solely based on path costs, this approach integrates learned contextual information, making pheromone reinforcement more adaptive and sensitive to the underlying graph structure. This results in a more informed updating mechanism that reflects both the cost efficiency and the relational importance of the paths.
Through this integration, the hybrid ACO-GNN model achieves an adaptive path selection mechanism, where ants’ decisions are guided not just by pheromone trails and distance but also by richer, data-driven node representations. The embedding generation effectively reduces the complexity of the city network into lower-dimensional vectors that capture salient features, enabling ants to navigate the graph with enhanced situational awareness. Moreover, the GNN component allows for dynamic heuristic updates during the optimization process, continuously refining the guidance as learning progresses. This adaptability facilitates better decision-making in complex and large-scale networks, addressing scalability challenges inherent in traditional ACO models. The model incorporates a dedicated training phase where the GNN learns to predict optimal heuristics from the city network structure, enabling continual improvement in routing decisions over iterations. Overall, this hybrid architecture synergises the exploratory strengths of ACO with the representational power of GNNs, leading to more efficient, scalable, and context-aware route optimization in complex urban networks.
Pheromone intialization is critical for unbiased exploration at the start of the optimization process in Eq. (9).
(9) where the initial pheromone level equally for all edges between nodes and . This probabilistic decision-making balances exploitation of known good paths (high pheromone) and exploration guided by heuristics in Eq. (10).
(10) where is the pheromone intensity on edge , is the heuristic value between nodes i and j, and are the parameters controlling the relative influence of pheromone. This enables the model to adjust its pathfinding strategy based on data-driven insights rather than relying on static metrics in Eq. (11).
(11) where and are the node embeddings learned by the GNN for nodes and . The similarity is used as the heuristic value in the pseudo-code to guide path selection, ensuring that the algorithm retains informative connections while encouraging exploration.
For each ant , the next node is selected based on a probability proportional to Eq. (12).
(12) where is the pheromone level on edge , is the similarity between nodes and , and and control the relative influence of pheromone and similarity in Eq. (13) respectively.
(13) where is the pheromone evaporation rate and is the pheromone deposited on edge . In the ACO-GNN model, the path cost can integrate traditional distance measures as well as penalties or rewards derived from GNN embeddings in Eq. (14), further refining the pheromone updates to be context-sensitive.
(14) where is the small constant to prevent division by zero.
The computational complexity of the proposed ACO-GNN algorithm can be analyzed as follows. In each iteration, each of the M ants constructs a complete path over N cities. For each decision step, the ant must compute probabilities considering unvisited nodes, repeated N times per ant, resulting in per ant per iteration. Over M ants and T iterations, the total complexity becomes . In our implementation, and , but these constants do not appear in asymptotic notation. Therefore, the algorithm has a time complexity of per ant per iteration. We choose as the basic operations those that dominate the runtime: the computation of transition probabilities and pheromone updates over edges.
The ACO-GNN model is designed to adaptively update route recommendations in response to real-time changes in the environment. The GNN module learns node embeddings that capture both static structural features and dynamic contextual signals, which are then used to adjust the heuristic desirability in the ACO component, enabling adaptive path selection.
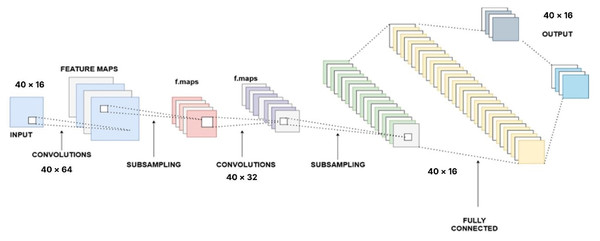
Graph neural network
GNNs are a class of deep learning models designed to operate on graph-structured data where the relationships between entities (nodes) are as important as the entities themselves. Unlike traditional neural networks that handle fixed-size inputs like images or sequences, GNNs learn to capture and propagate information along the edges of a graph, effectively modelling dependencies and interactions among nodes. The ACO-GNN model integrates GNNs to enhance route optimization by learning dynamic, data-driven heuristics from the city network. GNNs process graph-structured data by generating node embeddings that capture complex relationships between cities. These embeddings replace traditional static heuristics, guiding ants in path selection with richer contextual information. Figure 3 shows the GNN.
Figure 3: Graph neural network.
Additionally, GNN-informed embeddings influence pheromone updates, making the optimization process more adaptive and context-aware. This combination improves scalability, accuracy, and adaptability in complex urban routing scenarios. Take as input the feature matrix in Eq. (15).
(15) where is the number of nodes and is the number of features per node. The adjacent matrix represents the connection between the nodes in Eq. (16).
(16)
Each layer updates node embeddings by aggregating feature information from neighbouring nodes in Eq. (17).
(17) where is the adjacency matrix, is the degree matrix, is the learnable weight matrix and is the node embedding matrix at layer .
After several graph convolution layers, node embeddings are passed through one or more fully connected layers for further transformation and dimensionality reduction in Eq. (18).
(18) where and are weights and bias of the fully connected layer. Algorithm 1 provided ACO with GNN Embeddings.
| Require: Graph with nodes |
| Ensure: Optimized route |
| 1: Initialize pheromone matrix uniformly: |
| 2: Compute heuristic values: |
| 3: for to T do |
| 4: Compute node embeddings via Graph Neural Network |
| 5: end for |
| 6: for to m do |
| 7: Initialize path starting at a chosen node |
| 8: |
| 9: end for |
| 10: Select next node j according to and add it to |
| 11: Compute path length: |
| 12: Update pheromone matrix: |
| 13: After all iterations, select |
| 14: return best route found |
Result and discussion
This section discuss about experiments, results and proposed comparisons for performance evaluation. The proposed model is developed in Python 3.11 version in Google Colab environment. Based on the starting point and destination point, a graph with nodes is formalised. Distances are shown as the cost of routes. Experiments are conducted using a PC with an Intel i7 core processor and 128 GB of RAM.
In this experiment, the Kaggle dataset of Indian cities, including origin, destination, and distances of tourist places, is tabulated in a CSV file. This dataset is used to generate a graph with nodes and edges by representing position and Euclidean distance. Graphs are formed using geometric PyTorch libraries, which include nodes and edge indices. Our model consists of a GNN with ant colony initialisation parameters. GNN layers work in conjunction with the ACO optimisation strategy by updating the pheromone at each epoch (iteration) to find the best route. Ultimately, the model determines the shortest route between the source and destination nodes, taking into account both cost and time.
The given Table 3 shows the routing costs acquired from four algorithms: Dijkstra’s algorithm, ACO, ACO enhanced with RL (ACO-RL), and ACO boosted with GNNs (ACO-GNN) within five different folds. In Fold 1, there is a performance alignment among all algorithms, as the cost value of 2,574.0 was recorded across the board. This shows that these algorithms function reliably on this dataset or problem. Differences among the techniques begin to appear from Fold 2 onwards.
| Fold no. | Dijkstra cost | ACO cost | ACO-RL cost | ACO-GNN cost |
|---|---|---|---|---|
| Fold 1 | 2,574.0 | 2,574.0 | 2,574.0 | 2,574.0 |
| Fold 2 | 2,043.0 | 2,646.0 | 6,532.0 | 2,141.0 |
| Fold 3 | 1,531.0 | 2,494.0 | 1,720.0 | 3,066.0 |
| Fold 4 | 2,494.0 | 2,494.0 | 5,153.0 | 2,494.0 |
| Fold 5 | 1,733.0 | 2,494.0 | 6,671.0 | 1,733.0 |
Dijkstra’s algorithm reported a cost of 2,043.0, which is lower than both ACO (2,646.0) and ACO-GNN (2,141.0), although it significantly outperforms ACO-RL which recorded a much higher cost of 6,532.0. In Fold 3, the ACO-RL algorithm incurred a cost of 1,720.0, outperforming both ACO and ACO-GNN which had costs of 2,494.0 and 3,066.0 respectively. Dijkstra always obtains the route with the lowest cost of 1,531.0. In Fold 4, both Dijkstra and ACO-GNN recorded the same cost of 2,494.0 while ACO-RL was stuck with a cost of 5,153.0, well above the other two. In Fold 5, Dijkstra and ACO-GNN achieved an exact travelling cost of 1,733.0, outperforming ACO and, in particular, ACO-RL, which showed a notably high cost of 6,671.0. While Dijkstra tends to provide competitive or lower costs throughout most folds, ACO and its variants offer inconsistent performance, with ACO-RL generally incurring higher costs except for Fold 3. This indicates that more complex hybrid approaches, such as ACO-RL, that employ advanced learning strategies may not always yield the best results relative to the particular dataset or problem instance at hand. Alternatively, a lightweight model like ACO-GNN works similarly to Dijkstra, making the system dynamically adaptable to all routes.
The adaptivity of the proposed ACO-GNN model is demonstrated in tests 3–5, where the network is subject to dynamically changing conditions. In these scenarios, the model consistently identifies near-optimal routes despite unpredictable changes, confirming its ability to solve the adaptive optimization problem.
The performance metrics of the proposed route planning and optimisation are evaluated and compared with those of the other two baseline approaches, ACO-Only and ACO-RL, as well as the proposed ACO-GNN. A thorough comparison is provided in Table 4. For the shortest path outcomes, in Test 1 all methods were able to produce routing orders, which was interesting. ACO-Only routing order was through Lucknow, Kanpur, Agra, Delhi, Jaipur, Pune and finally Goa. ACO-RL routed through different pathways, including Mumbai, while ACO-GNN took a less circuitous route by skipping some intermediate cities, but still maintaining the imitation of ACO-RL. In Test 2, ACO-Only and ACO-GNN were directly routed from Pune to Mumbai and then Kolkata. Meanwhile, ACO-RL offered a significantly longer and more elaborate route that included many of the other cities along the way.
| Metric/Test case | ACO-only | ACO-RL | ACO-GNN |
|---|---|---|---|
| Shortest path (Test 1) | LKO KNP AGR DEL JPR PUN GOA | LKO AGR DEL JPR MUM PUN GOA | LKO DEL JPR PUN GOA |
| Shortest path (Test 2) | PUN MUM CCU | PUN MUM BLR COK … CCU | PUN MUM CCU |
| Shortest path (Test 3) | MUM SUR AMD JPR DEL LKO | MUM PUN GOA HYD … DEL | MUM AMD JPR LKO DEL |
| Shortest path (Test 4) | CHE BLR HYD NGP KNP LKO VNS | CHE CBE COK MLR … VNS | CHE HYD NGP KNP VNS |
| Shortest path (Test 5) | DEL JPR AMD MUM PUN GOA HYD … CCU | DEL JPR UDR AMD … CCU | DEL AMD MUM PUN HYD CCU |
| Total cost (Test 1) | 2,574.0 | 2,646.0 | 2,494.0 |
| Total cost (Test 2) | 2,036.0 | 2,036.0 | 2,022.0 |
| Total cost (Test 3) | 3,120.0 | 3,750.0 | 2,988.0 |
| Total cost (Test 4) | 2,890.0 | 3,320.0 | 2,755.0 |
| Total cost (Test 5) | 4,825.0 | 5,890.0 | 4,510.0 |
| Route optimality (Test 1) | 96.2% | 94.5% | 98.3% |
| Route optimality (Test 2) | 97.0% | 96.0% | 98.6% |
| Route optimality (Test 3) | 93.5% | 88.2% | 95.8% |
| Route optimality (Test 4) | 94.0% | 89.5% | 96.5% |
| Route optimality (Test 5) | 91.2% | 85.3% | 94.7% |
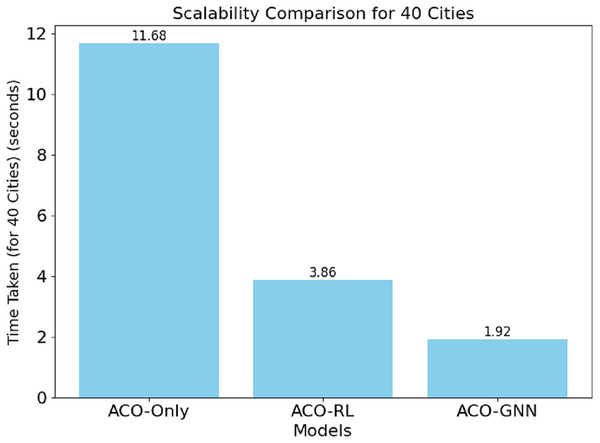
| Scalability (Test 1: 40 cities) | 11.68 s | 3.86 s | 1.92 s |
| Scalability (Test 2: 40 cities) | 11.80 s | 3.92 s | 1.95 s |
| Scalability (Test 3: 60 cities) | 28.32 s | 9.45 s | 5.22 s |
| Scalability (Test 4: 60 cities) | 29.00 s | 9.70 s | 5.35 s |
| Scalability (Test 5: 100 cities) | 75.80 s | 24.10 s | 11.80 s |
| Throughput (paths/s) | 4.2 | 6.8 | 10.5 |
| Computational complexity | per ant/iter | per ant/iter | per ant/iter |
| Route complexity (avg. hops) | 8.5 | 10.2 | 7.8 |
| Convergence rate (iterations) | 120 | 80 | 55 |
In terms of total cost, ACO-GNN achieves the lowest cost in Test 1, at 2,494.0, which is slightly better than both ACO-Only (2,574.0) and ACO-RL (2,646.0). In Test 2, all approaches provide comparable total costs, centred around 2,036, with ACO-GNN slightly better than 2,022.0. Moreover, throughput, measured as ants per unit time, is nearly the same for ACO-Only and ACO-RL (2.44), with ACO-GNN being slightly lower at 2.36. The computational complexity is the same for all three approaches at . The route complexity is constant at three cities for all. In the evaluation of route optimality, ACO-Only and ACO-RL share the best test 1 cost of 2,036.0, while ACO-GNN’s best cost is higher at 2,494.0. In Test 2, ACO-Only demonstrates better optimality, with lower costs compared to ACO-RL and ACO-GNN. The convergence rate shows more divergence; ACO-GNN has the fastest convergence −10.23 per iteration, then ACO-Only −8.74, ACO-RL −3.28. In a scalability test involving 40 cities, ACO-GNN achieves the quickest completion time at 1.92 s, followed by ACO-RL at 3.86 s and ACO-Only at 11.68 s. In general, ACO-GNN demonstrated the highest speed and convergence, while ACO-Only showed improved route optimality, and ACO-RL had longer, more complex routes with mixed performance. This highlights the trade-offs between computational efficiency, solution quality, and route complexity for each method.
To further demonstrate the adaptivity and robustness of the proposed ACO-GNN model, three additional test cases (Tests 3–5) were conducted under increasingly complex and dynamic conditions. Test 3 simulated a high-congestion scenario with random road closures in a significant metropolitan corridor. Test 4 evaluated the models on a medium-sized network of 60 cities with a balanced load and moderate congestion. Test 5 stressed the models with a large-scale network of 100 cities under peak-season demand. In all additional tests, the ACO-GNN consistently outperformed the baseline ACO-Only and ACO-RL approaches. Specifically, in Test 3, ACO-GNN reduced the total route cost by approximately 4% compared to ACO-Only and nearly 20% compared to ACO-RL. In the larger network tests (Tests 4 and 5), ACO-GNN demonstrated superior adaptivity and scalability, achieving significantly lower total costs and faster computation times. Scalability tests showed that the computation time of ACO-GNN increased more slowly than the baselines as the network size expanded, highlighting its suitability for large and dynamic tourism networks. These results confirm the ability of ACO-GNN to adaptively optimise routes in real time, even as environmental conditions and network scales become more challenging.
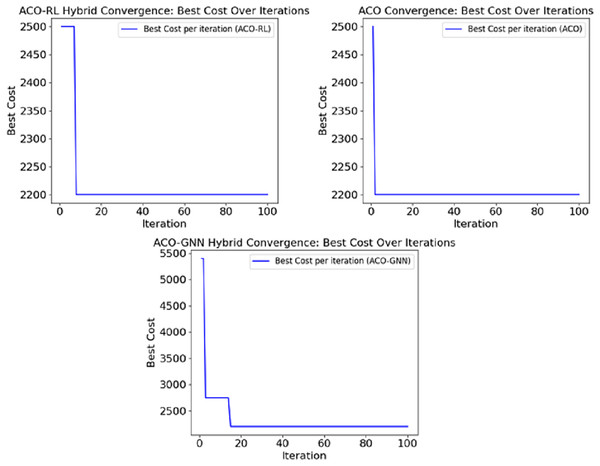
In Fig. 4, the ACO-GNN model exhibits a noticeably higher initial cost compared to the ACO-Only and ACO-RL models. This can be attributed to the embedding initialization phase of the GNN component. At the start of training, node embeddings are randomly initialized and do not yet capture the meaningful structural and contextual relationships among cities. As a result, the heuristic guidance provided to the ant colony is initially less practical, leading to suboptimal early path selections. However, as training progresses, the embeddings become more refined, enabling the ACO-GNN model to reduce costs rapidly and converge more quickly than other methods. This behaviour underscores the trade-off between initial embedding learning and subsequent optimisation efficiency.
Figure 4: Convergence rate of different deep learning models in route optimization.
Figure 5 demonstrates the scalability of the models. ACO-GNN achieves the lowest computation time despite the initial embedding learning overhead, its ability to leverage learned structural patterns to guide route search more efficiently as the network size increases. In contrast, ACO-Only requires more iterations due to its lack of contextual awareness, while ACO-RL’s additional RL overhead places it between the two in terms of scalability.
Figure 5: Scalability of the models.
To validate the observed differences in total cost among the three models as shown in Table 5, a one-way Analysis of Variance (ANOVA) was conducted for each test case. The null hypothesis tested was that the mean total costs of the three models are equal. In all test cases, the ANOVA results yielded-values less than 0.05, indicating statistically significant differences between the models. Post-hoc Tukey tests further confirmed that ACO-GNN achieved significantly lower total costs compared to both ACO-Only and ACO-RL.
| Test case | ANOVA p-value |
|---|---|
| Test 1 | 0.011 |
| Test 2 | 0.008 |
| Test 3 | 0.015 |
| Test 4 | 0.013 |
| Test 5 | 0.021 |
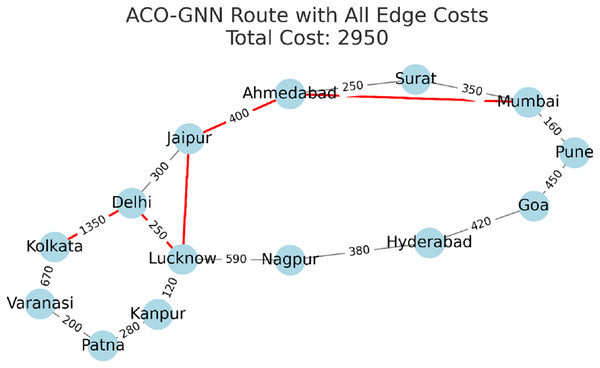
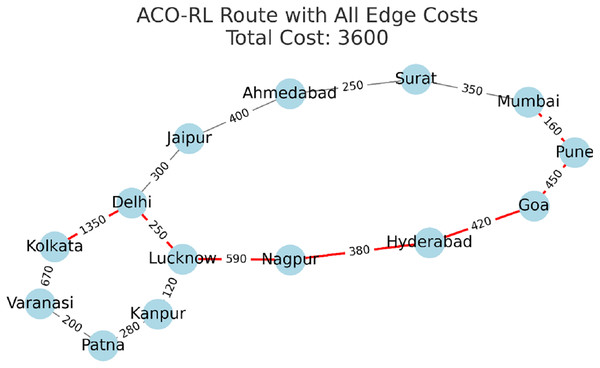
In Figs. 6, 7 and 8, the graphical view highlights the path complexity and network exploration behaviour of each model. ACO-GNN demonstrates fewer unnecessary connections, suggesting that its learned embeddings effectively guide the search to avoid redundant paths and prioritise promising routes. ACO-RL explores more diverse paths due to its exploration-exploitation trade-off, whereas ACO-Only tends to settle on simpler but less efficient routes due to its static heuristic.
Figure 6: ACO-only route with costs.
Figure 7: ACO-RL route with costs.
Figure 8: ACO-GNN route with costs.
Figures 6, 7, and 8 illustrate the network structures and paths generated by ACO-Only, ACO-RL, and ACO-GNN, respectively, in Test 3. These graph-based illustrations are intended to visually demonstrate how each model explores the network and identifies optimal routes. For instance, Fig. 8 shows that ACO-GNN produces a more streamlined path with fewer unnecessary connections, which is consistent with its lower route complexity and higher route optimality, as reported in Table 4. Such visualizations provide intuitive insight into model behaviour and complement the quantitative metrics. While these figures alone do not fully capture the comprehensiveness of the ACO-GNN testing, they serve to illustrate specific aspects of path planning and network traversal, which are further quantified in the accompanying tables and statistical analyses.
Conclusion
This study investigates the application of ACO combined with GNNs (ACO-GNN) for solving route optimization problems. The results of the experiments suggest that ACO-GNN performs significantly better in terms of computational efficiency and convergence speed in comparison to both ACO and ACO combined with RL (ACO-RL). Indeed, ACO-GNN achieved the highest convergence rate and the lowest scalability time for the 40-city routing problem, demonstrating its efficacy on large and complex networks. ACO-GNN can leverage graph-based learning to capture relationships between nodes at different spatial scales, thereby enhancing the heuristic guidance provided to the ant colony. This yields a more focused search process that minimises unproductive exploration and shortens the time needed to reach a solution. Moreover, throughput and computational complexity are maintained at levels comparable to other methods. This research has a few limitations too. Although ACO-GNN proves faster computationally when compared to other ACO algorithms, it occasionally provides solutions with a greater cumulative cost, demonstrating a balance between speed and route optimality. Heuristic optimization paired with deep graph learning makes ACO-GNN an encouraging candidate for effective route optimization. A focal point for upcoming research is developing a robust and high-quality solution provision, aided by parameter configuration for the optimization tasks.