Mining highly reliable dense subgraphs from uncertain weighted graphs for protein-protein interaction networks
- Published
- Accepted
- Received
- Academic Editor
- Davide Chicco
- Subject Areas
- Data Mining and Machine Learning, Data Science
- Keywords
- Graph mining, Greedy algorithms, Reliable dense subgraphs, Subgraphs, Uncertain weighted graphs
- Copyright
- © 2025 Duong and Nguyen
- Licence
- This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, reproduction and adaptation in any medium and for any purpose provided that it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Computer Science) and either DOI or URL of the article must be cited.
- Cite this article
- 2025. Mining highly reliable dense subgraphs from uncertain weighted graphs for protein-protein interaction networks. PeerJ Computer Science 11:e3304 https://doi.org/10.7717/peerj-cs.3304
Abstract
Graphs are widely used as essential modeling tools to represent protein-protein interaction networks. However, they are often subject to uncertainty due to noise or incomplete data collection. This research aims to address the challenges associated with uncertain weighted graphs, where each edge is characterized by both a probability of existence and a numerical weight. We propose two novel greedy algorithms, GreedyUWDS and GreedyBWDS, designed to extract dense and reliable subgraphs from uncertain weighted graphs. GreedyUWDS optimizes subgraph density by leveraging the expected weighted density metric, whereas GreedyBWDS introduces a flexible reliability threshold parameter to effectively balance density and reliability, enabling users to adjust the algorithm to prioritize either highly reliable subgraphs at the expense of density or greater density at the expense of reliability, thereby addressing a critical trade-off that previous methods have not effectively managed. Experimental validation on protein-protein interaction networks demonstrates that the proposed algorithms outperform existing techniques in terms of weighted edge density and subgraph reliability. Specifically, GreedyBWDS achieves approximately a 20% improvement in graph density over GreedyUWDS, while reducing runtime by a factor of 2.5. GreedyBWDS consistently identifies subgraphs with higher values for the combined density and reliability objective, and demonstrates significantly greater computational efficiency. These results underscore the flexibility and efficiency of our proposed approaches, offering practical solutions for analyzing uncertain weighted graphs in biological contexts, with a primary focus on protein-protein interaction networks. This research advances the field of graph mining by enabling users to fine-tune the balance between density and reliability according to their specific application requirements.
Introduction
Graph theory, the study of graphs and their properties, is a fundamental area of computer science. Graphs are widely used to represent complex systems, capturing relationships in biological systems such as protein-protein interaction networks (PPI). A central concept in this discipline is finding the densest subgraph, typically defined as the subgraph with the highest edge density, the ratio of the number of edges to the number of vertices (Dondi et al., 2021). Identifying such dense substructures is important for many applications. For example, in biology, discovering connected groups of entities can reveal community structures and functional modules. Traditionally, the densest subgraph problem has been studied using deterministic graphs; however, additional challenges arise when uncertainty is introduced into these graph models.
In uncertain weighted graphs, each edge is characterized by both a probability of existence and a numerical weight. This model captures not only the variability of connections, due to noise or incomplete data, but also their relative importance. For example, as noted by Rual et al. (2005), PPI networks (Szklarczyk et al., 2015) demonstrate that each protein bond can influence both structural and biological function, yet the presence or absence of these bonds is often uncertain. A graph that models this uncertainty is called an uncertain graph, and when weights are also assigned to edges, it becomes an uncertain weighted graph.
A key analytical challenge in uncertain weighted graphs is to identify subgraphs that are both dense and reliable. Focusing solely on density, without accounting for the reliability of edges, may result in dense subgraphs that rely on highly uncertain connections. Conversely, optimizing only for reliability could yield trivial subgraphs. Therefore, balancing both density and reliability is necessary to extract meaningful subgraphs from uncertain weighted graphs. An essential concept is the most reliable subgraph, consisting of edges with the highest collective probability of existence.
This research aims to develop an effective strategy for identifying subgraphs that are both dense and reliable in uncertain weighted graphs. We consider both connection density and edge reliability, striving for a balance that yields subgraphs with high density and high overall reliability of connections. This is especially important in applications such as PPI network analysis, where subgraphs must be both structurally dense and statistically reliable to be useful. Existing methods are insufficient because they typically optimize only one aspect—either density or reliability—or assume that all edges are unweighted (Lu, Huang & Huang, 2019). Classic densest subgraph algorithms ignore uncertainty, while previous work on reliable subgraphs in uncertain graphs does not account for varying edge weights.
Our approach provides practical tools specifically tailored for protein-protein interaction networks to address these complex challenges and is expected to make a significant contribution to the analysis of biological networks.
Related work
Researchers have shown great interest in identifying dense subgraphs, particularly in uncertain graph models. The probabilistic nature of edge existence makes the task of discovering dense and reliable subgraphs more challenging. Greedy approximation methods, such as the Charikar algorithm (Charikar, 2000), offer valuable insights into network density within specific contexts. Other studies, such as those by Khuller & Saha (2009) and Andersen & Chellapilla (2009), focus on enhancing subgraph density by reducing subgraph size, a problem known to be NP-hard. Additionally, Moreira, Campos & Meira (2020) developed methods for evaluating complex hierarchical structures within bipartite graphs, broadening the field and providing insights for future applications in healthcare research. Methods such as finding the densest k-connected subgraphs have also been studied (Bonchi et al., 2021), demonstrating the breadth of dense subgraph research.
Research on uncertain graphs began with fundamental work by Gao & Gao (2013), which led to the development of models such as graph reliability (Zou et al., 2010) and clustering approaches (Kollios, Potamias & Terzi, 2013). The concept of the largest clique in uncertain graphs was introduced by Zou & Zhu (2013), who also proposed methods for identifying highly probable cliques (fully connected subgraphs) in large uncertain graphs. Since finding large cliques is NP-hard, the idea was extended to quasi-cliques, which permit some missing edges, offering a trade-off between density and computational feasibility.
The densest subgraph in an uncertain graph was first formally discussed by Zou et al. (2010), who defined the expected subgraph density based on edge existence probabilities. Subsequently, Jin, Liu & Aggarwal (2011) addressed the problem of identifying reliable subgraphs by introducing reliability measures and developing sampling-based algorithms to find subgraphs that are highly likely to exist. However, their approach focuses solely on reliability and does not directly ensure high density.
In Lu, Huang & Huang (2019), the authors proposed the -subgraph method and an associated optimal subgraph algorithm to balance density and reliability. A subgraph was defined as “ -dense” if it remained dense after filtering out edges with probability below . While this approach improved the reliability of the resulting subgraph, it assumed equal edge weights (effectively treating the graph as unweighted) and applied a fixed threshold to all edges. These limitations of the -subgraph approach reduce its applicability to uncertain weighted graphs.
In contrast, our GreedyBWDS algorithm generalizes this idea by accommodating variable edge weights and dynamically applying the threshold during the greedy removal process, rather than as a one-time filter. Miyauchi & Takeda (2018) laid the groundwork for addressing weighted uncertainty in dense subgraph discovery. Additionally, the study in Cheng et al. (2014) on shortest-path algorithms provided further insights into uncertain weighted graphs and contributed to the development of our methodology.
More recently, a powerful framework for detecting dense subgraphs in graphs was introduced in Chen et al. (2024), offering a range of useful features for deterministic graphs. Regrettably, it cannot be applied to uncertain graphs.
In addition to previous works on densest subgraphs and cliques, researchers have extended other notions of cohesive subgraphs to uncertain graphs. For example, k-core decomposition, which identifies the maximal subgraph in which each vertex has at least k neighbors, has been adapted to probabilistic settings. In Luo et al. (2023), scalable parallel algorithms were proposed to identify densest subgraphs in undirected and directed graphs by leveraging k-core decomposition, achieving substantial performance improvements on large-scale networks. In Peng et al. (2018), efficient algorithms were developed to compute the probabilistic k-core of an uncertain graph, introducing models that retain vertices with a high probability of being connected to at least k others. Similarly, a k-truss, defined as a subgraph in which each edge participates in at least k–2 triangles, has also been extended to uncertain graphs. In Sun et al. (2021), the authors studied the probabilistic k-truss, the largest subgraph in which each edge belongs to at least k–2 triangles with a probability of at least gamma. These approaches aim to find dense substructures based on vertex degree or triangle count under uncertainty.
In Saha et al. (2023), the concept of the most probable densest subgraph in uncertain graphs was introduced, along with algorithms that prioritize subgraphs likely to exhibit dense structures while taking edge uncertainty into account. Expanding on this, Kawase, Miyauchi & Sumita (2023) explored multilayer networks and proposed stochastic methods that yield probability distributions over vertex subsets, enabling the discovery of dense subgraphs in complex systems. However, these methods generally focus on specific structural patterns such as cores or trusses, rather than directly optimizing a combined density-reliability objective. In contrast, we define a unified objective function capturing both edge density and reliability, and design algorithms to directly optimize this joint criterion.
The application of dense subgraph discovery has extended from theoretical settings to real-world applications. Dense subgraphs have been utilized in PPI network analysis (Rual et al., 2005), as well as in fraud detection (Ma et al., 2021). Such applications have deepened our understanding of dense subgraphs within these complex structures.
Recent research has focused on dynamic methods. For example, Bera et al. (2022) introduced novel methodologies for finding the densest sub-hypergraphs within larger graph frameworks. Furthermore, Map-Reduce approaches have been used to address high-density subgraph problems. However, applying these principles to real-time or streaming contexts remains challenging.
Another active area of related research is the use of dense subgraph mining for anomaly and fraud detection, especially in dynamic or streaming graphs. Hooi et al. (2016) introduced Fraudar, an algorithm for detecting fraudulent clusters in static graphs by identifying anomalously dense subgraphs, while accounting for camouflage, which refers to efforts by fraudsters to hide within normal patterns. Fraudar effectively identifies suspiciously dense bipartite substructures in rating or follower networks. Shin et al. (2017) proposed DenseAlert, which incrementally maintains dense sub-tensors in multi-aspect data and detects sudden increases in density. These works highlight the importance of efficient dense subgraph discovery in streaming and evolving contexts.
Yan et al. (2021) developed real-time anomaly detection frameworks based on dense subgraph identification in network streams, successfully handling dynamic and uncertain data. Bhatia et al. (2023) proposed a sketch-based streaming anomaly detection method that approximates graph structure on the fly to detect anomalies in real time, which implicitly involves tracking dense connectivity patterns in a dynamic graph. Jiang et al. (2022) introduced Spade, a real-time fraud detection framework that incrementally maintains dense subgraphs on evolving graphs to catch fraudulent groups nearly instantaneously. In addition, Sawlani & Wang (2020) proposed fully dynamic algorithms for maintaining the densest subgraphs in evolving graphs, improving upon previous static methods. All these advances address the challenges of finding dense substructures under various constraints.
Our proposed methods are complementary to the studies mentioned above. We specifically address the case of uncertain weighted graphs and introduce methods that explicitly balance density and reliability. This fills a niche not fully covered by prior works. While previous studies have focused on static vs. dynamic settings or on unweighted graphs, we address uncertain graphs with weighted edges and provide a tunable approach that allows users to emphasize reliability as needed.
Many recent approaches have addressed the problem of reliable subgraph mining in uncertain graphs. In Lu, Huang & Huang (2019), the authors introduced the β-subgraph method, defining a subgraph as -dense if it remains dense after removing all edges with probability less than . However, this method treats the graph as unweighted and applies a hard probability threshold, potentially discarding valuable edge information in weighted networks. Our GreedyBWDS algorithm generalizes this approach by allowing for arbitrary edge weights and providing a tunable parameter that enables a continuous trade-off between density and reliability, rather than a strict cut-off.
Similarly, the approach in Jin, Liu & Aggarwal (2011) focuses on maximizing the expected number of edges within a subgraph, but it relies on the probability that all edges exist simultaneously and does not consider edge weights. This results in high computational cost for large graphs, and limits its applicability in practical scenarios. By contrast, our proposed algorithms extend these objectives to weighted graphs, and leverage efficient greedy techniques that maintain theoretical guarantees while scaling to much larger networks.
In summary, the proposed GreedyUWDS and GreedyBWDS algorithms improve upon previous research by optimizing a joint density-reliability objective. Unlike prior densest subgraph algorithms, our GreedyBWDS includes an adjustable parameter that allows users to smoothly navigate the trade-off between subgraph density and edge reliability. This adaptability is particularly useful in applications such as PPI networks (our primary example). Precisely modeling uncertain relationships is essential, and different scenarios may require different balance points between density and reliability.
Preliminaries and definitions
This section introduces the notations and definitions used throughout the article. Table 1 presents the key notations and definitions essential for understanding the content.
| Notion | Explanation |
|---|---|
| G | An uncertain weighted graph |
| The set of deterministic vertices | |
| The set of random edges | |
| The edge incident to the vertices and | |
| Edge Weight | |
| Probability of the edge weight = | |
| The order of the graph | |
| The size of the graph | |
| The size of the corresponding complete graph | |
| The average edge weight |
Definition 1. An uncertain weighted graph is a semi-random discrete structure , where is the set of deterministic vertices, and is the set of random edges, each edge follows a Bernoulli distribution with weight or . An uncertain weighted subgraph is extracted from , where . In an uncertain weighted graph, the random edges are mutually independent.
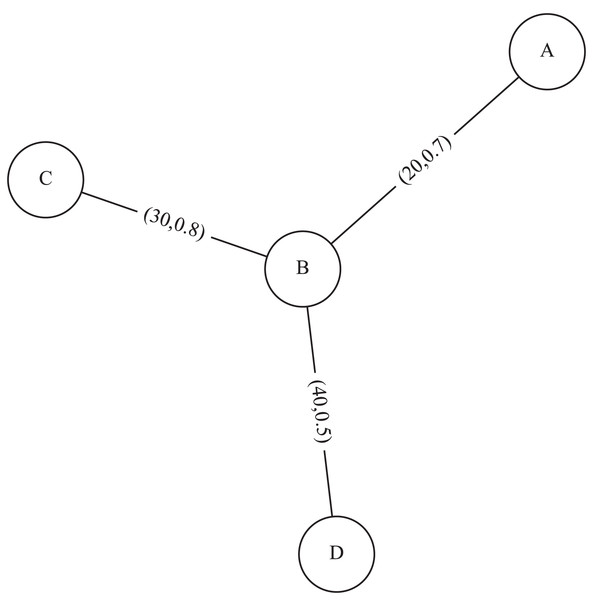
For example, Fig. 1 represents a simple uncertain weighted graph with three vertices , and their edge having probabilities: having a weight and a probability , having a weight and a probability , having a weight and a probability
Figure 1: An example of uncertain weighted graph.
Definition 2. An uncertain weighted subgraph is considered nontrivial if it satisfies the condition . We focus on nontrivial subgraphs because a single-edge subgraph, while trivially dense, is often not meaningful for our analysis of dense subgraphs.
Definition 3. The adjoint logarithmic reliability is defined in Eq. (1). By summing logarithms, we avoid numerical underflow that can occur when multiplying many probabilities. This approach provides a measure of subgraph reliability, where larger values indicate a higher joint probability that all the edges exist.
(1)
For example, the adjoint logarithmic reliability of the graph in Fig. 1 is calculated as .
Definition 4. The average edge weight is defined in Eq. (2)
(2)
For example, average edge weight of the graph in Fig. 1 is calculated as .
Definition 5. The standard deviation of edge weight is defined in Eq. (3).
(3)
This measures the variability of edge weight within the graph. A low value of indicates that the edges have similar probabilities, whereas a high value of suggests that some edges are much less certain than others.
For example, the standard deviation of edge weight of the graph in Fig. 1 is calculated
Definition 6. The edge weight density is defined in Eq. (4).
(4)
For example, the edge weight density of the graph in Fig. 1 is calculated as .
Problem statement
An important challenge in graph theory is to identify dense subgraphs in uncertain weighted graphs. Dense subgraphs consisting of closely connected vertices often contain important information about the properties of a graph. Therefore, extracting dense subgraphs from large graphs is an essential task in graph research.
However, advanced analytical techniques are required to extract dense and reliable subgraphs from uncertain graphs, especially when each edge has a different probability of existence. Furthermore, treating all edge weights equally often fails to capture the complexity of their interrelationships. Therefore, new methods are needed to incorporate edge weights, which represent the strength of relationships, into graph models.
Dense subgraphs in protein networks often reflect protein complexes and indicate how groups of proteins interact to perform specific biological functions. For example, the Fanconi protein complex is involved in DNA repair (Wang, 2007). The use of dense subgraphs in uncertain weighted graphs is essential for identifying and predicting previously unknown protein complexes.
The density of a graph with equals . The goal is to find a subset of vertices that has the highest density. Zou et al. (2010) described the concept of expected density in uncertain graphs and highlighted the challenge of finding dense subgraphs in such graphs. In uncertain graphs, both edges and weights are probabilistic, which makes the identification of dense and reliable subgraphs challenging (Jin, Liu & Aggarwal, 2011) examined the reliability of uncertain graphs by evaluating the reliability of their subgraphs and introduced the idea of subgraph reliability. This work also proposed sampling-based methods to find subgraphs with high reliability in uncertain graphs.
However, the subgraphs discovered using this method raise some concerns. For example, consider two uncertain subgraphs, A and B, both of which have the same expected density of . Subgraph A may consist of only a few edges, but each edge has a high probability of existence, indicating strong but sparse connections. In contrast, subgraph B may contain many more edges, reflecting a denser structure, but the probability of existence for each edge is very low. Although their expected densities are identical, it is not sufficient to compare graphs based solely on this measure. The reliability of a subgraph, which reflects the overall certainty of the connections, becomes an important criterion. As a result, the reliability of a subgraph is often prioritized over its density.
Lu, Huang & Huang (2019) developed a subgraph method and an optimal subgraph algorithm for finding dense and reliable subgraphs, with positive results in various real-world applications. However, these methods assume all edge weights are equal and therefore do not address the challenge of uncertainty in edge weights. The present research attempts to address the challenge of balancing density and reliability in the context of uncertain weighted graphs.
The problem of mining highly reliable dense subgraphs from uncertain weighted graphs is defined in Eq. (5).
(5)
This problem is NP-hard in general, as it generalizes the densest subgraph problem and also relates to finding high-probability subgraphs. Therefore, we seek heuristic or approximation algorithms that can efficiently find good solutions on large graphs. We design our methods for protein–protein interaction networks.
Proposed methods
We propose two algorithms for mining highly reliable dense subgraphs from uncertain weighted graphs: GreedyUWDS and GreedyBWDS.
GreedyUWDS extends the GreedyUDS method (designed for unweighted uncertain graphs) by incorporating edge weights and probabilities into the density computation, thus handling uncertainty in edge existence while optimizing subgraph density. GreedyUWDS uses expected weighted density metrics to guide the search for dense regions. At each step, it removes the vertex that contributes the least to the subgraph’s overall expected density. By doing this iteratively, the algorithm identifies a sequence of vertex-removal steps that yield progressively smaller subgraphs. Among all these subgraphs, it keeps track of the subgraph with the highest density measure encountered.
Similarly, the GreedyBWDS method is intended for finding dense and reliable subgraphs. This algorithm introduces a tunable parameter , which acts as a reliability threshold. The parameter allows us to filter out or downweight edges with low existence probability during the subgraph extraction process. By adjusting , we control the penalty for uncertain edges. A higher value of means that only very reliable edges contribute significantly, thus favoring reliability but potentially removing many edges and reducing density. In contrast, a lower value of is more permissive, favoring the retention of more edges and hence higher density, even if some edges are less reliable.
According to our experimental results, GreedyBWDS can be flexibly applied to a range of scenarios within protein-protein interaction networks by tuning parameter . In applications where reliability is paramount, a relatively high value of should be set to ensure that the edges in the output subgraph are mostly of high probability. In scenarios where having as many connections as possible is desired and some decrease in reliability is acceptable, a lower value of can be chosen to prioritize density. A key novelty of our approach is that it allows users to fine-tune the trade-off between density and reliability based on the specific needs of the application domain.
In addition to these improved approaches, we also consider a baseline brute-force method for finding the optimal subgraph with respect to our objective function. This approach is similar in principle to the GreedyUWDS algorithm. The brute-force technique examines all possible subgraphs in the graph and selects the one with the highest expected weighted density. While brute force is a useful benchmark for evaluating the performance of more advanced algorithms such as GreedyUWDS and GreedyBWDS, it is not suitable for large or complex graphs due to its inefficiency.
Both GreedyUWDS and GreedyBWDS have made significant strides in addressing the challenges of finding dense subgraphs in uncertain graph environments. These algorithms offer deeper insights into the density and reliability of uncertain weighted graphs, opening up new possibilities for future research and applications.
Brute force method
When searching for dense subgraphs in uncertain weighted graphs, the traditional brute-force technique serves as an important benchmark. The brute-force method analyzes every possible subset of vertices within the graph and evaluates each subset using expected weighted density, which incorporates both the overall weight of the edges and their probabilities of existence. While the brute-force approach guarantees an optimal solution by exhaustively considering all possible options, it faces a significant limitation in terms of computational complexity. For large graphs, as the number of vertices increases, the number of possible subsets grows exponentially, rendering the algorithm infeasible in practice. Specifically, the brute-force algorithm has time complexity of .
As a result, although brute force serves as a vital benchmark, it is typically used only in theoretical analyses or as a comparison method for small graphs. It is rarely recommended for large and complex graphs due to its severe performance limitations. Therefore, the GreedyUWDS and GreedyBWDS algorithms are generally preferred for finding dense and reliable subgraphs in uncertain weighted graphs.
GreedyUWDS method
Definition 7. The expected weighted degree of a vertex of the graph is calculated as the sum of probabilistic edge weight of incident edges (Eq. (6)).
(6)
For example, the expected weighted degree of vertex B of the graph in Fig. 1 is .
Definition 8. The expected weighted density of the uncertain weighted subgraph produced by the graph is defined in Eq. (7).
(7)
For example, the expected weighted density of the uncertain weighted graph in Fig. 1 is .
Definition 9. The subgraph argmax is referred to as the densest uncertain weighted subgraph.
The GreedyUWDS presented in this research is a modification of the minimal cut concept described in Jin, Liu & Aggarwal (2011) and is also based on the Charikar algorithm (Charikar, 2000). It has been adapted to capture the characteristics of uncertain weighted graphs. Algorithm 1 provides the full pseudocode for the algorithm.
| 1. Initialize best_subgraph and best_expected_weighted_density |
| 2. For i = n down to 2 do: |
| 3. Determine the expected weighted density for the current subgraph. |
| 4. Update the values of best_subgraph and best_expected_weighted_density as appropriate |
| 5. Calculate the expected weighted degree of each vertex and remove the worst one. |
| 6. End for |
| 7. Return best_subgraph and best_expected_weighted_density |
GreedyBWDS method
Definition 10. For a vertex and a set of edges and , its excess weighted degree is defined in Eq. (8).
(8) Given and the graph in Fig. 1, we have
Definition 11. Given a reliability threshold , the average excess weighted degree of graph is defined in Eq. (9).
(9)
The average excess weighted degree of the graph in Fig. 1 in case is:
The GreedyBWDS method is similar to the GreedyUWDS but uses the parameter b to control the selection. Based on the average excess weighted degree, it identifies the most reliable dense subgraph. The method determines the subgraph with the highest average excess weighted degree.
In addition, we use a min-heap to efficiently extract the best vertex. The improved version runs in time , where is the order of the graph.
| Input: Uncertain Weighted Graph of n vetices, and for each , and a value b |
| Output: A highly reliable dense subgraph |
| 1. Initialize best_subgraph and best_aewdg |
| 2. Initialize min_heap |
| 3. For each vertex v in the graph: |
| 4. Compute ewdg of v |
| 5. Insert v into min_heap |
| 6. For i = n down to 2: |
| 7. Compute aewdg of the current subgraph |
| 8. Update the values of best_subgraph and best_aewdg |
| 9. If len(minHeap) > 0: |
| 10. Extract the vertex v from the top of the min_heap |
| 11. End if |
| 12. Retrieve all neighbors of v |
| 13. Remove v from the graph |
| 14. For each neighbor of v: |
| 15. If the vertex is not in the min_heap: |
| 16. Calculate its ewdg and add it to min_heap |
| 17. End for |
| 18. End for |
| 19. Return best_subgraph |
The GreedyBWDS method relies on the parameter , which serves as a key threshold for determining the most reliable dense subgraph. The method effectively handles vertex evaluations by strategically using the average excess weighted degree as a critical variable in subgraph evaluation. It utilizes a min-heap structure to methodically find and remove vertices with the lowest excess degree. This process is repeated iteratively, reducing the graph’s complexity until it reaches a subgraph that is likely to be dense and reliable. This subgraph, characterized by its high average excess weighted degree, serves as the final output of the algorithm and provides valuable insights into the fundamental graph structure.
Scalability analysis
The scalability of the proposed methods, GreedyUWDS and GreedyBWDS, was investigated to determine their effectiveness on large-scale uncertain weighted graphs. GreedyUWDS has a time complexity of , where is the number of vertices, making it ideal for small to medium-sized networks. In contrast, GreedyBWDS leverages a min-heap data structure to improve runtime, resulting in a significant improvement in scalability and making it suitable for larger networks.
In comparison with other approaches, the brute-force method, with its exponential time complexity of , is computationally challenging for large networks but serves as a benchmark for small networks. The Charikar algorithm, designed for deterministic networks, has a time complexity of , where is the number of edges and is the number of vertices. While Charikar’s technique is efficient, it fails to account for uncertainty or edge weights, which limits its applicability in real-world scenarios. The proposed GreedyBWDS method provides a balance between computational efficiency and the ability to handle the complexity of uncertain weighted graphs. As a result, GreedyBWDS achieves higher performance in large-scale applications.
Trade-offs between density and reliability
Trade-offs between density and reliability is achieved through the use of dedicated evaluation metrics and tunable threshold parameters, enabling the algorithms to adapt to the requirements of specific applications. Density and reliability are combined into a single objective function to identify subgraphs that are both dense and reliable, ensuring that the resulting subgraph maintains structural consistency while addressing edge uncertainty.
The GreedyUWDS algorithm identifies the densest subgraph by maximizing probabilistic edge weight density while preserving high reliability scores. In contrast, the GreedyBWDS algorithm employs the parameter as a threshold to filter edges based on their degree and reliability. Adjusting the value of enables the algorithm to prioritize either density or reliability, depending on the application context. A larger value of emphasizes reliability, resulting in subgraphs with stronger and more dependable connections. Conversely, a lower value of is more permissive, potentially favoring density by retaining more edges, even if some are less reliable.
Experiment setup
We implemented all algorithms in Python 3.9.16. Experiments were conducted on a PC with an AMD Ryzen 5 5600H 3.3 GHz CPU, 8 GB of RAM, and Windows 10. Our implementation and datasets are publicly available in our GitHub repository to ensure reproducibility: https://github.com/dqakiet/CDNC1_222805401_DuongQuocAnhKiet_NguyenChiThien.git.
We compare the performance of the GreedyUWDS and GreedyBWDS algorithms in finding subgraphs that achieve high density, reliability, and efficiency. Both algorithms were applied to the same set of PPI networks. All networks were obtained from the STRING database (Szklarczyk et al., 2023) (https://string-db.org). The first two features in the database represent proteins, where “combine_score” feature indicates the probability of the protein connection. The remaining features are weights of the connection.
Following STRING’s scoring scheme, each channel score is stored as an integer . Scores of 0 indicate “no evidence” but still carry a baseline prior probability . To avoid undefined value in and preserve this background likelihood, we replaced any score of by before computing expected weighted density and adjoint logarithmic reliability. This substitution maintains all weights on the same 0–1,000 scale, ensuring that edges with no direct evidence are treated with baseline confidence rather than being artefactually removed. For comparison with GreedyUWDS, the default value for the parameter in the GreedyBWDS method is set to .
Table 2 provides an overview of the four PPI networks of varying scale and complexity used in our experiments: 579,138, 86,666, 1,811,976, and 511,145. These networks vary widely in scale, ranging from several thousand to hundreds of thousands of edges, and represent different organisms or experimental sources. For each network, we report only the number of vertices and edges to highlight the increasing scale and complexity. This information demonstrates the diversity and size of the PPI networks included in our study.
| PPI network | Number of vertices | Number of edges |
|---|---|---|
| 579,138 | 1,676 | 106,739 |
| 86,666 | 3,210 | 287,458 |
| 1,811,976 | 3,577 | 411,949 |
| 511,145 | 4,140 | 492,380 |
To further analyze the impact of weight assignment, we examined all available edge weight types for the four representative networks. Table 3 summarizes the average probabilistic edge weight and standard deviation of probabilistic edge weight, averaged over seven weight types: neighborhood (1), fusion (2), cooccurrence (3), coexpression (4), experimental (5), database (6), and textmining (7). These statistics highlight the diversity of edge reliability distributions, emphasizing the necessity for flexible algorithms capable of identifying dense and reliable subgraphs under heterogeneous weighting schemes.
| Network | Average probabilistic edge weight | Standard deviation of probabilistic edge weight |
|---|---|---|
| 579,138 | 39.855 | 240.845 |
| 86,666 | 33.013 | 212.309 |
| 1,811,976 | 33.987 | 195.935 |
| 511,145 | 35.605 | 242.330 |
We evaluate algorithm performance on the identified subgraphs using several key metrics: probabilistic edge weight density and adjoint logarithmic reliability. We also report the number of edges in the subgraphs, which indicates their size and helps contextualize the trade-off between quantity and certainty of connections. Because our algorithms are deterministic, performance metrics such as expected weighted density and aggregated logarithmic reliability remain consistent across runs. Therefore, we present only representative results without standard deviation. To summarize the trade-off between subgraph size, density, and reliability, we also report a composite objective function value calculated from the number of edges, probabilistic edge weight density, and adjoint logarithmic reliability.
To assess parameter sensitivity, we further investigated the effect of varying the b parameter in the GreedyBWDS algorithm on the largest network, 511,145, using weight type 5 and values ranging from to . This ablation study demonstrates the flexibility of GreedyBWDS and provides practical guidance for parameter selection in real-world biological networks.
Results and discussion
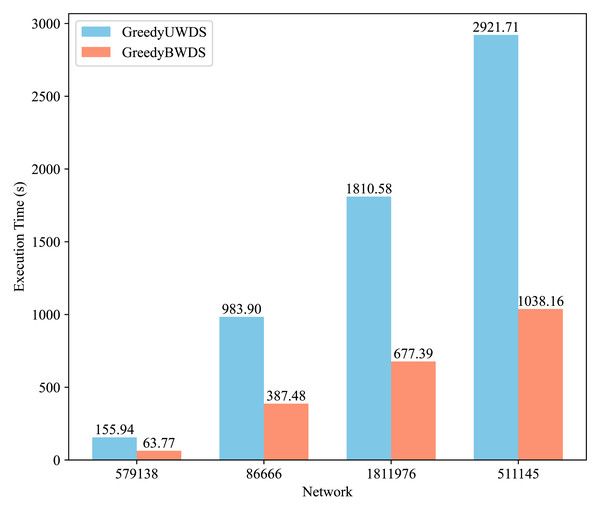
Figure 2 compares the execution times of the GreedyUWDS and GreedyBWDS algorithms on the four networks, averaged over seven weight types. It is evident that GreedyBWDS consistently achieves faster runtimes, being approximately times quicker than GreedyUWDS. In addition, as the network size increases, the performance advantage of GreedyBWDS becomes more significant. This highlights that GreedyBWDS not only outperforms GreedyUWDS in terms of efficiency for diverse weighting schemes, but also demonstrates significantly better scalability to larger PPI networks.
Figure 2: Comparison of execution time for GreedyUWDS and GreedyBWDS.
Table 4 provides a detailed comparison of GreedyUWDS and GreedyBWDS on the four networks, averaged over seven weight types. For each network, results are averaged across all seven STRING-defined weight types, with evaluations based on probabilistic edge weight density, adjoint logarithmic reliability, and the overall objective function value.
| Network | Density | Reliability | ||||
|---|---|---|---|---|---|---|
| UWDS | BWDS | UWDS | BWDS | UWDS | BWDS | |
| 579,138 | 781.3143 | 1,016.1 | −1,247.99 | −71.5143 | −1,117,810,485 | −230,411,294 |
| 86,666 | 745.7286 | 1,148.657 | −1,057.51 | −114.914 | −2,583,130,901 | −324,657,130 |
| 1,811,976 | 687.9286 | 844.1857 | −15,277.3 | −501.186 | −19,936,314,805 | −1,779,450,291 |
| 511,145 | 1,026.986 | 1,228.714 | −1,439.19 | −102.229 | −14,563,381,829 | −259,242,521 |
The findings reveal several important trends:
-
1.
Consistent superiority of GreedyBWDS: Across all networks, GreedyBWDS consistently identifies subgraphs with higher probabilistic edge weight density and higher adjoint logarithmic reliability compared to GreedyUWDS. For instance, the average probabilistic edge weight density achieved by GreedyBWDS is substantially greater than that of GreedyUWDS for all networks. This result indicates a clear advantage in discovering denser and more reliable subgraphs.
-
2.
Generalizability across networks: The strong performance of GreedyBWDS is not confined to a single network. The algorithm demonstrates robust and broadly applicable results, even when the underlying biological context or network scale differs.
-
3.
Algorithmic efficiency: In addition to its higher solution quality, GreedyBWDS demonstrates noticeably improved computational efficiency, as supported by the runtime analysis. This efficiency makes GreedyBWDS a practical choice for large-scale uncertain graph mining.
Overall, the results presented in Table 4 confirms that GreedyBWDS is both effective and efficient across diverse PPI networks. These outcomes support its suitability for mining highly reliable dense subgraphs in various uncertain weighted graph scenarios.
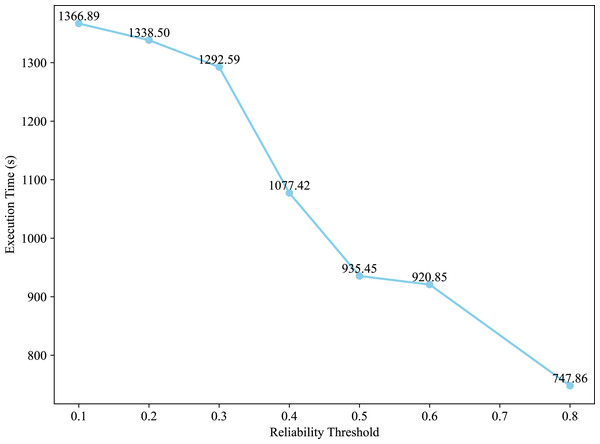
Figure 3 presents the execution time of the GreedyBWDS algorithm on the 511,145 network with different values of reliability threshold in case of “experimental (5)” weight type. As the value of grows, the algorithm’s execution time becomes faster. When the value is set to , the GreedyBWDS outputs are extremely similar to those produced by the GreedyUWDS method, indicating a level of density but a low degree of reliability. However, raising the value of results in a significant improvement not only in the density of the subgraph but also in reliability, objective .
Figure 3: Effect of the reliability threshold on execution time of the GreedyBWDS algorithm.
Table 5 shows the impact of varying parameter values on the quality of subgraph generated by the GreedyBWDS algorithm on the 511,145 network. As the value of increases, there is a corresponding improvement in all evaluation metrics, especially adjoint logarithmic reliability. This demonstrates GreedyBWDS’s adaptability in PPI network analysis, enabling flexible tuning according to the characteristics of each PPI network and the goals of the study.
| b | Number of edges | Density | Reliability | |
|---|---|---|---|---|
| 0.1 | 3,700 | 1,473.5 | −409.3 | −2,231,477,918.5 |
| 0.2 | 3,429 | 1,541.4 | −306 | −1,617,120,683.5 |
| 0.3 | 3,306 | 1,576 | −268 | −1,396,670,122.2 |
| 0.4 | 3,306 | 1,576 | −268 | −1,396,670,122.2 |
| 0.5 | 3,306 | 1,576 | −268 | −1,396,670,122.2 |
| 0.6 | 2,941 | 1,657.5 | −163.7 | −797,810,287.9 |
| 0.8 | 2,797 | 1,683.7 | −134.6 | −633,744,265.5 |
The parameter in GreedyBWDS serves as a threshold to filter out edges with low reliability. Adjusting directly affects the balance between subgraph density and reliability:
Low values of : The method favors density by including edges with lower probability. This increases the number of edges and the probabilistic edge weight density but significantly decreases adjoint logarithmic reliability. For instance, when , the number of edges increases, but reliability drops substantially.
Moderate values of ( ): The method provides a good trade-off between density and reliability. At , reliability increases dramatically, with only a slight decrease in edge count compared to lower thresholds. This indicates that moderate levels of are suitable for applications that require both density and reliability.
High values of ( ): The algorithm removes most low-reliability edges, resulting in fewer but much more reliable edges. For example, at , the number of edges decreases, but reliability increases sharply. This demonstrates the algorithm’s ability to adapt to applications requiring high reliability, such as identifying robust protein interactions in noisy networks.
These results highlight the flexibility of GreedyBWDS in adapting to diverse analysis requirements for protein-protein interaction networks by adjusting the parameter . Users can prioritize density, reliability, or a balance of both, depending on the specific objectives of PPI network analysis.
GreedyBWDS was compared to fundamental approaches such as the Charikar algorithm, brute force, and GreedyUWDS.
GreedyBWDS optimizes both density and reliability, opposing the Charikar method, which only considers density. This provides subgraphs with improved structural consistency in uncertain weighted graphs.
GreedyBWDS is more efficient than brute force for large networks, having a time complexity of . This makes it suitable for enormous networks such as STRING-DB.
Adaptability: GreedyUWDS promotes density despite uncertainty, but limits adaptability to balance density and reliability. GreedyBWDS, with parameter , compares to GreedyUWDS for situations demanding reliable subgraph mining.
GreedyBWDS typically outperforms basic methods on protein-protein interaction networks, achieving high density and reliability across all studied weight types. This demonstrates its suitability specifically for identifying dense subgraphs in uncertain weighted graphs arising from PPI networks. The parameter allows users to adjust the algorithm’s behavior, enabling a balance between density and reliability. This adaptability highlights the effectiveness of GreedyBWDS for protein-protein interaction analysis, allowing researchers to tailor results to the specific requirements of each PPI network.
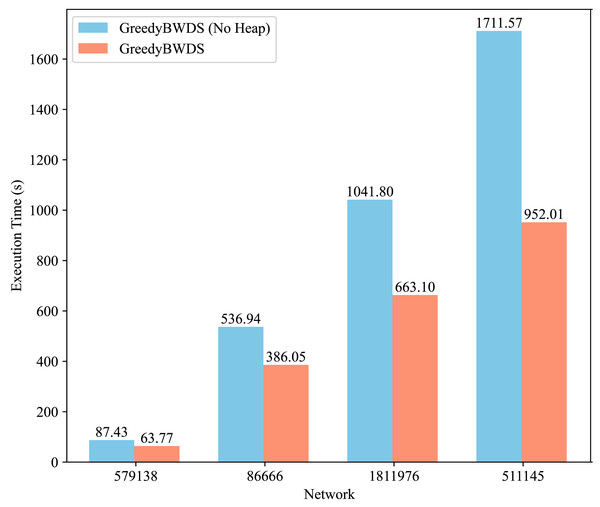
We conducted additional experiments to assess the contribution of specific components of our approach, specifically the min-heap optimization in GreedyBWDS. We modified GreedyBWDS to create a variant that does not use a min-heap. In this variant, at each iteration, we recompute the excess weighted degree of every remaining vertex to find the maximum, then remove that vertex and update its neighbors by scanning. This eliminates the overhead of maintaining a heap but increases the computation required for each iteration. We ran both versions on the same PPI networks using . Figure 4 presents the execution times for each network, averaged across all weight types. The results demonstrate that the min-heap version offers a significant performance advantage, particularly as the graph size increases. The heap-based GreedyBWDS was approximately times faster than the non-heap version across all networks tested. Both versions produced the same output subgraph. Thus the heap does not affect solution quality but substantially improves efficiency. This demonstrates that our proposed method is robust and highly scalable compared to baseline approaches, especially for large-scale networks.
Figure 4: Comparison of execution time for GreedyBWDS (No Heap) and GreedyBWDS.
Our experiments were conducted on a range of protein–protein interaction (PPI) networks with varying scales and organisms. The techniques we developed generalize robustly within the domain of large-scale PPI networks. While our results are promising for biological data, the applicability of our techniques beyond protein-protein interaction networks has not yet been verified. For example, STRING provides interaction networks for over organisms, covering more than million proteins and upwards of billion interactions. By applying our GreedyUWDS and GreedyBWDS algorithms to PPI networks of various sizes, from tens of thousands up to millions of vertices, we observed that the runtime scaling behavior and solution quality remained consistent across all networks. This consistency demonstrates that our methods are both scalable and robust across a wide range of PPI networks, regardless of the specific organism or graph size.
Conclusions
In this article, we present a methodology for extracting dense and reliable subgraphs from uncertain weighted graphs using two greedy algorithms, GreedyUWDS and GreedyBWDS. GreedyUWDS extends the classic densest subgraph approach to uncertain, weighted settings by using expected edge weights. GreedyBWDS introduces a threshold parameter that acts as a tunable filter for edge reliability. This allows users to select subgraphs that achieve a desired balance between density and reliability.
Through extensive experiments on PPI networks, we showed that the subgraphs identified by GreedyBWDS outperform those found by a baseline density-focused greedy algorithm in terms of both density and reliability. Notably, GreedyBWDS was able to find subgraphs that were approximately denser and more reliable, while also achieving significantly lower runtime.
This development enables a wide range of applications in the analyzing of protein-protein interaction networks and other large biological networks with uncertainty.
We acknowledge some limitations of our current work. First, although our algorithm was effective on PPI networks, its performance on other types of networks has not been evaluated in this study. Our focus was exclusively on undirected uncertain graphs derived from PPI data, and we did not verify the applicability of our methods beyond this context.
Additionally, our approach may not directly handle directed graphs or bipartite graphs without modification, which limits the scope of applicability. Handling directed uncertain graphs would require a redefinition of density in the context of directed graphs.
Another limitation is that we concentrated on finding a single dense subgraph. In many applications, there may be multiple disjoint or overlapping dense subgraphs of interest. Our algorithms, as presented, identify only the densest subgraph. Extending the approach to identify multiple dense and reliable subgraphs is an interesting direction for future work. For example, one could iteratively remove the identified subgraph and repeat the search on the residual graph, or incorporate diversification strategies to find a set of subgraphs. However, ensuring that these subgraphs are globally optimal or significant is non-trivial and was beyond the scope of our current work.
While our proposed methods GreedyBWDS and GreedyUWDS show promising performance compared to standard benchmarks such as Charikar’s method and brute-force approaches, we acknowledge that the experimental comparison could be further enriched by including more advanced baselines, such as probabilistic quasi-clique mining and probabilistic k-core decomposition. Nevertheless, our current comparison still provides meaningful insights, particularly in demonstrating the relative strength of GreedyBWDS in terms of expected edge density and reliability. In future work, we intend to include these advanced probabilistic baselines to provide a more comprehensive and competitive evaluation of our methods.
In future research, we plan to address these limitations. We will test the algorithm on different networks to evaluate its generality and adaptability. Additionally, we will work on methods to identify multiple subgraphs from a single graph. This could involve extending the greedy approach or applying hierarchical clustering techniques to the output subgraph structure in order to capture multiple dense regions that may exist. Another direction is to integrate our approach with dynamic graph algorithms. This would enable the method to update the dense subgraph solution as new edges appear or as edge weight probabilities change over time.
Overall, we believe that the techniques introduced in this research provide a useful new tool for graph analysis in uncertain environments. By enabling the discovery of subgraphs that are both dense and reliable, our work helps bridge the gap between purely structural graph mining and uncertainty-aware data analysis.