Predicting e-commerce product prices through the integration of variational mode decomposition and deep neural networks

Moving window structure

As shown in Fig. 1, the prediction structure employed in this article adopts a moving window format, where predictions within each window are independent and do not mutually influence one another. This logical framework serves a dual purpose: firstly, it simulates real trading scenarios, mitigating the occurrence of ex post prediction errors. Secondly, it satisfies the condition of parallelism across different time windows or within different IMFs within each window, thereby expediting the model training process (Nava, Di Matteo & Aste, 2018). Within the sliding window framework, each window’s data corresponds to the original time series.

Optimization of VMD based on fuzzy entropy

The variational problem is initially formulated by assuming the decomposition of the original signal f into k components. It is imperative to ensure that the decomposed sequence represents modal components with center frequency and finite bandwidth. Simultaneously, the task involves determining the estimated bandwidth of each modal sum to be the smallest. Additionally, the summation of all modes is required to be equal to the original signal, serving as a constraint. Subsequently, the corresponding constraint variational expression is established. (1)${\displaystyle \underset{\left\{u_k\right\},\left\{{\omega }_k\right\}}{min}\left\{\sum _k{∥{\partial }_t\left[\left(\delta \left(t\right)+j/\pi t\right)\mathrm{\ast }{u}_k\left(t\right)\right]e^{-j{\omega }_{k}t}∥}_2^2\right\}\mathrm{ s}.\mathrm{t}.\mathrm{ }\sum _{k=1}^K{u}_k=f}$

where K is the number of modes (positive integers) to be decomposed, and $\left\{u_k\right\},\left\{{\omega }_k\right\}$ are the first k modal component and the corresponding center frequency of the decomposed modes, where δ(t) is the Dirac function, and ∗ is the convolution operator.

To optimize the modal number in VMD decomposition, fuzzy entropy is employed in this study. The process of calculating fuzzy entropy for optimizing the VMD decomposition model is as follows:

Reconstruct the phase space of the original sequence to obtain a m vector (2)${\displaystyle \left\{{\mathrm{x}}_{\mathrm{i}}^{\mathrm{m}}\right\}\left(\mathrm{i}=1,2,\dots ,\mathrm{N}-\mathrm{m}+1\right).}$

Then, (3)${\displaystyle \left\{{\mathrm{x}}_{\mathrm{i}}^{\mathrm{m}}\right\}=\left\{\mathrm{x}\left(\mathrm{i}+\mathrm{j}\right)-{\mathrm{x}}_0\left(\mathrm{i}\right)\right\},\mathrm{j}=0,1,\dots ,\mathrm{m}-1}$

and, (4)${\displaystyle {\mathrm{x}}_0\left(\mathrm{i}\right)=\frac{1}{\mathrm{m}}\times \sum _{\mathrm{j}=0}^{\mathrm{m}-1}\mathrm{x}\left(\mathrm{i}+\mathrm{j}\right).}$ Calculate the distance between time series ${\mathrm{x}}_{\mathrm{i}}^{\mathrm{m}}$ and ${\mathrm{x}}_{\mathrm{j}}^{\mathrm{m}}$ . (5)${\displaystyle {\mathrm{d}}_{\mathrm{i},\mathrm{j}}^{\mathrm{m}}=\underset{\mathrm{k}\in \left(0,\mathrm{m}-1\right)}{max}\left|\left(\mathrm{x}\left(\mathrm{i}+\mathrm{k}\right)-{\mathrm{x}}_0\left(\mathrm{i}\right)\right)-\left(\mathrm{x}\left(\mathrm{j}+\mathrm{k}\right)-{\mathrm{x}}_0\left(\mathrm{j}\right)\right)\right|.}$ For a given n and r , use the fuzziness function $\mathrm{u}\left({\mathrm{d}}_{\mathrm{i},\mathrm{j}}^{\mathrm{m}},\mathrm{n},\mathrm{r}\right)$. Calculate the time series ${\mathrm{x}}_{\mathrm{i}}^{\mathrm{m}}$ with ${\mathrm{x}}_{\mathrm{j}}^{\mathrm{m}}$ the similarity of the time series with ${\mathrm{D}}_{\mathrm{i},\mathrm{j}}^{\mathrm{m}}\left(\mathrm{n},\mathrm{r}\right)=\mathrm{u}\left({\mathrm{d}}_{\mathrm{i},\mathrm{j}}^{\mathrm{m}},\mathrm{n},\mathrm{r}\right)$.

For the time series ${\mathrm{x}}_{\mathrm{i}}^{\mathrm{m}}$ , define the following function. (6)${\displaystyle {\varphi }^{\mathrm{m}}\left(\mathrm{n},\mathrm{r}\right)=\frac{1}{\mathrm{N}-\mathrm{m}}\sum _{\mathrm{i}=1}^{\mathrm{N}-\mathrm{m}}\left(\frac{1}{\mathrm{N}-\mathrm{m}-1}\sum _{\mathrm{j}=1,\mathrm{j}\ne \mathrm{i}}^{\mathrm{N}-\mathrm{m}}{\mathrm{D}}_{\mathrm{i},\mathrm{j}}^{\mathrm{m}}\right.}$

Define the fuzzy entropy: (7)${\displaystyle \mathrm{FE}\left(\mathrm{m},\mathrm{n},\mathrm{r},\mathrm{N}\right)=ln{\varphi }^{\mathrm{m}}\left(\mathrm{n},\mathrm{r}\right)-ln{\varphi }^{\mathrm{m}+1}\left(\mathrm{n},\mathrm{r}\right).}$

The calculation of fuzzy entropy is associated with the parameters m, n, and r. The embedding dimension (m) is typically set to 2, as it is computationally less intensive and more responsive to sequence changes. The similarity tolerance limit (r) is chosen as 0.2 times the standard deviation of the sequence (std), ensuring that r is not excessively large. The standard deviation of the sequence (std) is usually taken as the value of n, and n is commonly set to 1.

Since fuzzy entropy can measure the complexity of time series, based on this, optimization based on the minimum fuzzy entropy criterion VMD decomposition of modal K The specific steps of the optimization method are as follows: Firstly, given that K = 3,4, ⋯,14VMD model to decompose the original time series x(t)(t = 1,2, ⋯,N) model to adaptively decompose the original time series into K different scales of the IMF set of component sequences $\left\{{\mathrm{I}}_{\mathrm{i}}\left(\mathrm{t}\right)\right\}\left(\mathrm{i}=1,2\cdots ,\mathrm{K}\right)$. Then, the IMF components are calculated and ranked by the fuzzy entropy $\left\{{\mathrm{I}}_{\mathrm{i}}\left(\mathrm{t}\right)\right\}$. The IMF components exhibiting the least fuzzy entropy are designated as trend terms, while the remaining IMF components are denoted as stochastic disturbance terms. Subsequently, a comparative analysis of the fuzzy entropy associated with the trend term is conducted across varying decomposition values (K values) to ascertain the optimal number of decompositions. As the K value decreases, the fuzzy entropy of the trend term escalates, and conversely, with an increase in the K value, the fuzzy entropy of the trend term expands. However, with a continued rise in the K value, the fuzzy entropy demonstrates a tendency to gradually stabilize. Consequently, to prevent excessive decomposition, the inflection point, where the fuzzy entropy begins to stabilize, is identified as the modal number for the VMD decomposition.

DNN structure

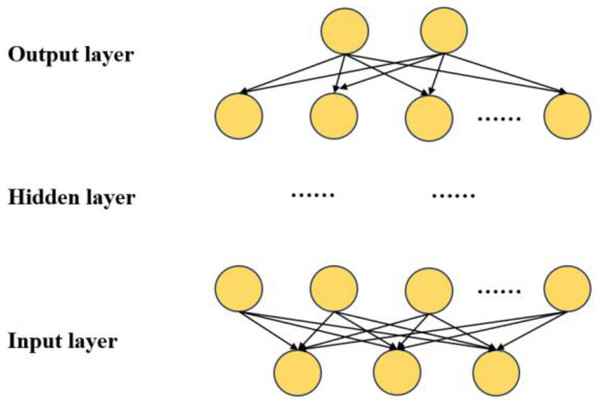
The network architecture of the DNN is depicted in Fig. 2, encompassing multiple hidden layers, an input layer, and an output layer (Aldahdooh et al., 2022). The input layer is denoted as $\mathrm{X}={\left[{\mathrm{x}}_1,{\mathrm{x}}_2,{\mathrm{x}}_{\mathrm{n}}\right]}^7$. The input data comprises a column vector denoted as n-dimensional. The dataset encompasses seven distinct types of information:

Daily product prices: Detailed price records for each day of the product.

Product dimensions: Numeric representation of product dimensions, including length, width, and height.

Seasonal sales volume: Quantification of the impact of seasonality on product sales volume, usually on a monthly or quarterly basis.

Competitor prices: Specific price details for comparable products offered by competitors.

User ratings: User-assigned ratings for a given product.

Promotion discount percentage: The specific percentage of product discount during promotional activities.

Inflation rate: The inflation rate within the economic environment, expressed as a percentage.

Once categorized and processed as output values, this data is transmitted from the input layer to the hidden layer, facilitating the establishment of the initial relationship between hidden inputs and outputs, as represented by Eq. (8). (8)${\displaystyle {\mathrm{R}}_1=\mathrm{f}\left({\mathrm{w}}_1\cdot \mathrm{X}+{\mathrm{b}}_1\right)}$

where R₁ represents the output matrix of the first hidden layer, while W_i and b_i stand for the weight parameter and threshold parameter between the input layer and the hidden layer.

If we designate the variable for the p-th element of the first hidden layer as r_1,p, where p is the index, then w_1,p represents the weight matrix between the input layer and the first hidden layer, and b_1,p represents the value corresponding to the first variable in the vector of values between the input layer and the first hidden layer. Each output value in the activation function is determined accordingly. (9)${\displaystyle {\mathrm{r}}_{1,\mathrm{p}}=\mathrm{F}\left(\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{w}}_{1,{\mathrm{p}}_{\mathrm{i}}}\cdot {\mathrm{X}}_{\mathrm{i}}+{\mathrm{b}}_{1,\mathrm{p}}\right)}$

According to the principle of DNN, the output of the previous hidden layer is the input of the next hidden layer, so the output of the first hidden layer of the DNN model is the input of the next hidden layer. m The output of the first hidden layer of the DNN model R_m of the first hidden layer of the DNN model is given by (10)${\displaystyle {\mathrm{R}}_{\mathrm{m}}=\mathrm{f}\left({\mathrm{w}}_{\mathrm{m}}\cdot {\mathrm{R}}_{\mathrm{m}-1}+{\mathrm{b}}_{\mathrm{m}}\right)}$

Input X after undergoing processing by the input layer, is forwarded to the hidden layer. Following the completion of processing in the hidden layer, the result is transmitted to the output layer. This process can be expressed as follows. (11)${\displaystyle \mathrm{y}=\mathrm{g}\left({\mathrm{W}}_{\mathrm{n}+1}\cdot {\mathrm{R}}_{\mathrm{n}}+{\mathrm{b}}_{\mathrm{n}+1}\right)}$

To enable the DNN for predicting the price movements of e-commerce products—up, down, or flat—the network structure is designed as outlined in Table 1.

The architectural design of the DNN takes into consideration the functions and parameters of different layers. The entire network comprises seven layers, including the input layer, two hidden layers, a dropout loss layer, and the output layer.

Commencing with the input layer, responsible for receiving raw data, the information proceeds to the first hidden layer. This layer encompasses 64 neurons, each associated with a feature from the input layer, with the objective of extracting key features from the input data. Subsequently, the second hidden layer, more intricate than the first, with 128 neurons, learns an abstract representation of the data at a deeper level. To prevent overfitting during training, a dropout loss layer is introduced between the two hidden layers. The dropout layer mitigates overfitting by randomly deactivating a number of neurons with a specific probability during training.

Ultimately, the output layer employs a sigmoid function as an activation function to determine the probability of belonging to the three categories. The sigmoid function maps output values between 0 and 1, representing the probability of belonging to each category, facilitating multi-category classification tasks.

To optimize training, adaptive learning rate methods and learning rate schedules are employed. Specifically, the Adam optimizer is used for its capability to adjust the learning rate dynamically based on the estimates of first and second moments of gradients. The Adam optimizer updates the weights as follows: ${\displaystyle \begin{array}{cc}\hfill & \hfill m_t={\beta }_1{m}_{t-1}+\left(1-{\beta }_1\right)\nabla {\mathfrak{L}}_t\\ \hfill & \hfill v_t={\beta }_2{v}_{t-1}+\left(1-{\beta }_2\right){\left(\nabla {\mathfrak{L}}_t\right)}^2\\ \hfill & \hfill {\hat{m}}_t=\frac{m_t}{1-{\beta }_1^L}\\ \hfill & \hfill {\hat{v}}_t=\frac{v_t}{1-{\beta }_2^L}\\ \hfill & \hfill W_t=W_{t-1}-\frac{\alpha {\hat{m}}_t}{\sqrt{{\hat{v}}_t}+ϵ}\end{array}}$

where m_t and v_t are the first and second moment estimates, respectively, β₁ and β₂ are decay rates for the moments, α is the learning rate, and ϵ is a small constant to prevent division by zero.

Additionally, learning rate schedules are implemented to adjust the learning rate during training. For example, a step decay schedule reduces the learning rate by a factor after a set number of epochs, allowing the model to converge more effectively over time.

VMD-DNN

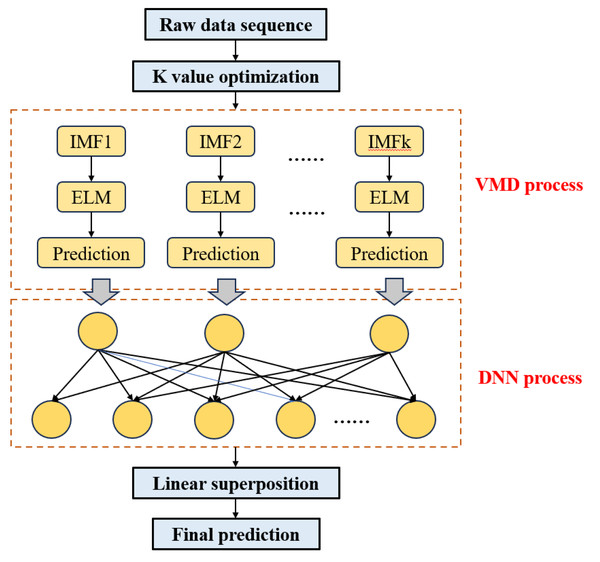
The block diagram illustrating the structure of the VMD-DNN price prediction model constructed in this article is depicted in Fig. 3.

The specific modeling steps are as follows:

Step 1: Optimization of K value. Calculate the fuzzy entropy of the trend term under various VMD decomposition modes and identify the optimal parameter values for decomposition based on the minimum fuzzy entropy criterion (K value).

Step 2: Time series decomposition. Following the determination of the optimal K value, employ the VMD model to adaptively decompose the original time series into a set of K IMF component sequences $\left\{{\mathrm{I}}_{\mathrm{i}}\left(\mathrm{t}\right)\right\}\left(\mathrm{i}=1,2,\dots ,\mathrm{K}\right)$.

Step 3: DNN input. Utilize the trained DNN model for each eigenmode function as input and obtain the corresponding prediction results.

Step 4: Integration prediction. Employ the ELM model to train and predict the trend and random interference terms within the IMF component. This process results in the predicted values of the IMF component ${\mathrm{s}}_{\mathrm{i}}=\left\{{\mathrm{s}}_1,{\mathrm{s}}_2,{\mathrm{s}}_3,\dots ,{\mathrm{s}}_{\mathrm{K}}\right\}$, then linearly sum the predicted values of IMF components s_i to derive the final prediction results.

The pseudo-code on which the VMD-DNN model runs is shown in Algorithm 1 .

Data sets

The utilized datasets for model training encompass three publicly available sources, contributing diverse and comprehensive information to enhance the model’s comprehension of the intricate relationship between products and prices.

Amazon Product Reviews Dataset (DOI 10.5281/zenodo.6657410): Derived from Amazon product reviews, this dataset includes extensive product information, user reviews, and ratings. It offers a substantial amount of data, potentially containing details pertinent to product prices. The inclusion of multiple data layers aids the model in capturing correlations between user feedback and pricing dynamics.

E-commerce Price Prediction Dataset (DOI 10.5281/zenodo.11237099): Sourced from Kaggle, a platform for open data science competitions, this dataset is tailored for e-commerce product price prediction. Encompassing various product categories and related features, it provides the model with diverse training instances, fostering experience in predicting prices within different contextual settings.

Online Retail Dataset (DOI 10.24432/C5BW33): Encompassing online retail information, this dataset comprises sales data, user behavior patterns, and price variations across diverse products. Analysis of this dataset facilitates the model’s understanding of price fluctuations under various conditions, thereby enhancing its proficiency in accurately predicting e-commerce product prices.

Experiments details and evaluation indicators

This article uses the CPU of Xeon^(R) E5-2640 v4, the GPU of 4*Nvidia Tesla V100 and the ubuntu system to complete the environment setup and model training. The deep learning framework is Tensorflow. Table 2 presents the experimental results for different batch size, learning rate, and activation function.

The analysis underscores that ReLU, with a batch size of 16 and a learning rate of 0.01, represents the most effective combination for achieving optimal model performance. This configuration not only delivers the highest accuracy but also minimizes the loss, thereby demonstrating superior robustness and stability. Although Tanh offers competitive performance, it does not reach the same level of effectiveness as ReLU. Sigmoid, while still useful in certain contexts, shows comparatively lower performance metrics. Consequently, ReLU is recommended as the preferred activation function for models requiring high accuracy and low loss, based on the results from this experimental evaluation.

To comprehensively assess the performance of various prediction models, this article employs root mean square error (RMSE), mean absolute percentage error (MAPE), mean absolute error (MAE), and direction symmetry (DS) as evaluation criteria (Ardiansyah, Majid & Zain, 2016). In this study, RMSE, MAPE, MAE, and DS serve as the evaluation metrics (Ardiansyah, Majid & Zain, 2016), with a lower RMSE, MAPE, and MAE indicative of higher prediction accuracy. Conversely, a higher value of DS signifies a better alignment with the actual data trend.

Results and Discussion

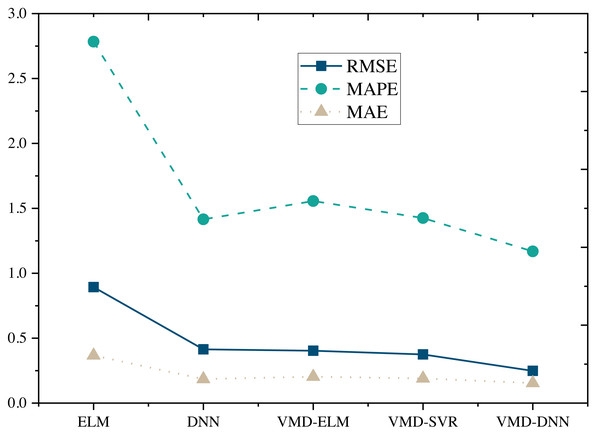
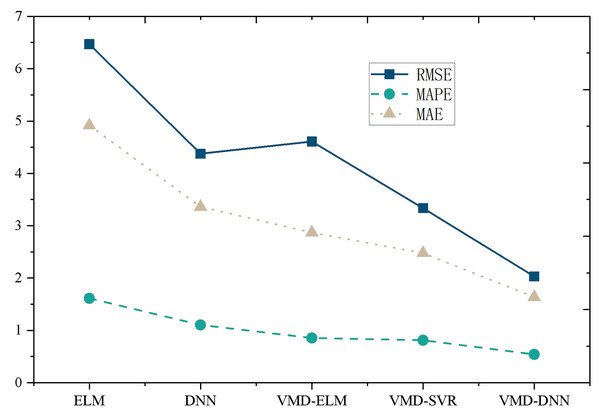
The performance comparison of models on the Amazon Product Reviews Dataset (Fig. 4) reveals that, in terms of RMSE, the VMD-DNN model outperforms others, achieving the lowest error value (0.2481). This superiority in accuracy positions the VMD-DNN model as a clear leader among the models. Furthermore, in terms of MAPE and MAE, the VMD-DNN model demonstrates the best performance, with values of 1.1686 and 0.1546, respectively, indicating closer proximity to true values compared to other models.

The DNN and VMD-SVR models also exhibit commendable performance, showcasing effective error reduction compared to the traditional ELM and VMD-ELM models. Conversely, the ELM model performs relatively poorly across all metrics, potentially due to its limitations in nonlinear modeling. In summary, the VMD-DNN model excels in e-commerce product price prediction, offering a robust solution to enhance prediction accuracy and practical utility.

Furthermore, upon comparing the single prediction model with the decomposition integration prediction model (Figs. 5 and 6), it is evident that all three error metrics and directional metrics of the decomposition integration prediction models surpass those of the single model. This observation underscores the effectiveness of the decomposition integration strategy.

Notably, the proposed VMD-DNN sub-model achieves an impressive MAPE of only 0.6578 on the E-commerce Price Prediction Dataset and 0.5414 on the Online Retail Dataset. The associated error reduction rates of 66.5% and 70.4%, respectively, compared to the single model, emphasize the substantial improvement achieved through the decomposition integration approach. Relative to other decomposition integration models, VMD-DNN excels in breaking down complex e-commerce product data into more manageable sub-sequences, alleviating the prediction burden on the single model. This enhancement augments its generalization capability, ultimately leading to optimal prediction performance.

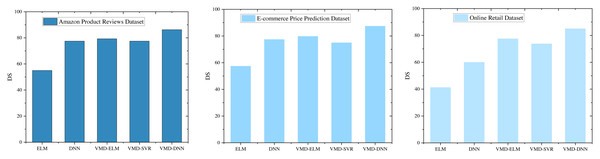
DS provides a more nuanced analysis of model performance across various datasets, as illustrated in Fig. 7. This metric offers insight into the consistency of model predictions in capturing directional trends, complementing traditional accuracy measures.

In the Amazon Product Reviews Dataset, the VMD-DNN model achieves a notable DS score of 86.25, highlighting its excellence in both prediction accuracy and directional alignment. This high DS score indicates that the VMD-DNN model not only performs well in terms of accuracy but also effectively captures the underlying trend directions. The VMD-ELM model also demonstrates significant performance with a DS score of 79.3, showcasing its ability to maintain good directional symmetry, albeit slightly behind the VMD-DNN model.

The exceptional performance of the VMD-DNN model is further confirmed in the E-commerce Price Prediction Dataset and the Online Retail Dataset, where it secures the highest DS scores of 87.5 and shows consistent performance across datasets. This consistency underscores the model’s robustness in maintaining both prediction accuracy and directional alignment. The VMD-ELM model, with DS scores of 79.8 and 79.3 in these datasets, maintains its competitive edge by showing reliable directional symmetry, although it remains slightly inferior to the VMD-DNN model.

In comparison, the DNN and VMD-SVR models exhibit similar DS scores across the datasets but are notably lower than those of the VMD-DNN and VMD-ELM models. The lower DS scores for these models suggest that while they exhibit some level of directional accuracy, there remains substantial room for improvement in capturing directional trends effectively.

The VMD-DNN model exhibits notable advantages in both directional symmetry and prediction performance, particularly in the task of e-commerce product price prediction. This robust performance enhances the model’s explanatory and practical utility. The VMD-ELM model, with its stability and commendable directional symmetry across datasets, emerges as a reliable alternative. The in-depth analyses presented here offer a comprehensive guide for selecting suitable prediction models, especially in scenarios where directional symmetry and interpretability are pivotal. Notably, the VMD-DNN and VMD-ELM models demonstrate strong performance in such scenarios.

To obtain final forecasts, the IMF decomposition results are linearly summed. Price forecast curves for e-commerce products in different price ranges are illustrated in Fig. 8 (400–600) and Fig. 9 (20–40), with actual observed values depicted in black for reference.

From the figures, it is evident that the predictions from VMD-ELM and VMD-SVR exhibit instability and the poorest alignment with the actual observations. In contrast, VMD-DNN demonstrates closer proximity to the actual observations than the single model. With the exception of occasional bias in the high-frequency subsequence in extreme cases, the predicted values for the remaining subsequences exhibit high compatibility with the actual values. Notably, the predicted trends closely mirror the actual trends.

The application of VMD to decompose the original e-commerce product price data, particularly within different price intervals, proves beneficial. This process effectively extracts and processes price fluctuation information, significantly enhancing the prediction performance of the DNN model.