RT-Cabi: an Internet of Things based framework for anomaly behavior detection with data correction through edge collaboration and dynamic feature fusion

Background

The Internet of Things (IoT) is transforming the way we work and live. As the number of these devices increases rapidly, we are faced with unprecedented challenges in data processing and security. The vast amount of data generated by IoT devices requires not only real-time processing but also in-depth analysis to ensure the efficiency and security of the systems. The market value of IoT is expected to reach $534.3 billion by 2025, increasing the demand for real-time data monitoring. The projected number of IoT connections via LEO satellites is also on the rise—from six million in 2022 to 22 million by 2027, with an annual compound growth rate of 25%, highlighting the importance of real-time data processing (https://iot-analytics.com/number-connected-iot-devices/). The network security threats faced by IoT devices are significant, with data showing that on average, each device is attacked within five minutes of connecting to the internet, and routers suffer an average of 5,200 attacks per month, underscoring the urgency of strengthening security measures (https://dataprot.net/statistics/iot-statistics/). The global number of IoT devices is expected to grow by 16%, reaching 16.7 billion by 2025 (https://iot-analytics.com/number-connected-iot-devices/). This reflects the scale of cross-industry integration and the ensuing data management challenges, highlighting the need for efficient processing solutions to address this trend.

As IoT technology continues to be widely applied, the security challenges it presents, particularly in identifying anomalous traffic behaviors, are becoming increasingly important (Lee, Pak & Lee, 2020). The diversity of IoT devices and the complexity of the data they generate make the patterns of abnormal behavior more varied and complex. Existing detection methods often struggle with this high-dimensional, complex data, finding it difficult to adapt and learn in a constantly changing environment (Injadat et al., 2020; Di Mauro et al., 2021). (1) The process of data collection often comes with errors and inconsistencies, leading to frequent occurrences of data loss or missing fields, not only increasing the difficulty of anomaly detection but also making the effective correction and completion of data an urgent problem to solve. (2) Considering the limited resources of IoT devices, such as processing power, storage space, and power, there is an urgent need for an efficient and energy-saving algorithm to address these challenges.

Therefore, facing the challenges of diversity in IoT devices, incompleteness of data, and limitations of device resources, traditional anomaly detection algorithms often fall short. This study introduced the RT-Cabi framework, which utilizes an adaptive edge collaboration mechanism, dynamic feature fusion and selection technology, and an optimized lightweight convolutional neural network (CNN) model. This approach not only improves data communication between sensors for better accuracy and completeness but also significantly lowers resource requirements.

Literature review

Our contributions

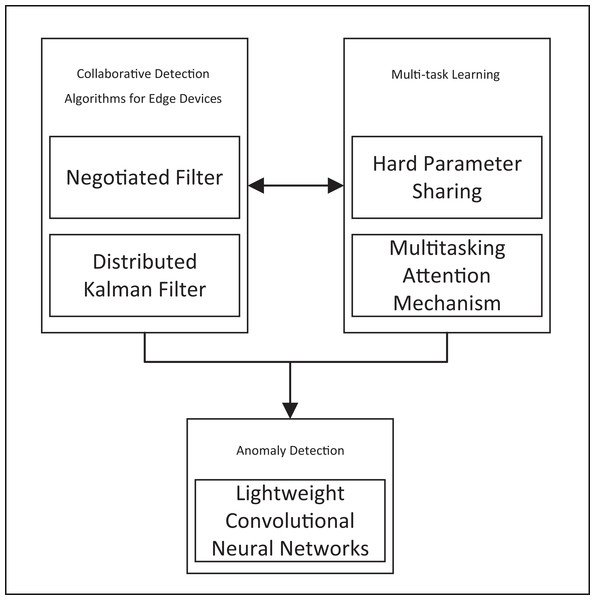
This study identifies gaps in data integrity, algorithm adaptability, and computational resource optimization, detailed in Table 1. We introduce a comprehensive solution, the RT-Cabi framework, shown in Fig. 1. Figure 1 illustrates the integration of various components, including negotiated filtering, distributed Kalman filtering, hard parameter sharing, multitasking attention mechanisms, and lightweight convolutional neural networks. These elements work together to enhance anomaly detection and collaborative detection algorithms for edge devices. The key contributions of our proposed framework are summarized as follows:

• Adaptive anomaly detection for IoT: We designed an edge collaborative framework based on adaptive parameter adjustment. This framework can capture environmental changes in real-time, dynamically adjust model parameters through weighted collaborative filtering and distributed Kalman filtering techniques. This approach ensures the model remains robust and responsive to new data patterns and anomalies.

• Data anomaly correction and imputation strategy: We developed a dynamic feature fusion and selection mechanism combining hard parameter sharing and multi-task learning technologies. By introducing adaptive weight adjustment and an advanced multi-task dynamic attention mechanism, this strategy can effectively handle common feature missing issues in the IoT environment. This ensures data integrity and enhances the overall reliability of the system.

• Mathematical collaborative optimization strategy: This study also proposes a set of mathematical collaborative optimization strategies, integrating methods from edge collaboration, feature fusion, and lightweight CNN optimization, forming a comprehensive model optimization scheme. This strategy reduces the computational demands and resource consumption in resource-constrained edge computing environments, making it practical for real-world IoT applications.

IoT anomaly detection model

Consider an IoT environment composed of N devices, denoted as $\mathcal{N}\stackrel{\mathrm{\Delta }}{=}\{1,\dots ,N\}$. Each device $i\in \mathcal{N}$ can collect and process a local dataset ${\mathcal{D}}_i$, containing $D_i$ samples $\{x_i^n{\}}_{n=1}^{D_i}$. These samples are independently and identically distributed (i.i.d.) drawn from the local distribution ${\mathcal{D}}_i$ of device $i$, with each sample $x_i^n$ including a training input and its corresponding label. Assume the data across devices is heterogeneous, i.e., the local distributions $\{{\mathcal{D}}_i\}$ are non-i.i.d.

Each device trains a local model composed of $d$ parameters, represented by the vector $\theta \in \mathrm{\Theta }\subset {\mathbb{R}}^d$, using its dataset. The training objective is to minimize the local objective function $f_i(\theta )$ based on the loss metric $l(\cdot ;\theta )$, with device $i$’s local objective defined as:

(1) $$f_i(\theta )=\frac{1}{D_i}\sum _{n=1}^{D_i}l(x_i^n;\theta ).$$

Thus, the goal of device $i$ is to find the parameters ${\theta }_i^{\ast }$ that minimize Eq. (1):

(2) $${\theta }_i^{\ast }=\arg \underset{\theta }{min}{f}_i(\theta ).$$

The server aims to train a global model with parameters $\theta$ using the data available from the user side. The global learning objective is given by the following equation:

(3) $$F(\theta )=\frac{1}{N}\sum _{i=1}^N{f}_i(\theta ).$$

Therefore, the server seeks to solve the following minimization problem:

(4) $${\theta }^{\ast }=\arg \underset{\theta }{min}F(\theta ).$$

We introduce adaptive parameters $\varphi$, allowing the model to dynamically adjust according to changes in the environment, to enhance the accuracy and adaptability of anomaly detection in the IoT environment. The problem is transformed into a multi-objective optimization issue of simultaneously optimizing $\theta$ and $\varphi$ to achieve optimal anomaly detection performance.

Motivation for adaptive edge collaboration framework: achieving efficient information sharing and task distribution

• Existing edge computing frameworks often use centralized management or information exchange mechanisms based on simple protocols, which struggle in handling dynamically changing network environments and diverse device capabilities (Hu & Huang, 2022). This limitation leads to inefficient information sharing, inability to flexibly allocate tasks, and severely restricts the system’s response speed and adaptability to change (Wang et al., 2022; Patsias et al., 2023).

• We propose an adaptive edge collaboration framework that integrates advanced algorithmic design, combining weighted collaborative filtering with distributed Kalman filtering. Its core innovation is the dynamic adjustment of task and resource allocation strategies in response to real-time network conditions and device capabilities, ensuring efficient resource use and quick task response under diverse conditions.

Mathematical model of the adaptive edge collaboration framework

We focus on how the adaptive edge collaboration framework enables effective information sharing and task allocation among multiple devices in an edge computing environment. The state at time $t$ is $x_t$, following the dynamic model:

(5) $$x_{t+1}=A{x}_t+B{u}_t+w_t$$where A is the state transition matrix, B is the control matrix, $u_t$ is the control input at time $t$, and $w_t$ is the process noise, assumed $w_t\sim \mathcal{N}(0,Q)$, with Q as the covariance matrix of the process noise.

The device observation at time $t$, $z_t$, is:

(6) $$z_t=H{x}_t+v_t$$where H is the observation matrix, and $v_t$ is the observation noise, assumed $v_t\sim \mathcal{N}(0,R)$, with R as the covariance matrix of the observation noise. Estimation accuracy improves by merging information from different devices, described by the collaborative filtering algorithm:

(7) $${\hat{x}}_{t|t}=\frac{\sum _{i=1}^N{K}_t^i{z}_t^i}{N}$$where $K_t^i$ is the Kalman gain of device $i$ at time $t$, and N is the total number of devices. Information fusion among devices uses a weighted collaborative filtering algorithm to enhance overall state estimation accuracy:

(8) $$\begin{array}{r}\begin{array}{cc}{\hat{x}}_{t|t}=& {\displaystyle (\sum _{i=1}^N\frac{\exp \left(-\frac{1}{2}||z_t^i-H{\hat{x}}_{t|t-1}^i|{|}_{{(R+Q)}^{-1}}^2\right)}{\sum _{k=1}^N\exp \left(-\frac{1}{2}||z_t^k-H{\hat{x}}_{t|t-1}^k|{|}_{{(R+Q)}^{-1}}^2\right)}{K}_t^i{z}_t^i}\\ & +{\displaystyle \sum _{j=1}^M\frac{\exp \left(-\frac{1}{2}||y_t^j-G{\hat{x}}_{t|t-1}^j|{|}_{{(S+P)}^{-1}}^2\right)}{\sum _{l=1}^M\exp \left(-\frac{1}{2}||y_t^l-G{\hat{x}}_{t|t-1}^l|{|}_{{(S+P)}^{-1}}^2\right)}{L}_t^j{y}_t^j)/(N+M)}\end{array}\end{array}$$where $K_t^i=P_{t|t-1}{H}^T(H{P}_{t|t-1}{H}^T+R{)}^{-1}$ and $L_t^j=P_{t|t-1}{G}^T(G{P}_{t|t-1}{G}^T+S{)}^{-1}$ are the Kalman gains of device $i$ and external information source $j$ at time $t$. Observations $z_t^i$ and $y_t^j$ come from device $i$ and external source $j$. Matrices H and G represent internal and external observation models. R, S, Q, and P are covariance matrices of observation noise, external source noise, process noise, and estimation error. ${\hat{x}}_{t|t-1}^i$ is device $i$’s state prediction based on prior information, used to generate the optimal estimate ${\hat{x}}_{t|t}$.

The distributed Kalman filtering algorithm lets each device update its state estimation based on local observations and neighbor information:

(9) $${\hat{x}}_{t+1|t}^i=A{\hat{x}}_{t|t}^i+B{u}_t^i+K_t^i(y_t^i-H{\hat{x}}_{t|t}^i)$$where $y_t^i$ is the observation of device $i$ at time $t$. Distributed Kalman filtering allows each device to use local observations and neighbor information to update its state estimate:

(10) $${\hat{x}}_{t+1|t}^i=A{\hat{x}}_{t|t}^i+B{u}_t^i+\left(\sum _{j\in {\mathcal{N}}_i}{\lambda }_{ij}{K}_t^j\right)(y_t^i-H{\hat{x}}_{t|t}^i)$$where H is the observation model matrix, ${\lambda }_{ij}$ is the neighbor weight coefficient, and ${\mathcal{N}}_i$ is the set of neighbor devices of device $i$.

In each iteration, devices share state estimates and observation information through the network, adapting to network conditions and device capabilities. Considering the information exchange and dynamic adjustment of adaptive parameters, we define the following mathematical model:

(11) $$I_t^i=\underset{j\in {\mathcal{N}}_i}{\oplus }\left\{\varphi \left({\alpha }_t^i{\hat{x}}_{t|t}^j+{\beta }_t^i{z}_t^j;{\gamma }_t^i{\mathrm{\Psi }}_t^i+{\delta }_t^i{\mathrm{\Omega }}_t^{ij}\right)\right\}$$where $\oplus$ represents advanced information fusion between device $i$ and its neighbor set ${\mathcal{N}}_i$. $\varphi$ is an advanced information processing function dynamically adjusted based on device capabilities and network state. ${\alpha }_t^i$, ${\beta }_t^i$, ${\gamma }_t^i$, and ${\delta }_t^i$ are dynamically adjusted weight coefficients. ${\mathrm{\Psi }}_t^i$ is a basic parameter set for adjusting the information processing, and ${\mathrm{\Omega }}_t^{ij}$ is an additional parameter set for the interaction between device $i$ and its neighbor $j$.

To adapt to changing network conditions and device capabilities, an adaptive parameter adjustment process updates the state estimate of device $i$:

(12) $${\hat{x}}_{t+1|t}^i=f\left({\hat{x}}_{t|t}^i,u_t^i,I_t^i;{\theta }_t^i\right)+{\gamma }_t^i\odot {\mathrm{\nabla }}_{\hat{x}}\mathcal{L}\left({\hat{x}}_{t|t}^i,I_t^i;\mathrm{\Theta }\right)$$where $f$ is the adaptive adjustment function, ${\theta }_t^i$ are dynamically adjusted parameters, ${\gamma }_t^i$ is an adaptive learning rate, $\odot$ is the Hadamard product, ${\mathrm{\nabla }}_{\hat{x}}\mathcal{L}$ is the gradient of the loss function $\mathcal{L}$ with respect to the state estimate ${\hat{x}}_{t|t}^i$, and $\mathrm{\Theta }$ includes all related model parameters and network condition indicators.

The proof is presented in the appendix.

Motivation for feature data selection and optimization: achieving dynamic feature fusion and selection for feature data optimization

• Existing feature selection and fusion techniques often fail to effectively address the challenges of dynamically changing data and complex inter-task relationships. These techniques, based primarily on a static data perspective, overlook the time-varying nature of IoT data streams and the complexity of interactions between devices, leading to limited model performance in a multi-task learning environment and difficulty in adapting to real-time application requirements (Tao et al., 2022; Wang et al., 2022; Patsias et al., 2023).

• To address these issues, we designed an innovative mechanism for dynamic feature fusion and selection. The core innovation of this mechanism is its ability to dynamically adjust feature selection strategies based on real-time data streams and task requirements, achieving intelligent selection of the most representative and relevant features from large-scale, multi-source feature sets.

Mathematical principles of dynamic feature fusion and selection

To delve into the mathematical principles of dynamic feature fusion and selection, we propose a multi-task learning (MTL) model that combines hard parameter sharing and a multi-task attention mechanism. First, we define the overall objective function of multi-task learning, considering the relatedness between tasks and their uniqueness. The overall objective function combines the loss functions of all tasks as follows:

(15) $$\begin{array}{rl}{\mathcal{L}}_{total}=& \sum _{i=1}^T{\alpha }_i{\mathcal{L}}_i\left(f_i\left(X;{\mathrm{\Theta }}_{shared},{\mathrm{\Theta }}_i\right),Y_i\right)+\lambda \sum _{j=1}^P||{\mathrm{\Theta }}_{shared}^j|{|}_2^2\\ & +\beta \sum _{i=1}^T\sum _{t=1}^N{\left(\frac{1}{Z_t}\sum _{k=1}^K\exp \left(-\frac{\left||X_t-{\mu }_{t|t-1}^k\right|{|}^2}{2{\sigma }^2}\right)\cdot \left(\mathrm{\Phi }\left(X_t,{\mathrm{\Theta }}_i^k\right)\right)-Y_{i,t}\right)}^2\end{array}$$where T is the total number of tasks; ${\alpha }_i$ represents the weight of the $i$th task; ${\mathcal{L}}_i$ is the loss function of the $i$th task; $f_i$ is the prediction function corresponding to the $i$th task; X represents the input features; $Y_i$ is the true label of the $i$th task; ${\mathrm{\Theta }}_{shared}$ represents the parameters shared across all tasks; ${\mathrm{\Theta }}_i$ is the task-specific parameters of the $i$th task; $\lambda$ is the weight of the regularization term; P is the number of shared parameters; $\beta$ is the weight for missing data imputation; N is the number of data points in the dataset; $Z_t$ is a normalization factor; K is the number of historical data points considered at each time step; ${\sigma }^2$ represents the variance of Gaussian noise; $\mathrm{\Phi }$ is a task-specific feature extraction function.

By considering the problem of multi-task learning (MTL) under a hard parameter sharing framework, we describe the structure and learning process of the model by introducing an equation for the parameter set of shared layers:

(16) $${\mathrm{\Theta }}_{shared}=\underset{j=1}{\overset{L}{\otimes }}{\mathbf{W}}_j$$where L represents the number of shared layers, ${\mathbf{W}}_j$ is the weight matrix of the $j$th layer, and $\otimes$ indicates the tensor product operation, used to describe the complex interaction between parameters of different layers.

The overall objective function of multi-task learning is expressed as:

(17) $${\mathcal{L}}_{total}=\sum _{i=1}^T{\alpha }_i{\mathcal{L}}_i\left(f_i\left(X;{\mathrm{\Theta }}_{shared},{\mathrm{\Theta }}_i\right),Y_i\right)+\lambda \sum _{j=1}^P||{\mathbf{W}}_j|{|}_F^2+\gamma \sum _{i=1}^T\sum _{j\ne i}^T{\rho }_{ij}||{\mathrm{\Theta }}_i-{\mathrm{\Theta }}_j|{|}_2^2$$where ${\mathrm{\Theta }}_i$ is the task-specific parameter set of the $i$th task; $\lambda$ and $\gamma$ are the weight parameters of the regularization terms; ${\rho }_{ij}$ represents the correlation adjustment parameter between tasks $i$ and $j$; $||\cdot |{|}_F$ and $||\cdot |{|}_2$ respectively indicate the Frobenius norm and $L_2$ norm.

To capture the dynamic relationships between tasks and optimize the process of multi-task learning, we introduce an adaptive weight adjustment mechanism based on task correlation:

(18) $${\alpha }_i(t)=\frac{\exp \left(-\eta \sum _{j\ne i}^T{\rho }_{ij}||{\mathrm{\Theta }}_i(t-1)-{\mathrm{\Theta }}_j(t-1)|{|}_2^2\right)}{\sum _{k=1}^T\exp \left(-\eta \sum _{l\ne k}^T{\rho }_{kl}||{\mathrm{\Theta }}_k(t-1)-{\mathrm{\Theta }}_l(t-1)|{|}_2^2\right)}$$where $\eta$ is the learning rate, $t$ represents the iteration count, and ${\alpha }_i(t)$ indicates the adaptive importance weight of task $i$ at iteration $t$.

To enhance the model’s capability in handling high-dimensional data and complex task relationships, we incorporate attention mechanisms from deep learning to dynamically focus on different tasks and features:

(19) $${\mathrm{\Theta }}_i^{attention}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\frac{{\mathrm{\Theta }}_{shared}^T{\mathrm{\Theta }}_i}{\sqrt{d_k}}\right){\mathrm{\Theta }}_{shared}$$where $d_k$ is a scaling factor to prevent the dot product from becoming too large in high-dimensional spaces.

Considering the complexity and diversity in a multi-task learning framework, we extend and deepen the original attention mechanism, introducing an advanced multi-task dynamic attention mechanism:

(20) $$A_i=\mathrm{S}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\frac{W_i^{\mathrm{a}\mathrm{t}\mathrm{t}}\cdot \tilde{h}+b_i^{\mathrm{a}\mathrm{t}\mathrm{t}}}{\sqrt{d_k}}+\sum _{j\ne i}^T{\mathrm{\Psi }}_{ij}(W_j^{\mathrm{a}\mathrm{t}\mathrm{t}}\cdot h+b_j^{\mathrm{a}\mathrm{t}\mathrm{t}})\right)$$where $A_i$ represents the dynamic attention weight vector for task $i$, $W_i^{\mathrm{a}\mathrm{t}\mathrm{t}}$ and $b_i^{\mathrm{a}\mathrm{t}\mathrm{t}}$ are the task-specific attention mechanism’s weight matrix and bias vector, respectively. Vector $\tilde{h}$ is an enhanced output of the shared layer through a feature completion mechanism.

For the dynamic completion issue of features in a multi-task learning environment, a feature completion mechanism is proposed:

(21) $$\tilde{h}=h\oplus \sigma \left(\sum _{n=1}^N{\mathrm{\Delta }}_n\odot \mathcal{M}(h;{\mathrm{\Phi }}_n)+\sum _{n=1}^N\left(1-{\mathrm{\Delta }}_n\right)\odot \left(V_n\cdot h+b_n\right)\right)$$where $h$ is the original output vector of the shared layer, $\mathrm{\Delta }$ represents a high-dimensional feature missing indicator vector, $\odot$ is element-wise multiplication, $\mathcal{M}$ is a feature completion model based on the parameter set ${\mathrm{\Phi }}_n$, $V_n$ and $b_n$ are the weight and bias in the completion model for handling non-missing features, $\sigma$ is a nonlinear activation function.

A parameterized dynamic adjustment layer is introduced into the feature completion mechanism for dynamic adjustment of the enhanced feature representation after feature completion:

(22) $${\tilde{h}}^{\ast }=\mathrm{\Gamma }\odot \tilde{h}+\mathrm{\Omega }\odot \left(h\oplus \sigma \left(\mathcal{F}(\tilde{h};{\mathrm{\Theta }}_{\mathcal{F}})+\mathcal{G}(h;{\mathrm{\Theta }}_{\mathcal{G}})\right)\right)$$where $\mathrm{\Gamma }$ and $\mathrm{\Omega }$ are matrices learned during training, ${\mathrm{\Theta }}_{\mathcal{F}}$ and ${\mathrm{\Theta }}_{\mathcal{G}}$ represent the parameter sets of these two functions.

Following this, a multi-task attention mechanism allows each task to select and emphasize the most important features for feature fusion, also considering the completion of missing features:

(23) $$F_i=\mathrm{S}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\frac{A_i\odot {\tilde{h}}^{\ast }}{\sqrt{d_k}}\right)$$where $F_i$ is the feature representation of the $i^{th}$ task after attention weighting and feature complementation, and $d_k$ is a scaling factor. Task-specific parameters ${\mathrm{\Theta }}_i$ are used to further process the features selected and fused by the attention mechanism, adapting to environmental changes and missing features:

(24) $$O_i=g_i\left(F_i;{\mathrm{\Theta }}_{adaptive}^i\right)=\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}\left({\mathrm{\Theta }}_{adaptive}^i\cdot F_i+b_i\right)$$where $O_i$ is the output of the $i^{th}$ task, $g_i$ is a non-linear transformation function for further processing the feature representation, and ${\mathrm{\Theta }}_{adaptive}^i$ is a task-specific parameter set adaptively adjusted to adapt to changes in network conditions and computational capabilities:

(25) $${\mathrm{\Theta }}_{adaptive}^i={\theta }_t^i\otimes {\mathrm{\Theta }}_i+\lambda \sum _{j\ne i}{\rho }_{ij}\left({\mathrm{\Theta }}_i-{\mathrm{\Theta }}_j\right)$$where $\otimes$ represents a parameter adjustment operation, ${\theta }_t^i$ is a coefficient dynamically adjusted according to task $i$’s specific requirements at time $t$, $\lambda$ is a regularization coefficient, and ${\rho }_{ij}$ represents a correlation adjustment parameter between task $i$ and task $j$.

To improve the model’s performance and generalization ability in handling multiple tasks, an integrated loss function is introduced, aiming to minimize the total loss of all tasks. (26) $$\begin{array}{rl}{\mathcal{L}}_{total}& =\sum _{i=1}^T{\alpha }_i{\mathcal{L}}_i\left(g_i\left(F_i;{\mathrm{\Theta }}_{adaptive}^i\right),Y_i\right)+\lambda \sum _{j=1}^P||{\mathrm{\Theta }}_{shared}^j|{|}_2^2\\ & +\beta \sum _{i=1}^T\sum _{t=1}^N{\left(\frac{1}{Z_t}\sum _{k=1}^K\exp \left(-\frac{\left||F_{i,t}-{\mu }_{t|t-1}^k\right|{|}^2}{2{\sigma }^2}\right)\cdot \left(\mathrm{\Psi }\left(F_{i,t},{{\mathrm{\Theta }}_{adaptive}^i}^k\right)\right)-Y_{i,t}\right)}^2\\ & +\eta \sum _{i=1}^T\left||{\mathrm{\Delta }}_i-\mathcal{M}(h_i;\mathrm{\Phi })\right|{|}_2^2\end{array}$$where ${\mathcal{L}}_i$ is the loss function of the $i^{th}$ task, ${\alpha }_i$, $\lambda$, $\beta$, and $\eta$ are hyperparameters adjusting the importance of each loss component, $||{\mathrm{\Theta }}_{shared}^j|{|}_2^2$ is a regularization term, ${\mathrm{\Delta }}_i$ is an indicator vector for missing features of the $i^{th}$ task, $\mathcal{M}$ is a feature complementation model, and $\mathrm{\Phi }$ are the parameters of the feature complementation model.

This addresses the feature complementation problem within the dynamic feature fusion and selection framework to enhance the robustness and accuracy of multi-task learning models in dealing with incomplete or noisy feature data.

The proof process is presented in the appendix.

Motivation for computational resource constraints in the IoT: enhancing edge computing efficiency

• Facing the issue of limited resources in edge devices within IoT applications, traditional computation-intensive models are often inapplicable due to their high computational power and storage space requirements. Existing strategies frequently overlook the resource constraints of edge computing, limiting the performance of edge devices (Xiong et al., 2020; Zikria et al., 2021; Mendez et al., 2022).

• We propose an optimized lightweight CNN framework that reduces computational demand through efficient activation functions, network pruning, and model compression. Additionally, it features a dynamic resource allocation mechanism that smartly adjusts task distribution according to device capabilities and network status, enhancing efficiency while preserving accuracy.

Dataset and experimental parameters introduction

In our study, we utilized two publicly available datasets: Edge-IIoT and UNSW_NB15, to evaluate the performance of our proposed model.

Edge-IIoT: The dataset is designed for the edge computing environment in Industrial Internet of Things (IIoT) (https://www.kaggle.com/datasets/mohamedamineferrag/edgeiiotset-cyber-security-dataset-of-iot-iiot), containing various normal and abnormal device behavior data, simulating network attacks such as DDoS and malware, suitable for edge computing security threat detection.

UNSW_NB15: The dataset, released by the University of New South Wales, Australia, is aimed at network intrusion detection research (https://www.kaggle.com/datasets/mrwellsdavid/unsw-nb15). It covers a diverse dataset of modern network attack characteristics, such as backdoors and DoS attacks, intended to support network security research, enhancing the generalization and robustness of intrusion detection systems.

Our experimental parameters are set as shown in Table 2.

Experimental deployment data

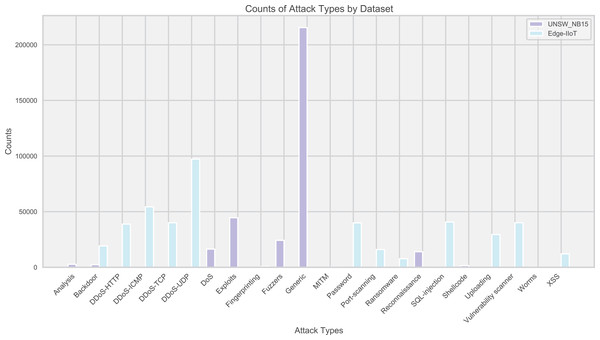
Edge-IIoT and UNSW_NB15 datasets were used to evaluate the IoT traffic anomaly detection model. These two datasets cover a variety of normal and abnormal traffic, reflecting the diversity of attack types. The distribution of attacks is intuitively displayed through bar charts (Fig. 2), guiding the model design and tuning.

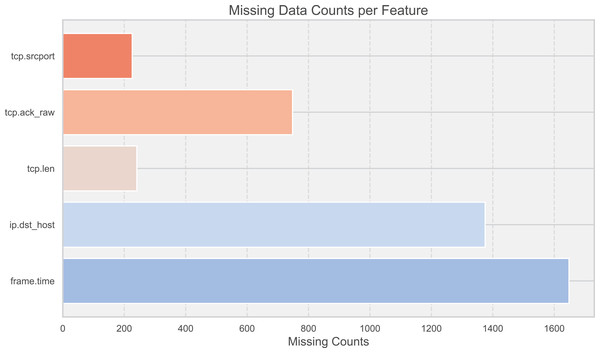
To enhance the robustness of the model, 10,000 records from each of the two datasets were randomly selected for testing. This sample size was chosen to ensure that the key characteristics of both datasets were adequately represented, providing a sufficient basis to validate the model’s performance. In the face of data missing and shifting (Fig. 3), corrections were made through a dynamic feature fusion strategy. Specifically, missing data were imputed using a combination of statistical methods and machine learning techniques, while shifting data distributions were adjusted using normalization techniques to ensure the accuracy of the results. The resource consumption of the RT-Cabi model is detailed in Table 3, covering time and space costs.To provide a comprehensive understanding of the training process, we conducted experiments over 20 training rounds. This number was chosen based on preliminary tests, which indicated that performance improvements plateaued after 20 rounds, making it an optimal choice for balancing training time and model efficiency.

The RT-Cabi model was deployed and completed training within 2 h for 20,000 samples, indicating that the training process, from initializing the model to finishing the final epoch, was efficient and time-effective. This deployment was conducted on a machine equipped with an NVIDIA Tesla V100 GPU, 32 GB RAM, and an Intel Xeon CPU. The deployment time can vary depending on the number of epochs, batch size, and the specific hardware used. With an average inference time of 10 milliseconds per sample, this makes the model suitable for IoT applications that require rapid response. The space cost of the model includes 50 MB for parameter storage and approximately 500 MB for intermediate data storage, making the overall resource consumption reasonable for resource-constrained devices.

To address concerns about the time complexity of feature selection, our framework incorporates an efficient feature selection mechanism that balances flexibility and computational efficiency, ensuring that predictive tasks are not delayed significantly, even in the presence of potential attacks. This approach is particularly suitable for resource-constrained IoT devices such as smart sensors, wearable devices, and edge computing nodes, where computational power and memory are limited. By optimizing the feature selection process, we ensure that these devices can maintain high performance and quick response times, essential for real-time applications.

Experimental results

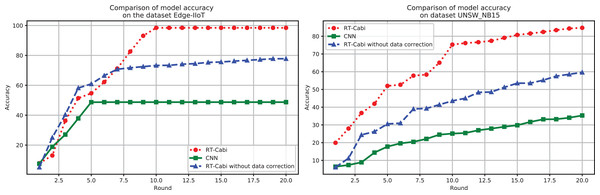
Figure 4 demonstrates the flexibility and superiority of the RT-Cabi model under various parameter settings and structures. In the Edge-IIoT dataset experiments, the model achieved a 97.15% accuracy rate after fine-tuning and feature engineering. Even without data correction, the accuracy rate was still 77.79%, showing strong robustness. In the UNSW_NB15 experiments, the accuracy rate increased from 75.59% to 84.75% after data correction, highlighting the importance of data preprocessing and the model’s adaptability to network security. In contrast, traditional CNNs, which serve as the baseline models in our study, showed significantly lower accuracy on both datasets than RT-Cabi, proving its advantages in processing IoT traffic. Traditional CNNs refer to standard convolutional neural networks without the optimizations and enhancements incorporated in RT-Cabi, such as dynamic feature fusion, adaptive parameter adjustment, and lightweight model compression.

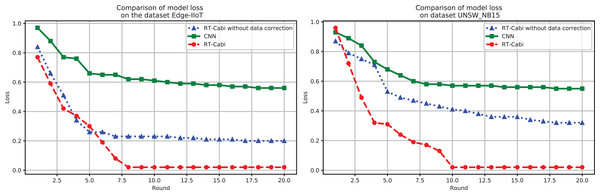
The performance of the RT-Cabi model is displayed through loss value analysis, as shown in Fig. 5. On the Edge-IIoT dataset, the loss value decreased from 1.03 to 0.006, showing its learning and optimization effects. Its performance on the UNSW_NB15 also demonstrated its generalization ability. These results not only confirm the efficiency and advanced nature of RT-Cabi in IoT anomaly detection but also provide guidance for future model design, helping to advance industrial IoT security research.

Comparison with cutting-edge research

Table 4 summarizes the accuracy comparison between the RT-Cabi model and other significant models from the literature. The RT-Cabi model achieved accuracies of 97.15% and 84.75% on the Edge-IIoT and UNSW_NB15 datasets, respectively, outperforming existing research. Compared to Zhang et al. (2021) and Singh et al. (2021), it showed an improvement of 1.45% and nearly 2%, respectively, demonstrating its effectiveness and advantages in the field of IoT anomaly detection. This underscores the potential of RT-Cabi as an efficient solution.