Multi-stage hybrid flow shop scheduling problem with lag, unloading, and transportation times

General HFS

The HFS has captured substantial interest within academic spheres and the manufacturing industry alike, thanks to its remarkable relevance and remarkable adaptability across a wide array of production systems. In make-to-order environments, there is a strong demand for flexible production systems, particularly because scheduling plans frequently face unforeseen disruptions. In the contemporary research landscape, there has been a discernible trend highlighting the efficacy of adaptable systems, such as the flexible flow shop, in adeptly managing the uncertainties characteristic of these environments (Fattahi, Hosseini & Jolai, 2013; Gen, Gao & Lin, 2009). Extensive literature exists regarding HFS, underscoring a substantial body of research and discourse within this references (Lee & Loong, 2019; Ribas, Leisten & Framiñan, 2010; Ruiz & Vázquez-Rodríguez, 2010; Tosun, Marichelvam & Tosun, 2020). These references provide comprehensive insights and detailed analyses of problems related to HFS. Below is a concise summary of recent publications that delve into different versions of the HFS.

Liu et al. (2024) examined the distributed HFS with blocking constraints. They proposed using greedy algorithms to tackle the problem, reducing idle machine time through active decoding techniques. Subsequently, a neighborhood search framework is implemented to increase the diversity of solutions. To generate effective initial solutions, they devised a heuristic rule centered on blocking constraints. Li et al. (2023a) addressed an HFS problem that incorporates energy considerations. To address this challenging problem, a multi-objective Mixed-Integer Linear Programming (MILP) approach is proposed. Furthermore, the article introduces both a Q-learning technique and an enhanced genetic algorithm as solutions tailored specifically for this problem. The investigation by Guan et al. (2023) explores various solution representations for the HFS, emphasizing their respective advantages and limitations. It also deals with the task of striking a balance between narrowing down the solution space and maintaining an efficient search process within the confines of the limited solution space. Liu et al. (2023) concentrate on the dynamic HFS with re-entrant jobs, integrating factors such as skill levels and worker fatigue into their analysis. They utilize a multi-agent technique reinforced by deep learning to achieve a solution that approaches optimality. Thorough experimental studies illustrate the effectiveness of the algorithm put forth. In the study by Ghodratnama, Amiri-Aref & Tavakkoli-Moghaddam (2023), researchers explore an MFFS problem that entails fuzzy maintenance time and robotic integration. They present a bi-objective mathematical model and utilize two multi-objective decision-making strategies: LP-metric and goal attainment (GA). The efficacy of these solution methods is evaluated and prioritized using the “TOPSIS” (Technique for Order of Preference by Similarity to Ideal Solution) methodology. In the study outlined in Huang et al. (2023), diverse uncertain parameters linked to the production process in HFS are considered. To tackle the problem, they introduce a two-stage stochastic programming approach. To address this challenge effectively, they propose a novel iteration of the pointer-based discrete differential evolution (PDDE) algorithm, referred to as H-PDDE. This variant is crafted to enhance the performance and efficiency of the PDDE algorithm, particularly tailored for addressing the specified problem.

Gholami & Sun (2023), address a distributed MFFS involving multiprocessor jobs. They frame the issue as a Markov Decision Process (MDP) and subsequently utilize a hybrid Q-learning-local search algorithm to resolve it. This approach combines the advantages of Q-learning, a reinforcement learning technique, with local search methods to effectively obtain near-optimal solutions for the given problem. In their work Tran et al. (2023), improved mathematical integer formulations are introduced for the HFS, integrating chaining time-lag and time-varying resources. To reinforce these formulations, researchers devise valid inequalities. These inequalities are subjected to testing and evaluation, with the findings demonstrating their performance. In Fernandez-Viagas, Molina-Pariente & Framinan (2018), a thorough investigation into constructive heuristics for the HFS is carried out. The assessed heuristics are put to experimental scrutiny and juxtaposed with four newly proposed counterparts. Two memory-centric constructive heuristics are unveiled, featuring a gradual integration of jobs into a partial sequence, while advantageous insertions are cataloged to form the eventual sequence. Furthermore, two constructive heuristics based on Johnson’s algorithm are put forth as an alternative strategy. In their work Li et al. (2023b), researchers addressed a challenge within the HFS related to batch processing in the sand casting industry. They introduced an upgraded cuckoo algorithm, integrating crossover and mutation operations to enhance its search capabilities. These enhancements were aimed at replacing the traditional long and short flight strategies within the cuckoo algorithm.

In their study (Wang et al., 2023), researchers investigate a distributed two-stage HFS issue related to maintenance requirements. They introduce a mixed integer programming model and suggest employing a genetic algorithm to tackle this challenge. In their study (Utama & Primayesti, 2022), researchers delve into the HFS, incorporating energy considerations. They present an optimization algorithm that employs the Hybrid Aquila Optimizer (HAO) to tackle this specific issue. Within their study (Shao, Shao & Pi, 2023), researchers explore the distributed heterogeneous MFFS that integrates lot-streaming. They unveil a mixed-integer linear programming model and suggest a series of constructive heuristics, alongside an iterated local search algorithm. These constructive heuristics, grounded in time-based rules, form a notable part of their approach.

Scheduling multiprocessor tasks entails the necessity for a task to be processed simultaneously by multiple parallel processors (machines). Researchers have paid particular attention to scheduling multiprocessor tasks in hybrid flow shops (HFSMT) due to its significance in real-world applications. In this context authors in Engin & Engin (2020) addressed a HFSMT problem. This study proposes a novel memetic algorithm that integrates both global and local search methods to address the challenges of HFSMT scheduling problems. An intensive experimental study on benchmark test problems demonstrates that the proposed algorithms surpass existing ones in performance. Additionally, in Engin & Engin (2018) a HFSMT under the environment of a common time window is examined. In this research, a new memetic algorithm in which a global search algorithm is accompanied with the local search mechanism is developed to solve the HFSMT with jobs having a common time window. Memetic algorithm is tested using HFSMT problems. In Kahraman et al. (2010), authors introduced a highly efficient parallel greedy algorithm for solving the HFSMT problem. Furthermore, they proposed four constructive heuristic methods to tackle HFSMT problems. Comparative computational results with previous works in the literature demonstrate the remarkable effectiveness of the proposed algorithms in terms of significantly reducing total completion time or makespan. Engin, Ceran & Yilmaz (2011) conducted a study that focused on an HFS scheduling problem involving multiprocessor tasks, where each job necessitates the use of more than one machine for processing. In their research, the authors proposed an efficient genetic algorithm specifically designed for tackling this problem.

HFS with lag times

In a recent study conducted by Tran et al. (2023), an improved and refined linear integer formulation is presented for the HFS. This advanced formulation takes into account time-varying resources and incorporates chaining time-lag constraints, thereby offering a more comprehensive approach to addressing the complexities of the problem. To enhance the robustness of the formulations, two valid inequalities are proposed. These inequalities serve to strengthen the mathematical models and improve their ability to accurately represent and solve the problem at hand. The revised formulations are evaluated through a benchmarking process, and the results indicate that the valid inequalities significantly improve their performance. Tran et al. (2021) Introduces a novel mathematical formulation for the HFS problem, which considers time-varying resources and exact time-lag constraints. A comparison of this formulation to others is made, and it is found that it always guarantees a feasible solution for all instances. In a study conducted by Harbaoui, Khalfallah & Bellenguez-Morineau (2018), a two-stage HFS problem incorporating precedence constraints, setup times, and lag times is examined and addressed. Due to the complexity of the studied problem, a hybrid genetic algorithm (HGA) is presented. The proposed procedures are successfully demonstrated to efficiently solve the problem under study within acceptable CPU time constraints. This outcome is the culmination of a rigorous experimental study. In a study conducted by Javadian et al. (2012), the HFS problem is investigated, taking into account both setup and lag times. In Authors proposed a mathematical model that solves efficiently small sizes instances. In addition, for medium and large sizes problems a meta-heuristic algorithm based on the immune algorithm is proposed. The computational results indicate that the proposed algorithm can generate near-optimal solutions in a short period of time. In Botta-Genoulaz (2000), authors studied the HFS problem under precedence constraints, lag times and due dates. In the latter research work, six new heuristics aiming to solve the problem are presented. An experimental study is performed to assess the performance and robustness of these algorithms, and the computational results substantiate the high quality of the obtained solutions.

HFS with transportation times

The authors in Gheisariha et al. (2021) investigated the HFS problem associated with transportation time, sequence setup time, and rework. To solve the problem, they proposed an efficient Enhanced Harmony Search Algorithm. In Lei et al. (2020), the HFS problem with dynamic transportation waiting time is examined, and a memetic algorithm is proposed to provide a near-optimal solution. In the work by Naderi, Zandieh & Shirazi (2009b), the authors focus on addressing the HFS problem that considers both setup time and transportation time. They propose an effective solution approach based on the electromagnetism metaheuristic to solve this problem. In Naderi et al. (2009a), the HFS problem with transportation and setup times is examined, with respective objective functions of total tardiness and total completion time. A proposed solution entails using a metaheuristic based on the simulated annealing algorithm in order to overcome this problem. Additionally, Zabihzadeh & Rezaeian (2016) conducted a study examining the HFS problem, with a specific focus on incorporating release dates and transportation time with robots. The objective of their study is to minimize the makespan in this context. Both ant colony optimization algorithm and genetic algorithms are proposed to solve this problem.

Zhong & Lv (2014) examined a two-stage HFS which considers the transportation times. In the latter problem, the machine-stage configuration involves two machines in the second stage and a single machine in the first stage. The transportation between stages is performed by a one-capacity transporter. To find a solution that is close to optimal, the researchers propose an efficient heuristic algorithm. Zhu (2012) addresses the HFS problem with batching restrictions and transportation times. In a specific case, the author suggests a heuristic approach with polynomial time complexity to address the problem. Furthermore, for the general case, a heuristic with pseudo-polynomial complexity is developed as a solution. Elmi & Topaloglu (2013) examines the HFS problem with robots’ transportation and blocking restrictions, proposing an efficient simulated annealing metaheuristic to minimize makespan. The presented algorithms are subjected to a comprehensive experimental evaluation. Chikhi et al. (2015) focus on examining the two-stage HFS problem that involves the inter-stage transportation with robots.  In the considered problem, the initial stage comprises two dedicated machines operating in parallel, while the subsequent stage is composed of a single machine. A thorough investigation of the problem and its various specific cases is conducted, including those that are considered NP-hard. In response to the NP-hard variants, the researchers develop two efficient heuristics.

HFS with unloading times

In their publication (Gupta & Tunc, 1994), the authors investigate the HFS problem that incorporates unloading times and setup times. The authors propose a set of heuristics, which are thoroughly evaluated through an experimental study. The results of the study show the efficiency and effectiveness of these algorithms in addressing the studied HFS problem. Botta-Genoulaz (2000) focuses on studying an HFS problem that considers both precedence constraints and unloading times. In order to provide a near-optimal solution for the addressed scheduling problem, the authors propose a set of six heuristic, which are demonstrated to be efficient through an extensive computational study. The authors of the study conducted by Low (2005) investigate an HFS problem that involves unloading and setup times. Notably, the parallel machines within each stage are unrelated, adding complexity to the problem. A heuristic algorithm is developed by the authors to obtain an initial feasible solution. A simulated annealing metaheuristic is then used to enhance this initial feasible solution. To assess the efficiency of the developed algorithms, an experimental study is conducted, providing substantial evidence of their effectiveness. A real-life HFS problem with unloading times and additional constraints is investigated in Gicquel et al. (2012). A mixed integer linear program (MILP) is proposed. This MILP is then improved by including several new inequalities. The obtained algorithm is providing optimal solution for the industrial test problems.

Research gap

Based on the current literature, the HFS scheduling problem involving lag times, transportation and unloading times has yet to be addressed. Therefore, there is a research gap that needs to be filled by studying this type of problem and developing effective procedures to solve it.

Definition of the studied problem

The HFS with lag time, transportation time, and unloading time (HFSULT) is defined as follows: A set of n tasks, denoted {J = 1, 2, …, n}, must be processed in a shop comprising a series of K production stages, denoted {ST = S₁, S₂, …, S_K}. Each stage, S_i contains m_i parallel machines which are identical, denoted M_i,1, M_i,2, …, M_i,mi $\left(\right.$i =1 $\left.,2,\dots ,K\right)$. To be consider as HFSULT, at least one stage contains more than one machine. It is also assumed that n is greater than the maximum of m_i for all i between 1 and K. The tasks must be processed consecutively, starting with stage S₁ and ending with stage S_K. Following the completion of processing in stage S_i, each task j is unloaded from the machine and then subjected to a lag time (such as cooling, cleaning, or fermentation) during which no further treatment is carried out. Once the lag time has elapsed, task j is transported to stage S_i+1(1 ≤ i ≤ K − 1). In the HFSULT problem, the processing time for task j in stage S_i is identical across all machines. Additionally, the machine responsible for processing a task j remains unavailable until the task is entirely unloaded. The following notations are utilized to describe the problem:

• pr_i,j: the processing time of task j at stage S_i.

• un_i,j: the unloading time of task j at stage S_i.

• lg_i,j: the lag time of task j at stage S_i.

• tr_i,j: the transportation time of task jfrom stage S_i to stage S_i+1(1 ≤ i ≤ K − 1).

Following the completion of task processing, it is crucial to note that the unloading operation may not commence immediately. The unloading and processing operations are completely separate, meaning that while a task is being unloaded or still present in the machine, the machine cannot be utilized for the processing of additional tasks. Additionally, it should be noted that during the lag time, neither transportation nor processing can be carried out.

The following assumptions serve as the basis for scheduling activities:

• No interruptions or preemption are allowed during processing.

• In a stage, each job is treated by only one machine.

• It is not possible for multiple jobs to be processed by the same machine simultaneously.

• Machines have the possibility to remain idle and await assignment for the next job.

• No breakdowns are assumed to occur with the machines.

• Between stages, buffers with an infinite capacity are assumed to be present.

• All jobs strictly follow a predefined route during processing. This route initiates from the first stage and progresses sequentially until reaching the final stage.

• There is no disparity in the processing time among the machines within each production stage since the machines are identical.

• pr_i,j, un_i,j, lg_i,j, and tr_i,j $\left(\right.$i =1 , …, K; j =1 $,\left.\dots ,n\right)$ are deterministic and have positive integer values.

• All machines and jobs are assumed to be available starting from time zero.

Finding a schedule π^∗, that optimized the makespan is the objective of this study. The makespan is defined as the maximum completion time and is represented by the following expression: (1)${\displaystyle C_{max}\left({\pi }^{\mathrm{\ast }}\right)=\underset{j\in J}{max}\left(c_{K,j}\left({\pi }^{\mathrm{\ast }}\right)\right)}$

Here, c_K,j(π^∗) is the exit time of job j from the system (leaving the last stage S_K). In addition, $c_{K,j}\left({\pi }^{\ast }\right)=C{U}_{K,j}\left({\pi }^{\ast }\right)+l{g}_{K,j}\left({\pi }^{\ast }\right)$ where $C{U}_{K,j}\left({\pi }^{\ast }\right)$ is the finishing date of the unloading operation of job j in S_K.

$F{H}_K,\left({\left(P{M}^{\left(l\right)}\right)}_{l=1}^K\right)\left|u{n}_{i,j},l{g}_{i,j},t{r}_{i,j}\right|C_{max}$ is the notation of the studied problem following the three-field notation (Graham et al., 1979).

Here, FH_K represents the problem type, where “FH” indicates that the problem is a flow shop hybrid scheduling problem, and K denotes the number of stages in the production process. The second part of the first field, $\left({\left(P{M}^{\left(l\right)}\right)}_{l=1}^K\right)$, describes the set of machines available for processing in each stage. This field specifies the existence of parallel machines, represented as $P{M}^{\left(l\right)}$, within each stage denoted as S_l.

The second field, $\left|u{n}_{i,j},l{g}_{i,j},t{r}_{i,j}\right|$, specifies the parameters of the problem, including unloading time un_i,j, lag time lg_i,j, and transportation time tr_i,j, for each job j in each stage S_i. Finally, C_max in the third field represents the objective function, which is to minimize the maximum completion time over all jobs.

The above points can be illustrated using the following example.

Example 1: Consider n = 4, K = 3, and m₃ = m₂ = m₁ = 2. Table 1 presents the processing times pr_i,j, unloading times pr_i,j, lag times lg_i,j, and transportation times tr_i,j for each job j in each stage S_i, (i = 1, 2, .., K and j ∈ J).

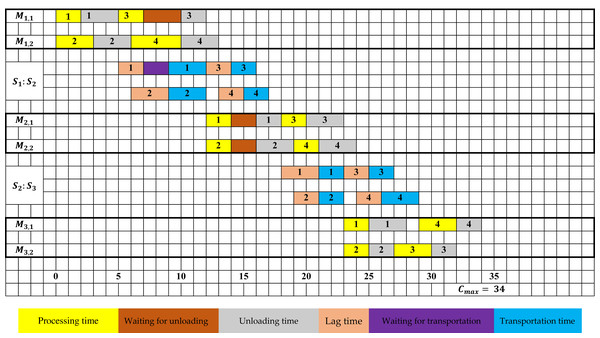
Figure 1 depicts a feasible scheduling solution with a makespan of C_max = 34 for the problem at hand, as per the example discussed earlier.

In Fig. 1, it can be observed that task 3 remains on machine M_1,1 even after its processing is completed at time 7. An unloading operation starts at time 10 and finishes at time 12. During this time window [7;10], the machine is not accessible and cannot be utilized for jobs treatment. This observation involves that the unloading operates independently of the required processing time.

Moreover, in the first stage, the lag time for task 1 starts once the unloading operation is completed, which occurs at time 5. The lag time period ends at time 7, but transportation is postponed until time 9. Hence, it can be inferred that the lag time is independent of the transportation operation.

Properties of the problem

The symmetric problem

This subsection is devoted to the introduction of the symmetric problem as well as its proprieties. Indeed, the study demonstrates that the optimal solutions for the original problem and its symmetric are equivalent and have the same makespan. As a result, to improve the solution quality, we conducted a systematic investigation of the symmetric problem.

Definition 3: The symmetric problem (backward) of $F{H}_K,\left({\left(P{M}^{\left(l\right)}\right)}_{l=1}^K\right)\left|u{n}_{i,j},l{g}_{i,j},t{r}_{i,j}\right|C_{max}$, involves beginning scheduling from the last stage S_K toward the first one S₁. By interchanging the roles of the stages, the symmetric (backward) problem can be derived, leading to a symmetric arrangement.

According to the aforementioned definition (definition 3), the following notations are presented. The forward problem is starting scheduling in the first stage, S₁, and ending at the last stage, S_K.

• The symmetric problem is starting scheduling in the last stage, S_K, and ending at the first stage, S₁.

Definition 4

• The following notations represent the stages and machines respectively in the context of the symmetric problem: $m_k^B=m_{K-k+1}$, and $S_k^B=S_{K-k+1}$ $\left(\right.$k =1 $,\left.\dots ,K\right)$.

• The machines are represented by the following notations: $M_{k,l}^B=M_{K-k+1,l}$ $\left(\right.$k =1 , …, K; l =1 $,\left.2,\dots ,m_k^B\right)$.

• The processing, unloading, lag , and transportation times of the backward (symmetric) problem are denoted respectively as follows: $p{r}_{k,j}^B,u{n}_{k,j}^B$ , $l{g}_{k,j}^B$ , and $t{r}_{k,j}^B$.

• We have: $t{r}_{k,j}^B=l{g}_{{}_{K-k+1},j}$, $p{r}_{k,j}^B=$ un_K−k+1,j, $l{g}_{k,j}^B=t{r}_{{}_{K-k+1},j}$, and $u{n}_{k,j}^B=p{r}_{{}_{K-k+1},j}$.

• $F{H}_K,\left({\left(P{M}^{\left(l\right)}\right)}_{l=1}^K\right)\left|u{n}_{k,j}^B,l{g}_{k,j}^B,t{r}_{k,j}^B\right|C_{\max }$ is the three-field notation of the symmetric problem.

This following result highlights the significance of exploring the symmetric problem.

Proposition 5: Every feasible solution for the forward problem $F{H}_K,\left({\left(P{M}^{\left(l\right)}\right)}_{l=1}^K\right)$ $\left|u{n}_{i,j},l{g}_{i,j},t{r}_{i,j}\right|C_{max}$ can be converted into a feasible solution for the symmetric problem $F{H}_K,\left({\left(P{M}^{\left(l\right)}\right)}_{l=1}^K\right)\left|u{n}_{i,j}^B,l{g}_{i,j}^B,t{r}_{i,j}^B\right|C_{max}$.

Furthermore, the makespans for both schedules exhibit similarity.

Proof. A feasible solution FS for the $F{H}_K,\left({\left(P{M}^{\left(l\right)}\right)}_{l=1}^K\right)$ $\left|u{n}_{i,j},l{g}_{i,j},t{r}_{i,j}\right|C_{max}$ problem can serve as the foundation for generating a feasible solution FS^B for the $F{H}_K,\left({\left(P{M}^{\left(l\right)}\right)}_{l=1}^K\right)\left|u{n}_{i,j}^B,l{g}_{i,j}^B,t{r}_{i,j}^B\right|C_{max}$ problem. This can be accomplished by maintaining identical sequences and assignments on each machine. In the forward problem, the time scale is denoted by ^′′t^′′, whereas in the backward problem, the time scale is represented by t^B, where t^B = C_max − t. The makespans of both feasible schedules FS and FS^B are identical since they share the same critical path. Similarly, utilizing the method outlined above, it becomes possible to convert a valid schedule obtained for the symmetric problem into an feasible schedule for the investigated problem.

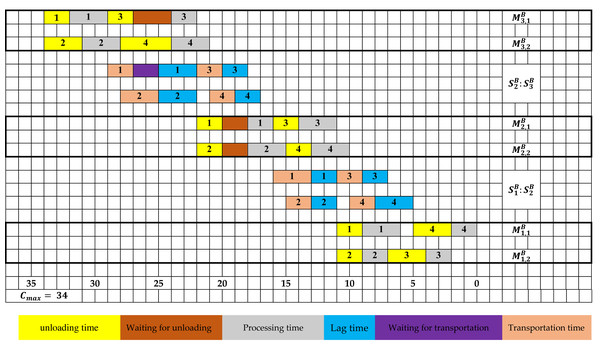
In order to illustrate the concept of symmetry, Example 1 is revisited, and Table 2 presents the processing, unloading, lag, and transportation times associated with the symmetric problem.

Table 2:

A symmetric problem’s processing, unloading, lag times, and transportation times.

j	1	2	3	4
$p{r}_{1,j}^B$	3	2	2	2
$u{n}_{1,j}^B$	2	2	3	3
$l{g}_{1,j}^B$	2	2	2	3
$t{r}_{1,j}^B$	3	2	2	2
$p{r}_{2,j}^B$	2	3	3	3
$u{n}_{2,j}^B$	2	2	2	2
$l{g}_{2,j}^B$	3	3	2	2
$t{r}_{2,j}^B$	2	3	2	2
$p{r}_{3,j}^B$	3	3	2	3
$u{n}_{3,j}^B$	2	3	2	4

DOI: 10.7717/peerjcs.2168/table-2

Figure 2 displays a feasible solution to the symmetric problem, which is achieved by reversing the time scale from “t” to (C_max − t).

Proposition 5 entails the following significant corollary.

Corollary 6: The $F{H}_K,\left({\left(P{M}^{\left(l\right)}\right)}_{l=1}^K\right)\left|u{n}_{i,j},l{g}_{i,j},t{r}_{i,j}\right|C_{max}$ problem and its symmetric counterpart, $F{H}_K,\left({\left(P{M}^{\left(l\right)}\right)}_{l=1}^K\right)\left|u{n}_{i,j}^B,l{g}_{i,j}^B,t{r}_{i,j}^B\right|C_{max}$, share the same optimal makespan.

Proof. This outcome directly follows from Proposition 5.

The subsequent proposed procedures, including lower bounds and heuristic, are systematically employed to tackle the symmetric problem, resulting in enhanced outcomes. This observation directly follows from Corollary 6.

In the following sections, useful notations will be presented.

In each stage $S_k\left(\right.$k =1 $,2,\left.\dots ,K\right)$ and for j ∈ J, re_k,j given below is the release date. (2)${\displaystyle \left\{\begin{array}{c}r{e}_{k,j}=\stackrel{k-1}{\sum _{i=1}}\left(p{r}_{i,j}+u{n}_{i,j}+l{g}_{i,j}+t{r}_{i,j}\right)\mathrm{if}k>1\hfill \\ r{e}_{k,j}=0\mathrm{if}k=1\hfill \end{array}\right.}$

For $S_k\left(\right.$k = 1 $\left.,2,\dots ,K\right)$ and for j ∈ J, qe_k,j given below is the delivery time. (3)${\displaystyle \left\{\begin{array}{c}q{e}_{k,j}=l{g}_{k,j}+t{r}_{k,j}\stackrel{K}{+\sum _{i=k+1}}\left(p{r}_{i,j}+u{n}_{i,j}+l{g}_{i,j}+t{r}_{i,j}\right)\mathrm{if}k<K\hfill \\ q{e}_{k,j}=0\mathrm{if}k=K\hfill \end{array}\right.}$

Furthermore, for each stage $S_k\left(\right.$k =1 $\left.,\dots ,K\right)$:

■ ${\overline{r{e}_{k,j}}}_{\left(i\right)}$ is the ith value in the increasingly sorted list of re_k,j’s (j = 1, …, n).

■ ${\overline{q{e}_{k,j}}}_{\left(i\right)}$ is the ith value in the increasingly sorted list of qe_k,j’s (j = 1, …, n).

■ ${\overline{\left(u{n}_{k,j}+p{r}_{k,j}\right)}}_{\left(i\right)}$ is the ith value in the increasingly sorted list of $\left(u{n}_{k,j}+p{r}_{k,j}\right)$’s (j = 1, …, n).

■ ${\overline{\left(l{g}_{k,j}+t{r}_{k,j}\right)}}_{\left(i\right)}$ is the ith value in the increasingly sorted list of tr_k,j’s (j = 1, …, n).

Lower bound based on capacity relaxation

Suppose that all stages, with the exception of one stage S_k are equipped with an infinite number of machines. Once a task reaches a relaxed stage, it undergoes immediate processing. Consequently, the scheduling problem for stage S_k can be represented as P_m| re_k,j, un_k,j, qe_k,j|C_max, where the problem characteristics encompass:1) the number of machines (m = m_k), 2) release dates (re_k,j), 3) unloading times (un_k,j), and 4) delivery times (qe_k,j).

To introduce further relaxation to this problem, one can exclude the idle time after the completion of task processing and the commencement of the unloading for each job. By applying this relaxation, we obtain a P_m| re_k,j, qe_k,j|C_max problem. In this scenario, each task j is assigned a processing time (pr_k,j + un_k,j). In their study (Carlier, 1987) of parallel machine scheduling with release and delivery (P_m|r_j, q_j|C_max), the researchers introduced a new lower bound. By using the aforementioned lower bound as a reference, we can derive the following lower bound specific to stage S_k. (4)${\displaystyle L{B}_k^S=⌈\frac{1}{m_k}\left(\stackrel{m_k}{\sum _{i=1}}{\overline{r{e}_{k,j}}}_{\left(i\right)}+\underset{j=1}{\sum ^n}p{r}_{k,j}+\underset{j=1}{\sum ^n}u{n}_{k,j}+\stackrel{m_k}{\sum _{i=1}}{\overline{q{e}_{k,j}}}_{\left(i\right)}\right)⌉.}$

Proof: For the problem P_m|r_j, q_j|C_max, Carlier (1987) established that $LB=⌈\frac{1}{m}\left(\stackrel{m}{\sum _{i=1}}{\overline{r_j}}_{\left(i\right)}+\underset{j=1}{\sum ^n}{p}_j+\stackrel{m}{\sum _{i=1}}{\overline{q_j}}_{\left(i\right)}\right)⌉$ is a lower bound. Here, ${\overline{r_j}}_{\left(i\right)}$ and ${\overline{q_j}}_{\left(i\right)}$ represent the ith release date and delivery time, respectively, sorted in increasing order. In stage S_k, let m = m_k, r_j = re_k,j, and q_j = qe_k,j . By omitting the idle time between the completion of a job’s processing and the beginning of its unloading operation (as a relaxation), we define p_j = pr_k,j + un_k,j Therefore, Therefore, ${\overline{r_j}}_{\left(i\right)}={\overline{r{e}_{k,j}}}_{\left(i\right)}$, ${\overline{q}}_{\left(i\right)}={\overline{q{e}_{k,j}}}_{\left(i\right)}$. Thus, the expression given in Eq. (4) indeed represents a lower bound for the studied problem.

It is important to note that Eq. (4) does not explicitly account for the transportation and lag times. However, these two parameters are implicitly considered and incorporated within ${\overline{r{e}_{k,j}}}_{\left(i\right)}$ and ${\overline{q{e}_{k,j}}}_{\left(i\right)}$.

Therefore, we can conclude that the following result can be derived.

Proposition 7: The following expression represents a lower bound with complexity O(Kn). (5)${\displaystyle L{B}^S=\underset{1\le k\le K}{max}\left\{L{B}_k^S\right\}.}$

Proof: Eq. (4) involves that $L{B}_k^S$ is a lower bound for P_mk| re_k,j, qe_k,j|C_max at stage S_k. By exploring all stages, the expression $L{B}^S={max}_{\begin{array}{c}\hfill 1\le k\le K\hfill \end{array}}\left\{L{B}_k^S\right\}$ yield a valid lower bound for the studied problem. The primary computational effort involved in calculating $L{B}_k^S$ is the sorting of ${\overline{r{e}_{k,j}}}_{\left(i\right)}$ and ${\overline{q{e}_{k,j}}}_{\left(i\right)}$, which has a time complexity of O(n). Therefore, by exploring all the K stages, the time complexity of LB^S is O(Kn).

An idle time based lower bound

This subsection aims to derive a secondary lower bound by introducing relaxation to a particular parallel machine scheduling problem. The purpose of this relaxation is to evaluate the minimum idle time within stage S_k. Specifically, we consider stage S_k−1 (if k ≥ 2) and stage S_k+1 if (if k < K). The scheduling problem under consideration is a parallel machine problem with release dates, with the objective of minimizing the sum of completion times. The notation of the above mentioned problem is $P_m\left|r_j\right|\sum C_j$. This problem is defined as follows. A set of m identical parallel machine has to process without preemption n jobs. Each job j is subject to a release date constraint (mentioned by r_j in the second field of the previous three-field notation). Each job j is processed during p_j = pr_k,j + un_k,j units of time in a machine. The primary objective of this problem is to identify a viable schedule that satisfies the specified constraints while minimizing the total completion time, represented by the sum of all task completion times ∑C_j. According to Yalaoui & Chu (2006), this problem is recognized as NP-hard.

$P_m\left|r_j\right|\sum C_j$ can be relaxed by permitting the job splitting. In this relaxed problem, jobs are permitted to be interrupted and resumed at any time, and they can also be executed concurrently on multiple machines. According to Yalaoui & Chu (2006), the Shortest Remaining Processing Time (SRPT) algorithm is capable of effectively solving this relaxation by employing job splitting, with a time complexity of O(nlog(n)). In simpler terms, the SRPT rule selects the job j with the shortest remaining processing time at any given time t. Following that, the available machines schedule portions of job j until either the entire job is processed or another available job with a shorter remaining processing time is found. For the problem $P_m\left|r_j\right|\sum C_j$ a lower bound is obtained by summing the n smallest completion times obtained by using the SRPT rule.

The sum of the l smallest completion times, obtained through the SRPT rule (splitting relaxation) within stage S_k, is denoted as JSRPM_k(l).

The second lower bound is presented below over Proposition 8.

Proposition 8: Let $L{B}_{2S}\left(k\right)$ expressed as follows. (6)${\displaystyle L{B}_{2S}\left(k\right)=⌈\frac{1}{m_k}\left(\right.JSRP{M}_{k-1}\left(m_k\right)+\underset{i=1}{\sum ^{m_k}}{\overline{\left(l{g}_{k-1,j}+t{r}_{k-1,j}\right)}}_{\left(i\right)}+\underset{j=1}{\sum ^n}\left(p{r}_{k,j}+u{n}_{k,j}\right)+\underset{i=1}{\sum ^{m_k}}{\overline{\left(l{g}_{k,j}+t{r}_{k,j}\right)}}_{\left(i\right)}+JSRP{M}_{k+1}\left(m_k\right)\left.\right)⌉.}$

Therefore, for the problem under study, $L{B}_{2S}\left(k\right)$ is a lower bound specific to stage S_k $\left(2\le k\le K\right)$. Furthermore, the time complexity of $L{B}_{2S}\left(k\right)$ is $O\left(nlogn\right)$.

Proof: When analyzing an optimal schedule with an optimal solution of $C_{max}^{\ast }$ and focusing on a specific stage S_k (where 2 ≤ k ≤ K), the following notations are utilized:

• f_i denotes the first task processed by the machine M_k,i.

• l_i represents the last task that was unloaded from the machine M_k,i.

• s_k,fi signifies the start time of processing task f_i on machine M_k,i.

• Pr_k,i: This represents the total processing time on machine M_k,i

• UN_k,i: This signifies the total unloading time on machine M_k,i

• Id_k,i: denotes the total idle time in machine M_k,i.

Clearly, we have: (7)${\displaystyle s_{k,f_i}+P{r}_{k,i}+I{d}_{k,i}+U{N}_{k,i}+q{e}_{k,l_i}\le C_{\max }^{\ast }.}$

Therefore, (8)${\displaystyle \sum _{i=1}^{m_k}{s}_{k,f_i}+\sum _{i=1}^{m_k}P{r}_{k,i}+\sum _{i=1}^{m_k}I{d}_{k,i}+\sum _{i=1}^{m_k}U{N}_{k,i}+\sum _{i=1}^{m_k}q{e}_{k,l_i}\le m_k{C}_{max}^{\ast },}$

In addition, (9)${\displaystyle \sum _{i=1}^{m_k}P{r}_{k,i}=\sum _{j=1}^n{p}_{k,j}\mathrm{and}\sum _{i=1}^{m_k}U{N}_{k,i}=\sum _{j=1}^{n}u{n}_{k,j}}$

Furthermore, (10)${\displaystyle \sum _{i=1}^{m_k}{\overline{q{e}_{k,j}}}_{\left(i\right)}\le \sum _{i=1}^{m_k}q{e}_{k,l_i}}$

In stage S_k−1, we have a parallel machine problem $P_{m_{\begin{array}{c}\hfill k-1\hfill \end{array}}}\left|r{e}_{k-1,j}\right|\sum C_j$ and, (11)${\displaystyle JSRP{M}_{k-1}\left(m_k\right)+\underset{i=1}{\sum ^{m_k}}{\overline{\left(l{g}_{k-1,j}+t{r}_{k-1,j}\right)}}_{\left(i\right)}\le \sum _{i=1}^{m_k}{s}_{k,f_i}.}$

Based on Eqs. (8), (9), (10) and (11), the following relationship can be established: (12)${\displaystyle ⌈\frac{1}{m_k}\left(JSRP{M}_{k-1}\left(m_k\right)+\underset{i=1}{\sum ^{m_k}}{\overline{t{r}_{k-1,j}}}_{\left(i\right)}+\underset{j=1}{\sum ^n}\left(p{r}_{k,j}+u{n}_{k,j}\right)+\stackrel{m_k}{\sum _{i=1}}{\overline{q{e}_{k,j}}}_{\left(i\right)}\right)⌉\le C_{\max }^{\ast }}$

By considering the symmetric problem and directing attention to stage S_k+1, one can illustrate the following: (13)${\displaystyle JSRP{M}_{k+1}\left(m_k\right)+\underset{i=1}{\sum ^{m_k}}{\overline{\left(l{g}_{k,j}+t{r}_{k,j}\right)}}_{\left(i\right)}\le \stackrel{m_k}{\sum _{i=1}}{\overline{q{e}_{k,j}}}_{\left(i\right)}}$

This ends the first part of the proof.

The main effort computing LB_2S(k), lies in determining $JSRP{M}_{k-1}\left(m_k\right)$ and $JSRP{M}_{k+1}\left(m_k\right)$ $\left(1\le k\le K\right)$, which takes O(nlogn) time.

The following corollary is presented as a direct consequence of the preceding proposition (Proposition 8).

Corollary 9: The expression for a valid lower bound on the problem can be formulated as follows: (14)${\displaystyle L{B}_{2S}=\underset{1\le k\le K}{max}\left\{L{B}_{2S}\left(k\right)\right\}}$

Additionally, the time complexity of LB_2S is O(Knlogn).

Proof: The lower bound LB_2S(k) is derived from the preceding proposition (Proposition 8). By taking the maximum value among all LB_2S(k) for 1 ≤ k ≤ K, denoted as $L{B}_{2S}={max}_{\begin{array}{c}\hfill 1\le k\le K\hfill \end{array}}\left\{L{B}_{2S}\left(k\right)\right\}$, we obtain a lower bound that has a time complexity of O(Knlog(n)).

A general lower bound

By jointly considering LB_S and LB_2S, the lower bounds can be enhanced to be more comprehensive and robust. The following expression represents this strengthened lower bound:

Corollary 13: A lower bound for the examined problem is expressed as follows. (15)${\displaystyle LB=max\left(L{B}_{2S},L{B}^S\right)}$

Proof. Obvious.

Initial feasible solution (Phase 1)

A constructive procedure is employed to generate a feasible schedule γ_i for each starting stage S_i(1 ≤ i ≤ K). The pseudocode for stage S_i is presented in Algorithm 1 as follows:

The first step involves solving the problem $P_{m_i}\left|r_j,u{n}_j,q_j\right|C_{\max }$ which is specific to stage S_i. This task is accomplished in Steps 1–2 by applying the ADAU heuristic. Moving on to the subsequent stage, S_i+1, the durations CU_i,j + lg_i,j + tr_i,j for each task j ∈ J are designated as the release dates r_j, where CU_i,j represents the completion unloading dates. Subsequently, the scheduling problem identified as $P_{m_{i+1}}\left|r_j,u{n}_j,q_j\right|C_{\max }$, as defined in Step 3.1, is tackled and resolved. This is achieved by utilizing the ADAU heuristic once again in Step 3.2. This process is repeated iteratively, starting from stage S_i+2 and continuing until stage S_K, with Steps 3.1–3.2 being executed in the same sequential order.

To achieve a comprehensive solution, iterative scheduling is utilized for the upstream stages S_i−1, …, S₁. More precisely, in stage S_i−1, a problem $P\left|r_j,u{n}_j\right|L_{\max }$ is formulated by assigning due dates d_j to each task j ∈ J, where the due dates are set equal to the starting time in stage S_i−1 (Step 5.1). Subsequently, in Step 5.2, ADAU is employed to generate a schedule with a maximum lateness $L_{\max }^{i-1}$. During this phase, two cases need to be addressed:

• Case 1: If the maximum lateness in Step 5.2 is greater than zero ($L_{\max }^{i-1}>0$), it is required to shift the starting time in the subsequent stages (S_i, …, S_K) to the right by $L_{\max }^{i-1}$ units of time.

• Case 2: Conversely, if the maximum lateness is less than or equal to zero ($L_{\max }^{i-1}\le 0$), the schedules in the subsequent stages (S_i, …, S_K) should be left-shifted by $L_{\max }^{i-1}$ units of time.

By implementing these adjustments, it ensures that the tasks are completed within their assigned due dates and maintains the overall feasibility of the solution.

Both in Case 1 and Case 2, it is essential to update the upper bound UB_i in Step 5.3 to reflect the adjusted starting times. The latter procedure is applied in each stage S_i−1, …, S₁. As a result, a feasible schedule γ_i is generated for the problem under investigation, ensuring that all the given constraints are satisfied. By modifying the starting stage S_i ($\left.1\le i\le K\right)$, K schedules γ₁, …, γ_K are obtained. From these schedules, the one with the minimum makespan UB is selected as the initial solution. By adopting this approach, the overall solution is guaranteed to achieve the minimum possible makespan while still being feasible within the given constraints of the problem.

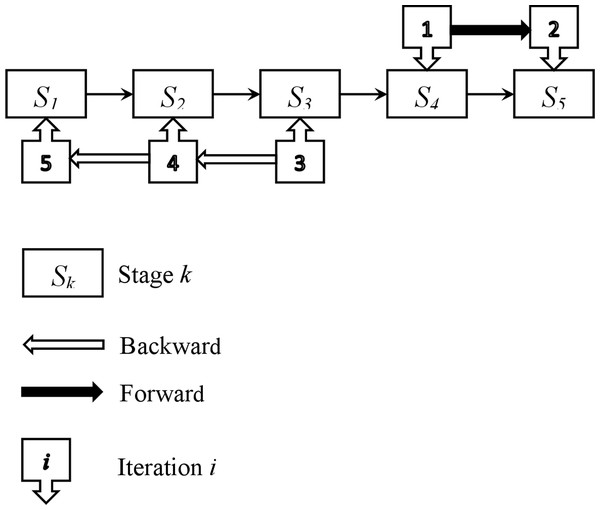
To simplify the presentation of the various steps in the above procedure (Phase 1), a straightforward example comprising five stages is provided. The entire process is illustrated in the self-contained Fig. 3.

In this example, stage 4 is chosen as the starting point (i = 4). A parallel machine problem is set up and solved. The same procedure is repeated for the subsequent stage (stage 5) as part of the forward process. For each iteration, a parallel machine problem is defined and solved. Once the last stage is reached, a backward procedure starts from stage 3 (i − 1 = 3), and continues with stages 2 and 1. For each of these stages, a parallel machine problem is defined and solved. By reaching the first stage, feasible solutions for all five stages are obtained. These solutions are not conflicting, and their combination provides a feasible solution for the studied problem. The ADAU heuristic is used to solve each parallel machine scheduling problem. If the starting stage is 1, 2, 3, or 5, four other feasible solutions are obtained, and the best one is kept as the initial feasible solution. Additionally, the parameters of the parallel machine problems are updated according to Step 3.1 and Step 5.3.

The enhancement phase (Phase 2)

The iterative improvement phase begins after obtaining the feasible schedule γ from Phase 1. A stopping criterion is set to determine when to terminate the improvement phase. In this phase, iterative refinements are applied to the schedules of all stages, excluding one specific stage (S_h), in order to enhance the solution. To facilitate the rescheduling process, it is crucial to address the problem denoted as $P_{m_h}\left|r_j,u{n}_j\right|L_{\max }$ as a fundamental aspect of the iterative adjustments. In the aforementioned problem, the release dates are defined as r_j = CU_h−1,j, where CU_h−1,j represents the completion unloading time of job j in the previous stage (S_h+1). Additionally, the due dates d_j are determined based on the scheduled start time T_h+1,j of the jobs in the next stage (S_h+1), denoted as d_j = T_h+1,j. In the last stage S_K, the due date d_j is assigned as the makespan UB (d_j = UB). After solving the rescheduling problem, two possible scenarios arise with respect to ADAU:

1. When $L_{\max }^h$ is negative (i.e., $L_{\max }^h<0$), it indicates that an improved solution has been achieved at stage S_h, with a makespan reduced by $\left|L_{\max }^h\right|$ units of time. In this case, a new schedule is created by shifting all tasks in stages from S_h to S_K to the left by $\left|L_{\max }^h\right|$ units of time. This adjustment guarantees that tasks are completed within their designated due dates and ensures the overall feasibility of the solution.

2. When $L_{\max }^h$ is greater than or equal to zero (i.e., $L_{\max }^h\ge 0$), it indicates that no improvement has been achieved in this case. The iterative process is repeated for the subsequent stages until the convergence criterion is satisfied.

Remark 14: The optimal solution $L_{max}^h$ of $P_{m_h}\left|r_j,u{n}_j\right|L_{max}$ guarantees feasibility by satisfying $L_{max}^h\le 0$. This condition is essential to guarantee that tasks are accomplished within their designated due dates, ensuring an optimal overall solution that adheres to the constraints of the problem.

Subsequently, we provide a pseudo-code ( Algorithm 2 ) that outlines the sequential steps of the improvement phase when initiating from stage S_h.

To commence the improvement phase, we begin by selecting an initial stage S_h for starting the procedure, where a problem $P_{m_h}\left|r_j,u{n}_j\right|L_{\max }$ is defined (Step 1). In Step 2, the problem $P_{m_h}\left|r_j,u{n}_j\right|L_{\max }$ is solved by applying the ADAU heuristic. If improvements are identified, Step 3 involves performing a rescheduling of stage S_h. Similarly, if enhancements are identified in Step 4, the upstream stages S_h−1 S_h−2, …, S₁ are subjected to rescheduling. When the heuristic procedure reaches the first stage in Step 3.2, the improvement phase is iteratively applied to each downstream stage S₂, S₃, …, S_K in Steps 5–8. During this process, Step 7.2 involves revisiting and rescheduling the upstream stages. The stopping criterion for the second phase is met when 2K-2 consecutive problems are solved without any improvement. The latter halting condition is represented by Step 9. This guarantees that the algorithm terminates either after a satisfactory number of iterations without any improvement or when an optimal solution is achieved.

The improvement phase operates on the feasible schedule γ derived from Phase 1 as its input. The proposed improvement phase can commence with any starting stage S_h ($\left.h=1,\dots ,K\right)$, and K improvement phases are carried out, each initiated with a different starting stage S_h ($\left.h=1,\dots ,K\right)$. As a result, K feasible schedules are generated, and the best schedule γ^∗ is chosen from among them. By exploring various starting stages, the algorithm can discover a diverse range of solutions and ultimately select the one with the lowest makespan that satisfies all the problem’s constraints. Incorporating multiple starting stages ensures the algorithm’s robustness and its ability to handle diverse scenarios and input data effectively.

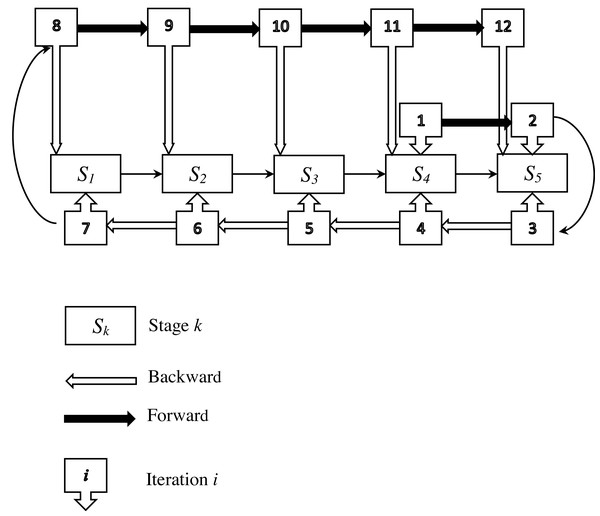
In the following, an example is provided to clearly explain the enhancement phase. This example involves five stages and assumes that an initial feasible solution has been obtained from phase 1. The entire process of this phase is illustrated in Fig. 4.

Stage 4 is chosen as the starting point (h = 4), where a parallel machine problem is set up and solved. This procedure is then repeated for the subsequent stage (stage 5) as part of the forward process. At each iteration, a parallel machine problem is defined and solved. Once the final stage (stage 5) is reached, a backward procedure begins from stage 5 and proceeds through stages 4, 3, 2, and 1 in that order. For each of these stages, a parallel machine problem is defined and solved. After reaching the first stage, a forward procedure starts again from stage 1 and continues to stage 5, with a parallel machine problem defined and solved at each stage. The backward and forward procedures are repeated until a stopping condition is met. These solutions are non-conflicting, and their combination provides a feasible solution for the problem under study. All parallel machine scheduling problems are solved using the ADAU heuristic. If the starting stage is 1, 2, 3, or 5, four other feasible solutions are generated, and the best one is retained as the improved solution.

Remark 15: By exploring the symmetric problem the algorithm can effectively explore a wider search space, enabling the identification of better solutions. Through the exploitation of problem symmetry, the algorithm can significantly reduce redundancy and eliminate duplicates within the search space. This optimization facilitates faster convergence and enhances the quality of the obtained solutions. In summary, incorporating the symmetric problem within the two-phase heuristic enhances the overall effectiveness and efficiency of the algorithm, enabling it to discover optimal or near-optimal solutions to the HFSULT problem more effectively.

Input instances

The test problems utilized in this study follow a similar generation approach as those in Vandevelde et al. (2005). More specifically, $K\in \left\{2,4,6,8,10\right\}$ and $n\in \left\{10,20,40,80\right\}$.

Table 3 presents the stage-machine configurations utilized in this study. It provides a comprehensive overview and details of the specific stage-machine combinations employed for the experimental analysis.

A noteworthy observation regarding the testbed is the presence of distinct patterns in the instances, stemming from their random distribution. These patterns can be characterized as follows:

• All-equal patterns: as 2-2-2-2-2-2-2-2-2-2.

• Increasing patterns: as 1-1-2-2-3-3-4-4-5-5.

• Top patterns: as 2-2-3-3-4-4-3-3-2-2.

• Valley patterns: as 5-4-3-2-1-1-2-3-4-5.

• Random patterns: as 1-3-2-4-1-3-2-4-1-4.

The pattern given in the stage-machine configurations expresses the number of machines assigned to each stage. For example, the pattern 1-3 signifies that we have two stages where the first one contains one machine while the second one has three machines.

p_k,j are generated randomly and uniformly in $\left[20,40\right]$.

The following distributions are employed to generate the unloading, lag, and transportation times:

• Type 1: un_k,j, lg_k,j, and tr_k,j are uniformly generated from $\left[1,10\right]$.

• Type 2: un_k,j, lg_k,j, and tr_k,j are uniformly generated from $\left[20,40\right]$.

• Type 3: un_k,j, lg_k,j, and tr_k,j are uniformly generated from $\left[20,60\right]$.

When considering unloading, lag, and transportation times, it is essential to consider the relative magnitude of their respective times in relation to the processing times. As an example, in the first type (Type 1), the unloading, lag, and transportation times are typically relatively minor compared to the processing time.

A total of 1,800 instances were generated by creating five instances for each combination of stage-machine configuration (S_k; m_k), number of tasks n, transportation time tr_k,j , processing time p_k,j, lag time lg_k,j, and unloading time un_k,j. The testbed encompasses a broad spectrum of problem sizes, machine distribution patterns, processing times, lag times, transportation times, and unloading times, rendering it highly diverse and well-suited for impartial evaluation of the proposed procedures.

The performance of the two-phase heuristic