Adaptive resilient containment control using reinforcement learning for nonlinear stochastic multi-agent systems under sensor faults

Guanzong Mo; Yixin Lyu

doi:10.7717/peerj-cs.2126

Introduction

Multi-agent systems (MASs) have garnered considerable attention due to their ability to organize vast and intricate systems into smaller, intercommunicating, easily coordinated, and manageable subsystems. Currently, MASs find widespread applications in various domains such as aircraft formation, sensor networks, data fusion, parallel computing and cooperative control of multiple robots (Antonio et al., 2021; Tang et al., 2016; Liu et al., 2020; Zhao et al., 2023; De Sá & Neto, 2023). As a class of classical control problems from cooperative control, the containment control approach guarantees the convergence of all followers to a dynamic convex hull formed by multiple leaders. Numerous findings on containment control have been documented in the last decade (Li et al., 2022; Li, Pan & Ma, 2022; Li et al., 2023; Liang et al., 2021).

It is noteworthy that optimal control, formally introduced by Bellman (1957) and Pontryagin et al. (1962) half a century ago, has become the foundation and prevailing design paradigm of modern control systems. The key to solving the optimal control problem lies in solving the Hamilton–Jacobi–Bellman (HJB) equation. Theoretically, solving optimal control based on the HJB equation is nearly impossible using analytical methods due to its strong nonlinearity (Beard, Saridis & Wen, 1996). Fortunately, Werbos (Werbos, 1992) introduced the approximate technique referred to as Adaptive Dynamic Programming (ADP) or Reinforcement Learning (RL), providing an effective method for solving the HJB equation. To date, this technique has witnessed significant development and achievements, as seen in Wen, Xu & Li (2023), Chen, Dai & Dong (2022), Gao & Jiang (2018), Zargarzadeh, Dierks & Jagannathan (2012), Zargarzadeh, Dierks & Jagannathan (2012), Li, Sun & Tong (2019), Song & Dyke (2013), Hu & Zhu (2015), Rajagopal, Balakrishnan & Busemeyer (2017), Wen, Xu & Li (2023). In Wen, Xu & Li (2023), RL was combined with backstepping to design actual controls and virtual controls, optimizing the overall control of high-order systems. In Chen, Dai & Dong (2022), this technique was applied to underactuated surface vessels, ensuring optimal tracking performance for ship control. Gao & Jiang (2018) addressed the computation problem of adaptive nearly optimal trackers without prior knowledge of system dynamics. In Zargarzadeh, Dierks & Jagannathan (2012), investigated neural network-based adaptive optimal control for nonlinear continuous-time systems with known dynamics in strict-feedback form. Zargarzadeh, Dierks & Jagannathan (2015) extended their work to address nonlinear continuous-time systems characterized by uncertain dynamics in strict feedback form. They accomplished this by adapting the standard backstepping technique, as outlined in Zargarzadeh, Dierks & Jagannathan (2015), transforming the optimal tracking problem into an equivalent optimal control problem and generating adaptive control inputs. Li, Sun & Tong (2019) presented a data-driven robust approximate optimal tracking scheme for a subset of strict-feedback single-input, single-output nonlinear systems characterized by the presence of unknown non-affine nonlinear faults and unmeasured states. In addition to deterministic nonlinear systems, various optimal control methods have been explored for stochastic systems in the past decade. The numerical techniques, proposed by Song & Dyke (2013), aimed to reduce system responses under extreme loading conditions with stochastic excitations. Hu & Zhu (2015) introduced a stochastic optimization-based bounded control strategy for multi-degree-of-freedom strongly nonlinear systems. In Rajagopal, Balakrishnan & Busemeyer (2017), an offline ADP method based on neural networks was developed to address finite-time stochastic optimal control problems. Specifically, in Wen, Xu & Li (2023) applied the RL strategy with the actor-critic architecture to stochastic nonlinear strict-feedback systems. However, for more complex nonlinear stochastic MASs, the above methods have not been fully studied. The challenges lie in the stability analysis process where the quadratic form of the Lyapunov function is no longer applicable, necessitating a reproof of system stability. Furthermore, in contrast to the single-agent stochastic strict-feedback system discussed in Wen, Xu & Li (2023a), we consider complex multi-agent systems. Many practical multi-agent systems, especially in areas like intelligent transportation and smart grids, tackle complex large-scale problems that surpass the capabilities of individual nonlinear systems. Therefore, research on nonlinear multi-agent systems is more meaningful.

Furthermore, in real-world scenarios, MASs comprise numerous actuators and sensors. Faults of some actuators or sensors can lead to the deviation from global control objectives. Therefore, investigating fault-tolerant control for MASs can enhance their safety and reliability. For instance, Ding et al. (2018) applied a region-based segmentation analysis to overcome caused by multiple sensor faults in strict-feedback systems. Wang et al. (2018) introduced a fault model to achieve fault-tolerant consensus for a multi-vehicle wireless network system with different actuator faults. Cao et al. (2021) fully considered consensus problems in MASs with sensor faults, utilizing neural networks not only for identifying unknown nonlinearities but also for designing adaptive compensatory controllers. Although there have been studies related to sensor faults, the conclusions from the above research cannot be directly applied to randomly occurring systems with statistical characteristics.

Inspired by the discussions above, This paper presents an enhanced backstepping control method tailored for a class of nonlinear stochastic strict-feedback MASs experiencing sensor faults. The primary contributions are summarized as follows:

(1) In this article, the optimal backstepping (OB) control method is extended to the nonlinear stochastic MASs with multiple leaders, which is more general than the consensus control results of MASs and can solve the optimal containment control problem.

(2) Suppressing sensor faults is important to enhance the system’s safety and reliability. To tackle the challenge posed by sensor faults in stochastic MASs, consideration is given to an adaptive neural network (NN) compensation control method. This method is designed to alleviate the adverse effects of sensor faults on the MASs.

(3) The proposed adaptive control scheme successfully solves the problem of contained control with sensor faults, and the designed RL optimization method can optimize the control of unknown or uncertain stochastic dynamic systems.

Preliminariers and Problem Formulation

Graph theory

In the context of a group of N + M agents, the associated directed graph 𝔊 can be described by $G = (V, E, Λ)$ , where 𝔙 = 1, 2, …, N, …, N + M constitutes a set of nodes, and $E = (j, i) \in V \times V$ represents a set of edges. The adjacency matrix is $Λ = [a_{i j}] \in R^{(N + M) \times (N + M)}$ , $(j, i) \in E$ implies that nodes j and i can share information with one another. a_ij is defined as (1) $a_{i j} = \{\begin{matrix} 1, if (i, j) \in E \\ 0, if (i, j) ⁄ \in E \end{matrix}$

where the set of neighbors for a node i is denoted by $N_{i} = j \in V : (j, i) \in E$ . The Laplacian matrix $L = {[l_{i j}]}_{(M + N) \times (M + N)} = D - Λ \in R^{(N + M) \times (N + M)}$ is defined as (2) $l_{i j} = \{\begin{matrix} - a_{i j}, if i \neq j \\ \sum_{j \in N_{i}} a_{i j}, if i = j \end{matrix}$

where 𝔇 = {diagd₁, …, d_N} represents the degree matrix and d_i = ∑_{j∈𝔑_i}a_ij. In this paper, the focus is on N + M agents, comprising N followers and M leaders, within a directed graph topology. It is assumed that each follower has at least one neighbor. Consequently, one can observe (3) $L = [\begin{matrix} L_{1} & L_{2} \\ 0_{M \times N} & 0_{M \times M} \end{matrix}]$

where 𝕃₁ ∈ ℝ^N×N, 𝕃₂ ∈ ℝ^N×M.

Assumption 1: Each follower is connected to a minimum of one leader through a directed path, while leaders themselves lack neighboring nodes.

Lemma 1: According to Assumption 1, the matrix 𝕃₁ issymmetric and positive definite, each element of $- L_{1}^{- 1} L_{2}$ is nonnegative scalar, and all row sums of $- L_{1}^{- 1} L_{2}$ equal to 1.

Assumption 2: (Yoo, 2013) The multiple leaders’ outputs y_ld, l ∈ (N + 1, …, N + M) and their derivatives ${\dot{y}}_{l d}, {\ddot{y}}_{l d}, \dots, y_{l d}^{(n)}$ are bounded.

Lemma 2: (Tong et al., 2011a) Existing continuously differentiable function V(t, x) ∈ ℝ⁺, it meets the conditions (4) $ν_{1} (∥ x ∥) \leq V (t, x) \leq ν_{2} (∥ x ∥)$ (5) $L V (t, x) \leq - a V (t, x) + c$

where a > 0, c > 0 are constants, ν1(⋅ ), ν2(⋅ ) are K ∞ functions, the differential Eq. (9) has a singular, robust solution, and subsequent inequality is satisfied: (6) $E [V (t, x)] \leq e^{- a t} V (0, x (0)) + \frac{c}{a} .$

Inequality Eq. (6) signifies that the solution x(t) showcases SGUUB when considering expectations.

Lemma 3: (Wang, Wang & Peng, 2015) Defining s_∗1 = [s_11,s₂₁, …, s_N1]^T, y_i = [y₁, y₂, …, y_N]^Twe have s_∗1 = 𝔏₁y_i + 𝔏₂y_ld. Then the following inequality holds: (7) $∥ y_{i} + L_{1}^{- 1} L_{2} y_{l d} ∥ \leq ∥ s_{* 1} ∥ / ∥ \bar{η} (L_{1}) ∥$

where $∥\bar{η} (L_{1})∥$ is the minimum singular value of 𝕃₁.

Lemma 4 (Young’s Inequality (Tong et al., 2011)): For all x, y ∈ ℝ+, the subsequent inequality is held: (8) $x y \leq \frac{1}{p} x^{p} + \frac{1}{q} y^{q}$

where p > 0, q < 0, 1/p + 1/q = 1.

Stochastic systems statement

Consider a group of nonlinear stochastic MASs described as follows: (9) $\{\begin{matrix} d x_{i m} = [x_{i m + 1} + f_{i m} ({\bar{x}}_{i m})] d t + ψ_{i m} ({\bar{x}}_{i m}) d w \\ d x_{i n} = [u_{i} + f_{i n} ({\bar{x}}_{i n})] d t + ψ_{i n} ({\bar{x}}_{i n}) d w \\ y_{i} = h (x_{i 1}) \end{matrix}$

where ${\bar{x}}_{i m} = {[x_{i 1, \dots,} x_{i m}]}^{T} \in R^{m} ($ m = 1 $, \dots, n - 1)$ represents the state vector. u_i ∈ ℝ denotes the control input, y_i ∈ ℝ is the system output. h(x_i1) = k_i(t)x_i1 + ρ_i(t) ,where k_i(t) and ρ_i(t) denote the parameters of sensor faults. f_im(⋅) ∈ ℝ^m and ψ_im(⋅) ∈ ℝ^m depict uncertain smooth functions. w ∈ ℝ^r denotes the independent r-dimensional standard Brownian motion.

Neural network approximation

It has been shown that a neural network (NN) can approximate any continuous function $F (x) : R^{n} \to R^{m}$ to a desired accuracy within a specified compact set Ω_x ⊂ ℝⁿ. The neural network approximation function can be represented as follows: (10) $F_{NN} (x) = W^{T} S (x)$

where W ∈ ℝ^q×m is the weight matrix, q is the quantity of neurons, $S (x) = {[s_{1} (x), \dots, s_{q} (x)]}^{T} \in R^{q}$ is the Gaussian basis function vector with $s_{i} (x) = exp (- {(x - ν_{i})}^{T}$ $(x - ν_{i}) / φ_{i}^{2}) \in R, ν_{i} = {[ν_{i 1}, \dots, ν_{in}]}^{T} \in R^{n}$ represents the centers of receptive fields, and φ_i is the width of the Gaussian function.

To fulfill Eq. (10), there must exist an ideal weight W^∗, and the function $F (x)$ can be rewritten as (11) $F (x) = W^{* T} S (x) + ɛ (x)$

where $ɛ (x) \in R^{m}$ is the approximation error required to meet $| | ɛ (x) | | \leq δ$ with δ being a positive constant.

The ideal weight matrix W^∗ can be shown as (12) $W^{*} = {arg min}_{W \in R^{p \times m}} \{sup_{x \in Ω_{x}} ∥ F (x) - W S (x) ∥\} .$

The Eq. (12) implies that the NN approximation error in Eq. (11) represents the minimum achievable deviation between $F (x)$ and $W^{T} S (x)$ .

Sensor faults

Within sensor fault model (Bounemeur, Chemachema & Essounbouli, 2018), the unspecified parameters adhere to $0 < {\bar{k}}_{i min} \leq k_{i} (t) \leq 1$ and $- {\bar{ρ}}_{i} \leq ρ_{i} (t) \leq {\bar{ρ}}_{i}$ , where ${\bar{k}}_{i min}$ > 0 represents the minimum sensor effectiveness, $- {\bar{ρ}}_{i}$ , ${\bar{ρ}}_{i}$ are the lower bound and the upper bound respectively. The parameters of the sensor fault models can be summarized as below:

If $k_{i} (t) = 1$ and ρ_i(t) is a constant, the sensor exhibits bias fault.
If $k_{i} (t) = 1$ , |ρ_i(t)| = ιt, 0 < ι ≪ 1, the sensor experiences a drift fault.
If $k_{i} (t) = 1$ , $| ρ_{i} (t) | < {\bar{ρ}}_{i}, ρ_{i} (t) \to 0$ , this signifies that the sensor has incurred a loss of accuracy.
If $0 < {\bar{k}}_{i m i n} \leq k_{i} (t) \leq 1$ , $ρ_{i} (t) = 0$ , this suggests that the sensor has undergone a loss of effectiveness.

Denote f_si = (k_i(t) − 1)x_i1 + ρ_i(t). Then y_i can be reformulated as y_i = x_i1 + f_si. The derivative of y_i can be rewritten as ${\dot{y}}_{i} = {\dot{x}}_{i 1} + f_{p s i}$ , where $f_{p s i} = {\dot{f}}_{s i}$ .

Operator 𝔏

For function V(t, x), calculate its differential operator 𝔏 as Mao, (2006) (13) $L V = \frac{\partial V}{\partial x^{T}} (f (x) + g (x) u (x)) + \frac{1}{2} T r \{ψ^{T} \frac{\partial^{2} v}{\partial x \partial x^{T}} ψ\}$

where Tr signifies the matrix trace.

Distributed Adaptive Optimal Containment Control

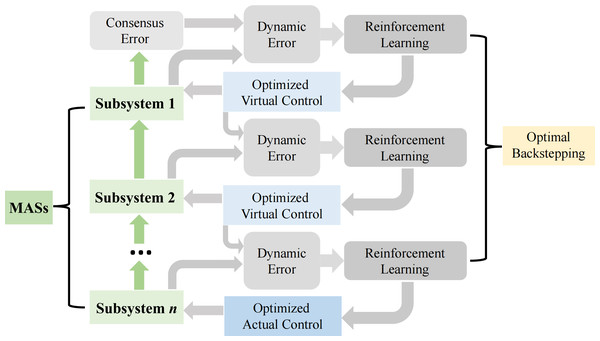
The backstepping technique is employed for controller design. Before we begin, to clearly demonstrate our ideas and process, let’s provide a brief overview using Fig. 1.

Figure 1: OB design in the i th agent, i = 1, …,n.

Download full-size image

DOI: 10.7717/peerjcs.2126/fig-1

Figure 1 illustrates the application process of RL in the design of optimized backstepping control. This process employs a Critic-Actor architecture to address the leader-following consensus control issue for nonlinear MASs. Within this method, the actor network is responsible for generating control actions, while the critic network evaluates the performance of the current control strategy. By iterating these two networks, the RL algorithm can learn an optimized control strategy that optimizes the control performance of the entire system.

Specifically, the optimal control problem is transformed into solving the HJB equation. However, due to the nonlinearity of the HJB equation, solving it directly is very challenging. To overcome this difficulty, a neural network-based RL method is proposed. This method derives the RL update rules from the negative gradient of a simple positive function, thereby avoiding the direct handling of multiple nonlinear terms in the HJB equation. This not only simplifies the algorithm but also relaxes the requirements for known system dynamics and persistent excitation.

During the RL learning process, the critic network first evaluates the performance of the current control strategy and provides it as feedback to the actor network. The actor network then adjusts its control actions based on this feedback, with the expectation of improving the system’s performance. In this way, the RL algorithm can continuously learn and optimize the control strategy through iteration until the optimal solution is found.

To start with, the i-th subsystem’s distributed containment error is defined as (14) $\begin{matrix} s_{i 1} = \sum_{j = 1}^{N} a_{i j} (y_{i} - y_{j}) + \sum_{ℓ = N + 1}^{N + M} a_{i ℓ} (y_{i} - y_{l d}) \\ s_{i m} = x_{i m} - α_{i m - 1} (m = 2, \dots, n) \end{matrix}$

where α_im−1 denotes the virtual controller. The OB control method is designed as follows.

Step 1: With Eq. (14) and Itô formula, the containment error can be calculated as follows: (15) $\begin{matrix} d s_{i 1} = [d_{i} (x_{i 2} + f_{p s i} + f_{i 1} (x_{i 1})) - \sum_{j = 1}^{N} a_{i j} ({\dot{x}}_{j 1} + {\dot{f}}_{s j}) - \sum_{ℓ = N + 1}^{N + M} a_{i l} {\dot{y}}_{l d}] d t + [d_{i} ψ_{i 1} (x_{i 1}) - \sum_{j = 1}^{N} ψ_{j 1} (x_{j 1})] d w = [d_{i} x_{i 2} - \sum_{j = 1}^{N} a_{i j} x_{j 2} + F_{i 1}] d t + Ψ_{i 1} d w \end{matrix}$

where: $\begin{matrix} F_{i 1} = d_{i} (f_{p s i} + f_{i 1} (x_{i 1})) - \sum_{j = 1}^{N} a_{i j} (f_{p s j} + f_{j 1} (x_{j 1})) - \sum_{ℓ = N + 1}^{N + M} a_{i ℓ} {\dot{y}}_{ℓ d} \\ Ψ_{i 1} = d_{i} ψ_{i 1} (x_{i 1}) - \sum_{j = 1}^{N} ψ_{j 1} (x_{j 1}) \end{matrix}$

Representing virtual control by α_i1, the performance index function is formulated as (16) $J_{i 1} (s_{i 1}) = \int_{t}^{\infty} c_{i 1} (s_{i 1} (s), α_{i 1} (s_{i 1} (s))) d s$

where $c_{i 1} (s_{i 1}, α_{i 1}) = s_{i 1}^{2} (t) + α_{i 1}^{2}$ is the cost function.

Replace $α_{i 1}^{}$ with $α_{i 1}^{*}$ (optimal virtual control) in Eq. (16), the function is obtained as (17) $J_{i 1}^{*} (s_{i 1}) = \int_{t}^{\infty} c_{i 1} (s_{i 1} (s), α_{i 1}^{*} (s_{i 1} (s))) d s$

According to the previous introduction, the function is given as follows: (18) $E [J_{i 1}^{*} (s_{i 1})] = min_{α_{i 1} \in Ψ (Ω)} [E [\int_{t}^{\infty} c_{i 1} (s_{i 1}, α_{i 1}) d s]$

where Ω is a predefined compact set containing origin. By viewing x_i2 as optimal control $α_{i 1}^{*}$ , the HJB equation linked with Eqs. (15) and (17) can be rewritten (19) $H_{i 1} (s_{i 1}, α_{i 1}^{*}, \frac{d J_{i 1}^{*} (s_{i 1})}{d s_{i 1}}) = s_{i 1}^{2} + α_{i 1}^{2} + \frac{d J_{i 1}^{*}}{d s_{i 1}} (d_{i} α_{i 1}^{*} + F_{i 1} - \sum_{j = 1}^{N} a_{i j} x_{j 2}) + \frac{1}{2} \frac{d^{2} f_{i 1}^{*}}{d s_{i 1}^{2}} Ψ_{i 1}^{T} Ψ_{i 1} = 0$

The optimal virtual controller $α_{i 1}^{*}$ can be derived by solving $\partial H_{i 1} / \partial α_{i 1}^{*} = 0$ as (20) $α_{i 1}^{*} = - \frac{1}{2} \frac{d J_{i 1}^{*} (s_{i 1})}{d s_{i 1}}$

To attain the tracking control, the term $\frac{d J_{i 1}^{*} (s_{i 1})}{d s_{i 1}}$ is partitioned as (21) $\frac{d J_{i 1}^{*} (s_{i 1})}{d s_{i 1}} = \frac{2 γ_{i 1}}{d_{i}} s_{i 1} + \frac{1}{2 β_{i 1} d_{i}} s_{i 1}^{3} + \frac{2}{d_{i}} h_{i 1} (x_{i 1}, s_{i 1}) + \frac{1}{d_{i}} J_{i 1}^{0} (x_{i 1}, s_{i 1})$

where γ_i1 > 0, β_i1 > 0 are two designed constants, h_i1(x_i1, s_i1) = F_i1 + s_i1||Ψ_i1||⁴ and $J_{i 1}^{0} (x_{i 1}, s_{i 1}) = - \frac{2 γ_{i 1}}{d_{i}} s_{i 1} - \frac{1}{2 β_{i 1} d_{i}} s_{i 1}^{3} - \frac{2}{d_{i}} h_{i 1} (x_{i 1}, s_{i 1}) + \frac{d J_{i 1}^{*} (s_{i 1})}{d s_{i 1}} \in R$ . Substituting Eqs. (21) into (20) yields (22) $α_{i 1}^{*} = \frac{1}{d_{i}} [- γ_{i 1} s_{i 1} - \frac{1}{4 β_{i 1}} s_{i 1}^{3} - h_{i 1} (x_{i 1}, s_{i 1}) - \frac{1}{2} J_{i 1}^{0} (x_{i 1}, s_{i 1})]$

Since two functions h_i1(x_i1, s_i1) and $J_{i 1}^{0} (x_{i 1}, s_{i 1})$ are uncertain yet continuous, they can be approximated by NN as (23) $h_{i 1} (x_{i 1}, s_{i 1}) = W_{h i 1}^{* T} S_{h i 1} (x_{i 1}, s_{i 1}) + ɛ_{h i 1} (x_{i 1}, s_{i 1})$ (24) $J_{i 1}^{0} (x_{i 1}, s_{i 1}) = W_{J i 1}^{T} S_{J i 1} (x_{i 1}, s_{i 1}) + ɛ_{J i 1} (x_{i 1}, s_{i 1})$

where $W_{h i 1}^{* T}$ ∈ℝ^p₁ and $W_{J i 1}^{* T}$ ∈ℝ^q₁ are the ideal NN weights, S_hi1(x_i1, s_i1) ∈ℝ^p₁ and S_Ji1(x_i1, s_i1) ∈ℝ^q₁ are basis function vectors, and ɛ_hi1(x_i1, s_i1) ∈ ℝ, ɛ_Ji1(x_i1, s_i1) ∈ ℝ denote approximation errors. Substitute Eqs. (23) and (24) into Eqs. (21) and (22), separately (25) $\frac{d f_{i 1}^{*} (s_{i 1})}{d s_{i 1}} = \frac{1}{d_{i}} [2 γ_{i 1} s_{i 1} (t) + \frac{1}{2 β_{i 1}} s_{i 1}^{3} (t) + 2 W_{h i 1}^{* T} S_{h i 1} (x_{i 1}, s_{i 1}) + W_{j i 1}^{* T} S_{j i 1} (x_{i 1}, s_{i 1}) + ɛ_{i 1}]$ (26) $α_{i 1}^{*} = \frac{1}{d_{i}} [- γ_{i 1} s_{i 1} (t) - \frac{1}{4 β_{i 1}} s_{i 1}^{3} (t) - W_{h i 1}^{* T} S_{h i 1} (x_{i 1}, s_{i 1}) - \frac{1}{2} W_{J i 1}^{* T} S_{J i 1} (x_{i 1}, s_{i 1}) - \frac{1}{2} ɛ_{i 1}]$

where ɛ_i1 = 2ɛ_hi1 + ɛ_Ji1. The optimal control Eq. (26) is unattainable due to the two ideal weights $W_{h i 1}^{* T}$ and $W_{J i 1}^{* T}$ are uncertain constant vectors.

To acquire an effective optimized virtual control, the implementation involves applying RL through the identifier-critic-actor architecture, utilizing the NNs. The uncertain function h_i1(x_i1, s_i1) of adaptive identifier is constructed in the following: (27) ${\hat{h}}_{i 1} (x_{i 1}, s_{i 1}) = {\hat{W}}_{h i 1}^{T} (t) S_{h i 1} (x_{i 1}, s_{i 1})$

where ${\hat{h}}_{i 1} (x_{i 1}, s_{i 1})$ is the identifier output, and ${\hat{W}}_{h i 1}^{T} (t) \in R^{p_{1}}$ is the NN weight. The weight experiences updates based on the following law: (28) ${\dot{\hat{W}}}_{h i 1} (t) = Γ_{i 1} (S_{h i 1} (x_{i 1}, s_{i 1}) s_{i 1}^{3} (t) - σ_{i 1} {\hat{W}}_{h i 1} (t))$

where Γ_i1 is a positive-definite constant matrix, σ_i1 > 0 is constant. Designing the critic to evaluate the control performance aligns with Eq. (25) as (29) $\frac{d {\hat{J}}_{i 1}^{*} (s_{i 1})}{d s_{i 1}} = \frac{1}{d_{i}} [2 γ_{i 1} s_{i 1} (t) + \frac{1}{2 β_{i 1}} s_{i 1}^{3} (t) + 2 {\hat{W}}_{h i 1}^{T} (t) S_{h i 1} (x_{i 1}, s_{i 1}) + {\hat{W}}_{c i 1}^{T} (t) S_{J i 1} (x_{i 1}, s_{i 1})]$

where $\frac{d {\hat{J}}_{i 1}^{*} (s_{i 1})}{d s_{i 1}} \in R^{}$ is the estimation of $\frac{d J_{i 1}^{*} (s_{i 1})}{d s_{i 1}}$ , ${\hat{W}}_{c i 1}^{T} \in R^{q_{1}}$ is the NN weight of critic. The weight experiences updates based on the following law: (30) ${\dot{\hat{W}}}_{c i 1} (t) = - γ_{c i 1} S_{J i 1} (x_{i 1}, s_{i 1}) S_{J i 1}^{T} (x_{i 1}, s_{i 1}) {\hat{W}}_{c i 1} (t)$

where γ_ci1 > 0 is constant. The formulation of the actor, responsible for executing the control action, corresponds to Eq. (25) as articulated below: (31) ${\hat{α}}_{i 1}^{*} = \frac{1}{d_{i}} [- γ_{i 1} s_{i 1} (t) - \frac{1}{4 β_{i 1}} s_{i 1}^{3} (t) - {\hat{W}}_{h i 1}^{T} (t) S_{h i 1} (x_{i 1}, s_{i 1}) - \frac{1}{2} {\hat{W}}_{a i 1}^{T} (t) S_{J i 1} (x_{i 1}, s_{i 1})]$

where ${\hat{α}}_{i 1}^{*}$ is the optimized virtual control, ${\hat{W}}_{a i 1}^{T} (t) \in R^{q_{1}}$ is the NN weight of actor. The weight experiences updates based on the following law: (32) ${\hat{W}}_{a i 1} (t) = - S_{J i 1} (x_{i 1}, s_{i 1}) S_{J i 1}^{T} (x_{i 1}, s_{i 1}) \times (γ_{a i 1} ({\hat{W}}_{a i 1} (t) - {\hat{W}}_{c i 1} (t)) + γ_{c i 1} {\hat{W}}_{c i 1} (t))$

where γ_ai1 > 0 is constant. These determined parameters, β_i1, γ_i1, γ_ci1, and γ_ai1, are selected to satisfy (33) $β_{i 1} > 0, γ_{i 1} > 3, γ_{a i 1} > \frac{β_{i 1}}{2}, γ_{a i 1} > γ_{c i 1} > \frac{γ_{a i 1}}{2}$

According to Eqs. (19), (29) and (31), the HJB equation is calculated as (34) $\begin{matrix} H_{i 1} (s_{i 1}, {\hat{α}}_{i 1}^{*}, \frac{d {\hat{J}}_{i 1}^{*}}{d s_{i 1}}) = s_{i 1}^{2} (t) + \frac{1}{d_{i}^{2}} (- γ_{i 1} s_{i 1} (t) - \frac{1}{4 β_{i 1}} s_{i 1}^{3} (t) - {\hat{W}}_{h i 1}^{T} (t) S_{h i 1} (x_{i 1}, s_{i 1}) \\ - {\frac{1}{2} {\hat{W}}_{a i 1}^{T} (t) S_{J i 1} (x_{i 1}, s_{i 1}))}^{2} + \frac{1}{d_{i}^{2}} [2 γ_{i 1} s_{i 1} (t) + \frac{1}{2 β_{i 1}} s_{i 1}^{3} (t) + 2 {\hat{W}}_{h i 1}^{T} (t) S_{h i 1} (x_{i 1}, s_{i 1}) \\ + {\hat{W}}_{c i 1}^{T} (t) S_{J i 1} (x_{i 1}, s_{i 1})] \times (- γ_{i 1} s_{i 1} (t) - \frac{1}{4 β_{i 1}} s_{i 1}^{3} (t) - {\hat{W}}_{h i 1}^{T} (t) S_{h i 1} (x_{i 1}, s_{i 1}) - \frac{1}{2} {\hat{W}}_{a i l}^{T} (t) \times \\ S_{J i l} (x_{i 1}, s_{i 1}) + f_{i 1} (x_{i 1}) + ψ_{i 1}^{T} (x_{i 1}) \frac{d w}{d t} - {\dot{y}}_{d}) + \frac{1}{2} \frac{d^{2} J_{i 1}^{*}}{d s_{i 1}^{2}} ∥ ψ_{i 1} (x_{i 1}) ∥^{2} \end{matrix}$

Building upon the preceding analysis, the optimized control ${\hat{α}}_{i 1}^{*}$ is foreseen as the sole solution to achieve $H_{i 1} (s_{i 1}, {\hat{a}}_{i 1}^{*}, (d {\hat{J}}_{i 1}^{*}) / (d s_{i 1})) \to 0 .$ Assuming the existence of $H_{i 1} (s_{i 1}, {\hat{a}}_{i 1}^{*}, \frac{d {\hat{J}}_{i 1}^{*}}{d s_{i 1}}) = 0$ and its unique solution, it is equivalent to the following equation: (35) $\frac{\partial H_{i 1} (s_{i 1}, {\hat{a}}_{i 1}^{*}, \frac{d {\hat{J}}_{i 1}^{*}}{d s_{i 1}})}{\partial {\hat{W}}_{a i 1}} = \frac{1}{2} S_{J i 1} (x_{i 1}, s_{i 1}) S_{J i 1}^{T} (x_{i 1}, s_{i 1}) \times ({\hat{W}}_{a i 1} (t) - {\hat{W}}_{c i 1} (t)) = 0$

Define the positive function P_i1(t) as (36) $P_{i 1} (t) = {({\hat{W}}_{a i 1} (t) - {\hat{W}}_{c i 1} (t))}^{T} ({\hat{W}}_{a i 1} (t) - {\hat{W}}_{c i 1} (t))$

It is evident that Eq. (35) is the equivalent to $P_{i 1} (t) = 0$ . Given the fact that $(\partial P_{i 1} (t)) / (\partial {\hat{W}}_{a i 1} (t)) = \begin{matrix} - (\partial P_{i 1} (t)) / (\partial {\hat{W}}_{c i 1} (t)) = 2 ({\hat{W}}_{a i 1} (t) - {\hat{W}}_{c i 1} (t)) \end{matrix}$ , the time derivative of $P_{i 1} (t)$ along with Eqs. (29) and (31) is (37) $\begin{matrix} \frac{d P_{i 1}}{d t} = \frac{\partial P_{i 1}}{\partial {\hat{W}}_{a i 1}^{T}} {\dot{\hat{W}}}_{a i 1} + \frac{\partial P_{i 1}}{\partial {\hat{W}}_{c i 1}^{T}} {\dot{\hat{W}}}_{c i 1} = - \frac{\partial P_{i 1}}{\partial {\hat{W}}_{a i 1}^{T}} S_{J i 1} S_{J i 1}^{T} (γ_{a i 1} ({\hat{W}}_{a i 1} - {\hat{W}}_{c i 1}) + γ_{c i 1} {\hat{W}}_{c i 1}) \\ = - γ_{a i 1} \frac{\partial P_{i 1}}{\partial {\hat{W}}_{a i 1}^{T}} S_{J i 1} S_{J i 1}^{T} ({\hat{W}}_{a i 1} - {\hat{W}}_{c i 1}) = - \frac{γ_{a i 1}}{2} \frac{\partial P_{i 1}}{\partial {\hat{W}}_{a i 1}^{T}} S_{J i 1} S_{J i 1}^{T} \frac{\partial P_{i 1}}{\partial {\hat{W}}_{a i 1}} \leq 0 \end{matrix}$

The inequality Eq. (37) suggests that the updating laws Eqs. (30) and (32) can ensure eventually. The key benefits of the RL design approach include: (1) comparatively, the optimized control algorithm demonstrates a substantially simpler structure than existing optimal methods, such as Vamvoudakis & Lewis (2010), Liu et al. (2013), Wen, Ge & Tu (2018). (2) this can alleviate the necessity for persistent excitation, a requirement prevalent in many optimal control methods. Replace x_i2 with $α_{i 1}^{*} + s_{i 2}$ in the dynamic Eq. (14) to have (38) $d s_{i 1} = [d_{i} ({\hat{α}}_{i 1}^{*} + s_{i 2}) + F_{i 1} - \sum_{j = 1}^{N} a_{i j} x_{j 2}] d t + Ψ_{i 1} d w$

The Lyapunov function candidate is designed as (39) $L_{i 1} = \frac{1}{4} s_{i 1}^{4} + \frac{1}{2} W_{h i 1}^{T} Γ_{i 1}^{- 1} W_{h i 1} + \frac{1}{2} W_{c i 1}^{T} W_{c i 1} + \frac{1}{2} W_{a i 1} W_{a i 1}$

where ${\tilde{W}}_{h i 1} (t) = {\hat{W}}_{h i 1} (t) - W_{h i 1}^{*}$ , ${\tilde{W}}_{c i 1} (t) = {\hat{W}}_{c i 1} (t) - W_{J i 1}^{*}$ and ${\tilde{W}}_{a i 1} (t) = {\hat{W}}_{a i 1} (t) - W_{J i 1}^{*}$ represent corresponding errors. Compute the 𝔏 of L_i1, along with Eqs. (28), (30), (32) and (39) to yield (40) $L L_{i 1} = s_{i 1}^{3} [d_{i} ({\hat{α}}_{i 1}^{*} + s_{i 2}) + F_{i 1} - \sum_{j = 1}^{N} a_{i j} x_{j 2}] + \frac{3}{2} s_{i 1}^{2} ∥ Ψ_{i 1} ∥^{2} + {\tilde{W}}_{h i 1}^{T} (S_{h i 1} s_{i 1}^{3} - σ_{i 1} {\hat{W}}_{h i 1}) - γ_{c i} {\hat{W}}_{c i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{c i 1} - {\tilde{W}}_{a i 1}^{T} S_{J i 1} S_{J i 1}^{T} [γ_{a i 1} ({\hat{W}}_{a i 1} - {\hat{W}}_{c i 1}) + γ_{c i 1} {\hat{W}}_{c i 1}]$

Design optimal virtual controller (41) ${\hat{α}}_{i 1}^{*} = \frac{1}{d_{i}} (- γ_{i 1} s_{i 1} - \frac{1}{4 β_{i 1}} s_{i 1}^{3} - {\hat{W}}_{h i 1}^{T} S_{h i 1} - \frac{1}{2} {\hat{W}}_{a i 1}^{T} S_{J i 1})$

and then Eq. (31) becomes (42) $\begin{matrix} L L_{i 1} = s_{i 1}^{3} [γ_{i 1} s_{i 1} - \frac{1}{4 β_{i 1}} s_{i 1}^{3} - {\hat{W}}_{h i 1}^{T} S_{h i 1} - \frac{1}{2} {\hat{W}}_{a i 1} S_{J i 1} + s_{i 2} d_{i} + F_{i 1} - \sum_{j = 1}^{N} a_{i j} x_{j 2}] + \frac{3}{2} s_{i 1}^{2} ∥ Ψ_{i 1} | |^{2} \\ + {\tilde{W}}_{h i 1}^{T} (s_{h i 1} s_{i 1}^{3} - σ_{i 1} {\hat{W}}_{h i 1}) - γ_{c i 1} {\tilde{W}}_{c i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{c i 1} - γ_{a i 1} {\tilde{W}}_{a i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{a i 1} + (γ_{a i 1} - γ_{c i 1}) \\ {\tilde{W}}_{a i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{c i 1} \end{matrix}$

With Young’s inequality Eq. (8), there are following results: (43) $d_{i} s_{i 1}^{3} s_{i 2} \leq \frac{3}{4} d_{i} s_{i 1}^{4} + \frac{1}{4} d_{i} s_{i 2}^{4}$ (44) $- s_{i 1}^{3} \sum_{j = 1}^{N} a_{i j} x_{j 2} \leq \frac{3}{4} s_{i 1}^{4} + \frac{1}{4} {(\sum_{j = 1}^{N} a_{i j} x_{j 2})}^{4}$ (45) $\frac{3}{2} s_{i 1}^{2} | | Ψ_{i 1} | |^{2} \leq s_{i 1}^{4} | | Ψ_{i 1} | |^{4} + \frac{9}{16}$ (46) $- \frac{1}{2} s_{i 1}^{3} {\hat{W}}_{a i 1}^{T} S_{J i 1} \leq \frac{1}{4 β_{i 1}} s_{i 1}^{6} + \frac{β_{i 1}}{4} {\hat{W}}_{a i 1} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{a i 1}$

Substituting inequalities Eqs. (43), (44), (45) and (46) into (42) has (47) $L L_{i 1} \leq - (γ_{i 1} - \frac{3}{4} d_{i} - \frac{3}{4}) s_{i 1}^{4} - s_{i 1}^{3} ({\hat{W}}_{h i 1}^{T} S_{h i 1} - h_{i 1}) + W_{h i 1}^{T} (S_{h i 1} s_{i 1}^{3} - σ_{i 1} {\hat{W}}_{h i 1}) - γ_{c i 1} {\tilde{W}}_{c i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{c i 1} - γ_{a i 1} {\tilde{W}}_{a i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{a i 1} + (γ_{a i 1} - γ_{c i 1}) {\tilde{W}}_{a i 1}^{T} S_{J i 1}^{T} S_{J i 1}^{T} {\hat{W}}_{c i 1} + \frac{β_{i 1}}{4} {\hat{W}}_{a i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{a i 1} + \frac{1}{4} {(\sum_{j = 1}^{N} a_{i j} x_{j 2})}^{4} + \frac{9}{16} + \frac{1}{4} d_{i} s_{i 2}^{4}$

where h_i1 = F_i1 + s_i1||Ψ_i1||⁴. Substituting Eqs. (24) into (47) results in the following inequality: (48) $\begin{matrix} L L_{i 1} \leq - (γ_{i 1} - \frac{3}{4} d_{i} - \frac{3}{4}) s_{i 1}^{4} + s_{i 1}^{3} ɛ_{h i} - σ_{i 1} {\tilde{W}}_{h i 1}^{T} {\hat{W}}_{h i 1} - γ_{c i 1} {\tilde{W}}_{c i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{c i 1} - \\ γ_{a i 1} {\tilde{W}}_{a i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{a i 1} + \frac{β_{i 1}}{4} {\hat{W}}_{a i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{a i 1} + (γ_{a i 1} - γ_{c i 1}) {\tilde{W}}_{a i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{c i 1} + \\ \frac{1}{4} {(\sum_{i = 1}^{N} a_{j i} x_{j 2})}^{4} + \frac{1}{4} d_{i} s_{i 2}^{4} + \frac{9}{16} \end{matrix}$

From the facts ${\tilde{W}}_{h i 1} (t) = {\hat{W}}_{h i 1} (t) - W_{h i 1}^{*}$ , ${\tilde{W}}_{c i 1} (t) = {\hat{W}}_{c i 1} (t) - W_{J i 1}^{*}$ and ${\tilde{W}}_{a i 1} (t) = {\hat{W}}_{a i 1} (t) - W_{J i 1}^{*},$ the following equations can be derived: (49) ${\tilde{W}}_{h i 1}^{T} {\hat{W}}_{h i 1} = \frac{1}{2} {\tilde{W}}_{h 1 i}^{T} {\tilde{W}}_{h i 1} + \frac{1}{2} {\hat{W}}_{h i 1}^{T} {\hat{W}}_{h i 1} - \frac{1}{2} W_{h i 1}^{* T} W_{h i 1}^{*}$ (50) ${\tilde{W}}_{c i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{c i 1} = \frac{1}{2} {\tilde{W}}_{c i 1}^{T} S_{J i 1}^{T} {\tilde{W}}_{c i 1} + \frac{1}{2} {\hat{W}}_{c i 1}^{T} S_{J i 1}^{T} {\hat{W}}_{c i 1} - \frac{1}{2} W_{J i 1}^{* T} S_{J i 1} S_{J i 1}^{T} W_{J i 1}^{*}$ (51) ${\tilde{W}}_{a i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{a i 1} = \frac{1}{2} {\tilde{W}}_{a i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\tilde{W}}_{a i 1} + \frac{1}{2} {\hat{W}}_{a i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{a i 1} - \frac{1}{2} W_{J i 1}^{* T} S_{J i 1} S_{J i 1}^{T} W_{J i 1}^{*}$

With Young’s inequality Eqs. (8) and limitation of (33), subsequent inequalities obtained: (52) $s_{i 1}^{3} ɛ_{h i 1} \leq \frac{3}{4} s_{i 1}^{4} + \frac{1}{4} ɛ_{h i 1}^{4}$ (53) $(γ_{a i 1} - γ_{c i 1}) {\tilde{W}}_{a i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{c i 1} \leq \frac{γ_{a i 1} - γ_{c i 1}}{2} {\tilde{W}}_{a i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\tilde{W}}_{a i 1} + \frac{γ_{a i 1} - γ_{c i 1}}{2} {\hat{W}}_{c i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\hat{W}}_{c i 1}$

Substituting Eqs. (49)–(53) into (48) yields (54) $L L_{i 1} \leq - (γ_{i 1} - \frac{3}{2} - \frac{3}{4} d_{i}) s_{i 1}^{4} - \frac{σ_{i 1}}{2} {\tilde{W}}_{h i 1}^{T} {\tilde{W}}_{h i 1} - \frac{γ_{c i 1}}{2} {\tilde{W}}_{c i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\tilde{W}}_{c i 1} - \frac{γ_{c i 1}}{2} {\tilde{W}}_{a i 1}^{T} S_{J i 1} S_{J i 1}^{T} {\tilde{W}}_{a i 1} - (γ_{c i 1} - \frac{γ_{a i 1}}{2}) {({\hat{W}}_{c i 1}^{* T} S_{J i 1})}^{2} - (\frac{γ_{a i 1}}{2} - \frac{β_{i 1}}{4}) {({\hat{W}}_{a i 1}^{T} S_{J i 1})}^{2} + B_{i 1} + \frac{d_{i}}{4} s_{i 2}^{4} + \frac{1}{4} {(\sum_{j = 1}^{N} a_{i j} x_{j 2})}^{4}$

where $B_{i 1} (t) = (\frac{γ_{c i 1}}{2} + \frac{γ_{a i 1}}{2}) {(W_{J i 1}^{* T} S_{J i 1})}^{2} + \frac{σ_{i 1}}{2} | | W_{h i 1}^{*} | |^{2} + \frac{1}{4} ɛ_{h i 1}^{4} + \frac{9}{16}$ and |B_i1(t)| ≤ b_i1, because all its terms are bounded, and $\frac{1}{4} {(\sum_{j = 1}^{N} a_{i j} x_{j 2})}^{4}$ will be handled in step 2′s h_i2(x_i2, s_i2).

Step m (2 ≤ m ≤ n − 1):Define the containment error as $s_{i m} = x_{i m} - {\hat{α}}_{i m - 1}^{*}$ . According to Eq. (9), the error dynamic, along with Eq. (13), is (55) $d s_{i m} = [x_{i m + 1} + f_{i m} (x_{i m}) - L {\hat{α}}_{i m - 1}^{*}] d t + Ψ_{i m} d w$

where $Ψ_{i m} = ψ_{i m} ({\bar{x}}_{i m}) - \sum_{j = 1}^{m - 1} \frac{\partial {\hat{α}}_{i m - 1}^{*}}{o x_{i j}} ψ_{i j}$ . Let α_im denote virtual controller, the performance index function can be defined as (56) $J_{i m} (s_{i m}) = \int_{t}^{\infty} c_{i m} (s_{i m} (s), α_{i m} (s_{i m} (s))) d s$

where $c_{i m} (s_{i m}, α_{i m}) = s_{i m}^{2} (t) + α_{i m}^{2}$ is the cost function. Denoted $α_{i m}^{*}$ as the optimal virtual controller, substitute $α_{i m}^{*}$ into Eq. (56), the function can be rewritten as (57) $J_{i m}^{*} (s_{i m}) = \int_{t}^{\infty} c_{i m} (s_{i m} (s), α_{i m}^{*} (s_{i m} (s))) d s .$

Similar to Step 1, Eq. (57) manifests the subsequent characteristic (58) $E [J_{i m}^{*} (s_{i m})] = min_{α_{i m} \in Ψ (Ω)} E [J_{i m} (s_{i m})] .$

By viewing x_im+1(t) as optimal control $α_{i m}^{*}$ , the HJB equation relate to Eqs. (55) and (57) is (59) $H_{i m} (s_{i m}, α_{i m}^{*}, \frac{d J_{i m}^{*}}{d s_{i m}}) = s_{i m} + α_{i m}^{*} 2 + \frac{d J_{i m}^{*}}{d s_{i m}} \times (α_{i m}^{*} + f_{i m} + Ψ_{i m} \frac{d w}{d t} - L {\hat{α}}_{i m - 1}^{*}) + \frac{1}{2} \frac{d^{2} J_{i m}^{*}}{d s_{i m}^{2}} Ψ_{i m}^{T} Ψ_{i m} = 0$

where (dw)/(dt) represents the white noise. Besides, $α_{i m}^{*}$ is obtained by solving $(\partial H_{i m}) / (\partial α_{i m}^{*}) = 0$ as (60) $α_{i m}^{*} = - \frac{1}{2} \frac{d J_{i m}^{*}}{d s_{i m}}$

To attain the containment control, the term $(d J_{i m}^{*} (s_{i m})) / (d s_{i m})$ is segmented as (61) $\frac{d J_{i m}^{*}}{d s_{i m}} = 2 γ_{i m} s_{i m} + \frac{1}{2 β_{i m}} s_{i m}^{3} + 2 h_{i m} + J_{i m}^{0}$

where γ_im > 0 and β_im > 0 are two designed constants, $h_{i 2} = f_{i 2} + s_{i 2} | | Ψ_{i m} | |^{4} - \frac{1}{4} {(\sum_{j = 1}^{N} a_{i j} x_{j 2})}^{4} \in R$ , $h_{i m} = f_{i m} + s_{i m} | | Ψ_{i m}^{} | |^{4} \in R (m \geq 3)$ , and $J_{i m}^{0} = - 2 γ_{i m} s_{i m} - \frac{1}{2 β_{i m}} s_{i m}^{3} - 2 h_{i m} + \frac{d J_{i m}^{*}}{d s_{i m}} \in R$ . By substituting Eqs. (61) into (60), optimal control transforms into (62) $α_{i m}^{*} = - γ_{i m} s_{i m} - \frac{1}{4 β_{i m}} s_{i m}^{3} - h_{i m} - J_{i m}^{0}$

Since two functions $h_{i m} ({\bar{x}}_{i m}, s_{i m})$ and $J_{i m}^{0} ({\bar{x}}_{i m}, s_{i m})$ are uncertain yet continuous, they can be approximated by NN as (63) $h_{i m} ({\bar{x}}_{i m}, s_{i m}) = W_{h i m}^{* T} S_{h i m} ({\bar{x}}_{i m}, s_{i m}) + ɛ_{h i m} ({\bar{x}}_{i m}, s_{i m})$ (64) $J_{i m}^{0} ({\bar{x}}_{i m}, s_{i m}) = W_{J i m}^{T} S_{J i m} ({\bar{x}}_{i m}, z_{i m}) + ɛ_{J i m} ({\bar{x}}_{i m}, s_{i m})$

where $W_{h i m}^{* T} \in R^{p_{m}}$ and $W_{J i m}^{* T} \in R^{q_{m}}$ are the ideal NN weights, S_him(x_im, s_im) ∈ℝ^p_m, S_Jim(x_im, s_im) ∈ℝ^q_m are basis vectors, ɛ_him(x_im, s_im) ∈ ℝ, ɛ_Jim(x_im, s_im) ∈ ℝ are bounded approximation errors. Substituting Eqs. (63) and (64) into Eqs. (61) and (62) has (65) $\frac{d J_{i m}^{*} (s_{i m})}{d s_{i m}} = 2 γ_{i m} s_{i m} + \frac{1}{2 β_{i m}} s_{i m}^{3} + 2 W_{h i m}^{* T} S_{h i m} ({\bar{x}}_{i m}, s_{i m}) + W_{J i m}^{* T} S_{J i m} ({\bar{x}}_{i m}, s_{i m}) + ɛ_{i m}$ (66) $α_{i m}^{*} = - γ_{i m} s_{i m} - \frac{1}{4 β_{i m}} s_{i m}^{3} - W_{h i m}^{* T} S_{h i m} - \frac{1}{2} W_{J i m}^{* T} S_{J i m} - \frac{1}{2} ɛ_{i m}$

where ɛ_im = 2ɛ_him + ɛ_Jim.The optimal control Eq. (66) is impractical due to the two ideal weights $W_{h i m}^{* T}$ and $W_{Jim}^{* T}$ are uncertain. To obtain a practical optimized control, RL is constructed based on Eqs. (65) and (66) as follows. The adaptive identifier is formulated as follows: (67) ${\hat{h}}_{i m} ({\bar{x}}_{i m}, s_{i m}) = {\hat{W}}_{h i m}^{T} S_{h i m} ({\bar{x}}_{i m}, s_{i m})$

where ${\hat{h}}_{i m} (x_{i m}, s_{i m})$ is the identifier output, ${\hat{W}}_{h i m}^{T} (t) \in R^{p_{m}}$ is the NN weight. The weight experiences updates based on the following law: (68) ${\dot{\hat{W}}}_{h i m} = Γ_{i m} (S_{h i m} ({\bar{x}}_{i m}, s_{i m}) s_{i m}^{3} - σ_{i m} {\hat{W}}_{h i m})$

where Γ_im is a positive-definite constant matrix, σ_im > 0 is constant. The critic is designed in the following: (69) $\frac{d {\hat{J}}_{i m}^{*} (s_{i m})}{d s_{i m}} = 2 γ_{i m} s_{i m} + \frac{1}{2 β_{i m}} s_{i m}^{3} + 2 {\hat{W}}_{h i m}^{T} S_{h i m} + {\hat{W}}_{c i m}^{T} S_{J i m}$

where $d {\hat{J}}_{i m}^{*} (s_{i m}) / d s_{i m} \in R^{}$ is the estimation of $d J_{i m}^{*} (s_{i m}) / d s_{i m}$ , ${\hat{W}}_{c i m}^{T} (t) \in R^{q_{m}}$ is the NN weight of critic. The weight experiences updates based on the following law: (70) ${\dot{\hat{W}}}_{c i m} = - γ_{cim} S_{J i m} S_{J i m}^{T} {\hat{W}}_{c i m}$

where γ_cim > 0 is constant. The actor is designed as follows: (71) ${\hat{α}}_{i m}^{*} = - γ_{i m} s_{i m} - \frac{1}{4 β_{i m}} s_{i m}^{3} - {\hat{W}}_{h i m}^{T} S_{h i m} - \frac{1}{2} {\hat{W}}_{a i m} S_{J i m}$

where ${\hat{α}}_{i m}^{*}$ is the optimized virtual control, ${\hat{W}}_{a i m}^{T} (t) \in R^{q_{m}}$ is the NN weight of actor. The weight experiences updates based on the following law: (72) ${\dot{\hat{W}}}_{a i m} = - S_{J i m} S_{J i m}^{T} (γ_{a i m} ({\hat{W}}_{a i m} - {\hat{W}}_{c i m}) + γ_{c i m} {\hat{W}}_{c i m})$

where γ_aim > 0 are constant. These designed parameters, β_im, γ_im, γ_cim and γ_aim satisfy the following conditions:

(73) $β_{i m} > 0, γ_{i m} > 4, γ_{a i m} > \frac{β_{i m}}{2}, γ_{a i m} > γ_{c i m} > \frac{γ_{a i m}}{2} .$

Define containment error of the step m+1 as $s_{i m + 1} = x_{i m + 1} - α_{i m + 1}^{*}$ . Replace x_im+1 with $α_{i m + 1}^{*} + s_{i m + 1}$ in the dynamic Eq. (55) to have (74) $d s_{i m} = ({\hat{α}}_{i m}^{*} + s_{i m + 1} + f_{i m} - L {\hat{α}}_{i m - 1}^{*}) d t + Ψ_{i m} d w$

Select the Lyapunov function candidate: (75) $L_{i m} = \sum_{j = 1}^{m - 1} L_{i j} + \frac{1}{4} s_{i m}^{4} + \frac{1}{2} {\tilde{W}}_{h i m}^{T} {\tilde{W}}_{h i m} + \frac{1}{2} {\tilde{W}}_{c i m}^{T} {\tilde{W}}_{c i m} + \frac{1}{2} {\tilde{W}}_{a i m}^{T} {\tilde{W}}_{a i m}$

where $L_{i j} = \frac{1}{4} s_{i j}^{4} + \frac{1}{2} {\tilde{W}}_{h i j}^{T} Γ_{i j}^{- 1} {\tilde{W}}_{h i j} + \frac{1}{2} {\tilde{W}}_{c i j}^{T} {\tilde{W}}_{c i j} + \frac{1}{2} {\tilde{W}}_{a i j}^{T} {\tilde{W}}_{a i j}$ , and ${\tilde{W}}_{h i m} (t) = {\hat{W}}_{h i m} (t) - W_{h i m}^{*}$ , ${\tilde{W}}_{c i m} (t) = {\hat{W}}_{c i m} (t) - W_{J i m}^{*}$ and ${\tilde{W}}_{a i m} (t) = {\hat{W}}_{a i m} (t) - W_{J i m}^{*}$ . Computing the infinitesimal generator 𝔏 of L_im, along with Eqs. (68), (70), (72) and (74) has (76) $L L_{i m} = \sum_{j = 1}^{m - 1} L L_{i j} + s_{i m}^{3} ({\hat{α}}_{i m}^{*} + s_{i m + 1} + f_{i m} - L {\hat{α}}_{i m - 1}^{*}) + \frac{3}{2} s_{i m}^{2} | | Ψ_{i m} | |^{2} + {\tilde{W}}_{h i m}^{T} (S_{h i m} s_{i m}^{3} - σ_{i m} {\hat{W}}_{h i m}) - γ_{c i m} {\tilde{W}}_{c i m}^{T} S_{J i m} S_{J i m}^{T} {\hat{W}}_{c i m} - {\tilde{W}}_{a i n}^{T} S_{J i m} S_{J i m}^{T} [γ_{a i m} ({\hat{W}}_{a i m} - {\hat{W}}_{c i m}) + γ_{c i m} {\hat{W}}_{c i m}]$

Substituting the virtual control Eqs. (71) into (76) holds (77) $L L_{i m} = \sum_{i = 1}^{m - 1} L L_{i j} + s_{i m}^{3} (- γ_{i m} s_{i m} - \frac{1}{4 β_{i m}} s_{i m}^{3} - {\hat{W}}_{h i m}^{T} S_{h i m} - \frac{1}{2} {\hat{W}}_{a i m}^{T} S_{J i m} + s_{i m + 1} + f_{i m} - L {\hat{α}}_{i m - 1}^{*}) + \frac{3}{2} s_{i m}^{2} | | Ψ_{i m} | |^{2} + {\tilde{W}}_{h i m}^{T} (S_{h i m} s_{i m}^{3} - σ_{i m} {\hat{W}}_{h i m}) - γ_{c i m} {\tilde{W}}_{c i m}^{T} S_{J i m} S_{J i m}^{T} {\hat{W}}_{c i m} - {\tilde{W}}_{a i n}^{T} S_{J i m} S_{J i m}^{T} [γ_{a i m} ({\hat{W}}_{a i m} - {\hat{W}}_{c i m}) + γ_{c i m} {\hat{W}}_{c i m}] \leq \sum_{j = 1}^{m - 1} L L_{i j} - (γ_{i m} - \frac{3}{2}) s_{i m}^{4} + \frac{β_{i m}}{4} {\hat{W}}_{a i m}^{T} S_{J i m} S_{J i m}^{T} {\hat{W}}_{a i m} + \frac{1}{4} s_{i m + 1}^{4} + \frac{1}{4} L {\hat{α}}_{i m + 1}^{*} + \frac{9}{16} - {\tilde{W}}_{h i m}^{T} (S_{h i m} s_{i m}^{3} - h_{i m}) + {\tilde{W}}_{h i m}^{T} (S_{h i m} s_{i m}^{3} - σ_{i m} {\hat{W}}_{h i m}) - γ_{c i m} {\tilde{W}}_{c i m}^{T} S_{J i m} S_{J i m}^{T} {\hat{W}}_{c i m} - γ_{a i m} {\tilde{W}}_{a i m}^{T} S_{J i m} S_{J i m}^{T} {\hat{W}}_{a i m} + (γ_{a i m} - γ_{c i m}) {\tilde{W}}_{a i m}^{T} S_{J i m} S_{J i m}^{T} {\tilde{W}}_{c i m}$

From the fact $- s_{i m}^{3} (t) L {\hat{α}}_{i m - 1}^{*} \leq (3 / 4) s_{i m}^{4} (t) + (1 / 4) {(L {\hat{α}}_{i m - 1}^{*})}^{4}$ and previous results, following numerous operations resembling those in Eqs. (43)–(54) in Step 1, (87) can be expressed as (78) $\begin{matrix} L L_{i m} \leq \sum_{j = 1}^{m - 1} (- a_{i j} L_{i j} + b_{i j}) - (γ_{i m} - 4) s_{i m}^{2} - \frac{σ_{i m}}{2 λ_{Γ_{i m}^{- 1}}^{m a x}} {\tilde{W}}_{h i m}^{T} Γ_{i m}^{- 1} {\tilde{W}}_{h i m} \\ - \frac{γ_{c i m}}{2} λ_{S_{J i m}}^{m i n} {\tilde{W}}_{c i m}^{T} {\tilde{W}}_{c i m} - \frac{γ_{c i m}}{2} λ_{S_{J i m}}^{m i n} {\tilde{W}}_{c i m}^{T} {\tilde{W}}_{c i m} + B_{i m} + \frac{1}{4} s_{i m + 1}^{4} \end{matrix}$

where $λ_{Γ_{i m}^{- 1}}^{m a x}$ is the maximal eigenvalue of $Γ_{i m}^{- 1}$ , $λ_{S_{J i m}}^{m i n}$ is the minimal eigenvalue of $S_{J i m} S_{J i m}^{T}$ .

And $B_{i m} = (\frac{γ_{c i m}}{2} + \frac{γ_{a i m}}{2}) {(W_{J i m}^{* T} S_{J i m})}^{2} + \frac{σ_{i m}}{2} | | W_{h i m}^{*} | |^{2} + \frac{1}{4} {(L {\hat{α}}_{i m - 1}^{*})}^{4} + \frac{1}{4} ɛ_{h i m}^{4} + \frac{9}{16}$ ,which satisfied |B_im| ≤ b_im.Define $a_{i m} = min \{4 (γ_{i m} - 4), \frac{σ_{i m}}{λ_{Γ_{i m}^{- 1}}^{m a x}}, γ_{c i m} λ_{S_{J i m}}^{m i n}\}$ , and then Eq. (78) can become the following one: (79) $L L_{i m} \leq \sum_{j = 1}^{m} (- a_{i j} L_{i j} + b_{i j}) + \frac{1}{4} s_{i m + 1}^{4}$

Step n: The optimized control u_i is obtained here. Based on Eq. (9), $s_{i n} = x_{i n} - {\hat{α}}_{i n - 1}^{*}$ can be derived from Eq. (13) as follows: (80) $d s_{i n} = (u_{i} + f_{i n} ({\bar{x}}_{i n}) - L {\hat{α}}_{n - 1}^{*}) d t + Ψ_{i n} d w$

where $Ψ_{i n} = ψ_{i n} - \sum_{j = 1}^{n - 1} \frac{\partial α_{i n - 1}}{\partial x_{i j}} ψ_{i j}$ .The performance index function related to Eq. (80) can be written as (81) $J_{i n} (s_{i n}) = \int_{t}^{\infty} c_{i n} (s_{i n} (s), u_{i} (s_{i n} (s))) d s$

where $c_{i n} (s_{i n}, u_{i}) = sin 2 + u_{i}^{2}$ is cost function. Denoted $u_{i}^{*}$ as optimal control, the function can be rewritten as (82) $J_{i n}^{*} (s_{i n}) = \int_{t}^{\infty} c_{i n} (s_{i n} (s), u_{i}^{*} (s_{i n} (s))) d s$

The function Eq. (82) implies the following property: (83) $E [J_{i n}^{*} (s_{i n})] = min_{u_{i} \in Ψ (Ω)} E [J_{i n} (s_{i n})]$

The HJB equation related to Eqs. (80) and (82) is (84) $H_{i n} (s_{i n}, u_{i}^{*}, \frac{d J_{i n}^{*}}{d s_{i n}}) = sin 2 + u_{i}^{* 2} + \frac{d J_{i n}^{*}}{d s_{i n}} (u_{i}^{*} + f_{j n} - L {\hat{α}}_{i n - 1}^{*} + Ψ_{i n} \frac{d w}{d t}) + \frac{1}{2} \frac{d^{2} J_{i n}^{*}}{d sin 2} Ψ_{i n}^{T} Ψ_{i n} = 0$

Solving $(\partial H_{i n}) / (\partial u_{i}^{*}) = 0$ yields (85) $u_{i}^{*} = - \frac{1}{2} \frac{d J_{i n}^{*} (s_{i n})}{d s_{i n}}$

Split the term $\frac{d J_{i n}^{*}}{d s_{i n}}$ as (86) $\frac{d J_{i n}^{*}}{d s_{i n}} = 2 γ_{i n} s_{i n} + \frac{1}{2 β_{i n}} sin 3 + 2 h_{i n} + J_{i n}^{0}$

where γ_in > 0 and β_in > 0 are two designed constants, and h_in = f_in + s_in||Ψ_in||⁴ ∈ ℝ, $J_{i n}^{0} = - 2 γ_{i n} s_{i n} - \frac{1}{2 β_{i n}} sin 3 - 2 h_{i n} + \frac{d J_{i n}^{*}}{d s_{i n}} \in R .$ Substituting Eqs. (86) into (85) has (87) $u_{i}^{*} = - γ_{i n} s_{i n} - \frac{1}{4 β_{i n}} sin 3 - h_{i n} - \frac{1}{2} J_{i n}^{0}$

Since the unknown functions $h_{i n} ({\bar{x}}_{i n}, s_{i n})$ and $J_{n}^{0} ({\bar{x}}_{i n}, s_{i n})$ are continuous, which can be approximated by NN as (88) $h_{i n} ({\bar{x}}_{i n}, s_{i n}) = W_{h i n}^{* T} S_{h i n} ({\bar{x}}_{i n}, s_{i n}) + ɛ_{h i n} ({\bar{x}}_{i n}, s_{i n})$ (89) $J_{n}^{0} ({\bar{x}}_{i n}, s_{i n}) = W_{J i n}^{* T} S_{J i n} ({\bar{x}}_{i n}, s_{i n}) + ɛ_{J i n} ({\bar{x}}_{i n}, s_{i n})$

where $W_{h i n}^{* T}$ ∈ℝ^p_n, $W_{J i n}^{* T} \in R^{q_{n}}$ are the ideal NN weights, S_hin(x_in, s_in) ∈ ℝ^p_n and S_Jin(x_in, s_in) ∈ ℝ^q_n are the basis function vectors, ɛ_hin(x_in, s_in) ∈ ℝ, ɛ_Jin(x_in, s_in) ∈ ℝ are the bounded approximation errors. Substituting Eqs. (88) and (89) into Eqs. (86) and (87) yields (90) $\frac{d J_{i n}^{*}}{d s_{i n}} = 2 γ_{i n} s_{i n} + \frac{1}{2 β_{i n}} sin 3 + 2 W_{h i n}^{* T} S_{h i n} + W_{J i n}^{* T} S_{J i n} + ɛ_{i n}$ (91) $u_{i}^{*} = - γ_{i n} s_{i n} - \frac{1}{4 β_{i n}} sin 3 - W_{h i n}^{* T} S_{h i n} - \frac{1}{2} W_{J i n}^{* T} S_{J i n} - \frac{1}{2} ɛ_{i n}$

where ɛ_in = 2ɛ_hin + ɛ_Jin.The adaptive identifier is formulated as (92) ${\hat{h}}_{i n} ({\bar{x}}_{i n}, s_{i n}) = {\hat{W}}_{h i n}^{T} S_{h i n} ({\bar{x}}_{i n}, s_{i n})$

where ${\hat{h}}_{i n} (x_{i n}, s_{i n})$ is the identifier output, ${\hat{W}}_{h i n}^{T} (t) \in R^{p_{n}}$ is the NN weight of identifier.

The weight experiences updates based on the following law: (93) ${\dot{\hat{W}}}_{h i n} = Γ_{i n} (S_{h i n} ({\bar{x}}_{i n}, s_{i n}) sin 3 - σ_{i n} {\hat{W}}_{h i n})$

where Γ_in is a positive-definite constant matrix, σ_in > 0 is constant. The critic is (94) $\frac{d {\hat{J}}_{i n}^{*} (s_{i n})}{d s_{i n}} = 2 γ_{i n} s_{i n} + \frac{1}{2 β_{i n}} sin 3 + 2 {\hat{W}}_{h i n}^{T} S_{h i n} ({\bar{x}}_{i n}, s_{i n}) + {\hat{W}}_{c i n}^{T} S_{J i n} ({\bar{x}}_{i n}, s_{i n})$

The weight experiences updates based on the following law: (95) ${\dot{\hat{W}}}_{c i n} = - γ_{c i n} S_{J i n} ({\bar{x}}_{i n}, s_{i n}) S_{J i n}^{T} ({\bar{x}}_{i n}, s_{i n}) {\hat{W}}_{c i n}$

where γ_cin is a constant. The actor is (96) ${\hat{u}}_{i}^{*} = - γ_{i n} s_{i n} - \frac{1}{4 β_{i n}} sin 3 - {\hat{W}}_{h i n}^{T} (t) S_{h i n} ({\bar{x}}_{i n}, s_{i n}) - \frac{1}{2} {\hat{W}}_{a i n}^{T} S_{J i n} ({\bar{x}}_{i n}, s_{i n})$

The weight experiences updates based on the following law: (97) ${\dot{\hat{W}}}_{a i n} = - S_{J i n} ({\bar{x}}_{i n}, s_{i n}) S_{J i n}^{T} ({\bar{x}}_{i n}, s_{i n}) \times (γ_{a i n} ({\hat{W}}_{a i n} - {\hat{W}}_{c i n}) + γ_{c i n} {\hat{W}}_{c i n})$

These parameters are required to meet the following limitation: (98) $β_{i n} > 0, γ_{i n} > 4, γ_{a i n} > \frac{β_{i n}}{2}, γ_{a i n} > γ_{c i n} > \frac{γ_{a i n}}{2} .$

Select the Lyapunov function candidate for overall backstepping control as (99) $L_{i n} = \sum_{j = 1}^{n - 1} L_{i j} + \frac{1}{4} sin 4 + \frac{1}{2} {\tilde{W}}_{h i n}^{T} Γ_{i n}^{- 1} {\tilde{W}}_{h i n} + \frac{1}{2} {\tilde{W}}_{c i n}^{T} {\tilde{W}}_{c i n} + \frac{1}{2} {\tilde{W}}_{a i n}^{T} {\tilde{W}}_{a i n}$

where ${\tilde{W}}_{h i n} (t) = {\hat{W}}_{h i n} (t) - W_{h i n}^{*}$ , ${\tilde{W}}_{c i n} (t) = {\hat{W}}_{c i n} (t) - W_{J i n}^{*}$ , ${\tilde{W}}_{a i n} (t) = {\hat{W}}_{a i n} (t) - W_{J i n}^{*}$ . Compute 𝔏 of L_in, along with Eqs. (80), (93), (95) and (97), and then apply (96), resulting in the following: (100) $\begin{matrix} L L_{i n} = \sum_{j = 1}^{n - 1} L L_{i j} + sin 3 (- γ_{i n} s_{i n} - \frac{1}{4 β_{i n}} sin 3 - {\hat{W}}_{h i n}^{T} S_{h i n} - \frac{1}{2} {\hat{W}}_{a i n}^{T} S_{J i n} + f_{i n} - L {\hat{α}}_{n - 1}^{*}) + \\ \frac{3}{2} s_{i n} | | Ψ_{i n} | |^{2} + {\tilde{W}}_{h i n}^{T} (S_{h i n} sin 3 - σ_{i n} {\hat{W}}_{h i n}) - γ_{c i n} {\tilde{W}}_{c i n}^{T} S_{J i n} S_{J i n}^{T} {\hat{W}}_{c i n} - W_{a i n}^{T} S_{J i n} S_{J i n}^{T} \\ [γ_{a i n} ({\hat{W}}_{a i n} - {\hat{W}}_{c i n}) + γ_{c i n} {\hat{W}}_{c i n}] \end{matrix}$

The following expression is derived from Eqs. (100): (101) $L L_{i n} \leq \sum_{j = 1}^{n - 1} (- a_{i j} L_{i j} + b_{i j}) - (γ_{i n} - 4) sin 4 - \frac{σ_{i n}}{2 λ_{Γ_{i n}^{- 1}}^{m a x}} {\tilde{W}}_{h i n}^{T} Γ_{i n}^{- 1} {\tilde{W}}_{h i n} - \frac{γ_{c i n}}{2} λ_{s_{J i n}}^{m i n} {\tilde{W}}_{c i n}^{T} {\tilde{W}}_{c i n} - \frac{γ_{c i n}}{2} λ_{s_{J i n}}^{m i n} {\tilde{W}}_{a i n}^{T} {\tilde{W}}_{a i n} + B_{i n}$

where $λ_{Γ_{i n}^{- 1}}^{m a x}$ is the maximal eigenvalue of $Γ_{i n}^{- 1}$ , $λ_{S_{J i n}}^{m i n}$ is the minimal eigenvalue of $S_{J i n} S_{J i n}^{T} .$ And $B_{i n} = (\frac{γ_{c i n}}{2} + \frac{γ_{a i n}}{2}) {(W_{J i n}^{* T} S_{J i n})}^{2} + \frac{σ_{i n}}{2} | | W_{h i n}^{*} | |^{2} + \frac{1}{4} {(L {\hat{α}}_{i n - 1}^{*})}^{4} + \frac{1}{4} ɛ_{h i n}^{4} + \frac{9}{16}$ ,which satisfied |B_in| ≤ b_in.Let $a_{i n} = min 4 (γ_{i n} - 4), σ_{i n} / (λ_{Γ_{i n}^{- 1}}^{max}), γ_{c i n} λ_{S_{J i n}}^{min}$ , and then Eq. (101) can become the following one (102) $L L_{i n} \leq \sum_{j = 1}^{n} (- a_{i j} L_{i j} + b_{i j}) .$

Stability Analysis

Theorem 1: Consider MASs described by Eq. (13) and subjected to Assumptions 1-2, operating within a directed graph and employing the adaptive laws Eqs. (32), (72) and (97), together with the virtual controllers Eqs. (31) and (71), and the actual controller Eq. (96), the containment control protocol unequivocally guarantees the SGUUB of all signals within the closed-loop system. Furthermore, for a given ∀t > 0, tuning the design parameters leads the containment error to converge within an arbitrarily small neighborhood, as expressed: (103) $| | y_{i} + L_{1}^{- 1} L_{2} y_{ℓ d} | | \leq \bar{ɛ}$

Proof: Consider the overall Lyapunov function L given by: (104) $L = \sum_{i = 1}^{N} \sum_{j = 1}^{n} L_{i j}$

Define $a_{i} = min \{a_{i 1}, a_{i 2}, \dots, a_{i j}\}$ and $b_{i} = \sum_{j = 1}^{n} b_{i j}$ . Subsequently, Eq. (104) can be expressed as (105) $L L | \leq - a_{i} L + b_{i}$

Based on Lemma 2, the following inequality is deduced from Eq. (105): (106) $E (L) \leq e^{- a_{i} t} L (0) + \frac{b_{i}}{a_{i}}$ (107) $E (L) \leq E [L (0)] + \frac{b_{i}}{a_{i}}$

For s_∗1 = [s₁₁, s₂₁, …, s_N1]^T, based on the definition of L_in and Eq. (99) (108) $E (| | s_{* 1} | |^{4}) \leq E {(s_{11}^{2} + s_{21}^{2} + \dots + s_{N 1}^{2})}^{2} \leq E (s_{11}^{4} + s_{21}^{4} + \dots + s_{N 1}^{4}) \leq 4 N (E [L (0)] + \frac{b_{i}}{a_{i}})$

where N denotes quantity of follower agents. With Eq. (99), for ∀ɛ > 0: (109) $E [L (0)] + \frac{b_{i}}{a_{i}} \leq \frac{\bar{ɛ}}{8} {(\bar{η} (L_{1}))}^{4}$

Taking Eq. (109) and Lemma 3 into account to obtain (110) $E (| | y_{i} + L_{1}^{- 1} L_{2} y_{ℓ d} | |) \leq \frac{E (| | s_{* 1} | |^{4})}{| | \bar{η} (L_{i}) | |^{4}} \leq \bar{ɛ}$

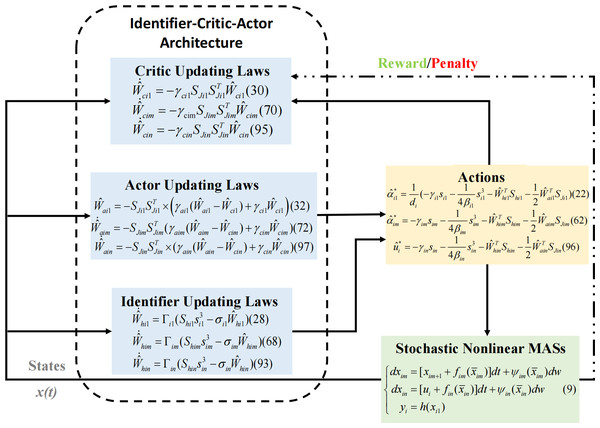
The proof is completed and the RL control strategy process diagram is illustrated in Fig. 2.

Figure 2: The RL control scheme.

Download full-size image

DOI: 10.7717/peerjcs.2126/fig-2

Simulation Example

In this section, the effectiveness of OB, RL and containment control is illustrated by a numerical example. For the nonlinear stochastic MASs consisting of 4 followers and 2 leaders, the following system dynamics are considered: (111) $\{\begin{matrix} d x_{i 1} = [0.9 x_{i 2} - 0.8 x_{i 1}^{2} sin (x_{i 2})] d t + ψ_{i 1} ({\bar{x}}_{i 1}) d w \\ d x_{i 2} = [u_{i} + 0.9 sin (x_{i 1})] d t + ψ_{i 2} ({\bar{x}}_{i 2}) d w \end{matrix}$

where x_i1, x_i2 ∈ ℝ, u ∈ ℝ is the control input, $ψ_{i 1} ({\bar{x}}_{i 1}) = 0.3 sin (x_{i 1})$ , $ψ_{i 2} ({\bar{x}}_{i 2}) = 0.01 sin (0.1 sin (x_{i 1}))$ .The leaders are defined as: (112) $\{\begin{matrix} y_{5 r} = 0.1 sin (2 t) - 0.1 \\ y_{6 r} = 0.45 - 0.5 e^{- (t + 2)} \end{matrix}$

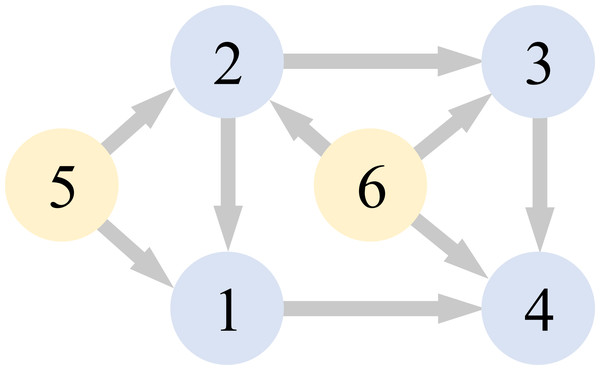
The communication graph that we used in the simulation is visualized in Fig. 3.

According to Fig. 3, the Laplacian matrix as: (113) $L = [\begin{matrix} 2 & - 1 & 0 & 0 & - 1 & 0 \\ 0 & 2 & 0 & 0 & - 1 & - 1 \\ 0 & - 1 & 3 & - 1 & 0 & - 1 \\ - 1 & 0 & 0 & 2 & 0 & - 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}] .$

The NN update parameters are designed as: γ_ai1 = 20, γ_ai2 = 15, γ_ci1 = 14, γ_ci2 = 14, σ_i1 = 14. The design parameters for the optimized virtual control action ${\hat{α}}_{i}^{*}$ corresponding to Eq. (41) are: γ_i1 = 12, β_i1 = 5. The parameters of the optimized actual control action corresponding to Eq. (42) are set as γ_i2 = 5, β_i2 = 2.

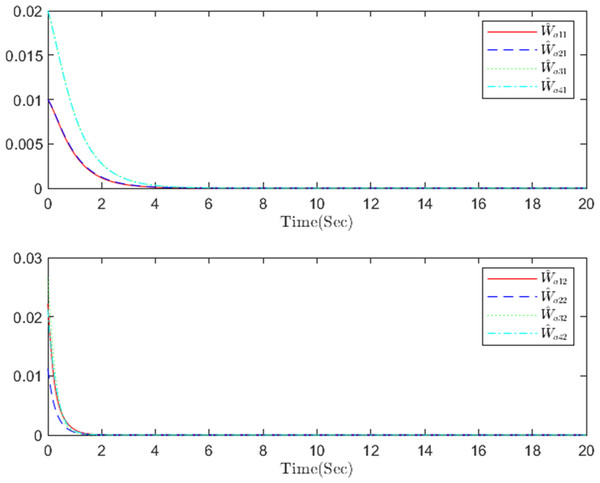
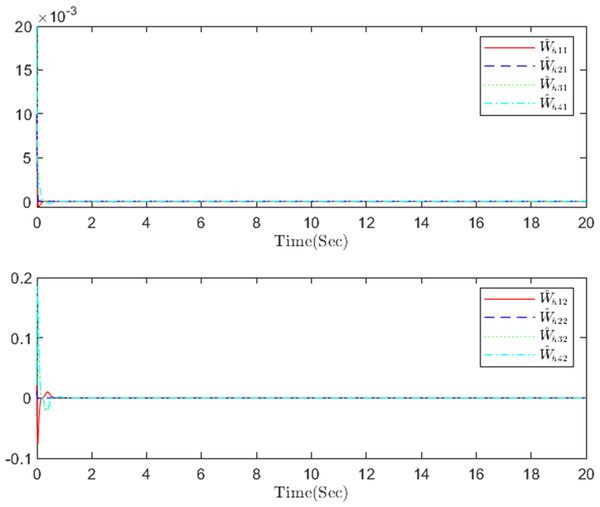
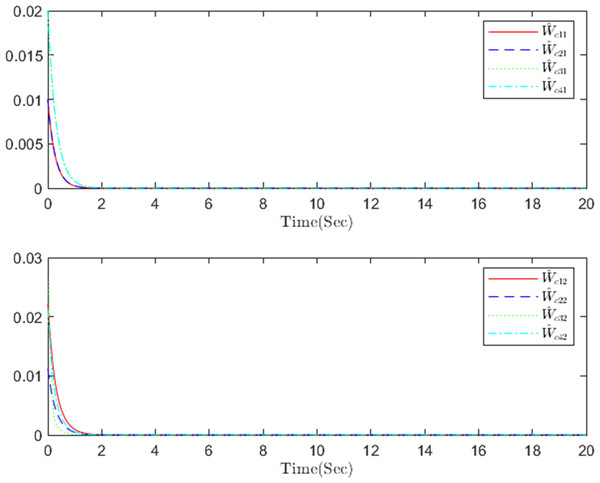
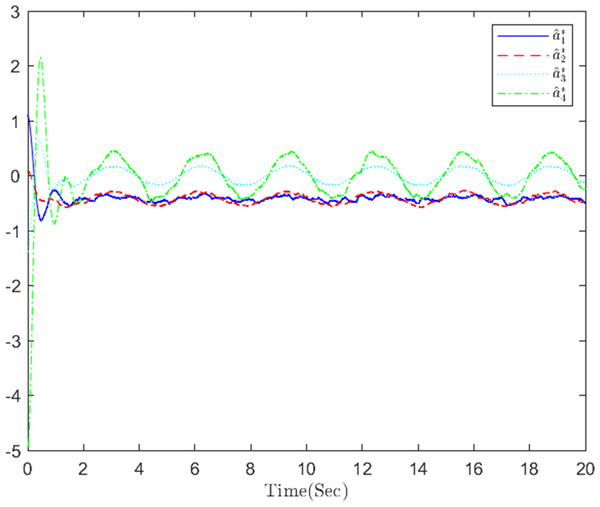
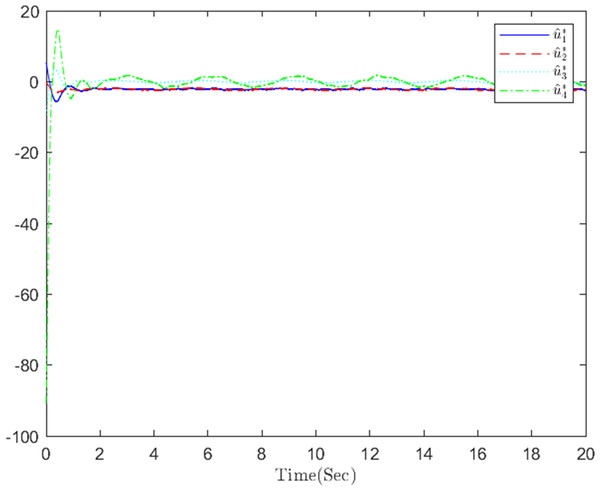
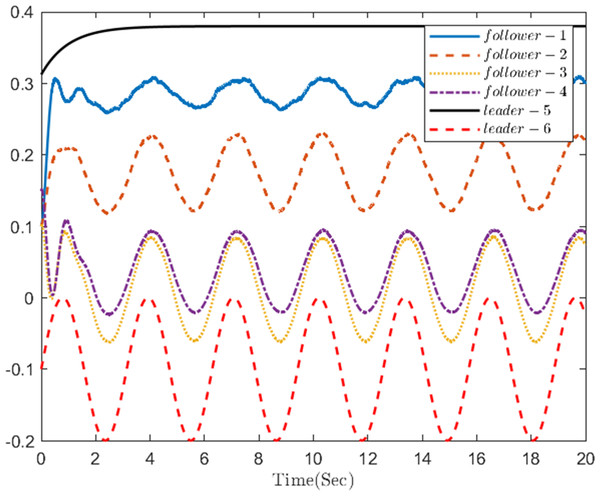
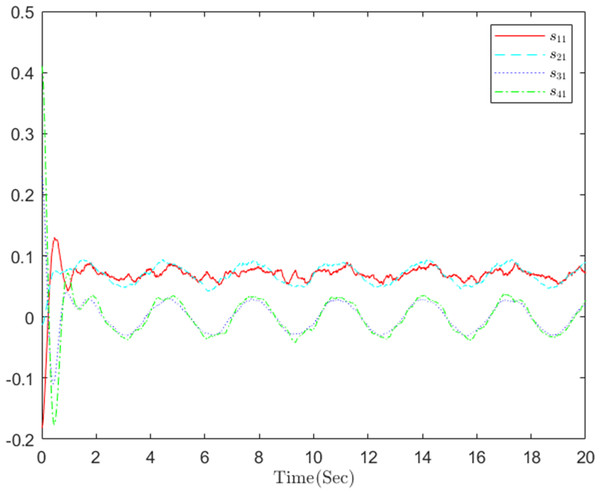
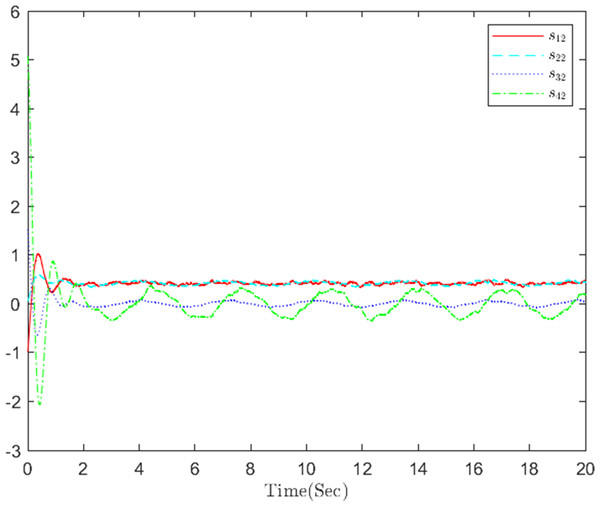
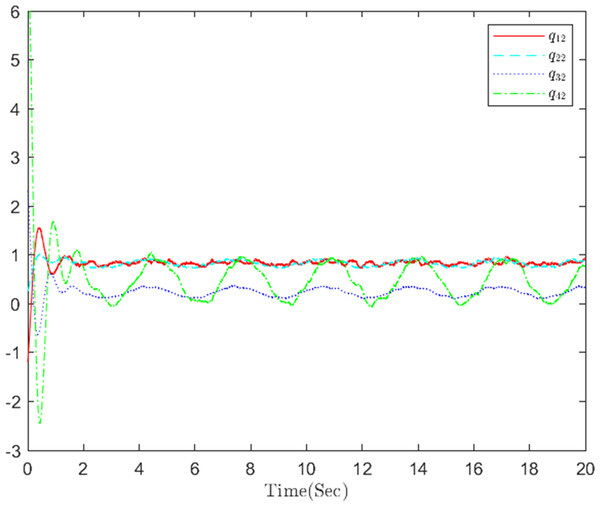
The simulation results, illustrating the application of the proposed OB method for stochastic nonlinear MASs, are presented in Figs. 4–12. Figure 4–6 depict the boundedness of the actor, identifier, and critic NN weights. The actor for performing the control action ${\hat{α}}_{i}^{*}$ and the optimized control actor ${\hat{u}}_{i}^{*}$ are illustrated in Figs. 7–8. Figure 9 displays the trajectories of leaders and followers, demonstrating the asymptotic convergence of all followers to the convex hull formed by the leaders. The distributed containment errors are shown in Figs. 10–11. The results verify that all closed-loop system signals are SGUUB. The simulation results demonstrate that the OB method used in MASs can achieve the desired control performance. Besides, Fig. 12 is the error curve without considering the adaptive compensation scheme in this paper. By comparing simulation results, it can be seen that through RL, adjusting the adaptive rate accelerates the convergence speed of the optimization algorithm, allowing sensor errors to converge more quickly.

Figure 4: The actor NN weight a in step m.

Download full-size image

DOI: 10.7717/peerjcs.2126/fig-4

Figure 5: The identifier NN weight h in step m.

Download full-size image

DOI: 10.7717/peerjcs.2126/fig-5

Figure 6: The critic NN weight c in step m.

Download full-size image

DOI: 10.7717/peerjcs.2126/fig-6

Figure 7: The optimized virtual control action in step 1.

Download full-size image

DOI: 10.7717/peerjcs.2126/fig-7

Figure 8: The optimized actual control action in step 2.

Download full-size image

DOI: 10.7717/peerjcs.2126/fig-8

Figure 9: The trajectories of four followers and two leaders.

Download full-size image

DOI: 10.7717/peerjcs.2126/fig-9

Figure 10: The distributed containment errors s in step 1.

Download full-size image

DOI: 10.7717/peerjcs.2126/fig-10

Figure 11: The distributed containment errors s in step 2.

Download full-size image

DOI: 10.7717/peerjcs.2126/fig-11

Figure 12: The distributed containment errors q in step 2.

Download full-size image

DOI: 10.7717/peerjcs.2126/fig-12

Conclusion

This article introduces an optimized backstepping control based on RL, which has been developed and applied to a class of nonlinear stochastic strict-feedback MASs experiencing sensor faults. Crafting virtual and actual controls as optimized solutions for their respective subsystems, an overall optimization of the backstepping control has been achieved. To address sensor faults, an adaptive neural network compensation control method has been constructed. Utilizing the RL framework based on neural network approximation, the rules for updating RL have been deduced from the negative gradient of a basic positive function linked to the HJB equation. In comparison with existing methods, not only did this approach significantly simplify the RL algorithm, but it also relaxed the requirements for known dynamics and persistent excitation. Additionally, the proposed control scheme has that the outputs of all followers converge to the dynamic convex hull formed by the leaders.

Supplemental Information

Simulation Code

The reinforcement learning (RL) framework based on neural network approximation is employed, deriving RL update rules from the negative gradient of a simple positive function correlated with the Hamilton–Jacobi-Bellman (HJB) equation. This significantly simplifies the RL algorithm while relaxing the constraints for known dynamics and persistent excitation.

DOI: 10.7717/peerj-cs.2126/supp-1

Download

[1] Antonio VTJ, Adrien G, Manuel A-M, Jean-Christophe P, Laurent C, Damiano R, Didier T. 2021. Event-triggered leader-following formation control for multi-agent systems under communication faults: application to a fleet of unmanned aerial vehicles. Journal of Systems Engineering and Electronics 32(5):1014-1022

[2] Beard R, Saridis G, Wen J. 1996. Improving the performance of stabilizing controls for nonlinear systems. IEEE Control Systems Magazine 16(5):27-35

[3] Bellman RE. 1957. Dynamic programming. Princeton: Princeton Univ. Press.

[4] Bounemeur A, Chemachema M, Essounbouli N. 2018. Indirect adaptive fuzzy fault-tolerant tracking control for MIMO nonlinear systems with actuator and sensor failures. ISA Transactions 79:45-61

[5] Cao L, Li H, Dong G, Lu R. 2021. Event-triggered control for multiagent systems with sensor faults and input saturation. IEEE Transactions on Systems, Man, and Cybernetics: Systems 51(6):3855-3866

[6] Chen L, Dai S-L, Dong C. 2022. Adaptive optimal tracking control of an underactuated surface vessel using actor—critic reinforcement learning. IEEE Transactions on Neural Networks and Learning Systems 7520-7533

[7] De Sá DFS, Neto JVDF. 2023. Multi-agent collision avoidance system based on centralization and decentralization control for UAV applications. IEEE Access 11:7031-7042

[8] Ding Z, An LW, Li XJ, Zhang QL. 2018. Adaptive fault-tolerant control for nonlinear systems with multiple sensor faults and unknown control directions. IEEE Transactions on Neural Networks & Learning Systems 29(9):4436-4446

[9] Gao W, Jiang Z-P. 2018. Learning-based adaptive optimal tracking control of strict-feedback nonlinear systems. IEEE Transactions on Neural Networks and Learning Systems 29(6):2614-2624

[10] Hu RC, Zhu WQ. 2015. Stochastic optimal bounded control for MDOF nonlinear systems under combined harmonic and wide-band noise excitations with actuator saturation. Probabilistic Engineering Mechanics 39:87-95

[11] Li T, Bai W, Liu Q, Long Y, Chen CLP. 2023. Distributed fault-tolerant containment control protocols for the discrete-time multiagent systems via reinforcement learning method. IEEE Transactions on Neural Networks and Learning Systems 34(8):3979-3991

[12] Li Z, Cao L, Pan Y, Zhang P. 2022. Adaptive resilient containment control for nonlower triangular multiagent systems with time-varying delay and sensor faults. Journal of the Franklin Institute 359(17):9759-9781

[13] Li Z, Pan Y, Ma J. 2022. Disturbance observer-based fuzzy adaptive containment control of nonlinear multi-agent systems with input quantization. International Journal of Fuzzy Systems 24(1):574-586

[14] Li Y, Sun K, Tong S. 2019. Observer-based adaptive fuzzy fault-tolerant optimal control for SISO nonlinear systems. IEEE Transactions on Cybernetics 49(2):649-661

[15] Liang H, Zhang L, Sun Y, Huang T. 2021. Containment control of semi-markovian multiagent systems with switching topologies. IEEE Transactions on Systems, Man, and Cybernetics: Systems 51(6):3889-3899

[16] Liu D, Huang Y, Wang D, Wei Q. 2013. Neural-network-observerbased optimal control for unknown nonlinear systems using adaptive dynamic programming. International Journal of Control 86(9):1554-1566

[17] Liu X, Yu J, Feng Z, Gao Y. 2020. Multi-agent reinforcement learning for resource allocation in IoT networks with edge computing. China Communications 17(9):220-236

[18] Mao X. 2006. Stochastic differential equations and applications (2nd edition). New York: Academic.

[19] Pontryagin LS, Boltyanskii VG, Gamkrelidze RV, Mishchenko EF. 1962. The mathematical theory of optimal processes. New York, NY: Interscience.

[20] Rajagopal K, Balakrishnan SN, Busemeyer JR. 2017. Neural network-based solutions for stochastic optimal control using path integrals. IEEE Transactions on Neural Networks and Learning Systems 28(3):534-545

[21] Song W, Dyke S. 2013. Optimal feedback design for nonlinear stochastic systems using the pseudospectral method. International Journal of Non-Linear Mechanics 55:70-78

[22] Tang Y, Xing X, Karimi HR, Kocarev L, Kurths J. 2016. Tracking control of networked multi-agent systems under new characterizations of impulses and its applications in robotic systems. IEEE Transactions on Industrial Electronics 63(2):1299-1307

[23] Tong S, Li Y, Li Y, Liu Y. 2011. Observer-based adaptive fuzzy backstepping control for a class of stochastic nonlinear strict-feedback systems. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics) 41(6):1693-1704

[24] Vamvoudakis KG, Lewis FL. 2010. Online actor-critic algorithm to solve the continuous-time infinite horizon optimal control problem. Automatica 46(5):878-888

[25] Wang W, Wang D, Peng Z. 2015. Distributed containment control for uncertain nonlinear multi-agent systems in non-affine pure-feedback form under switching topologies. Neurocomputing 152:1-10

[26] Wang BH, Wang JC, Zhang B, Chen WS, Zhang ZQ. 2018. Leader-follower consensus of multivehicle wirelessly networked uncertain systems subject to nonlinear dynamics and actuator fault. IEEE Transactions on Automation Science & Engineering 15(2):492-505

[27] Wen G, Ge SS, Tu F. 2018. Optimized backstepping for tracking control of strict-feedback systems. IEEE Transactions on Neural Networks and Learning Systems 29(8):3850-3862

[28] Wen G, Xu L, Li B. 2023a. Optimized backstepping tracking control using reinforcement learning for a class of stochastic nonlinear strict-feedback systems. IEEE Transactions on Neural Networks and Learning Systems 34(3):1291-1303