A dual-population Constrained Many-Objective Evolutionary Algorithm based on reference point and angle easing strategy

Introduction

The constrained multi-objective optimization problem (CMOP) is a type of problem that widely occurs often in real-life scenarios (Zhao et al., 2023; Wang et al., 2023). One major characteristic of CMOPs is the involvement of diverse and complex constraints related to decision variables or objective functions, which makes it difficult to find ideal or approximately ideal solutions. The theoretical model of CMOPs can be presented as: ${\displaystyle \begin{array}{cc}minimize\hfill & F\left(x\right)={\left(f_1\left(x\right),...,f_j\left(x\right)\right)}^T\hfill \\ subjectto\hfill & x\in S\hfill \\ \hfill & g_m\left(x\right)\ge 0,j=1,2,...,M;\hfill \\ \hfill & h_n\left(x\right)=0,k=1,2,...,N.\hfill \end{array}}$

Where x = (x₁, …, x_j)^T denotes the decision vector, and j describes the decision variables count, and x ∈S, addition S ∈Rn is the search area. g_m(x) and h_n(x) represent the m-th inequality constraint and the n-th equality constraint, respectively. m indicates the number of objectives. When m ≥4, the equation can be used to describe a constrained many-objective optimization problem (CMaOP). Many real-world applications involve CMaOPs, such as scheduling optimization (Sindhu & Mukherjee, 2018; Zhang et al., 2017; Zhang et al., 2021), routing problems (Li et al., 2017; Shen et al., 2022; Shen et al., 2023; Guo et al., 2023), portfolio optimization (Hemici & Zouache, 2023; Wang, Huang & Wang, 2023; Setiawan & Rosadi, 2020), and water resource allocation (Wang, Wang & Li, 2020).

For a CMaOP, the extent of the constraint violation (CV) of the p-th constraint for a solution x is formulated as follows: ${\displaystyle {\phi }_p\left(x\right)=\left\{\begin{array}{c}max\left(0,g_p\left(x\right)\right),p=1,\dots ,l\hfill \\ max\left(0,\left|h_p\left(x\right)\right|\right),p=l+1,\dots .,q\hfill \end{array}.\right.}$

The total CV can be determined by: ${\displaystyle \phi \left(x\right)=\sum _{j=1}^p{\phi }_j\left(x\right).}$

Over the past few decades, there have been continuous efforts made to solve CMOPs. Algorithms often need to find new and better feasible solutions by bypassing the infeasible regions. Therefore, transforming the original problem into a multi-population-based cooperative optimization problem is an often used approach (Bao et al., 2023; Liang et al., 2023a). Relevant evidence indicates which methods can effectively balance objectives and constraints (Liang et al., 2023b). Previous algorithms have been successful in solving traditional constraint multi-objective optimization problems (CMOPs). However, they have encountered limitations when it comes to constrained many-objective optimization problems (CMaOPs). These challenges predominantly stem from the following:

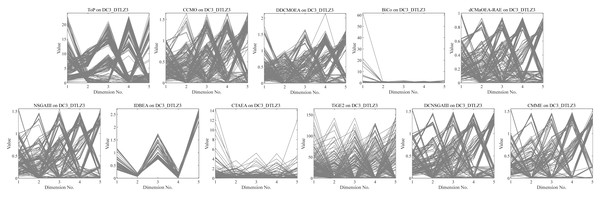
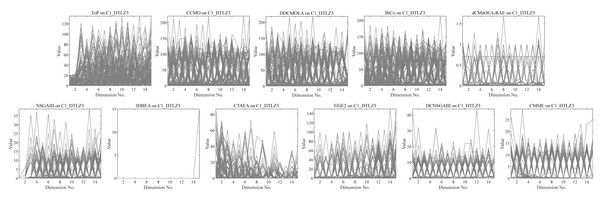
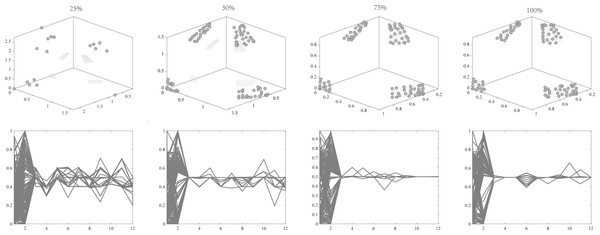
• They get stuck in local optima caused by overemphasizing convergence. To illustrate the drawbacks of traditional selection strategies, we present the following example. Figure 1 demonstrates the evolution of decision variables and objective values for three traditional optimization algorithms—CTAEA (Li et al., 2019), NSGAIII (Jain & Deb, 2014), and IDBEA (Asafuddoula, Ray & Sarker, 2015)—tackling the C1-DTLZ3 (Jain & Deb, 2014) problem. As iterations progress, these algorithms gradually approach the optimal CPFs but often get stuck in local optima. Simultaneously, there is a gradual reduction in the diversity of their decision variables, which is not coincidental. These behaviors are controlled by their selection strategies to move toward CPFs, it is necessary to promptly eliminate poorly performing solutions. However, this might also prevent the population from finding the final CPF. To further support this, we conducted multiple runs and obtained a notably ideal result. Figure 2 displays the distribution of decision variables and objective values in this ideal result. It is evident that the entire population is uniformly distributed over the CPF, with a significant portion of its decision variables distributed around 0.5. In the results depicted in Fig. 1, the presence of decision variables at 0.5 gradually diminishes with further iterations because these solutions perform poorly in the current environment. However, these solutions are crucial for the population’s progression towards CPFs. As a result, some solutions that might not perform well in the current context but are instrumental for the overall optimization process were discarded. It is important to note the distinction in our study compared to Wang & Xu (2020), which focused on infeasible solutions that show good convergence, or Ming et al. (2023a), which concentrated on suboptimal solutions tailored for the current population. Instead, our study prioritized solutions that perform poorly in the current environment but contribute to the overall optimization process. This highlights the need to ease the population’s convergence pressure, which is crucial in CMaOPs, as it might prevent the population from converging to CPFs in time. Employing a multi-population collaborative approach is effective but it also brings forth the second issue.

• In the process of population collaboration, it is crucial to strike a balance between exploring feasible and infeasible regions. While exploring infeasible regions, it is also important to avoid missing feasible areas caused by excessively rapid convergence (Zeng, Cheng & Liu, 2023), which could result in inefficiency and waste of computational resources. This balance becomes more fragile in CMaOPs. To address this issue, Zeng, Cheng & Liu (2023) divided the archive into an inverse archive and a diversity archive, which enables better performance across various types of problems. However, the algorithm relies on the distance between solutions, making them susceptible to local optima influences in smaller dimensions with different value ranges. Moreover, distances lose meaning in higher dimensions (Myszkowski & Laszczyk, 2021). Similarly, Li et al. (2019) used two archives, CA and DA, to store convergence and diversity solutions. However, in CMaOPs, updating a solution in the archive often requires traversing the entire population for convergence or diversity, which is inefficient. Furthermore, mating-selection strategies lead to deficiencies in exploring new feasible regions (Yang et al., 2023). Some dual-population algorithms (Bao et al., 2023; Ming et al., 2022) utilize a bidirectional search strategy. This approach involves rapidly converging an infeasible solution towards Unconstrained Pareto fronts (UPFs). Subsequently, together with the population of exploring feasible solutions, it gradually moves towards CPFs from both directions. This method proves highly effective in CMOPs. However, in CMaOPs, the emergence of numerous nondominated solutions weakens the population’s convergence toward the PF (Zou et al., 2023; Elarbi, Bechikh & Ben Said, 2021). This prevents the traditional method from moving the population closer toward PF in time. There is a critical need for a search strategy that explores infeasible solutions while balancing convergence and diversity.

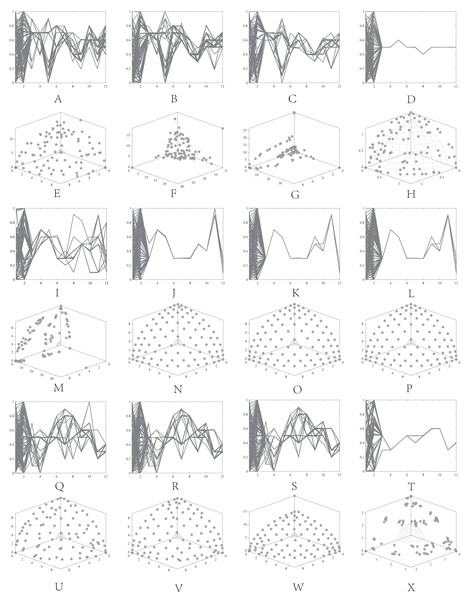
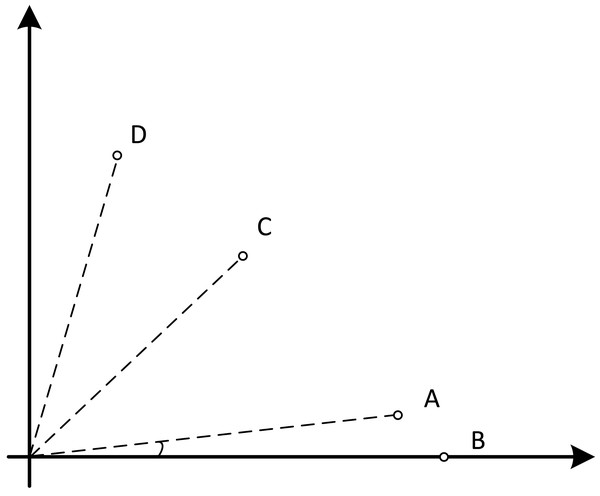
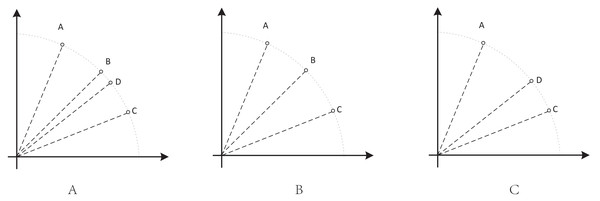
• In MaOPs, preserving diversity among solutions, aiming for their uniform distribution along the PF, remains crucial. Two representative approaches to achieving this are reference points (Jain & Deb, 2014) and angles among solutions (He & Yen, 2017). The former ensures uniformity across the solution space by generating reference vectors, while the latter promptly eliminates poor-quality solutions based on the angles between them. However, in CMaOPs, the scenario differs: the reference points might be uniform, while the CPF might not be, indicating that traditional reference point-based methods cannot guarantee uniform solution distribution (Wang, Huang & Pan, 2023). Similarly, the angle-based approach has its drawbacks. To illustrate the limitations of these traditional strategies, consider the following artificial scenario depicted in Fig. 3, which demonstrates the selection process. The solutions—A, B, C, and D——are four non-dominated solutions, where B has a y-coordinate of 0 and one solution needs to be eliminated. If the angle-based method is applied, A or B would be chosen from the AB pair: Solutions dominating B would also have a y-coordinate of 0. Comparatively, the solution space dominating B would be less than that of A. In this case, eliminating A seems like a favorable choice. However, it would drive the population closer to the x-axis. In MaOPs, such a strategy could severely damage population diversity. If B is eliminated, there might appear non-dominated solutions with a y-coordinate of 0 but an extremely high x-coordinate, especially in problems with multimodal attributes like DC3-DTLZ3 (Li et al., 2019). When B has been eliminated, any new solutions of this type would be non-dominated, consequently compromising the overall quality of the population. The optimization problem of irregular PFs can be effectively addressed by employing neural networks (Wang, Huang & Pan, 2023; Liu et al., 2020), which produces favorable outcomes. However, it has been noted by Ming et al. (2023c) that the excessive integration of multiple techniques tends to complicate the algorithm. Additionally, while some problems have a uniform CPFs, others might not. Algorithms need to balance both scenarios to provide a series of high-performance solutions.

These challenges lead to varying degrees of reduced efficiency when using traditional methods in CMaOPs. Striking the right balance between feasibility, convergence, and diversity has been a critical challenge.

The motivation for this article is as follows:

As a type of meta-heuristic algorithm, the evolutionary algorithm does not rely on problem continuity or differentiability, making it highly suitable for solving CMOPs, particularly CMaOPs with intricate constraints. However, it should be noted that there is no universally versatile meta-heuristic algorithm capable of effectively addressing all types of optimization problems. This concept is known as the No Free Lunch (Wang et al., 2020; Del Ser et al., 2019). The verification of this theorem also underscores the necessity for continuous theoretical research on meta-heuristic algorithms.

In contrast to other evolutionary algorithms that have undergone substantial development, there has been limited research on CMaOEAs, especially with methods based on multi-population collaborative techniques. However, the performance decreased significantly when using existing CMOEAs to handle CMaOPs (Ming et al., 2023c). Hence, conventional multi-objective optimization algorithms are not suitable for CMaOPs, leaving ample room for advancement and potential when using CMaOEA to handle CMaOPs.

The design of effective CMaOEAs requires a proper balance among convergence, diversity, and feasibility (Ming et al., 2023c). Traditional multi-population collaborative algorithms perform well in CMOPs. An improved multi-population collaborative algorithms could yield better performance and results in CMaOPs if appropriate consideration is given to the feasibility.

In this article, a unique dual-population constrained many-objective evolutionary algorithm based on reference point and angle easing strategy (dCMaOEA-RAE) was developed. This method effectively resolves CMaOPs by striking a balance feasibility, convergence, and diversity. Specifically, we divided the population into two parts: the main population (called PopulationMain) was responsible for searching feasible zones. A selection strategy was proposed to optimize the distribution of the population in discrete and irregular CPFs by combining reference points and angles. The other auxiliary population (called PopulationExplore) was dedicated to exploring infeasible regions. We retained some current poor but beneficial solutions for the evolutionary process by slowing down the convergence rate of some solutions, thereby uncovering new and superior areas of feasible solutions.

The primary achievements of this study can be briefly described as follows:

• For the main population (PopulationMain), the process involves selecting non-dominated sets from parents and offspring that using the constraints. Subsequently, the solution region was divided into a series of sub-regions using reference vectors. Within each region, the closest solutions to the reference line were initially chosen to ensure the distribution of solutions in the outcome. Then, among the remaining solutions, those closer in angle within the current region and adjacent regions were eliminated. The aim of this was to ensure a more uniform distribution within the population.

• For the auxiliary population (PopulationExplore), solutions were selected in pairs using binary tournaments based on angular distance, favoring solutions with better dominance relationships and distances from the ideal point. This approach enhanced diversity while guiding the population to spread in various directions within the search space. This balance the convergence and diversity, which led the population to superior feasible solution regions.

• Extensive experiments encompassing three test suites with a total of 77 benchmark problems were conducted. The goals were to confirm the effectiveness and competitiveness of dCMaOEA-RAE against 10 advanced CMOEA/CMAOEA methods.

The following is the structure of the remainder of this article: Section ‘Related work’ offers a short review of the related work on reference point adaptation methods and their underlying motivations. Section ‘Proposed algorithm’ explains the overall structure of the dCMaOEA-RAE with a detailed description of its components. Section ‘Experimental results and analysis’ analyzes the experimental setup and comprehensive experiments conducted. Finally, Section ‘Conclusions’ concludes this article, and highlights further directions for research.

Related work

Proposed Algorithm

Overview of the proposed dCMaOEA-RAE

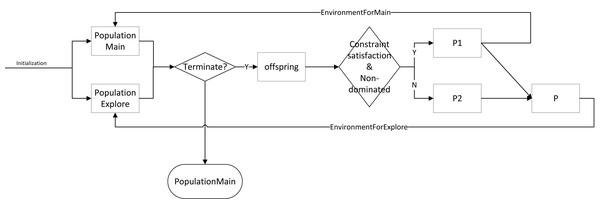
dCMaOEA-RAE maintains two populations, both of size N. The main population, PopulationMain, is responsible for exploring feasible solutions and providing a uniformly distributed final result with strong convergence. The exploration population, PopulationExplore, explores infeasible solutions to discover new, better feasible solution regions. Additionally, different selection strategies are applied to the two populations to fulfill their distinct functions. Algorithm 1  outlines the overall framework of dCMaOEA-RAE. In the beginning, each population is initialized and reference points are generated. Subsequently, the populations enter an evolutionary loop. Parents are selected using binary tournament which is based on non-dominated sorting. This generates offspring, P’. The offspring and parents together undergo environmental selection. The environmental selection process is conducted differently for the two populations: feasible non-dominated solutions that meet the constraints undergo the environmental selection strategy of the main population. These solutions are screened, based on angles, to eliminate crowded solutions and then form the new generation of the main population. The remaining solutions undergo the environmental selection strategy of the exploration population, creating a new generation of the exploration population. This cycle continues until completion. The proposed algorithm’s process flow is illustrated in Fig. 4.

 
_______________________ 
 Algorithm 1: Framework of dCMaOEA-RAE                               _________ 
  1  Input: N (Population size), (Maximum generation) 
  2  Output: (final Population set) 
  3  Z ← Reference_point_Generation(N); 
  4  Pmain,Pexp lore ← Initialization(N); 
  5  t ← 0; 
  6  repeat 
     7   FrontNo ← nondominated_sorting(Pmain ∪ Pexp lore); 
8   MatingPool ← Select n solutions by FrontNo based 
    binary-tournament-selection method as mating parents; 
9   P’ = OperatorGAhalf(MatingPool); 
10   P = Pmain ∪ Pexp lore ∪ P 
11   Calculate the CV values of solutions in P 
12   FrontNo ← nondominated_sorting(P) 
13   Pm← FrontNo==1 and CV==0 
14   Pm = EnvironmentSelectionForMain(Pm,Z) 
15   Pe← P-Pm 
16   Pe = EnvironmentSelectionForExplore(Pe,Z) 
17   t ← t + 1 
18  until t < tmax;    

Environmental selection of PopulationMain

After obtaining a range of feasible non-dominated solutions that exceeded the population size, an environmental selection process was required. As all the solutions within this set are non-dominated, this step focuses on enhancing diversity. Algorithm 2  delineated the population selection process. The search space was divided into subspaces using pre-generated weight vectors and each solution was associated with the vector perpendicularly closest (Line 1). This step effectively reduced the computational complexity. For each subspace, the algorithm first identified the solution closest to the weight vector and designated it as ‘the key of this vector’ (Line 2). Following this, we identified the weight vector associated with the highest number of connected solutions, denoted by z. (Line 4). We calculated the angles between the solution set S (excluding ‘key’) associated with the vector z and the set comprising themselves along with adjacent weight vectors (Line 6). The method is further illustrated by Fig. 5, which depicts a hyperplane composed of ten weight vectors (A-J) in a three-objective environment. For F, its adjacent weight vectors were C, E, I, and J. We found the pair of solutions with the smallest angle. At least one solution in this pair should be from set P. If the other solution was not part of set S, we eliminated the other solution (Lines 8-11). Otherwise, we compared these two solutions with the second smallest angle excluding each other. This was used as the criteria for diversity. And eliminated the solution with the smaller angle (Line 13-14). The process continued iteratively utill the number of solutions was same as N.

 
_______________________________________________________________________________________________________ 
  Algorithm 2: EnvironmentSelectionForMain                                _________ 
  1  Input: P (The Population), Z (Reference point), N (Population Size) 
  2  Output: P 
  3  Normalize P; 
  4  Assign each solution of P to the nearest reference point by the 
      perpendicular distance. 
  5  In the set of solutions connected to each reference point, the solution 
      with the shortest distance is selected and named as the ’key’ of each 
      reference point. 
  6  repeat 
     7   Find the reference point that connects the largest number of 
    solutions in the same reference point, denoted as z. 
8   The solutions associated with the vector z are denoted as S, while 
    the set of solutions belonging to the reference vectors adjacent to z 
    is denoted as S’. 
9   Calculate the Angle between (S - key) and (S’ ∪ S), and the result is 
    denoted as R. 
10   Find the pair of solutions with the smallest Angle in R, denoted as 
    A and B. 
11   if A / ∈ S then 
    12   discard B 
13   else if B / ∈ S then 
    14   discard A 
15   else 
    16   compute the Angle of the second closest solution of A and B 
apart from each other, denoted a_ and b_. If a_ > b_ then 
eliminate B from P and vice versa. 
17   end 
18  until size of P > N;    

 
_______________________________________________________________________________________________________ 
  Algorithm 3: EnvironmentSelectionForExplore                             _________ 
  1  Input: P (The Population), Z (Reference point) 
  2  Output: P(The screened population) 
  3  Calculate the minimum angle among the solutions of the set of solutions 
      that connect the same reference point, denoted as Angle_min. If there 
      is only 0 or 1 solution in the solution set, the Angle is denoted as inf. 
  4  FrontNo ← nondominated_sorting(P) 
  5  Cons ← The distance of the solution from the origin 
  6  Normalize P 
  7  repeat 
     8   Find the reference point where the minimum value in Angle_min lies 
    and identify the pair of solutions with the smallest angle, denoted 
    as A and B; 
9   if FrontNo(A) > FrontNo(B) then 
    10   Eliminate A from P; 
11   else if FrontNo(A) < FrontNo(B) then 
    12   Eliminate B from P; 
13   else 
    14   The solution with larger Cons is eliminated; 
15   end 
16   Update Angle_min 
17  until size of P > N; 
18  return P;    

Remark

Certainly, it is important to note the significant differences between the use of reference points and angles in the search methods of these two populations.

The main population aims for an even distribution to ensure the outcome. We used the ‘key’ solution to maintain uniform distribution, particularly in cases of a uniform CPF. In situations with non-uniform CPFs, we calculated the angle with adjacent reference vectors, allowing the solutions to distribute as evenly as possible. In Fig. 6, we demonstrate the effectiveness of this strategy through an artificial selection scenario: Fig. 6A comprises four non-dominated solutions, A, B, C, and D, where ABC divides the solution space into four quarters and D is near B. If we needed to eliminate one solution it would be either B or D. Our proposed search strategy accurately eliminated D by calculating the angle between BD and other solutions.

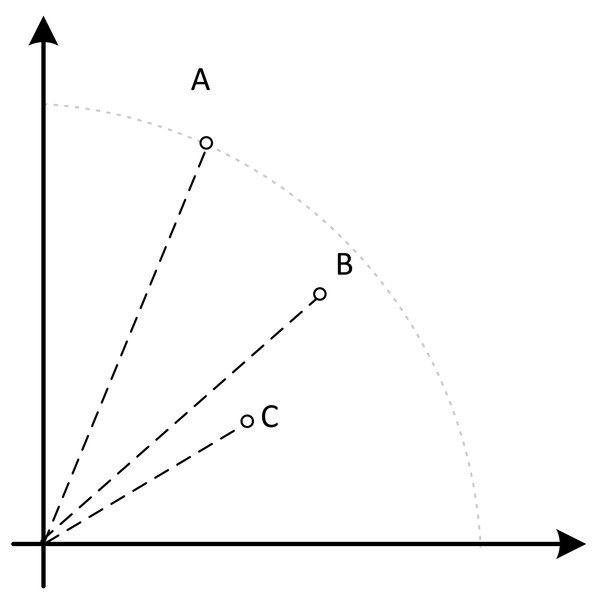
For the auxiliary population tasked with exploring infeasible solutions, achieving maximum uniformity, unlike the main population, was not crucial. Instead, it aimed to slow down convergence pressure through angle-based strategies, preserving some sub-optimal yet beneficial solutions throughout the evolution process. As the main population used non-dominated sorting to decrease convergence pressure, the overall convergence pressure was guaranteed. Additionally, while comparing non-dominant layers and their distance from the origin are somewhat similar but different, we illustrated this distinction through an example: Fig. 7 displays three solutions, A, B, and C, within a selection environment where one needs elimination. It is clear that AC is non-dominated, and B is dominated by C. When considering their distances from the origin, C < B < A, which would lead to the elimination of A. However, when considering the dominance layer, B is to be eliminated, which is the intended outcome. Therefore, by first comparing dominance layers and then distances, we achieved our intended objective.

Experimental Results and Analysis

A concise overview of the experimental setup and algorithm parameters is included in this section. We then evaluated our designed method against ten advanced CMOEAs/CMaOEAs on three representative benchmark suites containing a total of 77 test problems. A performance analysis was carried out on the results. All experiments were performed using PlatEMO (Tian et al., 2017).

Comparison results

The designed algorithm was compared with the ten methods mentioned previously. Values such as “NaN” and “0.0000e+0” signify that the results were too distant from the true Pareto front to compute the metric. We used symbols “+”, “-”, and “=” respectively to indicate results that were statistically superior to dCMaOEA-RAE, significantly inferior to dCMaOEA-RAE, or similar to dCMaOEA-RAE. The result with the best performance in each problem had been bolded. Within the Friedman ranking, in addition to the best data, we bolded the second-best data.

Comparison results on DTLZ test problem

Table 3 presents the Friedman rankings of eleven algorithms across various objective quantities in the C-DTLZ and DC-DTLZ test problems. It is evident that dCMaOEA-RAE consistently outperformed other algorithms across all three metrics. CMME and DCNSGAIII, as recent CMaOEAs, exhibited relatively good performance. These test sets included diverse feasible regions and offered a comprehensive evaluation of algorithm performance. Tables 4, 5 and 6 report the IGD, IGDp, and HV performance indices for the test problems, respectively. Looking at the three metrics collectively, it is apparent that dCMaOEA-RAE achieved the highest number of superior rankings in all three metrics. Specifically 34, 31, and 35, respectively, exceeded more than half of the total. Particularly notable performances were observed in C1-DTLZ3, DC1-DTLZ3, DC2-DTLZ1, and DC3-DTLZ3. Due to the complex nature of the constraints, the designed algorithm faced significant challenges in dealing with these types of problems, yet it outperformed other algorithms. For instance, C1-DTLZ3 encounter infeasible obstacles when approaching the PFs and DC2-DTLZ1 contained extensive infeasible regions, which showed the ability of dCMaOEA-RAE to reach superior CPFs through such regions. For example, DC1-DTLZ3 had a narrow feasible region, while DC3-DTLZ3’s CPF consisted of a couple of segmented, narrow, tapered strips and a flexible sheet area above the PF. dCMaOEA-RAE strengthened population diversity in the auxiliary population through binary tournaments. It guided the main population toward the precise exploration of minute feasible regions. Additionally, algorithms like CCMO are competitive in solving some problems such as C2-DTLZ2, DC1-DTLZ1, and DC2-DTLZ3 in the 3-objective problems. This competitiveness stems from CCMO’s utilization of a weak cooperation approach, where two independent populations evolve. This enhances certain aspects of diversity and enables the discovery of smaller feasible regions. However, the slow convergence of the CCMO as the number of objectives grows prevents it from being suitable for CMaOPs. Furthermore, it is notable that dCMaOEA-RAE exhibited relatively inferior performance in D1-DTLZ1 and DC1-DTLZ1. This could be due to the simplicity of these test problems in terms of the constraint complexity, where even using the straightforward CDP of NSGA-III yielded reasonably good performance.

Table 1:

The upper limit of the fitness estimates for different problems.

Problem	M = 3	M = 5	M = 8	M = 10	M = 15
C1-DTLZ1	46,000	127,200	124,800	276,000	204,000
C1-DTLZ3	92,000	318,000	390,000	966,000	680,000
C2-DTLZ2	23,000	74,200	78,000	207,000	136,000
C3-DTLZ4	69,000	265,000	312,000	828,000	544,000
DC-DTLZ and MW	69,000	265,000	312,000	828,000	544,000
CF	40,000	80,000	140,000	180,000	240,000

DOI: 10.7717/peerjcs.2102/table-1

Table 2:

The population size of different problems.

Problem	M = 3	M = 5	M = 8	M = 10	M = 15
C-DTLZ, DC-DTLZ and MW	92	212	156	276	136
CF	92	126	156	220	240

DOI: 10.7717/peerjcs.2102/table-2

Table 3:

The Friedman rankings of eleven algorithms across various objective quantities in DTLZ test problems.

	Igd ranking	Igdp ranking	Hv ranking
NSGAIII	3.89	3.97	4.60
IDBEA	8.20	8.22	8.47
CTAEA	4.40	3.99	4.47
TiGE2	7.59	7.12	7.82
DCNSGAIII	3.50	3.57	4.47
CMME	3.62	3.42	4.71
ToP	8.75	8.76	6.68
CCMO	6.20	6.45	5.62
DDCMOEA	6.75	7.00	6.00
BiCo	6.43	6.72	5.86
dCMaOEA-RAE	1.36	1.48	1.98

DOI: 10.7717/peerjcs.2102/table-3

Notes:

The best results are in bold.

Table 4:

The IGD performance values of dCMaOEA-RAE and other schemes on DTLZ benchmark problems.

Problem	M	NSGAIII	IDBEA	CTAEA	TiGE2	DCNSGAIII	CMME	ToP	CCMO	DDCMOEA	BiCo	dCMaOEA-RAE
C1_DTLZ1	3	2.0452e−2 (8.62e−4) =	4.3115e−1 (6.06e−2) -	2.2959e−2 (3.13e−4) -	2.7828e−1 (6.90e−2) -	2.0328e−2 (2.04e−4) =	2.0270e−2 (1.09e−4) =	NaN (NaN)	2.0796e−2 (1.43e−4) -	2.0929e−2 (1.90e−4) -	2.1079e−2 (2.43e−4) -	2.0304e−2 (1.06e−4)
	5	5.2035e−2 (3.62e−4) -	4.6390e−1 (7.21e−2) -	5.9488e−2 (4.48e−4) -	3.2485e−1 (7.57e−2) -	5.2180e−2 (2.13e−4) -	5.2317e−2 (3.29e−4) -	NaN (NaN)	5.2123e−2 (3.83e−4) -	5.2182e−2 (3.52e−4) -	5.2005e−2 (2.94e−4) =	5.1809e−2 (3.13e−4)
	8	9.5924e−2 (6.26e−4) -	4.9600e−1 (7.32e−2) -	1.2051e−1 (2.62e−3) -	4.4614e−1 (7.41e−2) -	9.9733e−2 (1.08e−2) -	9.8088e−2 (4.73e−3) -	4.4803e−1 (0.00e+0) =	1.0814e−1 (6.34e−3) -	1.0586e−1 (1.35e−3) -	1.0352e−1 (9.60e−4) -	9.5362e−2 (3.70e−4)
	10	1.0859e−1 (3.77e−4) -	4.7535e−1 (9.26e−2) -	1.3984e−1 (1.92e−3) -	4.7119e−1 (3.66e−2) -	1.1141e−1 (9.27e−3) -	1.1105e−1 (7.93e−3) =	3.3122e−1 (7.98e−2) -	1.1906e−1 (8.58e−3) -	1.1743e−1 (1.64e−3) -	1.1234e−1 (8.15e−4) -	1.0777e−1 (4.01e−4)
	15	1.8217e−1 (3.43e−3) =	5.7091e−1 (4.73e−2) -	2.1316e−1 (7.48e−3) -	4.9683e−1 (2.94e−2) -	1.7852e−1 (9.79e−3) =	1.7490e−1 (1.14e−2) +	3.5315e−1 (7.93e−2) -	2.0141e−1 (1.60e−2) -	2.0306e−1 (1.60e−2) -	1.6217e−1 (4.91e−3) +	1.8093e−1 (2.25e−3)
C1_DTLZ3	3	4.5626e+0 (4.01e+0) -	6.7824e+0 (2.84e+0) -	7.4347e−2 (1.90e−2) -	6.7013e+0 (2.77e+0) -	4.3189e+0 (4.02e+0) -	2.7092e+0 (3.82e+0) -	2.5549e+0 (3.74e+0) -	5.5936e−2 (6.16e−4) -	5.9077e−2 (1.23e−2) -	1.1201e+0 (2.76e+0) -	5.4471e−2 (5.79e−6)
	5	5.9626e+0 (5.41e+0) -	1.0480e+1 (3.46e+0) -	8.9830e+0 (4.88e+0) -	8.1656e+0 (5.06e+0) -	5.2901e+0 (5.61e+0) -	7.0263e+0 (5.68e+0) -	4.6736e+0 (5.19e+0) -	1.8980e−1 (4.11e−3) -	2.5247e−1 (5.80e−2) -	1.9953e−1 (1.81e−2) -	1.6511e−1 (5.45e−5)
	8	6.4110e+0 (5.71e+0) -	1.0124e+1 (4.20e+0) -	8.8411e+0 (4.85e+0) -	1.1572e+1 (2.72e+0) -	5.2733e+0 (5.71e+0) -	8.7426e+0 (4.98e+0) -	2.1311e+1 (2.24e+0) -	1.1604e+2 (1.93e+1) -	1.2365e+2 (1.70e+1) -	1.0942e+2 (9.85e+0) -	3.1542e−1 (4.01e−4)
	10	3.5311e+0 (5.49e+0) -	1.2517e+1 (5.13e+0) -	1.1578e+1 (5.44e+0) -	1.1682e+1 (5.76e+0) -	4.6522e+0 (6.39e+0) -	1.1051e+1 (5.87e+0) -	2.2314e+1 (1.91e+0) -	1.5002e+2 (1.55e+1) -	1.4579e+2 (1.48e+1) -	1.3473e+2 (1.57e+1) -	4.1996e−1 (4.59e−4)
	15	1.3161e+1 (3.96e+0) -	1.4881e+1 (7.23e−15) -	9.3568e+0 (6.24e+0) -	1.4107e+1 (3.45e+0) -	1.2142e+1 (5.18e+0) -	1.3874e+1 (2.48e+0) -	2.2541e+1 (1.52e+0) -	1.8118e+2 (1.05e+1) -	1.7849e+2 (7.35e+0) -	1.7511e+2 (7.15e+0) -	6.2513e−1 (1.07e−2)
C2_DTLZ2	3	4.8388e−2 (3.82e−4) -	8.0929e−1 (1.87e−1) -	5.6440e−2 (1.21e−3) -	1.4636e−1 (2.94e−2) -	4.8131e−2 (4.14e−4) -	5.5408e−2 (9.57e−4) -	1.5413e−1 (2.63e−1) -	4.4865e−2 (6.60e−4) +	4.5238e−2 (7.34e−4) +	4.5092e−2 (5.79e−4) +	4.6736e−2 (4.47e−4)
	5	1.3880e−1 (3.21e−4) -	9.0861e−1 (1.95e−1) -	1.4675e−1 (1.21e−3) -	2.2595e−1 (1.51e−2) -	1.3864e−1 (8.98e−4) -	1.4490e−1 (1.22e−3) -	2.0163e−1 (4.13e−3) -	1.4317e−1 (1.91e−3) -	1.4302e−1 (2.45e−3) -	1.3954e−1 (1.29e−3) -	1.3730e−1 (3.72e−4)
	8	3.0943e−1 (1.66e−1) -	1.3201e+0 (1.37e−1) -	2.3839e−1 (1.75e−3) -	2.9756e−1 (5.99e−3) -	2.6084e−1 (6.99e−2) -	2.3830e−1 (2.46e−3) -	7.6692e−1 (2.10e−1) -	2.7862e−1 (5.88e−3) -	3.0119e−1 (1.12e−1) -	2.7864e−1 (4.68e−3) -	2.3475e−1 (1.03e−3)
	10	2.9867e−1 (8.17e−2) -	1.2785e+0 (1.23e−1) -	3.3770e−1 (4.50e−2) -	3.9815e−1 (3.68e−2) -	2.9453e−1 (7.55e−2) -	2.8284e−1 (2.65e−3) -	7.6441e−1 (2.07e−1) -	3.7589e−1 (5.37e−2) -	3.8182e−1 (5.30e−2) -	3.0048e−1 (3.34e−3) -	2.5342e−1 (1.75e−3)
	15	4.0315e−1 (1.95e−1) -	1.4436e+0 (1.27e−1) -	2.6972e−1 (5.49e−3) +	3.5847e−1 (1.54e−2) -	3.2636e−1 (7.16e−2) -	2.6685e−1 (6.67e−3) =	1.0485e+0 (4.41e−2) -	4.0502e−1 (1.17e−1) -	3.7823e−1 (3.44e−2) -	3.5942e−1 (4.34e−3) -	2.7792e−1 (3.85e−2)
C3_DTLZ4	3	1.6714e−1 (2.29e−1) -	4.9293e−1 (3.69e−1) -	1.1251e−1 (2.84e−3) -	1.9931e−1 (1.08e−2) -	1.4715e−1 (1.89e−1) =	1.0837e−1 (2.90e−3) -	1.4903e−1 (4.12e−3) -	1.7413e−1 (2.26e−1) -	1.2544e−1 (1.35e−1) -	1.0162e−1 (1.71e−3) -	9.6727e−2 (6.76e−3)
	5	2.4577e−1 (9.07e−4) +	4.2896e−1 (6.00e−2) -	2.9058e−1 (2.70e−3) -	4.1223e−1 (1.71e−2) -	2.9674e−1 (1.26e−1) -	2.8014e−1 (2.23e−3) -	4.3753e−1 (2.15e−2) -	2.9621e−1 (5.60e−3) -	2.9659e−1 (4.37e−3) -	3.1528e−1 (6.81e−3) -	2.4646e−1 (9.17e−4)
	8	4.8463e−1 (8.85e−2) -	7.8663e−1 (1.00e−1) -	5.4737e−1 (3.61e−3) -	6.3383e−1 (5.52e−3) -	6.5925e−1 (7.66e−2) -	5.3235e−1 (4.01e−2) -	1.1467e+0 (2.29e−1) -	2.1495e+0 (1.55e−2) -	2.1532e+0 (2.35e−2) -	1.0767e+0 (5.14e−2) -	4.5240e−1 (1.37e−3)
	10	5.7647e−1 (2.95e−2) -	7.4832e−1 (6.16e−2) -	6.2254e−1 (5.49e−3) -	7.4351e−1 (1.01e−2) -	6.8257e−1 (2.99e−2) -	6.1341e−1 (5.10e−3) -	1.5677e+0 (2.24e−1) -	2.2620e+0 (8.41e−3) -	2.2605e+0 (9.40e−3) -	1.2231e+0 (6.93e−2) -	5.6575e−1 (1.92e−3)
	15	8.8392e−1 (7.18e−2) -	1.2092e+0 (2.13e−1) -	8.0478e−1 (8.14e−4) =	8.6019e−1 (1.05e−2) -	8.9130e−1 (6.60e−2) -	8.0885e−1 (1.06e−2) -	2.0933e+0 (1.65e−1) -	2.4880e+0 (9.28e−3) -	2.4897e+0 (9.81e−3) -	1.7600e+0 (1.66e−1) -	8.0729e−1 (7.30e−3)
DC1_DTLZ1	3	1.4171e−2 (2.08e−4) -	8.5097e−2 (7.94e−2) -	1.5193e−2 (2.86e−4) -	6.9675e−1 (3.91e−1) -	1.3659e−2 (1.71e−4) -	1.5771e−2 (1.93e−4) -	3.9118e−2 (5.26e−2) -	1.2028e−2 (9.49e−5) +	1.2193e−2 (1.54e−4) +	1.2155e−2 (1.76e−4) +	1.3441e−2 (1.79e−4)
	5	3.9838e−2 (1.66e−4) -	1.0296e−1 (8.89e−2) -	4.2027e−2 (4.10e−4) -	4.1156e−1 (1.82e−1) -	4.0467e−2 (1.37e−4) -	4.2269e−2 (3.45e−4) -	1.4487e+0 (2.95e+0) -	4.2931e−2 (8.93e−4) -	4.3592e−2 (1.10e−3) -	4.3503e−2 (8.31e−4) -	3.9222e−2 (2.01e−4)
	8	7.9405e−2 (3.49e−4) -	1.5747e−1 (1.01e−1) -	8.3722e−2 (7.83e−4) -	4.4538e−1 (1.39e−1) -	7.9243e−2 (5.95e−3) -	7.9963e−2 (7.57e−4) -	1.9710e+0 (3.14e+0) -	9.5292e−1 (7.71e−1) -	2.4032e+0 (1.71e+0) -	2.7226e+0 (6.16e+0) -	7.8712e−2 (4.62e−4)
	10	8.6661e−2 (2.54e−3) -	1.3065e−1 (6.75e−2) -	9.4437e−2 (2.20e−3) -	3.8517e−1 (1.32e−2) -	9.1340e−2 (1.57e−2) =	7.8762e−2 (2.11e−3) +	9.0116e−1 (2.35e+0) -	1.5949e+1 (2.66e+1) -	8.4254e+0 (1.31e+1) -	6.6049e+1 (4.30e+1) -	8.5535e−2 (3.50e−4)
	15	1.2831e−1 (4.74e−4) =	3.7718e−1 (1.00e−1) -	1.4233e−1 (6.33e−3) -	4.7192e−1 (1.85e−1) -	1.3542e−1 (6.46e−3) -	1.3437e−1 (6.44e−3) -	1.6273e+0 (2.72e+0) -	1.7559e+2 (3.41e+1) -	1.9601e+2 (3.27e+1) -	1.7509e+2 (4.41e+1) -	1.2824e−1 (3.56e−5)
DC1_DTLZ3	3	4.6182e−2 (8.08e−4) -	7.5739e−1 (6.20e−1) -	4.3119e−2 (1.24e−3) -	2.4204e+0 (6.29e−1) -	4.5442e−2 (8.81e−4) -	5.0164e−2 (2.60e−3) -	1.8304e+0 (2.63e+0) -	3.5491e−2 (2.87e−4) +	1.1967e−1 (1.22e−2) -	3.6419e−2 (6.04e−4) +	3.9421e−2 (9.47e−4)
	5	1.4439e−1 (7.55e−4) -	8.8198e−1 (4.30e−1) -	2.1898e−1 (2.90e−2) -	1.9932e+0 (5.10e−1) -	1.4426e−1 (7.68e−4) -	1.4814e−1 (1.26e−3) -	2.7296e+0 (1.49e+0) -	1.5380e−1 (3.49e−3) -	2.3892e−1 (4.90e−2) -	1.5655e−1 (5.05e−3) -	1.4282e−1 (8.97e−4)
	8	4.6456e−1 (1.06e−1) -	1.4782e+0 (6.35e−1) -	4.8976e−1 (3.74e−2) -	1.8398e+0 (4.67e−1) -	4.3037e−1 (1.13e−1) -	4.8240e−1 (7.81e−2) -	1.9521e+1 (6.68e+0) -	9.7315e+1 (1.04e+1) -	9.6550e+1 (9.92e+0) -	9.2617e+1 (1.15e+1) -	3.2833e−1 (3.88e−2)
	10	5.0848e−1 (3.36e−2) -	1.1976e+0 (1.52e−1) -	5.0451e−1 (2.88e−2) -	1.5937e+0 (2.42e−1) -	4.7635e−1 (5.52e−2) -	5.3172e−1 (4.02e−2) -	2.1042e+1 (5.77e+0) -	1.2820e+2 (1.96e+1) -	1.2783e+2 (2.22e+1) -	1.2017e+2 (1.64e+1) -	4.2703e−1 (3.11e−2)
	15	7.0664e−1 (5.26e−2) -	1.4486e+0 (4.16e−1) -	7.5391e−1 (6.29e−2) -	1.3974e+0 (1.14e−1) -	7.2232e−1 (6.14e−2) -	6.7388e−1 (1.68e−2) -	1.9561e+1 (6.34e+0) -	1.8314e+2 (7.12e+0) -	1.8222e+2 (6.10e+0) -	1.7097e+2 (7.49e+0) -	6.0801e−1 (1.53e−2)
DC2_DTLZ1	3	1.4121e−1 (5.47e−2) -	4.4372e−1 (1.10e−1) -	2.3142e−2 (1.64e−4) -	3.4230e−1 (3.88e−2) -	1.4038e−1 (2.59e−1) -	3.9740e−2 (4.97e−2) =	NaN (NaN)	2.1163e−2 (1.74e−4) -	2.1303e−2 (2.77e−4) -	8.4539e−2 (7.37e−2) -	2.0585e−2 (3.16e−5)
	5	1.1904e−1 (5.13e−2) -	4.4879e−1 (1.56e−1) -	6.1253e−2 (3.40e−4) -	3.6741e−1 (7.46e−2) -	8.7978e−2 (6.54e−2) -	6.6678e−2 (3.63e−2) -	NaN (NaN)	5.6980e−2 (1.04e−3) -	5.7216e−2 (1.01e−3) -	8.3301e−2 (4.46e−2) -	5.2703e−2 (1.24e−5)
	8	1.5374e−1 (2.95e−2) -	5.0946e−1 (1.44e−1) -	1.2430e−1 (7.27e−4) -	4.0216e−1 (7.02e−2) -	1.1450e−1 (2.95e−2) -	1.0856e−1 (2.59e−2) =	NaN (NaN)	NaN (NaN)	2.2591e−1 (0.00e+0) =	NaN (NaN)	9.7173e−2 (4.00e−5)
	10	1.6371e−1 (3.41e−2) -	6.4506e−1 (1.47e−1) -	1.4338e−1 (1.04e−3) -	4.3323e−1 (6.80e−2) -	1.1603e−1 (1.53e−2) -	1.1535e−1 (1.98e−2) =	NaN (NaN)	2.3380e−1 (7.98e−3) -	2.4261e−1 (0.00e+0) =	2.1240e−1 (0.00e+0) =	1.0924e−1 (9.25e−5)
	15	2.6711e−1 (4.90e−2) -	7.5599e−1 (7.79e−2) -	2.1687e−1 (4.12e−3) -	4.6611e−1 (1.28e−1) -	2.0479e−1 (3.87e−2) -	2.2509e−1 (5.07e−2) =	NaN (NaN)	NaN (NaN)	NaN (NaN)	NaN (NaN)	1.8312e−1 (9.08e−4)
DC2_DTLZ3	3	NaN (NaN)	NaN (NaN)	5.1407e−1 (1.36e−1) -	5.3954e−1 (2.34e−1) -	5.6252e−1 (7.92e−4) -	5.6290e−1 (3.93e−3) -	NaN (NaN)	5.5577e−2 (5.55e−4) +	1.2880e−1 (1.66e−1) -	5.6653e−1 (3.75e−3) -	7.7453e−2 (8.03e−2)
	5	5.9767e−1 (1.53e−3) -	1.3285e+0 (1.12e−1) -	3.0578e−1 (1.65e−1) -	5.9047e−1 (1.69e−1) -	6.3286e−1 (7.44e−2) -	6.0501e−1 (9.68e−3) -	NaN (NaN)	5.1390e−1 (2.02e−1) -	6.2292e−1 (6.59e−2) -	6.3820e−1 (1.88e−2) -	1.6504e−1 (1.24e−4)
	8	8.1512e−1 (4.09e−2) -	1.5661e+0 (7.73e−2) -	4.1644e−1 (1.10e−1) =	1.1275e+0 (4.48e−1) -	7.6298e−1 (6.29e−2) -	6.9270e−1 (1.49e−2) -	NaN (NaN)	8.2310e−1 (0.00e+0) =	NaN (NaN)	NaN (NaN)	3.7867e−1 (6.42e−2)
	10	8.4419e−1 (3.12e−2) -	1.6222e+0 (6.41e−2) -	4.3850e−1 (4.61e−2) =	9.8833e−1 (1.93e−1) -	7.8365e−1 (1.32e−1) -	7.9176e−1 (1.05e−2) -	9.5967e−1 (0.00e+0) =	8.6445e−1 (0.00e+0) =	8.4945e−1 (0.00e+0) =	8.5563e−1 (6.60e−3) -	4.4248e−1 (3.25e−2)
	15	1.0026e+0 (1.98e−2) -	1.7053e+0 (1.46e−3) -	6.3739e−1 (1.87e−2) -	1.4889e+0 (1.88e−1) -	9.5856e−1 (1.09e−1) -	9.7664e−1 (6.12e−3) -	1.1355e+0 (1.38e−1) -	NaN (NaN)	NaN (NaN)	NaN (NaN)	6.2688e−1 (1.30e−2)
DC3_DTLZ1	3	1.8985e−1 (1.01e−1) -	9.2166e+0 (1.21e+1) -	9.2066e−3 (2.70e−4) -	2.0076e+0 (1.25e+0) -	1.5542e−2 (2.93e−2) -	9.8425e−2 (8.07e−2) -	3.6156e+0 (2.94e+0) -	7.2053e−3 (8.90e−5) +	7.5990e−3 (3.66e−4) +	5.7873e−2 (7.50e−2) =	8.1517e−3 (1.02e−4)
	5	1.0734e−1 (5.16e−2) -	6.0361e+0 (9.03e+0) -	3.2263e−2 (5.22e−3) -	1.0480e+0 (5.36e−1) -	2.8726e−2 (1.52e−2) -	5.3204e−2 (4.84e−2) -	8.7646e+0 (7.34e+0) -	1.8746e−2 (6.67e−4) +	1.9470e−2 (6.96e−4) +	2.6404e−2 (2.91e−2) -	2.1367e−2 (7.46e−4)
DC3_DTLZ3	3	1.4704e+0 (4.10e−1) -	1.0056e+1 (9.17e+0) -	4.8771e−2 (3.30e−2) -	4.0190e+0 (1.08e+0) -	6.2978e−1 (3.10e−1) -	9.3609e−1 (4.52e−1) -	1.0109e+1 (3.88e+0) -	3.3601e−2 (2.87e−2) -	3.4534e−1 (1.98e−1) -	9.0422e−1 (3.76e−1) -	2.3069e−2 (4.38e−4)
	5	9.2709e−1 (4.17e−1) -	3.1616e+0 (1.60e+0) -	9.7792e−2 (1.36e−2) -	3.4930e+0 (9.29e−1) -	3.8017e−1 (2.44e−1) -	7.3050e−1 (2.84e−1) -	9.3152e+0 (6.55e+0) -	2.8038e−1 (2.09e−1) -	6.4652e−1 (1.49e−1) -	6.8763e−1 (2.53e−1) -	7.8344e−2 (1.85e−3)
	8	1.6474e+0 (5.88e−1) -	2.7607e+0 (5.51e−1) -	2.3947e−1 (6.44e−2) -	3.5893e+0 (1.14e+0) -	8.4779e−1 (6.01e−1) -	1.2897e+0 (3.60e−1) -	2.0797e+1 (5.84e+0) -	5.3433e+1 (1.11e+1) -	4.6698e+1 (1.08e+1) -	4.3766e+1 (9.50e+0) -	1.8735e−1 (2.87e−2)
	10	1.4446e+0 (6.44e−1) -	2.4439e+0 (5.79e−1) -	2.0325e−1 (6.70e−2) =	3.4611e+0 (9.84e−1) -	5.6973e−1 (3.24e−1) -	9.5002e−1 (3.52e−1) -	1.7307e+1 (4.91e+0) -	6.8489e+1 (9.43e+0) -	6.0150e+1 (9.55e+0) -	6.5345e+1 (8.19e+0) -	1.9546e−1 (8.80e−2)
	15	3.4727e+0 (1.44e+0) -	7.0692e+0 (5.93e+0) -	3.1701e+0 (6.91e−1) -	3.6492e+0 (1.27e+0) -	7.1588e−1 (2.45e−1) -	2.3985e+0 (5.99e−1) -	4.0817e+1 (5.82e+0) -	1.2969e+2 (4.01e+1) -	9.9678e+1 (1.42e+1) -	1.3491e+2 (2.96e+1) -	1.5429e−1 (1.73e−2)
+/-/=		1/42/3	0/46/0	1/42/4	0/47/0	0/43/4	2/38/7	0/35/2	6/36/2	4/37/3	4/36/3

DOI: 10.7717/peerjcs.2102/table-4

Notes:

The best results are in bold.

Comparison results on MW and CF test problem

Table 7 presents the Friedman ranking of the 11 algorithms in the MW and CF test problems with different numbers of objectives, respectively. Known for their discrete irregularity and small feasible ratios, MW and CF highlighted the robust integrated capability of dCMaOEA-RAE in navigating infeasible regions and exploring minute irregular feasible solutions. It is evident that dCMaOEA-RAE consistently secured the top position across all indicators and test problems. It was closely followed by CMME. Tables 8, 9 and 10 illustrate the detailed results of the algorithms using different metrics. CMME was effective certain effectiveness due to its enhanced mating and environmental selection. However, its performance was relatively unstable, resulting in higher standard deviations. Meanwhile, dCMaOEA-RAE demonstrated favorable execution in MW8, CF4, and CF12. These problems encompass various scenarios such as multimodal landscapes, irregular CPFs, convex shapes, and small feasible regions. This showcased dCMaOEA-RAE’s adeptness in tackling these complexities, which are challenging for other algorithms.

Table 5:

The IGDp performance values of dCMaOEA-RAE and other schemes on DTLZ benchmark problems.

Problem	M	NSGAIII	IDBEA	CTAEA	TiGE2	DCNSGAIII	CMME	ToP	CCMO	DDCMOEA	BiCo	dCMaOEA-RAE
C1_DTLZ1	3	1.5071e−2 (9.98e−4) -	3.4300e−1 (5.89e−2) -	1.6368e−2 (2.70e−4) -	2.0904e−1 (5.56e−2) -	1.4712e−2 (3.60e−4) =	1.4676e−2 (1.07e−4) =	NaN (NaN)	1.5076e−2 (3.51e−4) -	1.5154e−2 (3.29e−4) -	1.5405e−2 (4.84e−4) -	1.4676e−2 (1.47e−4)
	5	3.7117e−2 (1.93e−4) -	3.9090e−1 (7.37e−2) -	4.1657e−2 (3.23e−4) -	2.5660e−1 (6.84e−2) -	3.7066e−2 (1.26e−4) -	3.7268e−2 (1.88e−4) -	NaN (NaN)	3.6398e−2 (2.58e−4) +	3.6446e−2 (2.59e−4) +	3.6230e−2 (2.70e−4) +	3.6910e−2 (1.82e−4)
	8	6.3453e−2 (2.63e−4) -	4.2557e−1 (7.79e−2) -	8.5570e−2 (2.87e−3) -	3.7210e−1 (7.69e−2) -	6.4649e−2 (4.69e−3) -	6.4857e−2 (3.95e−3) -	3.8029e−1 (0.00e+0) =	7.3596e−2 (3.21e−3) -	7.2479e−2 (1.26e−3) -	6.8557e−2 (8.36e−4) -	6.2733e−2 (1.71e−4)
	10	6.8922e−2 (4.28e−4) -	4.1215e−1 (1.01e−1) -	1.0167e−1 (2.13e−3) -	4.0702e−1 (3.91e−2) -	7.0627e−2 (5.44e−3) -	7.2273e−2 (8.50e−3) =	2.6124e−1 (8.76e−2) -	8.1057e−2 (3.47e−3) -	8.0229e−2 (1.45e−3) -	7.3970e−2 (8.14e−4) -	6.8387e−2 (3.60e−4)
	15	1.2163e−1 (4.06e−3) -	5.2070e−1 (5.15e−2) -	1.6630e−1 (8.85e−3) -	4.4015e−1 (3.11e−2) -	1.1811e−1 (1.25e−2) =	1.1411e−1 (1.60e−2) +	2.8383e−1 (8.82e−2) -	1.4231e−1 (1.06e−2) -	1.4273e−1 (9.04e−3) -	1.1198e−1 (5.50e−3) +	1.1982e−1 (2.67e−3)
C1_DTLZ3	3	4.5493e+0 (4.02e+0) -	6.7784e+0 (2.85e+0) -	3.7412e−2 (2.46e−2) -	6.6561e+0 (2.83e+0) -	4.3051e+0 (4.03e+0) -	2.6882e+0 (3.83e+0) -	2.5388e+0 (3.75e+0) -	2.3800e−2 (4.84e−4) -	2.8914e−2 (1.68e−2) -	1.0915e+0 (2.77e+0) -	2.2516e−2 (5.70e−5)
	5	5.9199e+0 (5.45e+0) -	1.0469e+1 (3.49e+0) -	8.9443e+0 (4.95e+0) -	8.0714e+0 (5.16e+0) -	5.2435e+0 (5.65e+0) -	6.9822e+0 (5.73e+0) -	4.6065e+0 (5.24e+0) -	1.0212e−1 (7.25e−3) -	1.8576e−1 (7.38e−2) -	1.1577e−1 (2.58e−2) -	6.2004e−2 (6.08e−5)
	8	6.3259e+0 (5.80e+0) -	1.0061e+1 (4.30e+0) -	8.7839e+0 (4.93e+0) -	1.1529e+1 (2.79e+0) -	5.1740e+0 (5.79e+0) -	8.6753e+0 (5.08e+0) -	2.1294e+1 (2.24e+0) -	1.1603e+2 (1.93e+1) -	1.2365e+2 (1.70e+1) -	1.0942e+2 (9.85e+0) -	1.2206e−1 (5.31e−4)
	10	3.3633e+0 (5.58e+0) -	1.2420e+1 (5.29e+0) -	1.1533e+1 (5.51e+0) -	1.1579e+1 (5.90e+0) -	4.4943e+0 (6.49e+0) -	1.0965e+1 (6.01e+0) -	2.2295e+1 (1.91e+0) -	1.5002e+2 (1.55e+1) -	1.4579e+2 (1.48e+1) -	1.3473e+2 (1.57e+1) -	1.7495e−1 (1.78e−4)
	15	1.3117e+1 (4.04e+0) -	1.4850e+1 (9.03e−15) -	9.2640e+0 (6.34e+0) -	1.4056e+1 (3.53e+0) -	1.2075e+1 (5.30e+0) -	1.3848e+1 (2.53e+0) -	2.2521e+1 (1.52e+0) -	1.8118e+2 (1.05e+1) -	1.7849e+2 (7.35e+0) -	1.7511e+2 (7.15e+0) -	2.4861e−1 (2.05e−2)
C2_DTLZ2	3	2.1372e−2 (2.37e−4) -	6.3197e−1 (1.17e−1) -	2.3856e−2 (8.28e−4) -	6.1040e−2 (9.35e−3) -	2.1214e−2 (3.01e−4) -	2.3871e−2 (4.98e−4) -	9.8479e−2 (1.66e−1) -	2.0700e−2 (7.61e−4) =	2.0353e−2 (7.63e−4) =	2.0966e−2 (4.57e−4) -	2.0447e−2 (3.32e−4)
	5	5.5624e−2 (2.75e−4) -	6.7427e−1 (1.39e−1) -	5.6095e−2 (6.62e−4) -	8.3355e−2 (4.45e−3) -	5.7154e−2 (5.30e−4) -	5.7630e−2 (7.30e−4) -	1.4749e−1 (6.41e−3) -	8.0053e−2 (4.70e−3) -	7.7944e−2 (4.67e−3) -	7.6340e−2 (2.56e−3) -	5.5350e−2 (2.84e−4)
	8	1.3996e−1 (1.58e−1) -	9.8003e−1 (1.56e−1) -	6.0517e−2 (8.35e−4) +	6.8137e−2 (1.44e−3) +	9.4139e−2 (5.59e−2) -	6.5080e−2 (3.53e−3) +	6.3935e−1 (1.58e−1) -	1.8715e−1 (1.89e−2) -	2.0550e−1 (9.89e−2) -	1.8829e−1 (1.51e−2) -	7.4946e−2 (1.53e−3)
	10	1.1811e−1 (5.17e−2) -	9.0742e−1 (1.35e−1) -	1.4630e−1 (2.42e−2) -	1.6031e−1 (1.31e−2) -	1.1885e−1 (5.33e−2) -	1.0104e−1 (7.09e−4) -	6.3353e−1 (1.49e−1) -	2.7440e−1 (2.83e−2) -	2.7052e−1 (2.89e−2) -	2.2964e−1 (1.21e−2) -	9.6858e−2 (1.46e−3)
	15	1.8442e−1 (2.04e−1) =	1.0801e+0 (1.69e−1) -	6.1199e−2 (1.48e−3) +	7.6436e−2 (1.35e−2) -	1.0765e−1 (5.17e−2) -	6.4462e−2 (4.27e−3) +	8.4881e−1 (4.40e−2) -	3.1274e−1 (9.18e−2) -	2.9106e−1 (1.72e−2) -	2.8147e−1 (3.70e−3) -	7.3645e−2 (2.69e−2)
C3_DTLZ4	3	8.1424e−2 (1.04e−1) -	3.0240e−1 (2.36e−1) -	6.1324e−2 (2.73e−3) -	9.2891e−2 (3.91e−3) -	7.7509e−2 (8.48e−2) -	5.6539e−2 (2.04e−3) -	1.1098e−1 (6.11e−3) -	9.1339e−2 (1.00e−1) -	7.0274e−2 (5.96e−2) -	6.1555e−2 (2.72e−3) -	5.1679e−2 (5.38e−3)
	5	1.1982e−1 (3.19e−3) =	2.6732e−1 (4.22e−2) -	1.4618e−1 (2.01e−3) -	1.7275e−1 (8.94e−3) -	1.5202e−1 (5.97e−2) -	1.3551e−1 (1.68e−3) -	3.2848e−1 (1.85e−2) -	1.9558e−1 (6.87e−3) -	1.9549e−1 (6.97e−3) -	2.1764e−1 (8.24e−3) -	1.2111e−1 (2.55e−3)
	8	2.6476e−1 (5.25e−2) =	4.8561e−1 (4.53e−2) -	2.4637e−1 (1.41e−3) -	2.8048e−1 (2.06e−3) -	3.6549e−1 (6.55e−2) -	2.4301e−1 (1.78e−2) -	9.8181e−1 (2.17e−1) -	2.1174e+0 (1.66e−2) -	2.1210e+0 (2.21e−2) -	8.4204e−1 (7.49e−2) -	2.4287e−1 (2.33e−3)
	10	2.8542e−1 (1.41e−2) =	4.4309e−1 (4.32e−2) -	2.9814e−1 (2.67e−3) -	3.7084e−1 (1.09e−2) -	3.5775e−1 (4.38e−2) -	2.8302e−1 (3.49e−3) -	1.3896e+0 (2.32e−1) -	2.2284e+0 (9.38e−3) -	2.2265e+0 (1.06e−2) -	9.7925e−1 (9.13e−2) -	2.8104e−1 (8.99e−4)
	15	5.0147e−1 (9.69e−2) -	7.6127e−1 (2.14e−1) -	4.0003e−1 (4.78e−4) +	4.5801e−1 (1.04e−2) -	5.0953e−1 (8.36e−2) -	4.0187e−1 (5.14e−3) +	1.9129e+0 (2.14e−1) -	2.4356e+0 (1.00e−2) -	2.4366e+0 (1.10e−2) -	1.4336e+0 (2.32e−1) -	4.0669e−1 (1.06e−2)
DC1_DTLZ1	3	1.0188e−2 (3.36e−4) -	5.9860e−2 (5.73e−2) -	1.0676e−2 (2.41e−4) -	6.3877e−1 (4.09e−1) -	9.7869e−3 (2.38e−4) -	1.1292e−2 (2.06e−4) -	3.4279e−2 (5.34e−2) -	8.6929e−3 (2.44e−4) +	9.0721e−3 (4.35e−4) +	8.8226e−3 (4.32e−4) +	9.4730e−3 (1.52e−4)
	5	2.8071e−2 (1.68e−4) -	7.5701e−2 (7.52e−2) -	2.8782e−2 (3.05e−4) -	3.4897e−1 (1.90e−1) -	2.8384e−2 (1.59e−4) -	2.9380e−2 (2.75e−4) -	1.4320e+0 (2.96e+0) -	2.9986e−2 (6.57e−4) -	3.1803e−2 (1.13e−3) -	3.1071e−2 (7.60e−4) -	2.7511e−2 (2.06e−4)
	8	4.9284e−2 (3.08e−4) -	1.1482e−1 (9.17e−2) -	5.5199e−2 (6.80e−4) -	3.8672e−1 (1.50e−1) -	4.9115e−2 (3.16e−3) -	5.1719e−2 (8.18e−4) -	1.9325e+0 (3.17e+0) -	9.3636e−1 (7.79e−1) -	2.3949e+0 (1.72e+0) -	2.7066e+0 (6.16e+0) -	4.8935e−2 (4.24e−4)
	10	5.5262e−2 (1.05e−3) -	9.1598e−2 (6.62e−2) -	6.6001e−2 (2.20e−3) -	3.3369e−1 (1.38e−2) -	5.9687e−2 (9.38e−3) -	5.0651e−2 (2.46e−3) +	8.5308e−1 (2.36e+0) -	1.5943e+1 (2.66e+1) -	8.4220e+0 (1.31e+1) -	6.6049e+1 (4.30e+1) -	5.4699e−2 (3.58e−4)
	15	7.4143e−2 (9.39e−4) =	3.0707e−1 (1.11e−1) -	9.0981e−2 (4.49e−3) -	4.1096e−1 (1.95e−1) -	7.6779e−2 (4.96e−3) -	7.6754e−2 (4.30e−3) -	1.5758e+0 (2.75e+0) -	1.7559e+2 (3.41e+1) -	1.9601e+2 (3.27e+1) -	1.7509e+2 (4.41e+1) -	7.4060e−2 (4.41e−4)
DC1_DTLZ3	3	1.6203e−2 (7.38e−4) -	7.2363e−1 (6.17e−1) -	1.6831e−2 (8.74e−4) -	2.3042e+0 (6.63e−1) -	1.6513e−2 (7.26e−4) -	1.7507e−2 (1.22e−3) -	1.7876e+0 (2.64e+0) -	1.4190e−2 (6.95e−4) =	8.0907e−2 (1.60e−2) -	1.4054e−2 (4.70e−4) +	1.4419e−2 (3.03e−4)
	5	4.8471e−2 (3.79e−4) -	6.4856e−1 (4.60e−1) -	7.6827e−2 (9.02e−3) -	1.8042e+0 (5.49e−1) -	4.8692e−2 (6.71e−4) -	4.9736e−2 (9.46e−4) -	2.6777e+0 (1.53e+0) -	8.3787e−2 (5.83e−3) -	1.7425e−1 (6.03e−2) -	8.8537e−2 (6.01e−3) -	4.8206e−2 (6.44e−4)
	8	2.4523e−1 (1.13e−1) -	1.1572e+0 (6.92e−1) -	2.1490e−1 (4.59e−2) -	1.5979e+0 (5.21e−1) -	2.1918e−1 (1.15e−1) -	2.0597e−1 (4.43e−2) -	1.9492e+1 (6.72e+0) -	9.7313e+1 (1.04e+1) -	9.6549e+1 (9.92e+0) -	9.2615e+1 (1.15e+1) -	1.2875e−1 (3.00e−2)
	10	2.3071e−1 (3.88e−2) -	8.3413e−1 (1.14e−1) -	1.9902e−1 (1.20e−2) -	1.2943e+0 (2.85e−1) -	2.1556e−1 (6.08e−2) =	2.2052e−1 (1.72e−2) -	2.1015e+1 (5.80e+0) -	1.2820e+2 (1.96e+1) -	1.2782e+2 (2.22e+1) -	1.2017e+2 (1.64e+1) -	1.8044e−1 (1.81e−2)
	15	3.6545e−1 (8.55e−2) -	1.0587e+0 (4.81e−1) -	4.0432e−1 (1.08e−1) -	1.0242e+0 (1.45e−1) -	3.9700e−1 (1.01e−1) -	2.9844e−1 (1.97e−2) -	1.9525e+1 (6.39e+0) -	1.8314e+2 (7.12e+0) -	1.8222e+2 (6.10e+0) -	1.7097e+2 (7.49e+0) -	2.4723e−1 (2.18e−2)
DC2_DTLZ1	3	1.4040e−1 (5.65e−2) -	4.1064e−1 (9.82e−2) -	1.6410e−2 (3.64e−4) -	2.5655e−1 (3.47e−2) -	1.2849e−1 (2.41e−1) -	3.4643e−2 (5.17e−2) =	NaN (NaN)	1.5119e−2 (4.08e−4) -	1.5513e−2 (7.99e−4) -	8.1403e−2 (7.66e−2) -	1.4738e−2 (1.75e−4)
	5	1.1338e−1 (5.85e−2) -	4.0660e−1 (1.53e−1) -	4.3221e−2 (2.56e−4) -	2.9019e−1 (7.33e−2) -	7.5801e−2 (6.89e−2) =	5.3527e−2 (4.14e−2) =	NaN (NaN)	4.3852e−2 (1.57e−3) -	4.4832e−2 (1.69e−3) -	7.6669e−2 (4.77e−2) -	3.7589e−2 (3.96e−5)
	8	1.4102e−1 (3.95e−2) -	4.5940e−1 (1.47e−1) -	9.0082e−2 (9.09e−4) -	3.2493e−1 (7.34e−2) -	8.5652e−2 (4.06e−2) =	7.9495e−2 (3.59e−2) -	NaN (NaN)	NaN (NaN)	2.1694e−1 (0.00e+0) =	NaN (NaN)	6.3804e−2 (1.49e−4)
	10	1.4286e−1 (4.52e−2) -	6.0198e−1 (1.52e−1) -	1.0586e−1 (1.10e−3) -	3.6727e−1 (7.10e−2) -	7.5415e−2 (2.04e−2) -	7.8057e−2 (2.87e−2) -	NaN (NaN)	2.0939e−1 (2.52e−2) -	2.3065e−1 (0.00e+0) =	2.0059e−1 (0.00e+0) =	6.8932e−2 (1.00e−4)
	15	2.3120e−1 (6.31e−2) -	7.1874e−1 (8.29e−2) -	1.7049e−1 (5.05e−3) -	4.0874e−1 (1.37e−1) -	1.5173e−1 (5.11e−2) -	1.7862e−1 (6.78e−2) =	NaN (NaN)	NaN (NaN)	NaN (NaN)	NaN (NaN)	1.2195e−1 (1.12e−3)
DC2_DTLZ3	3	NaN (NaN)	NaN (NaN)	5.0295e−1 (1.50e−1) -	4.1451e−1 (3.39e−1) -	5.6204e−1 (7.77e−4) -	5.6240e−1 (3.76e−3) -	NaN (NaN)	2.5172e−2 (1.69e−3) +	9.9415e−2 (1.68e−1) -	5.6567e−1 (3.68e−3) -	4.8172e−2 (8.28e−2)
	5	5.8544e−1 (1.47e−3) -	1.1968e+0 (6.67e−2) -	1.9624e−1 (1.80e−1) -	3.7730e−1 (2.49e−1) -	6.0997e−1 (4.83e−2) -	5.9176e−1 (8.30e−3) -	NaN (NaN)	4.8620e−1 (2.30e−1) -	6.0770e−1 (8.59e−2) -	6.2759e−1 (1.86e−2) -	6.2047e−2 (6.82e−5)
	8	7.1946e−1 (2.62e−2) -	1.3449e+0 (5.88e−2) -	1.9755e−1 (1.37e−1) =	8.3837e−1 (4.89e−1) -	6.9204e−1 (3.97e−2) -	6.4366e−1 (4.78e−3) -	NaN (NaN)	7.8606e−1 (0.00e+0) =	NaN (NaN)	NaN (NaN)	1.5498e−1 (3.21e−2)
	10	7.3825e−1 (2.74e−2) -	1.3606e+0 (2.45e−2) -	1.6340e−1 (4.04e−2) +	6.6764e−1 (1.92e−1) -	6.6327e−1 (1.71e−1) -	6.9057e−1 (4.48e−3) -	7.5380e−1 (0.00e+0) =	8.1869e−1 (0.00e+0) =	8.0284e−1 (0.00e+0) =	8.1081e−1 (9.59e−3) -	1.8389e−1 (1.40e−2)
	15	8.2436e−1 (2.18e−2) -	1.4065e+0 (1.78e−3) -	2.5376e−1 (1.83e−2) +	1.2206e+0 (2.03e−1) -	7.5877e−1 (1.70e−1) -	7.8952e−1 (3.78e−3) -	9.6822e−1 (1.82e−1) -	NaN (NaN)	NaN (NaN)	NaN (NaN)	2.5884e−1 (1.75e−2)
DC3_DTLZ1	3	1.8963e−1 (1.02e−1) -	9.2109e+0 (1.21e+1) -	6.4401e−3 (2.25e−4) -	1.9866e+0 (1.26e+0) -	1.2833e−2 (2.98e−2) -	9.6676e−2 (8.24e−2) -	3.6118e+0 (2.94e+0) -	5.2763e−3 (2.52e−4) +	6.2000e−3 (7.51e−4) -	5.6977e−2 (7.56e−2) -	5.7532e−3 (1.16e−4)
	5	1.0550e−1 (5.47e−2) -	6.0264e+0 (9.03e+0) -	2.2297e−2 (3.94e−3) -	1.0259e+0 (5.49e−1) -	1.8314e−2 (8.07e−3) -	4.6251e−2 (5.19e−2) -	8.7615e+0 (7.34e+0) -	1.2866e−2 (5.80e−4) +	1.5066e−2 (1.16e−3) =	2.1411e−2 (3.04e−2) -	1.4656e−2 (7.67e−4)
DC3_DTLZ3	3	1.4702e+0 (4.10e−1) -	1.0041e+1 (9.17e+0) -	2.5030e−2 (2.75e−2) -	3.9622e+0 (1.10e+0) -	6.2874e−1 (3.12e−1) -	9.3571e−1 (4.52e−1) -	1.0102e+1 (3.89e+0) -	2.2802e−2 (3.19e−2) -	3.1587e−1 (2.16e−1) -	9.0262e−1 (3.76e−1) -	8.3682e−3 (5.55e−4)
	5	9.2330e−1 (4.18e−1) -	3.1029e+0 (1.62e+0) -	3.6526e−2 (9.16e−3) -	3.4067e+0 (9.54e−1) -	3.5355e−1 (2.70e−1) -	7.2354e−1 (2.86e−1) -	9.2965e+0 (6.57e+0) -	2.4476e−1 (2.24e−1) -	6.3199e−1 (1.63e−1) -	6.8480e−1 (2.53e−1) -	2.9814e−2 (1.26e−3)
	8	1.6388e+0 (5.91e−1) -	2.6413e+0 (5.86e−1) -	1.1580e−1 (4.07e−2) -	3.5271e+0 (1.17e+0) -	8.0235e−1 (6.24e−1) -	1.2803e+0 (3.64e−1) -	2.0791e+1 (5.84e+0) -	5.3431e+1 (1.11e+1) -	4.6694e+1 (1.08e+1) -	4.3764e+1 (9.50e+0) -	9.0387e−2 (2.96e−2)
	10	1.4288e+0 (6.42e−1) -	2.3043e+0 (6.11e−1) -	1.0824e−1 (3.12e−2) +	3.3303e+0 (1.02e+0) -	4.8189e−1 (3.09e−1) -	9.2788e−1 (3.60e−1) -	1.7295e+1 (4.92e+0) -	6.8487e+1 (9.43e+0) -	6.0148e+1 (9.55e+0) -	6.5343e+1 (8.19e+0) -	1.2956e−1 (4.21e−2)
	15	3.4292e+0 (1.45e+0) -	6.9724e+0 (5.97e+0) -	3.1329e+0 (6.98e−1) -	3.5671e+0 (1.27e+0) -	6.7397e−1 (2.49e−1) -	2.3755e+0 (5.97e−1) -	4.0806e+1 (5.82e+0) -	1.2969e+2 (4.01e+1) -	9.9677e+1 (1.42e+1) -	1.3491e+2 (2.96e+1) -	5.9004e−2 (2.50e−2)
+/-/=		0/41/5	0/46/0	6/40/1	1/46/0	0/42/5	5/37/5	0/35/2	5/35/4	2/37/5	4/38/1

DOI: 10.7717/peerjcs.2102/table-5

Notes:

The best results are in bold.

Table 6:

The HV performance values of dCMaOEA-RAE and other schemes on DTLZ benchmark problems.

Problem	M	NSGAIII	IDBEA	CTAEA	TiGE2	DCNSGAIII	CMME	ToP	CCMO	DDCMOEA	BiCo	dCMaOEA-RAE
C1_DTLZ1	3	8.3079e−1 (9.63e−3) -	8.1384e−2 (6.91e−2) -	8.3313e−1 (4.44e−3) -	3.0228e−1 (9.86e−2) -	8.3546e−1 (5.14e−3) =	8.3557e−1 (3.30e−3) =	NaN (NaN)	8.3238e−1 (6.38e−3) -	8.3264e−1 (6.65e−3) -	8.3142e−1 (5.85e−3) -	8.3668e−1 (3.15e−3)
	5	9.7357e−1 (4.68e−3) =	9.7600e−2 (9.50e−2) -	9.7664e−1 (1.68e−3) +	4.1091e−1 (1.74e−1) -	9.7730e−1 (2.65e−3) +	9.7655e−1 (4.20e−3) +	NaN (NaN)	9.7420e−1 (8.26e−3) -	9.7612e−1 (3.08e−3) +	9.7372e−1 (3.90e−3) =	9.7429e−1 (3.07e−3)
	8	9.7893e−1 (1.34e−2) -	1.0138e−1 (8.57e−2) -	9.9099e−1 (7.62e−3) +	2.0892e−1 (1.51e−1) -	9.8851e−1 (9.15e−3) =	9.9064e−1 (9.05e−3) +	1.9269e−1 (0.00e+0) =	9.7697e−1 (1.68e−2) -	9.7169e−1 (2.73e−2) -	9.9304e−1 (2.14e−3) +	9.8708e−1 (6.19e−3)
	10	9.9386e−1 (8.00e−3) =	1.3252e−1 (1.17e−1) -	9.9857e−1 (1.57e−3) +	1.6268e−1 (5.70e−2) -	9.9641e−1 (3.67e−3) =	9.9648e−1 (3.24e−3) =	4.7593e−1 (2.01e−1) -	9.8585e−1 (1.66e−2) -	9.8821e−1 (1.21e−2) -	9.9726e−1 (1.44e−3) =	9.9628e−1 (2.35e−3)
	15	9.8987e−1 (1.51e−2) =	3.7705e−2 (5.21e−2) -	9.9672e−1 (4.40e−3) +	1.3674e−1 (5.46e−2) -	9.9904e−1 (1.68e−3) +	9.9473e−1 (6.73e−3) +	4.5187e−1 (1.80e−1) -	9.7278e−1 (2.57e−2) -	9.7465e−1 (3.16e−2) -	9.9397e−1 (6.78e−3) =	9.9443e−1 (3.17e−3)
C1_DTLZ3	3	2.4047e−1 (2.80e−1) -	7.0244e−2 (1.83e−1) -	5.3015e−1 (4.06e−2) -	0.0000e+0 (0.00e+0) -	2.4159e−1 (2.81e−1) -	3.7197e−1 (2.68e−1) -	2.8998e−1 (2.34e−1) -	5.5833e−1 (8.94e−4) -	5.4974e−1 (2.74e−2) -	4.8312e−1 (1.93e−1) -	5.5951e−1 (9.75e−5)
	5	2.8929e−1 (3.88e−1) -	6.0718e−2 (2.07e−1) -	1.5756e−1 (2.94e−1) -	0.0000e+0 (0.00e+0) -	3.4392e−1 (4.00e−1) -	3.1487e−1 (3.93e−1) -	3.1292e−2 (5.77e−2) -	7.6360e−1 (8.34e−3) -	6.2188e−1 (1.29e−1) -	7.4071e−1 (4.20e−2) -	8.1268e−1 (3.91e−4)
	8	3.8594e−1 (4.52e−1) -	6.7505e−2 (2.33e−1) -	9.3339e−2 (2.14e−1) -	0.0000e+0 (0.00e+0) -	4.6273e−1 (4.44e−1) -	1.5470e−1 (3.18e−1) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	9.2377e−1 (4.09e−4)
	10	5.7396e−1 (4.76e−1) -	1.5151e−2 (3.45e−2) -	7.6375e−2 (2.12e−1) -	0.0000e+0 (0.00e+0) -	5.7572e−1 (4.72e−1) -	1.9406e−1 (3.58e−1) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	9.6960e−1 (2.38e−4)
	15	6.2260e−2 (2.37e−1) -	0.0000e+0 (0.00e+0) -	3.6518e−2 (1.39e−1) -	0.0000e+0 (0.00e+0) -	1.1863e−1 (3.05e−1) -	1.6573e−2 (9.08e−2) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	9.7806e−1 (2.12e−2)
C2_DTLZ2	3	5.0596e−1 (1.55e−3) -	4.4350e−2 (4.23e−2) -	5.0400e−1 (2.50e−3) -	4.0805e−1 (2.15e−2) -	5.0219e−1 (2.25e−3) -	5.0292e−1 (2.45e−3) -	4.1234e−1 (1.30e−1) -	5.1319e−1 (1.58e−3) +	5.1392e−1 (1.50e−3) +	5.1238e−1 (1.60e−3) +	5.0966e−1 (1.87e−3)
	5	7.5435e−1 (1.16e−3) -	6.8357e−2 (6.12e−2) -	7.4050e−1 (1.97e−3) -	6.5522e−1 (1.43e−2) -	7.4789e−1 (2.07e−3) -	7.4383e−1 (1.81e−3) -	5.2333e−1 (1.83e−2) -	7.3029e−1 (4.57e−3) -	7.3504e−1 (4.48e−3) -	7.3563e−1 (2.98e−3) -	7.5518e−1 (7.24e−4)
	8	7.7736e−1 (1.61e−1) -	2.9518e−2 (4.41e−2) -	7.9456e−1 (6.73e−3) -	7.8054e−1 (1.02e−2) -	8.2090e−1 (4.81e−2) -	7.9791e−1 (2.33e−2) -	2.4464e−1 (9.70e−2) -	7.7460e−1 (1.45e−2) -	7.6116e−1 (1.08e−1) -	7.7791e−1 (1.16e−2) -	8.4337e−1 (1.23e−3)
	10	8.8403e−1 (2.61e−2) -	5.3786e−2 (5.15e−2) -	8.7656e−1 (4.53e−3) -	8.7053e−1 (7.11e−3) -	8.8440e−1 (2.66e−2) -	8.8678e−1 (7.23e−4) -	2.7555e−1 (1.18e−1) -	8.3972e−1 (9.91e−3) -	8.4168e−1 (7.36e−3) -	8.3985e−1 (7.27e−3) -	9.0091e−1 (1.21e−3)
	15	8.5497e−1 (2.23e−1) -	2.6259e−2 (3.08e−2) -	9.3111e−1 (4.11e−3) -	8.6271e−1 (2.03e−2) -	9.3501e−1 (2.49e−2) -	9.4281e−1 (5.05e−3) -	1.7040e−1 (5.61e−2) -	8.6617e−1 (1.20e−1) -	8.9485e−1 (9.76e−3) -	9.0964e−1 (6.90e−3) -	9.5419e−1 (1.36e−2)
C3_DTLZ4	3	7.6826e−1 (8.07e−2) -	5.8664e−1 (1.48e−1) -	7.8483e−1 (1.75e−3) -	7.6185e−1 (3.01e−3) -	7.7262e−1 (6.57e−2) -	7.8802e−1 (1.42e−3) -	7.5108e−1 (4.54e−3) -	7.6293e−1 (7.65e−2) -	7.7913e−1 (4.57e−2) -	7.8602e−1 (1.77e−3) -	7.9176e−1 (3.85e−3)
	5	9.6444e−1 (6.33e−4) =	8.9923e−1 (2.56e−2) -	9.5706e−1 (6.58e−4) -	9.4841e−1 (2.77e−3) -	9.5397e−1 (2.30e−2) -	9.5980e−1 (5.37e−4) -	8.9026e−1 (8.92e−3) -	9.4627e−1 (2.02e−3) -	9.4633e−1 (2.09e−3) -	9.3852e−1 (3.04e−3) -	9.6418e−1 (4.87e−4)
	8	9.9365e−1 (5.77e−3) =	9.4139e−1 (2.46e−2) -	9.9435e−1 (1.28e−4) -	9.9226e−1 (2.35e−4) -	9.8274e−1 (8.96e−3) -	9.9470e−1 (1.51e−3) -	6.0447e−1 (1.91e−1) -	4.6487e−2 (4.96e−3) -	4.7454e−2 (5.64e−3) -	6.8927e−1 (5.55e−2) -	9.9592e−1 (1.21e−4)
	10	9.9930e−1 (3.41e−4) =	9.8939e−1 (4.92e−3) -	9.9903e−1 (3.95e−5) -	9.9750e−1 (5.26e−4) -	9.9740e−1 (1.61e−3) -	9.9917e−1 (7.54e−5) -	3.8396e−1 (1.71e−1) -	8.5281e−2 (4.30e−3) -	8.6897e−2 (3.72e−3) -	6.5068e−1 (6.80e−2) -	9.9941e−1 (2.50e−5)
	15	9.9907e−1 (1.30e−3) -	8.9733e−1 (1.89e−1) -	9.9998e−1 (3.35e−6) +	9.9965e−1 (1.01e−4) -	9.9887e−1 (2.12e−3) -	9.9997e−1 (1.70e−5) +	1.2437e−1 (7.96e−2) -	6.1290e−2 (5.04e−3) -	5.9072e−2 (4.18e−3) -	2.9820e−1 (8.53e−2) -	9.9996e−1 (3.26e−5)
DC1_DTLZ1	3	6.2853e−1 (1.80e−3) -	4.7633e−1 (1.30e−1) -	6.2711e−1 (8.56e−4) -	4.4992e−2 (7.19e−2) -	6.2523e−1 (1.56e−3) -	6.2462e−1 (2.53e−3) -	5.3679e−1 (1.04e−1) -	6.3120e−1 (1.03e−3) =	6.3008e−1 (1.30e−3) -	6.3007e−1 (1.70e−3) =	6.3080e−1 (7.35e−4)
	5	7.7271e−1 (1.02e−3) -	6.5021e−1 (1.86e−1) -	7.7004e−1 (6.49e−4) -	1.0812e−1 (5.02e−2) -	7.6993e−1 (8.79e−4) -	7.7093e−1 (8.96e−4) -	2.3086e−1 (2.55e−1) -	7.7030e−1 (8.49e−4) -	7.6717e−1 (2.62e−3) -	7.6534e−1 (1.59e−3) -	7.7335e−1 (2.79e−4)
	8	7.9422e−1 (1.97e−4) -	6.4863e−1 (2.37e−1) -	7.9142e−1 (1.56e−3) -	1.0051e−1 (5.52e−2) -	7.9418e−1 (3.63e−3) -	7.9443e−1 (3.26e−4) =	1.2615e−1 (1.33e−1) -	5.7474e−2 (1.35e−1) -	1.9399e−2 (7.75e−2) -	2.2937e−2 (7.98e−2) -	7.9450e−1 (2.41e−4)
	10	7.9615e−1 (1.87e−4) -	7.2697e−1 (1.82e−1) -	7.9611e−1 (8.32e−5) -	1.0508e−1 (2.29e−2) -	7.9096e−1 (1.80e−2) -	7.9620e−1 (1.07e−3) =	2.0599e−1 (1.35e−1) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	7.9640e−1 (6.24e−5)
	15	7.9780e−1 (5.25e−5) -	2.1553e−1 (1.25e−1) -	7.9690e−1 (6.67e−4) -	9.7776e−2 (3.14e−2) -	7.9701e−1 (8.79e−4) -	7.9692e−1 (1.77e−3) -	1.3018e−1 (1.43e−1) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	7.9782e−1 (1.26e−5)
DC1_DTLZ3	3	4.6770e−1 (1.21e−3) -	4.4299e−2 (9.85e−2) -	4.5969e−1 (2.38e−3) -	0.0000e+0 (0.00e+0) -	4.6689e−1 (1.75e−3) -	4.6456e−1 (1.75e−3) -	1.2582e−1 (1.55e−1) -	4.7178e−1 (1.19e−3) +	4.8450e−1 (3.04e−2) +	4.7192e−1 (9.03e−4) +	4.7020e−1 (6.42e−4)
	5	7.6343e−1 (8.32e−4) -	1.5999e−1 (1.91e−1) -	6.9317e−1 (2.77e−2) -	0.0000e+0 (0.00e+0) -	7.6326e−1 (1.11e−3) -	7.6066e−1 (1.70e−3) -	6.7052e−3 (2.15e−2) -	7.3878e−1 (6.61e−3) -	6.3025e−1 (1.21e−1) -	7.3260e−1 (7.72e−3) -	7.6433e−1 (6.39e−4)
	8	6.7891e−1 (2.12e−1) -	3.8186e−2 (5.80e−2) -	7.2227e−1 (9.72e−2) -	0.0000e+0 (0.00e+0) -	7.2117e−1 (2.11e−1) -	7.2086e−1 (1.15e−1) -	2.7222e−3 (1.49e−2) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	8.8759e−1 (2.46e−2)
	10	8.6427e−1 (6.05e−2) -	1.1858e−1 (7.32e−2) -	9.0575e−1 (1.34e−2) -	4.3598e−5 (1.67e−4) -	8.8727e−1 (8.32e−2) -	8.5660e−1 (3.52e−2) -	1.6414e−3 (8.99e−3) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	9.3396e−1 (2.37e−2)
	15	7.7122e−1 (1.99e−1) -	4.0233e−2 (2.95e−2) -	5.3964e−1 (2.87e−1) -	1.3883e−2 (3.04e−2) -	6.9292e−1 (2.23e−1) -	8.7544e−1 (5.45e−2) -	8.9910e−4 (4.92e−3) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	9.6829e−1 (2.64e−2)
DC2_DTLZ1	3	5.3565e−1 (1.38e−1) -	4.1253e−2 (4.80e−2) -	8.3793e−1 (8.03e−4) -	2.2592e−1 (6.28e−2) -	6.6866e−1 (3.24e−1) -	7.9298e−1 (1.26e−1) =	NaN (NaN)	8.4021e−1 (9.28e−4) -	8.3918e−1 (1.91e−3) -	6.7809e−1 (1.87e−1) -	8.4132e−1 (3.90e−4)
	5	8.8733e−1 (7.15e−2) -	9.4441e−2 (8.46e−2) -	9.7703e−1 (2.35e−4) -	3.1664e−1 (1.98e−1) -	9.1189e−1 (1.52e−1) =	9.6040e−1 (5.05e−2) =	NaN (NaN)	9.7553e−1 (1.02e−3) -	9.7512e−1 (9.53e−4) -	9.3350e−1 (7.07e−2) -	9.7981e−1 (1.25e−4)
	8	9.4308e−1 (2.81e−2) -	8.6927e−2 (8.75e−2) -	9.9630e−1 (1.49e−4) -	3.1972e−1 (1.85e−1) -	9.8299e−1 (2.83e−2) -	9.8646e−1 (2.53e−2) =	NaN (NaN)	NaN (NaN)	8.9944e−1 (0.00e+0) =	NaN (NaN)	9.9760e−1 (5.02e−5)
	10	9.8137e−1 (1.18e−2) -	3.5186e−2 (5.71e−2) -	9.9945e−1 (3.38e−5) -	2.5602e−1 (1.71e−1) -	9.9853e−1 (4.84e−3) =	9.9742e−1 (6.90e−3) =	NaN (NaN)	9.6718e−1 (2.83e−3) -	9.6177e−1 (0.00e+0) =	9.6774e−1 (0.00e+0) =	9.9968e−1 (1.69e−5)
	15	9.7648e−1 (1.39e−2) -	6.2107e−3 (2.28e−2) -	9.9983e−1 (4.90e−5) -	2.5592e−1 (2.64e−1) -	9.9098e−1 (1.48e−2) =	9.8683e−1 (1.42e−2) =	NaN (NaN)	NaN (NaN)	NaN (NaN)	NaN (NaN)	9.9992e−1 (7.81e−6)
DC2_DTLZ3	3	NaN (NaN)	NaN (NaN)	5.5219e−2 (1.37e−1) -	1.4459e−1 (1.67e−1) -	7.7810e−3 (2.66e−4) -	7.2387e−3 (1.58e−3) -	NaN (NaN)	5.5615e−1 (2.58e−3) +	4.6617e−1 (1.84e−1) -	1.3183e−2 (7.65e−4) -	5.2320e−1 (1.03e−1)
	5	7.1128e−2 (1.04e−3) -	2.6517e−4 (5.24e−4) -	5.9045e−1 (2.82e−1) -	3.2567e−1 (2.40e−1) -	6.1863e−2 (1.41e−2) -	5.7198e−2 (1.80e−2) -	NaN (NaN)	2.3767e−1 (3.15e−1) -	7.1011e−2 (1.08e−1) -	5.1734e−2 (1.04e−2) -	8.1290e−1 (5.15e−4)
	8	9.4008e−2 (2.98e−2) -	7.8746e−4 (1.68e−3) -	8.1248e−1 (2.46e−1) =	2.5644e−1 (3.05e−1) -	1.1812e−1 (3.80e−2) -	1.5532e−1 (4.23e−2) -	NaN (NaN)	6.0427e−2 (0.00e+0) =	NaN (NaN)	NaN (NaN)	8.9720e−1 (2.79e−2)
	10	1.9009e−1 (3.83e−2) -	5.1470e−4 (1.20e−3) -	9.5124e−1 (9.40e−2) =	2.7150e−1 (2.02e−1) -	2.7644e−1 (2.20e−1) -	1.3179e−1 (1.11e−1) -	5.1449e−2 (0.00e+0) =	1.2294e−1 (0.00e+0) =	1.2314e−1 (0.00e+0) =	9.4961e−2 (4.02e−3) -	9.5968e−1 (1.77e−2)
	15	2.0471e−2 (1.55e−2) -	0.0000e+0 (0.00e+0) -	9.5590e−1 (2.43e−2) -	1.4640e−2 (4.07e−2) -	1.1581e−1 (2.93e−1) -	0.0000e+0 (0.00e+0) -	7.6188e−2 (8.71e−2) -	NaN (NaN)	NaN (NaN)	NaN (NaN)	9.7109e−1 (1.80e−2)
DC3_DTLZ1	3	1.0301e−1 (1.18e−1) -	5.0216e−4 (2.75e−3) -	5.2385e−1 (3.52e−3) -	4.7724e−3 (1.82e−2) -	5.1341e−1 (7.88e−2) -	2.7861e−1 (2.20e−1) -	1.8447e−3 (7.04e−3) -	5.3458e−1 (1.44e−3) +	5.3150e−1 (2.74e−3) -	3.9225e−1 (1.99e−1) -	5.3403e−1 (1.29e−3)
	5	3.3519e−2 (5.65e−2) -	0.0000e+0 (0.00e+0) -	8.8720e−2 (1.34e−2) -	0.0000e+0 (0.00e+0) -	1.2609e−1 (7.73e−3) -	9.1221e−2 (5.15e−2) -	1.7315e−3 (9.48e−3) -	1.4590e−1 (1.19e−3) +	1.3700e−1 (4.01e−3) =	1.3026e−1 (3.55e−2) -	1.3680e−1 (1.54e−3)
DC3_DTLZ3	3	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	3.2375e−1 (5.53e−2) -	0.0000e+0 (0.00e+0) -	1.2013e−2 (6.58e−2) -	0.0000e+0 (0.00e+0) -	4.9475e−3 (2.71e−2) -	3.4162e−1 (5.41e−2) =	2.0874e−1 (1.74e−1) -	0.0000e+0 (0.00e+0) -	3.6432e−1 (1.79e−3)
	5	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	5.2809e−1 (2.60e−2) -	0.0000e+0 (0.00e+0) -	2.2979e−1 (2.86e−1) -	0.0000e+0 (0.00e+0) -	3.6063e−3 (1.98e−2) -	2.9958e−1 (2.52e−1) -	3.3183e−2 (1.27e−1) -	0.0000e+0 (0.00e+0) -	5.8852e−1 (2.50e−3)
	8	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	4.9611e−1 (6.96e−2) -	0.0000e+0 (0.00e+0) -	1.3614e−1 (2.78e−1) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	7.0329e−1 (3.00e−2)
	10	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	6.5133e−1 (4.80e−2) -	0.0000e+0 (0.00e+0) -	3.1313e−1 (3.60e−1) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	7.6613e−1 (2.81e−2)
	15	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	3.3276e−3 (1.33e−2) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	2.9572e−2 (3.65e−2)
+/-/=		0/40/6	0/46/0	5/40/2	0/47/0	2/39/6	4/34/9	0/35/2	5/35/4	3/37/4	3/35/5

DOI: 10.7717/peerjcs.2102/table-6

Notes:

The best results are in bold.

Table 7:

The Friedman ranking of the 11 algorithms in the MW and CF test problems.

	MW			CF
	Igd ranking	Igdp ranking	Hv ranking	Igd ranking	Igdp ranking	Hv ranking
NSGAIII	3.58	3.41	3.66	4.25	4.40	4.78
IDBEA	10.16	10.19	9.96	8.33	8.02	8.71
CTAEA	5.73	5.04	4.22	4.19	4.28	4.25
TiGE2	8.75	8.39	7.31	6.21	5.58	4.84
DCNSGAIII	3.78	3.52	3.61	3.50	3.81	3.82
CMME	3.30	2.95	3.38	3.45	2.90	3.02
ToP	7.20	7.53	7.90	8.04	8.16	8.07
CCMO	5.73	6.08	6.13	7.05	7.29	7.14
DDCMOEA	5.45	5.79	6.00	6.97	7.29	6.98
BiCo	5.04	5.93	6.22	7.17	7.45	7.13
dCMaOEA-RAE	1.96	1.86	2.31	1.52	1.49	1.94

DOI: 10.7717/peerjcs.2102/table-7

Notes:

The best results are in bold.

Effects of the proposed selection strategy

The proposed dual-population mechanism is further validated in this subsection by employing two variants of dCMaOEA-RAE. We adopted the reference point selection strategy from Jain & Deb (2014) to replace the selection strategy of the subject and exploration populations in the dCMaOEA-RAE algorithm, denoted as dCMAOEA-RAE-I and dCMAOEA-RAE-II, respectively. In C-DTLZ and DC-DTLZ experiments with identical parameters as in Section ‘Experimental settings’, we compared these aforementioned variants and are presented in Table 11. It is worth noting that even when the CPF is non-uniform, the selection strategy for the main population maintained a favorable distribution. Furthermore, the auxiliary population’s selection strategy effectively guided the population towards discovering a superior feasible solution region. Figure 8 shows the effectiveness of the three methods used in the DC3-DTLZ3 problem. It is evident that dCMAOEA-RAE-I failed to achieve a uniform distribution on the CPF, while dCMAOEA-RAE-II was unable to locate the CPF within the given time frame. dCMAOEA-RAE achieved the best performance.

Table 8:

The IGD performance values of dCMaOEA-RAE and other schemes on MW and CF benchmark problems.

Problem	M	NSGAIII	IDBEA	CTAEA	TiGE2	DCNSGAIII	CMME	ToP	CCMO	DDCMOEA	BiCo	dCMaOEA-RAE
MW4	3	4.1346e−2 (1.03e−4) +	5.3510e−1 (1.68e−1) -	4.6574e−2 (3.86e−4) -	9.2444e−2 (2.68e−2) -	4.1775e−2 (3.05e−4) -	4.1772e−2 (2.55e−3) -	NaN (NaN)	4.2790e−2 (3.94e−4) -	4.3134e−2 (4.43e−4) -	4.3125e−2 (4.31e−4) -	4.1556e−2 (8.50e−5)
	5	1.0481e−1 (5.10e−5) -	6.2830e−1 (1.63e−1) -	1.2460e−1 (7.45e−4) -	1.4335e−1 (4.64e−3) -	1.0504e−1 (1.16e−4) -	1.0471e−1 (4.73e−5) -	3.4736e−1 (2.11e−1) -	1.2323e−1 (1.90e−3) -	1.2415e−1 (2.59e−3) -	1.2582e−1 (2.54e−3) -	1.0466e−1 (4.81e−5)
	8	1.9815e−1 (1.79e−2) =	7.3962e−1 (1.92e−1) -	2.4861e−1 (1.22e−3) -	2.5424e−1 (1.29e−2) -	1.9563e−1 (1.09e−2) -	1.9424e−1 (5.16e−3) -	3.3111e−1 (1.79e−1) -	3.4269e−1 (1.21e−2) -	3.1111e−1 (1.20e−2) -	3.3144e−1 (1.04e−2) -	1.9345e−1 (9.29e−5)
	10	2.1732e−1 (6.17e−4) -	7.4992e−1 (1.78e−1) -	2.8787e−1 (1.50e−3) -	2.6195e−1 (4.54e−3) -	2.2966e−1 (1.83e−2) -	2.1779e−1 (7.00e−4) -	2.7979e−1 (7.59e−3) -	3.6658e−1 (7.92e−3) -	3.7324e−1 (7.58e−3) -	3.4167e−1 (7.16e−3) -	2.1565e−1 (4.79e−4)
	15	3.7106e−1 (1.43e−3) -	6.1677e−1 (8.02e−2) -	4.3220e−1 (1.54e−2) -	8.9734e−1 (1.45e−1) -	3.7025e−1 (2.30e−3) =	3.6383e−1 (3.40e−3) +	3.3544e−1 (6.68e−3) +	3.8830e−1 (5.74e−3) -	3.8721e−1 (5.39e−3) -	3.6461e−1 (7.79e−3) +	3.7002e−1 (2.57e−3)
MW8	3	5.5978e−2 (8.98e−3) -	8.0068e−1 (1.77e−1) -	5.5650e−2 (4.03e−3) -	1.3725e−1 (1.03e−1) -	4.9512e−2 (2.66e−3) -	5.6059e−2 (2.87e−3) -	7.5520e−1 (3.05e−1) -	4.9376e−2 (5.24e−3) =	5.0773e−2 (6.52e−3) -	4.7367e−2 (1.50e−3) =	4.6914e−2 (1.06e−3)
	5	1.7251e−1 (5.93e−2) -	1.0041e+0 (1.35e−1) -	1.7079e−1 (2.01e−3) -	9.4621e−1 (1.03e−1) -	1.5286e−1 (2.83e−4) +	1.5402e−1 (3.15e−3) -	6.9024e−1 (4.27e−1) -	1.6384e−1 (2.70e−3) -	1.6491e−1 (2.46e−3) -	1.6445e−1 (2.87e−3) -	1.5297e−1 (1.57e−4)
	8	3.3806e−1 (5.45e−2) -	1.1610e+0 (1.23e−1) -	3.5481e−1 (2.62e−3) -	1.1195e+0 (5.39e−2) -	3.1421e−1 (3.61e−2) -	3.1036e−1 (1.08e−2) -	5.1666e−1 (2.29e−1) -	4.2377e−1 (5.63e−3) -	3.8674e−1 (6.09e−3) -	4.0797e−1 (6.46e−3) -	3.0702e−1 (3.70e−4)
	10	4.0071e−1 (2.18e−2) -	1.2049e+0 (1.01e−1) -	4.1210e−1 (2.18e−3) -	1.1830e+0 (5.14e−2) -	4.0145e−1 (2.81e−2) -	4.0576e−1 (1.00e−2) -	4.6236e−1 (5.63e−3) -	4.8420e−1 (4.96e−3) -	4.8514e−1 (3.60e−3) -	4.7549e−1 (4.31e−3) -	3.9335e−1 (3.39e−4)
	15	6.3583e−1 (1.26e−2) -	1.2613e+0 (1.10e−1) -	6.4977e−1 (4.49e−3) -	1.2661e+0 (3.78e−2) -	6.3590e−1 (1.41e−2) -	6.2361e−1 (1.99e−3) =	6.4753e−1 (8.01e−3) -	6.8639e−1 (5.22e−3) -	6.8641e−1 (4.75e−3) -	6.7954e−1 (4.56e−3) -	6.2297e−1 (1.11e−3)
MW14	3	1.4173e−1 (6.05e−2) -	2.4198e+0 (4.30e−1) -	1.1203e−1 (7.44e−3) -	1.6621e−1 (8.43e−3) -	1.3470e−1 (2.36e−2) -	1.3348e−1 (5.32e−3) -	3.9380e−1 (5.07e−1) -	1.0776e−1 (1.86e−2) -	1.0422e−1 (2.57e−3) +	1.0359e−1 (3.47e−3) +	1.0718e−1 (2.33e−3)
	5	3.5957e−1 (3.79e−2) =	2.5722e+0 (6.35e−1) -	3.0796e−1 (5.24e−3) =	5.1383e−1 (1.07e−1) -	3.7462e−1 (3.84e−2) -	5.9738e−1 (7.17e−2) -	7.6569e−1 (1.06e−1) -	3.3206e−1 (5.00e−3) =	3.2991e−1 (7.00e−3) =	3.4341e−1 (1.19e−2) =	3.4779e−1 (6.39e−2)
	8	8.4285e−1 (1.81e−2) -	2.2333e+0 (2.56e−1) -	1.0653e+0 (3.23e−2) -	1.6886e+0 (1.66e−1) -	8.5748e−1 (2.45e−2) -	8.9219e−1 (4.80e−2) -	1.1373e+0 (3.17e−2) -	1.0958e+0 (8.18e−3) -	9.6001e−1 (2.06e−2) -	9.7758e−1 (1.20e−2) -	8.2505e−1 (1.58e−2)
	10	1.1364e+0 (2.70e−2) -	2.6975e+0 (1.64e−1) -	1.4082e+0 (4.57e−2) -	2.2269e+0 (8.02e−2) -	1.1661e+0 (3.05e−2) -	1.1100e+0 (5.22e−2) -	1.3607e+0 (1.33e−2) -	1.2092e+0 (2.07e−2) -	1.2016e+0 (1.65e−2) -	1.1445e+0 (8.87e−3) -	1.0287e+0 (3.38e−2)
	15	3.3138e+0 (5.26e−2) -	3.9256e+0 (1.29e−1) -	3.0267e+0 (9.82e−2) -	4.5330e+0 (3.33e−2) -	3.2478e+0 (5.32e−2) -	2.9776e+0 (1.27e−1) -	2.3851e+0 (1.59e−2) +	2.2046e+0 (4.51e−3) +	2.2060e+0 (3.90e−3) +	2.2208e+0 (6.17e−3) +	2.8376e+0 (1.07e−1)
Problem	M	NSGAIII	IDBEA	CTAEA	TiGE2	DCNSGAIII	CMME	ToP	CCMO	DDCMOEA	BiCo	dCMaOEA-RAE
CF4	3	2.7874e−1 (2.36e−1) -	1.9639e+0 (5.03e−1) -	1.3014e−1 (1.13e−1) -	3.1715e−1 (1.81e−1) -	1.3509e−1 (7.97e−2) -	3.0527e−1 (3.29e−1) -	1.8169e+0 (0.00e+0) =	1.4601e−1 (1.37e−1) =	2.4416e−1 (2.33e−1) =	1.4671e−1 (1.67e−1) -	1.0281e−1 (6.06e−2)
	5	5.1186e−1 (3.53e−1) -	1.7146e+0 (7.15e−1) -	3.8089e−1 (1.52e−1) -	7.0498e−1 (3.67e−1) -	3.7751e−1 (2.53e−1) -	4.2964e−1 (2.60e−1) -	1.9103e+0 (2.33e−1) -	4.6312e−1 (2.69e−1) -	3.2679e−1 (1.80e−1) =	3.5408e−1 (1.65e−1) -	2.4837e−1 (7.57e−2)
	8	7.3985e−1 (3.45e−1) -	1.4417e+0 (5.13e−1) -	5.5977e−1 (1.74e−1) -	8.5278e−1 (5.71e−1) -	6.2013e−1 (2.12e−1) -	5.7799e−1 (7.47e−2) -	1.7747e+0 (8.05e−1) -	1.0621e+0 (3.96e−1) -	1.1457e+0 (5.08e−1) -	1.1823e+0 (4.13e−1) -	5.0722e−1 (2.23e−1)
	10	6.7419e−1 (1.24e−1) -	1.1133e+0 (3.34e−1) -	5.8305e−1 (1.33e−1) =	7.7031e−1 (2.71e−1) -	6.2555e−1 (2.94e−2) -	6.5622e−1 (3.80e−2) -	1.7666e+0 (9.80e−1) -	1.3395e+0 (3.48e−1) -	1.2291e+0 (3.44e−1) -	1.5427e+0 (4.84e−1) -	5.2266e−1 (2.64e−2)
	15	8.8459e−1 (4.42e−1) -	1.0728e+0 (1.36e−1) -	7.1502e−1 (1.90e−1) =	7.6792e−1 (9.57e−2) -	7.8034e−1 (1.39e−2) -	7.8149e−1 (3.94e−2) -	1.7647e+0 (7.64e−1) -	1.8277e+0 (6.25e−1) -	2.4202e+0 (1.34e+0) -	1.8478e+0 (7.73e−1) -	6.8444e−1 (7.63e−2)
CF8	3	3.9755e−2 (1.64e−3) -	1.1639e+0 (4.42e−1) -	1.0639e−1 (2.95e−2) -	8.6543e−2 (8.95e−3) -	4.3037e−2 (1.56e−3) -	4.0327e−2 (8.39e−4) -	7.0123e−1 (3.23e−1) -	3.7801e−2 (1.34e−3) =	3.8347e−2 (1.09e−3) -	3.8073e−2 (1.40e−3) =	3.7546e−2 (9.19e−4)
	5	1.7553e−1 (2.60e−2) -	1.0117e+0 (4.14e−1) -	2.1613e−1 (5.33e−2) -	2.0680e−1 (1.00e−2) -	1.8213e−1 (6.87e−3) -	1.6425e−1 (4.45e−3) -	8.1078e−1 (1.48e−1) -	1.9636e−1 (1.05e−2) -	1.7891e−1 (7.62e−3) -	2.0177e−1 (7.94e−3) -	1.5310e−1 (4.78e−3)
	8	2.3475e−1 (1.34e−2) -	6.3313e−1 (1.81e−1) -	3.9845e−1 (1.62e−1) -	3.2142e−1 (3.92e−2) -	2.2564e−1 (1.95e−2) -	2.1694e−1 (1.35e−2) =	6.7238e−1 (1.37e−1) -	7.0495e−1 (1.01e−1) -	7.1514e−1 (1.16e−1) -	8.2211e−1 (1.59e−1) -	2.1246e−1 (7.63e−3)
	10	2.9697e−1 (2.49e−2) -	7.9193e−1 (1.96e−1) -	4.2456e−1 (1.20e−1) -	3.8367e−1 (4.47e−2) -	2.9648e−1 (3.08e−2) -	3.0264e−1 (1.99e−2) -	6.7894e−1 (7.12e−2) -	1.0749e+0 (1.05e−1) -	9.9753e−1 (9.53e−2) -	1.1600e+0 (2.44e−1) -	2.4757e−1 (1.86e−2)
	15	3.1541e−1 (2.25e−2) =	7.3267e−1 (1.01e−1) -	3.7981e−1 (1.81e−2) -	4.8627e−1 (4.87e−2) -	2.7887e−1 (1.89e−2) +	2.7830e−1 (1.81e−2) +	6.9293e−1 (8.91e−2) -	1.4265e+0 (2.58e−1) -	1.6848e+0 (9.48e−2) -	1.6510e+0 (1.93e−1) -	3.1348e−1 (1.19e−2)
CF12	3	4.8641e−1 (3.01e−1) -	1.1384e+0 (4.25e−1) -	1.5854e−1 (2.58e−1) -	3.3710e−1 (2.96e−1) -	1.1978e−1 (2.38e−1) -	2.0562e−1 (2.41e−1) -	8.0750e−1 (2.73e−1) -	1.2534e−1 (2.68e−1) =	1.2139e−1 (1.92e−1) =	6.9080e−2 (1.41e−1) =	4.5687e−2 (6.05e−2)
	5	3.5444e−1 (2.88e−1) -	8.7013e−1 (3.99e−1) -	1.8317e−1 (1.68e−1) =	4.1561e−1 (1.12e−1) -	2.3564e−1 (2.22e−1) -	2.0452e−1 (1.22e−1) -	4.4233e−1 (1.77e−1) -	3.9534e−1 (2.39e−1) -	2.6854e−1 (1.61e−1) -	4.2466e−1 (2.28e−1) -	1.2527e−1 (2.75e−2)
	8	3.2852e−1 (1.36e−1) -	5.8694e−1 (9.36e−2) -	3.3983e−1 (8.80e−2) -	4.7955e−1 (9.13e−2) -	2.8077e−1 (1.11e−1) -	2.6319e−1 (3.47e−2) -	4.0280e−1 (7.65e−2) -	7.6433e−1 (7.39e−2) -	7.5671e−1 (7.49e−2) -	7.8730e−1 (2.80e−2) -	2.0841e−1 (2.31e−2)
	10	3.4037e−1 (6.52e−2) -	5.3685e−1 (1.04e−1) -	3.0463e−1 (6.32e−2) -	5.6965e−1 (9.14e−2) -	3.0606e−1 (7.40e−2) -	3.0401e−1 (2.01e−2) -	3.5304e−1 (3.65e−2) -	8.5742e−1 (3.75e−2) -	8.1686e−1 (6.66e−2) -	8.1813e−1 (3.55e−2) -	2.2183e−1 (1.85e−2)
	15	3.0488e−1 (1.13e−1) =	5.3377e−1 (1.04e−1) -	4.8640e−1 (8.85e−2) -	6.3978e−1 (3.16e−2) -	3.6300e−1 (1.29e−1) -	2.7465e−1 (2.70e−2) +	3.5823e−1 (2.49e−2) -	1.0110e+0 (3.37e−2) -	1.0934e+0 (3.53e−2) -	8.7825e−1 (3.15e−2) -	2.7757e−1 (6.48e−2)
+/-/=		0/13/2	0/15/0	0/12/3	0/15/0	1/14/0	2/12/1	0/14/1	0/12/3	0/12/3	0/13/2

DOI: 10.7717/peerjcs.2102/table-8

Notes:

The best results are in bold.

Table 9:

The IGDp performance values of dCMaOEA-RAE and other schemes on MW and CF benchmark problems.

Problem	M	NSGAIII	IDBEA	CTAEA	TiGE2	DCNSGAIII	CMME	ToP	CCMO	DDCMOEA	BiCo	dCMaOEA-RAE
MW4	3	2.9289e−2 (1.03e−4) +	4.2468e−1 (1.58e−1) -	3.2597e−2 (2.71e−4) -	6.3474e−2 (1.63e−2) -	2.9571e−2 (2.29e−4) =	2.9623e−2 (2.04e−3) -	NaN (NaN)	3.0663e−2 (4.53e−4) -	3.0932e−2 (4.53e−4) -	3.1015e−2 (4.29e−4) -	2.9557e−2 (1.29e−4)
	5	7.4796e−2 (7.03e−5) -	5.0429e−1 (1.61e−1) -	8.8288e−2 (5.45e−4) -	9.9578e−2 (3.04e−3) -	7.5102e−2 (1.43e−4) -	7.4678e−2 (6.44e−5) +	2.8461e−1 (1.74e−1) -	9.4456e−2 (1.70e−3) -	9.4854e−2 (2.38e−3) -	9.8683e−2 (2.63e−3) -	7.4730e−2 (7.12e−5)
	8	1.2979e−1 (9.87e−3) -	5.8795e−1 (2.04e−1) -	1.8021e−1 (1.46e−3) -	1.7057e−1 (7.94e−3) -	1.2823e−1 (4.97e−3) -	1.2786e−1 (4.50e−3) -	2.6204e−1 (1.54e−1) -	3.0516e−1 (2.05e−2) -	2.7824e−1 (1.93e−2) -	2.9891e−1 (1.57e−2) -	1.2754e−1 (1.83e−4)
	10	1.3713e−1 (5.73e−4) -	6.1016e−1 (1.99e−1) -	2.1316e−1 (1.51e−3) -	1.7944e−1 (4.32e−3) -	1.4487e−1 (1.11e−2) -	1.3768e−1 (5.31e−4) -	2.1757e−1 (8.55e−3) -	3.2563e−1 (1.47e−2) -	3.3593e−1 (1.31e−2) -	3.0570e−1 (1.26e−2) -	1.3581e−1 (5.27e−4)
	15	2.5309e−1 (2.03e−3) -	4.5806e−1 (8.82e−2) -	3.3969e−1 (2.11e−2) -	7.7342e−1 (1.61e−1) -	2.5193e−1 (3.41e−3) =	2.4334e−1 (4.98e−3) +	2.2496e−1 (8.13e−3) +	2.9788e−1 (6.89e−3) -	2.9638e−1 (6.52e−3) -	2.7074e−1 (9.05e−3) -	2.5177e−1 (3.62e−3)
MW8	3	3.9993e−2 (1.42e−2) -	5.7774e−1 (9.08e−2) -	3.3213e−2 (9.00e−3) -	7.0014e−2 (5.32e−2) -	2.8480e−2 (6.68e−3) -	3.2699e−2 (6.96e−3) -	5.1278e−1 (2.02e−1) -	3.2390e−2 (9.86e−3) -	3.4976e−2 (1.07e−2) -	2.5398e−2 (4.45e−3) -	2.3117e−2 (4.69e−3)
	5	7.0555e−2 (2.88e−2) -	7.4154e−1 (7.69e−2) -	6.9426e−2 (3.12e−3) -	5.6557e−1 (9.53e−2) -	5.9255e−2 (2.50e−3) -	6.0619e−2 (3.94e−3) -	5.1355e−1 (2.94e−1) -	9.9077e−2 (5.55e−3) -	1.0132e−1 (5.79e−3) -	1.0259e−1 (5.12e−3) -	5.8090e−2 (1.41e−3)
	8	1.3577e−1 (3.06e−2) -	8.5910e−1 (8.38e−2) -	1.3838e−1 (4.46e−3) -	7.3811e−1 (4.13e−2) -	1.2060e−1 (2.03e−2) -	1.1870e−1 (5.41e−3) =	3.9139e−1 (1.74e−1) -	3.2516e−1 (9.41e−3) -	2.9701e−1 (8.61e−3) -	3.1057e−1 (1.10e−2) -	1.1446e−1 (1.31e−3)
	10	1.6430e−1 (1.40e−2) =	8.4317e−1 (5.78e−2) -	1.4699e−1 (3.24e−3) +	7.7858e−1 (3.46e−2) -	1.6406e−1 (1.83e−2) =	1.5094e−1 (8.88e−3) +	3.2069e−1 (1.32e−2) -	3.7183e−1 (7.68e−3) -	3.7267e−1 (5.58e−3) -	3.6790e−1 (6.13e−3) -	1.5847e−1 (2.07e−4)
	15	2.5413e−1 (1.25e−2) -	8.2425e−1 (1.07e−1) -	2.7904e−1 (5.16e−3) -	8.3885e−1 (2.98e−2) -	2.5562e−1 (1.42e−2) -	2.3796e−1 (2.83e−3) =	3.9988e−1 (1.48e−2) -	5.3852e−1 (1.30e−2) -	5.3698e−1 (1.03e−2) -	5.3801e−1 (9.76e−3) -	2.3786e−1 (3.33e−4)
MW14	3	9.0654e−2 (4.74e−2) -	1.3525e+0 (7.16e−2) -	6.3732e−2 (6.30e−3) +	8.5369e−2 (5.71e−3) -	8.3313e−2 (1.49e−2) -	7.7527e−2 (4.80e−3) -	3.1444e−1 (4.32e−1) -	7.1622e−2 (1.21e−2) -	6.9085e−2 (3.32e−3) -	6.7223e−2 (3.63e−3) =	6.5913e−2 (2.88e−3)
	5	2.5164e−1 (2.71e−2) -	1.6923e+0 (2.39e−1) -	1.8814e−1 (4.90e−3) +	2.9914e−1 (4.64e−2) -	2.6388e−1 (2.77e−2) -	4.4066e−1 (7.58e−2) -	6.7475e−1 (1.23e−1) -	2.2313e−1 (4.57e−3) =	2.2090e−1 (4.88e−3) =	2.6601e−1 (7.40e−3) -	2.2524e−1 (3.29e−2)
	8	6.0095e−1 (1.82e−2) -	1.6448e+0 (2.44e−1) -	8.2161e−1 (4.28e−2) -	9.7918e−1 (1.29e−1) -	6.1068e−1 (1.57e−2) -	6.0961e−1 (2.01e−2) -	9.3345e−1 (5.24e−2) -	8.5644e−1 (1.64e−2) -	7.0419e−1 (2.68e−2) -	7.5409e−1 (1.99e−2) -	5.5625e−1 (1.02e−2)
	10	6.8197e−1 (1.38e−2) -	1.7954e+0 (1.32e−1) -	1.0278e+0 (4.30e−2) -	1.2109e+0 (4.29e−2) -	7.0376e−1 (1.82e−2) -	6.8679e−1 (2.60e−2) -	1.0212e+0 (2.81e−2) -	9.7390e−1 (2.92e−2) -	9.6252e−1 (2.42e−2) -	8.9199e−1 (1.40e−2) -	6.2209e−1 (1.65e−2)
	15	1.5370e+0 (3.28e−2) -	1.9926e+0 (1.17e−1) -	1.8635e+0 (4.55e−2) -	2.4193e+0 (2.87e−2) -	1.5042e+0 (3.45e−2) -	1.6214e+0 (1.41e−1) -	1.5120e+0 (1.85e−2) -	1.3596e+0 (3.33e−2) =	1.3643e+0 (2.48e−2) -	1.4821e+0 (3.19e−2) -	1.3495e+0 (3.76e−2)
+/-/=		1/13/1	0/15/0	3/12/0	0/15/0	0/12/3	3/10/2	1/13/0	0/13/2	0/14/1	0/14/1
Problem	M	NSGAIII	IDBEA	CTAEA	TiGE2	DCNSGAIII	CMME	ToP	CCMO	DDCMOEA	BiCo	dCMaOEA-RAE
CF4	3	2.5749e−1 (2.48e−1) -	1.9349e+0 (4.94e−1) -	1.0778e−1 (1.23e−1) =	2.7235e−1 (2.08e−1) -	1.1140e−1 (9.26e−2) -	2.8786e−1 (3.41e−1) -	1.7723e+0 (0.00e+0) =	1.3125e−1 (1.46e−1) =	2.3481e−1 (2.40e−1) =	1.3039e−1 (1.75e−1) =	7.9945e−2 (7.23e−2)
	5	4.6652e−1 (3.79e−1) -	1.6673e+0 (7.29e−1) -	3.1371e−1 (1.77e−1) -	6.1577e−1 (4.18e−1) -	3.0539e−1 (2.79e−1) -	3.6565e−1 (2.90e−1) -	1.9036e+0 (2.44e−1) -	4.2723e−1 (2.90e−1) -	2.8740e−1 (2.02e−1) -	3.0548e−1 (1.90e−1) -	1.6527e−1 (1.04e−1)
	8	6.0122e−1 (4.24e−1) -	1.3679e+0 (5.52e−1) -	4.2633e−1 (2.35e−1) -	7.4308e−1 (6.19e−1) -	4.4543e−1 (2.89e−1) -	3.9912e−1 (1.60e−1) -	1.7444e+0 (8.22e−1) -	9.7088e−1 (4.37e−1) -	1.0620e+0 (5.51e−1) -	1.1019e+0 (4.60e−1) -	3.4447e−1 (2.81e−1)
	10	4.7550e−1 (2.01e−1) -	9.6959e−1 (3.97e−1) -	4.1533e−1 (1.87e−1) -	5.9737e−1 (3.44e−1) -	3.8232e−1 (9.90e−2) -	4.4791e−1 (1.32e−1) -	1.7040e+0 (1.03e+0) -	1.2273e+0 (3.76e−1) -	1.1269e+0 (3.87e−1) -	1.4596e+0 (5.21e−1) -	2.9085e−1 (4.97e−2)
	15	6.8697e−1 (5.09e−1) -	9.0722e−1 (2.11e−1) -	5.0084e−1 (2.38e−1) -	5.2603e−1 (1.83e−1) -	5.1275e−1 (1.25e−1) -	5.3619e−1 (1.58e−1) -	1.7417e+0 (7.70e−1) -	1.6453e+0 (6.89e−1) -	2.2494e+0 (1.43e+0) -	1.7250e+0 (8.22e−1) -	4.4977e−1 (1.70e−1)
CF8	3	3.1652e−2 (1.94e−3) -	1.1386e+0 (4.73e−1) -	8.5985e−2 (2.06e−2) -	6.0930e−2 (6.76e−3) -	3.7001e−2 (1.72e−3) -	3.0683e−2 (7.98e−4) -	6.9780e−1 (3.25e−1) -	3.2867e−2 (1.70e−3) -	3.3349e−2 (1.27e−3) -	3.3070e−2 (1.80e−3) -	2.9468e−2 (1.01e−3)
	5	1.1606e−1 (1.13e−2) -	9.0091e−1 (4.76e−1) -	1.3901e−1 (4.64e−2) -	1.0173e−1 (6.84e−3) -	1.2223e−1 (6.03e−3) -	9.7557e−2 (3.71e−3) -	7.7930e−1 (1.54e−1) -	1.6096e−1 (1.34e−2) -	1.5010e−1 (8.61e−3) -	1.6823e−1 (9.00e−3) -	9.0641e−2 (3.57e−3)
	8	1.6626e−1 (1.16e−2) -	4.5019e−1 (2.51e−1) -	2.9224e−1 (1.59e−1) -	1.5502e−1 (1.64e−2) -	1.6170e−1 (1.47e−2) -	1.2843e−1 (5.95e−3) +	6.3877e−1 (1.47e−1) -	6.5518e−1 (1.16e−1) -	6.7043e−1 (1.24e−1) -	7.6669e−1 (1.91e−1) -	1.4202e−1 (9.04e−3)
	10	1.8864e−1 (1.84e−2) -	5.7974e−1 (2.60e−1) -	2.7780e−1 (1.11e−1) -	1.9705e−1 (2.25e−2) -	1.9541e−1 (2.13e−2) -	1.5847e−1 (8.78e−3) =	6.2191e−1 (8.30e−2) -	1.0119e+0 (1.21e−1) -	9.3561e−1 (1.19e−1) -	1.0793e+0 (2.77e−1) -	1.5876e−1 (1.47e−2)
	15	2.5077e−1 (2.40e−2) -	5.3343e−1 (1.58e−1) -	2.4071e−1 (1.27e−2) -	2.6381e−1 (2.25e−2) -	2.3607e−1 (1.65e−2) -	1.7904e−1 (1.19e−2) +	6.3907e−1 (9.60e−2) -	1.3891e+0 (2.91e−1) -	1.6652e+0 (1.13e−1) -	1.6332e+0 (2.15e−1) -	2.2342e−1 (1.19e−2)
CF12	3	3.8140e−1 (3.05e−1) -	1.0455e+0 (4.42e−1) -	1.5463e−1 (2.60e−1) -	3.0743e−1 (3.11e−1) -	1.1515e−1 (2.39e−1) -	1.9649e−1 (2.40e−1) -	7.3841e−1 (2.89e−1) -	1.2271e−1 (2.69e−1) =	1.1983e−1 (1.92e−1) -	6.6585e−2 (1.42e−1) =	4.1701e−2 (6.16e−2)
	5	3.0979e−1 (2.77e−1) -	7.7571e−1 (4.18e−1) -	1.6041e−1 (1.75e−1) =	3.4556e−1 (1.24e−1) -	2.1588e−1 (2.30e−1) -	1.7765e−1 (1.33e−1) -	3.9326e−1 (1.63e−1) -	3.7825e−1 (2.44e−1) -	2.5649e−1 (1.64e−1) -	4.0799e−1 (2.34e−1) -	1.0132e−1 (3.18e−2)
	8	2.6319e−1 (1.32e−1) -	4.1857e−1 (1.21e−1) -	2.8634e−1 (1.03e−1) -	3.9054e−1 (1.07e−1) -	2.1781e−1 (1.28e−1) -	2.0438e−1 (4.80e−2) -	3.4100e−1 (8.98e−2) -	7.3697e−1 (9.46e−2) -	7.2558e−1 (9.66e−2) -	7.8037e−1 (2.94e−2) -	1.5545e−1 (3.19e−2)
	10	2.7927e−1 (8.13e−2) -	3.8577e−1 (1.28e−1) -	2.4053e−1 (7.44e−2) -	4.8997e−1 (1.10e−1) -	2.3407e−1 (8.52e−2) -	2.2826e−1 (2.57e−2) -	2.8170e−1 (4.36e−2) -	8.3995e−1 (4.44e−2) -	7.9354e−1 (8.68e−2) -	8.0399e−1 (4.35e−2) -	1.5412e−1 (2.55e−2)
	15	2.1264e−1 (1.40e−1) =	3.7450e−1 (1.29e−1) -	4.1921e−1 (1.04e−1) -	5.4726e−1 (3.67e−2) -	2.7843e−1 (1.55e−1) -	1.7495e−1 (3.61e−2) =	2.4987e−1 (2.01e−2) -	9.8260e−1 (3.76e−2) -	1.0658e+0 (3.91e−2) -	8.5561e−1 (3.35e−2) -	1.8532e−1 (8.48e−2)
+/-/=		0/14/1	0/15/0	0/13/2	0/15/0	0/15/0	2/11/2	0/14/1	0/13/2	0/14/1	0/13/2

DOI: 10.7717/peerjcs.2102/table-9

Notes:

The best results are in bold.

Table 10:

The HV performance values of dCMaOEA-RAE and other schemes on MW and CF benchmark problems.

Problem	M	NSGAIII	IDBEA	CTAEA	TiGE2	DCNSGAIII	CMME	ToP	CCMO	DDCMOEA	BiCo	dCMaOEA-RAE
MW4	3	8.4145e−1 (1.08e−4) +	2.3817e−1 (9.33e−2) -	8.3812e−1 (2.84e−4) -	7.7874e−1 (2.80e−2) -	8.4107e−1 (3.45e−4) =	8.4071e−1 (3.79e−3) -	NaN (NaN)	8.3983e−1 (5.83e−4) -	8.3959e−1 (5.83e−4) -	8.3914e−1 (5.40e−4) -	8.4112e−1 (1.44e−4)
	5	9.7987e−1 (1.42e−4) =	2.5165e−1 (8.31e−2) -	9.7694e−1 (2.15e−4) -	9.6827e−1 (2.11e−3) -	9.7980e−1 (1.33e−4) =	9.7988e−1 (1.50e−4) +	7.0289e−1 (2.37e−1) -	9.7335e−1 (7.11e−4) -	9.7311e−1 (9.90e−4) -	9.7028e−1 (1.14e−3) -	9.7980e−1 (1.36e−4)
	8	9.9713e−1 (2.01e−3) =	2.5338e−1 (9.73e−2) -	9.9625e−1 (1.35e−4) -	9.8708e−1 (6.65e−3) -	9.9750e−1 (5.78e−4) =	9.9754e−1 (2.22e−4) =	8.9256e−1 (2.10e−1) -	9.7439e−1 (3.49e−3) -	9.8316e−1 (2.28e−3) -	9.7518e−1 (2.04e−3) -	9.9758e−1 (5.23e−5)
	10	9.9968e−1 (2.27e−5) =	2.5479e−1 (1.14e−1) -	9.9944e−1 (2.77e−5) -	9.9858e−1 (3.97e−4) -	9.9902e−1 (1.80e−3) =	9.9968e−1 (1.37e−5) =	9.9412e−1 (9.99e−4) -	9.9332e−1 (4.29e−4) -	9.9302e−1 (3.61e−4) -	9.9418e−1 (3.02e−4) -	9.9967e−1 (1.96e−5)
	15	9.9990e−1 (1.02e−5) -	6.3492e−1 (1.25e−1) -	9.9986e−1 (1.50e−5) -	2.4233e−1 (1.50e−1) -	9.9990e−1 (7.66e−6) =	9.9990e−1 (1.01e−5) -	9.9976e−1 (3.31e−5) -	9.9992e−1 (8.87e−6) +	9.9992e−1 (1.02e−5) +	9.9993e−1 (8.97e−6) +	9.9990e−1 (1.09e−5)
MW8	3	5.1180e−1 (2.47e−2) -	6.0227e−2 (4.48e−2) -	5.1631e−1 (1.59e−2) -	4.3885e−1 (9.40e−2) -	5.3113e−1 (1.17e−2) -	5.1983e−1 (1.28e−2) -	1.1356e−1 (1.29e−1) -	5.2841e−1 (1.79e−2) -	5.2341e−1 (1.88e−2) -	5.4133e−1 (7.78e−3) =	5.4121e−1 (8.41e−3)
	5	7.9491e−1 (3.93e−2) -	4.9124e−2 (3.14e−2) -	7.8761e−1 (4.73e−3) -	1.4422e−1 (5.68e−2) -	8.1026e−1 (2.86e−3) -	8.0784e−1 (5.90e−3) -	2.8673e−1 (2.49e−1) -	7.6652e−1 (7.43e−3) -	7.6249e−1 (7.65e−3) -	7.6013e−1 (7.46e−3) -	8.1157e−1 (1.77e−3)
	8	9.0627e−1 (2.86e−2) -	5.5880e−2 (3.60e−2) -	9.0678e−1 (4.21e−3) -	1.2706e−1 (2.40e−2) -	9.1896e−1 (1.60e−2) -	9.2039e−1 (3.85e−3) -	5.2887e−1 (1.65e−1) -	6.9051e−1 (1.78e−2) -	7.5224e−1 (1.66e−2) -	7.2151e−1 (1.95e−2) -	9.2357e−1 (8.28e−4)
	10	9.6606e−1 (9.22e−3) -	7.6649e−2 (2.52e−2) -	9.6408e−1 (1.36e−3) -	1.2046e−1 (2.66e−2) -	9.6550e−1 (1.43e−2) =	9.6760e−1 (1.91e−3) -	7.3265e−1 (2.11e−2) -	7.8154e−1 (9.06e−3) -	7.7941e−1 (8.40e−3) -	7.8296e−1 (9.39e−3) -	9.6948e−1 (1.91e−4)
	15	9.8076e−1 (8.48e−3) -	1.4583e−1 (1.61e−1) -	9.3112e−1 (7.04e−3) -	1.1517e−1 (3.28e−2) -	9.7927e−1 (9.93e−3) -	9.8822e−1 (4.46e−3) -	7.3366e−1 (2.97e−2) -	7.0558e−1 (9.71e−3) -	7.0550e−1 (8.88e−3) -	6.9588e−1 (1.64e−2) -	9.9046e−1 (1.24e−4)
MW14	3	4.5879e−1 (2.83e−2) -	1.3010e−2 (6.73e−3) -	4.6637e−1 (3.77e−3) -	4.4582e−1 (4.54e−3) -	4.6379e−1 (7.79e−3) -	4.6464e−1 (3.70e−3) -	3.5887e−1 (1.61e−1) -	4.6872e−1 (6.28e−3) -	4.7030e−1 (3.63e−3) -	4.6572e−1 (4.10e−3) -	4.7200e−1 (2.36e−3)
	5	3.5753e−1 (1.61e−2) -	3.3504e−3 (7.86e−3) -	3.9543e−1 (3.88e−3) +	3.6694e−1 (1.62e−2) =	3.5286e−1 (1.91e−2) -	2.7439e−1 (2.08e−2) -	1.4241e−1 (4.90e−2) -	3.8912e−1 (3.12e−3) +	3.9010e−1 (2.31e−3) +	3.7165e−1 (2.79e−3) =	3.7269e−1 (1.59e−2)
	8	2.2297e−1 (5.40e−3) -	7.7490e−3 (1.13e−2) -	2.4924e−1 (6.82e−3) =	2.5048e−1 (1.98e−2) +	2.2710e−1 (7.45e−3) -	2.1931e−1 (1.82e−2) -	7.1659e−2 (1.66e−2) -	1.3412e−1 (1.21e−2) -	1.6040e−1 (9.08e−3) -	1.8116e−1 (9.99e−3) -	2.3804e−1 (2.19e−2)
	10	2.0448e−1 (3.94e−3) -	5.9731e−3 (1.03e−2) -	2.3281e−1 (5.15e−3) +	2.4060e−1 (1.02e−2) +	2.0460e−1 (4.41e−3) -	2.1629e−1 (1.22e−2) =	8.3505e−2 (2.35e−2) -	9.8631e−2 (2.09e−2) -	8.7729e−2 (1.93e−2) -	1.0571e−1 (2.06e−2) -	2.1926e−1 (6.31e−3)
	15	1.5314e−1 (2.81e−3) -	1.5010e−1 (6.97e−3) -	1.5495e−1 (2.72e−3) -	1.0444e−1 (4.94e−3) -	1.4540e−1 (2.01e−3) -	1.5952e−1 (3.96e−3) =	1.5091e−1 (1.43e−2) -	5.0262e−3 (4.34e−3) -	3.8760e−3 (3.44e−3) -	4.5549e−3 (9.60e−3) -	1.5950e−1 (3.10e−3)
+/-/=		1/11/3	0/15/0	2/12/1	2/12/1	0/9/6	1/10/4	0/14/0	2/13/0	2/13/0	1/12/2
Problem	M	NSGAIII	IDBEA	CTAEA	TiGE2	DCNSGAIII	CMME	ToP	CCMO	DDCMOEA	BiCo	dCMaOEA-RAE
CF4	3	2.1851e−1 (1.39e−1) -	0.0000e+0 (0.00e+0) -	3.2993e−1 (1.08e−1) =	1.6366e−1 (1.21e−1) -	3.1812e−1 (1.03e−1) -	2.2409e−1 (1.47e−1) -	0.0000e+0 (0.00e+0) =	3.0642e−1 (1.31e−1) =	2.3407e−1 (1.47e−1) -	3.1949e−1 (1.32e−1) -	3.5245e−1 (8.95e−2)
	5	1.4248e−2 (1.94e−2) -	0.0000e+0 (0.00e+0) -	2.2867e−2 (1.81e−2) -	1.0441e−2 (1.34e−2) -	2.8453e−2 (2.06e−2) -	2.4517e−2 (2.64e−2) -	0.0000e+0 (0.00e+0) -	1.6121e−2 (1.97e−2) -	3.2761e−2 (2.77e−2) -	2.6162e−2 (2.06e−2) -	5.7694e−2 (2.60e−2)
	8	6.8585e−4 (7.51e−4) -	2.7990e−7 (1.29e−6) -	5.5645e−4 (4.88e−4) -	2.1065e−4 (3.95e−4) -	1.0133e−3 (6.83e−4) -	1.3023e−3 (1.07e−3) =	0.0000e+0 (0.00e+0) -	9.9240e−8 (2.70e−7) -	2.6130e−7 (9.19e−7) -	2.3805e−6 (6.21e−6) -	1.3651e−3 (8.93e−4)
	10	5.7391e−5 (5.13e−5) -	3.1228e−7 (8.93e−7) -	2.5140e−5 (1.96e−5) -	3.7022e−5 (3.77e−5) -	1.0095e−4 (5.25e−5) =	1.1084e−4 (1.05e−4) =	0.0000e+0 (0.00e+0) -	2.2733e−11 (8.99e−11) -	1.9845e−9 (1.06e−8) -	6.1339e−9 (3.21e−8) -	1.2048e−4 (2.76e−5)
	15	8.3250e−8 (8.70e−8) =	6.3372e−11 (1.61e−10) -	1.3009e−8 (1.23e−8) -	6.2761e−8 (4.98e−8) -	1.2302e−7 (7.58e−8) +	1.4354e−7 (1.12e−7) +	0.0000e+0 (0.00e+0) -	7.7199e−16 (3.62e−15) -	3.1682e−15 (9.49e−15) -	2.3660e−15 (9.48e−15) -	9.6979e−8 (5.33e−8)
CF8	3	2.2498e−1 (2.72e−3) -	3.7582e−3 (1.10e−2) -	1.6136e−1 (2.08e−2) -	1.9275e−1 (7.88e−3) -	2.1746e−1 (2.22e−3) -	2.2573e−1 (1.57e−3) -	7.0995e−3 (1.47e−2) -	2.2579e−1 (2.10e−3) -	2.2531e−1 (1.55e−3) -	2.2433e−1 (2.19e−3) -	2.2680e−1 (1.60e−3)
	5	2.6927e−1 (1.29e−2) -	1.0666e−2 (1.62e−2) -	2.3169e−1 (6.21e−2) -	2.8069e−1 (9.69e−3) -	2.6228e−1 (8.43e−3) -	2.9133e−1 (4.99e−3) -	1.6904e−3 (3.06e−3) -	2.1877e−1 (1.47e−2) -	2.3418e−1 (1.03e−2) -	2.0919e−1 (1.01e−2) -	3.0242e−1 (4.74e−3)
	8	7.0072e−2 (1.03e−2) -	1.0188e−2 (8.94e−3) -	3.6058e−2 (3.85e−2) -	9.3233e−2 (7.72e−3) +	7.0002e−2 (1.36e−2) -	1.0138e−1 (6.13e−3) +	1.7981e−4 (4.74e−4) -	9.3405e−5 (2.92e−4) -	1.0920e−4 (5.65e−4) -	3.8865e−5 (2.13e−4) -	8.2937e−2 (6.07e−3)
	10	1.2409e−1 (1.72e−2) -	4.8998e−3 (5.36e−3) -	8.4751e−2 (4.19e−2) -	1.2798e−1 (1.85e−2) -	1.1367e−1 (1.59e−2) -	1.5730e−1 (5.07e−3) +	1.7567e−3 (1.81e−3) -	5.1527e−8 (2.82e−7) -	9.2729e−6 (5.06e−5) -	1.4456e−5 (7.92e−5) -	1.5109e−1 (7.48e−3)
	15	1.0529e−2 (4.47e−3) -	5.9518e−4 (1.27e−3) -	3.8934e−2 (5.49e−3) +	3.5485e−2 (9.58e−3) =	5.7219e−3 (2.66e−3) -	2.4147e−2 (4.10e−3) -	1.0581e−4 (1.25e−4) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	0.0000e+0 (0.00e+0) -	3.4936e−2 (2.89e−3)
CF12	3	3.8683e−1 (2.11e−1) -	4.2158e−2 (7.32e−2) -	5.6890e−1 (2.59e−1) -	3.4110e−1 (2.22e−1) -	6.3439e−1 (2.06e−1) -	4.9787e−1 (2.77e−1) -	6.5318e−2 (8.63e−2) -	6.4245e−1 (2.30e−1) =	6.1007e−1 (2.18e−1) =	6.8629e−1 (1.54e−1) =	7.0904e−1 (1.17e−1)
	5	7.0639e−1 (2.84e−1) -	1.2679e−1 (1.16e−1) -	8.7269e−1 (2.01e−1) -	6.0749e−1 (2.02e−1) -	8.2216e−1 (2.52e−1) -	8.6234e−1 (1.58e−1) -	4.5740e−1 (1.57e−1) -	5.7809e−1 (3.20e−1) -	7.4101e−1 (2.30e−1) -	5.2243e−1 (2.70e−1) -	9.4250e−1 (3.27e−2)
	8	8.3101e−1 (1.66e−1) -	2.9044e−1 (8.27e−2) -	8.6778e−1 (1.02e−1) -	8.1219e−1 (1.69e−1) -	8.9698e−1 (1.58e−1) =	9.1898e−1 (7.88e−2) -	6.9062e−1 (9.47e−2) -	2.6858e−1 (4.48e−2) -	2.7911e−1 (5.48e−2) -	2.6118e−1 (2.30e−2) -	9.7087e−1 (2.17e−2)
	10	9.7140e−1 (3.72e−2) -	3.0165e−1 (8.13e−2) -	9.8856e−1 (2.73e−2) -	8.3423e−1 (1.83e−1) -	9.7873e−1 (4.03e−2) =	9.8856e−1 (5.68e−3) -	8.2950e−1 (3.84e−2) -	3.3259e−1 (2.30e−2) -	4.1362e−1 (3.30e−2) -	3.8638e−1 (1.76e−2) -	9.9038e−1 (5.79e−3)
	15	8.2411e−1 (1.20e−1) -	3.1671e−1 (7.34e−2) -	9.4826e−1 (7.77e−2) -	9.2284e−1 (2.93e−2) -	9.4371e−1 (1.07e−1) =	9.1963e−1 (8.64e−2) -	8.7218e−1 (9.69e−2) -	3.4662e−1 (2.29e−2) -	2.2330e−1 (2.19e−2) -	5.1265e−1 (2.42e−2) -	9.7434e−1 (6.94e−2)
+/-/=		0/14/1	0/15/0	1/13/1	1/13/1	1/10/4	3/10/2	0/14/1	0/13/2	0/14/1	0/14/1

DOI: 10.7717/peerjcs.2102/table-10

Notes:

The best results are in bold.

Table 11:

The IGD performance of dCMaOEA-RAE and the variants on DTLZ benchmark problems.

Problem	M	dCMaOEA-RAE-I	dCMaOEA-RAE-II	dCMaOEA-RAE
C1_DTLZ1	3	2.0307e−2 (1.63e−4) =	2.0479e−2 (5.54e−4) =	2.0304e−2 (1.06e−4)
	5	5.1975e−2 (1.97e−4) =	6.1374e−2 (5.13e−2) -	5.1809e−2 (3.13e−4)
	8	9.5552e−2 (4.64e−4) -	1.0287e−1 (1.21e−2) -	9.5362e−2 (3.70e−4)
	10	1.0781e−1 (3.40e−4) =	1.1133e−1 (5.99e−3) -	1.0777e−1 (4.01e−4)
	15	1.8056e−1 (3.54e−3) =	1.8646e−1 (6.00e−3) -	1.8093e−1 (2.25e−3)
C1_DTLZ3	3	5.4470e−2 (4.84e−6) =	2.2349e+0 (3.55e+0) -	5.4471e−2 (5.79e−6)
	5	1.6510e−1 (4.01e−5) =	2.4353e+0 (4.25e+0) -	1.6511e−1 (5.45e−5)
	8	3.1541e−1 (5.37e−4) =	4.8279e+0 (5.41e+0) -	3.1542e−1 (4.01e−4)
	10	4.1997e−1 (4.15e−4) =	2.5805e+0 (4.71e+0) -	4.1996e−1 (4.59e−4)
	15	6.2727e−1 (1.07e−2) =	1.0509e+1 (6.08e+0) -	6.2513e−1 (1.07e−2)
C2_DTLZ2	3	4.7274e−2 (4.76e−4) -	4.7139e−2 (5.42e−4) -	4.6736e−2 (4.47e−4)
	5	1.3763e−1 (3.99e−4) -	1.3775e−1 (3.98e−4) -	1.3730e−1 (3.72e−4)
	8	2.4102e−1 (2.64e−2) -	2.4176e−1 (2.07e−2) -	2.3475e−1 (1.03e−3)
	10	2.5928e−1 (2.13e−3) -	2.6511e−1 (5.23e−2) -	2.5342e−1 (1.75e−3)
	15	2.8690e−1 (4.83e−2) =	2.7273e−1 (2.16e−2) +	2.7792e−1 (3.85e−2)
C3_DTLZ4	3	1.2057e−1 (1.36e−1) =	9.3242e−2 (5.43e−4) +	9.6727e−2 (6.76e−3)
	5	2.4665e−1 (9.25e−4) =	2.4623e−1 (1.17e−3) =	2.4646e−1 (9.17e−4)
	8	4.5868e−1 (3.11e−2) =	4.5755e−1 (3.35e−2) =	4.5240e−1 (1.37e−3)
	10	5.6612e−1 (2.08e−3) =	5.6809e−1 (1.90e−3) -	5.6575e−1 (1.92e−3)
	15	8.0926e−1 (1.33e−2) =	8.0865e−1 (1.04e−2) -	8.0729e−1 (7.30e−3)
DC1_DTLZ1	3	1.3872e−2 (2.32e−4) -	1.3633e−2 (2.21e−4) -	1.3441e−2 (1.79e−4)
	5	3.9356e−2 (1.80e−4) -	3.9801e−2 (1.79e−4) -	3.9222e−2 (2.01e−4)
	8	7.8816e−2 (3.73e−4) =	7.9226e−2 (3.57e−4) -	7.8712e−2 (4.62e−4)
	10	8.5651e−2 (2.45e−4) =	8.5942e−2 (2.73e−4) -	8.5535e−2 (3.50e−4)
	15	1.2824e−1 (3.14e−5) =	1.2822e−1 (2.07e−4) =	1.2824e−1 (3.56e−5)
DC1_DTLZ3	3	4.3553e−2 (9.34e−4) -	4.1805e−2 (1.07e−2) -	3.9421e−2 (9.47e−4)
	5	1.4300e−1 (7.63e−4) =	1.4290e−1 (9.92e−4) =	1.4282e−1 (8.97e−4)
	8	3.3113e−1 (4.32e−2) =	4.2799e−1 (9.94e−2) -	3.2833e−1 (3.88e−2)
	10	4.2458e−1 (3.37e−2) =	4.5276e−1 (3.55e−2) -	4.2703e−1 (3.11e−2)
	15	6.1091e−1 (1.98e−2) =	7.0825e−1 (8.42e−2) -	6.0801e−1 (1.53e−2)
DC2_DTLZ1	3	2.0576e−2 (2.74e−5) =	2.5392e−2 (2.63e−2) =	2.0585e−2 (3.16e−5)
	5	5.2706e−2 (1.63e−5) =	5.2703e−2 (1.08e−5) =	5.2703e−2 (1.24e−5)
	8	9.7176e−2 (5.01e−5) =	1.0520e−1 (1.64e−2) =	9.7173e−2 (4.00e−5)
	10	1.0926e−1 (8.35e−5) =	1.2099e−1 (2.56e−2) =	1.0924e−1 (9.25e−5)
	15	1.8335e−1 (8.73e−4) =	1.9088e−1 (2.87e−2) =	1.8312e−1 (9.08e−4)
DC2_DTLZ3	3	8.8731e−2 (1.13e−1) =	5.6710e−1 (8.12e−3) -	7.7453e−2 (8.03e−2)
	5	1.6503e−1 (7.61e−5) =	5.8769e−1 (7.98e−2) -	1.6504e−1 (1.24e−4)
	8	3.6504e−1 (6.94e−2) =	7.2973e−1 (6.67e−2) -	3.7867e−1 (6.42e−2)
	10	4.4066e−1 (4.17e−2) =	7.9912e−1 (3.39e−2) -	4.4248e−1 (3.25e−2)
	15	6.3066e−1 (1.64e−2) =	9.8775e−1 (1.77e−2) -	6.2688e−1 (1.30e−2)
DC3_DTLZ1	3	9.8363e−3 (3.60e−4) -	1.1807e−2 (1.80e−2) -	8.1517e−3 (1.02e−4)
	5	2.2668e−2 (8.43e−4) -	2.1306e−2 (4.72e−4) =	2.1367e−2 (7.46e−4)
DC3_DTLZ3	3	3.2289e−2 (1.81e−2) -	6.6723e−1 (2.40e−1) -	2.3069e−2 (4.38e−4)
	5	8.2585e−2 (3.19e−3) -	5.4976e−1 (1.42e−1) -	7.8344e−2 (1.85e−3)
	8	1.7583e−1 (4.57e−2) +	8.7158e−1 (3.96e−1) -	1.8735e−1 (2.87e−2)
	10	2.2435e−1 (8.87e−2) =	7.1864e−1 (2.46e−1) -	1.9546e−1 (8.80e−2)
	15	1.7843e−1 (6.40e−2) =	1.0644e+0 (5.13e−1) -	1.5429e−1 (1.73e−2)
+/-/=		1/12/34	2/34/11

DOI: 10.7717/peerjcs.2102/table-11

Notes:

The best results are in bold.

Intuitive experimental results

To provide a visual representation of the experimental outcomes, Figs. 9, 10, 11 and 12 show the parallel coordinates of the final nondominated solutions that were achieved by the 11 algorithms in problems like DC3-DTLZ3, DC1-DTLZ3, and C1-DTLZ3, with five, eight, and 15 objectives, respectively. To demonstrate the efficacy of the designed algorithm, we magnified part of the images. It is evident that dCMaOEA-RAE attains a more diverse and superior set of feasible solutions than the other algorithms. This further supports the high performance of the designed environmental selection strategy in enhancing the population’s search for better feasible regions. It directed the main population to be evenly distributed within the feasible region. Additionally, Fig. 13 illustrates the evolution process concerning changes in the objective space and decision variables for both the main and exploration populations. The proposed algorithm managed to maintain certain suboptimal solutions, thereby preventing the decision variables from becoming overly uniform and avoiding local optima.

Conclusions

Within this report, we introduced a novel dual-population constrained many-objective optimization algorithm named dCMaOEA-RAE. This approach addresses the issue of reduced performance in traditional algorithms that happens. Specifically, we designed two distinct search strategies for the two populations to ensure that the population could identify the optimal feasible regions in a timely manner. We found that coordination between different populations when using dCMaOEA-RAE reached a satisfactory balance between feasibility, convergence, and diversity. However, there are still some limitations to be addressed. For instance, further enhancements are needed in the performance of dCMaOEA-RAE when dealing with problems featuring small feasible regions. The number of poor solutions retained in this method is fixed, which may affect the efficiency of population search. In addition, using the most efficient method possible to ensure the uniform distribution of the population on the irregular CPFs has also become a challenge. The above problems are likely to be solved by the theory of swarm intelligence algorithms. We suggest focusing on exploring this research field. In the future, we will make an attempt to add the theory of swarm intelligence algorithm and machine learning to create simple and efficient optimization algorithms that would enhance their effectiveness in handling CMaOPs.

Supplemental Information