Fast and exact fixed-radius neighbor search based on sorting

Introduction

This work is concerned with the retrieval of nearest neighbors, a fundamental data operation. Given a data point, this operation aims at finding the most similar data points using a predefined distance function. Nearest neighbor search has many applications in computer science and machine learning, including object recognition (Philbin et al., 2007; Nister & Stewenius, 2006), image descriptor matching (Silpa-Anan & Hartley, 2008), time series indexing (Keogh & Ratanamahatana, 2005; Chakrabarti et al., 2002; Yagoubi et al., 2020), clustering (Ester et al., 1996; Campello, Moulavi & Sander, 2013; Gallego et al., 2018; Alshammari, Stavrakakis & Takatsuka, 2021; Gallego, Rico-Juan & Valero-Mas, 2022; Li et al., 2020), particle simulations (Groß, Köster & Krüger, 2019), molecular modeling (Galvelis & Sugita, 2017), pose estimation (Shakhnarovich, Viola & Darrell, 2003), computational linguistics (Kaminska, Cornelis & Hoste, 2021), and information retrieval (Geng et al., 2008; Wang et al., 2015).

There are two main types of nearest neighbor (NN) search: k-nearest neighbor and fixed-radius near neighbor search. Fixed-radius NN search, also referred to as radius query, aims at identifying all data points within a given distance from a query point; see Bentley (1975b) for a historical review. The most straightforward way of finding nearest neighbors is via a linear search through the whole database, also known as exhaustive or brute force search. Though considered inelegant, it is still widely used, e.g., in combination with GPU acceleration (Garcia, Debreuve & Barlaud, 2008).

Existing NN search approaches can be broadly divided into exact and approximate methods. In many applications, approximate methods are an effective solution for performing fast queries while allowing for a small loss. Well-established approximate NN search techniques include randomized $k$-d trees (Silpa-Anan & Hartley, 2008), hierarchical k-means (Nister & Stewenius, 2006), locality sensitive hashing (Indyk & Motwani, 1998), HNSW (Malkov & Yashunin, 2020), and ScaNN (Guo et al., 2020). Considerable drawbacks of most approximate NN search algorithms are their potentially long indexing time and the need for the tuning of additional hyperparameters such as the trade-off between recall vs index and query time. Furthermore, to the best of our knowledge, all approximate NN methods for which open-source implementations (such as Guo et al., 2020; Bernhardsson, 2023; Dong, Moses & Li, 2011; Malkov & Yashunin, 2020) are available only address the k-nearest neighbor problem, not the fixed-radius problem discussed here.

In this article we introduce a new exact approach to fixed-radius NN search based on sorting, referred to as SNN for short. Some of the appealing properties of SNN are

1. simplicity: SNN has no hyperparameters except for the necessary search radius

2. exactness: SNN is guaranteed to return all data points within the search radius

3. speed: SNN demonstrably outperforms other exact NN search algorithms like, e.g., methods based on tree structures

4. flexibility: the low indexing time of SNN makes it applicable in an online streaming setting.

The rest of this article is organized as follows. In “Related Work”, we provide a brief review of existing work on NN search. In “Sorting-Based NN Search”, we introduce our sorting-based NN method, detailing its indexing and query phases. “Computational Considerations” contains computational considerations regarding the efficient implementation of SNN and its behavior in floating-point arithmetic. Theoretical performance analysis is provided in “Theoretical Analysis”. “Experimental Evaluation” contains performance comparisons of our algorithm to other state-of-the-art NN methods, as well as an application to DBSCAN clustering. We then conclude in “Conclusions”. (A preprint of this work is available on arXiv (Chen & Güttel, 2023)).

Related work

NN search methods can broadly be classified into approximate or exact methods, depending on whether they return exact or approximate answers to queries (Cayton & Dasgupta, 2007). It is widely accepted that for high-dimensional data there are no exact NN search methods which are asymptotically more efficient than exhaustive search; see, e.g., (Muja, 2013, Chap. 3) and Francis-Landau & Durme (2019). Exact NN methods based on $k$-d tree (Bentley, 1975a; Friedman, Bentley & Finkel, 1977), balltree (Omohundro, 1989), VP-tree (Yianilos, 1993), cover tree (Beygelzimer, Kakade & Langford, 2006), and RP tree (Dasgupta & Sinha, 2013) only perform well on low-dimensional data. This shortcoming is often referred to as the curse of dimensionality (Indyk & Motwani, 1998). However, note that negative asymptotic results do not rule out the possibility of algorithms and implementations that perform significantly (by orders of magnitude) faster than brute force search in practice, even on real-world high-dimensional data sets.

To speedup NN search, modern approaches generally focus on two aspects, namely indexing and sketching. The indexing aims to construct a data structure that prunes the search space for a given query, hopefully resulting in fewer distance computations. Sketching, on the other hand, aims at reducing the cost of each distance computation by using a compressed approximate representation of the data.

The most widely used indexing strategy is space partitioning. Some of the earliest approaches are based on tree structures such as $k$-d tree (Bentley, 1975a; Friedman, Bentley & Finkel, 1977), balltree (Omohundro, 1989), VP-tree (Yianilos, 1993), and cover tree (Beygelzimer, Kakade & Langford, 2006). The tree-based methods are known to become inefficient for high-dimensional data. One of the remedies are randomization (e.g., Dasgupta & Sinha, 2013; Ram & Sinha, 2019) and ensembling (e.g., the FLANN nearest neighbor search tool by Muja & Lowe (2009), which empirically shows competitive performance against approximate NN methods). Another popular space partitioning method is locality-sensitive hashing (LSH); see, e.g., Indyk & Motwani (1998). LSH leverages a set of hash functions from the locality-sensitive hash family and it guarantees that similar queries are hashed into the same buckets with higher probability than less similar ones. This method was originally introduced for the binary Hamming space by Indyk & Motwani (1998), and it was later extended to the Euclidean space (Datar et al., 2004). In Bawa, Condie & Ganesan (2005) a self-tuning index for LSH based similarity search was introduced. A partitioning approach based on neural networks and LSH was proposed in Dong et al. (2020). Another interesting method is GriSPy (Chalela et al., 2021), which performs fixed-radius NN search using regular grid search—to construct a regular grid for the index—with the possibility of working with periodic boundary conditions. This method, however, has high memory demand because the grid computations grow exponentially with the space dimension.

This article focuses on exact fixed-radius NN search. The implementations available in the most widely used scientific computing environments are all based on tree structures, including findNeighborsInRadius in MATLAB (The MathWorks Inc., 2022), NearestNeighbors in scikit-learn (Pedregosa et al., 2011), and spatial in SciPy (Virtanen et al., 2020). This is in contrast to our SNN method introduced below which does not utilise any tree structures.

Sorting-based nn search

Suppose we have $n$ data points $p_1,\dots ,p_n\in {\mathbb{R}}^d$ (represented as column vectors) and $d\ll n$. The fixed-radius NN problem consists of finding the subset of data points that is closest to a given query point $q\in {ℝ}^d$ (may be out-of-sample) with respect to some distance metric. Throughout this article, the vector norm $\left|\right|\cdot \left|\right|=\left|\right|\cdot |{|}_2$ is the Euclidean one, though it also possible to identify nearest neighbors with other distances such as

• cosine distance: assuming normalized data (with $||u||=||v||=1$), the cosine distance is

  $$\mathrm{c}\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}(u,v)=1-\cos (\theta )=1-\frac{u^{T}v}{||u||||v||}=1-u^{T}v\in [0,2].$$Hence, the cosine distance can be computed from the Euclidean distance via $$2\mathrm{c}\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}(u,v)=2-2u^{T}v=u^{T}u-2u^{T}v+v^{T}v=||u-v|{|}^2.$$

• angular distance: the angular distance $\theta \in [0,\pi ]$ between two normalized vectors $u,v$ satisfies

  $$\theta \le \alpha \mathrm{i}\mathrm{f}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{n}\mathrm{l}\mathrm{y}\mathrm{i}\mathrm{f}||\mathrm{u}-\mathrm{v}|{|}^2\le 2-2\cos (\alpha ).$$ Therefore, closest angle neighbors can be identified via Euclidean distance.

• maximum inner product similarity (see, e.g., Bachrach et al., 2014): for not necessarily normalized vectors we can consider the transformed data points ${\tilde{p}}_i=[\sqrt{{\xi }^2-||p_i|{|}^2},p_i^T{]}^T$ with $\xi :=\underset{i}{max}||p_i||$ and the transformed query point $\tilde{q}=[0,q^T{]}^T$. Then

  $$||{\tilde{p}}_i-q|{|}^2=||{\tilde{p}}_i|{|}^2+||\tilde{q}|{|}^2-2{\tilde{p}}_i^T\tilde{q}={\xi }^2+||q|{|}^2-2p_i^{T}q\ge 0.$$Since $\xi$ and $q$ are independent of the index $i$, we have $\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}{\mathrm{n}}_i||{\tilde{p}}_i-\tilde{q}|{|}^2=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}{\mathrm{x}}_i{p}_i^{T}q$.

• Manhattan distance: since $|p_i-q|{|}_2\le \left|\right|p_i-q|{|}_1$, any points satisfying $|p_i-q|{|}_1\text{>}R$ must necessarily satisfy $\left|\right|p_i-q|{|}_2\text{ >}R$. Hence, the sorting-based exclusion criterion proposed in section 3.2 to prune the query search space can also be used for the Manhattan distance.

Our algorithm, called SNN, will return the required indices of the nearest neighbors in the Euclidean norm, and can also return the corresponding distances if needed. SNN uses three essential ingredients to obtain its speed. First, a sorting-based exclusion criterion is used to prune the search space for a given query. Second, pre-calculated dot products of the data points allow for a reduction of arithmetic complexity. Third, a reformulation of the distance criterion in terms of matrices (instead of vectors) allows for the use of high-level basic linear algebra subprograms (BLAS, Blackford et al., 2002). In the following, we explain these ingredients in more detail.

Query

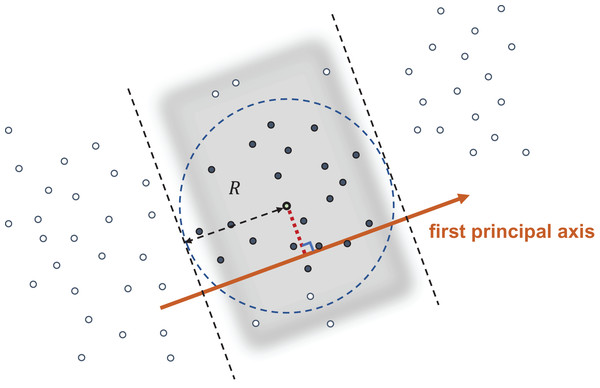
Given a query point $q$ and user-specified search radius R, we want to retrieve all data points $p_i$ satisfying $||p_i-q||\le R$. Figure 1 illustrates our approach. We first compute the mean-centered query $x_q:=q-\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}(\{p_j\})$ and the corresponding score ${\alpha }_q:=x_q^T{v}_1$. By utilizing the Cauchy–Schwarz inequality, we have

(2) $$|{\alpha }_i-{\alpha }_q|=|v_1^T{x}_i-v_1^T{x}_q|\le ||x_i-x_q||.$$

Since we have sorted the $x_i$ such that ${\alpha }_1\le {\alpha }_2\le \cdots \le {\alpha }_n$, the following statements are true:

$$\mathrm{i}\mathrm{f}{\alpha }_q-{\alpha }_{j_1}>R\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{m}\mathrm{e}{\mathrm{j}}_1,\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{n}||x_i-x_q||>R\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}i\le j_1;$$

$$\mathrm{i}\mathrm{f}{\alpha }_{j_2}-{\alpha }_q>R\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{o}\mathrm{m}\mathrm{e}{\mathrm{j}}_2,\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{n}||x_i-x_q||>R\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}i\ge j_2.$$

As a consequence, we only need to consider candidates $x_i$ whose indices are in $J:=\{j_1+1,j_1+2,\dots ,j_2-1\}$ and we can determine the smallest subset by finding the largest $j_1$ and smallest $j_2$ satisfying the above statements, respectively. As the ${\alpha }_i$ are sorted, this can be achieved via binary search in $O(\log n)$ operations. Note that the indices in J are continuous integers, and hence it is memory efficient to access $X(J,:)$, the submatrix of X whose row indices are in J. This will be important later.

Finally, we filter all data points in the reduced set $X(J,:)$, retaining only those data points whose distance to the query point $x_q$ is less or equal to R, i.e., points satisfying $||x_j-x_q|{|}^2\le R^2$. The query phase is summarized in Algorithm 2.

Algorithm 2:

SNN query.

1: Input: Query vector q; user-specified radius R; output from Algorithm 1

2: Compute $x_q:=q-\mu$

3: Compute the sorting score of xq, i.e., ${\alpha }_q:=x_q^T{v}_1$

4: Select candidate index range J so that $|{\alpha }_j-{\alpha }_q|\le R$ for all $j\in J$

5: Compute $d:=\overline{x}(J)-X(J,:{)}^T{x}_q$ using the precomputed $\overline{x}=[\overline{x_i}]$

6: Return: Points xj with $d_j\le (R^2-x_q^T{x}_q)/2$ according to Eq. (4)

DOI: 10.7717/peerj-cs.1929/table-9

Computational considerations

The compute-intensive step of the query procedure is the computation of

(3) $$||x_j-x_q|{|}^2=(x_j-x_q{)}^T(x_j-x_q)$$for all vectors $x_j$ with indices $j\in J$. Assuming that these vectors have $d$ features, one evaluation of Eq. (3) requires $3d-1$ floating point operations (flop): $d$ flop for the subtractions, $d$ flop for the squaring, and $d-1$ flop for the summation. In total, $|J|(3d-1)$ flop are required to compute all |J| squared distances. We can equivalently rewrite (Eq. (3)) as $||x_j-x_q|{|}^2=x_j^T{x}_j+x_q^T{x}_q-2x_j^T{x}_q$ and instead verify the radius condition as

(4) $$\frac{1}{2}{x}_j^T{x}_j-x_j^T{x}_q\le \frac{R^2-x_q^T{x}_q}{2}.$$

This form has the advantage that all the squared-and-halved norms $\overline{x_j}=(x_j^T{x}_j)/2$ ( $i=1,2,\dots ,n$) have been precomputed during the indexing phase. Hence, in the query phase, the left-hand side of Eq. (4) can be evaluated for all |J| points $x_j$ using only $2d|J|$ flop: $(2d-1)|J|$ for the inner products and |J| subtractions.

Merely counting flop, Eq. (4) saves about 1/3 of arithmetic operations over (Eq. (3)). An additional advantage results from the fact that all inner products in Eq. (4) can be computed as $X(J,:{)}^T{x}_q$ using level-2 BLAS matrix-vector multiplication (gemv), resulting in further speedup on modern computing architectures. If multiple query points are given, say $x_q^{(1)},\dots ,x_q^{(l)}$, a level-3 BLAS matrix-matrix multiplication (gemm) evaluates $X(J,:{)}^T[x_q^{(1)},\dots ,x_q^{(l)}]$ in one go, where J is the union of candidates for all $l$ query points.

One may be concerned that the computation using Eq. (4) incurs more rounding error than the usual Formula (3). We now prove that this is not the case. First, note that division or multiplication by 2 does not incur rounding error. Using the standard model of floating point arithmetic, we have $fl(a\circ b)=(a\circ b)(1\pm \delta )$ for any elementary operation $\circ \in \{+,-,\times ,/\}$, where $0\le \delta \le u$ with the unit roundoff $u$ (Higham, 2002, Chap. 1). Suppose we have two vectors $x$ and $y$ where $x_i$ and $y_i$ denote their respective coordinates. Then computing

$$s_d:=\sum _{i=1}^d{(x_i-y_i)}^2=(x-y{)}^T(x-y)$$in floating point arithmetic amounts to evaluating

$$\begin{array}{l}{\widehat{s}}_1=fl\left({\left(x_1-y_1\right)}^2\right)=fl{\left(\left(x_1-y_1\right)\right)}^2.\left(1\pm \delta \right)={\left(x_1-y_1\right)}^2{\left(1\pm \delta \right)}^3\\ {\widehat{s}}_2=fl\left({\widehat{s}}_1+\left(x_2-y_2\right)\right)=\left({\widehat{s}}_1+{\left(x_2-y_2\right)}^2{\left(1\pm \delta \right)}^3\right).\left(1\pm \delta \right)\\ ={\left(x_1-y_1\right)}^2{\left(1\pm \delta \right)}^4+{\left(x_2-y_2\right)}^2{\left(1\pm \delta \right)}^4,\text{and\hspace{0.17em}so\hspace{0.17em}on}.\end{array}$$

Continuing this recursion we arrive at

$$\begin{array}{rl}{\hat{s}}_d=& (x_1-y_1{)}^2(1\pm \delta {)}^{d+2}+(x_2-y_2{)}^2(1\pm \delta {)}^{d+2}+(x_3-y_3{)}^2(1\pm \delta {)}^{d+1}\\ & +\cdots +(x_d-y_d{)}^2(1\pm \delta {)}^4.\end{array}$$

Assuming $ju<1$ and using (Higham, 2002, Lemma 3.1) we have

$$(1\pm \delta {)}^j=1+{\theta }_j,\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}|{\theta }_j|\le \frac{ju}{1-ju}:={\gamma }_j.$$

Hence,

$$\begin{array}{rl}& |(x-y{)}^T(x-y)-fl((x-y{)}^T(x-y))|\\ & \le |{\theta }_{d+2}(x_1-y_1{)}^2+{\theta }_{d+2}^{\mathrm{\prime }}(x_2-y_2{)}^2+{\theta }_{d+1}(x_3-y_3{)}^2+\\ & \cdots +{\theta }_4(x_d-y_d{)}^2|\\ & \le |{\theta }_{d+2}|(x_1-y_1{)}^2+|{\theta }_{d+2}^{\mathrm{\prime }}|(x_2-y_2{)}^2+|{\theta }_{d+1}|(x_3-y_3{)}^2+\\ & \dots +|{\theta }_4|(x_d-y_d{)}^2|\\ & \le {\gamma }_{d+2}(x-y{)}^T(x-y),\end{array}$$showing that the left-hand side of Eq. (3) can be evaluated with high relative accuracy.

A very similar calculation can be done for the formula

$$x^{T}x+y^{T}y-2x^{T}y=s_d,$$the expression that is used to derive (Eq. (4)). Using the standard result for inner products (Higham, 2002, eq. (3.2))

$$\begin{array}{rl}fl(x^{T}y)=& x_1{y}_1(1\pm \delta {)}^d+x_2{y}_2(1\pm \delta {)}^d+x_3{y}_3(1\pm \delta {)}^{d-1}\\ & +\cdots +x_d{y}_d(1\pm \delta {)}^2,\end{array}$$one readily derives

$$|(x-y{)}^T(x-y)-fl(x^{T}x+y^{T}y-2x^{T}y)|\le {\gamma }_{d+2}(x-y{)}^T(x-y),$$the same bound on the relative accuracy of floating-point evaluation as obtained for (3).

Theoretical analysis

The efficiency of the SNN query in Algorithm 2 is dependent on the number of pairwise distance computations that are performed in Step 5, depending on the size of the index set |J|. If the index set J is the full $\{1,2,\dots ,n\}$, then the algorithm reduces to exhaustive search over the whole dataset $\{x_1,x_2,\dots ,x_n\}$, which is undesirable. For the algorithm to be most efficient, |J| would exactly coincide with the indices of data points $x_i$ that satisfy $||x_i-x_q||\le R$. In practice, the index set J will be somewhere in between these two extremes. Thus, it is natural to ask: How likely is it that $|{\alpha }_i-{\alpha }_q|\le R$, yet $||x_i-x_q||>R$?

First note that, using the singular value decomposition (Eq. (1)) of the data matrix X, we can derive an upper bound on $||x_i-x_q||$ that complements the lower bound (Eq. (2)). Using that $x_i^T=e_i^{T}X=e_i^{T}U\mathrm{\Sigma }{V}^T$, where $e_i\in {\mathbb{R}}^n$ denotes the $i$th canonical unit vector, and denoting the elements of U by $u_{ij}$, we have

$$\begin{gathered} ||x_i-x_q|{|}^2=|{\alpha }_i-{\alpha }_q{|}^2+\left||[(u_{i2}-u_{q2}),\dots ,(u_{id}-u_{qd})]\hat{\mathrm{\Sigma }}\right|{|}^2 \\ \le |{\alpha }_i-{\alpha }_q{|}^2+||u_i-u_q|{|}^2\cdot ||\hat{\mathrm{\Sigma }}|{|}^2 \\ \le |{\alpha }_i-{\alpha }_q{|}^2+2{\sigma }_2^2 \end{gathered}$$with $\widehat{\Sigma }=\left(\begin{array}{ccc}{\sigma }_2& & \\ & \ddots & \\ & & {\sigma }_d\end{array}\right)$ Therefore,

(5) $$|{\alpha }_i-{\alpha }_q{|}^2\le ||x_i-x_q|{|}^2\le |{\alpha }_i-{\alpha }_q{|}^2+2{\sigma }_2^2$$and the gap in these inequalities depends on ${\sigma }_2$, the second singular value of X. Indeed, if ${\sigma }_2=0$, then all data points $x_i$ lie on a straight line passing through the origin and their distances correspond exactly to the difference in their first principal coordinates. This is a best-case scenario for Algorithm 2 as all candidates $x_j$, $j\in J$, found in Step 4 are indeed also nearest neighbors. If, on the other hand, ${\sigma }_2$ is relatively large compared to ${\sigma }_1$, the gap in the inequalities (Eq. (5)) becomes large and $|{\alpha }_i-{\alpha }_q|$ may be a crude underestimation of the distance $||x_i-x_q||$.

In order to get a qualitative understanding of how the number of distance computations in Algorithm 2 depends on the various parameters (dimension $d$, singular values of the data matrix, query radius R, etc.), we consider the following model. Let $\{x_i{\}}_{i=1}^n$ be a large sample of points whose $d$ components are normally distributed with zero mean and standard deviation $[1,s,\dots ,s]$, $s<1$, respectively. These points describe an elongated “Gaussian blob” in ${\mathbb{R}}^d$, with the elongation controlled by $s$. In the large data limit $(n\to \mathrm{\infty })$ the singular values of the data matrix $X=[x_1,\dots ,x_n{]}^T$ approach $\sqrt{n},s\sqrt{n},\dots ,s\sqrt{n}$ and the principal components approach the canonical unit vectors $e_1,e_2,\dots ,e_d$. As a consequence, the principal coordinates ${\alpha }_i=e_1^T{x}_i$ follow a standard normal distribution, and hence for any $c\in \mathbb{R}$ the probability that $|{\alpha }_i-c|\le R$ is given as

$$P_1=P_1(c,R)=\frac{1}{\sqrt{2\pi }}\underset{c-R}{\overset{c+R}{\int }}{e}^{-r^2/2}\mathrm{d}r.$$

On the other hand, the probability that $||x_i-[c,0,\dots ,0{]}^T||\le R$ is given by

(6) $$\begin{array}{l}{P}_2=P_2(c,R,s,d)\\ =\frac{1}{\sqrt{2\pi }}{\displaystyle {\int }_{c-R}^{c+R}{e}^{-r^2/2}}\cdot F\left(\frac{R^2-{(r-c)}^2}{s^2};d-1\right)\text{d}r,\end{array}$$where F denotes the ${\chi }^2$ cumulative distribution function. In this model we can think of the point $x_q:=[c,0,\dots ,0{]}^T$ as a query point, and our aim is to identify all data points $x_i$ within a radius R of this query point.

Since $||x_i-x_q||\le R$ implies that $|{\alpha }_i-c|\le R$, we have $P_1\ge P_2$. Hence, the quotient $P_2/P_1$ can be interpreted as a conditional probability of a point $x_i$ satisfying $||x_i-x_q||\le R$ given that $|e_1^T{x}_i-c|\le R$, i.e.,

$$P=P(||x_i-x_q||\le R||e_1^T{x}_i-c|\le R)=P_2/P_1.$$

Ideally, we would like this quotient $P=P_2/P_1$ be close to $1$, and it is now easy to study the dependence on the various parameters. First note that $P_1$ does not depend on $s$ nor $d$, and hence the only effect these two parameters have on P is via the factor $F\left(\frac{R^2-{(r-c)}^2}{s^2};d-1\right)$ in the integrand of $P_2$. This term corresponds to the probability that the sum of squares of $d-1$ independent Gaussian random variables with mean zero and standard deviation $s$ is less or equal to $R^2-(r-c{)}^2$. Hence, $P_2$ and therefore P are monotonically decreasing as $s$ or $d$ are increasing. This is consistent with intuition: as $s$ increases, the elongated point cloud $\{x_i\}$ becomes more spherical and hence it gets more difficult to find a direction in which to enumerate (sort) the points naturally. And this problem gets more pronounced in higher dimensions $d$.

We now show that the “efficiency ratio” P converges to $1$ as R increases. In other words, the identification of candidate points $x_j$, $j\in J$, should become relatively more efficient as the query radius R increases. (Here relative is meant in the sense that candidate points become more likely to be fixed-radius nearest neighbors as R increases. Informally, as $R\to \mathrm{\infty }$, all $n$ data points are candidates and also nearest neighbors and so the efficiency ratio must be $1$.) First note that for an arbitrarily small $\epsilon >0$ there exists a radius $R_1>1$ such that $P_1(c,R_1-1)>1-\epsilon$. Further, there is a $R_2>1$ such that

$$F(\frac{R_2^2-(r-c{)}^2}{s^2};d-1)>1-\epsilon \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}r\in [c-R_2+1,c+R_2-1].$$

To see this, note that the cumulative distribution function F increases monotonically from $0$ to $1$ as its first argument increases from $0$ to $\mathrm{\infty }$. Hence there exists a value T for which $F(t,d-1)>1-\epsilon$ for all $t\ge T$. Now we just need to find $R_2$ such that

$$\frac{R_2^2-{(r-c)}^2}{s^2}\ge T\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}r\in [c-R_2+1,c+R_2-1].$$

The left-hand side is a quadratic function with roots at $r=c\pm R_2$, symmetric with respect to the maximum at $r=c$. Hence choosing $R_2$ such that

$$\frac{R_2^2-{([c+R_2-1]-c)}^2}{s^2}=T,\mathrm{i}.\mathrm{e}.,R_2={\left(\frac{T{s}^2+1}{2}\right)}^{1/2},$$or any value $R_2$ larger than that, will be sufficient. Now, setting $R=max\{R_1,R_2\}$, we have

$$P_2\ge \frac{1}{\sqrt{2\pi }}{\int }_{c-R+1}^{c+R-1}{e}^{-r^2/2}\cdot F(\frac{R^2-(r-c{)}^2}{s^2};d-1)dr\ge (1-\epsilon {)}^2.$$

Hence, both $P_1$ and $P_2$ come arbitrarily close to $1$ as R increases, and so does their quotient $P=P_2/P_1$.

Experimental evaluation

Our experiments are conducted on a compute server with two Intel Xeon Silver 4114 2.2G processors, 1.5 TB RAM, with operating system Linux Debian 11. All algorithms are forced to run in a single thread with the same settings for fair comparison. We only consider algorithms for which stable Cython or Python implementation are freely available. Our SNN algorithm is implemented in native Python (i.e., no Cython is used), while scikit-learn’s (Pedregosa et al., 2011) $k$-d tree and balltree NN algorithms, and hence also scikit-learn’s DBSCAN method, use Cython for some part of the computation. Numerical values are reported to four significant digits. The code and data to reproduce the experiments in this article can be downloaded from https://github.com/nla-group/snn.

Near neighbor query on synthetic data

We first compare $k$-d tree, balltree, and SNN on synthetically generated data to study their dependence on the data size $n$ and the data dimension $d$. We also include two brute force methods, the one in scikit-learn (Pedregosa et al., 2011) (denoted as brute force 1) and another one implemented by us (denoted as brute force 2) which exploits BLAS level-2 (One might say that brute force 2 is equivalent to SNN without index construction and without search space pruning.). The leaf size for scikit-learn’s $k$-d tree and balltree is kept at the default value 40. The $n$ data points are obtained by sampling from the uniform distribution on $[0,1{]}^d$.

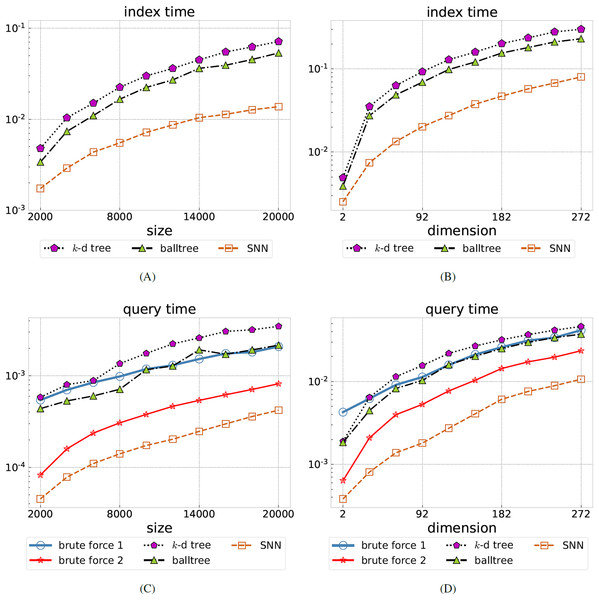
For the first test we vary the number of data points $n$ (the index size) from 2,000 to 20,000 in increments of 2,000. The number of features is either $d=2$ or $d=50$. We then query the nearest neighbors of each data point for varying radius R. The ratio of returned data points relative to the overall number of points is listed in Table 1. As expected, this ratio is approximately independent of $n$. We have chosen the radii R so that a good order-of-magnitude variation in the ratio is obtained, in order to simulate queries with small to large returns. The timings of the index and query phases of the various NN algorithms are shown in Fig. 2 (left). Note that the brute force methods do not require the construction of an index. Among $k$-d tree, balltree, and SNN, our method has the shortest indexing phase. The query time is obtained as an average over all queries, over the two considered dimensions $d\in \{2,50\}$, and over all considered radii R.SNN performs best, with the average query time being between 5 and 9.7 times faster than balltree (the fastest tree-based method). We have verified that for all methods, when run on the same datasets with the same radius parameter, the set of returned points coincide.

Table 1:

The table shows the ratio of returned data points from the synthetic uniformly distributed dataset, relative to the overall number of points $n$, as the query radius R and the dimension $d$ is varied; The ratios confirm that our parameter choices lead to queries over a wide order-in-magnitude variation of query return sizes.

	$n$	2,000	4,000	6,000	8,000	10,000	12,000	14,000	16,000	18,000	20,000
Varying $n$ ( $d=2$)	$R=0.02$	0.1243%	0.1245%	0.1232%	0.1234%	0.1236%	0.1236%	0.1238%	0.1238%	0.1232%	0.1234%
	$R=0.05$	0.755%	0.7561%	0.7506%	0.7522%	0.7532%	0.7508%	0.7531%	0.7534%	0.7511%	0.751%
	$R=0.08$	1.852%	1.87%	1.879%	1.871%	1.882%	1.879%	1.879%	1.871%	1.881%	1.875%
	$R=0.11$	3.434%	3.46%	3.433%	3.449%	3.44%	3.459%	3.454%	3.44%	3.452%	3.453%
	$R=0.14$	5.487%	5.42%	5.443%	5.456%	5.438%	5.454%	5.442%	5.432%	5.449%	5.417%
Varying $n$ ( $d=50$)	$R=2.0$	0.01732%	0.01674%	0.01818%	0.01763%	0.01752%	0.01717%	0.01734%	0.01726%	0.0175%	0.0174%
	$R=2.1$	0.07652%	0.07361%	0.07286%	0.07502%	0.07777%	0.07414%	0.07571%	0.07737%	0.07486%	0.07722%
	$R=2.2$	0.2873%	0.2843%	0.2912%	0.2863%	0.2879%	0.2857%	0.2862%	0.2903%	0.2888%	0.2892%
	$R=2.3$	0.9608%	0.9235%	0.9316%	0.9184%	0.9129%	0.929%	0.9065%	0.9195%	0.9166%	0.9303%
	$R=2.4$	2.514%	2.624%	2.623%	2.544%	2.526%	2.511%	2.542%	2.558%	2.584%	2.562%
	$d$	2	32	62	92	122	152	182	212	242	272
Varying $d$ ( $n=$ 10,000)	$R=0.5$	48.11%	0%	0%	0%	0%	0%	0%	0%	0%	0%
	$R=2.0$	100.0%	11.08%	3.9e−05%	0%	0%	0%	0%	0%	0%	0%
	$R=3.5$	100.0%	100.0%	88.78%	4.613%	0.001981%	0%	0%	0%	0%	0%
	$R=5.0$	100.0%	100.0%	100.0%	100.0%	98.03%	45.5%	1.886%	0.005933%	2e−06%	0%
	$R=6.5$	100.0%	100.0%	100.0%	100.0%	100.0%	100.0%	100.0%	98.99%	74.06%	17.15%

DOI: 10.7717/peerj-cs.1929/table-1

For the second test we fix the number of data points at $n=10,000$ and vary the dimension $d=2,32,\dots ,272$. We perform queries for five selected radii as shown in Table 1. The table confirms that we have a wide variation in the number of returned data points relative to the overall number of points $n$, ranging from empty returns to returning all data points. The indexing and query timings are shown in Fig. 2 (right). Again, among $k$-d tree, balltree, and SNN, our method has the shortest indexing phase. The query time is obtained as an average over all $n$ query points and over all considered radii R. SNN performs best, with the average query time being between 3.5 and 6 times faster than balltree (the fastest tree-based method).

Comparison with GriSPy

GriSPy (Chalela et al., 2021), perhaps the most recent work on fixed-radius NN search, is an exact search algorithm which claims to be superior over the tree-based algorithms in SciPy. GriSPy indexes the data points into regular grids and creates a hash table in which the keys are the cell coordinates, and the values are lists containing the indices of the points within the corresponding cell. As there is an open-source implementation available, we can easily compare GriSPy against SNN. However, GriSPy has a rather high memory demand which forced us to perform a separate experiments with reduced data sizes and dimensions as compared to the ones in the previous “Near Neighbor Query on Synthetic Data”.

Again we consider $n$ uniformly distributed data points in $[0,1{]}^d$, but now with (i) varying data size from $n=1,000$ to $100,000$ and averaging the runtime of five different radius queries with $R=0.05,0.1,\dots ,0.25$, and (ii) varying dimension over $d=2,3,4$. The precise parameters and the corresponding ratio of returned data points are listed in Table 2. All queries are repeated 1,000 times and timings are averaged. Both experiments (i) and (ii) use the same query size as the index size.

Table 2:

The table shows the ratio of returned data points from the synthetic uniformly distributed dataset, relative to the overall number of points $n$, as the data volumn $n$, query radius R and the dimension $d$ is varied.

	$n$	1,000	2,154	4,641	10,000	21,544	46,415	100,000
Varying $n$ ( $d=3$)	$R=0.05$	0.05%	0.05%	0.048%	0.049%	0.05%	0.05%	0.049%
	$R=0.10$	0.37%	0.37%	0.36%	0.38%	0.37%	0.37%	0.37%
	$R=0.15$	1.2%	1.2%	1.2%	1.2%	1.2%	1.2%	1.2%
	$R=0.20$	2.6%	2.6%	2.6%	2.7%	2.7%	2.6%	2.6%
	$R=0.25$	4.8%	4.8%	4.8%	4.9%	4.9%	4.9%	4.7%
	$d$	2	3	4
Varying $d$ ( $n=$ 10,000)	$R=0.05$	0.75%	0.05%	0.0029%
	$R=0.10$	2.9%	0.38%	0.042%
	$R=0.15$	6.1%	1.2%	0.2%
	$R=0.20$	10%	2.7%	0.59%
	$R=0.25$	15%	4.9%	1.3%

DOI: 10.7717/peerj-cs.1929/table-2

The index and query timings are illustrated in Fig. 3. We find that SNN indexing is about an order of magnitude faster than GriSPy over all tested parameters. For the experiment (i) where the data size is varied, we find that SNN is up to two orders of magnitude faster than GriSPy. For experiment (ii), we see that the SNN query time is more stable than GriSPy with respect to increasing data dimension.

Conclusions

We presented a fixed-radius nearest neighbor (NN) search method called SNN. Compared to other exact NN search methods based on $k$-d tree or balltree data structures, SNN is trivial to implement and exhibits faster index and query time. We also demonstrated that SNN outperforms different implementations of brute force search. Just like brute force search, SNN requires no parameter tuning and is straightforward to use. We believe that SNN could become a valuable tool in applications such as the MultiDark Simulation (Klypin et al., 2016) or the Millennium Simulation (Boylan-Kolchin et al., 2009). We also demonstrated that SNN can lead to significant performance gains when used for nearest neighbor search within the DBSCAN clustering method.

While we have demonstrated SNN speedups in single-threaded computations on a CPU, we believe that the method’s reliance on high-level BLAS operations makes it suitable for parallel GPU computations. A careful CUDA implementation of SNN and extensive testing will be subject of future work.