J-score: a robust measure of clustering accuracy

J-Score

Let D represent a data set containing N samples that are categorized into T true classes. Clustering analysis of D produces K hypothetical clusters, each containing a disjoint subset of N. The class and cluster assignments of these samples are stored in a matrix M, which has N rows and two columns. For a given sample in row i, the first column corresponds to the class label t_i ∈ T and the second column corresponds to the cluster assignment k_i ∈ K. For a specific pair of class t and cluster k, the sets V_t and V_k consist of samples for which M_i∈1:N,1 = t and M_i∈1:N,2 = k, respectively. The Jaccard index is calculated as (1)${\displaystyle I_{t,k}=\frac{\left|V_t\cap V_k\right|}{\left|V_t\cup V_k\right|}}$ where —?— denote the size of a set.

Distribution of J-Score

Proposition 1. J-score is bounded between (0, 1], with the maximum value of 1 reached when hypothetical clusters match true classes perfectly.

Proof of Proposition 1. Based on the theorem of Jaccard index (Cheetham & Hazel, 1969), I_t,k in Eq. (1) ranges from 0 when V_t and V_kshare no common data point (i.e., $\left|V_t\cap V_k\right|=0$) to 1 when data points in V_t and V_k overlap completely (i.e., $\left|V_t\cap V_k\right|=\left|V_t\cup V_k\right|$). It is easy to derive that I_t in Eq. (2) obtains the maximum value of 1 when class t is paired with a perfectly matched cluster. Similarly, I_k in Eq. (3) maximizes to 1 when cluster k is paired with a perfectly matched class.

Lemma 1.1 If all classes have perfectly matched clusters and vice versa, R and P in Eq. (4) equal to 1 regardless of the fraction of data points in each class and cluster, giving rise to J = 1.

Lemma 1.2 If at least one class or cluster cannot find a perfectly matched counterpart, the corresponding I_t and I_k will be less than 1. Consequently, R and P will be less than 1, resulting in J < 1.

Because Lemma 1.1 and 1.2 exhaust all possible scenarios of bidirectional matches, J-score has a maximum value of 1 when classes and clusters have complete agreement. Meanwhile, bidirectional matching ensures that each and every class will be matched to a cluster sharing at least one data point, and vice versa. Therefore, R, P, and J are all non-zero positive values.

Proposition 2. The baseline value of J-score is obtained from clustering results from a useless algorithm that randomly assigns data points into an arbitrary number of clusters. This baseline value is not constant.

Proof of Proposition 2. A useless clustering algorithm implies M_i,1 and M_i,2 are independent. By this definition, we derive the following lemmas.

Lemma 2.1. Denote V_t,k = V_t∩V_k as the set of data points that have class label t ∈ T and belong to cluster k ∈ K. Because a useless clustering algorithm produces M where M_i,1 and M_i,2 are independent, $Pr\left(M_{i,1}=t,M_{i,2}=k\right)=Pr\left(M_{i,1}=t\right)\cdot Pr\left(M_{i,2}=k\right)$. As $Pr\left(M_{i,1}=t\right)=\frac{\left|V_k\right|}{N}$ and $Pr\left(M_{i,2}=k\right)=\frac{\left|V_t\right|}{N}$, the expected value of $\left|V_{t,k}\right|=$ $N\cdot \frac{\left|V_k\right|}{N}\cdot \frac{\left|V_t\right|}{N}=\frac{\left|V_k\right|\left|V_t\right|}{N}$.

Lemma 2.2. Denote $f\left(x\right)=\frac{ax}{bx+c}$ with x, a, b, c > 0. Because $\frac{d}{dx}f\left(x\right)=\frac{ac}{{\left(bx+c\right)}^2}$ is strictly greater than zero, $f\left(x\right)$ is a strictly increasing function.

For a given class-cluster pair (t, k), the Jaccard index in Eq. (1) $I_{t,k}=\frac{\left|V_t\cap V_k\right|}{\left|V_t\cup V_k\right|}=\frac{\left|V_{t,k}\right|}{\left|V_t|+|V_k\right|-\left|V_{t,k}\right|}$. By Lemma 2.1, I_t,k can be reduced to $\frac{\left|V_t\right|\left|V_k\right|/N}{\left|V_t|+|V_k\right|-\left|V_t\right|\left|V_k\right|/N}=\frac{\left|V_t\right|\left|V_k\right|}{\left(N-\left|V_t\right|\right)\left|V_k\right|+N\left|V_t\right|}$. Lemma 2.2 shows I_t,k strictly increases as $\left|V_k\right|$ increases. Thus, Eq. (2) $I_t={max}_{\mathit{kϵK}}\left(I_{t,k}\right)$ is further reduced to $\frac{\left|V_t\right|\left|V_{k\text{\_}max}\right|}{\left(N-\left|V_t\right|\right)\left|V_{k\text{\_}max}\right|+N\left|V_t\right|}\equiv I_{0t}$, where $\left|V_{k\text{\_}max}\right|$ is the maximum of $\left\{\left|V_{k\in K}\right|\right\}$. Similarly, I_k in Eq. (3) is reduced to $\frac{\left|V_k\right|\left|V_{t\text{\_}max}\right|}{\left(N-\left|V_k\right|\right)\left|V_{t\text{\_}max}\right|+N\left|V_k\right|}\equiv I_{0k}$, where $\left|V_{t\text{\_}max}\right|$ is the maximum of $\left\{\left|V_{t\in T}\right|\right\}$. According to Eq. (4), $J_0=\frac{2\times R_0\times P_0}{R_0+P_0}$, where $R_0={\sum }_{t\in T}\left(\frac{\left|V_t\right|}{N}{I}_{0t}\right)$, and $P_0={\sum }_{k\in K}\left(\frac{\left|V_k\right|}{N}{I}_{0k}\right)$. Because R₀ and P₀ are strictly positive, J₀ is strictly positive. J₀ is also a function of $\left\{\left|V_{k\in K}\right|\right\}$ and $\left\{\left|V_{tt\in T}\right|\right\}$ as $\left|V_{k\text{\_}max}\right|$, $\left|V_{t\text{\_}max}\right|$ are functions of $\left\{\left|V_{k\in K}\right|\right\}$ and $\left\{\left|V_{t\in T}\right|\right\}$.

J₀ is the J-score by comparing clustering results from a useless algorithm with the true class labels. J₀ varies by the number of true and hypothetical clusters and has no single value. For example, suppose that the N data points are equally distributed across the total |K| clusters and total |T| true classes, i.e., |V_k| = N/|K| and $\left|V_t\right|=\mathrm{N}/\left|T\right|$. Using the formula in Proposition 2, $J_0=\frac{1}{\left|T\right|+\left|K\right|-1}$, which decreases as |T| or |K| increases. This means the minimum value of J-score varies even for the same data set. It maximizes when all data points are grouped into a single cluster. It minimizes when each data point is assigned to a separate cluster.

Simulations to evaluate performance

To simulate an input data set D with known class labels, we generated random numbers based on Gaussian distributions G(μ, 0.05) where µ is the mean and 0.05 is the fixed standard deviation. Data points generated from the same Gaussian distribution belonged to the same class. We then mixed data points of different classes to produce the input data. Class labels of these data points were ground truth.

Given an input data set D with N data points, we used three approaches to simulate a hypothetical partition structure. The first approach simulated a pre-determined partition structure, in which the total number of clusters K, the size of each cluster N_k, and the assignment of each data point to a cluster were specified manually. The second approach simulated a random partition structure. Here, only the value of K was pre-specified. N_k was determined by randomly choosing K integers that summed to $N={\sum }_1^K{N}_k$. Assignment of data points to clusters was also random, which was achieved by first repeating each k value by N_k times to create an ordered list of cluster labels, then permutating these labels. The third approach simulated splitting or merging classes. Given the pre-specified value of K, classes to be split or merged and the splitting ratio were randomly selected under the constraint that $N={\sum }_1^K{N}_k$.

Analysis of real datasets

We used two benchmark datasets to evaluate the performance of J-score and other accuracy measures. The first data set contains observations of 150 iris plants categorized into three true classes (50 Setosa, 50 Versicolor, and 50 Virginica) (Anderson, 1935). The second data set contains information of 178 wines categorized into three true classes (59 cultivar_1, 71 cultivar_2, and 48 cultivar_3) (Aeberhard, Coomans & DeVel, 1994). We performed K-means clustering analysis and agglomerative hierarchical clustering analysis of the scaled features. For K-means clustering, we used the kmeans() function in R with the default Hartigan-Wong algorithm, 10 random initialization sets (nstart =10), and 10 maximum iterations (iter.max =10), and tested a series of K values from 2 to 10. For hierarchical clustering, we used the dist() function in R to calculate pairwise Euclidean distance, the hclust() function to build a dendrogram with the “ward.D2” algorithm, and the cutree() function with a series of K values from 2 to 10 to create disjoint clusters. Given the true classes in the input data and the clusters identified from clustering analysis, we computed various accuracy measures to find the best number of clusters that maximizes the accuracy. Ideally, the best number of clusters shall be 3 for both the Iris data set and the Wine data set. Deviation from the expected number indicates errors associated with a specific accuracy measure.

Computation and comparison of various accuracy measures

We compared J-score with commonly used clustering accuracy measures. To compute ARI, RI, NMI, NVI, and V-measure, we used the R/aricode and R/clevr packages. To compute F- and H-score, we used an in-house developed R functions based on the published algorithms (Meilă & Heckerman, 2001; Fung, Wang & Ester, 2003).

J-Score addresses the “problem of matching”

The “problem of matching” arises when an accuracy measure fails to consider the presence of stray clusters in the evaluation process. J-score addresses this issue via bidirectional set matching, which enables the recovery of stray clusters. To illustrate the advantages of bidirectional over unidirectional set matching, we conducted simulation experiments in which the number of hypothetical clusters was set to be equal to, less than, or greater than the number of true classes. For each scenario, we measured the similarity between the true partition structure and the hypothetical partition structure using H-score and F-score, which utilizes unidirectional T → K matching, as well as J-score, which incorporates bidirectional matching.

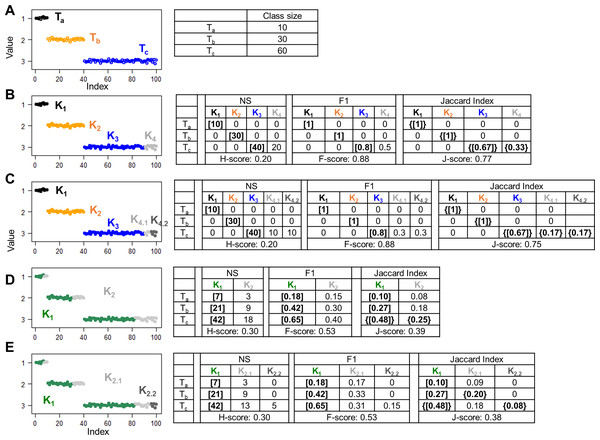
For ground truth, we generated 100 random numbers D_i ( i = 1, …, 100) belonging to three classes. Specifically, D_1,…,10 from a Gaussian distribution G(1, 0.05) constituted class T_a, D_11,…,40 ∈ G(2, 0.05) constituted class T_b, and D_41,…,100 ∈ G(3, 0.05) constituted class T_c (Fig. 1A). We first examined hypothetical partition structures that contained more clusters than classes. In one simulation, we grouped the data points into four clusters (Fig. 1B). Clusters K₁ and K₂ consisted of all data points from classes T_a and T_b, respectively; Cluster K₃ consisted of D_41,…,80 that are two thirds of data points from T_c; and cluster K₄ consisted of the remaining data points from T_c. Because the number of hypothetical clusters exceeded the number of true classes, stray clusters were inevitable. Indeed, all three approaches despite using different T → K algorithms, identified K₁, K₂, and K₃ as the cluster best matched to T_a, T_b, and T_c, respectively, and left K₄ unmatched. The H-score (0.20) and the F-score (0.88) were calculated based on the goodness of T_a → K₁,  T_b → K₂, and T_c → K₃ matches, with no information contributed by K₄. The “problem of matching” occurred when we split the unmatched K₄ cluster into two clusters K_4.1 and K_4.2 (Fig. 1C). This splitting obviously reduced the overall accuracy of the partition structure. But H-score and F-score remained unchanged because K_4.1 and K_4.2 were stray clusters and did not contribute to the final scores. J-score rescued these stray clusters in the K → T matching step, identifying T_c as the class best matched to K_4.1 and K_4.2. Then, all clusters and classes contributed information to the final J-score. As expected, the J-score dropped from 0.77 to 0.75 after the splitting.

Stray clusters exist even when there are fewer clusters than classes. In one simulation, we created a hypothetical partition structure consisting of two clusters. Specifically, cluster K₁ mixed 70% of the data points from each class. The remaining data points were grouped into cluster K₂ (Fig. 1D). After the T → K matching step, K₁ was repeatedly identified as the best matched cluster for all three classes, leaving K₂ as a stray cluster. In another hypothetical partition structure, we kept cluster K₁ untouched and split K₂ into K_2.1 and K_2.2 that were stray clusters as well (Fig. 1E). Again, because these two hypothetical partition structures differ only by stray clusters, H-score and F-score failed to distinguish them. J-score correctly reported a higher value for the first structure than the second structure (0.39 vs. 0.38).

J-score reflects correct inference of class numbers

An important objective of cluster analysis is to infer the number of classes in input data. A robust accuracy measure shall reward a hypothetical partition structure if it contains the correct number of clusters and penalize incorrect ones, as well as accounting for assignment of individual data points to each cluster. Using simulated data and real benchmark data sets, we examined how J-score and other measures varied with the number of clusters. Because H-score and NVI measure distances, we converted them to 1-H and 1-NVI, respectively, to measure similarities.

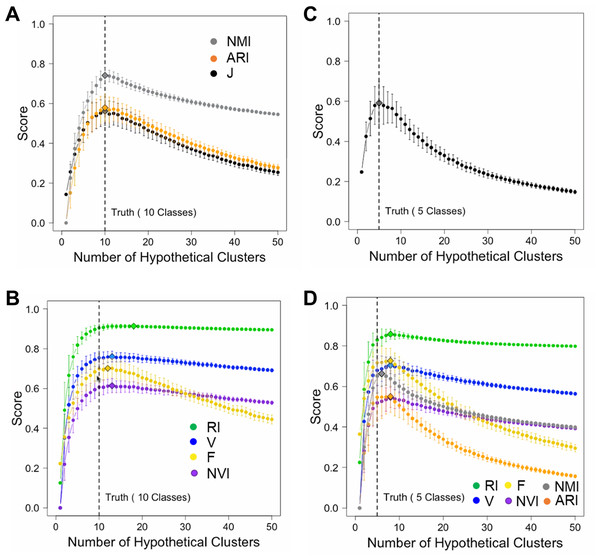
To minimize the confounding effect between class number inference and data point assignment, we simulated hypothetical partition structures by splitting or merging true classes. For ground truth, we generated 1,000 random numbers belonging to 10 classes. We varied the number of clusters K from 1 to 50. For each hypothetical partition structure, we computed seven accuracy measures including J-score, F-score, V-measure, RI, ARI, NMI, and NVI. We repeated this process 200 times for each K value and examined the mean and variance of each score. Since the number of true classes was 10, we expected these scores should peak at K = 10. This was indeed the case for J-score, F-score, ARI, and NMI (Fig. 2A). These scores also decreased sharply as K deviated from 10, penalizing both deficient and excessive clusters. However, V-measure, RI, and NVI peaked incorrectly at K = 13, overestimating the number of classes (Fig. 2B). These two measures penalized excessive clusters only slightly. Even when K = 50 corresponding to overestimation by 400%, these scores decreased only by 5% from their peak values. To examine if J-score remains robust when the number of classes decreases and the class size increases, we simulated 1,000 random numbers belonging to five classes. Again, J-score peaked at correct inferences of class counts (Fig. 2C) while all the other scores overestimated (Fig. 2D). These results are consistent with previous reports of biases towards excessive clusters using existing accuracy measures (Amelio & Pizzuti, 2015; Lei et al., 2017; Vinh, Epps & Bailey, 2010). J-score is vigorous in this perspective.

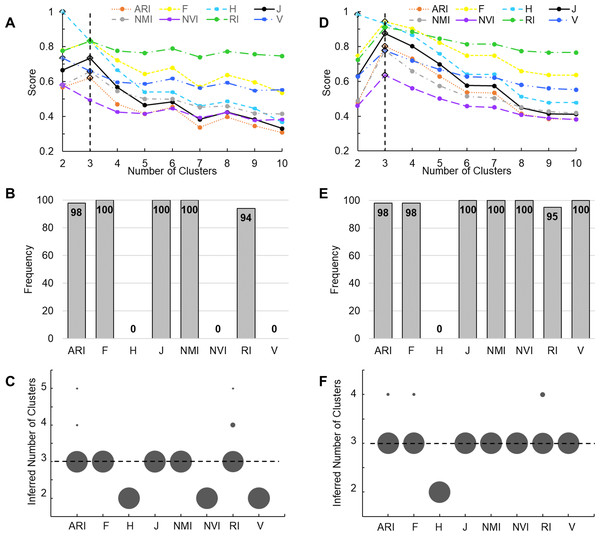
We then examined the performance of these accuracy measures by applying them to clustering results of two real datasets. The first benchmark data set contains 150 iris plants belonging to three true classes. We performed K-means clustering of these plants. A key initial parameter of K-means is the number of clusters (K) to partition the data points into. Because K is unknown in priori, we varied K from 2 to 10. A robust accuracy measure is expected to maximize when K is equal to the number of true classes. Indeed, J-score, along with ARI, RI, F-score, and NMI, peaked at K = 3, identifying the correct number of clusters. H-score, NVI, and V-measure maximized at K = 2, underestimating the number of clusters (Fig. 3A). To further examine the performance of these measures, we randomly sampled 90% of the Iris data set and repeated the above analysis 100 times. J-score, F-score, and NMI were the top performers, maximizing at K = 3 across all 100 tests (Fig. 3B). Conversely, H-score, NVI, and V-measure always underestimated the number of clusters, maximizing at K = 2 across all tests (Fig. 3C). ARI and RI made overestimations in 2% and 5% of the tests, respectively, maximizing at K = 4 or 5.

The second benchmark data set contains 178 wines belonging to three true classes. We performed agglomerative hierarchical clustering of these wines. Although hierarchical clustering does not need to know the value of K when building dendrograms, this information is required when cutting the tree to create disjoint clusters. We again varied K from 2 to 10. All measures except H-score maximized at K = 3 (Fig. 3D). We then randomly sampled 90% of the Wine data set and repeated the analysis 100 times. J-score, NMI, NVI, and V-measure were the top performers, maximizing at K = 3 across all 100 tests (Fig. 3E). ARI, F-score, and RI made overestimations in 2–5% of the tests (Fig. 3F). H-score always made underestimations, maximizing at K = 2.

These results from analyzing simulated data and real data consistently supported that J-score is robust at inferring the correct number of clusters.

J-score has a relatively stable baseline

The establishment of a baseline for an accuracy measure serves as a reference point to evaluate the performance of clustering algorithms and assess their ability to capture meaningful patterns in the data. It is important to note that the baselines of most clustering accuracy measures are not constant (Vinh, Epps & Bailey, 2010). In the proof of Proposition 2, we showed that the baseline of J-score is also not constant. To further investigate this phenomenon, we examined how the baseline of each measure varies using simulated data sets and real data sets.

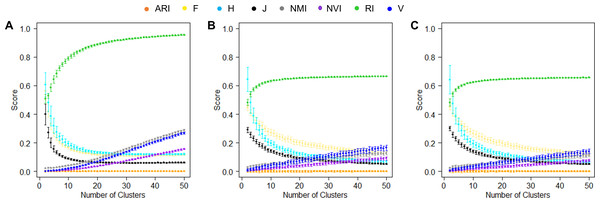
In the simulation experiments, we computed similarities between two random hypothetical partition structures. Specifically, we simulated 1,000 random numbers, randomly assigned them to K clusters, and varied K values from 2 to 50. For each K, we generated two random hypothetical partition structures and measured their similarities using various measures. We repeated this process 50 times for each K value. Because these partition structures were random, their mean pairwise similarities shall be close to the lowest value of the corresponding accuracy measure and stay constant regardless of the K value. This was indeed the case for ARI that is designed deliberately to maintain a stable baseline at 0 (Fig. 4A). The second best was J-score, with the baseline stabilized around 0.08 after the K value reached 12 and higher, i.e., the mean cluster size was less than 83. However, when K was small, many data points were grouped together simply by chance, leading to high similarities between random partition structures and consequently high baseline values. Similar to J-score, the baselines of F-score and H-score quickly dropped as K increased but stabilized at a higher value (0.16). Conversely, the baselines of NMI, NVI, and V-measure steadily increased with the K value, showing no signs of stabilization across the entire range of K values tested. This pattern was consistent with the previous reports that these measures were biased towards overestimating the number of clusters (Amelio & Pizzuti, 2015; Vinh, Epps & Bailey, 2010). The baseline of RI looked the most different from the others, quickly approaching 1 as K increased.

We also examined the baselines of these accuracy measures in real datasets. Specifically, we randomly assigned the 150 iris plants (Fig. 4B) or 175 wines (Fig. 4C) to K clusters with K varied from 2 to 50. For each K, we generated a random clustering structure, measured its similarity to the true partition structure, and repeated this process 50 times. Unlike the simulated data where the two random clustering structures had the same value of K, this analysis using real data sets allowed the K value to be different from the number of true classes. The baselines of the various accuracy measures observed in this analysis were largely consistent with those observed in the simulated data. The only exception was RI, the baseline of which approached 0.6 instead of 1, reflecting the large impact of the numbers of clusters in two partition structures on this measure.