Determining population structure from k-mer frequencies

Population structure of human superpopulations from k-mer frequencies using PCA

For each sample, we computed the frequencies of canonical k-mers (k-mer or its reverse complement, whichever comes first lexicographically) of length 21 bp. Frequencies were computed from the fasta file using Jellyfish (Marcais & Kingsford, 2011) (version 2.2.10), a tool for fast, memory-efficient counting of k-mers in the DNA sequence. When choosing the length of k-mers we were initially guided by a general rule used by alignment-free methods for sequence comparisons—shorter k-mers are more likely to be present in a sequence (e.g., 1-mers); thus they are less informative in analyzing closely related genomes (Bernard, Chan & Ragan, 2016); however, longer k-mers are more unique to particular species and are therefore more useful for similarity identification across species (Greenfield & Röhm, 2013). Moreover, widely used alignment-free sequence comparison tools such as mash found a k-mer length of 21 to give accurate estimates of sequence similarities (Ondov et al., 2016). We examined alternate values of k (k-mer frequency length) in our simulations (see below).

We filtered out singletons (k-mers of frequency one) to account for possible errors produced by the sequencer (Melsted & Pritchard, 2011). For this purpose, the flag -L 2 is used when analyzing the k-mer content of the sequence with Jellyfish. We then sorted each k-mer frequency profile in alphabetical order and calculated the intersection of k-mer profiles across all samples. We used the intersection to ensure accurate counts, as singletons may be sequencing errors and were not counted; thus, including such k-mers could introduce the uncertainty of assigning counts of either 1 or 0. The resulting output is a count of each k-mer of size 21 that is found in all samples.

We performed a PCA on vectors of k-mer frequencies of each sample in python (version 3.6.6) using the scikit-learn (sklearn) library (Pedregosa et al., 2011) (version 0.23.2). We normalized the data (frequencies of k-mers) by scaling all the values to be between 0 and 1 using the StandardScaler function from the scikit-learn (sklearn) library (Fränti & Sieranoja, 2018). Normalization of the dataset is a necessary step due to PCA calculating a new projection of the dataset with new axes based on the standard deviation of the variables (Jolliffe & Cadima, 2016). Variables with different standard deviations (high versus low) will have different weights for axes calculation. Normalization of data allows for uniform standard deviation across all variables, thus PCA calculates axes with all variables having equal weight. We visualized the projection of the two PCs with the most variance using a scatter plot from the matplotlib package (Hunter, 2007).

To identify populations, we used K-means clustering based on the PCs (Ding & He, 2004; Lee, Abdool & Huang, 2009) using the scikit-learn (sklearn) library (version 0.23.2). We found the optimal number of principal components that capture the greatest amount of variance in the data by plotting the explained variances in a scree plot. We used the explained variance ratio as a metric to evaluate the usefulness of the principal components and to choose how many components to use in the model (Jombart, Devillard & Balloux, 2010). The explained variance ratio is the percentage of variance that is attributed by each of the selected components. To avoid overfitting the model we chose the number of components to include in the model by adding the explained variance ratio of each component until we reach a total of around 80%, which is considered an adequate amount of variance to derive informative results (Jolliffe & Cadima, 2016). We used these PCs to cluster samples into different numbers of groups (k from 1–10). We determined the optimal number of clusters (K) by using the “elbow method” heuristic approach (Yuan & Yang, 2019). The sum of the squared distances to the nearest cluster center (aka inertia) was measured using the K-means model for each k. From the scree plot, we determined the “elbow point”, i.e., the point after which the inertia starts decreasing in a linear fashion. We clustered the dataset by fitting the numbers of PCs with 80% of the variance into the K-means model with k number of clusters.

Because the PCs with 80% of the variance caused undecidability in the K-means clustering algorithm, we hypothesized that the dataset contains noise that suppresses the true biological signal, and only a small fraction of k-mers “drive” (dominate) the data. From the scree plots of PC variance and K-means inertia plots, we saw that the variance is spread out, mostly equally, through all the PCs. Commonly, the first three PCs contain most of the variance of the data (around 80%), however, our dataset shows that the first three PCs have only a slightly higher variance than the rest of the PCs. Nevertheless, when using the first two PCs we saw deterministic results by K-means and they matched the expected results. Thus, we used the first two PCs throughout this work.

The analysis of the dataset including all five superpopulations showed strong differentiation of the AFR superpopulation from the rest of the superpopulations. Thus, we repeated the analysis for four superpopulations excluding AFR, with 24 samples of a single origin as identified by The 1000 Genomes Project Consortium et al. (2015) (AMR_PEL, EAS_JPT, EUR_TSI, and SAS_ITU).

Differentiating human populations with k-mer frequencies using PCA

Because we were able to differentiate human superpopulations, we examined whether this approach could differentiate populations within those superpopulations. We obtained an additional 12 samples (six per population) of European ancestry and East Asian ancestry originating from single-origin populations (The 1000 Genomes Project Consortium et al., 2015):

1. Finnish population in Finland (FIN) of European ancestry.

2. Dai Chinese population in Xishuangbanna, China (CDX) of East Asian ancestry.

Genomes for each individual were obtained as described above. We repeated our analysis with these six populations from four superpopulations (excluding AFR). These additional samples allow us to establish how this approach differentiates samples hierarchically (i.e., whether all six populations are differentiated or whether only the four superpopulations are supported). Methods such as STRUCTURE often require separate examination of individual clusters to determine large-scale and fine-scale population structure separately (O’Neill et al., 2013).

Populations from multiple ancestral origins

To determine whether we could identify populations of more complex origin, we selected samples from populations that were previously identified as comprising roughly equal parts fractional membership of two ancestral populations (The 1000 Genomes Project Consortium et al., 2015) from the same superpopulation (we refer to these as “multiple-origin” populations). We obtained six samples from the Han Chinese population in Beijing China of mixed East Asian ancestry (CHB). In our prior analysis the two ancestral populations within East Asia are represented by JPT and CDX. We obtained an additional six samples from Utah residents of Northern and Western European ancestry (CEU). In our prior analysis Northern European ancestry is represented by the FIN population, while Western European ancestry is represented by TSI. Genomes for each individual were obtained as described above. We repeated our analysis with these eight populations from four superpopulations (AMR_PEL, EAS_CDX, EAS_CHB, EAS_JPT, EUR_CEU, EUR_FIN, EUR_TSI, and SAS_ITU; excluding AFR).

Because we continued to differentiate the four superpopulations, we focused a subsequent analysis on the single East Asian (EAS) superpopulation with 18 samples (12 single-origin and six multiple-origin; EAS_CDX, EAS_CHB, and EAS_JPT) to determine our ability to identify population origin as in STRUCTURE (Pritchard, Stephens & Donnelly, 2000). We repeated our PCA analysis on these samples alone. Additionally, we repeated the analysis on the single European (EUR) superpopulation with 18 samples (12 single-origin and six multiple-origin; EUR_CEU, EUR_FIN, EUR_TSI).

Comparison of k-mer/PCA results to SNP/fastSTRUCTURE

To compare our k-mer frequency-based PCA approach, we assessed population identifiability in the same datasets from the 1000 Genomes Project using SNPs and fastStructure (Raj, Stephens & Pritchard, 2014, version 1.0). This tool is a computationally efficient alternative to the STRUCTURE method (Pritchard, Stephens & Donnelly, 2000). We extracted SNPs for each group of samples using bcftools (version 1.12) to merge the vcf files generated previously from cram files. Data was then converted to bed format using PLINK (version 2.00a3.7). fastStructure was run with K values ranging from two to six for all datasets except in the case where there were eight potential populations. The chooseK script included in fastStructure was employed to determine the optimal K values. Finally, the distruct script included in fastStructure was used to create plots for the selected optimal K value(s).

K-mer frequency approach applied to simulated data

To further investigate the use of k-mer based methods in population structure analyses, we applied the same approach to simulated data, where the true population structure was known. We initially simulated three populations using a genome size of 10⁷ bp. Simulations were performed in SLiM (Haller & Messer, 2017) in the GUI (SliMguiLegacy version 3.7.1) using a random starting sequence, neutral mutations at a rate of 10⁻⁷ and a recombination rate of 10⁻⁸. The initial effective population size of the starting population was set to 500, and this population was expanded to 1,000 after 2,000 generations. A second population of 180 was added in generation 3,500, and a third population of 180 was added in generation 4,500. Minimal migration was allowed. Six genomes per population were sampled at generation 7,000. This model was loosely based on the human population model of Gravel et al. (2011), although with fewer generations due to time and computational limitations, and no population expansion.

K-mers were counted as above using Jellyfish (Marcais & Kingsford, 2011) (version 2.2.10), a PCA was produced based on the intersection of k-mers across samples, and K-means clustering was used to identify groupings. Because our initial approach using k-mers of size 21 produced no k-mers with counts greater than two, and even fewer k-mers common to all samples, we used k-mers of size 9. K-mer size was chosen by examining k-mer frequency distributions and selecting a size with a symmetrical distribution.

The simulation was repeated with genomes sampled at 5,500 generations. This simulation was then repeated with exponential growth in the second and third populations following the establishment of the third population (similar to expected population expansion in humans). Finally, we used the simulation without growth and added a fourth population that was the product of equal migration from populations 2 and 3. After a single generation, this population was isolated.

To examine the impact of hybrid-origin populations more precisely, we adapted a SLiM simulation population structure recipe for adding subpopulations. We started with three populations of effective populations sizes of 500, 500, and 200. The smaller population experienced 10 generations of equal origin from the larger two. After this, migration was reduced to 0.02% of the smaller population originating from each of the larger populations in each generation (probabilistically) and each of the larger populations experiencing origin of 0.02% from the smaller population. Genomes were sampled after 5,500 generations. We used a k-mer size of 11 for this and subsequent simulations based on k-mer distributions. Simulations were repeated with migration of 0.2% and 2% to examine the impacts of higher migration rates on detection of populations.

Comparison of simulated data results using fastSTRUCTURE

For comparison, we examined population differentiation in our simulated datasets using fastStructure (Raj, Stephens & Pritchard, 2014) (version 1.0) as described earlier. We extracted the biallelic sites from the simulated whole genome alignments and converted them to STRUCTURE format using a custom script. We ran fastStructure for K values of 2–6 and used the chooseK script to select the optimal range of K values. We used the distruct script to generate plots for the optimal value(s) of K.

Population structure from a number of shared k-mers between sequence pairs

For comparison with our k-mer frequency-based PCA approach, we examined population identifiability in our human datasets using mash (Ondov et al., 2016) (version 2.1.1). mash can be used to build phylogenies for family-level data and shows promise for population genetic analyses of polyploid sequences (VanWallendael & Alvarez, 2022). The principle behind mash is that each sequence is converted into a MinHash sketch, a vastly reduced representation of a sequence, then two sketches are compared by calculating the fraction of shared k-mers between a pair of sequences (Jaccard index). Finally, the mash distance is calculated, which estimates the rate of sequence mutation under a simple evolutionary model. mash has been investigated for basic population genetic analyses of polyploid and diploid species (VanWallendael & Alvarez, 2022) and showed some promising results in the population stratification of plants.

For each sample we built mash sketches using a mash sketch command with -m 2 flag to filter out single k-mers, -k N flag to analyze the k-mer length of N, and -s M flag to build sketches of size M. We repeated the process for parameters of -k N = 21, 24, 27, 29, 32 and -s M = 1,000, 3,000, 5,000, 7,000, 8,000, 9,000, 10,000, 12,000, 15,000, 18,000, 20,000, 23,000, 25,000, 28,000, 30,000 to compare the results for a different set of parameters. We calculated pairwise distances between each pair of samples using mash and used the distances to build a neighbor-joining tree (NJ) for each set of parameters—k-mer length and sketch size. mash does not assign samples by population thus to verify that grouping by superpopulation we checked for monophyly of each of the groups in the NJ tree by superpopulation label. We used the is.monophyletic function in the ape (version 5.0) R package (Paradis & Schliep, 2019) to check whether each population was monophyletic in the resulting tree and ggplot2 (Wickham, 2016) (version 3.3.4) to plot the Boolean values for whether the tree with all the populations contained clades that are all monophyletic.

Population structure of five human superpopulations shows two major groups

To differentiate samples from the five human superpopulations identified by the 1000 Genomes Project (The 1000 Genomes Project Consortium et al., 2015) we used principal component analysis with a K-means clustering algorithm. 80% of the variance was captured by 21 PCs. The first two PCs contained 14.5% of the variance.

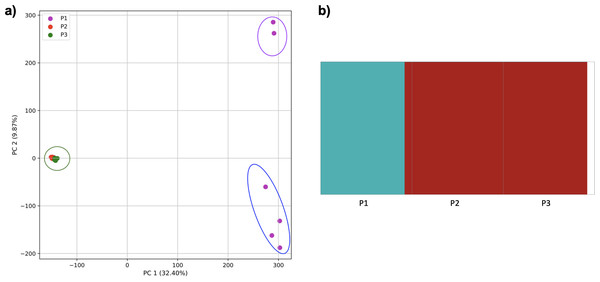
Using 21 PCs, which hold 80% of the variance, caused undecidability in the K-means clustering algorithm where no obvious inflection (“elbow”) point was observed (Fig. 1A). However, using the first two PCs, which hold 14.5% of the variance, showed deterministic results in K-means clustering (Fig. 1B). Thus, we applied K-means clustering to the first two PCs throughout this study. The African superpopulation was strongly differentiated from all other samples along PC1. The “elbow point” of the K-means scree plot (when the change in the value of inertia is no longer significant) indicated the samples grouped into three clusters. There was a strong differentiation of samples of African Ancestry (AFR_LWK) from all other populations on PC1, and differentiation within this population along PC2 (Fig. 2). In contrast, the fastStructure SNP-based approach assigned the individuals to a single population (Fig. SA1).

Population structure from four human superpopulations shows four groups

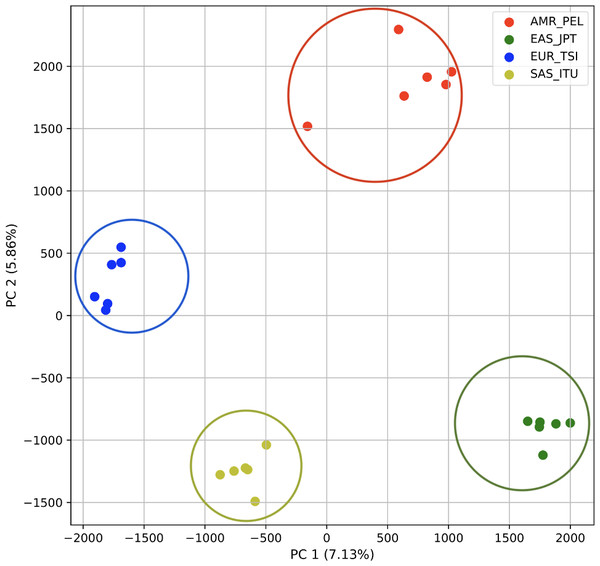
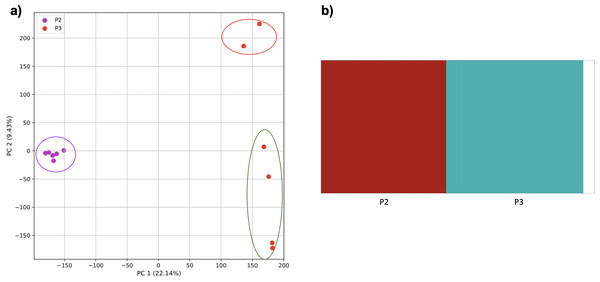
To determine whether we could differentiate the non-African populations we repeated the PCA analysis excluding AFR_LWK samples. 80% of the variance was captured by 18 PCs. The first two PCs contained 13% of the variance. Plotting the first two PCs, we observe four distinct groups corresponding to the four superpopulations (Fig. 3). The elbow point of the K-means scree plot indicated the samples grouped into four clusters (Fig. SA2). In contrast, the fastStructure SNP-based approach assigned the individuals to a single population (Fig. SA3).

Population structure from four human superpopulations including samples of multiple ancestral origin

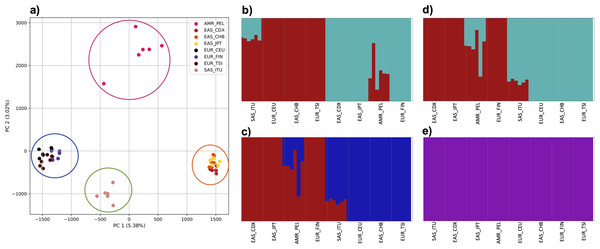
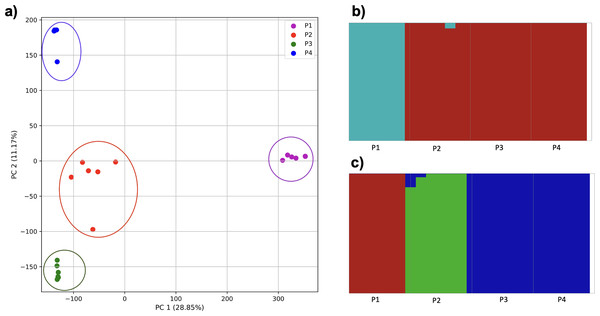
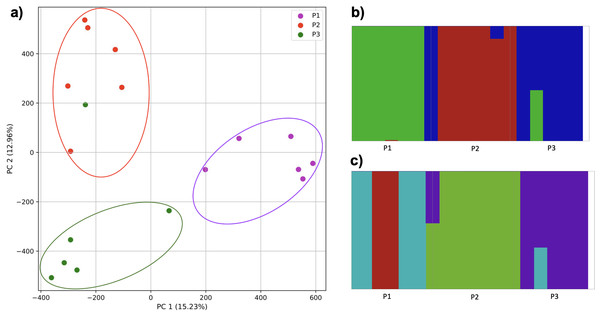
To examine the ability of this approach to provide information about samples from populations identified as having ancestry from multiple populations within a single superpopulation (as identified by the 1000 Genomes Project), we repeated the PCA analysis with additional “multiple-origin” samples from EAS and EUR superpopulations. 80% of the variance was captured by 36 PCs. The first two PCs contained 8.4% of the variance. Plotting the first two PCs, we observe four distinct groups corresponding to the four superpopulations; individual populations were not clearly differentiated (Fig. 4A). The “elbow point” of the K-means scree plot indicated the samples grouped into four clusters (Fig. SA4). On the other hand, the fastStructure SNP-based approach selected a K value between 1–5; however, fastStructure plots assigned individuals either to a single population (Fig. 4E), or wholly or partly to one of two populations, which did not correspond to expected population differentiation or that identified by our k-mer/PCA approach (Figs. 4B–4D).

Population structure from three populations of single and multiple origins

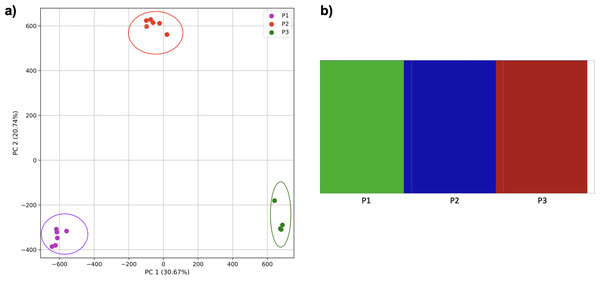
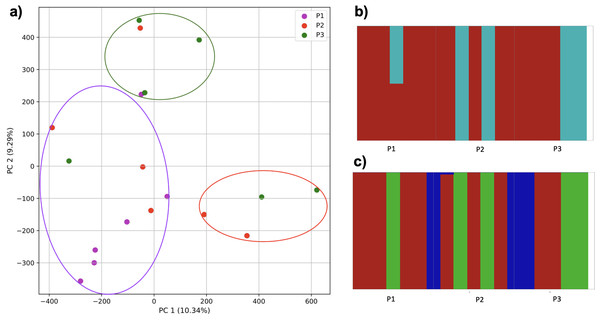
To further examine our ability to understand populations with samples identified as having multiple origins, we repeated the PCA analysis with our samples from the East Asian superpopulation. 80% of the variance was captured by 14 PCs. The first two PCs contained 13% of the variance. Plotting the first two PCs, we observe three distinct groups corresponding to the three populations CDX, CHB, and JPT (superpopulation EAS), with the CHB population placed in between CDX and JPT populations (Fig. 5). The “elbow point” of the K-means scree plot suggested three populations, although it was difficult to distinguish between three to five, suggesting the samples formed a continuous grouping (Fig. SA5). When samples were assigned to three populations these corresponded to the known populations, with one exception. In contrast, the fastStructure SNP-based approach assigned the individuals to a single population (Fig. SA6).

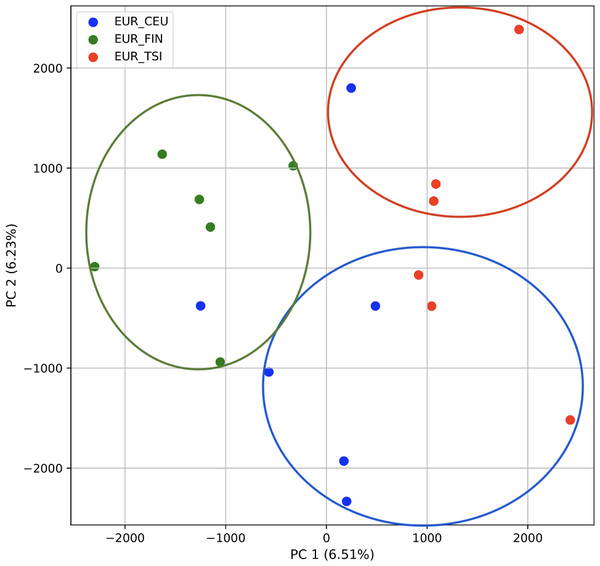
We also repeated the PCA analysis with samples from the European superpopulation with samples of both single and multiple origin. 80% of the variance was captured by 14 PCs. The first two PCs contained 13% of the variance. Plotting the first two PCs, the three populations CEU, FIN, and TSI (superpopulation EUR) appear visually differentiated along PC 1, with CEU (Northern and Western ancestry) placed in between FIN (Northern) and TSI (Western) (Fig. 6). As for the prior analysis, the “elbow point” of the K-means scree plot suggested three populations, although the angle differentiation was not strong, suggesting the samples formed weaker groupings than the superpopulations (Fig. SA7). While the visual scatter plot of the PCA appears to suggest differentiation along PC 1 nearly consistent with the expected population groupings, there is discordance between sample populations and K-means assignments. This is because K-means clusters individuals into genetically homogeneous subpopulations by placing each observation to the cluster with the nearest mean (Fränti & Sieranoja, 2018). On the other hand, the fastStructure SNP-based approach assigned the individuals into a single population (Fig. SA8).

Accuracy of K-means clustering

The adjusted mutual information (AMI) score for K-means clusters and the expected clusters from the analysis of the five superpopulations of non-admixed origin was 0.35 but improved to 1.0 when excluding AFR. The AMI for K-means clusters and the expected clusters of the four superpopulations including samples of admixed and non-admixed origin was 1.0. When analyzing individual superpopulations including samples of admixed and non-admixed origin to differentiate populations, the AMI was 0.83 for the populations in EAS, and 0.43 for the populations in EUR. For the explained variance plots and for the cumulative explained variance plots see Figs. SA9–SA18.

Memory usage when analyzing population structure with k-mer frequencies

These analyses (using k-mer length of 21) stored a dictionary data structure with k-mer content for each sequence. The dictionary of 48 vectors of k-mers and their frequencies occupied 41Gb of space in a pickled (compressed) format. Reduction of space to 38Gb was possible by calculating the intersection of k-mers across all vectors. Generating these data structures required an HPC node with at least 250Gb of RAM for the dictionary compression step. Additionally, calculating PCA on this dataset required ∼239Gb of RAM, and took 2 h 36 min and 51 s of job wall-clock time on a 36-core HPC node. For simulations of 10 million base pairs and 18–24 samples, analyses took just a few minutes.

Accuracy of population structure estimates from k-mer frequencies using simulations

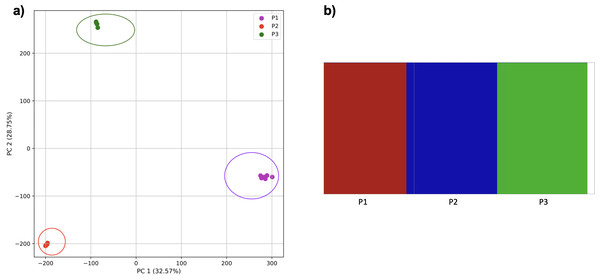
To examine the use of this approach in greater depth we simulated populations and sampled genomes from each. In our initial simple three-population simulation (Fig. 7), we clearly identified the three populations using k-mer frequencies with PCA and K-means clustering. The fastStructure SNP-based approach also assigned the individuals in the three populations correctly.

Reducing the time interval between the establishment of the third population and sampling did not affect the results either for our approach (Fig. 8) or from fastStructure.

However, when the second and third populations experienced exponential growth, they were grouped together in the PCA (separated from population 1 along PC1) and by K-means clustering, while the oldest population was separated into two groups (along PC2) (Fig. 9). fastStructure also grouped the second and third populations, although it did not separate population 1 into two groups.

When these two populations were analyzed without population three, they were separated by the PCA and K-means clustering (Fig. 10). fastStructure also separated the populations successfully, but only suggested the two clusters accurately.

For the four populations simulation, where the fourth population originated from a mix of two others, followed by isolation, all four populations were separate, with population 1 differentiated along PC1 and the remaining along PC2 (Fig. 11). In contrast, fastStructure supported either two or three populations, but was unable to differentiate all four successfully. In the former case, population 1 was separated from all others (i.e. matching PC1 of the k-mer approach), while in the latter population 1 and 2 were each separate, while 3 and 4 were grouped together.

In using simulations to examine hybrid-origin and subsequent migration more closely, isolated populations of hybrid origin were rapidly differentiable from other populations (Fig. 12) using both approaches.

As migration increased, populations became more difficult to differentiate. Populations with limited (≤0.2% of parents from each origin population entering the hybrid population and vice versa) were differentiated, but had some overlap and contained one mis-assigned individual in the clustering (Fig. 13). The fastStructure approach suggested either three or four clusters. In the 3-population scenario, the first population was strongly differentiated (i.e., matching PC1 of the k-mer approach), with the addition of the partial assignment of an individual from population 3. Five individuals from population 2 were strongly differentiated with the addition of an individual from population 3. The remaining individuals from population 3 were strongly differentiated with the addition of an individual from population 2 and the partial assignment of the individual to population 1.

When divided into four clusters, two individuals from population 1 formed a cluster, the four remaining individuals formed a cluster along with partial assignment of a single individual from population 3. Population 2 formed a cluster combined with one individual from population 3 (as in the k-mer approach), although one individual was only partially assigned, and the five remaining individuals from population 3 formed a cluster.

As migration was increased further, populations could not be differentiated (Fig. 14). While the k-mer approach with K-means identified three clusters, these did not match the simulated populations. Similarly, fastStructure identified either two or three populations. In the former scenario, one cluster consisted of two individuals from population 3 and three from population 2, and 50% assignment of an individual from population 1. In the latter, cluster 1 consisted of 5 individuals from population 1, 3 from population 2, and 2 from population 3; cluster 2 consisted of 1 from population 1, 2 from population 2, and 2 from population 3; cluster 3 consisted of 1 from population 2 and 2 from population 3.

Population structure from k-mer presence alone

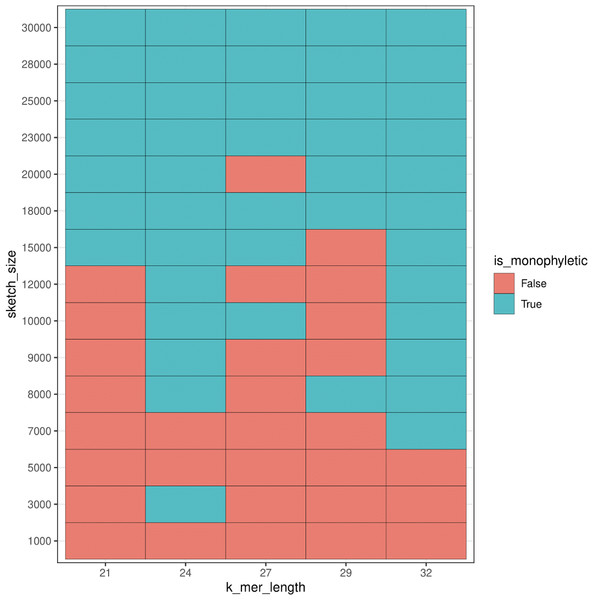
For additional comparison with our PCA approach, we used mash to estimate population structure from the human samples. Monophyly of the superpopulation groups was observed on the unrooted tree for various parameters of k-mer length (k) and sketch size (s) (Figs. SA19–SA22). Specifically, the trend of accurate grouping by population was observed with shorter k-mer length and higher sketch size, and conversely lower sketch size and longer k-mer length produced trees with monophyletic groupings of samples by population (Fig. 15).

While we saw a general trend of improved accuracy with low k-mer length and higher sketch size, and conversely longer k-mers and smaller sketch size, we saw exceptions in the accuracy trend for various parameters. For example, k-mer length 24 and sketch size 3,000 produced accurate results, however, the accuracy dropped with setting k = 24 and s = 5,000 and 7,000, and the accuracy picked up again when k = 24 and s = 8,000–30,000. While this test case allowed us to compare results to the ground truth, it is difficult to select a priori the parameters that produce accurate results.

Population identification

We hypothesize that our initial observation of two larger clusters in the data from the five human superpopulations (Africa and all others) reflects the effects of the high genetic variation and population-specific alleles in the African populations due to humans originating in Africa, combined with the bottlenecks and subsequent population expansion of other populations (Campbell & Tishkoff, 2008; Gravel et al., 2011). While similar substructure was not found by the 1000 Genomes Project when using SNPs, it is accurate that non-African populations share common ancestry with each other more recently than they do with African individuals. We observed that simulations produced similar differentiation in the results from the three-population model with population expansions, but not in the constant-size model, confirming that an out-of-Africa model with subsequent population expansion may produce the observations from the empirical data. Alternatively, Kulohoma (2018) found structure within the LWK samples corresponding to outlier individuals, who may be from different tribes, which could also explain differentiation within the African samples.

Excluding the African superpopulation, k-mer-based PCA grouped the samples by their expected superpopulation, with the majority of variation among superpopulations. This result was consistent with analyses based on SNPs (The 1000 Genomes Project Consortium et al., 2015) by the 1000 Genomes Project. PCA analysis of individual superpopulations similarly differentiates populations as expected in prior work. These results are consistent with the results from our simulations, in which populations were easily differentiated by our approach.

For populations identified as having multiple origins using SNPs, k-mer-based PCA places samples in between the two populations representing the two ancestral populations. The continuum in the placement of samples of multiple origins likely corresponds to the fractional membership of samples as determined by the 1000 Human Genomes Project. Specifically, given two populations, additional samples with origin similar to both are placed on the coordinates along edges joining the centers of the established populations (Patterson, Price & Reich, 2006). While it is not surprising that these samples are not accurately assigned to a third population, as this same result was found by the 1000 Genomes Project (The 1000 Genomes Project Consortium et al., 2015), three populations were identified by K-means and the third intermediate population was largely comprised of the expected mixed samples.

K-mers versus marker genotypes

Importantly, k-mer frequencies can be simpler to count and process when compared to using marker genotypes (e.g., SNPs). Thus, the k-mer-based approach has particular potential to be useful for non-model organisms (Russell et al., 2017). Such non-model organisms do not have established SNP panels or information on allele frequencies from which population structure can be identified using model-based approaches and marker genotype data. In organisms without a reference genome (Bendaoud et al., 2022), a typical way to discover SNPs to analyze variation is through restriction digests and several computational pipelines (Puritz, Hollenbeck & Gold, 2014). On the other hand, generation of k-mer profiles from genome sequences, even of non-model organisms, is a straightforward task where subsequences of length k are counted along the genome and no markers have to be identified. While sequencing whole genomes can be more costly than RADseq, whole genome sequencing promotes reuse of data and is becoming more cost effective. Therefore, the method described in this paper provides a functional alternative to model-based approaches where genome data lacks information on SNPs and provided the goal of the analysis is to only identify the population structure present in the dataset. It may also act as a complementary approach to analyses where larger numbers of individuals were sequenced for smaller allele panels.

When analyzing genotype data, a number of preprocessing steps to evaluate data quality are necessary (Pritchard, Stephens & Donnelly, 2000; Alhusain & Hafez, 2018), as population structure estimation using genetic markers is susceptible to genotyping errors (Pompanon et al., 2005). This evaluation includes an assessment of SNP call rates, minor allele frequencies (MAFs), verification of the HWE assumptions, and relatedness between individuals. Additionally, the identification of ancestry informative markers, which constitute a minimal number of markers needed to obtain population structure, is necessary to ensure the accuracy of the results (Alhusain & Hafez, 2018). In contrast, k-mer frequencies can be viewed as summary statistics of a genome resulting from SNPs. While errors in k-mer counts occur due to sequencing or genotyping errors, these can easily be identified as k-mers of low frequency. The overwhelming majority of k-mers of frequency 1 are not found in a genome and thus are most likely due to sequencing errors and therefore can easily be discarded (Melsted & Pritchard, 2011). While in this analysis we use the available reference genome for alignment to produce a genome for each sample, k-mer frequencies should not be significantly affected by using a draft genome assembly.

Model-based population analysis methods can also be limited by inadequate sample sizes and the number of markers analyzed (Lawson, Van Dorp & Falush, 2018). These methods depend on an estimation of allele frequency that is sensitive to small samples (Gao & Starmer, 2008; Porras-Hurtado et al., 2013). In contrast, our PCA-based k-mer frequency approach does not depend on allele frequency estimation and thus is not affected by sample size (Alhusain & Hafez, 2018). We were able to produce accurate results with as few as six samples per population.

The PCA-based approach also has the advantage of operating without a preset number of populations and no modeling assumption requirements (Patterson, Price & Reich, 2006; Lee, Abdool & Huang, 2009). This makes the analysis of population structure using a non-model-based approach an appealing choice. The application of PCA and K-means to k-mer profiles of genomes makes it easy to detect a number of populations (clusters) present in the dataset, which is a major parameter in the model-based method that is required to be set in advance.

However, it is important to recognize that the k-mer and SNP-based approaches may deliver different types of information. While a more complex but sophisticated method such as STRUCTURE describes the population structure by probabilistic assignment to classes, the PCA combined with K-means, provides a graphical and quantitative representation of population structure along axes of variation in the dataset. Thus, the goal of the investigation of population structure should be taken into consideration when deciding which approach is more applicable for the analysis.

Consideration of computational efficiency

The PCA-based approach is computationally efficient and can handle genomic marker data for thousands of individuals (Paschou et al., 2007). PCA also demonstrated efficiency when applied to k-mer frequencies in our study. However, the k-mer approach has some limitations. While it is effective for analyzing datasets with a limited number of samples, the large memory burden associated with k-mer analysis poses a significant challenge when applied to larger datasets. The memory requirements increase with k-mer length, as does the computational power needed to calculate distances between sequences based on k-mer frequencies. Additionally, shorter k-mers tend to be less informative, whereas longer k-mers offer greater specificity but demand more resources. This creates a tradeoff between specificity, computational efficiency, and memory requirements. Approaches such as down sampling (sketching) or compressing the k-mer space may help address these limitations and improve the feasibility of k-mer analysis for larger datasets.

Identification of population structure based on the number of shared k-mers

mash’s identification of all five superpopulations, suggests that mash has an adequate amount of sensitivity to differentiate samples by superpopulation even with the presence of samples with greater variation (AFR). However, grouping individuals into populations based on k-mer presence using mash distances was more difficult than using PCA and k-mer frequencies. mash produced accurate groupings (samples were placed on the tree according to the superpopulation) only for particular combinations of k-mer length and sketch size, and accuracy was not necessarily predictable. We were able to identify the k-mer length that produced accurate results by checking with the results produced by the 1000 Genome Project; however, finding the right parameter for k-mer length would be hard without knowing the correct population structure in advance. Thus, while mash is a robust tool for identifying genome relationships on a species level (Zielezinski et al., 2017), on a population level, in comparison to the PCA approach, mash showed less viable performance for differentiating populations due to its high sensitivity to parameter selection which is unknown in advance.

Whole genome sequences versus raw sequencing reads

Our study utilized k-mers derived from whole genome sequences (WGS) to enhance accuracy and minimize the impact of sequencing errors and artifacts. We used this approach to ensure that k-mers may be used successfully to determine population structure. However, an optional approach, especially for non-model organisms without an assembled genome, may be to use k-mers directly from raw sequencing reads (Rahman et al., 2018). Raw reads are inherently error-prone while having variation in read coverage that affects k-mer frequencies; however, it may be possible to address these challenges through filtering (e.g., removing rare k-mers) and trimming techniques, with tools like mash effectively mitigating errors and contamination. This direct approach not only avoids the need for a reference genome, but bypasses the alignment step, potentially streamlining the analysis and improving computational efficiency. Future work should consider the steps necessary to match the effectiveness of genome-based k-mer analysis that we observe here while using read-based k-mer counts.