Improving plant miRNA-target prediction with self-supervised k-mer embedding and spectral graph convolutional neural network

K-mer frequency counter

DNA/RNA sequences, being the building blocks of genetics, demonstrate discernible structures and patterns due to their biochemical composition. This consistency makes tools derived from information theory, such as cross-entropy, suitable for performing frequency analysis on these sequences (Compeau, Pevzner & Tesler, 2011). Many of the methods used in this analysis break down each individual sequence into numerical components. These components often include frequencies that stem from the incidence of word types or substrings of a definite length (k-mers) within the sequences. The frequency analysis of k-mers is a valuable technique in genomics as it enables the characterization of DNA/RNA sequences into quantifiable units. If two sequences display high degrees of similarities, their respective distributions of derived k-mer frequencies also align; they echo these similarities, subsequently creating a correlation signature. In contrast, sequences that are dissimilar or unrelated will showcase contrasting frequency distributions. Recognizing this principle, we employ a counter to meticulously transform miRNA and target gene sequence information into numerical descriptors based on k-mer frequencies, thereby converting bio-information into digestible mathematical representation. Specifically, we employ an iterative fragment selection approach for each sequence, treating it as an assembly of length k. A sequence of length m, for instance, can be disassembled into m-k+1 sequence fragments, akin to a puzzle being separated into smaller pieces. The miRNA sequence comprises four bases that are fundamental to the genetic code: adenine (A), uracil (U), cytosine (C), and guanine (G). For example, in a scenario where we select a k-value of 7 during an experiment, this allows us to generate sequence fragments akin to AAAAAAA, AAAAAAU, AAAAAAC, AAAAAAG, …, and GGGGGGG, thus yielding an extensive palette of 16,384 (4^7) unique combinations. Such variations demonstrate the richness of genetic data. Consequently, the process transforms the character sequences of miRNA and target genes into a structured, standardized numerical matrix with N × 16,384, where N is the total number of miRNA and target, providing a format that is highly advantageous for further computational analysis and machine learning algorithms.

K-mer frequency counter

Embeddings are known to represent the underlying characteristics of semantics, enabling convolutional neural models to effectively capture hidden deep semantics. In the field of genomics, it has been demonstrated that k-mer embeddings offer superior performance and advantages for deep learning models (Fang, Deng & Li, 2022; Trabelsi, Chaabane & Ben-Hur, 2019). Motivated by these findings, we have designed a self-supervised deep neural network (SDNN) comprising four convolution layers, aimed at extracting deep semantics from the k-mer frequency matrix. In our approach, the frequency vector of each sequence serves as the input for SDNN and undergoes deep self-encoding and self-decoding, a process that is iterated multiple times in a loop. To facilitate learning in each fully connected layer, we apply a hyperbolic tangent activation function, which effectively centers the data around zero and enhances the subsequent layer’s learning process. The final output of embedding learner is a matrix ${\mathrm{M}}_{\mathrm{k}\mathrm{m}\mathrm{e}\mathrm{r}}\in {\mathbb{R}}^{\left({\mathrm{N}}_{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}}+{\mathrm{N}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}\right)\times {\mathrm{N}}_{\mathrm{e}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{d}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{g}}}$, where ${\mathrm{N}}_{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}}$ and ${\mathrm{N}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$ is the number of miRNA and target gene, respectively. ${\mathrm{N}}_{\mathrm{e}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{d}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{g}}$ is the dimensions of learning embeddings.

Heterogeneous graph construction

To represent known associations between miRNA and target genes more effectively, a heterogeneous graph was constructed based on miRNA-target associations, target similarity network and miRNA similarity network. Let the heterogeneous is $G=\left(\mathcal{v},\epsilon \right)$, where $\mathcal{v}=\left({\mathrm{N}}_{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}},{\mathrm{N}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}\right)$ representing ${\mathrm{N}}_{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}}$ miRNA nodes and ${\mathrm{N}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$ target gene nodes and $\epsilon$ is a set of edges between nodes. Suppose that the labels of some links, $\epsilon$ in $G$ are given, the goal is to predict if there is any potential link between any miRNA-target pair that have not yet previously been established.

Here, we denote miRNA-target association as a binary matrix ${\mathrm{A}}^{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}-\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}\in {\left\{0,1\right\}}^{{\mathrm{N}}_{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}}\times {\mathrm{N}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}}$. ${\mathrm{A}}_{\mathrm{i},\mathrm{j}}^{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}-\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$ is equal to 1, if a miRNA ${\mathcal{m}}_i$ has association with a target ${\mathcal{t}}_j$; otherwise ${\mathrm{A}}_{\mathrm{i},\mathrm{j}}^{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}-\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}=0$. The pairwise similarities between ${\mathrm{N}}_{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}}$ miRNA are denoted as a similarity matrix ${\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}}$ with ${\mathrm{S}}_{\mathrm{i},\mathrm{j}}^{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}}$ as its $\left(\mathrm{i},\mathrm{j}\right)$th entry; the pairwise similarities between ${\mathrm{N}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$ target genes are denoted as a similarity matrix ${\mathrm{S}}^{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$ with ${\mathrm{S}}_{\mathrm{i},\mathrm{j}}^{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$ as its $\left(\mathrm{i},\mathrm{j}\right)$th entry. The similarities in ${\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}}$ or ${\mathrm{S}}^{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$ can be measured based on the k-mer frequency matrix by cosine or Jaccard based on a general threshold 0.5 (Cheng et al., 2015; Guo et al., 2021b; Xie et al., 2020). Mathematically, the heterogeneous graph $G$ can be represented by an adjacency matrix ${\mathrm{A}}_{\mathrm{H}}$:

(1) $$\begin{array}{c}{\mathrm{A}}_{\mathrm{H}}=\left[\begin{array}{cc}{\mathrm{S}}^{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}}& {\mathrm{A}}^{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}-\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}\\ {{\mathrm{A}}^{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}-\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}}^{\mathrm{T}}& {\mathrm{S}}^{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}\end{array}\right]\in {\mathbb{R}}^{\left({\mathrm{N}}_{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}}+{\mathrm{N}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}\right)\times \left({\mathrm{N}}_{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}}+{\mathrm{N}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}\right)}\end{array}$$

Graph convolutional network

GCN (Kipf & Welling, 2016) and its variants (Defferrard, Bresson & Vandergheynst, 2016; Du et al., 2017; Hamilton, Ying & Leskovec, 2017; Veličković et al., 2017) generally learn node features through a three-step process: message passing, aggregation and representation update. The critical step is feature aggregation, in which a node aggregates feature information from its topology neighbors and itself in each convolution layer. The GCN model relies on the adjacent matrix of graph and the feature matrix of nodes. For a given miRNA-target heterogeneous graph $\mathrm{G}={\mathrm{A}}_{\mathrm{H}}$, each node in a GCN network generally contains its own features that belong to the feature matrix ${\mathrm{M}}_{\mathrm{k}\mathrm{m}\mathrm{e}\mathrm{r}}$ (Kipf & Welling, 2016), so an identity matrix is always added to the adjacency matrix:

(2) $$\begin{array}{c}{\hat{\mathrm{A}}}_{\mathrm{H}}={\mathrm{A}}_{\mathrm{H}}+{\mathrm{I}}_{\mathrm{H}}\end{array}$$where ${\mathrm{A}}_{\mathrm{H}}$ is the adjacency matrix of heterogeneous graph as Formula (1), ${\mathrm{I}}_{\mathrm{H}}$ is the identity matrix.

Current approaches to designing localized convolutional filters on graphs can be roughly classified into two categories: spatial and spectral approaches. Spatial-based approaches construct the filter localization based on local information from neighboring nodes, which may be limited in terms of matching local neighbors (Bruna et al., 2013). On the other hand, spectral-based approaches rely on the spectrum of the graph Laplacian for filter design (Kipf & Welling, 2016). A well-defined localization operator on graphs was introduced by employing a Kronecker delta function implemented in the spectral domain. In contrast to spatial-based approaches, spectral-based approaches typically exhibit superior performance in graph learning (Ayat et al., 2019; Ding et al., 2021; Huang et al., 2019a). As the number of nodes and dimensions of feature vectors in graph $\mathrm{G}$ usually thousands or tens of thousands. It is time consuming for traditional spatial approach when decomposing the Laplacian matrix spectrum, and convolutional operation often directly performs on global that weakens the local information (Bruna et al., 2013). Therefore, a spectral approach that rely on the spectrum of graph Laplacian was proposed (Defferrard, Bresson & Vandergheynst, 2016). Unlike the traditional spatial approach, the graph convolution in spectral approach is defined on graph as the product of the input signal and the filter ${\mathrm{g}}_{\theta }$ in the Fourier domain. Let us denote the symmetric normalized Laplacian matrix of ${\mathrm{A}}_{\mathrm{H}}$ is ${\mathrm{L}}_{\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{l}}$:

(3) $$\begin{array}{c}{\mathrm{L}}_{\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{l}}={\mathrm{U}}_{\mathrm{H}}{\mathrm{\Lambda }}_{\mathrm{H}}{{\mathrm{U}}_{\mathrm{H}}}^{\mathrm{t}}\end{array}$$where ${\mathrm{U}}_{\mathrm{H}}$ is the eigenvector matrix and ${\mathrm{\Lambda }}_{\mathrm{H}}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\lambda }_1,{\lambda }_2,{\lambda }_3,\dots ,{\lambda }_{{\mathrm{N}}_{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}}+{\mathrm{N}}_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}}\right)$ is the diagonal matrix of eigenvalues.

Here, the Fourier transform of ${\mathrm{M}}_{\mathrm{k}\mathrm{m}\mathrm{e}\mathrm{r}}$ is represented as ${{\mathrm{U}}_{\mathrm{H}}}^{\mathrm{t}}{\mathrm{M}}_{\mathrm{k}\mathrm{m}\mathrm{e}\mathrm{r}}$. However, that calculation of getting eigenvector matrix and eigenvalues diagonal matrix is expensive with the increasing scale of graph. Thus, a modified GCN based on Chebyshev polynomials ${\mathrm{T}}_{\mathrm{K}}\left(\mathrm{x}\right)=2\mathrm{x}{\mathrm{T}}_{\mathrm{K}-1}\left(\mathrm{x}\right)-{\mathrm{T}}_{\mathrm{K}-2}\left(\mathrm{x}\right)$ was used here for features representation to reduce the computational complexity (Defferrard, Bresson & Vandergheynst, 2016). As a result, the filter ${\mathrm{g}}_{\theta }$ can be defined and represented as follows:

(4) $$\begin{array}{c}{\mathrm{g}}_{\theta }\left({\mathrm{\Lambda }}_{\mathrm{H}}\right)=\sum _{\mathrm{K}=0}^{\mathrm{K}}{\theta }_{\mathrm{K}}{\mathrm{T}}_{\mathrm{K}}\left({\tilde{\mathrm{\Lambda }}}_{\mathrm{H}}\right)\end{array}$$

(5) $$\begin{array}{c}{\mathrm{g}}_{\theta }\ast {\mathrm{M}}_{\mathrm{k}\mathrm{m}\mathrm{e}\mathrm{r}}=\sum _{\mathrm{K}=0}^{\mathrm{K}}{\theta }_{\mathrm{K}}{\mathrm{T}}_{\mathrm{K}}\left({\tilde{\mathrm{L}}}_{\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{l}}\right){\mathrm{M}}_{\mathrm{k}\mathrm{m}\mathrm{e}\mathrm{r}}\end{array}$$where $\theta \in {\mathbb{R}}^{\mathrm{K}}$ is a vector of Chebyshev coefficients, ${\tilde{\mathrm{\Lambda }}}_{\mathrm{H}}={\displaystyle \frac{2{\mathrm{\Lambda }}_{\mathrm{H}}}{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}-{\mathrm{I}}_{\mathrm{H}}}$, ${\tilde{\mathrm{L}}}_{\mathrm{H}}={\displaystyle \frac{2{\mathrm{L}}_{\mathrm{H}}}{{\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}}-{\mathrm{I}}_{\mathrm{H}}}$, ${\mathrm{I}}_{\mathrm{H}}$ is the identity matrix and K is the K^th-order neighborhood.

Since the Chebyshev polynomials are recursively (Hammond, Vandergheynst & Gribonval, 2011), the formulation can be simplified by limiting K = 1 (Kipf & Welling, 2016). Finally, the spectral GCN can be represented as:

(6) $$\begin{array}{c}{\mathrm{g}}_{\theta }\ast {\mathrm{M}}_{\mathrm{k}\mathrm{m}\mathrm{e}\mathrm{r}}=CELU\left(\theta \left({\mathrm{D}}_{\mathrm{H}}^{-{\displaystyle \frac{1}{2}}}\left({\mathrm{I}}_{\mathrm{N}}+{\mathrm{A}}_{\mathrm{H}}\right){\mathrm{D}}_{\mathrm{H}}^{-{\displaystyle \frac{1}{2}}}\right)\right)\end{array}$$

(7) $$\begin{array}{c}\left[\begin{array}{c}{\mathrm{H}}_{\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{l}}^{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}}\\ {\mathrm{H}}_{\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{l}}^{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}\end{array}\right]={\mathrm{g}}_{\theta }\ast {\mathrm{M}}_{\mathrm{k}\mathrm{m}\mathrm{e}\mathrm{r}}\end{array}$$where ${\mathrm{D}}_{\mathrm{H}}$ is the diagonal matrix with diagonal entry ${\left[{\mathrm{D}}_{\mathrm{H}}\right]}_{\mathrm{i},\mathrm{j}}={\sum }_{\mathrm{j}}{\left[{\mathrm{A}}_{\mathrm{H}}\right]}_{\mathrm{i},\mathrm{j}}$, ${\mathrm{H}}_{\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{l}}^{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}}$ is the embedding of miRNA and ${\mathrm{H}}_{\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{l}}^{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$ is the embedding of target genes.

Edge representation construction and probabilities prediction

After GCN encoding, we concatenate ${\mathrm{H}}^{\mathrm{m}\mathrm{i}\mathrm{R}\mathrm{N}\mathrm{A}}$ and ${\mathrm{H}}^{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$ as the feature vector for each miRNA-target pairs, so as a result, the features of each miRNA-target pairs are the combination of the features of its miRNA and target gene. Then, the multilayer perceptron (MLP) is used as a supervised learning model to predict the association probabilities. The MLP contains three fully connected layers. The input for MLP is miRNA-target pair feature vector, which is extracted using the GCN. Since the prediction can be deemed as a two-class problem, we chose a sigmoid activation function for the final layer.

Overall loss and optimization

For model training, we used the binary cross-entropy (BCE) loss function and the Adam optimizer for learning model parameters. The BCE $\mathcal{B}$ can be represented as follow:

(8) $$\begin{array}{c}B=-{\displaystyle \frac{\sum _{\mathrm{i},\mathrm{j}\in \mathcal{Y}\cup {\mathcal{Y}}^{-}}\left({\mathrm{y}}_{\mathrm{i}\mathrm{j}}\log {\hat{\mathrm{y}}}_{\mathrm{i}\mathrm{j}}+\left(1-{\mathrm{y}}_{\mathrm{i}\mathrm{j}}\right)\log \left(1-{\hat{\mathrm{y}}}_{\mathrm{i}\mathrm{j}}\right)\right)}{\mathrm{N}}}\end{array}$$where N is the number of pairs, ${\mathrm{y}}_{\mathrm{i}\mathrm{j}}$ is the true label of the edges, which will be 1 or 0, $\mathcal{Y}$ and ${\mathcal{Y}}^{-}$ denote the set of all nodes contained in the positive edges set and negative edges set, respectively.

To mitigate the issue of overfitting, we employ ${\mathrm{L}}_2$-regularization:

(9) $$\begin{array}{c}{\mathrm{L}}_2={\displaystyle \frac{\lambda }{2\mathrm{N}}\sum _{\omega }{\omega }^2}\end{array}$$where $\lambda$ is a hyperparameter, $\omega$ is an element in the parameter matrices $\mathrm{W}$.

As a result, the overall loss function for training is $\mathcal{L}=\mathcal{B}+{\mathrm{L}}_2$. The whole model via back propagation algorithm in an end-to-end manner can be trained.

Evaluation metrics

After constructing the framework, the final step involves evaluating the performance of our model to provide users with an understanding of its utility and weaknesses. Model evaluation is conducted using five-fold cross-validation (5-CV). We categorize all recognized miRNA-target pairs as the positive dataset and evenly divide them into five portions. An unknown miRNA-target pair suggests that no evidence from biological experimentation can confirm the association between the miRNA and target nodes. All such unspecified miRNA-target associations constitute the negative dataset. For each iteration, we select four-fifths of the positive samples and an equivalent number of randomly chosen negative examples as the training set. In contrast, the test set comprises the remainder of the positive dataset and all the remaining negative samples (Su et al., 2022; Xuan et al., 2022). The accuracy of the model is evaluated using the receiver operating characteristic curve (ROC). As a primary evaluation metric, the area under the ROC curve (AUROC) is adopted. Considering its bias towards imbalanced datasets, the precision-recall curve (PRC) is also utilized, with the area under the PRC curve (AUPRC) chosen as another primary evaluation metric. The performance of our model can be assessed using AUROC or AUPRC without requiring specific thresholds. Additionally, other evaluation metrics including accuracy (ACC), recall (REC), precision (PRE), and F1-score (F1) are calculated as follows:

(10) $$\begin{array}{c}ACC={\displaystyle \frac{\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}}{\mathrm{T}\mathrm{P}+\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P}+\mathrm{F}\mathrm{N}}}\end{array}$$

(11) $$\begin{array}{c}REC={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}}\end{array}$$

(12) $$\begin{array}{c}PRE={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}}\end{array}$$

(13) $$\begin{array}{c}F1={\displaystyle \frac{2\times \mathrm{R}\mathrm{E}\mathrm{C}\times \mathrm{P}\mathrm{R}\mathrm{E}}{\mathrm{R}\mathrm{E}\mathrm{C}+\mathrm{P}\mathrm{R}\mathrm{E}}}\end{array}$$where TP is true positive, FP is false positive, FN is false negative, and TN is true negative in the predicting results.

Hyperparameters and model implementation

Prediction performance is contingent on several hyperparameters. The efficacy of model training is particularly influenced by two critical hyperparameters. We conducted a series of combinatorial experimental tests. The first is the learning rate of the optimizer $\mathrm{l}\mathrm{r}\in \left\{0.00001,0.00005,0.0001,0.00015,0.00003\right\}$, which essentially determines the step size at each iteration while moving toward a minimum of a loss function. The second is the number of epochs $\mathrm{n}\mathrm{e}\in \left\{500,1,000,2,000,3,000,5,000\right\}$, dictating the number of times the learning algorithm will work through the entire training dataset. Our study involved iteratively testing on four distinct plant datasets. Our results revealed that a learning rate of 0.0001 is optimal, maintaining a delicate balance between adequate learning speed and prevention of any overshoots. Consequently, in our model, we adhered to this learning rate for training. Simultaneously, we found it beneficial to set the number of epochs to 3000, giving the model ample opportunity to learn from the data without overfitting. As for the L2-regularization coefficient $\mathrm{L}\in \left\{0.0001,0.0005,0.001,0.002,0.004\right\}$, a parameter used to prevent overfitting by discouraging complex models, we set it to 0.0005. During the optimization process, priority was given to one specific parameter for adjustments, while the other two parameters were held constant at their nominal values. Following each optimization cycle, the optimal value of the parameter was used to redefine its nominal value.

Our model, kmerPMTF, was realized using the robust capabilities of the PyTorch framework (v2.0.0) (Paszke et al., 2019), built specifically for high-performance machine learning. Additional functionality was incorporated from numpy (v1.23.5), pandas (v1.5.3). Other key resources included the PyTorch Geometric (v2.3.0) (Fey & Lenssen, 2019), a geometric deep learning extension library for PyTorch, and scikit-learn (v1.2.2) (Pedregosa et al., 2011), a free software machine learning library for Python. Both the training and testing stages were performed using CUDA v11.0 on Tesla V100S, embracing the power of GPU acceleration to train our model and perform predictions efficiently.

Design of the kmerPMTF framework

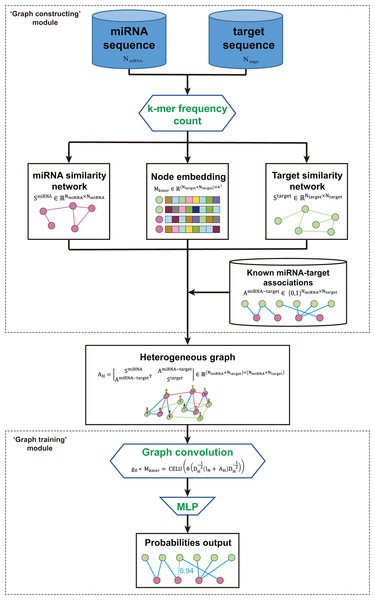
The kmerPMTF is an open-source python command-line utility that serves as a fast and reliable framework for predicting plant miRNA-target associations (MTA). It utilizes the deep learning graph convolution theory to train a specific model for a given plant. The kmerPMTF framework consists of two modules: a ‘graph constructing’ module, which constructs a miRNA-target graph from the sequences of specific plant miRNAs and target genes, and a ‘graph training’ module, which utilizes a graph convolutional network to learn the representations and train a specific plant prediction model (Fig. 1). The main reason for having both modules is that distinct graph construction approach probably contributes to the graph training module. Besides, by adjusting the training parameters according to different datasets, an optimal prediction model for specific plants can be obtained. Therefore, splitting the framework into two modules can enhance the ease of use and the degree of customization. This will allow users to easily train suitable models for different plants using the kmerPMTF framework.

The ‘graph constructing’ module consists of two components: a k-mer frequency counter, which counts the frequency of k-mer, and a learner, which learns embeddings. This module takes the nucleotide sequences of both miRNA and target gene as input. The k-mer frequency is utilized to compute the similarity that is necessary for constructing a heterogeneous graph and feeding it to a self-supervised deep neural network (SDNN) that learns embeddings serve as attributes for the graph nodes. Next, integrate the miRNA similarity, target gene similarity, known miRNA-target pairs, and k-mer frequency as a heterogeneous graph to generate an output that can be used for graph convolution operations (Fig. S1A). The ‘graph training’ module consists of a series of graph neural network layers that comprise a typical graph convolutional network (GCN) architecture. The purpose of this architecture is to learn the topological structure and node semantics from the graph. The heterogeneous graph constructed by the previous module serves as input to this module. After extracting node representation through three layers of graph convolution, we pair the nodes to obtain edge representations, which are then fed into a multilayer perceptron (MLP) to compute the probabilities of all edges in the heterogeneous graph. We consider the prediction of associations between miRNA and target gene as a link prediction task. The probabilities of the predicted edges between miRNA and target gene are regarded as the probability of a regulatory relationship between a specific miRNA and gene (Fig. S1B).

The kmerPMTF outperforms published methods

The primary goal of kmerPMTF is to predict the binary classification of miRNA-target gene. We evaluated the effectiveness and performance of kmerPMTF by comparing it with popular deep learning and traditional machine learning methods. Four typical plant datasets, namely Arabidopsis thaliana, Oryza sativa, Solanum lycopersicum, and Prunus persica, were employed in the comparison. Arabidopsis thaliana is a classic model plant which has been widely used in plant genetic studies (Koornneef & Meinke, 2010; Somerville & Koornneef, 2002), the other three are representative model plants in the field of crops, vegetables and fruit trees (Aranzana et al., 2019; Izawa & Shimamoto, 1996; Kimura & Sinha, 2008), respectively. All the miRNA information and known miRNA-target gene pairs are obtained from Plant miRNA Encyclopedia project (PmiREN) (Guo et al., 2021a), which provides high-confidence MIR and regulatory relationships by integrating several databases and many datasets. The four plant genome datasets used in our study contained a range of 27,416 to 42,189 genes and 221 to 699 MIRs. The number of pairs formed between miRNA and their target genes ranged from 2,181 to 17,809 (Table 1).

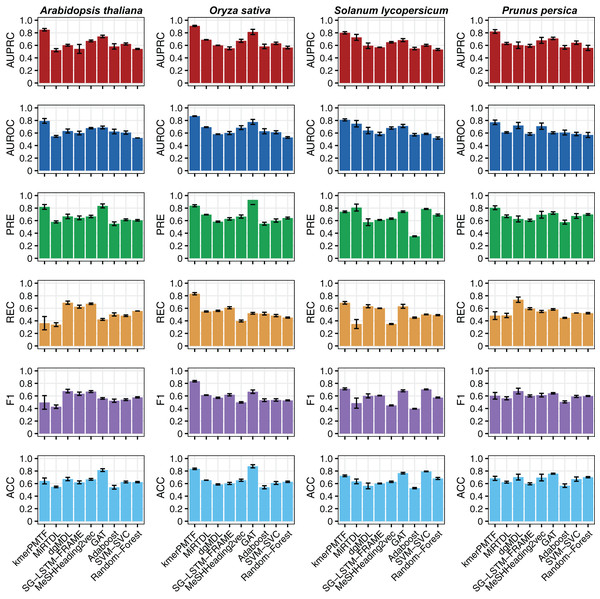
For the deep learning comparison, we selected MiRTDL (Cheng et al., 2015), dgMDL (Luo et al., 2019) and SG-LSTM-FRAME (Xie et al., 2020). MiRTDL utilizes the traditional convolutional neural network (CNN) model, whereas dgMDL employs the multimodal deep belief network (DBN), which can be regarded as a stack of restricted Boltzmann machine. In contrast, SG-LSTM-FRAME is designed based on a random walk strategy to predict potential relationships. Furthermore, to demonstrate the efficacy of graph convolutional network in extracting deep topological semantics, we conducted experiments using our datasets in the MeSHHeading2vec framework (Guo et al., 2021b) and graph attention networks (GAT) (Veličković et al., 2017), which employs graph embedding and graph neural networks. We configured the parameters of the aforementioned methods in accordance with the recommended guidelines of the author. All four of these methods are categorized under deep learning. We tested our plant datasets using these models. Besides, to exemplify the effectiveness of deep learning, we conducted experiments on our dataset using traditional machine learning techniques. Specifically, we applied the Adaboost, SVM-SVC and random forest algorithms to our data. All the results consistently indicate that kmerPMTF is the optimal choice for the plant datasets, as it achieves the highest AUPRC values of 0.84, 0.91, 0.80 and 0.82 in Arabidopsis thaliana, Oryza sativa, Solanum lycopersicum and Prunus persica, respectively (Fig. 2 and Fig. S2).

Parametric sensitivity analysis

As different parametric can affect model performance, we explored the parameters of graph construction, embedding generation and model training of our experiments. We first explored the influence of the length of k-mer selected for the frequency counter. For four models in this work, we set the k-mer length to be 7 bp. This value is within the range of typical transcription factor binding site lengths (5–9 bp) (Stormo, 2000; Tsai et al., 2006; Yu, Lin & Li, 2016). To test the robustness of our framework, we further set a series of k-mer lengths (5, 7, 9 bp) within this range for testing. The results showed that for the four plants selected in this study, although the model performed best when the k-mer length was 7 bp, the influence of different k-mer lengths on the fluctuations of the models AUPRC and AUROC did not exceed 5% and 8%, respectively. Secondly, we explored different methods of generating similarity network. Cosine and Jaccard similarity were tested, and we discovered that cosine similarity might be more suitable in our cases. Thirdly, we tested k-mer embedding dimensions used as node attributes for graph convolution. We selected different dimensions from the range of 16–512 for testing. The results show that when the dimension is greater than or equal to 128, the performance is improved by 2–5%, while the RAM consumption is increased by three times compared when it is less than 128. Our experiments demonstrate that selecting the appropriate hyperparameter k-mer can enhance the model effect. Additionally, our framework mitigates the impact of inaccurate k-mer selection on performance reduction.

Examination of the graph components

Our framework, kmerPMTF, is constructed with its foundation firmly anchored on the established principles of the ChebNet graph convolutional model. kmerPMTF skillfully leverages the nuanced semantics of sequence k-mer, forming a comprehensive heterogeneous graph. This, in turn, creates a rich tapestry of information, ripe for analysis by our model. Further adding a level of sophistication, the framework employs a spectral graph convolutional network. This method facilitates the extraction of profound and detailed representations, which prove instrumental for accurate and precise predictions. As part of our rigorous validity checks and to assess the robustness of kmerPMTF, we adopt an experimental approach during the training phase. Certain components from the heterogeneous graph are deliberately omitted in this process. The objective of this strategy is to zero in on the individual contributions of the elements and test the framework’s capability to sustain its performance amidst these variable conditions. In parallel, we also design and implement a node feature elimination strategy. This systematic approach is aimed at assessing the degree to which each k-mer embedding is necessary and contributes to the overall success of the model. We initiate five model variations as follows, each evolved from the original and expressing a unique set of parameters and settings.

• – miT+TT+mimi: It is a Chebyshev GCN model that uses a graph with all elements but lacks node features.

• – miT+TT+feat: It is a Chebyshev GCN model that uses a graph including node features but lacks a miRNA-miRNA semantics similarity network.

• – miT+TT: It is a Chebyshev GCN model that uses a graph which lacks both node features and miRNA-miRNA semantics similarity network.

• – miT+mimi+feat: It is a Chebyshev GCN model that uses a graph including node features but lacks a target-target semantics similarity network.

• – miT+mimi: It is a Chebyshev GCN model that uses a graph which lacks both node features and target-target semantics similarity network.

Upon employing a 5-fold cross-validation for each variant model, a significant decrease in the AUROC is observably evident when compared with the original model (miT+TT+mimi) (Table 2). The integration of features from miRNA and target genes markedly improves the model’s capability to assimilate multiple strata of representation, thereby potentially amplifying its performance.

Case studies

In this section, we conduct case studies to further validate the predictive performance of the model kmerPMTF in real situations. In peach, the gene PpTIR1 (Prupe.4G037400 and Prupe.4G037200) as a target of miR393a and miR393b and have been verified using the GUS assay (Ma et al., 2023). We also select miR171c and miR408 in Arabidopsis as a case, which is involved in plant growth and development, stress response and hormone signaling (Gao et al., 2022; Pei et al., 2023). As biologists are more interested in the top prediction, we finally choose the top five associated target genes from the prediction results and validate them on the latest database PmiREN (Guo et al., 2021a) and TarDB (Liu et al., 2021) (Table 3). We can find that all the top five target genes have been supported by existing databases and experiment study. The results from the case studies suggest that kmerPMTF is an effective tool in plant miRNA-target pair prediction.