Linking multi-level population dynamics: state, role, and population

General concept of multiple descriptions of ecological community

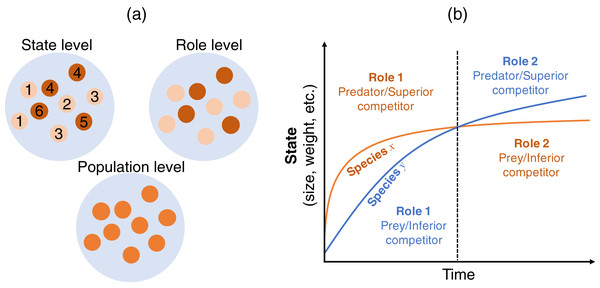
This section describes how the Lotka–Volterra model is derived as a population-level description from more detailed descriptions (state and role; Fig. 1A). I start with a state-level discussion of the situation presented in Fig. 1B, where the largest information can be incorporated. Then, we derive the role-level and population-level dynamics by scaling-up the focal level of the population dynamics, where we assume a simple situation where two species and two roles are considered. This approach is justified because the state-based dynamics contain information on the role- (if any) and population-level dynamics, but the opposite is not true. That is, scaling-up provides a simpler model but loses some information.

Notably, one can control the specificity (i.e., information) of the model by choosing what to scale up. Here, I demonstrate the role-level information is carried over to the Lotka–Volterra (population-level) model that contains larger information than the ordinary one where the interaction coefficients between species are fixed constant. The Lotka–Volterra model derived here provides an insight into the connection with nature where diverse interspecific interaction patterns are observed between species. The ordinary Lotka–Volterra model is readily recovered from the model by losing the information of role-shift (i.e., giving a fixed interaction strength). The role-level model contains the information of the Lotka–Volterra model, so the knowledge of the Lotka–Volterra model is applicable to the role-level model to some extent. By so doing, the connection to a different level of description becomes clear. I will demonstrate this in the following section.

State-level dynamics

I begin with a state-level model that describes the N-species dynamics in which each individual of a species changes its state (e.g., age or weight) throughout its lifetime. The starting point is the common McKendrick–von Foerster equation (Murray, 2004). I extend this model by introducing the effects of intra- and inter-specific competition among the N species. The population dynamics of species i in state s, n_i(s,t), can be described as

(1) $$\frac{\mathrm{\partial }{n}_i\left(s,t\right)}{\mathrm{\partial }t}+\frac{\mathrm{\partial }g\left(s\right)n_i\left(s,t\right)}{\mathrm{\partial }s}=-d_i{n}_i\left(s,t\right)-n_i\left(s,t\right)\sum _{j=1}^N{\int }_0^{\mathrm{\infty }}{a}_{i\left(s\right)j\left(s^{\prime }\right)}{n}_j\left(s^{\prime },t\right)d{s}^{\prime },$$where g(s) is the rate of growth in state s on the state axis and d_i is the death rate of species i. a_i(s)j(s′) is the (nonnegative) interaction strength between state s of species i and state s′ of species j. The second term on the right-hand side accounts for the nonlinear effects of population dynamics, and is the fundamental difference from the size-structured community model (Hartvig, Andersen & Beyer, 2011) and physiologically structured population model (De Roos et al., 2008; Metz & Diekmann, 1986), in which nonlinearity appears in the term g(s) where, for instance, predation effects are incorporated (i.e., these are quasilinear equations). Note that Eq. (1) has the same form as the aforementioned models, except for the explicit nonlinearity, and it can be reduced to these models by removing the nonlinear term and defining g(s) accordingly. Equation (1) is complemented with the boundary conditions

(2) $$n_i\left(0,t\right)={\int }_0^{\mathrm{\infty }}{b}_i\left(s\right)n_i\left(s,t\right)ds+\sum _{j=1}^N{\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}{\hat{b}}_{i\left(s\right)j\left(s^{\prime }\right)}{n}_i\left(s,t\right)n_j\left(s^{\prime },t\right)dsd{s}^{\prime },$$where b_i(s) is the birth rate of species i in state s and ${\hat{b}}_{i\left(s\right)j\left(s^{\prime }\right)}$ is the birth rate of species i in state s as the result of predation on species j in state s′. Note that a cannibalistic interaction can be considered by setting ${\hat{b}}_{i\left(s\right)i\left(s^{\prime }\right)}>0$. These values are described as

(3a) $$b_i\left(s\right)=\{\begin{array}{ll}\mathrm{n}\mathrm{o}\mathrm{n}-\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e},\hfill & i\left(s\right)ismatured\\ 0,\hfill & otherwise\end{array},$$

(3b) $${\hat{b}}_{i\left(s\right)j\left(s^{\mathrm{\prime }}\right)}=\{\begin{array}{ll}\mathrm{n}\mathrm{o}\mathrm{n}-\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\hfill & i\left(s\right)preysonj\left(s^{\mathrm{\prime }}\right)\\ 0,\hfill & otherwise\end{array}$$where the notation i(s) indicates species i in state s. To describe the two-species role-level dynamics in the main text, the number of species is fixed to two, denoted as n_x and n_y, respectively, instead of n_i.

This is an N-species generalization of the nonlinear size-structured model discussed in Hastings (1987) and Nisbet & Gurney (1982).

Role-level dynamics

The state-level model can be scaled-up to describe the dynamics of different roles in each species, and a variable corresponding to each role can be used to obtain the role-level dynamics. I assume that state development over time causes the ontogenetic diet/trophic niche shift in a well-mixed region; i.e., role shift. Here, I am interested in the general effect of this role shift on the population dynamics. For this purpose, I discuss the simplest possible situation, in which the rate of state growth is a constant g(s) = 1, the number of species is two (represented by x and y), and the number of roles is two, and only species y changes its role. y₁ and y₂ are non-overlapping role groups in population y, and y₁ is assumed to be earlier stage than y₂, where the role shift occurs in state s₁. Integrating n_x and n_y accordingly, these are described as

(4) $$x={\int }_0^{\mathrm{\infty }}{n}_x\left(s,t\right)ds,y_1={\int }_0^{s_1}{n}_y\left(s,t\right)ds,y_2={\int }_{s_1}^{\mathrm{\infty }}{n}_y\left(s,t\right)ds.$$

Hence, by integrating over state s in Eq. (1), the role-level model becomes (see Section “Derivation of the role-level dynamics”):

(5a) $$\frac{dx}{dt}=x\left(r_x+\sum _{\mathcal{X}\in \left\{x,y_1,y_2\right\}}{a}_{x\mathcal{X}}\mathcal{X}\right),$$

(5b) $$\frac{d{y}_1}{dt}=y_1\left(r_{y_1}+\sum _{\mathcal{X}\in \left\{x,y_1,y_2\right\}}{a}_{y_1\mathcal{X}}\mathcal{X}\right)-m{y}_1+\left(b_{y_2}+I_A{a}_{y_{2}x}x\right)y_2,$$

(5c) $$\frac{d{y}_2}{dt}=y_2\left(-d_{y_2}+\sum _{\mathcal{Y}\in \left\{y_1,y_2\right\}}{a}_{y_2\mathcal{Y}}\mathcal{Y}+\left(1-I_A\right)a_{y_{2}x}x\right)+m{y}_1,$$where $r_{\mathcal{X}}$ is the growth rate of $\mathcal{X}\in \left\{x,y_1,y_2\right\}$, which can be either a species or a role (simply referred to as “type” hereafter). $r_{\mathcal{X}}$ can further be decomposed into $b_{\mathcal{X}}-d_{\mathcal{X}}$, where $b_{\mathcal{X}}$ and $d_{\mathcal{X}}$ are the birth rate and death rate of type $\mathcal{X}$, respectively. $a_{\mathcal{X}{\mathcal{X}}^{\mathrm{\prime }}}$ represents the interaction strength between type $\mathcal{X}$ and ${\mathcal{X}}^{\mathrm{\prime }}\in \left\{x,y_1,y_2\right\}$; a positive sign indicates that type ${\mathcal{X}}^{\mathrm{\prime }}$ has a positive influence on the population of type $\mathcal{X}$, and vice versa. $\sum {}_{\mathcal{X}}$ represents the sum over the variables. m is the transition rate from type y₁ to y₂. I_A is an indicator variable that is equal to 1 if y₂ is a predator and equal to 0 otherwise.

Equation (5) has a similar form to the Lotka–Volterra-type model, but a major difference is that the birth event of role y₂ increases the population number of role y₁, and the transition rate m mediates the effect of the role shift.

The generalization of the role-level model is straightforward, and Section “Generalizations of the role-level model” describes generalized role-level models in which (i) species y has n roles; (ii) species x and y have n′ and n roles, respectively; and (iii) N species have (n₁, … , n_N) roles (n_i is the number of roles of species i). Via Eq. (5), various role-shift scenarios can be described: (i) from inferior/superior competitor to superior/inferior competitor; (ii) from competitor to predator; and (iii) from prey to predator. The specific forms of these models are provided in Section “Specific form of the role-level model”.

Population-level dynamics

By further scaling-up the focal level of the population dynamics, the role-level model can be converted into the population-level model. This process aggregates the two roles y₁ and y₂ into a single variable. I introduce a new variable $\overline{y}$(t) = y₁(t) + y₂(t), and let y₁(t) = (1 − α(t)) $\overline{y}$(t) and y₂(t) = α(t) $\overline{y}$(t), where α(t) $\in$ [0,1] is the proportion of y₂ in species y at time t (i.e., α(t) = y₂(t)/(y₁(t) + y₂(t))). By summing Eqs. (5b) and (5c), Eq. (5) becomes

(6) $$\begin{array}{l}\frac{{\displaystyle dx}}{{\displaystyle dt}}=x\left(r_x+a_{x}x+a_{x\overline{y}}\left(t\right)\overline{y}\right),\\ \frac{{\displaystyle d\overline{y}}}{{\displaystyle dt}}=\overline{y}\left(r_{\overline{y}}\left(t\right)+a_{\overline{y}}\left(t\right)\overline{y}+a_{\overline{y}x}\left(t\right)x\right),\end{array}$$where Eq. (6) has the form of the Lotka–Volterra model, but the parameters $r_{\overline{y}}$, $a_{x\overline{y}}$, $a_{\overline{y}x}$, and $a_{\overline{y}}$ are time-dependent because the role-level information is carried over. Therefore, Eq. (6) contains larger information than the usual Lotka–Volterra model. These parameters are described as

(7a) $$r_{\overline{y}}\left(t\right)=\left(1-\alpha \left(t\right)\right)r_{y_1}+\alpha \left(t\right)r_{y_2},$$

(7b) $$a_{x\overline{y}}\left(t\right)=\left(1-\alpha \left(t\right)\right)a_{x{y}_1}+\alpha \left(t\right)a_{x{y}_2},$$

(7c) $$a_{\overline{y}x}\left(t\right)=\left(1-\alpha \left(t\right)\right)a_{y_{1}x}+\alpha \left(t\right)a_{y_{2}x},$$

(7d) $$a_{\overline{y}}\left(t\right)={\left(1-\alpha \left(t\right)\right)}^2{a}_{y_1}+\left(a_{y_1{y}_2}+a_{y_2{y}_1}\right)\alpha \left(t\right)\left(1-\alpha \left(t\right)\right)+\alpha {\left(t\right)}^2{a}_{y_2}.$$

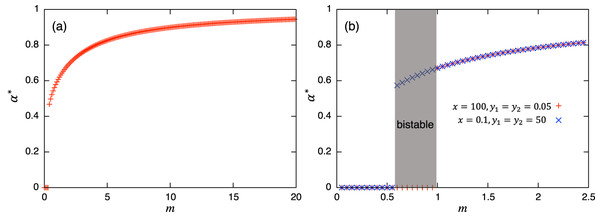
Values of α = 0 or 1 correspond to the usual (unstructured) Lotka–Volterra model, giving constant interaction coefficients. This Lotka–Volterra model can also be derived directly from Eq. (1) by scaling-up to a population level with a constant interaction strength (a_xy, a_yx). The magnitude of α is mediated by the transition rate m: a larger value of α is realized with a larger transition rate m, and vice versa. Note that each parameter in the role-shift model appears in the parameters in Eq. (7), and these mediate the effects of roles in the population-level model. While these coefficients change dynamically over time, α(t) converges to an equilibrium α* = y*₂/(y*₁ + y*₂) if there is no periodic solution in the role-level dynamics. Hence, if there is a unique and stable nontrivial equilibrium, the stability of the equilibrium can be discussed via the ordinary analytical tools of the Lotka–Volterra model, such as isoclines. If there is a periodic solution such as the limit cycle or chaos, α(t) does not converge and this approach fails. There is ample literature about the stability issue of dynamical systems (e.g., Hirsch, Smale & Devaney, 2012; Strogatz, 2014), including the one in the Lotka–Volterra model (e.g., Hofbauer & Sigmund, 1998; Kot, 2001; Murray, 2004) where various methods for evaluating the stability of equilibrium can be found. Similarly, if the concerned system exhibits bistability, α(t) does not converge to a unique value, and again, the equilibrium analysis via the population-level model fails: the investigation of the role-level dynamics is necessary. Following analysis and numerical simulations suggest that the concerned role-level and population-level dynamics do not have a periodic solution, but these can exhibit bistability. To summarize the discussions above, Fig. 2 shows examples of the relationship between equilibrium value of α and m. Both panels show the increasing trends of α* as the transition rate m increases. Fig. 2B demonstrates the existence of bistability, and the presented equilibrium analysis cannot apply to this region.

Effect of role shift on interaction strength of population-level dynamics

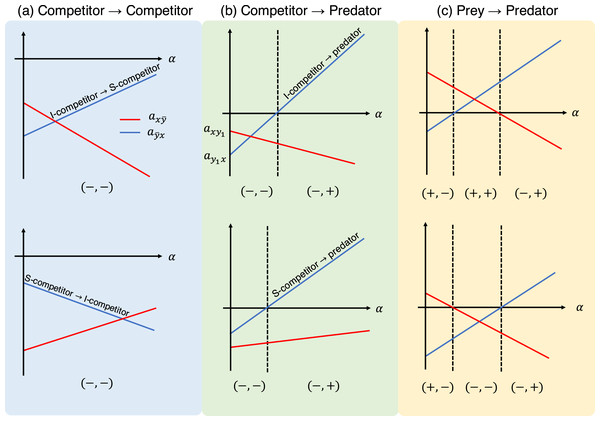
As stated in the previous section, the parameters in the role-level model appear in the parameters of the population-level model (Eq. (7)). Hence, it is important to ask how the role shift affects the interaction strength between species ( $a_{x\overline{y}},a_{\overline{y}x}$) in the population-level model. From Eq. (7), it is apparent that $a_{x\overline{y}}$ and $a_{\overline{y}x}$ are monotonic increasing or decreasing functions of the proportional parameter α, depending on the signs of $a_{x{y}_2}-a_{x{y}_1}$ and $a_{y_{2}x}-a_{y_{1}x}$. Figure 3 shows schematic examples of the interaction coefficients in the population-level model as a function of the proportional parameter α. When the two roles are both competitors (i.e., inferior and superior competitors; Fig. 3A), the interaction coefficients ( $a_{x\overline{y}},a_{\overline{y}x}$) have the signs (−, −). Namely, the population-level model exhibits the features of the competition model. When the role shift is from competitor to predator (Fig. 3B), the signs of the interaction coefficients are either (−, −) or (−, +). The largest number of combinations is realized when the role shift is from prey to predator (Fig. 3C), which could produce the combinations (−, −), (−, +), (+, −), or (+, +), providing more diverse dynamics than the other role-shift scenarios. Curiously, the combinations (−, −) and (+, +) are not realized, given a single set of parameters, by changing the proportional parameter α (Fig. 3C, top and bottom).

Coexistence and bistability of role-level and population-level dynamics

Using the interaction coefficients in the population-level model, I now investigate the role- and population-level dynamics. In two-species population models, analysis via isoclines provides an outline of the dynamics (Murray, 2004). However, in the population-level model, the parameters in Eq. (7) vary with time, and ordinary isocline analysis is not directly applicable. Instead, I focus on the equilibrium properties of the dynamics, which can be determined by the configuration of isoclines in equilibrium. The equilibrium isoclines of the population-level model (Eq. (6)) are given by

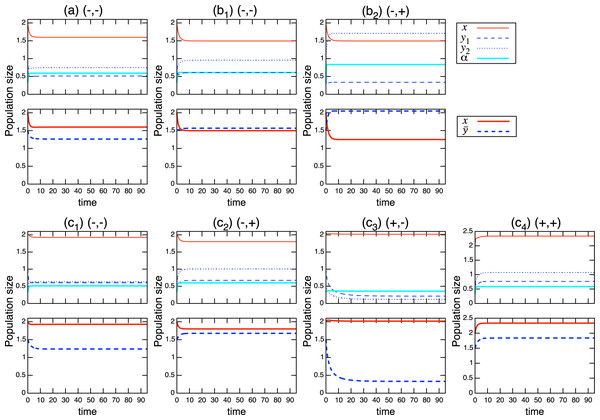
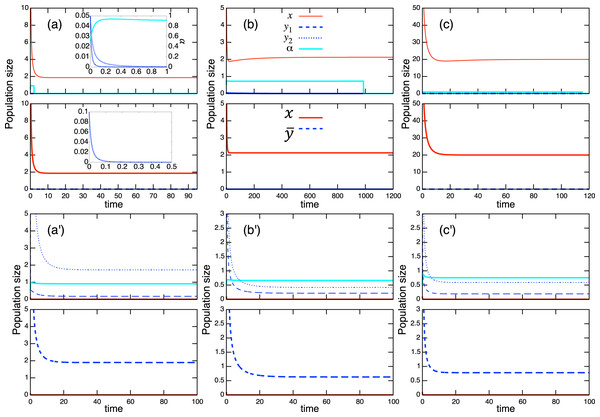
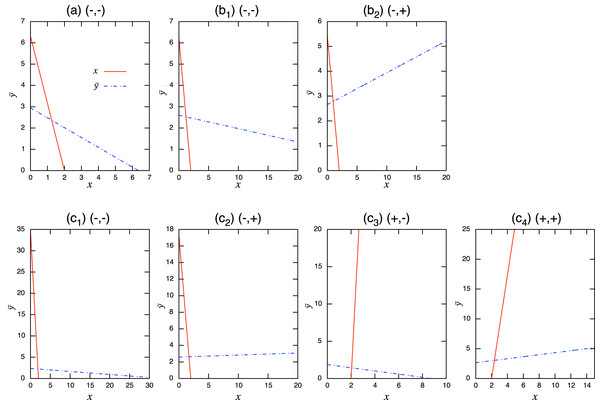
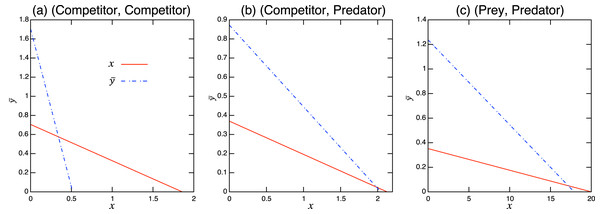
(8) $$\begin{array}{l}\overline{y}=-\frac{{\displaystyle 1}}{{\displaystyle a_{x\overline{y}}^{\ast }}}\left(r_x+a_{x}x\right),\\ \overline{y}=-\frac{{\displaystyle 1}}{{\displaystyle a_{\overline{y}}^{\ast }}}\left(r_{\overline{y}}^{\ast }+a_{\overline{y}x}^{\ast }x\right),\end{array}$$where * denotes equilibrium. Using these isoclines, it is straightforward to obtain the coexistence condition of the population-level dynamics (see Fig. A.1). For example, when the role shift is from inferior competitor to superior competitor and the interaction coefficients are $a_{x\overline{y}}\left(t\right)<0$ and $a_{\overline{y}x}\left(t\right)<0$, the coexistence condition is $a_{\overline{y}x}^{\ast }/a_x<r_{\overline{y}}^{\ast }/r_x<a_{\overline{y}}^{\ast }/a_{x\overline{y}}^{\ast }$. The full list can be found in Table A.1 and these are numerically verified. Examples of population-level dynamics and the corresponding role-level dynamics are presented in Fig. 4 for the case in which two species coexist. The parameter values used in the role-level dynamics are listed in Table A.2. These numerical calculations confirm that the role- and population-level dynamics are consistent in terms of the equilibrium values of two species.

Considering the possible signs of the interaction coefficients in the population-level model (Fig. 3), bistability can occur in all role-shift scenarios. In this case, analysis via the equilibrium isoclines immediately provides the necessary conditions. The conditions for bistability are listed in Table A.3. Figure 5 shows the role-level and population-level dynamics under bistability conditions. The parameter values used in the role-level dynamics are listed in Table A.4. The upper figures (Figs. 3A–3C) show that species x excludes species y, while the lower figures (Figs. 3B′ and 3C′) show the opposite situation. There is clearly an agreement between the role- and population-level dynamics at equilibrium. The equilibrium isoclines of the population-level model is shown in Fig. A.2.

As expected, the aggregation of roles into the population-level dynamics does not always work under bistability conditions, because the values of the proportional parameter α differ in the two stable states. When the mismatch of equilibrium values between the role- and population-level dynamics is minor in simulations with randomly generated parameter values (ca. 0.24% over 10⁵ random parameter sets; see Section “Mathematical discussion of the role-level model” for more details), it is safe to analyze the role-level dynamics instead of the corresponding population-level effects.

Mathematical discussion of the role-level model

Derivation of the role-level dynamics

The population dynamics of species i in state s (e.g., size, age), n_i(s,t), are described by Eq. (1) in the main text.¹ The connection to the role-level dynamics (and consequently the population-level dynamics) is demonstrated by considering the simplest possible situation with a constant rate of state growth g(s) = 1. Let the number of species be fixed to two, denoted by n_x and n_y, respectively, instead of n_i. Furthermore, assume that species y has a role-shift property and each role is described by y₁ and y₂, where the role shift occurs in state s₁. Hence, the population size of these roles are described by $x={\int }_0^{\mathrm{\infty }}{n}_x\left(s,t\right)ds,y_1={\int }_0^{s_1}{n}_y\left(s,t\right)ds$, and $y_2={\int }_{s_1}^{\mathrm{\infty }}{n}_y\left(s,t\right)ds$. Now, the interaction coefficients depend on the species or role (type, hereafter) $\mathcal{X}\in \left\{x,y_1,y_2\right\}$, rather than the state. Hence, the subscripts of interaction strength a_i(s)j(s′) in Eq. (1) are replaced with the label of the role.

Integrating both sides of Eq. (1) over all possible s $\in$ [0,∞) yields

(A.1a) $$\frac{dx}{dt}=n_x\left(0\right)-d_{x}x-x\sum _{\mathcal{X}\in \left\{x,y_1,y_2\right\}}{a}_{x\mathcal{X}}\mathcal{X},$$

(A.1b) $$\frac{d{y}_1}{dt}=n_y\left(0\right)-n_y\left(s_1\right)-d_{y_1}{y}_1-y_1\sum _{\mathcal{X}\in \left\{x,y_1,y_2\right\}}{a}_{y_1\mathcal{X}}\mathcal{X},$$

(A.1c) $$\frac{d{y}_2}{dt}=n_y\left(s_1\right)-d_{y_2}{y}_2-a_{y_1}{y}_1^2-y_2\sum _{\mathcal{X}\in \left\{x,y_1,y_2\right\}}{a}_{y_2\mathcal{X}}\mathcal{X},$$where n_x(0) and n_y(0) represent the recruitment of species x and y, respectively, and $\sum {}_{\mathcal{X}}$ represents the sum over variables $\mathcal{X}\in \left\{x,y_1,y_2\right\}$. As an example, n_x(0) is obtained from the integration of the second term on the left-hand side in Eq. (1) with i = x: ${\int }_0^{\mathrm{\infty }}\mathrm{\partial }{n}_x\left(s,t\right)/\mathrm{\partial }sds=n\left(\mathrm{\infty },t\right)-n\left(0,t\right)=-n\left(0,t\right)$. Under the assumption of homogeneity within a role (i.e., all individuals with a certain role are identical), n_x(0) = b_xx ( = ∫ b_xn_x(s,t)ds) and n_y(0) = b_y1y₁ + b_y2y₂ + I_Aa_y2xxy₂, where $b_{\mathcal{X}}$ is the birth rate of type $\mathcal{X}$ and a_y2x is the reproductive term under the predation of species x by type y₂. Additionally, I_A is an indicator variable with a value of 1 if y₂ is a predator role and a value of 0 otherwise. n_y(s₁) represents a shift from type y₁ to type y₂. This can be described as my₁, where m is the transition rate. By summarizing these discussions, and noting that the net growth rate is described by $r_{\mathcal{X}}=b_{\mathcal{X}}-d_{\mathcal{X}}$, Eq. (A.1) corresponds to role-level dynamics defined in Eq. (5) in the main text. I define the coefficient matrix of Eq. (5) as

(A.2) $$\left(\begin{array}{lll}{a}_x\hfill & a_{x{y}_1}\hfill & a_{x{y}_2}\hfill \\ a_{y_{1}x}\hfill & a_{y_1}\hfill & a_{y_1{y}_2}\hfill \\ a_{y_{2}x}\hfill & a_{y_2{y}_1}\hfill & a_{y_2}\hfill \\ \hfill & \hfill & \hfill \end{array}\right),$$where $a_{\mathcal{X}\mathcal{X}}$ is denoted as $a_{\mathcal{X}}$ for brevity. The signs of the components of the coefficient matrices for the three situations of (i) inferior competitor to superior competitor, (ii) competitor to predator, and (iii) prey to predator become

(A.3) $$\left(\mathrm{i}\right)\left(\begin{array}{lll}-\hfill & -\hfill & -\hfill \\ -\hfill & -\hfill & -\hfill \\ -\hfill & -\hfill & -\hfill \\ \hfill & \hfill & \hfill \end{array}\right),\left(\mathrm{i}\mathrm{i}\right)\left(\begin{array}{lll}-\hfill & -\hfill & -\hfill \\ -\hfill & -\hfill & -\hfill \\ +\hfill & -\hfill & -\hfill \\ \hfill & \hfill & \hfill \end{array}\right),\left(\mathrm{i}\mathrm{i}\mathrm{i}\right)\left(\begin{array}{lll}-\hfill & +\hfill & -\hfill \\ -\hfill & -\hfill & -\hfill \\ +\hfill & -\hfill & -\hfill \\ \hfill & \hfill & \hfill \end{array}\right).$$

Table A.1:

Coexistence conditions in the population-level model (Eq. (6)).

Signs of ( $a_{x\overline{y}},a_{\overline{y}x}$)	Coexistence condition
Competitor (y1) → Competitor (y2)
(i) (−, −)	${\displaystyle \frac{a_{\overline{y}x}^{\ast }}{a_x}<\frac{r_{\overline{y}}^{\ast }}{r_x}<\frac{a_{\overline{y}}^{\ast }}{a_{x\overline{y}}^{\ast }},\left(r_x>0,r_{\overline{y}}^{\ast }>0\right)}$
Competitor (y1) → Predator (y2)
(ii.a) (−, −)	Same as (i)
(ii.b) (−, +)	$\{\begin{array}{l}\frac{r_{\overline{y}}^{*}}{r_x}>\frac{a_{\overline{y}x}^{*}}{a_x},\left(r_x>0,r_{\overline{y}}^{*}<0\right)\\ \frac{r_{\overline{y}}^{*}}{r_x}<\frac{a_{\overline{y}}^{*}}{a_{x\overline{y}}^{*}},\left(r_x>0,r_{\overline{y}}^{*}>0\right)\end{array}$
Prey (y1) → Predator (y2)
(iii.a) (−, −)	Same as (i)
(iii.b) (−, +)	Same as (ii.b)
(iii.c) (+, −)	$\{\begin{array}{l}\frac{r_{\overline{y}}^{*}}{r_x}<\frac{a_{\overline{y}}^{*}}{a_{x\overline{y}}^{*}},\left(r_x<0,r_{\overline{y}}^{*}>0\right)\\ \frac{r_{\overline{y}}^{*}}{r_x}>\frac{a_{\overline{y}x}^{*}}{a_x},\left(r_x>0,r_{\overline{y}}^{*}>0\right)\end{array}$
(iii.d) (+, +)	$\{\begin{array}{l}\frac{a_{\overline{y}}^{*}}{a_{x\overline{y}}^{*}}<\frac{a_{\overline{y}x}^{*}}{a_x},\left(r_x>0,r_{\overline{y}}^{*}>0\right)\\ \frac{a_{\overline{y}}^{*}}{a_{x\overline{y}}^{*}}<\frac{a_{\overline{y}x}^{*}}{a_x}\frac{r_{\overline{y}}^{*}}{r_x}>\frac{a_{\overline{y}x}^{*}}{a_x},\left(r_x>0,r_{\overline{y}}^{*}<0\right)\\ \frac{a_{\overline{y}}^{*}}{a_{x\overline{y}}^{*}}<\frac{a_{\overline{y}x}^{*}}{a_x}\frac{r_{\overline{y}}^{*}}{r_x}<\frac{a_{\overline{y}}^{*}}{a_{x\overline{y}}^{*}},\left(r_x<0,r_{\overline{y}}^{*}>0\right)\end{array}$

DOI: 10.7717/peerj.13315/table-1

Table A.2:

Parameter values used in Fig. 4.

Panel	bx	by1	by2	dx	dy1	dy2	ax	${\mathit{a}}_{x{y}_1}$	${\mathit{a}}_{x{y}_2}$	${\mathit{a}}_{y_{1}x}$	${\mathit{a}}_{y_1}$	${\mathit{a}}_{y_1{y}_2}$	${\mathit{a}}_{y_{2}x}$	${\mathit{a}}_{y_2{y}_1}$	${\mathit{a}}_{y_2}$	m
a	1.2	0	1.2	0.2	0.1	0.1	−0.5	−0.1	−0.2	−0.2	−0.5	−0.1	−0.1	−0.1	−0.5	1.0
b1	1.2	0	1.2	0.2	0.1	0.1	−0.5	−0.1	−0.2	−0.2	−0.5	−0.1	0.1	−0.1	−0.5	1.0
b2	1.2	0	1	0.2	0.1	0.1	−0.5	−0.1	−0.2	−0.2	−0.5	−0.1	0.1	−0.1	−0.5	5.0
c1	1.2	0	1	0.2	0.1	0.1	−0.5	0.15	−0.2	−0.2	−0.5	−0.1	0.15	−0.1	−0.5	0.5
c2	1.2	0	1	0.2	0.1	0.1	−0.5	0.15	−0.2	−0.2	−0.5	−0.1	0.15	−0.1	−0.5	1.0
c3	1.2	0	1	0.2	0.1	0.1	−0.5	0.15	−0.2	−0.2	−0.5	−0.1	0.15	−0.1	−0.5	0.1
c4	1.2	0	1	0.2	0.1	0.1	−0.5	0.15	−0.2	−0.2	−0.5	−0.1	0.2	−0.1	−0.5	1.0

DOI: 10.7717/peerj.13315/table-2

Table A.3:

Bistability conditions in the population-level model (Eq. (6)).

Signs of ( ${\mathit{a}}_{x\overline{y}}^{\ast },a_{\overline{y}x}^{\ast }$)	Coexistence condition
Competitor (y1) → Competitor (y2)
(i) (−, −)	${\displaystyle \frac{a_{\overline{y}}^{\ast }}{a_{x\overline{y}}^{\ast }}<\frac{r_{\overline{y}}^{\ast }}{r_x}<\frac{a_{\overline{y}x}^{\ast }}{a_x},\left(r_x>0,r_{\overline{y}}^{\ast }>0\right)}$
Competitor (y1) → Predator (y2)
(ii) (−, −)	Same as (i)
Prey (y1) → Predator (y2)
(iii.a) (−, −)	Same as (i)
(iii.b) (+, +)	$\{\begin{array}{l}\frac{a_{\overline{y}}^{*}}{a_{x\overline{y}}^{*}}>\frac{a_{\overline{y}x}^{*}}{a_x},\left(r_x<0,r_{\overline{y}}^{*}<0\right)\\ \frac{a_{\overline{y}}^{*}}{a_{x\overline{y}}^{*}}>\frac{a_{\overline{y}x}^{*}}{a_x}\frac{r_{\overline{y}}^{*}}{r_x}<\frac{a_{\overline{y}x}^{*}}{a_x}\left(r_x>0,r_{\overline{y}}^{*}<0\right)\\ \frac{a_{\overline{y}}^{*}}{a_{x\overline{y}}^{*}}>\frac{a_{\overline{y}x}^{*}}{a_x}\frac{r_{\overline{y}}^{*}}{r_x}>\frac{a_{\overline{y}}^{*}}{a_{x\overline{y}}^{*}},\left(r_x<0,r_{\overline{y}}^{*}>0\right)\end{array}$

DOI: 10.7717/peerj.13315/table-3

Table A.4:

Parameter values used in Fig. 5.

Panel	bx	by1	by2	dx	dy1	dy2	ax	${\mathit{a}}_{x{y}_1}$	${\mathit{a}}_{x{y}_2}$	${\mathit{a}}_{y_{1}x}$	${\mathit{a}}_{y_1}$	${\mathit{a}}_{y_1{y}_2}$	${\mathit{a}}_{y_{2}x}$	${\mathit{a}}_{y_2{y}_1}$	${\mathit{a}}_{y_2}$	m
a	0.68	0	0.57	0.13	0.19	0.29	−0.296	−0.564	−0.805	−0.808	−0.272	−0.905	−0.406	−0.222	−0.034	3.81
b	0.67	0	0.65	0.4	0.17	0.37	−0.127	−0.487	−0.823	−0.933	−0.564	−0.069	0.252	−0.370	−0.09	0.95
c	0.55	0	0.8	0.29	0.28	0.26	−0.013	0.922	−0.956	−0.537	−0.621	−0.858	0.042	−0.448	−0.279	1.59

DOI: 10.7717/peerj.13315/table-4

Numerical error search

In the population-level dynamics (Eq. (6)) in the main text, the isolines at equilibrium are not unique for cases of bistability. This is the source of the mismatch in equilibrium values between the role-level and population-level dynamics. To check the match between the two models, 10⁵ parameter sets were randomly generated and the equilibrium values of the role-level and population-level dynamics were checked for each of the parameters. I counted a parameter set as mismatch if the equilibrium values satisfied with $|x^{\ast }-x_{pop}^{\ast }|+|y_1^{\ast }+y_2^{\ast }-{\overline{y}}^{\ast }|>{10}^{-3}$ where $x_{pop}^{\ast }$ is the equilibrium of species x in the population-level model. Each parameter sets were examined with two initial conditions to check bistability. The parameter sets were generated in the following manner:

(B.1) $$\begin{array}{l}{b}_Z\sim U\left[0,1\right],d_Z\sim U\left[0,0.5\right],a_Z\sim U\left[-1,0\right],|a_{ZZ}|\sim U\left[0,1\right],m\sim U\left[0,20\right],\end{array}$$where Z = {x,y₁,y₂}, a_ZZ represents all possible heterogeneous pairs of {x,y₁,y₂}, and U[a,b] is a uniform distribution over the range [a,b]. The role-shift scenario was chosen at random, and the signs of a_ZZ were chosen accordingly. I found 238 parameter sets (ca. 0.24%) that caused inconsistent equilibrium values. All these cases led to a bistability condition in the population-level model, but the role-level dynamics instead converged to a stable equilibrium for cases (i), (ii), and (iii.a), or to one of the equilibria regardless of stability for case (iii.b) in Table A.4.