The performance of a modified EWMA control chart for monitoring autocorrelated PM2.5 and carbon monoxide air pollution data

Modified EWMA chart

Roberts (1959) first proposed the EWMA control chart that is very effectively at detecting small process changes. This chart’s design parameters are the multiples of widths of the control limit and smoothing parameter. The EWMA statistic is defined as (1)${\displaystyle Z_t=\left(1-\lambda \right)Z_{t-1}+\lambda X_t,}$ where 0 < λ ≤ 1 is smoothing parameter and X_t, t = 1, 2, 3, … isa sequence of autocorrelated observations with the starting value is the process target mean Z₀ = μ₀.

The respective upper and lower control limits for the EWMA chart are (2)${\displaystyle UCL={\mu }_0+H\sigma \sqrt{\frac{\lambda }{2-\lambda }\left[1-{\left(1-\lambda \right)}^{2i}\right]},}$ (3)${\displaystyle LCL={\mu }_0-H\sigma \sqrt{\frac{\lambda }{2-\lambda }\left[1-{\left(1-\lambda \right)}^{2i}\right]},}$ where H is the width of the control limit and σ is the process standard deviation. The term $\left[1-{\left(1-\lambda \right)}^{2i}\right]$ is close to 1 as i becomes large. Hence, the respective upper and lower control limit will approach their respective steady-state value as (4)${\displaystyle UCL={\mu }_0+H\sigma \sqrt{\frac{\lambda }{2-\lambda }},}$ and (5)${\displaystyle LCL={\mu }_0-H\sigma \sqrt{\frac{\lambda }{2-\lambda }}.}$

Later, modified EWMA control chart was introduced by Patel & Divecha (2011). They corrected the inertia problem caused by errors in the EWMA statistic by considering past changes as well as the latest change in the process. The modified EWMA chart is useful for detecting process changes in observations that are autocorrelated or independent normally distributed. Recently, Khan, Aslam & Jun (2017) proposed a new control statistic structure that developed from the modified EWMA control chart as follow: (6)${\displaystyle Z_t=\left(1-\lambda \right)Z_{t-1}+\lambda X_t+k\left(X_t-X_{t-1}\right),}$ where λ is the smoothing parameter; X_t, t = 1, 2, 3, … is a sequence of autocorrelated observations; k is a constant; and the starting value is the process target mean Z₀ = μ₀. It is similar to the EWMA statistic but with the last term extended.

This chart generates a false alarm when the Z_n value violates the specified control limit. In general, the upper and lower control limit are respectively given by (7)${\displaystyle UCL={\mu }_0+L\sigma \sqrt{\frac{\lambda +2k\lambda +2k^2}{2-\lambda }},}$ and (8)${\displaystyle LCL={\mu }_0-L\sigma \sqrt{\frac{\lambda +2k\lambda +2k^2}{2-\lambda }},}$ where L and σ is the width of the control limit of modified EWMA procedure and process standard deviation, respectively.

Method of evaluating ARL for moving average order q model

A time series is a series of data points ordered in time, and the goal of a time series analysis is usually to make a forecast of the future using time as an independent variable. A usual characteristic of a time series is autocorrelation, which is correlation between observations in the same dataset at different points in time. In other words, autocorrelated data portrays the similarity between observations as a function of the time lag between them. In a time series analysis, an MA(q) process is a common approach for modeling a univariate time series for which the error depends linearly on the current and numerous past values of the error term. (9)${\displaystyle X_t=\mu +{\epsilon }_t-{\theta }_1{\epsilon }_{t-1}-{\theta }_2{\epsilon }_{t-2}-\cdots -{\theta }_q{\epsilon }_{t-q},}$ where µis the mean of the series, ε_t is a white noise process assumed to be exponentially distributed, θ_i is a process coefficient, and the starting value of ε₀= s is given.

Let L(u) denote the ARL for an MA(q) process with exponential white noise on a modified EWMA control chart (see Appendix A1 for the proof) that there exists only one solution of the integral equation (see Appendix A2). It is obtained by deriving a Fredholm integral equation of the second kind as follows: (10)${\displaystyle L\left(u\right)=1-\frac{\lambda e^{\frac{\left(1-\lambda \right)u}{{\alpha }_0\left(\lambda +k\right)}}\left[e^{-\frac{b}{{\alpha }_0\left(\lambda +k\right)}}-1\right]}{\lambda e^{\frac{-\mu }{{\alpha }_0}}\cdot e^{\frac{v+\left(\lambda {\theta }_1+{\theta }_{1}k\right)s+\left(\lambda {\theta }_2+{\theta }_{2}k\right){\epsilon }_{t-2}+\cdots +\left(\lambda {\theta }_q+{\theta }_{q}k\right){\epsilon }_{t-q}}{{\alpha }_0\left(\lambda +k\right)}}+e^{-\frac{\lambda b}{{\alpha }_0\left(\lambda +k\right)}}-1},}$ with in-control process parameter α₀ and out-of-control process parameter α₁ > α₀.

Numerical results

The ARLs of the explicit formulas are derived using a Fredholm integral equation of the second type, those of the numerical integral equation method are approximated using the Gauss-Legendre quadrature rule with 1,000 nodes, and the control ARL is set to ARL₀ = 500. The numerical approximation of the numerical integral equation and the exact result of the explicit formulas to measure the accuracy in the comparative study according to the relative error is defined as (11)${\displaystyle \epsilon =\frac{|L\left(u\right)-\hat{L}\left(u\right)|}{L\left(u\right)}\times 100\text{\%},}$ where L(u) is derived from the ARL using the explicit formulas and $\hat{L}\left(u\right)$ is an approximation of the ARL with the numerical integral equation. The numerical results are reported in Tables 1, 2 and 3.

Computation of the ARL by using the explicit formulas and the numerical integral equation method on the modified EWMA control chart were carried out with a varied smoothing parameters (λ = 0.05, 0.10, 0.15 and 0.2); constant k = 1; in-control process parameter α₀ = 1; out-of-control process parameter α₁ = (1 + δ)α₀, where δ is the shift size set as 0.001, 0.003, 0.005, 0.01, 0.05, 0.10, 0.50 or 1.00; and in-control process was ARL₀ = 500 (Tables 1 and 2). The parameters were set as μ = 2; coefficients θ₁ =  − 0.3, θ₂ = 0.5 with λ = 0.05, 0.1 and θ₁ = 0.1, θ₂ = 0.3 with λ = 0.15, 0.2 for an MA(2) process; and coefficients θ₁ = 0.3, θ₂ = 0.5, θ₃ = 0.7 with λ = 0.05, 0.1 and θ₁ =  − 0.5, θ₂ =  − 0.3, θ₃ =  − 0.5 with λ = 0.15, 0.2 for an MA(3) process. The results indicate that when the smoothing parameter was increased, the value of ARL₁ was reduced.

The results in Tables 1 and 2 show that the analytically explicit expression of the ARL was in excellent agreement with the approximated ARL obtained from the numerical integral equation (NIE) method. The computational time for the numerical integral equation method was around 21 and 23 s for the MA(2) and MA(3) processes, respectively, while the explicit formulas required a computational time of less than one second for both.

Table 3 reports the ARL values obtained by using the explicit formulas and numerical integral equation method. The parameters were set as μ = 2; coefficient parameters θ₁ =  − 0.3, θ₂ = 0.7, θ₃ =  − 0.5 for MA(3) process; λ = 0.1; and k was varies as 5λ, 10λ, 20λ, or 50λ. The results revealed that when the constant k was large, ARL₁ was reduced.

The performances of the standard and modified EWMA control charts were also compared. These were obtained by the explicit expression when varying λ (0.05 and 0.10) for both control charts, as reported in Tables 4 and 5. The observations were from the MA(2) and MA(3) processes with θ₁ =  − 0.1, θ₂ =  − 0.3, and θ₁ = 0.7, θ₂ = 0.7, θ₃ =  − 0.1, respectively, for μ = 2, k = 1, and ARL₀ = 500. The last row is the relative mean index (RMI) defined as (12)${\displaystyle RMI=\frac{1}{n}\sum _{i=1}^n\left[\frac{AR{L}_{{\delta }_i}-AR{L}_{{\delta }_i}^{\text{smallest}}}{AR{L}_{{\delta }_i}^{\text{smallest}}}\right],}$ where ARL_δidenotes the ARLs of the EWMA and modified EWMA control charts obtained via the explicit formulas for each shift size and $AR{L}_{{\delta }_i}^{\text{smallest}}$ denotes the smallest of the ARLs for each shift size.

The results in Table 4 show that when λ = 0.05, the performance of the modified EWMA control chart was better than the standard one for shift sizes of 0.001, 0.003, 0.005, 0.01, 0.05, 0.10 and 0.30, whereas for shift size of 0.50, 1.00, and 2.00, the small RMI of the modified EWMA chart was 0.057529 while that the RMI of the EWMA control chart was 3.266348. When λ = 0.1,  0.15 and 0.2, the modified EWMA control chart was more powerful than the standard one for all cases of shift size with the zero RMI. The results indicate that overall, the modified EWMA control chart was better than the standard one at detecting process changes.

Application of the modified EWMA chart

PM2.5 and CO gas air pollutants are being constantly emitted, which is likely to increase over time in the winter and summer seasons. When the levels of these air pollutants are high (>50 µg/m³ for PM2.5 (https://en.wikipedia.org/wiki/Air_quality_guideline) and >10,000 ppm for CO (https://www.airqualitynow.eu/download/CITEAIR-Comparing_Urban_Air_Quality_across_Borders.pdf)), the quality of the ambient air is unhealthy to humans. Increasing PM2.5 concentration can lead to coughing, breathing difficulties, and eye irritation and can be deadly to humans.

Table 5 contains a comparison of the ARLs of the modified and standard EWMA control charts obtained via the explicit formulas. PM2.5 and CO measurements were taken every day in January and May, respectively, 2020 by the Pollution Control Department, Thailand. There were small and abrupt changes in the PM2.5 and CO level data in the Din Daeng district of Bangkok (where there is a high volume of traffic) from measurements near a busy road (Chuersuwan et al., 2008). The PM2.5 and CO air pollution level data were tested for autocorrelation in the observations. The Box-Jenkins technique was applied to the two air pollution datasets to determine whether they fit forecast time series data models. The models with the lowest Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) values were considered as optimal. Moreover, t-test statistics proved that the two datasets were autocorrelated. The parameter values for the MA(1) and MA(2) processes were fitted and provided 51.163 for the mean and -0.723 and -0.380 for the coefficients, respectively. The PM2.5 level was found to be significant for the MA(2) process.

The efficiency of the modified EWMA procedure was also emphasized by its performance with the CO level data for the Din Daeng district, Bangkok, Thailand. Table 6 displays the ARLs of the modified and traditional EWMA control charts. The explicit formulas were used for measuring the ARLs of the CO gas level. The data were collected every day in May 2020. The analysis for an MA autocorrelated process resulted in a mean of 1.198 and −0.662, −0.479, and −0.495 for the coefficients of the MA(1), MA(2), and MA(3) processes. The results of the PM2.5 and CO air pollutant data indicate that the modified EWMA control chart was more effective than the standard one for detecting small shifts, and so confirms that it is excellent for monitoring unusual observations with undesirable values in a timely manner for all cases of exponential smoothing parameter.

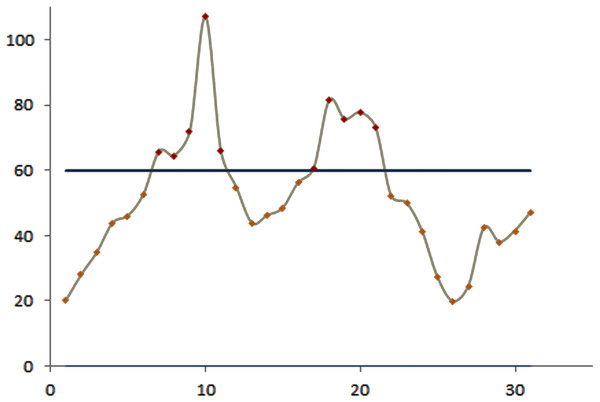
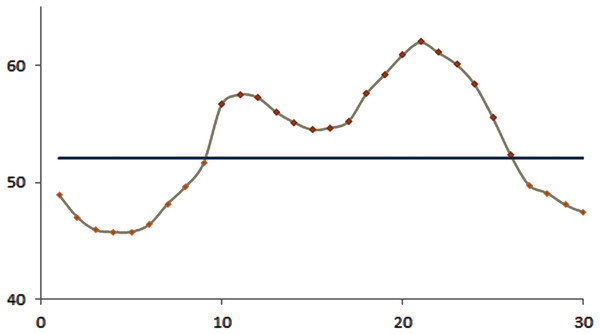
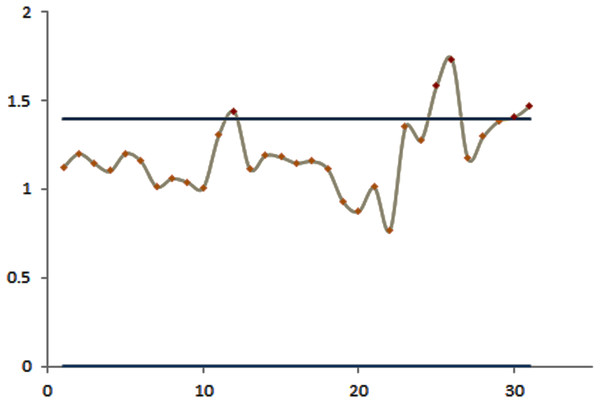
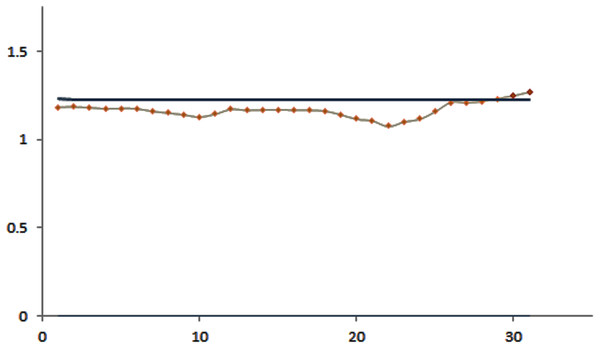
The efficacy of the control charts was visualized by plotting graphs to showcase the effective results obtained from the proposed procedure in a comparative study. Figure 1 shows that the modified EWMA control chart detected upper PM2.5 shifts at the 7th to 11th and 17th to 21st observations. On the other hand, the standard EWMA control chart only detected shifts at the 10th to 26th observations, as illustrated in Fig. 2. Figure 3 exhibits that the modified EWMA chart detected upper CO level shifts at the 12th, 25th to 26th, and 30th to 31st observations. On the contrary, the original EWMA chart only detected upper CO level shifts at the 30th to 31st observations, as shown in Fig. 4.

The modified EWMA control chart detected the upper change in PM2.5 level at the 7th observation (i.e., the 7th January), which marked the beginning of extreme changes in PM2.5 emissions at the upper level. Meanwhile, the standard EWMA control chart detected the change at the 10th observation (i.e., the 10th January). Although the CO gas level emissions were low and harmless to the human body, the performance of the modified EWMA control chart for detecting the change in CO gas emissions was exemplary.