DC-TSCM: an interpretable dual-channel traditional Chinese medicine syndrome classification model via semantic-structural fusion

Data collection and preprocessing

The dataset employed in this study is derived from the TCM-Syndrome Differentiation (SD) corpus (Ren et al., 2022), the first publicly available high-quality resource for TCM syndrome differentiation. It comprises 54,152 authentic TCM clinical records. To ensure the quality of the dataset, we cleaned the data, removed duplicate entries, and retained only prescriptions with both complete clinical description and physique detection data. In addition, we standardized syndrome names and four diagnostic information according to the WHO international standard terminologies on traditional Chinese medicine and Clinic terminology of traditional Chinese medical diagnosis and treatment (State Administration for Market Regulation & Standardization Administration of the People’s Republic of China, 2021). For example, semantically similar expressions such as “mental fatigue,” “lassitude,” and “low spirit” were unified into “mental fatigue”, achieving semantic alignment and improving feature interpretability and reproducibility. On this basis, we identified 24 high-frequency and representative syndrome types, covering patterns according to the eight principles (yang, yin, heat, cold, excess, deficiency, exterior, interior pattern) and patterns of the zang–fu organs and meridians (heart system, lung system, spleen system, liver system, kidney system, multiple zang-fu organs patterns, meridian and collateral patterns).

To address the large variation in sample sizes across syndrome categories, we employed a random up-sampling and down-sampling strategy to balance the dataset. It controlled the number of samples in each class to approximately 320 ± 50. This adjustment not only mitigated bias caused by class imbalance but also ensured the clinical representativeness and diversity of the dataset. Detailed dataset statistics are presented in Table 1. Each prescription record contains a set of clinical description, a set of physique detection, a set of chief complaint, and an associated TCM syndrome. The chief complaint content is only used to construct nodes in the heterogeneous graph. Physique detection data usually consists of multiple independent symptom elements. We divided the physique detection content into multiple TCM symptom elements to enable the graph structure to capture the potential associations among different elements. An example physique detection entry reads: “clear mind, fair spirit, moderate form, clear speech, red lips; normal skin, no blotchy rash …… no swelling of both lower limbs, red tongue, white moss, slippery pulse”. Using regular-expression filtering and TCM symptom dictionary matching, we identified 988 distinct symptom elements (e.g., “tongue red”, “deep pulse”, “poor appetite”). These elements form the basis for the subsequent heterogeneous graph construction. However, this rule-based approach enabled efficient symptom extraction, it had limited adaptability to diverse clinical expressions.

Problem definition

TCM syndrome classification is typically defined as a long-text classification task. Its goal is to identify the TCM syndrome category corresponding to the patient given a set of clinical description and physique detection. TCM syndrome differentiation dataset $D={\left\{\left(X_i,Y_i\right)\right\}}_{i=1}^N$, where each prescription sample $X_i$ contains a clinical description text $T_{desc}$ and a set of physique detection elements $E_{det}=\left\{e_1,e_2,\dots ,e_m\right\}$. The label $Y_i$ is a specific TCM syndrome category, which is taken from the syndrome category set $S=\left\{s_1,s_2,\dots ,s_k\right\}$. The objective of this study is to design a classifier $f$ that maps an input prescription $X_i$ to its corresponding syndrome label $Y_i$. Its output is expressed as $f\left(X_i\right)=\widehat{Y_i}$, where $\widehat{Y_i}$ is the predicted syndrome category for prescription $X_i$.

Dual-channel TCM syndrome classification model

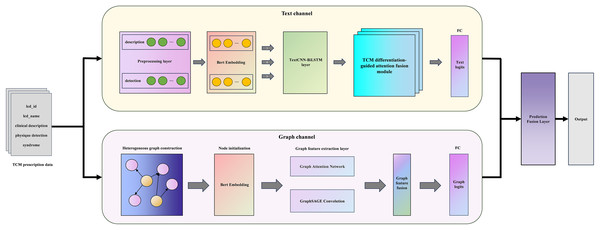
The whole model is mainly composed of a sequence-based text channel and a structural graph channel, as illustrated in Fig. 1. Specifically, in the text channel, we use BERT-TextCNN-BiLSTM to obtain the deep semantics of prescription texts. TDAF is introduced to integrate the idea of TCM syndrome differentiation guidance into the model, which improves the interpretability of the model. In parallel, the graph channel constructs a unique TCM differentiation heterogeneous graph with initialized node features and leverages GAT-GraphSAGE to capture local neighbor attention and global distribution information. The following sections will describe the architecture of DC-TSCM and its module operation process in detail.

Word embedding module

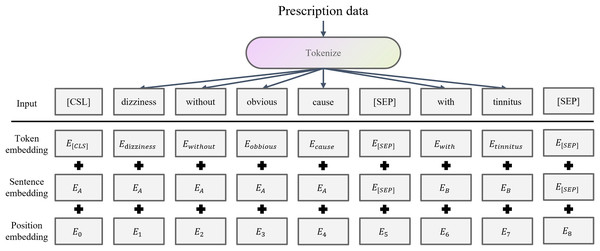
The preprocessed prescription text sequences are fed into BERT (Devlin et al., 2019), which converts each word in the clinical description and physique detection texts into its corresponding word embedding vectors. It maps discrete symbols to continuous representations. BERT has been widely used in medical clinical applications by taking advantage of its bidirectional Transformer architecture and context-aware word embedding (Chaudhari et al., 2022; Mulyar, Uzuner & McInnes, 2021; Nishigaki et al., 2023; Rasmy et al., 2021). BERT word embedding is shown in the Fig. 2.

For a TCM prescription, the clinical description sequence is $x_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}=\left\{x_1^d,x_2^d,\dots ,x_{L_d}^d\right\}$ and physique detection sequence is $x_{\mathrm{d}\mathrm{e}\mathrm{t}}=\left\{x_1^t,x_2^t,\dots ,x_{L_t}^t\right\}$. Each sequence is encoded by BERT as follows:

(1) $$H_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}=\mathrm{B}\mathrm{E}\mathrm{R}\mathrm{T}\left(x_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}\right)\in {\mathbb{R}}^{L_d\times d};H_{\mathrm{d}\mathrm{e}\mathrm{t}}=\mathrm{B}\mathrm{E}\mathrm{R}\mathrm{T}\left(x_{\mathrm{d}\mathrm{e}\mathrm{t}}\right)\in {\mathbb{R}}^{L_t\times d}$$where $d$ is the hidden dimension, $L_d$ and $L_t$ are the actual lengths of the clinical description and physique detection inputs, respectively.

Semantic encoding module

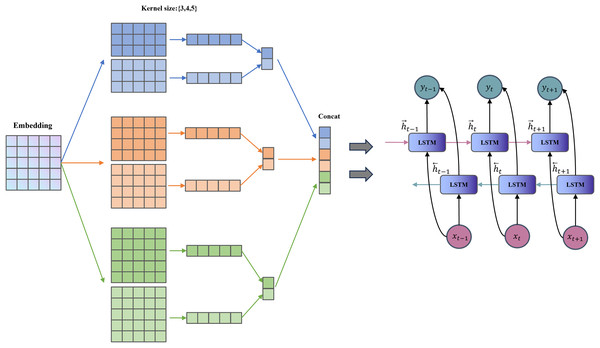
TextCNN has a simple structure and few parameters (Chen, 2015). It uses convolution kernels to extract n-gram features within a fixed window, which is suitable for capturing keywords at the “symptom element” level in TCM texts (e.g., “red tongue with yellow fur” and “slippery pulse”). BiLSTM (Graves, Fernández & Schmidhuber, 2005) further captures the long-range dependencies and contextual features between words. It enhances the understanding of contextual semantics in symptoms, such as the implicit temporal and state-related associations between “dry mouth” and “restless sleep”. The combination of TextCNN and BiLSTM is complementary, allowing the model to not only recognize the local symptom vocabulary combinations but also pay attention to the overall semantic logic. It aligns with the comprehensive differentiation concept of TCM. The TextCNN-BiLSTM layer framework is shown in Fig. 3.

For each branch, we first apply a TextCNN to extract local features. To accommodate 1-D convolution, the two BERT output matrices are transposed:

(2) $$H_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}^{\prime }=H_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}^{\mathrm{\top }}\in {\mathbb{R}}^{d\times L_d};H_{\mathrm{d}\mathrm{e}\mathrm{t}}^{\prime }=H_{\mathrm{d}\mathrm{e}\mathrm{t}}^{\mathrm{\top }}\in {\mathbb{R}}^{d\times L_t}.$$

For each channel and each convolution-kernel size $k\in \left\{k_1,k_2,k_3\right\}$, we perform the following operation:

(3) $$\begin{array}{rl}{C}_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}^{\left(k\right)}& =\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}\left(\mathrm{C}\mathrm{o}\mathrm{n}{\mathrm{v}}_{\mathrm{k}}\left(\mathrm{P}\mathrm{a}\mathrm{d}\left(H_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}^{\prime }\right)\right)+b^{\left(k\right)}\right)\in {\mathbb{R}}^{c\times L_d}\\ C_{\mathrm{d}\mathrm{e}\mathrm{t}}^{\left(k\right)}& =\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}\left(\mathrm{C}\mathrm{o}\mathrm{n}{\mathrm{v}}_{\mathrm{k}}\left(\mathrm{P}\mathrm{a}\mathrm{d}\left(H_{\mathrm{d}\mathrm{e}\mathrm{t}}^{\prime }\right)\right)+b^{\left(k\right)}\right)\in {\mathbb{R}}^{c\times L_t}\end{array}$$where $\mathrm{P}\mathrm{a}\mathrm{d}(\cdot )$ is a symmetric or asymmetric padding operation calculated based on the size of the convolution kernel, ensuring that the output length is the same as the original sequence. $c$ is the number of output channels of each group of convolution kernels. Concatenate the convolution outputs of different sizes in the channel dimension:

(4) $$\begin{array}{rl}{C}_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}& =\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\left(C_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}^{\left(k_1\right)},C_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}^{\left(k_2\right)},C_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}^{\left(k_3\right)}\right)\in {\mathbb{R}}^{\left(c\cdot 3\right)\times L_d}\\ C_{\mathrm{d}\mathrm{e}\mathrm{t}}& =\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\left(C_{\mathrm{d}\mathrm{e}\mathrm{t}}^{\left(k_1\right)},C_{\mathrm{d}\mathrm{e}\mathrm{t}}^{\left(k_2\right)},C_{\mathrm{d}\mathrm{e}\mathrm{t}}^{\left(k_3\right)}\right)\in {\mathbb{R}}^{\left(c\cdot 3\right)\times L_t}.\end{array}$$

Transpose the TextCNN output into sequence format for input to BiLSTM respectively:

(5) $$C_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}^{\prime }=C_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}^{\mathrm{\top }}\in {\mathbb{R}}^{L_d\times \left(c\cdot 3\right)};C_{\mathrm{d}\mathrm{e}\mathrm{t}}^{\prime }=C_{\mathrm{d}\mathrm{e}\mathrm{t}}^{\mathrm{\top }}\in {\mathbb{R}}^{L_t\times \left(c\cdot 3\right)}.$$

The BiLSTM models long-range and contextual dependencies, producing:

(6) $$O_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}=\mathrm{B}\mathrm{i}\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M}\left(C_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}^{\prime }\right)\in {\mathbb{R}}^{L_d\times 2h};O_{\mathrm{d}\mathrm{e}\mathrm{t}}=\mathrm{B}\mathrm{i}\mathrm{L}\mathrm{S}\mathrm{T}\mathrm{M}\left(C_{\mathrm{d}\mathrm{e}\mathrm{t}}^{\prime }\right)\in {\mathbb{R}}^{L_t\times 2h}$$where $h$ is the number of hidden units in each unidirectional LSTM; the output dimension $2h$ reflects the concatenation of forward and backward representations.

TDAF module

In TDAF, we first take the symptom set $\left\{s_i\right\}$ and the corresponding label syndrome $y$ for each case in the TCM differentiation heterogeneous graph. For each $s_i$, the count is accumulated to the matrix $C\left[s_i,y\right]$, and the row is normalized to obtain the differentiation weight matrix $P_{\mathrm{a}\mathrm{t}\mathrm{t}}\left[i,j\right]=\frac{C\left[s_i,y_j\right]}{{\sum }_{j^{\prime }}C\left[s_i,y_{j^{\prime }}\right]}$. Therefore, the model can dynamically modulate the attention allocation between clinical description and physique detection features under the guidance of the differentiation weight matrix. It reflects the differentiated attention to diverse diagnostic information in the TCM diagnosis process. The differentiation weight matrix $P_{att}$ was constructed exclusively from the training set, and remained fixed during validation and testing to ensure consistent data partitioning.

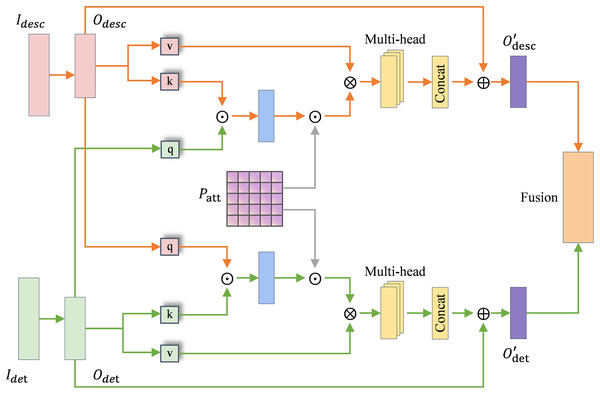
The attention module in TDAF is shown in Fig. 4, where the orange stream and green stream represent the clinical description and physique detection channels, respectively. $I_{desc}$ and $I_{det}$ denote the raw input matrices of each channel. $O_{desc}$ and $O_{det}$ represent the encoded feature embeddings obtained after semantic encoding module processing, which serve as the inputs to the TDAF attention module. The attention mechanism modulated by $P_{att}$ is formulated as:

(7) $$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}{\mathrm{n}}_{\mathrm{T}\mathrm{C}\mathrm{M}}\left(Q,K,V;P_{\mathrm{a}\mathrm{t}\mathrm{t}}\right)=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left({\displaystyle \frac{Q{K}^{\mathrm{\top }}}{\sqrt{d_k}}\odot P_{att}}\right)V$$where $O_{desc}$ and $O_{det}$ are linearly projected to obtain $Q,K,$ and $V$, and $\odot$ denotes element-wise multiplication.

The module performs two-way cross-attention between the clinical description and physique detection features. Specifically, the description features are refined under the guidance of detection information, and vice versa:

(8) $$\begin{array}{rl}{O}_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}^{\prime }& =\mathrm{L}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}\left(O_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}+\mathrm{D}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}\left(\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}{\mathrm{n}}_{\mathrm{T}\mathrm{C}\mathrm{M}}\left(O_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}},O_{\mathrm{d}\mathrm{e}\mathrm{t}},O_{\mathrm{d}\mathrm{e}\mathrm{t}};P_{\mathrm{a}\mathrm{t}\mathrm{t}}\right)\right)\right)\\ O_{\mathrm{d}\mathrm{e}\mathrm{t}}^{\prime }& =\mathrm{L}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}\left(O_{\mathrm{d}\mathrm{e}\mathrm{t}}+\mathrm{D}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}\left(\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}{\mathrm{n}}_{\mathrm{T}\mathrm{C}\mathrm{M}}\left(O_{\mathrm{d}\mathrm{e}\mathrm{t}},O_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}},O_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}};P_{\mathrm{a}\mathrm{t}\mathrm{t}}\right)\right)\right)\end{array}.$$

In each branch, multi-head attention is employed to capture diverse inter-feature dependencies, and the outputs of different heads are concatenated before residual fusion.

After the bidirectional refinement, global average pooling is applied to obtain the joint feature representation:

(9) $$f_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}}=\left[f_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}},f_{\mathrm{d}\mathrm{e}\mathrm{t}}\right]=\left[{\displaystyle \frac{1}{L}\sum _{i=1}^L{O}_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c},i}^{\prime },{\displaystyle \frac{1}{L}\sum _{i=1}^L{O}_{\mathrm{d}\mathrm{e}\mathrm{t},i}^{\prime }}}\right]\in {\mathbb{R}}^{4h}.$$

The basis gating vector is obtained through a linear transformation and sigmoid activation:

(10) $$g_0=\sigma \left(W_g{f}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}}+b_g\right)\in {\mathbb{R}}^{2h}.$$

To incorporate prior differentiation knowledge from the co-occurrence matrix $C$, we first aggregate the evidence of each syndrome category $y_j$ across all observed symptoms $\left\{s_k\right\}$ in the current case:

(11) $$z_j=\sum _{k}C\left[s_k,y_j\right],j=1,\dots ,N_c$$and derive the “differentiation confidence” over the syndrome dimension via a softmax:

$$p_j={\displaystyle \frac{\exp \left(z_j\right)}{{\sum }_{j^{\prime }}\exp \left(z_{j^{\prime }}\right)}}$$

(12) $$P_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}}=\sum _{j=1}^{N_c}{p}_j{\mathbf{e}}_j\in {\mathbb{R}}^{N_c}$$where ${\mathbf{e}}_j$ is the one-hot vector corresponding to the $j$-th syndrome category and $N_c$ is the number of syndrome classes. Since $P_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}}$ resides in the label space ${\mathbb{R}}^{N_c}$, while the feature gate $g_0$ lies in the feature space ${\mathbb{R}}^{2h}$, we introduce a learnable semantic projection to align the two spaces:

(13) $$P_{\mathrm{g}\mathrm{a}\mathrm{t}\mathrm{e}}=\sigma \left(W_s{P}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}}+b_s\right)\in {\mathbb{R}}^{2h}$$where $W_s\in {\mathbb{R}}^{2h\times N_c}$ and $b_s\in {\mathbb{R}}^{2h}$ are trainable parameters. Using the gated differentiation weight $P_{\mathrm{g}\mathrm{a}\mathrm{t}\mathrm{e}}$, we compute the final gating vector as:

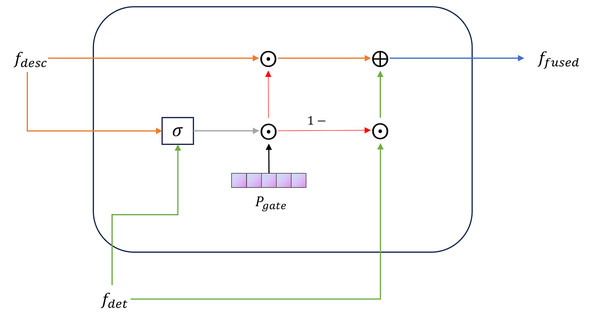
(14) $$g=g_0\odot P_{\mathrm{g}\mathrm{a}\mathrm{t}\mathrm{e}}.$$TDAF simulates the dynamic weight distribution of “observation, auscultation, inquiry, and pulse feeling” in TCM diagnosis, which improves the model’s fit and interpretability for TCM syndrome classification tasks. The final fused representation is as follows:

(15) $$f_{\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{e}\mathrm{d}}=g\odot f_{\mathrm{d}\mathrm{e}\mathrm{s}\mathrm{c}}+\left(1-g\right)f_{\mathrm{d}\mathrm{e}\mathrm{t}}.$$The gated fusion module in TDAF is shown in Fig. 5. Finally, the fused vector is linearly projected and mapped to the syndrome-category space:

(16) $$\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}{\mathrm{s}}_{\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}}=W_c{f}_{\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{j}}+b_c=W_c\left(W_p{f}_{\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{e}\mathrm{d}}+b_p\right)+b_c.$$

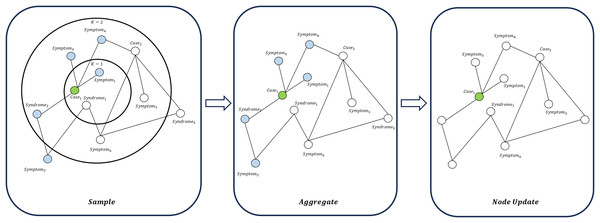
Heterogeneous graph construction

We transform TCM prescription data into a heterogeneous graph to represent the structured relationships between different clinical entities in TCM syndrome differentiation. Formally, the heterogeneous graph is denoted $G=\left(V,E\right)$, where $V=V_{case}\cup V_{syndrome}\cup V_{symptom}$ is the set of all nodes, and $E$ comprises all edge types. Each node $v$ has a $d$-dimensional initial vector ${\mathbf{x}}_v\in {\mathbb{R}}^d$. The specific steps for constructing the heterogeneous graph are as follows:

Nodes: The TCM syndrome differentiation heterogeneous graph contains three types of entity nodes. Each node is initialized with BERT-based feature embeddings to encode its semantic representations:

• Case nodes: Each clinical record is modeled as a case node, combining clinical description and chief complaint features. Their feature vectors are fused with a 0.2:0.8 weight ratio, emphasizing the main diagnostic cues in the chief complaint, and enriching them with supplementary symptom information from the clinical description.

• Syndrome nodes: Each standardized syndrome label corresponds to a syndrome node, represented by a feature vector derived from its standardized text.

• Symptom nodes: Each independent symptom extracted from the preprocessed physique detection text is represented as a symptom node.

Edges: Based on domain knowledge and statistical co-occurrence analysis, we define four types of directed edge relationships to connect these nodes:

• Case-to-Syndrome edges: Connect each case node with its actual corresponding syndrome node, reflecting the direct diagnostic relationship between clinical cases and their identified syndromes.

• Case-to-Symptom edges: Link each case node to all symptom elements extracted from its physique detection text, following the TCM principle that syndromes are inferred from observed symptoms.

• Symptom-to-Syndrome edges: Established when a symptom element and a syndrome co-occur in at least five cases (threshold = 5). It effectively filters out random co-occurrences while retaining weak but clinically significant associations.

• Case-to-Case edges: Self-loop connections are added to enhance the stability of message propagation during graph learning.

Graph feature extraction module

In the TCM differentiation heterogeneous graph, the nodes are diverse and the structure is characterized by hierarchical complexity and non-uniformity. It exhibits irregular connection patterns among nodes. The semantic significance of different nodes is also uneven. For instance, “white tongue coating” frequently appears across syndromes but contributes unequally to classification. Accordingly, within the graph feature extraction layer, we employ a hybrid GAT-GraphSAGE approach to extract both local and global structural features. GAT assigns different weights to neighboring nodes through the attention mechanism (Veličković et al., 2017). It is suitable for processing the local non-uniform contribution relationship between “cases-symptoms-syndromes” and improving the model’s sensitivity to typical symptoms. The node update process in GAT is shown in Fig. 6. The feature update of a node $v$ under edge type $t$ can be expressed as:

(17) $${\mathbf{h}}_v^{\left(\mathrm{G}\mathrm{A}\mathrm{T}\right)}=\sigma \left(\sum _{u\in {\mathcal{N}}_t\left(v\right)}{\alpha }_{vu}^{\left(t\right)}{W}_{\mathrm{g}\mathrm{a}\mathrm{t}}{\mathbf{h}}_u^{\left(l\right)}\right)$$where ${\alpha }_{vu}^{\left(t\right)}$ is the normalized attention coefficient, $W_{\mathrm{g}\mathrm{a}\mathrm{t}}$ is a learnable weight matrix, and $\sigma (\cdot )$ is typically a rectified linear unit (ReLU) activation. For each neighbor $u$, the unnormalized attention score is computed by:

(18) $$e_{vu}^{\left(t\right)}=\mathrm{L}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{y}\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}({\left({\mathbf{a}}^{\left(\mathit{t}\right)}\right)}^{\mathrm{\top }}[W_{\mathrm{g}\mathrm{a}\mathrm{t}}{\mathbf{h}}_v^{\left(l\right)}||W_{\mathrm{g}\mathrm{a}\mathrm{t}}{\mathbf{h}}_u^{\left(l\right)}])$$where ${\mathbf{a}}^{\left(\mathit{t}\right)}$ is the learnable attention vector, and || denotes vector concatenation. The normalized attention coefficient is then obtained using a softmax function:

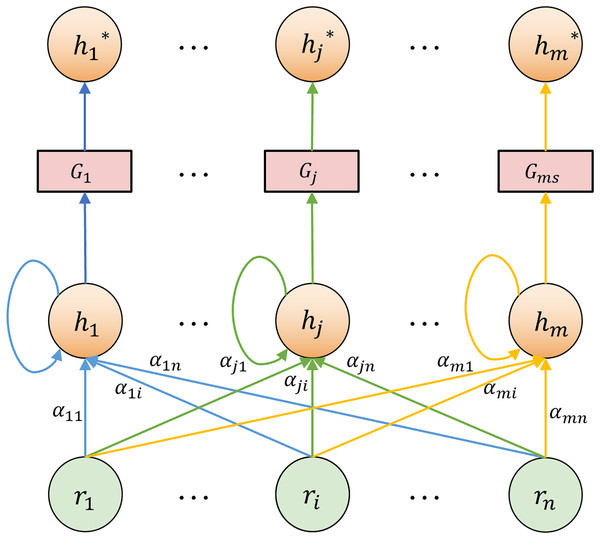
(19) $${\alpha }_{vu}^{\left(t\right)}={\displaystyle \frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(e_{vu}^{\left(t\right)}\right)}{{\sum }_{u^{\prime }\in {\mathcal{N}}_t\left(v\right)}\mathrm{e}\mathrm{x}\mathrm{p}\left(e_{v{u}^{\prime }}^{\left(t\right)}\right)}.}$$GraphSAGE aggregates information using a neighbor sampling-based approach and is applicable to large-scale graph data (Hamilton, Ying & Leskovec, 2017), as illustrated in Fig. 7. GraphSAGE can better capture the macro-topological structure and potential global patterns between “cases-symptoms-syndromes”. The update of a node $v$ is expressed as:

(20) $${\mathbf{h}}_v^{\left(\mathrm{S}\mathrm{A}\mathrm{G}\mathrm{E}\right)}=\sigma \left(W_{\mathrm{s}\mathrm{a}\mathrm{g}\mathrm{e}}\cdot \mathrm{A}\mathrm{G}\mathrm{G}\left(\left\{{\mathbf{h}}_u^{\left(l\right)}:u\in {\mathcal{N}}_t\left(v\right)\right\}\right)+b_{\mathrm{s}\mathrm{a}\mathrm{g}\mathrm{e}}\right)$$where $\mathrm{A}\mathrm{G}\mathrm{G}(\cdot )$ represents the aggregation function, and $W_{\mathrm{s}\mathrm{a}\mathrm{g}\mathrm{e}},b_{\mathrm{s}\mathrm{a}\mathrm{g}\mathrm{e}}$ are trainable parameters. The combined use of GAT and GraphSAGE allows the model to learn the strong representation ability of local key symptoms for syndromes. It also learns the overall connection and distribution rules between symptom elements, syndromes, and cases in the graph. This design is particularly suitable for dealing with the structure of “multiple symptoms corresponding to one medical history” and “multiple symptoms pointing to one syndrome” in TCM.

Graph feature fusion module

In the graph feature fusion layer, we combine the outputs of GAT and GraphSAGE through a weighted sum:

(21) $${\mathbf{h}}_v^{\left(\mathrm{f}\mathrm{u}\mathrm{s}\mathrm{e}\mathrm{d}\right)}=\alpha \cdot {\mathbf{h}}_v^{\left(\mathrm{G}\mathrm{A}\mathrm{T}\right)}+\left(1-\alpha \right)\cdot {\mathbf{h}}_v^{\left(\mathrm{S}\mathrm{A}\mathrm{G}\mathrm{E}\right)}$$where $\alpha$ controls the relative contribution of each branch. With $\alpha \in \left(0,1\right)$, the attention mechanism of GAT and the robust aggregation ability of GraphSAGE can be simultaneously utilized. It allows the final fused node representation to not only reflect the importance of local key neighbors but also maintain the robustness of the global features.

A larger $\alpha$ value causes the model to prioritize the GAT branch, improving its ability to capture sparse but critical clinical associations. This is common in cases with rare syndromes or those with few typical symptoms. In contrast, a smaller $\alpha$ value enhances the influence of the GraphSAGE branch, making the model more stable and generalizable in scenarios with dense neighborhoods or overlapping symptoms. Since our dataset contains mostly high-frequency and symptom-overlapping syndromes, the graph fusion coefficient $\alpha$ was set to 0.4 after multiple experiments.

The final node representation ${\mathbf{h}}_{\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}}^{\left(L\right)}$ is fed into a fully connected layer, and the final output can be expressed as:

(22) $$\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}{\mathrm{s}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}=W_{\mathrm{f}\mathrm{c}}{\mathbf{h}}_{\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{e}}^{\left(L\right)}+b_{\mathrm{f}\mathrm{c}}$$where $\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}{\mathrm{s}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}$ represents the graph channel’s standalone predictions for the case’s syndrome category.

Dual-channel fusion strategy

The outputs of the text and graph channels are integrated through a weighted summation:

(23) $$\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\mathrm{s}=\lambda \cdot \mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}{\mathrm{s}}_{\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}}+\left(1-\lambda \right)\cdot \mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}{\mathrm{s}}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}}$$where $\lambda \in \left[0,1\right]$ controls the relative contribution of the two channels.

When channel integration factor $\lambda$ approaches 1, the model relies primarily on the text channel. It is preferable for datasets where clinical descriptions are semantically rich but symptom relations are sparse or noisy. When $\lambda$ approaches 0, the model emphasizes the graph channel. It is suitable for datasets with dense and reliable relational structures. In this case, graph-based aggregation helps the model capture implicit diagnostic patterns and suppress noise propagation. This flexible integration mechanism ensures that the advantages of both types of TCM prescription information are effectively utilized, thus enhancing the overall classification performance. Through extensive experiments, $\lambda$ was set to 0.5, achieving a balanced trade-off between attention sensitivity and aggregation stability.

Finally, the fused logits are transformed into the probability distribution of each category:

(24) $$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{e}\mathrm{s}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\mathrm{s}\right)={\displaystyle \frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\mathrm{s}\right)}{{\sum }_{j=1}^C\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}{\mathrm{s}}_j\right)}}$$where $C$ denotes the total number of syndrome categories.

Experimental settings

We screened 8,280 complete TCM prescription records from the TCM-SD database, covering 24 representative types of TCM syndromes. Each record contained two input modalities: clinical description and physique detection, and a syndrome label as the prediction target. The dataset was split into training, validation, and test sets in the ratio of 80%, 10% and 10%, respectively, with the proportion of each syndrome class kept nearly identical across the three subsets (variance <0.5%).

All experiments were carried out in a PyTorch 2.2 environment. The device was equipped with an NVIDIA GeForce RTX 4060 Ti 8GB graphics card and 16 GB of system memory, and the model training was performed in the GPU environment. The model was implemented using the AdamW optimizer with an initial learning rate of 1e−5, optimized with the cross-entropy loss function. The batch size was set to 20. The network was trained for 50 epochs with early stopping (patience = 10) to prevent overfitting. The dropout rate was set to 0.4. Regarding the core network configuration, BERT served as the base encoder with a hidden size of 768. The TextCNN module adopted kernel sizes 3, 4, and 5. The BiLSTM layer contained 64 hidden units. The TDAF module was composed of 2 attention layers and four attention heads. The model’s hyperparameter and network parameter settings are detailed in Tables 2 and 3, respectively.

Evaluation metrics

In order to comprehensively measure the DC-TSCM in the multi-classification task of TCM syndrome, this study used precision, recall, F1-score and accuracy. All metrics were calculated on the test set and Macro-average was used. The metrics are defined as follows:

(25) $$\begin{array}{c}\mathrm{M}\mathrm{a}\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}={\displaystyle \frac{1}{K}{\sum }_{i=1}^K{P}_i={\displaystyle \frac{1}{K}{\sum }_{i=1}^K{\displaystyle \frac{T{P}_i}{T{P}_i+F{P}_i}}}}\hfill \\ \mathrm{M}\mathrm{a}\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}={\displaystyle \frac{1}{K}{\sum }_{i=1}^K{R}_i={\displaystyle \frac{1}{K}{\sum }_{i=1}^K{\displaystyle \frac{T{P}_i}{T{P}_i+F{N}_i}}}}\hfill \\ \mathrm{M}\mathrm{a}\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{F}1={\displaystyle \frac{1}{K}{\sum }_{i=1}^{K}F{1}_i={\displaystyle \frac{1}{K}{\sum }_{i=1}^K{\displaystyle \frac{2P_i{R}_i}{P_i+R_i}}}}\hfill \\ \mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}={\displaystyle \frac{1}{K}{\sum }_{i=1}^{K}Accurac{y}_i={\displaystyle \frac{1}{K}{\sum }_{i=1}^K{\displaystyle \frac{T{P}_i+T{N}_i}{N}}}}\hfill \end{array}$$where $K=24$ is the number of syndrome categories, $N$ is the total number of test set samples, $T{P}_i,T{N}_i,F{P}_i,F{N}_i$ denote the true-positive, true-negative, false-positive, and false-negative counts for class $i$, respectively.

Additionally, this study used the receiver operating characteristic (ROC) curve to intuitively evaluate the classification ability of the model. The ROC curve plots the false positive rate (FPR) on the horizontal axis and the true positive rate (TPR) on the vertical axis. A ROC curve approaching the top-left corner (TPR = 1, FPR = 0) indicates superior classification performance, whereas a curve nearing the diagonal line (TPR = FPR) implies poorer performance. The area under curve (AUC) is widely used as a quantitative measure to evaluate the overall classification effectiveness of the model.

Comparative experiments

To evaluate the effectiveness of our model, we compared it with several relevant baselines and state-of-the-art approaches.

• Support Vector Machine (SVM) (Cortes & Vapnik, 1995), Random Forest (RF) (Breiman, 2001), eXtreme Gradient Boosting (XGBoost) (Chen & Guestrin, 2016) and K-Nearest Neighbors (KNN) (Guo et al., 2003): These algorithms serve as classical baselines capable of handling structured and text-based features, offering interpretable yet limited nonlinear modeling capacity.

• TextCNN and TextRCNN (Lai et al., 2015): TextCNN uses convolutional structures to effectively extract local semantic features from TCM prescription texts. TextRCNN combines recurrent and convolutional structures to capture long-term dependencies within clinical description.

• BERT, MLM as correction BERT (MacBERT) (Cui et al., 2020), Zhong Yi BERT (ZY-BERT) (Ren et al., 2022) and Chief Complaint Syndrome Differentiation (CCSD) (Zhao et al., 2024): BERT serves as a foundational pre-trained language model for capturing contextual semantics from prescription texts. MacBERT is an enhanced Chinese BERT model that improves semantic representation through a masked correction pre-training objective. ZY-BERT is a BERT model pre-trained on the TCM-SD corpus for TCM-specific language understanding. CCSD enhances token-level and label-level attention on ZY-BERT to capture syndrome–symptom relationships and introduces focal loss.

• TextGCN (Yao, Mao & Luo, 2019), GAT, GraphSAGE and Pre-trained Semantic Interaction-based Inductive Graph Neural Network (PaSIG) (Wang et al., 2025): TextGCN learns global word co-occurrence structures, making it suitable for capturing latent associations between symptoms and syndromes. GAT applies an attention mechanism to assign adaptive weights to nodes, effectively highlighting key symptom features in complex clinical relationships. GraphSAGE aggregates neighborhood information for inductive learning, capturing the macro-topological structure among TCM entities. PaSIG is an inductive GNN framework that constructs a text–word heterogeneous graph. It leverages an asymmetric structure, gated fusion, and subgraph propagation for efficient text classification.

The experimental results are summarised in Table 4.

Traditional machine learning models performed poorly overall, with precision generally below 70%. Because these methods rely on fixed, hand-crafted features, they struggle to fully capture the complex TCM symptom expressions in prescriptions.

In contrast, text classification models have significantly improved performance and effectively modeling the complex symptom interactions in clinical description and physique detection. Notably, ZY-BERT outperformed both BERT and MacBERT across all evaluation metrics, indicating that domain-specific pre-training on TCM corpora enhances the model’s semantic understanding of specialized terminology and syndrome expressions. Furthermore, CCSD model achieved the highest performance among text classification models (accuracy = 0.8242, F1 = 0.8238, recall = 0.8246, precision = 0.8324).

GNN-based models further enhance TCM knowledge representation by explicitly encoding the structural relationships among cases, symptom elements, and syndromes. PaSIG achieved the best performance within this category (83.25% accuracy, 83.23% F1-score, 83.20% recall, 83.48% precision), illustrating that incorporating pre-trained semantic interaction effectively strengthens representation learning in text-graph structures.

Our proposed DC-TSCM achieved the best overall performance across all evaluation metrics: accuracy (89.19%), F1-score (89.30%), recall (89.47%), and precision (90.13%). Compared with the current mainstream TCM syndrome classification model CCSD, DC-TSCM improved accuracy by approximately 6.77%. It also outperformed the best baseline model PaSIG by 5.94%. The double asterisks (**) following DC-TSCM metrics indicate statistically significant improvements over the best baseline model, as verified by a two-tailed paired t-test at the 0.01 significance level. These substantial gains can be attributed to the model’s dual-channel architecture, which integrates the differentiation principles of TCM diagnosis into its design. By jointly leveraging semantic representations from textual and graph modalities, DC-TSCM effectively captures contextual prescription semantics and structural relationships among TCM entities. It achieves more comprehensive and robust syndrome classification.

Ablation experiments

In this section, in order to clarify the role of each submodule and specific framework combination in DC-TSCM, we referenced prevalent TCM syndrome classification frameworks (Chen et al., 2024; Hu et al., 2022; Liu et al., 2025, 2020; Teng et al., 2023; Zhao et al., 2022). We conducted ablation studies under identical data splits and hyperparameter settings, and designed nine variants:

• Text-only: Completely remove the graph channel and keep only the text channel.

• Graph-only: Completely remove the text channel and keep only the graph channel.

• R-GAT: Keep the GraphSAGE branch but remove the GAT branch.

• R-SAGE: Keep the GAT branch but remove the GraphSAGE branch.

• R-GFL: Replace TDAF with feature concatenation followed by a fully connected layer.

• TC-G: TextCNN-BiLSTM layer is changed to use only TextCNN.

• LR-G: TextCNN-BiLSTM layer is changed to use LSTM-RCNN.

• CBL-G: TextCNN-BiLSTM layer is changed to use CNN-BiLSTM.

• T-MGCN: Graph feature extraction layer is changed to use only multi-graph neural network.

As shown in Table 5, text-only and graph-only achieved precision around 0.83, a modest gain over traditional baselines. The R-GAT and R-SAGE variants improved accuracy by approximately 4–5% relative to single-channel models but remain 1.6–1.7% below full DC-TSCM. This result confirms the complementary advantages of GAT in capturing local neighbor information and GraphSAGE in modeling global graph structure in graph channels. When TDAF is replaced by naive concatenation and a fully connected layer, accuracy declines to 0.8202. It underscores TDAF’s effectiveness in dynamically weighting clinical description and physique detection features in line with the TCM “observation, auscultation, inquiry, and pulse feeling” syndrome differentiation principle. Among text-channel variants, TCNN-G, LR-G, and CBL-G underperformed relative to DC-TSCM, further validating the superiority of the TextCNN-BiLSTM combination for capturing TCM textual logic. The T-MGCN variant, in which the graph feature extraction layer is replaced by a multi-graph convolutional network, also performed worse than DC-TSCM. It demonstrates that the combination of GAT and GraphSAGE better captures the complex and multidimensional semantics involved in TCM structural relationship modeling. Collectively, each submodule of DC-TSCM improves the ability to discriminate and generalize complex symptoms in TCM.

Visualization analysis

To further evaluate the classification ability of the DC-TSCM, we conducted a visual analysis of syndrome–symptom co-occurrence patterns, the syndrome multi-classification confusion matrix, and the ROC curves in different syndromes.

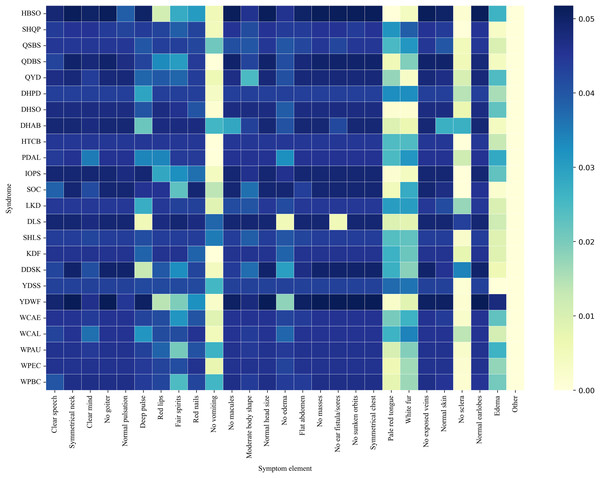
Figure 8 presents a co-occurrence heatmap illustrating the associations between syndromes and representative symptom elements. The color intensity reflects the degree of co-occurrence, with darker colors indicating higher frequencies. Notably, Yang deficiency with water flooding (YDWF) highly co-occurred with symptoms such as Edema and Deep pulse. Wind-cold attacking the external (WCAE) and wind-cold attacking the lung (WCAL) displayed strong associational patterns with white fur and pale red tongue. Another noticeable pattern was that the “No sclera” element exhibited a relatively high co-occurrence frequency with disharmony of liver and stomach (DLS), while showing very low or nearly zero co-occurrence with most other syndromes.

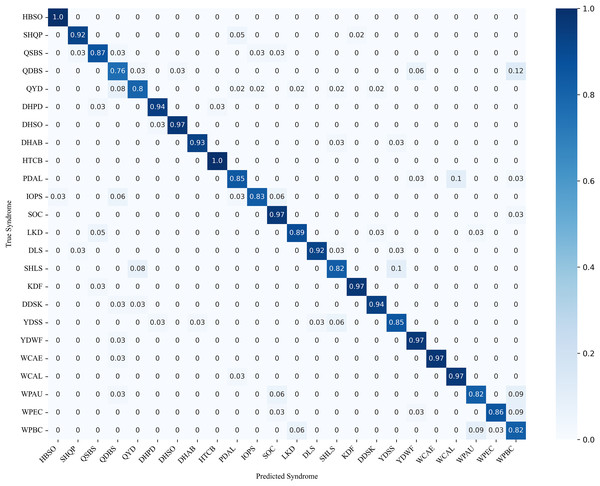
Figure 9 illustrates the confusion matrix of syndrome classification, showing the predictive performance of DC-TSCM across different syndromes. Overall, the model achieved high predictive accuracy, with heart blood stasis obstruction (HBSO) and heat toxin congestion and binding (HTCB) exhibiting the highest correct-classification rates. However, it was also found that some syndromes such as qi deficiency with blood stasis (QDBS) were easily misclassified as wind and phlegm blocking collaterals (WPBC), with a probability of 12%. Phlegm and dampness accumulating in the lung (PDAL) also had a certain probability of being misclassified as wind and phlegm attacking the upper (WPAU). These results demonstrate that the proposed model effectively differentiates between most syndromes in the multi-class classification task.

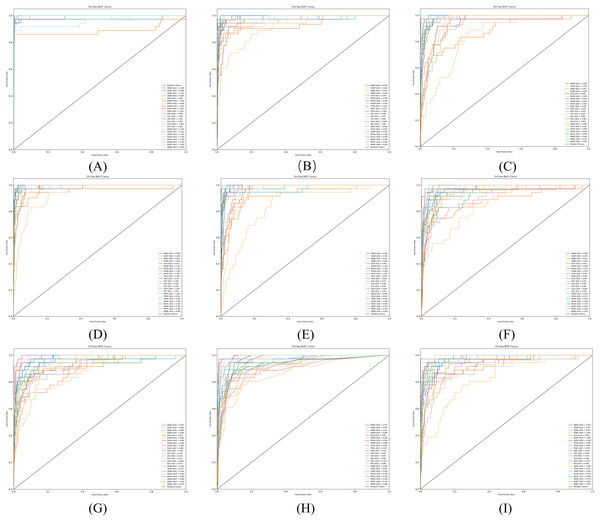
Figure 10 shows that the proposed DC-TSCM demonstrates outstanding discriminative performance on a 24-class TCM syndrome multi-classification task. The AUC ranges from 0.5 to 1.0, with higher values indicating superior classification performance of the model. In the Fig. 10A, QDBS had an AUC of 0.89, the lowest among all syndromes. WPBC achieved an AUC of 0.96, slightly lower than most categories. The ROC curves of the remaining 22 syndromes closely approached the top-left corner, with the highest AUC reached 1.00. Collectively, DC-TSCM exhibits robust discriminative capability, underscoring its robustness in multi-class syndrome classification tasks.