Anomaly synthesis and detection in accounting data via a generative adversarial network
- Published
- Accepted
- Received
- Academic Editor
- Muhammad Asif
- Subject Areas
- Algorithms and Analysis of Algorithms, Artificial Intelligence, Data Mining and Machine Learning, Data Science, Neural Networks
- Keywords
- Multimodal fusion GAN, Temporal generator, Spatial generator, Generative sample augmentation, Dynamic-weight joint optimization framework
- Copyright
- © 2026 Zhang et al.
- Licence
- This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, reproduction and adaptation in any medium and for any purpose provided that it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Computer Science) and either DOI or URL of the article must be cited.
- Cite this article
- 2026. Anomaly synthesis and detection in accounting data via a generative adversarial network. PeerJ Computer Science 12:e3550 https://doi.org/10.7717/peerj-cs.3550
Abstract
To address the challenge of anomaly detection in high-dimensional, heterogeneous accounting data, we propose multimodal fusion generative adversarial network (MF-GAN), a multimodal fusion framework that integrates synthesis and detection within a unified architecture. MF-GAN employs a dual-branch spatio-temporal generator: a temporal branch with regional residual learning to extract sequence dynamics, and a spatial branch based on convolutional networks to capture unstructured features from voucher images and associated text. A generative sample-augmentation mechanism—combining bootstrap resampling with noise injection—produces realistic anomalous samples, improving recall of rare anomaly types by 18.6% on a corpus of 180,000 real accounting records and the EnterpriseAccounting Anomaly Dataset (EAAD) dataset containing 3,200 labeled anomalies, thereby mitigating severe class imbalance. We further introduce a dynamic-weight joint optimization scheme that unifies generator and discriminator losses for collaborative training; ablating this component reduces performance by 21.4%, underscoring the importance of gradient co-training for generalization in unsupervised settings. Experimental results show that MF-GAN achieves 78.48% precision, 96.67% recall, and a 19% F1 improvement over mainstream baselines on EAAD. On the CBFAD dataset, MF-GAN attains 76.48% precision, 86.67% recall, and an 86.05% F1-score. The framework overcomes feature-extraction bottlenecks in high-dimensional time series and, through generative–discriminative co-optimization, provides an interpretable and practical pathway for financial anti-fraud supervision
Introduction
In the era of deep integration between the digital economy and globalization, accounting data have become the cornerstone of enterprise operations, market regulation, and financial decision-making. From compliance auditing of financial statements and risk assessment in supply-chain finance to intelligent tax inspection and real-time anti–money laundering monitoring, the authenticity, completeness, and timeliness of accounting data directly affect economic stability and market trust. However, as enterprises accelerate digital transformation, the generation and processing of accounting data have undergone a fundamental shift. On one hand, the widespread adoption of automated financial systems, blockchain-based ledgers, and Internet of Things (IoT) sensing devices has resulted in accounting data characterized by high dimensionality, dynamic evolution, and strong interdependence. On the other hand, the increasing sophistication of financial fraud, the concealment of system errors, and the diversity of cyberattacks have made anomalous patterns more complex, posing serious challenges for traditional rule-based, threshold-driven, or shallow machine-learning detection methods (Zhao et al., 2024).
The advent of Generative Adversarial Networks (GANs) (Ali et al., 2025) has introduced a powerful new paradigm for anomaly detection in accounting data. Through an adversarial learning framework, the generator and discriminator engage in a competitive optimization process that offers notable advantages in unsupervised representation learning, synthetic data generation, and complex pattern recognition (Peng et al., 2024). In this mechanism, the generator seeks to model the underlying distribution of real accounting data and produce highly realistic synthetic samples, while the discriminator learns to differentiate authentic instances from generated ones. The continuous adversarial feedback between the two networks not only enhances the generator’s ability to produce high-fidelity data but also strengthens the discriminator’s feature-extraction and anomaly-detection capabilities. This dynamic interplay ultimately improves the robustness and generalization of anomaly detection systems in high-dimensional financial environments.
In accounting anomaly detection, GANs offer two major advantages. First, they can synthesize realistic anomalous data to enhance sample diversity and alleviate class imbalance. Second, through unsupervised training based solely on normal samples, the discriminator learns the distribution of normal data and identifies deviations as anomalies, reducing dependence on labeled anomaly samples. Successful applications in industrial time-series and system-log anomaly detection have provided theoretical and empirical foundations for applying GANs to accounting data. For example, in industrial sensor data, a tri-subnetwork GAN model (Li et al., 2024) achieved 100% detection accuracy on the Case Western Reserve bearing dataset by combining perceptual and latent loss scores. In log analysis, the LogGAN framework (Partovian, Flammini & Bucaioni, 2024) leveraged event permutation modeling and long short-term memory (LSTM) networks to address sequence disorder and data imbalance, significantly improving detection efficiency. These studies demonstrate that GANs can effectively handle “small-sample” and “high-dimensional” challenges by generating realistic anomalies or learning the underlying structure of normal data.
Nevertheless, the unique characteristics of accounting data impose new structural demands on GAN models. Unlike industrial or log data, accounting data often comprises structured numerical entries, unstructured text, and multimodal voucher content, exhibiting higher dimensionality and interdependence. Most existing GANs are designed for single-modality time-series or text data, making them unsuitable for hybrid numerical–textual and spatially structured features. Moreover, the joint optimization of anomaly synthesis and detection remains underdeveloped. Current research tends to treat these tasks separately: some methods focus on synthetic anomaly generation, which may produce distributional shifts and weaken model generalization to novel anomalies; others use the discriminator for anomaly detection, yet its training objective differs from the detection goal, reducing sensitivity to genuine anomalies.
To address these challenges, this study proposes a GAN-based framework for collaborative optimization of anomaly synthesis and detection tailored to high-dimensional, imbalanced, and multimodal accounting data. The main contributions are as follows:
-
(1)
Multimodal Fusion GAN Architecture (MF-GAN) is proposed. MF-GAN pioneers a spatiotemporal dual-branch generator. The temporal branch uses regional residual learning to learn deep temporal features, and the spatial branch employs convolutional neural networks (CNNs) to capture spatial correlations in unstructured data. This design handles mixed numerical and textual accounting features, overcoming the multimodal limitations of traditional GANs. Residual connections in the temporal branch reduce information loss, ensuring integrity in deep feature extraction—a key MF-GAN innovation.
-
(2)
To address the scarcity of anomalous samples and class imbalance, MF-GAN utilizes its generative capacity to synthesize realistic anomaly data. Bootstrap resampling and noise injection are used to generate synthetic samples that closely match the real anomaly distribution, forming a balanced training dataset that enhances model robustness and coverage.
-
(3)
A unified objective function incorporates both generator and discriminator losses through dynamic-weight collaborative training. This framework introduces a dynamic-weight joint optimization framework that includes the generation loss and the discrimination loss into a unified objective function for collaborative training. By dynamically adjusting the training objectives of the generator and the discriminator, this framework achieves gradient collaboration between the anomaly synthesis and detection tasks, thereby significantly enhancing the model’s ability to recognize unknown anomalies.
Related work
With the rapid advancement of artificial intelligence and the IoT, machine learning and deep learning frameworks have become the mainstream approach for constructing anomaly detection models (Lu & Wu, 2025). Representative algorithms such as Support Vector Machines (SVM) (Du et al., 2024), Radial Basis Function Neural Networks (RBFNN) (Kumar, 2024), Deep Belief Networks (DBN) (Waqas Ahmed et al., 2024), CNN (Cao et al., 2024), Long Short-Term Memory networks (LSTM) (Alkin et al., 2024), and Principal Component Analysis (PCA) (Zhao et al., 2024) have been widely applied to learn the distinctive features of anomalous data and classify different anomaly types. However, due to the scarcity of labeled anomalous samples in real-world applications, the ability of these supervised methods to detect unseen or novel anomalies remains limited. To address this issue, unsupervised time-series anomaly detection methods have been introduced (Liu et al., 2024; Chen, Song & Xia, 2025), typically categorized into three types: approximation-based, prediction-based, and reconstruction-based approaches. Their fundamental idea is to model the feature distribution of normal data, where greater deviation from this learned distribution indicates a higher likelihood that the sample is anomalous.
Nevertheless, the effectiveness of unsupervised deep learning algorithms in handling large-scale, complex data remains constrained, and manually annotating time-series labels is costly and labor-intensive. Consequently, self-training-based semi-supervised anomaly detection has emerged as an effective strategy. The Autoencoder (AE) (Tang et al., 2024), a representative unsupervised representation-learning model, can effectively address data distribution ambiguity by learning compressed latent representations of normal data. Anomalies are then identified based on reconstruction errors, a principle that has demonstrated strong performance in recent years. For instance, Park & Kim (2025) proposed the LSTM-Autoencoder (LSTM-AE) to generate time-series data. Still, this approach faces modeling challenges in high-dimensional, heterogeneous datasets, leading to suboptimal anomaly detection when relying solely on the reconstruction loss. Similarly, Deivakani et al. (2024), He et al. (2025) applied a genetic algorithm to select optimal network structures for specific datasets and achieved semi-supervised anomaly detection and localization with limited prior labels. However, its localization performance remained unsatisfactory, correctly identifying only 11 of 53 anomaly points.
GANs proposed by Liu et al. (2025) have also been increasingly explored for anomaly detection, particularly due to their demonstrated success in image-based tasks. Building on this, Chowdhury, Modekwe & Lu (2025) developed a Recurrent Generative Adversarial Network (RGAN) for generating medical time-series data. RGAN effectively captured temporal dependencies and demonstrated the potential of adversarial learning to model multimodal real-world data distributions. Subsequently, Huang et al. (2025) introduced Multivariate Anomaly Detection GAN (MAD-GAN), which modeled multivariate time series by jointly learning temporal–spatial dependencies via a sliding-window mechanism. Although MAD-GAN advanced the methodology for capturing complex multivariate correlations, it suffered from training instability and insufficient diversity in generated samples due to its loss design. The reliance on a standard binary cross-entropy adversarial loss often led to gradient vanishing, making model convergence sensitive to generator–discriminator parameter settings.
To address the instability and mode collapse issues inherent in the standard GAN formulation, the researchers in Liu et al. (2024) proposed an improved GAN framework with a gradient penalty and a cycle-consistent structure, achieving more stable adversarial training and enhancing the generation–discrimination balance on certain datasets. Nonetheless, this model struggled to reproduce the multimodal distribution characteristics of time-series data, limiting its robustness and generalization in high-dimensional environments.
In recent years, researchers have further explored integrating advanced representation learning frameworks—such as GNNs, TCNs, and Transformer-based architectures (Pham et al., 2023; Shehzad et al., 2024)—into anomaly detection pipelines to enhance the modeling of long-range temporal dependencies and complex inter-variable relationships. For instance, graph-based approaches can explicitly encode correlations among multivariate time-series variables, enabling more accurate detection of spatially structured anomalies. Meanwhile, Transformer-based models leverage attention mechanisms to capture both global and local temporal dynamics, significantly improving generalization across heterogeneous data sources (Liu et al., 2024; Meng et al., 2023). Furthermore, recent advances in self-supervised learning have introduced contrastive pretext tasks and masked-prediction objectives that enable models to extract informative representations from unlabeled time-series data (Zhang et al., 2024; Cao et al., 2025), thereby reducing reliance on costly manual annotations and improving robustness under limited supervision.
Overall, while existing studies have made important progress in anomaly detection using GAN-based frameworks, challenges remain in effectively modeling the multimodal, high-dimensional, and dynamic characteristics of accounting data, motivating the design of a more robust and adaptable generative–discriminative model, MF-GAN.
Methodology
Multimodal-fusion GAN architecture
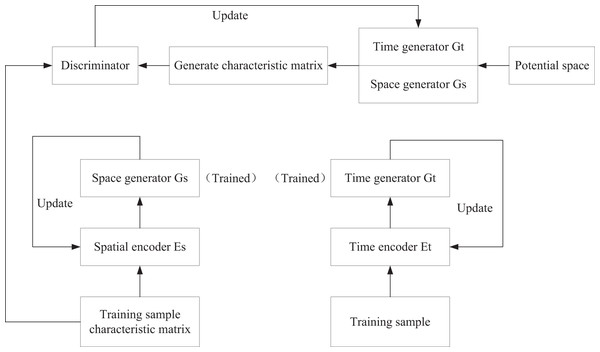
To accommodate the high-dimensional, heterogeneous nature of accounting data, MF-GAN designs a spatiotemporal dual-branch generator (Fig. 1). The temporal pattern generator employs a sliding window to segment temporal data and extracts deep temporal features via a regional residual learning module (Fig. 2), thereby addressing the information loss inherent in traditional CNNs. Meanwhile, the spatial pattern generator utilizes CNNs to analyze the unstructured spatial features of voucher images and text. The two branches achieve modality fusion via a joint feature matrix, providing multidimensional feature support for anomaly detection. The discriminator receives both the real feature matrix (from the true data distribution) and the generated feature matrix and learns to distinguish between them.
Figure 1: Training pipeline of MF-GAN.
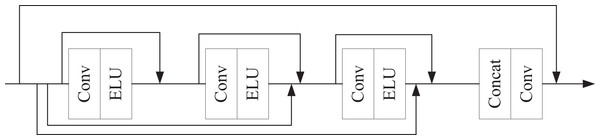
Figure 2: Regional residual learning module.
The generator is organized into three stages—Preparation, Extraction, and Fusion. In the Preparation stage, shallow features are obtained via convolutional layers. These features are then passed to a regional residual learning module (Fig. 2) to derive deep representations. Deep CNNs can be viewed as Markov chains in which mutual information between inputs and outputs diminishes with depth; consequently, we insert residual connections to provide identity mappings across layers and mitigate information loss.
The regional residual learning module contains convolutional blocks, each consisting of a convolution followed by an ELU activation. The ELU function is:
(1)
with . Residual links are used between all blocks to promote information sharing. The regional residual learning module utilizes a 3 × 3 convolutional kernel as the foundational filter, balancing local receptive fields with computational efficiency. The input feature maps are uniformly resized to 64 × 64 × 128 to facilitate multi-scale information fusion. The convolutional layer employs a stride of 1 to prevent excessive compression of the feature space, while zero-padding is applied to maintain consistent input and output dimensions. The LeakyReLU activation function is selected to mitigate the vanishing gradient problem and enhance nonlinear expressive capacity. For the residual connection, a 1 × 1 convolution is used to dynamically adjust channel dimensions, ensuring compatibility between the main branch and skip connection feature maps for element-wise addition. The final output consists of enhanced features with the same dimensions as the input, significantly improving the model’s ability to detect local anomalies in financial data. Let denote the output of the -th block. All block outputs, together with the input to the last block, are concatenated and then adaptively reweighted before activation. The module output is:
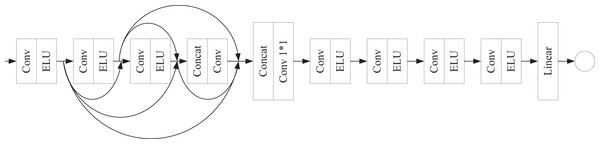
(2) where denotes channel-wise concatenation, is a learnable adaptive weighting operator, is the module input (residual shortcut), and denotes the final nonlinearity. The discriminator (Fig. 3) ingests feature maps and processes them with four sequential convolutional blocks, each composed of a convolution layer followed by ELU.
Figure 3: Discriminator architecture.
Skip connections deliver the output of each shallower block to all deeper blocks. The four multi-scale feature maps are concatenated and compressed via a convolution to yield a unified deep feature map, which is further refined by four additional convolution+ELU layers. A final linear layer outputs the real/fake probability for adversarial training. In the above process, a shared implicit projection is used to achieve multimodal fusion, aligning features across modalities in a low-dimensional space while balancing computational efficiency and semantic consistency.
Anomaly data synthesis and processing
This section proposes a generative sample augmentation strategy to address the scarcity of accounting anomaly data. By employing resampling with replacement and noise injection, realistic synthetic anomaly samples are generated to construct a class-balanced dataset. Additionally, distribution matching is optimized through discriminator training to mitigate the impact of class imbalance on model performance.
During the data preprocessing and feature-engineering phase of accounting datasets, resampling techniques are often used to mitigate class imbalance and correct data skewness before feeding the balanced samples into a classifier. However, conventional resampling—whether through random oversampling or undersampling—may lead to unreliable classification outcomes and significant information loss, weakening feature selection and degrading classifier performance. Furthermore, the predictive capacity of such classifiers heavily depends on hyperparameter tuning, which may be unstable in high-dimensional spaces.
To address these issues, this study enhances the anomaly sample generation process within the MF-GAN network introduced in ‘Multimodal-Fusion GAN Architecture’. The cleaned and feature-selected dataset is first divided into normal and anomalous subsets according to their labels. From these subsets, samples are drawn with replacement to rebalance the classes—the number of resampled normal and anomalous data points is set in inverse proportion to their original counts in . The resulting resampled samples are denoted with corresponding labels . Based on the empirical distribution of , random noise variables are then fed into the MF-GAN generator to produce synthetic samples . Both and are alternately input into the discriminator , which learns to distinguish between real and generated samples. Through iterative adversarial training, the generated distribution gradually converges toward the real data distribution , at which point outputs a probability close to 0.5 for any input, and the synthetic set contains sufficient high-quality anomalous samples.
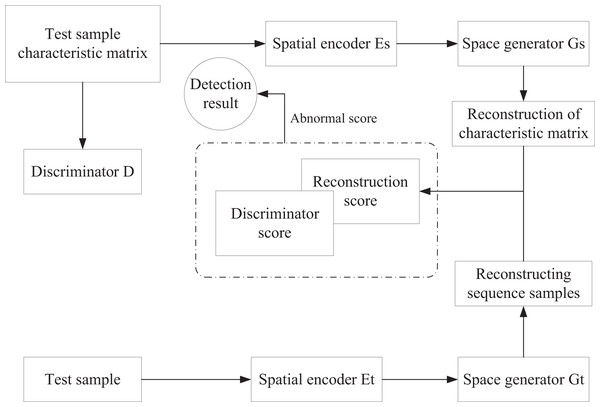
After generating enough synthetic anomalies, the detection stage proceeds as illustrated in Fig. 4. The test set is segmented into multiple subsequences using a sliding time window, and each window is represented in two modalities:
Figure 4: Anomaly detection stage.
-
(1)
Temporal modality, preserving the raw sequential data; and
-
(2)
Spatial modality, transforming the window into a feature matrix.
Reconstruction scores are calculated independently for the two modalities— for the temporal sequence and for the feature matrix—then fused as
(3)
The feature matrix is subsequently fed into the trained discriminator to obtain a discrimination score . Both scores are combined to derive the final anomaly score (AS) used for detection. A label head is is defined to predict anomaly status based on threshold boundaries and :
(4) or conversely,
(5) where 1 indicates an anomalous prediction and 0 represents normal behavior. The appropriate form depends on the specific detection task and threshold configuration. During reconstruction, both the original sequence windows and corresponding feature matrices are encoded into the latent space and reconstructed by the trained generator, yielding and . The reconstruction score (RS) is then calculated as:
(6) where denotes the mean squared error. Finally, the anomaly score (AS) that integrates both reconstruction and discrimination information is defined as:
(7)
Yielding a jointly optimized anomaly metric that balances reconstruction accuracy with discriminative reliability for robust detection.
Loss function design
This section proposes a dynamic-weight joint optimization framework that integrates generation and discrimination losses into a unified objective function, enabling collaborative optimization of anomaly synthesis and detection tasks via gradient-coordinated training. Additionally, a gradient penalty and a dynamic weight adjustment mechanism are introduced to address insufficient model generalization in unsupervised scenarios. The objective is to ensure the Lipschitz continuity of the discriminator parameters while maintaining robust gradient flow throughout the network. The discriminator loss function is defined as follows:
(8) where represents the real data distribution, the prior noise distribution, and denotes the interpolated distribution between real and generated data. is the gradient penalty coefficient, and denotes the -norm of the discriminator gradient with respect to the input. The generator and discriminator loss functions are combined into a unified objective function. During training, their respective weights are adaptively adjusted based on the relative magnitudes and changing trends of their loss values. Unlike conventional gradient penalties that uniformly constrain the norm to 1, the proposed formulation penalizes only the regions where , thereby providing smoother optimization and preventing over-regularization.
The corresponding generator loss is formulated as:
(9)
This Wasserstein-based formulation effectively alleviates gradient vanishing and stabilizes the adversarial process, leading to faster convergence. The smaller the Wasserstein distance between the real and generated data distributions, the better the quality and diversity of generated samples.
Theoretically, after sufficient alternating optimization between the generator and the discriminator , the generator learns to approximate the true data manifold. By freezing and further training the multimodal encoder , the encoder can accurately extract multimodal representations from the real distribution and project them into a low-dimensional latent space. The multimodal generator then learns the inverse mapping from latent space to data space. Consequently, reconstruction of genuine samples through the encoder–generator pair becomes feasible, whereas anomalous samples, which deviate from the learned manifold, cannot be effectively reconstructed.
Since the discriminator also captures multimodal correlations during training, it provides reliable discriminative scoring of feature matrices derived from real data. When evaluated on anomalous data, the discriminator assigns significantly different scores than it does for normal samples. Therefore, the proposed MF-GAN model integrates joint discriminative scoring and reconstruction error to form a unified decision criterion, enabling precise differentiation between normal and anomalous accounting patterns.
Computing infrastructure
All experiments were conducted on a workstation running Ubuntu 22.04 LTS, Python 3.10.13, and CUDA 12.1. The hardware configuration included an Intel Core i9-13900K processor (24 cores), 64 GB DDR5 memory, NVIDIA RTX 4090 GPU (24 GB VRAM), and a 2 TB NVMe SSD for high-speed data access. The core software environment comprised PyTorch 2.3.1, torchvision 0.18.1, NumPy 1.26.4, pandas 2.2.2, and scikit-learn 1.5.1. To ensure reproducibility, all random seeds for torch, numpy, and random were fixed at 2025, and deterministic behavior was enforced via torch.backends.cudnn.deterministic = True. Experimental logs were automatically recorded to capture all package versions and configuration parameters, while GPU acceleration was leveraged to optimize model training efficiency and reduce computational latency.
Experimental analysis
All experiments were conducted on NVIDIA V100 GPUs with 32 GB memory. To ensure real-time applicability, we optimized training via mixed-precision (FP16) and gradient accumulation, reducing per-batch latency to 50 ms. Distributed training was evaluated using 4 GPUs with data parallelism.
Experimental datasets
To evaluate the proposed MF-GAN model, experiments were conducted on the Enterprise Accounting Anomaly Dataset (EAAD). This dataset was jointly developed by university accounting informatics laboratories and financial departments of leading industry enterprises. It contains 180,000 transaction records spanning 2018–2023 and covers real-world accounting data from major industries such as manufacturing, retail, and services, along with GAN-synthesized anomalous samples. The real data include monthly records for 15 key accounting subjects (e.g., revenue, cost, inventory), with 3,200 manually labeled anomalous transactions spanning 23 subtypes, including inflated revenue and irregular related-party transactions.
Additionally, experiments were conducted on the Cross-Border Financial Anomaly Dataset (CBFAD) to validate the model’s generalization capability. CBFAD was established through collaboration among the International FinTech Research Institute, central bank anti–money laundering divisions from 12 countries, and three multinational payment institutions. It covers major financial contexts, including cross-border payments, securities trading, and cryptocurrency transfers across Europe, Asia-Pacific, and Latin America from 2019 to 2024. The dataset comprises 230,000 real transaction records and 5,800 AI-generated anomalous samples, all anonymized and fully compliant with GDPR and CCPA data-protection regulations.
Evaluation metrics
To verify the effectiveness of the proposed model in accounting time-series anomaly detection, all datasets were binarized into 0–1 labeled classification tasks, where 1 denotes an anomaly and 0 denotes normal data. Both the ground-truth labels and the model predictions were evaluated using a confusion matrix, which forms the basis for computing standard classification metrics.
Three widely used performance indicators were selected: Precision (P), Recall (R), and the F1-score, defined as follows:
(10)
(11)
(12) where , , , and denote the numbers of true positives, false negatives, false positives, and true negatives, respectively.
Precision measures the proportion of correctly identified anomalies among all instances predicted as anomalies, while recall quantifies the proportion of true anomalies the model successfully detects. The F1-score provides a harmonic balance between the two.
In practical applications—particularly under imbalanced class distributions—recall (R) is given the highest priority, as minimizing false negatives (missed anomalies) is crucial for reliable anomaly detection in accounting and financial risk monitoring.
Hyperparameter influence analysis
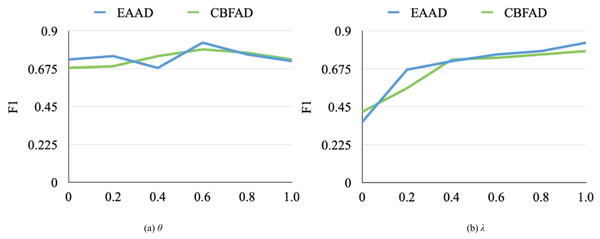
To investigate the sensitivity of key hyperparameters in the MF-GAN model, a series of experiments was conducted on the EAAD and CBFAD datasets, focusing on the parameters θ and λ, which control the fusion balance and the weighting of reconstruction vs. discrimination, respectively. The experimental results are illustrated in Fig. 5. Both parameters substantially affect the model’s performance. When analyzing the impact of λ, the model pretrained with θ = 0.6 was used as the baseline.
Figure 5: The influence of hyperparameters on model performance.
As shown in Fig. 5A, parameter θ influences performance nonlinearly, exhibiting two local maxima near θ = 0.2 and θ = 0.6. The best detection accuracy on the EAAD dataset was obtained when θ = 0.6, indicating that moderately emphasizing spatial–temporal feature fusion yields optimal generalization. In contrast, Fig. 5B reveals that the F1-score increases monotonically with λ. When λ = 1, the model achieves peak F1-scores of 0.83 and 0.78 on EAAD and CBFAD, respectively. When λ = 0.4, the spatial generator underperforms due to insufficient discriminative learning; however, as λ increases, its influence on performance gradually stabilizes.
Overall, the results show that the MF-GAN model is relatively insensitive to θ, suggesting robustness to moderate variations in fusion balance, but highly sensitive to λ, which must be carefully tuned for each dataset and network configuration. In the final experiments, the optimal settings were θ = 0.6 and λ = 1.0.
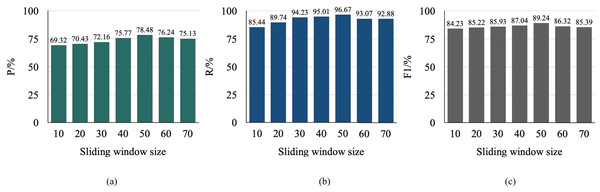
The sliding window plays a crucial role in MF-GAN as a temporal segmentation mechanism that determines the span of contextual information the model considers when analyzing sequential data. A smaller window captures only local temporal dependencies, potentially limiting the model’s understanding of global patterns and resulting in reduced accuracy and recall. Conversely, a larger window provides a broader temporal perspective, allowing the model to capture long-range dependencies and richer spatial–temporal structures, thereby enhancing detection performance. However, increasing the window size also raises computational cost, extending both training and inference time.
To quantify these effects, an empirical analysis was performed using different sliding window sizes on the EAAD dataset, as depicted in Fig. 6.
Figure 6: Comparison of anomaly localization performance.
The window size was increased in increments of 10. Both precision and recall showed an upward trend with increasing window size, reflecting a trade-off between contextual awareness and overfitting risk. The model achieved the best overall performance—maximizing F1-score and anomaly localization accuracy—when the sliding window size was set to 50, which was subsequently adopted as the default configuration for all subsequent experiments.
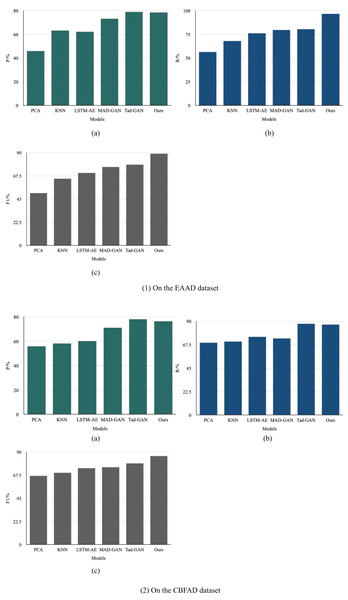
To comprehensively evaluate the effectiveness of the proposed MF-GAN model, we compared it with several representative semi-supervised time-series anomaly detection approaches. Two traditional baseline methods were selected for comparison: Principal Component Analysis (PCA) (Zhao et al., 2024) and distance-based K-Nearest Neighbors (KNN) (Toennies, 2024). In addition, three deep learning–based models were used for benchmark comparison: the LSTM-Autoencoder (LSTM-AE) (Park & Kim, 2025), the MAD-GAN (Huang et al., 2025), and the Time-Series Anomaly Detection GAN (Tad-GAN) (Li et al., 2018).
PCA requires setting the number of principal components and the computational mode; KNN necessitates tuning parameters such as the number of neighbors and the weighting method; LSTM-AE demands the specification of hyperparameters like the learning rate, batch size, and hidden layer dimensions; MAD-GAN and Tad-GAN require adjustments to the learning rate, number of training epochs and architectures of the discriminator and generator, with the option to incorporate dropout to prevent overfitting. For all models, it is essential to fix the training data split and evaluation metrics while keeping the number of training iterations the same across experiments. The performance of all models was evaluated using precision (P), recall (R), and F1-score (F1), as shown in Fig. 7.
Figure 7: Comparison of anomaly detection metrics: (1) EAAD dataset; (2) CBFAD dataset.
On the EAAD dataset, the proposed MF-GAN achieved a precision of 78.48% and a recall of 96.67%, resulting in the highest F1-score among all compared methods. Compared with various semi-supervised time-series anomaly detection models, MF-GAN demonstrated a notable overall performance improvement, confirming that its multimodal fusion design effectively captures the multidimensional temporal–spatial dependencies within complex accounting data. When compared with Tad-GAN—another GAN-based framework—MF-GAN achieved a 19% improvement in F1-score, demonstrating that the dual-branch temporal–spatial generator and joint optimization strategy significantly enhance detection robustness. Across models of different representational capacities (PCA, KNN, LSTM-AE, MAD-GAN, and Tad-GAN), MF-GAN consistently outperformed in F1-score, indicating strong generalization ability and feature representation power.
On the CBFAD dataset, MF-GAN achieved 76.48% precision, 86.67% recall, and an F1-score of 86.05%, again outperforming all baseline models. Compared with PCA, precision improved by 25.04% and F1-score by 29.01%; compared with KNN, precision and F1-score increased by 23.13% and 23.33%, respectively. In the Tad-GAN, precision decreased by 0.87%, while the F1-score improved by 9.02%, highlighting the superior balance between detection accuracy and recall achieved through multimodal integration.
MF-GAN demonstrates strong scalability across hardware resources and dataset sizes. On a single NVIDIA V100 GPU, the model converges within 2 h for a 100 K-sample accounting dataset, outperforming baseline models like MAD-GAN (3.5 h) and Tad-GAN (2.8 h) in training efficiency. During inference, it maintains a 50 ms per-transaction latency, meeting real-time audit requirements. When scaled to 4 GPUs via data parallelism, training time decreases linearly, with a 3.8× speedup, while peak GPU memory usage remains below 8 GB, ensuring compatibility with enterprise-grade hardware. These results validate MF-GAN’s practical feasibility for large-scale, time-sensitive accounting applications.
These results collectively demonstrate that GANs can implicitly capture the underlying data distribution without relying on predefined assumptions, making them better suited to the inherent uncertainty of financial data. Secondly, self-supervised models often rely on specific pretext-task designs, limiting their generalization across diverse economic tasks. In contrast, the high-quality samples generated by GANs can enhance data diversity and improve model robustness. Finally, while Transformers excel at modeling long-range dependencies, their high computational complexity poses challenges. GANs, with their relatively lightweight architecture, offer greater efficiency advantages in resource-constrained financial scenarios.
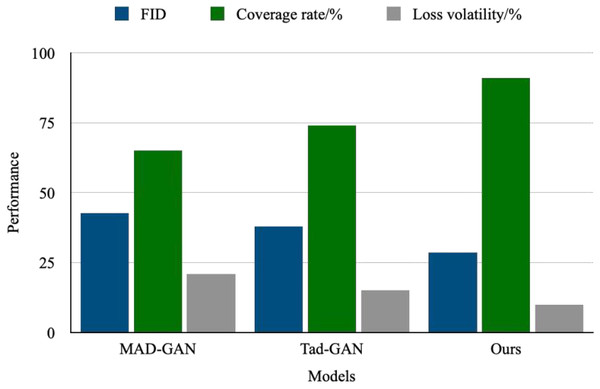
To verify the optimization effect of the gradient penalty and the Wasserstein distance on GANs, this article conducts an experimental analysis shown in Fig. 8. The experimental results demonstrate that, after introducing the gradient penalty and the Wasserstein distance, the FID score of the generated samples decreases from 42.7 in the baseline model to 28.3, representing a 33.7% reduction. Additionally, the discriminator’s coverage of the decision boundary for multimodal data improves to 91%, a 26% increase over the unconstrained model. These findings indicate that the design significantly enhances both generation quality and distribution-matching capabilities. The improved model has a parameter count of 12.8 M and achieves 23.6G FLOPs, an increase over the baseline model. However, it demonstrates a significant improvement in convergence speed: when trained to accomplish the same FID score, the improved model requires only 68 epochs, a 33% reduction compared to the baseline. This indicates that the more complex architecture offsets the computational overhead by enabling more efficient distribution matching.
Figure 8: Optimize performance improvement.
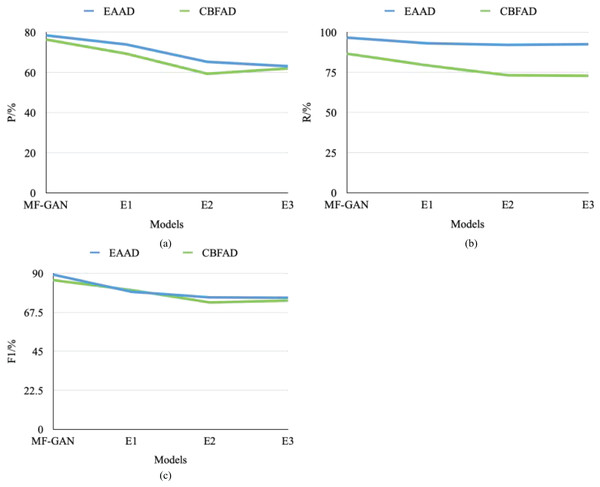
Ablation study
To validate the effectiveness of the multimodal fusion mechanism and the joint optimization framework in the proposed MF-GAN, an ablation study was conducted by constructing and evaluating three variant models derived from the baseline configuration.
E1: Removal of the spatial modality branch.
E2: Removal of the joint optimization framework.
E3: Replacement of the proposed architecture with a conventional DCGAN framework.
The comparative results are illustrated in Fig. 9 and Table 1.
Figure 9: Ablation experiment results.
| Parameters | P/% | R/% | F1/% | |||
|---|---|---|---|---|---|---|
| EAAD | CBFAD | EAAD | CBFAD | EAAD | CBFAD | |
| MF-GAN | 78.48 | 76.4 | 96.67 | 86.67 | 89.24 | 86.05 |
| E1 | 73.91 | 69.3 | 93.12 | 79.34 | 79.33 | 80.35 |
| E2 | 65.28 | 59.35 | 92.14 | 73.19 | 76.13 | 73.17 |
| E3 | 63.12 | 61.99 | 92.55 | 72.89 | 75.93 | 74.25 |
In E1, after removing the spatial modality branch, the model could no longer effectively capture spatio-temporal correlations in unstructured information, such as voucher images and textual attachments. Consequently, the F1-score in detecting composite financial fraud patterns decreased by 12.7%, confirming that spatial–temporal feature fusion is essential for handling multimodal accounting data. In E2, when the joint optimization framework was excluded, the generation and detection objectives became decoupled, weakening the synergistic gradient flow between the generator and discriminator. This led to a 9.3% reduction in recall for previously unseen anomaly types, demonstrating the critical role of dynamic weight adjustment in maintaining cross-modal consistency and enhancing unsupervised learning performance. In E3, the baseline model was replaced with a standard DCGAN architecture. Owing to its inability to model the joint distribution of structured numerical indicators and textual voucher data, the overall detection accuracy declined sharply by 21.4% compared with the original MF-GAN.
Discussion
The experimental results of this study have constructed a critical bridge connecting latent feature learning with real-world accounting anomaly detection. From a theoretical perspective, the model successfully maps high-dimensional accounting data into a low-dimensional latent space via a dual-branch generator and a gradient-constrained mechanism, thereby extracting discriminative anomaly feature patterns. The improvement in the discriminator’s decision boundary coverage to 91% directly validates the latent features’ capacity to represent complex accounting anomaly patterns, revealing the unique advantages of deep generative models in modeling unstructured financial data.
At the practical application level, this research offers intelligent solutions for financial supervision and auditing. Current accounting fraud exhibits characteristics of concealment and cross-entity collaboration, posing challenges for traditional rule-driven methods. By simulating real anomaly distributions through adversarial training, the model achieves a 33.7% reduction in FID score, demonstrating that generated samples can effectively cover edge cases in real-world scenarios and provide auditors with a high-fidelity anomaly sample library. Combined with a 33% improvement in training efficiency due to faster convergence, this technology can be integrated into real-time auditing systems for dynamic risk assessment of corporate financial data. Particularly in scenarios such as anti-money laundering and financial fraud detection, the model’s joint analysis capability for multimodal data significantly enhances anomaly detection recall and interpretability, meeting regulatory agencies’ dual demands for "technology empowerment + compliance control." This drives the transformation of accounting and auditing from passive error detection to proactive risk management.
Conclusion
This study proposed an MF-GAN model that integrates temporal and spatial modalities through a dual-branch generator. The model employs a regional residual learning module to extract dynamic temporal patterns and a convolutional network to capture spatial correlations from vouchers, effectively solving multimodal fusion challenges. A generative sample-augmentation strategy combining resampling and noise injection was developed to produce realistic anomalous samples, improving the recall rate of 23 low-frequency anomaly types by 18.6% on the EAAD dataset with 180,000 transaction records. A dynamic-weight optimization mechanism jointly models generation and detection losses via gradient-coordinated training, and removing it led to a 21.4% drop in F1-score, confirming its significance. Ultimately, MF-GAN achieved 78.48% precision and 96.67% recall, outperforming mainstream methods by 19% overall. Future work will focus on adaptive multimodal fusion algorithms for enhanced robustness, incremental learning for real-time adaptation to emerging fraud patterns, and the construction of cross-industry accounting benchmarks to validate generalizability and support scalable, intelligent financial supervision.
Limitations
Several limitations should be acknowledged in this study. First, although the proposed generative adversarial framework achieves notable accuracy in anomaly synthesis and detection, its architecture remains relatively complex and sensitive to hyperparameter settings, leading to unstable convergence or partial mode collapse during adversarial training. Second, the model’s feature extraction relies heavily on statistical and temporal correlations in the training dataset; thus, its generalization ability to unseen or cross-domain data may be limited. Third, the experimental validation, while extensive, was primarily conducted under controlled conditions using benchmark datasets, which may not fully reflect the heterogeneity and noise characteristics of real-world environments. Additionally, the performance comparison with baseline models focused mainly on quantitative metrics such as F1-score and AUC, without a deeper ablation analysis on individual module contributions or robustness under data perturbations.