Membrane computing approach to nurse rostering: enhanced scheduling efficiency with tissue-like P system (TLPS) algorithm
- Published
- Accepted
- Received
- Academic Editor
- Siddhartha Bhattacharyya
- Subject Areas
- Human-Computer Interaction, Algorithms and Analysis of Algorithms, Artificial Intelligence, Optimization Theory and Computation, Software Engineering
- Keywords
- Nurse rostering problem, Tissue like p system algorithm, Meta-heuristic, Genetic algorithm, Harmony search algorithm
- Copyright
- © 2026 Sharif and Agoyi
- Licence
- This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, reproduction and adaptation in any medium and for any purpose provided that it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Computer Science) and either DOI or URL of the article must be cited.
- Cite this article
- 2026. Membrane computing approach to nurse rostering: enhanced scheduling efficiency with tissue-like P system (TLPS) algorithm. PeerJ Computer Science 12:e3492 https://doi.org/10.7717/peerj-cs.3492
Abstract
Healthcare facilities require a significant amount of resources and the effective management of these resources to ensure efficient healthcare delivery. Rostering and scheduling of nurse shifts in healthcare facilities is a significant challenge facing healthcare facilities across the globe. This work investigates the application of the tissue-like P systems (TLPS) algorithm to effectively solve complex NRP. Conventional solutions to nurse rostering problems (NRP) are continually challenged by factors such as suboptimal schedules stemming from challenges such as comprehensive and competing constraints satisfaction. The proposed NRP algorithm is based on the principles of membrane computing, which uses the principles of object shifts between membranes using communicated rules. The proposed approach was designed, implemented, and applied to the National University of Malaysia Medical Center’s nurse scheduling context for a period of 14 days. Results of the experiments carried out show a significant improvement in scheduling adequacy with adherence to all nurse rostering requirements. Results of the experiment demonstrate reduced total penalty costs involved in the use of conventional NRP algorithms. Experimental results also show that the proposed TLPS produces better quality rosters compared with other algorithms, such as the genetic algorithm (GA) and harmony search algorithm (HSA) that have been previously proposed for the National University of Malaysia Medical Center’s dataset. This study presents a robust, scalable, and feasible solution to NRP that supports adequate healthcare management.
Introduction
Healthcare facilities and hospitals generally consist of large wards which are staffed with employees for different tasks, and for different hours of the day (Villarreal et al., 2023). This makes the requirement of staffing very diverse and requires compounded specifications to ensure schedules are adequately created and efficiently meet the requirements of optimal healthcare delivery in the hospitals (Almalawi et al., 2023). Creation of work schedules are complex tasks which require intricate details, and they are particularly challenging in the context of hospitals (Sharma et al., 2023). Hospital staffing and scheduling is predominantly solved using manual or conventional approaches, where roasters are created for the staff and the employees involved in the schedules contribute to its development (O’Connell et al., 2024). However, this manual approach towards scheduling is time consuming, and often leads to suboptimal outcomes in ensuring adequate healthcare delivery (Klyve, Senthooran & Wallace, 2023).
Nurses are considered one of the most critical resources of a hospital or healthcare facility, they affect both the overall resource requirement of a hospital and the quality of healthcare provided (Cavanagh et al., 2024). Hence, rostering of nurses is a critical operation that requires adequate planning and execution to ensure good healthcare delivery in hospitals. Rostering of nurses or nurse rostering problem (NRP) is generally regarded as a NP-hard problem, this implies its challenge as a computationally intractable problem to be solved by deterministic approaches (Ceschia et al., 2023). Nurse rosters must be able to account for what are considered as hard constraints; essential factors for feasible schedule, and soft constraints; preferable but not essential for healthcare delivery (Chen, De Causmaecker & Dou, 2023; Hadwan & Ayob, 2009). Both hard and soft constraints of nurse rostering are inherently complex and resource competing, and finding a single fit all nurse rostering solution continues to be challenged by this (den Hartog, Hoogeveen & van der Zanden, 2023). This challenge has been approached by several studies proposing automated scheduling methods. The proposed methods over the years include mathematical programming (Thomas, 2024), heuristic approaches (Chen, De Causmaecker & Dou, 2023), and meta heuristic approaches (Muklason et al., 2024). Some examples of meta-heuristic algorithms include genetic algorithms (GAs), simulated annealing (SA), tabu search (TS).
Research problem
Management of nurses in hospitals and other kinds of healthcare facilities continue to challenge the delivery of healthcare, particularly in the context of efficient human resources allocation (Wang et al., 2023). NRP is among the most critical challenges of nurse’s management in hospitals, as it is a process which requires distribution of human resources across multiple wards, and time schedules while also adhering to best practices of healthcare delivery (Booker et al., 2024). NRP as a problem is compounded with the need to balance quality of healthcare delivery and also cost or resource efficiency for the delivery (Wynendaele et al., 2025). Manual methods which are often used to solve the NRP challenge are resource inefficient, and often lead to gaps in services delivery and operational costs. Despite the existence of various computational approaches to address the NRP, there remains a need for more effective, adaptable, and scalable solutions that can handle the dynamic and multifaceted nature of hospital environments (Bebien et al., 2024).
Contribution of study
This study seeks to address the gap of NRP by exploring the potential of a novel bio-inspired algorithm. The tissue-like P systems (TLPS), is proposed in this study to optimize nurse rostering, offering a robust solution to this pervasive problem in healthcare management. The complex and NP hard problem challenges of healthcare management are approached using the computational techniques and parallel processing approach of TLPS in this study. The research proposes a novel approach of optimizing hospital nurse scheduling in a manner that considers both hard and soft constraints optimally. The contributions of this study can be outlined as follows:
-
-
The proposed approach of TLPS for NRP adequately factors both hard and soft constraints of NRP.
-
-
The proposed approach shows efficiency in its applications in this study, and also provides scalability and adaptability to resource allocation.
-
-
The study demonstrates the efficiency of bio inspired computing to achieve feasible solutions.
-
-
The study also demonstrates the performance of the TLPS approach for NRP to be more efficient compared to other approaches, such as GA and HAS on UKMMC dataset
Literature review
The complexity of NRP has attracted significant research interest since the 1970s because of the challenges it posed to healthcare management and delivery (Ngoo et al., 2022). However, despite the decades of research and resources invested in it, literature still indicates a significant challenge of NRP on healthcare delivery and management (Goh et al., 2022). NRP is a challenge that can impact other rostering scenarios that have similar requirements as NRP in healthcare management (Hadwan, 2022). Some of the critical factors that contribute to the challenges of NRP are the ever evolving policies and regulations of healthcare management and delivery in different parts of the world (Klyve, Senthooran & Wallace, 2023). Differences in regulations and policies, operational environment, contractual agreements of nurses, and other such factors do not have a single consensus on the most effective in solving the NRP challenge (Evangeline & Angel, 2023).
To deal with NRP, many methods have been presented so far. In this context, many articles have summarized such methods and provided their overview. For instance, ‘A Survey of the Nurse Rostering Solution Methodologies: The State-of-the-Art and Emerging Trends’ have provided a detailed overview, which show different approaches and possible solutions (Ngoo et al., 2022). For examples of these methods: cyclic approach, semi cyclic approach, and non-cyclic approach (Turhan & Bilgen, 2022).
Cyclic rostering approach is a well-structured approach to rostering, the structured characteristics of the approach imposes constraints stemming for structural rigidity (Alkallak & Shaban, 2022; Chen, Dou & De Causmaecker, 2022). However, cyclic rostering is challenged by its inability to accommodate impromptu changes such as increase in staffing demand and absence of staff (Guo & Bard, 2022; Fourati, Smaoui & Kamoun, 2023). Non cyclic approaches great flexibility and accommodate dynamic rostering and management (Anderson et al., 2023), also associated with significant time resource inefficient (Breugem et al., 2023). Optimization methods, such as linear, integer, or mixed integer programming, have been employed to address the nurse scheduling problem in various studies such as Taş, Jabali & Van Woensel (2014). Additionally, goal programming and constraint programming have been utilized in Weng et al. (2018).
In recent years, heuristic and meta-heuristic methods have become increasingly popular because they could find real-life optimal solutions to schedule nurses’ duties, which has been extremely difficult to implement (Thomas, 2024). To solve the NRP, these approaches have been widely applied. Their robustness, as compared to other methods, has been the main reason behind using these approaches. Usually, they can generate reasonable, acceptable, and feasible solutions within a limited time, even when there is a wide range of input data. Their duration to find a solution was very short compared to other approaches. Exact optimization normally needs longer computational time to generate optimal solutions for combinatorial problems. Contrary to that, heuristic approaches generate satisfactory results in a short time, but meta-heuristic processes are more advanced compared to heuristic methods (Ngoo et al., 2022).
Membrane computing P system
Membrane computing P system is a paradigm of computing that is inspired by the functional and architectural characteristics of living cells, they are often referred to as P systems (Păun & Păun, 2006). P systems computing is characterized by the use of inherent parallel and distributed functions which are synonymous with cellular structures of biological membranes (Jiang et al., 2012). The conceptualization of P systems was introduced by Păun (2000). This is based on tissue like P systems the use of multiple single membrane cells which contain sub modules that interact with one another directly using established and open communication channels (Song, Zhang & Pan, 2017; Martín-Vide et al., 2003). P systems have over the years been applied in computational algorithms which include their use in software development, this is among other several biological inspired computing algorithms (Liu et al., 2023). Both theoretical and applications of P systems suggest the systems remain functional and efficient given their diversity in controlling rule applications such as scheduling and rostering (Dong et al., 2023).
P systems are notably efficient in their enhanced parallelism and their ability to function using a distributed approach of multiple functions at a time (Leporati et al., 2023). P systems generate exponential workspaces using a linear time frame which have efficient modular processes working as a system, as is the case of cell membranes (Song, Zhang & Pan, 2017). P systems offer a versatile framework of modeling discrete processes which are characterized by efficient scalability, inherent compartmentalization, programmability, and discrete data handling (Jiang et al., 2012). P systems have seen successful applications in domains of biology, fault diagnosis, fuzzy reasoning, and computational systems (Zhou et al., 2024).
Methodology
This study proposes the use of a TLPS in approaching the NRP challenge of efficiently designing nurse rosters and schedules. The study designs and applies the TLPS approach while also evaluating its performance while considering its adaptability in scenarios of scalability and different nurse rostering cases. The evaluation of the proposed approach focuses on the NRP requirements of a defined schedule, which involves both hard and soft rostering constraints. Where performance evaluation is characterized by the adherence to hard constraints and adequate management of soft constraints
Research case
This study is conducted using the context of the National University of Malaysia Medical Center (UKMMC), the UKMMC is a healthcare facility which staffs over 1,400 nurses (Hadwan et al., 2013). At UKMMC Medical Center, head nurse is responsible to generate the roster for the nurses, s/he spends a lot of time in addition to the effort that are used to generate this roster, next steps provide more details about generating roster for nurses by head nurse at UKM Medical Center:
-
-
Nurses write the request and preference in the request book and submit to the head nurse.
-
-
Head nurse has decision to accept or reject the nurse preference, and then prepare the master plan and initial roster.
-
-
Department of nursing check the roster and also has decision to approve the roster or to ask the head nurse to repair the roster again.
The head nurse serving at each ward starts generating a master plan before s/he fills up the nurses’ request book. Later, the head nurse constructs the initial roster, but while doing so, s/he either accepts or rejects the nurses’ preferences, which are based on the criteria for acceptance. After that, the head nurse needs approval, so s/he sends the initial roster to the nursing department. If the nursing department approves it, it is distributed among the nurses as the final roster; otherwise, it is revised and amended. After that, the head nurse resends it back for approval.
The research is designed to propose an approach which considers the constraints requirements of nurse rostering which has a total of eight hard constraints labeled H1–H8, and five soft constraints labeled S1–S5 as outlined in Table 1. The constraints outlined in Table 1 are requirements set out for best practices of ensuring rostering and scheduling of nurses are both feasible and qualitative. The study also uses the demands of the minimum required number of nurses for each shift schedule in a day to propose the approach in this study. Table 2 outlines the rostering requirements of the UKMMC for each shift of the day and each department as represented in a sub dataset for a given week. The study also considers the required shift patterns of nurses rostering and schedule, where shift patterns are categorized to ensure there is ethical and policy regulation of the number of shifts of nurses to ensure adequate healthcare delivery. There are three categories of shift patterns which are defined as prohibited patterns, undesirable patterns, and desirable patterns. The prohibited patterns are the shift patterns that violate the hard constraints requirements, undesired adhere to hard constraints but do not have efficient use of soft constraints, and desirable adhere to both hard and soft constraints. The three categories of shift patterns are outlined in Table 3.
| Constraint | Description |
|---|---|
| H1 | All shifts must have at least the requested number of nurses. |
| H2 | Nurses cannot work more than one shift per day |
| H3 | The minimum number of days off for each nurse is two days off in the scheduling period. |
| H4 | At least one senior nurse must be scheduled for each shift. |
| H5 | Each nurse should not be scheduled on an isolated day. This constraint presents the minimum number of consecutive days that any nurse should work. This is normally 2 consecutive days for full time nurses. |
| H6 | The maximum working days for each nurse are 12 days for each fourteen days and the minimum are 10 days. |
| H7 | The maximum consecutive working days that nurses can work is 4 days. |
| H8 | For all night shifts, it must be in the form of four consecutive night shifts followed by two days off. This indicates that nurses should not be assigned individual night shifts. |
| S1 | Attempt to give a fair number of working days and days off to all of the nurses. |
| S2 | Make an attempt to provide at least one off day each weekend during the schedule period. |
| S3 | Try to give four consecutive morning shifts followed by one day off. |
| S4 | Try giving a nurse a day off after their fourth straight evening shift. |
| S5 | Attempt to give an evening shift after the day off that follows the night shift. |
| Departments | Nurses | MS (7-2) | ES (2-9) | NS (9-7) | MS (7-2) | ES (2-9) | NS (9-2) |
|---|---|---|---|---|---|---|---|
| CICU-Dep | 11n | 3n | 3n | 2n | 2n | 2n | 2n |
| Surgery-Dep | 18n | 4n | 4n | 3n | 4n | 4n | 2n |
| MDI-Dep | 19n | 4n | 4n | 3n | 4n | 4n | 2n |
| 50N-Dep | 50n | 10n | 10n | 10n | 10n | 10n | 10n |
| GICU-Dep | 73n | 16n | 16n | 15n | 15n | 15n | 14n |
Note:
Xn, is how many nurses needed for each shift; MS, is morning period; ES, is evening period; NS, is night period. CICU (Cardiac Intensive Care Unit); GICU (General Intensive Care Unit); MD1 (Medical Ward 1).
| Prohibited patterns | Undesirable patterns | Desirable patterns |
|---|---|---|
| NNNNM | MMEEXM | XMMMMXX |
| NNNNE | NNNNXXN | EEEEX |
| MNX | NNNNXXM | NNNNXX |
| ENX | MMMM | NNNNXXE |
| XMX | MEME | NNNNXXX |
Note:
X, Day off; M, Morning; E, Evening; and N, Night.
The proposed approach of this study primarily focuses on the minimization of the penalty of the rostering for a specific scheduling period, given a coverage requirement with a fixed number of nurses and defined set of constraints. Penalties in scheduling and rostering are characterized as violations of defined required constraints.
Mathematical model
This study uses the notations for mathematical formulation of UKMMC Medical Center nurse rostering problem presented as follows:
: represents the set of available nurses at the scheduling period i ;
: represents senior nurses, ;
: represents the set of days;
: represents the set of weights;
: represents the set of shifts;
: represents the set of night shift;
: represents the day where ;
: represents the shift where ;
: represents weight where ;
: represents possible shifts where ;
: represents the demand for day on shift ;
: represents the starting date for shifts .
: represents a decision variable, if nurse has working day ( ) on shift ( ); or otherwise;
represents a decision variable, if shifts are worked by nurse ; or otherwise.
The study focused about minimizing total violation of soft constraints for NRP at UKM Medical Center as following:
Minimize the total violation of (S01) which aims to give a fair number of days off and working days to all the nurses.
Minimize the total violation of (S02) which aims to give each nurse a minimum of one off day on the weekend in the scheduled period.
Minimize the total violation of (S03) which represents every four consecutive morning shifts of a nurse should be followed by one day off.
Minimize the total violation of (S04) which represents every four consecutive evening shifts of a nurse should be followed by one day off.
Minimize the total violation of (S05) which is give an evening shift after the day off comes after a night shift.
The model
The study uses the weighted method approach as in Hadwan & Ayob (2010), where the objective function minimizes the total penalty to violations of soft constraints. Nurse rostering problem at UKMMC Medical Center has possible shifts which are: morning shifts, evening shifts, night shifts and day off shifts. These shifts represented by respectively. The objective function for this study is to minimize total penalties that occur due to violating the soft constraints during generating the roster.
Objective function is:
The WT1, WT2, WT3, WT4 and WT5 are the weights connected with goals (1, 2, 3, 4, 5). Subject to
(H01)
(H02)
(H03)
(H04)
(H05(a))
(H05(b))
(H06)
(H07a)
(H07b)
(H08)
(S01)
(S02)
(S03)
(S04)
(S05a)
(S05b)
The hard constraints for UKMMC are Eqs. (H01) to (H08); where Eq. (H01) is used to ensure that the demand is satisfied all times. Constraint Eq. (H02) is used ensure that each nurse works one shift per day at the most, to cover constraints Eq. (H03) which is one senior nurse should be scheduled at each shift. To ensure that each nurse not to give an isolated working day, constraint Eq. (H04) is used. Constraint Eq. (H05a) used to ensure that the maximum number of working days for each nurse is 12 days during the whole rostering period. Furthermore, constraint Eq. (H05b) to ensures that the minimum number of working days for each nurse is not more than 10 days during the whole rostering period. Meanwhile, to ensure the maximum number of consecutives working days for each nurse is 4 days, a constraint Eq. (H06) is used. Constraints (Eqs. (H07a), (H07b)) ensure that the shifts are covered exactly for each nurse. According to each nurse should have at least two days off during the scheduling period, Constraint Eq. (H08) is stated. To give a fair number of working days and days off for each nurse, constraint Eq. (S01) is used. Constraint Eq. (S02) is used to give one day off in the weekend for each nurse during the scheduling period. Constraints Eqs. (S03) and (S04) try to give consecutive morning or evening shifts. Constraints (Eqs. (S05a) and (S05b)) try to give an evening shift after the day off followed by the four consecutive night shifts. The constraints Eqs. (S01) to (S05b) are soft constraints; ) represents the amount of negative deviations for any nurse which is represented by i from goal 1, likewise for each goal positive deviations are penalized.
Tissue like P system (TLPS) algorithm
Several single-membrane or cells evolve in a common environment that provides the basis for TLPS. They have object multi-sets, while some cells directly communicate through channels between them. All cells communicate through their environment. For inter- cellular communication, channels are already given, or it is possible to establish them dynamically.
A structure of a TLPS (degree ≥ 1):
(1) where:
Γ is an object represents non-empty set of symbols;
Γ is the set of objects, that are initially located in the environment, with arbitrary many copies;
, …., (1 ≤ ≤ ) are strings representing multisets over Γ, describing the initial contents of the d cells;
(1 ≤ ≤ ) are a set of rules related to the region;
is the output membrane structure of to save the output of the result.
The membrane structure of a TLPS is inspired by the constructing of tissues and the communicating substances between two or more cells (membranes), it is represented by a graph of nodes the cells, by applying communication rules the arcs will be existing between two membranes of cells, then they are communicated by (symport/antiport) rules.
In symport rules, a group of objects is transported simultaneously from one membrane (or cell) to another in a single direction. Conversely, antiport rules involve a bidirectional exchange, where objects move in opposite directions between two membranes. This work examines TLPS utilizing communication rules based on symport and antiport mechanisms. These rules are denoted as (i, h/k, j), where i and j range over the set {0, …, d} with i ≠ j, and h, k are multisets over the object alphabet Γ, with |hk| > 0. If both h and k are non-empty, the rule is classified as an antiport rule; otherwise, it is a symport rule. A rule is applicable when multiset h exists in membrane i and k exists in membrane j.
Symport and antiport rules are expressed as follows:
Symport rule:
(2) where is an object in membrane or cell is transferred to membrane or cell . represent rule number.
Antiport rule:
(3) In this scenario, object u is transferred from membrane i to j, while simultaneously object v moves from membrane j to i. This mechanism enables a bidirectional transfer of objects between membranes.
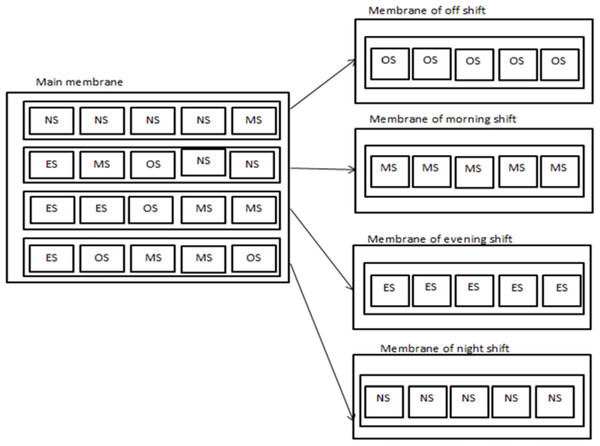
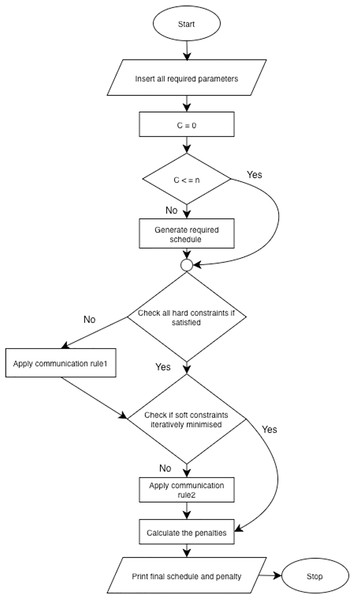
The proposed TPLS algorithm used in this study is based on the biological technique of modular processing. The proposed TLPS in this study is designed to use five primary membranes, where each membrane contains a key element representing shift schedules. The five membranes interact with each other based on a set of predefined constraints as presented in Table 1. The interactions between the five membranes ensures a final feasible and best case scheduling or roster of nurses. Figure 1 illustrates the flow chart of the TLPS algorithm proposed in this study.
Figure 1: TPLS algorithm flow.
Step 1: Five membranes are created, each corresponding to a table: the Main membrane, Membrane of off shift, Membrane of morning shift, Membrane of evening shift, and Membrane of night shift following the TLPS framework. These tables collaborate to develop a feasible nurse schedule for the Malaysia Medical Center.
Step 2: The membranes of shifts or tables are populated with objects representing different shifts as inputs, while the Main membrane generates the final output. night shifts, off-day shifts, morning shifts, and evening shifts are randomly allocated to the membranes as in Fig. 2.
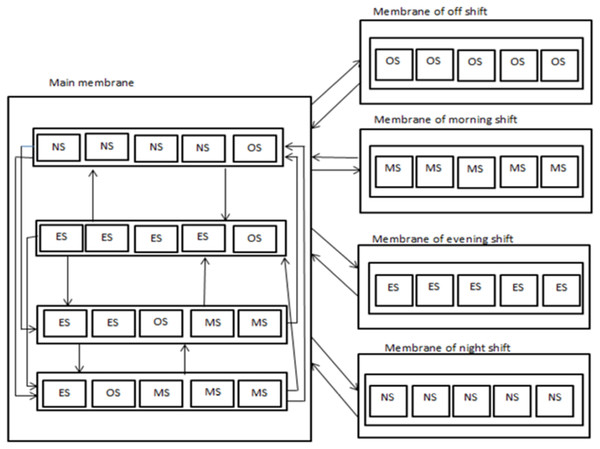
Step 3: Communication rule1 is applied between the membranes or tables, considering specific conditions (hard constraints). Connections between membranes are managed through antiport, symport, or uniport mechanisms, enabling the transfer of shifts between tables according to the defined rules. While communication rule 2 is applied between the membranes to satisfy soft constraints as much as possible as in Fig. 3.
Figure 2: Main membrane with shift membranes and applying communication.
Figure 3: Main membrane with communication rule 2 to generate feasible solution.
Each gap junction is connected through antiport, symport, or uniport mechanisms, enabling the transfer of shifts between membranes or tables according to defined rules and conditions. These mechanisms play a crucial role in facilitating the redistribution of shifts within the system.
Diversification mechanism
The TLPS algorithm uses random shift allocations to initiate solution search which serves as a form of diversification. The second step of the algorithm’s flow allocates the shifts randomly to the membranes. The initial random distribution of shifts ensures a broad exploration of solutions across the five membranes representing shifts; main, off, morning, evening, and night shift membranes. Varying initial configurations ensures the algorithm avoids premature convergence, and optimally discovers a wide range of solutions to choose the best from.
Intensification mechanism
TLPS archives intensification using an iterative rule based refinement process. The algorithm carries out a continuous application of communication rule 1 and rule 2 between its membranes. Communication rule 1 primarily focuses on satisfying the hard constraints requirements, which are essential requirements. The algorithm reiterates the shifts when the schedule fails to meet the requirements of the hard constraints; until it finally meets the constraint requirements. The effective correction in iteration to ensure hard constraints are met drives the algorithm to a feasible scheduling solution. After the communication rule 1 satisfies the hard constraints, then communication rule 2 is applied to satisfy soft constraints. Communication rule 2 aims to satisfy soft constraints by reducing the penalties of the scheduling. The algorithm intensifies the search for a higher quality schedule with the lowest incurred penalties.
Move acceptance strategy
TLPS algorithm uses an implicit and deterministic move acceptance approach, this is guided strictly by the rules of constraint satisfaction and penalty minimization. Each move is represented by the transfer of shifts between membranes, using the antiport, symport, or uniport mechanisms. The transfers of shifts between membranes is not random, and are executed based on the defined conditions of the hard and soft constraints. All shifts that satisfy all the hard constraints are accepted and maintained. All shifts that lead to a reduction in penalty cost are implicitly accepted. The algorithm continuously checks for constraints compliance. The system effectively accepts moves that improve the roster’s quality by reducing its penalty score.
This study applies the proposed TLPS algorithm on a schedule requirement of the UKMMC for a total of five different departments, these are the surgery, CICU (Cardiac Intensive Care Unit), MD1 (Medical Ward 1), GICU (General Intensive Care Unit), and N50 departments. The required nurses and shifts for each department are ascertained, and schedules are generated for the required nurses in each department accordingly. The generated shifts are cross examined to ensure if each shift schedule covers the demand of the departments as required. Where the schedules are lacking in meeting the demand requirements, the shifts are reiterated until the schedule allocation meets the requirement. Once a schedule is determined to meet the required number of nurses in every shift, the schedule is checked to ensure compliance with hard and soft constraints. Figure 4 illustrates the flowchart of the proposed TLPS algorithm process for NRP scheduling. Table 4 shows the penalty weight assigned to each constraint. Also, following is a detailed pseudocode approach to the NRP scheduling algorithm.
Figure 4: Algorithm flowchart for the proposed TLPS.
| Soft constraint | Weight | Penalty function | Violation measurement factor |
|---|---|---|---|
| Give fair number of working days and days off to all the nurses. | 100 | Linear | Number of days when there was an insufficient number of nurses to meet the minimum workday requirements |
| Give each nurse at least one day off on the weekends during the scheduled period. | 100 | Linear | Number of days when there is no day off on weekends |
| Give four consecutive morning shifts followed by one day off. | 10 | Linear | Four consecutive morning shifts |
| Give four consecutive evening shifts followed by one day off. | 10 | Linear | Four consecutive evening shifts |
| Give an evening shift after the day off, followed by a night shift. | 1 | Linear | Number of morning shifts after four consecutive night shifts followed by two days off |
Input: Days, Nurses, Shifts, Constraints (Hard and Soft)
Output: Feasible and optimized nurse schedule
Begin
Step 1: Initialization
Initialize membrane structure M
Initialize the population of candidate schedules within membranes
Define communication rules for information exchange between membranes
Set termination condition ← False
Step 2: Evolution Process
While (termination condition == False) do
Scatter initial shifts randomly into elementary membranes
For each elementary membrane mi in M do
Determine the number of iterations for mi
For i = 1 to d do
Execute communication rules between membranes
Update local schedules within mi
End For
End For
Step 3: Combine results
Collect and output the best main schedule candidate
End While
Step 4: Feasibility Phase—Satisfy Hard Constraints
While (no feasible solution exists) do
For i = 1 to 8 do
Apply communication rules that address hard constraints
Calculate penalties due to hard constraint violations
If (all hard constraints are satisfied) then
feasible solution ← True
End If
End For
End While
Step 5: Optimization Phase—Minimize Soft Constraint Violations
For j = 1 to 5 do
While (penalties due to soft constraint violations remain high) do
Apply communication rules that reduce soft constraint penalties
Check that all hard constraints remain satisfied
Compute new penalties for current schedule
If (new penalties < previous penalties) then
penalties ← new penalties
Else
penalties ← previous penalties
End If
End While
End For
Step 6: Final Output
Output the optimized main schedule with minimal soft constraint violations
End
Experimental setup
The proposed TLPS algorithm is designed and implemented on nurse scheduling for five departments of the UKMMC. The scheduling experiment was carried out for an 11 to 73 nurses shift for a period of 2 weeks. Performance of the proposed algorithm is evaluated based on the penalties of the performance of the algorithm. The TPLS algorithm is implemented using the C# programming language, and experiments are carried out using Intel platform with a 2.66 GHz Core TM processor and 4 GB of RAM. The penalty weights used range from 194 to 1,280, with execution time between 0.005 and 0.041 s.
Results
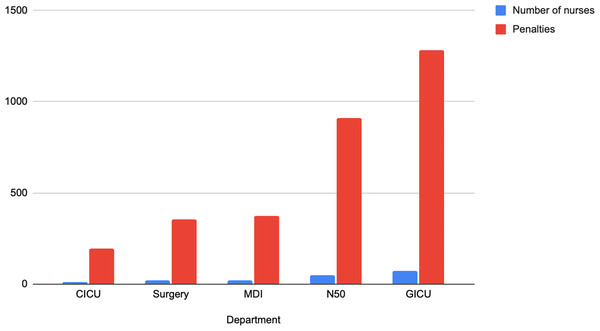
This section presents the results of experiments carried out using the proposed TLPS algorithm, and other algorithms are ablation experiments to determine a comparative performance. The algorithms used in the ablation experiments are the GA and HSA. Table 5 shows the experimental results for the observed penalties for each department, the required number of nurses and the period of the schedules also the construction time for each department.
| Department | Number of nurses | Schedule period (days) | Penalties | Construction time (seconds) |
|---|---|---|---|---|
| CICU | 11 | 14 | 194 | 0.004 |
| Surgery | 18 | 14 | 354 | 0.011 |
| MDI | 19 | 14 | 374 | 0.009 |
| N50 | 50 | 14 | 910 | 0.027 |
| GICU | 73 | 14 | 1,280 | 0.041 |
In Figs. 5 and 6, the penalties due to violation of soft constraints are reduced after applying the TLPS algorithm. Also the time taken to construct the roster is reduced, where it can construct a roster with less penalties and time.
Figure 5: The relation between number of nurses and the penalties of using TLPS.
Figure 6: The relation between number of nurses and the construction time of TLPS.
Comparison of genetic algorithm, harmony search algorithm, and TLPS using the UKMMC dataset
The genetic algorithm (GA) is a metaheuristic inspired by the principles of natural selection, operating on a population of candidate solutions that evolve through selection, crossover, and mutation. In contrast, the harmony search algorithm (HSA) is a more recent bio-inspired technique that draws its analogy from the musical process of improvisation, where harmony is iteratively refined to achieve an optimal composition. In this study, both GA and HSA, along with the TLPS, are evaluated on the UKMMC dataset as proposed by Hadwan et al. (2013).
In this study the performance of HSA and GA on the UKMMC dataset was compared with TLPS algorithm performance. Table 6 shows the main details about these comparisons.
| Department | GA (Hadwan et al., 2013) | Time | DP | HAS (Hadwan et al., 2013) | Time | DP | TLPS | Time | DP |
|---|---|---|---|---|---|---|---|---|---|
| CICU | 2,791 | 81.2 | 2 | 310 | 185.1 | 5 | 194 | 0.004 | 11 |
| Surgery | 3,680 | 96 | 3 | 221 | 115.3 | 8 | 354 | 0.011 | 14 |
| MDI | 4,219 | 99.6 | 5 | 339 | 127 | 9 | 374 | 0.009 | 16 |
| N50 | 1,021 | 847 | 18 | 821 | 175 | 21 | 910 | 0.027 | 50 |
| GICU | 1,850 | 274 | 24 | 1,481 | 295.2 | 27 | 1,280 | 0.041 | 76 |
| Total | 13,561 | 1,397.8 | 52 | 3,127 | 897.6 | 70 | 3,112 | 0.092 | 167 |
Note:
Time, time in seconds; DP, desirable patterns.
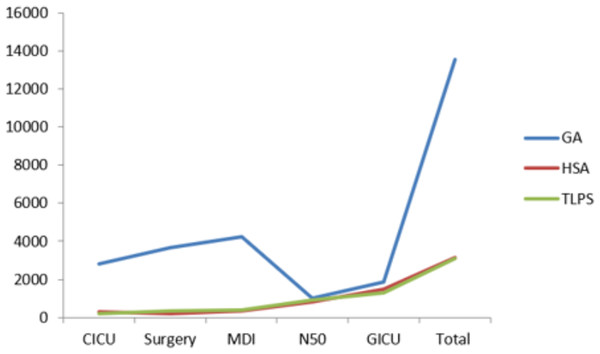
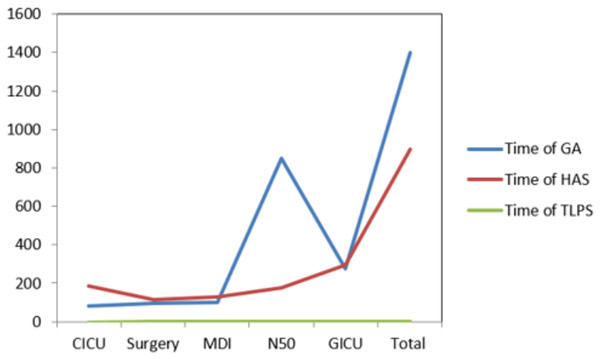
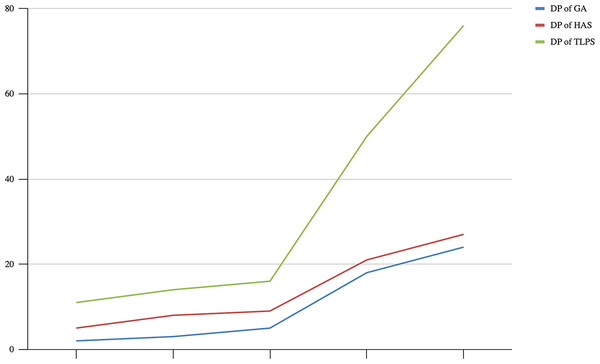
The results of the experiments indicate a significant performance improvement using the TLPS algorithm, especially compared to previously proposed algorithms. The resulting penalty weights as seen using the TLPS algorithm indicate good and feasible performance of the TLPS algorithm for NRP. Also, not only is there a significant lower total penalty weight, but the time taken for the construction of the schedules is significantly lower and desirable patterns obtained from applying TLPS are improved than both of the desirable patterns obtained by GA and HSA. Figure 7 illustrates the relation between number of nurses and the objective functions of the compared algorithms and the proposed approach. Figure 8 illustrates the relation between number of nurses and the construction time of the proposed approach compared to other algorithms: GA and HSA. Figure 9 illustrates the relation between number of nurses and the desirable patterns for the proposed approach and compared algorithms; GA and HSA
Figure 7: The relation between number of nurses and the objective function for GA, HAS, and TLPS algorithms.
Figure 8: The relation between number of nurses and the construction time of GA, HAS and TLPS algorithms.
Figure 9: The relation between number of nurses and the desirable patterns obtained by applying GA, HAS and TLPS algorithms.
Based on the results presented in Table 6, TLPS demonstrates the best performance across the critical metrics; construction time, total penalty, and desirable patterns. The TLPS approach achieved a total penalty of 3,112 across all the tested departments, this is significantly lower than the penalties incurred by both GA and HSA which have 13,561 and 3,127 respectively. A lower penalty indicates a roster adheres to soft constraints effectively which leads to efficient nurse schedules. The proposed TLPS algorithm also significantly reduced the construction time, where it constructed the roster in a total time of 0.092 s for all the required departments. Compared to the construction time of both GA and HSA having 1,397.8 and 897.6 s, this is a significantly improved construction time.
Desirable patterns (DP) relate to the quality and optimization of generated nurse rosters. DP considers the context of three categories of shift patterns, these are prohibited, undesirable, and desirable patterns. Prohibited patterns are the shift patterns which violate hard constraints, undesirable patterns adhere to hard constraints but do not efficiently adhere to soft constraints, and DP adhere to both hard and soft constraints. DP are generated or calculated with each successful minimization of soft constraints violations after hard constraints have been successfully adhered to. The more soft constraints violations have been minimized the more DPs are created and counted, as illustrated in Table 3. The proposed TLPS algorithm also resulted in a total of 167 desirable patterns (DP) across all the departments. This DP figure is significantly higher than the DP achieved in both GA and HSA which have 52 and 70 respectively. A higher number of DP indicates a better quality of generated roster; adhering to preferred requirements of scheduling.
Conclusions
The nurse rostering problem (NRP) is a challenge facing healthcare facilities in ensuring there is adequate rostering of nurses to enable the delivery of good healthcare and management. This study proposed the use of the TLPS algorithm to solve NRP. The proposed TLPS approach was designed and applied on real world data from the National University of Malaysia Medical Center (UKMMC). The performance of the proposed method shows significant performance in designing feasible nurse schedules while also adhering to the hard and soft constraints requirements. The proposed TLPS algorithm does not only produce a feasible solution to NRP but it also does so with exceptional timing. The results of this research show a good performance improvement using the proposed method compared with GA and HSA, and also providing a scalable solution to NRP which continuously challenges previous methods of solving NRP.
This study addresses the research gap for more effective, adaptable, and scalable NRP solutions in dynamic hospital environments. The study is aimed at mitigating existing limitations of NRP such as inefficiency and suboptimal approaches to manual nurse rostering approaches. The proposed TLPS algorithm for NRP provides an automated and significantly more effective solution to NRP. The inherent complexities of NRP makes it computational intractable for deterministic approaches, TLPS uses the advantages of computational parallel processing using its membrane computing to handle this complexity. Existing proposed approaches are often challenged in handling the comprehensive constraints of NRP, and the proposed TLPS is designed to adequately factor the different kinds of constraints and their requirements to efficiently minimize penalties.
Recommendation and future work
This study recommends further exploration of the proposed TLPS algorithm, further applications should include experimenting on other datasets and healthcare facility contexts. This will ensure the scalability of the TLPS algorithm is tested for suitability in different NRP. This study also recommends researching and investigating the applicability and feasibility of the TLPS algorithm on other scheduling problem contexts outside of NRP. Ultimately, the potential of the TLPS algorithm could be enhanced through more extensive testing across different datasets, leading to even more robust and scalable solutions for workforce management.