Node disjoint path construction algorithm in the folded divide-and-swap cube

Ying Gao; Lantao You; Yuejuan Han; Yunsong Zhang

doi:10.7717/peerj-cs.3458

Node disjoint path construction algorithm in the folded divide-and-swap cube

Ying Gao¹, Lantao You^1,2, Yuejuan Han ³, Yunsong Zhang¹

1School of Information Engineering, Suzhou Industrial Park Institute of Services Outsourcing, Suzhou, China

2Provincial Key Laboratory for Computer Information Processing Technology, Soochow University, Suzhou, China

3School of Computer Science and Technology, Soochow University, Suzhou, China

DOI: 10.7717/peerj-cs.3458

Published: 2026-01-27
Accepted: 2025-11-17
Received: 2025-07-11

Academic Editor: Michele Pasqua

Subject Areas: Algorithms and Analysis of Algorithms, Distributed and Parallel Computing, Optimization Theory and Computation, Scientific Computing and Simulation, Theory and Formal Methods
Keywords: Node-disjoint path, Folded divide-and-swap cube, Interconnection network

Copyright: © 2026 Gao et al.
Licence: This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, reproduction and adaptation in any medium and for any purpose provided that it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Computer Science) and either DOI or URL of the article must be cited.

Cite this article: Gao Y, You L, Han Y, Zhang Y. 2026. Node disjoint path construction algorithm in the folded divide-and-swap cube. PeerJ Computer Science 12:e3458 https://doi.org/10.7717/peerj-cs.3458

The authors have chosen to make the review history of this article public.

Abstract

The folded divide-and-swap cube FDSC_n (n = 2^d, d ≥ 1) is a new hypercube variant, which has many superior properties compared to the hypercube. FDSC_n is suitable as a candidate topology for data center networks. In this article, we investigate the one-to-one node disjoint path problem of FDSC_n. We first present an algorithm to construct a path between any two distinct nodes u and v based on the structural characteristics of FDSC_n. Then we develop an algorithm to build d + 2 node disjoint paths between any two different nodes in FDSC_n, and show that the maximum length of these paths shall not exceed n + 9.

Introduction

Supercomputers are high-performance computing systems that can perform complex tasks at an unprecedented speed. These systems typically consist of thousands or even millions of processors. An interconnection network, which is the fundamental topological structure of a supercomputer, plays a vital role in the performance of a supercomputer. The topology structure of an interconnection network is always modeled with a graph $G = (V (G), E (G))$ , where $V (G)$ is the processor set and $E (G)$ is the set of communication links connecting these processors. In a graph, a path is a sequence of distinct vertices $⟨ μ_{0}, μ_{1}, \dots, μ_{k} ⟩$ such that each pair of consecutive vertices $μ_{i}$ and $μ_{i + 1}$ is connected by an edge in $E (G)$ , where $0 \leq i \leq k - 1$ . The length of a path P, denoted by $L (P)$ , is the number of edges it contains. The distance between two vertices $μ$ and $ν$ , denoted by $d (μ, ν)$ , is the length of the shortest path connecting them. The diameter of G is the maximum distance between any two vertices in G. A vertex $μ \in V (G)$ is a neighbor of $ν \in V (G)$ if there exists an edge $(μ, ν) \in E (G)$ . The neighborhood of $ν$ , denoted by $N (ν)$ , is the set of all neighbors of $ν$ . Let $S \subseteq V (G)$ . Then $N (S) = {ν \in V (G) | μ \in S, (ν, μ) \in E (G)$ and $ν \notin S}$ and $N [S] = N (S) \cup V (S)$ . In this work, the terms “vertex” and “node” are used interchangeably.

One-to-one node-disjoint paths between any two distinct nodes $μ$ and $ν$ in a graph refer to a set of paths that do not share any common nodes except the end nodes $μ$ and $ν$ . Since each path is independent with the other ones, node-disjoint paths allow data to be transmitted through multiple paths. In distributed computing systems, node-disjoint paths are essential for fault-tolerant communication between different nodes. By using multiple disjoint paths, supercomputers can continue to function properly even when some nodes become unavailable due to hardware failures or network issues. There are many works on disjoint path problem in hypercubes (Saad & Schultz, 1988), crossed cubes (Kulasinghe, 1997), twisted cubes (Chang, Wang & Hsu, 1999), m $\ddot{o}$ bius cubes (Kocik & Kaneko, 2017), balanced hypercubes (Cheng, Hao & Feng, 2014; Liu et al., 2024), folded hypercubes (Lai, 2021; Liu, 2010), bcube (Fan et al., 2023), $k$ -ary $n$ -cube networks (Lv et al., 2024), enhanced hypercubes (Ma, Guo & Li, 2022), dcell networks (Wang et al., 2016), dragonfly networks (Wu et al., 2022), and alternating group graphs (You et al., 2015).

The $n$ -dimensional hypercube $Q_{n}$ which has network cost $O (n^{2})$ is one of the most important interconnection networks. The divide-and-swap cube $D S C_{n}$ is a newly proposed hypercube variant, which reduces the network cost to $O (n \log n)$ (Kim et al., 2019), while $D S C_{n}$ and $Q_{n}$ have the same number of nodes. To reduce the diameter of $D S C_{n}$ , the folded divide-and-swap cube $F D S C_{n}$ is proposed. The upper bounds of diameters of $D S C_{n}$ and $F D S C_{n}$ are $\frac{5 n}{4} - 1$ and $n - 1$ ( $n = 2^{d}, d \geq 2$ ), respectively (Kim et al., 2019). Both $D S C_{n}$ and $F D S C_{n}$ are hierarchical networks. Besides, $D S C_{n}$ and $F D S C_{n}$ are Hamiltonian and Hamiltonian-connected. Chang et al. (2021) pointed out that $F D S C_{n}$ is suitable as a candidate topology for data center networks, and they proposed a recursive construction of a dual-CIST for $F D S C_{n}$ . Zhao & Chang (2023) investigated the generalized connectivity on $D S C_{n}$ . Zhou et al. (2024) determined the $g$ -extra connectivity $(0 \leq g \leq 10)$ of the divide-and-swap cube $D S C_{n}$ . $F D S C_{n}$ has a node degree of $\log n + 2$ , which is much lower than most of the hypercube variants. Lower node degree reduces hardware costs, as it requires fewer ports per server/switch, minimizing the expense of network adapters and cabling. $F D S C_{n}$ has the smallest network cost among all hypercube variants, which proves $F D S C_{n}$ ’s superiority in balancing performance and resource usage. Besides, $F D S C_{n}$ exhibits double exponential scalability, which surpasses many traditional interconnection topologies (e.g., bcube, dcell) and meets the demand for connecting massive numbers of servers in modern data centers.

In this work, we investigate the one-to-one node disjoint path problem of $F D S C_{n}$ . Let $μ$ and $ν$ be any two distinct nodes in $F D S C_{n}$ where $n = 2^{d}$ and $d \geq 1$ . We give an algorithm to construct $d + 2$ disjoint paths between $μ$ and $ν$ . The main contributions of this work are shown as below:

We present an algorithm QP to construct a path between any two distinct nodes $μ$ and $ν$ based on the structural characteristics of $F D S C_{n}$ . This algorithm can quickly locate the subgraph where these two vertices are located, thereby reducing the scale of the path constructing problem.
We develop an algorithm O2OMain to build $d + 2$ disjoint paths between any two different nodes in $F D S C_{n}$ and show that the maximum length of these paths shall not exceed $n + 9$ .

Preliminaries

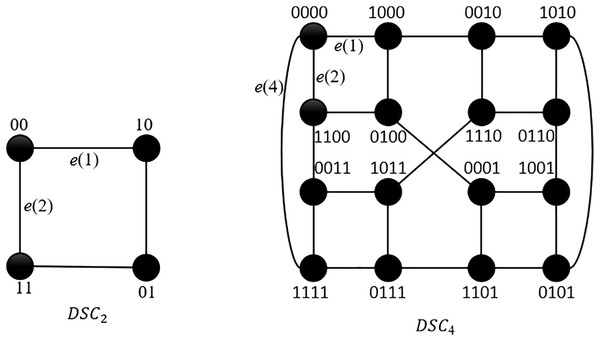
In this section, we give the formal definition of $D S C_{n}$ and $F D S C_{n}$ . Each node $μ$ in $D S C_{n}$ is denoted by an $n$ -bit binary string, where $μ = x_{1} x_{2} \dots x_{n}$ with $x_{i} \in {0, 1}$ for $1 \leq i \leq n$ . $D S C_{n}$ is defined as follows.

Definition 1. (Kim et al., 2019) For any integers $n = 2^{d}$ and $d \geq 1$ , $D S C_{n}$ has $2^{n}$ nodes, each of which is represented by an $n$ -bit binary string, where $μ = x_{1} x_{2} \dots x_{n} = s_{1} s_{2} s_{3}$ and $x_{i} \in {0, 1}$ with $1 \leq i \leq n$ . For each $k$ with $1 \leq k \leq d$ , $s_{1} = x_{1} x_{2} \dots x_{\frac{n}{2^{k}}}$ , $s_{2} = x_{\frac{n}{2^{k}} + 1} x_{\frac{n}{2^{k}} + 2} \dots x_{\frac{n}{2^{k - 1}}}$ and $s_{3} = x_{\frac{n}{2^{k - 1}} + 1} x_{\frac{n}{2^{k - 1}} + 2} \dots x_{n}$ . If $k = 1$ , then $μ = s_{1} s_{2}$ and $s_{3}$ is empty. If node $v$ satisfies one of the following conditions, then $(μ, v) \in E (D S C_{n})$ .

(1)

$v = {\bar{x}}_{1} x_{2} \dots x_{n}$ , where ${\bar{x}}_{1}$ is the complement of $x_{1}$ . Here, $(μ, v)$ is called an $e (1)$ -edge.
(2)

$v = {\begin{matrix} {\bar{s}}_{1} {\bar{s}}_{2} s_{3} & i f s_{1} = s_{2}, \\ s_{2} s_{1} s_{3} & i f s_{1} \neq s_{2} \end{matrix}$ Here, $(u, v)$ is called an $e (\frac{2 n}{2^{k}})$ -edge.

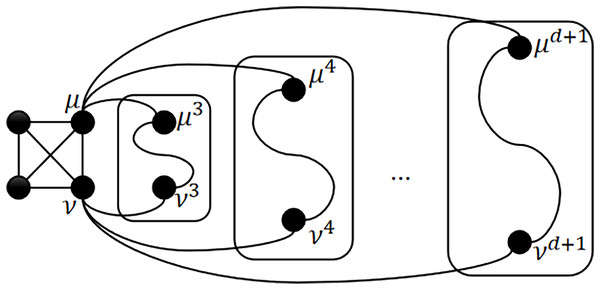
$D S C_{2}$ and $D S C_{4}$ are shown in Fig. 1. Each node in $D S C_{n}$ has $d + 1$ neighbors. Hence, $D S C_{n}$ is $(d + 1)$ -regular. If $ν$ is connected to $μ$ with an $e (1)$ -edge, then we call $ν$ the 1-neighbor of $μ$ , denoted by $μ^{1}$ ; If $ν$ is connected to $μ$ with an $e (\frac{2 n}{2^{k}})$ -edge ( $1 \leq k \leq d$ ), then we call $ν$ the $i$ -neighbor of $μ$ , denoted by $μ^{i}$ , where $i = d + 2 - k$ (See Table 1).

$DS{C_{2}}$DSC2
and
$DS{C_{4}}$DSC4
. — Figure 1: $D S C_{2}$ and $D S C_{4}$ .

Download full-size image

DOI: 10.7717/peerj-cs.3458/fig-1

Table 1:

Relationship between the values of

k

, edge types, neighboring nodes and label

s_{1} s_{2}

μ

Symbols	Values
$k$	$d$	$d - 1$	$\dots$	$2$	$1$
$e (\frac{2 n}{2^{k}}) = e (2^{d + 1 - k})$	$e (2^{1})$	$e (2^{2})$	$\dots$	$e (2^{d - 1})$	$e (2^{d})$
$u^{i} (i = d + 2 - k)$	$u^{2}$	$u^{3}$	$\dots$	$u^{d}$	$u^{d + 1}$
$s_{1} s_{2}$	$x_{1} \dots x_{2^{1}}$	$x_{1} x_{2} \dots x_{2^{2}}$	$\dots$	$x_{1} x_{2} \dots x_{2^{d - 1}}$	$x_{1} x_{2} \dots x_{2^{d}}$

DOI: 10.7717/peerj-cs.3458/table-1

Definition 2. Let $x_{2^{h} + 1} x_{2^{h} + 2} \dots x_{2^{d}}$ be a specific ( $2^{d}$ − $2^{h}$ )-digit binary string where $1 \leq h \leq d$ and $d \geq 1$ . Define $D S C_{2^{h}} \cdot x_{2^{h} + 1} x_{2^{h} + 2} \dots x_{2^{d}}$ as a subgraph of $D S C_{2^{d}}$ induced by ${a_{1} a_{2} \dots a_{2^{h}} x_{2^{h} + 1} x_{2^{h} + 2} \dots x_{2^{d}} | a_{1} a_{2} \dots a_{2^{h}}$ is a $2^{h}$ -digit binary string}. We call $D S C_{2^{h}} \cdot x_{2^{h} + 1} x_{2^{h} + 2} \dots x_{2^{d}}$ an embeded $D S C_{2^{h}}$ of $D S C_{2^{d}}$ with the identifier $x_{2^{h} + 1} x_{2^{h} + 2} \dots x_{2^{d}}$ .

For example, $D S C_{2} \cdot 00$ is an embeded $D S C_{2}$ induced by ${0000, 1000, 0100, 1100}$ in Fig. 1, where 00 is the identifier. The rightmost 2-digit binary string of each node in $D S C_{2} \cdot 00$ is same, which is 00. Let $μ = x_{1} \dots x_{2^{k}} x_{2^{k} + 1} x_{2^{k} + 2} \dots x_{2^{d}}$ with $1 \leq k \leq d - 1$ . According to Definition 2, node $μ$ belongs to $D S C_{2^{k}} \cdot x_{2^{k} + 1} x_{2^{k} + 2} \dots x_{2^{d}}$ . For two different nodes $μ$ and $ν$ of $D S C_{2^{d}}$ , if the rightmost ( $2^{d}$ − $2^{k}$ )-digit binary strings of $μ$ and $ν$ are same, or only the leftmost $2^{k}$ -digit binary strings of $μ$ and $ν$ are different, then $μ$ and $ν$ belong to the same $D S C_{2^{k}} \cdot x_{2^{k} + 1} x_{2^{k} + 2} \dots x_{2^{d}}$ . In this work, we say that $D S C_{2^{d}}$ is an embeded subgraph of its own, where the identifier is empty.

From Table 1, we can see that only the leftmost $2^{i - 1}$ -digit binary strings of $u^{i}$ and $u$ are different. Hence, $u^{i}$ and $u$ are in the same embeded $D S C_{2^{i - 1}} (2 \leq i \leq d + 1)$ . In this work, in order to simplify the expression, we may omit the identifier of the embeded subgraph sometimes.

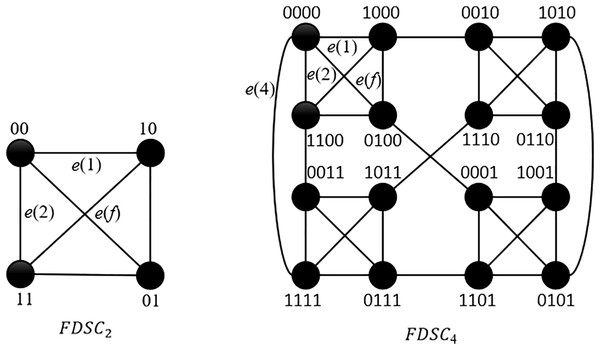
Next, we give the definition of $F D S C_{n}$ . For any integer $n$ with $n = 2^{d}$ and $d \geq 1$ , $F D S C_{n}$ is built based on $D S C_{n}$ by adding an edge to each node of $D S C_{n}$ . Hence, $F D S C_{n}$ is $(d + 2)$ -regular.

Definition 3. (Kim et al., 2019) $V (F D S C_{n}) = V (D S C_{n})$ , $E (F D S C_{n}) = E (D S C_{n}) \cup E_{f}$ , where $E_{f} = {(u, v) | u = x_{1} x_{2} x_{3} \dots x_{n}$ and $v = x_{1} {\bar{x}}_{2} x_{3} \dots x_{n}}$ . An edge in $E_{f}$ is called an $e (f)$ -edge.

If $ν$ is connected to $μ$ with an $e (f)$ -edge, then we call $ν$ the 0-neighbor of $μ$ , denoted by $μ^{0}$ . $F D S C_{2}$ and $F D S C_{4}$ are shown in Fig. 2. By the definition of $F D S C_{n}$ , the concept of embeded subgraph can also apply to $F D S C_{n}$ . Hence, we have the following properties:

$FDS{C_{2}}$FDSC2
and
$FDS{C_{4}}$FDSC4
. — Figure 2: $F D S C_{2}$ and $F D S C_{4}$ .

Download full-size image

DOI: 10.7717/peerj-cs.3458/fig-2

Property 1. For any node $μ \in V (F D S C_{n})$ with $n = 2^{d}$ and $d \geq 1$ , there exist the following properties:

(1)

If the rightmost ( $2^{d}$ − $2^{k}$ )-digit binary strings of $μ$ and $ν$ are the same, or only the leftmost $2^{k}$ -digit binary strings of $μ$ and $ν$ are different where $1 \leq k \leq d$ , then $μ$ and $ν$ are in the same embeded $F D S C_{2^{k}}$ .
(2)

$μ$ has $k + 2$ neighbors ${μ^{0}, μ^{1}, μ^{2}, \dots, μ^{k + 1}}$ in the embeded $F D S C_{2^{k}}$ of $F D S C_{n}$ , where $1 \leq k \leq d$ .
(3)

$μ^{0}$ , $μ^{1}$ , $μ^{2}$ and $μ$ are in the same embeded $F D S C_{2}$ .

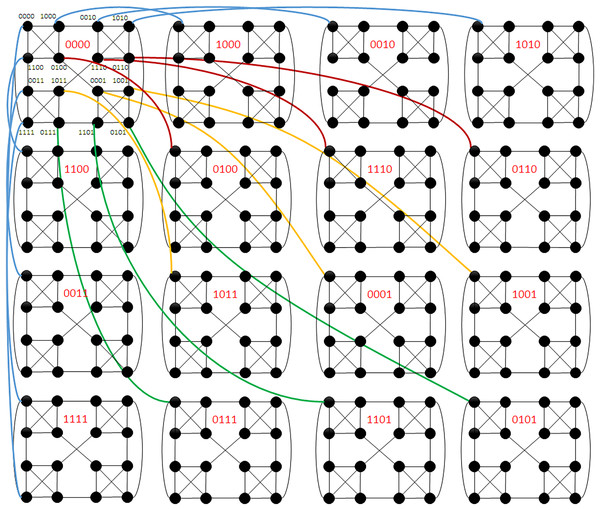
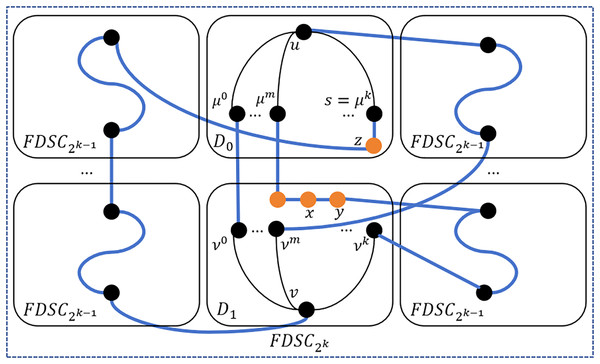
Suppose $D = F D S C_{2^{k}}$ is an embeded subgraph of $F D S C_{n}$ , where $n = 2^{d}, d \geq 2$ and $2 \leq k \leq d$ . The direct subgraph of D is callled a module of D. D can be decomposed into $2^{2^{k - 1}}$ embeded subgraph $F D S C_{2^{k - 1}} s$ , each of which is a module of $F D S C_{2^{k}}$ . For example, in Fig. 3, suppose $D = F D S C_{8}$ , then D can be decomposed into $2^{4}$ embeded $F D S C_{4} s$ . Let $μ = x_{1} x_{2} \dots x_{n} = A B C$ , where $A = x_{1} x_{2} \dots x_{2^{k - 1}}$ is the address in a module and $B = x_{2^{k - 1} + 1} x_{2^{k - 1} + 2} \dots x_{2^{k}}$ is the address of the module in D. For example, in Fig. 3, suppose $D = F D S C_{8}$ , then ${0000, 0001, \dots, 1111}$ are the module addresses of the $16$ embeded $F D S C_{4} s$ in D. Suppose $D = F D S C_{4} \cdot 0000$ , then ${00, 01, 10, 11}$ are the module addresses of the four embeded $F D S C_{2} s$ in D. Each module in $F D S C_{2^{k}}$ is denoted by $D_{B_{i}}$ where $B_{i}$ ( $1 \leq i \leq 2^{2^{k - 1}}$ ) is the module address. Each node $μ$ in $D_{B_{i}}$ has $k + 1$ interior neighbors ${u^{0}, u^{1}, \dots, u^{k}}$ inside $D_{B_{i}}$ and $u^{k + 1}$ is the external neighbor outside $D_{B_{i}}$ . Any two distinct modules in D are connected by at least one edge, which is called a bridge edge.

A partial view of
$FDS{C_{8}}$FDSC8
. — Figure 3: A partial view of $F D S C_{8}$ .

Download full-size image

DOI: 10.7717/peerj-cs.3458/fig-3

Property 2. (Kim et al., 2019) For any two distinct modules $D_{B_{i}}$ and $D_{B_{j}}$ in $F D S C_{2^{k}}$ with identifier B where $2 \leq k \leq d$ and $1 \leq i \neq j \leq 2^{2^{k - 1}}$ , there exist the following properties:

(1)

if $B_{i} \neq {\bar{B}}_{j}$ , then there is one bridge edge $(B_{j} B_{i} B, B_{i} B_{j} B)$ between modules $D_{B_{i}}$ and $D_{B_{j}}$ .
(2)

if $B_{i} = {\bar{B}}_{j}$ , there are two bridge edges $(B_{i} B_{i} B, {\bar{B}}_{i} {\bar{B}}_{i} B)$ and $(B_{j} B_{i} B, B_{i} B_{j} B)$ between modules $D_{B_{i}}$ and $D_{B_{j}}$ .

For example, in Fig. 3, suppose $D = F D S C_{8}$ . For modules $F D S C_{4} \cdot 0000$ and $F D S C_{4} \cdot 1111$ in D, there are two bridge edges (00000000, 11111111) and (11110000, 00001111). For modules $F D S C_{4} \cdot 0000$ and $F D S C_{4} \cdot 1000$ in D, there is one bridge edge (00001000, 10000000). Suppose $D = F D S C_{4} \cdot 0000$ . For modules $F D S C_{2} \cdot 00$ and $F D S C_{2} \cdot 11$ in D, there are two bridge edges (00000000, 11110000) and (11000000, 00110000). For modules $F D S C_{2} \cdot 00$ and $F D S C_{2} \cdot 01$ in D, there is one bridge edge (01000000, 00010000).

Let $μ = x_{1} x_{2} \dots x_{2^{d}}$ and $ν = y_{1} y_{2} \dots y_{2^{d}}$ be two distinct nodes in different modules $D_{B_{i}}$ and $D_{B_{j}}$ of the same $F D S C_{2^{k}}$ where $2 \leq k \leq d$ . Then, $B_{i} = x_{2^{k - 1} + 1} x_{2^{k - 1} + 2} \dots x_{2^{k}}$ is the module address of $D_{B_{i}}$ , and $B_{j} = y_{2^{k - 1} + 1} y_{2^{k - 1} + 2} \dots y_{2^{k}}$ is the module address of $D_{B_{j}}$ . If we replace the first $2^{k - 1}$ bits of $μ$ with $B_{j}$ to obtain node $s$ , and replace the first $2^{k - 1}$ bits of $ν$ with $B_{i}$ to obtain node $t$ , then $(s, t)$ is a bridge edge between $D_{B_{i}}$ and $D_{B_{j}}$ .

For example, in Fig. 3, suppose $μ = 00000000$ , $ν = 01010000$ and $D = F D S C_{4} \cdot 0000$ with $k = 2$ . Then $μ$ is in module $D_{B_{i}}$ with $B_{i} = 00$ and $ν$ is in module $D_{B_{j}}$ with $B_{j} = 01$ . If we replace the first 2 bits of $μ$ with $B_{j}$ , then we get node $s = 01000000$ . And if we replace the first 2 bits of $ν$ with $B_{i}$ , then we get node $t = 00010000$ . Then, (01000000, 00010000) is a bridge edge between $D_{00}$ and $D_{01}$ . We list some acronyms and notations in Table 2, which will be used in this work.

Table 2:

Acronyms and notations.

Symbol	Definition
$F D S C_{n} (n = 2^{d}, d \geq 1)$	An $n$ -dimensional folded divide-and-swap cube
$F D S C_{2^{k}} (1 \leq k \leq d)$	An embeded subgraph of $F D S C_{n} (n = 2^{d})$
$F D S C_{2^{k - 1}} (2 \leq k \leq d)$	A direct embeded subgraph of $F D S C_{2^{k}}$ or a module of $F D S C_{2^{k}}$
${μ^{i} \| 0 \leq i \leq k}$	The interior neighbor set of $μ$ inside the $F D S C_{2^{k - 1}}$ where $μ$ lies
$μ^{k + 1}$	The external neighbor of $μ$ in $F D S C_{2^{k}}$ outside the $F D S C_{2^{k - 1}}$ where $μ$ lies
$M_{u}$	The module which node $u$ is connected to
$M_{S}$	The module set ${M_{t} \| t \in S}$

DOI: 10.7717/peerj-cs.3458/table-2

Construction of a path between any two distinct nodes in $F D S C_{n}$

In this section, we will give two basic algorithms which will be used to build a path between any two distinct nodes in $F D S C_{n}$ . Let $μ = x_{1} x_{2} \dots x_{n}$ and $ν = y_{1} y_{2} \dots y_{n}$ be any two distinct nodes in $F D S C_{n}$ and $k = m a x {i | x_{2^{i - 1} + 1} x_{2^{i - 1} + 2} \dots x_{2^{i}} \neq y_{2^{i - 1} + 1} y_{2^{i - 1} + 2} \dots y_{2^{i}}$ with $2 \leq i \leq d}$ . If $k$ exists, then $x_{1} x_{2} \dots x_{2^{k}} \neq y_{1} y_{2} \dots y_{2^{k}}$ and $x_{2^{k} + 1} x_{2^{k} + 2} \dots x_{n} = y_{2^{k} + 1} y_{2^{k} + 2} \dots y_{n}$ . By Property 1(1), $μ$ and $ν$ are in the same embeded $F D S C_{2^{k}} \cdot x_{2^{k} + 1} x_{2^{k} + 2} \dots x_{2^{d}} (2 \leq k \leq d)$ . Otherwise, $μ$ and $ν$ are in the same embeded $F D S C_{2} \cdot x_{3} x_{4} \dots x_{2^{d}}$ .

If $μ$ and $ν$ are in the same embeded $F D S C_{2^{k}}$ where $2 \leq k < d$ , then they are also in the same embeded $F D S C_{2^{k + 1}}$ . For example, suppose $μ = 00000000$ and $ν = 11110000$ . Then these two nodes are in the same $F D S C_{4} \cdot 0000$ , and we can also consider that $μ$ and $ν$ are in the same $F D S C_{8}$ . Hence, $2^{k}$ is the minimum common dimension of the embeded subgraph where $μ$ and $ν$ lie. We give an algorithm to get the minimum common dimension for $μ$ and $ν$ as follows.

As shown in Fig. 3, for nodes $μ = 00000000$ and $ν = 10110101$ where $d = 3$ , since $x_{5} x_{6} x_{7} x_{8} \neq y_{5} y_{6} y_{7} y_{8}$ , then algorithm MinCommonDimension returns 3. Hence, $2^{3}$ is the minimum common dimension of the embeded subgraph, and $μ$ , $ν$ are in the same embeded $F D S C_{8}$ . For nodes $μ = 00000000$ and $ν = 00110000$ where $d = 3$ , since $x_{5} x_{6} x_{7} x_{8} = y_{5} y_{6} y_{7} y_{8}$ and $x_{3} x_{4} \neq y_{3} y_{4}$ , then algorithm MinCommonDimension returns 2, and $μ$ , $ν$ are in the same embeded $F D S C_{4} \cdot 0000$ . For nodes $μ = 00000000$ and $ν = 10000000$ where $d = 3$ , since $x_{5} x_{6} x_{7} x_{8} = y_{5} y_{6} y_{7} y_{8}$ and $x_{3} x_{4} = y_{3} y_{4}$ , then algorithm MinCommonDimension returns 1, and $μ$ , $ν$ are in the same embeded $F D S C_{2} \cdot 000000$ .

Next, we use a recursive algorithm to build a path between any two different nodes. Let $μ$ and $ν$ be any two distinct nodes in $F D S C_{n}$ . If $μ$ and $ν$ are in the same embeded $F D S C_{2}$ , then $⟨ μ, ν ⟩$ is the required path. If $μ$ and $ν$ are in the same embeded $F D S C_{2^{k}} (2 \leq k \leq d)$ where $2^{k}$ is the minimum common dimension of the embeded subgraph in which $μ$ and $ν$ lie, then $μ$ and $ν$ are in different $F D S C_{2^{k - 1}}$ s. We select nodes $s$ and $t$ where $μ$ and $s$ , $ν$ and $t$ are in the same $F D S C_{2^{k - 1}}$ respectively, and $(s, t)$ is the bridge edge connecting these two $F D S C_{2^{k - 1}} s$ . For nodes $μ$ and $s$ , $ν$ and $t$ , we use the same method to build the paths between them. Therefore, we can adopt a recursive construction approach to build the path between $μ$ and $ν$ . The detailed algorithm is shown as below.

Each node exists in a certain embeded subgraph. In line 1, we get the minimum common dimension of the embeded subgraph where $μ$ and $ν$ lie with Algorithm 1; In lines 2–4, if $μ$ and $ν$ exist in the same $F D S C_{2}$ , we return the required path $⟨ μ, ν ⟩$ , since $F D S C_{2}$ is a complete graph. If $μ$ and $ν$ lie in the same embeded $F D S C_{2^{k}} (2 \leq k \leq d)$ , we need to get the bridge edge which connects the $F D S C_{2^{k - 1}}$ s where $μ$ and $ν$ lie. In line 5, we get node $s$ by replacing $x_{1} x_{2} \dots x_{2^{k - 1}}$ of $μ$ with $y_{2^{k - 1} + 1} y_{2^{k - 1} + 2} \dots y_{2^{k}}$ of $ν$ . In line 6, we get node $t$ by replacing $y_{1} y_{2} \dots y_{2^{k - 1}}$ of $ν$ with $x_{2^{k - 1} + 1} x_{2^{k - 1} + 2} \dots x_{2^{k}}$ of $μ$ . Then, $(s, t)$ is the required bridge edge.

Algorithm 1:

MinCommonDimension (

μ, ν, d

Input: Nodes

μ = x_{1} x_{2} \dots x_{n}

ν = y_{1} y_{2} \dots y_{n}

, and

d \geq 1.

Output: an integer k where 2^k is the minimum common dimension of the embeded subgraph in which μ and ν lie.

1: for

i = d; i \geq 2; i - -

2: if

x_{2^{i - 1} + 1} x_{2^{i - 1} + 2} \dots x_{2^{i}} \neq y_{2^{i - 1} + 1} y_{2^{i - 1} + 2} \dots y_{2^{i}}

then

k \leftarrow i

;

4: return k;

5: end if

6: end for

7: return

k \leftarrow 1

;

DOI: 10.7717/peerj-cs.3458/table-4

Algorithm 2:

QP (

μ, ν, d

Input: Nodes

μ = x_{1} x_{2} \dots x_{n}

ν = y_{1} y_{2} \dots y_{n}

and

d \geq 1

Output: a path P between μ and ν in FDSC_n.

k \leftarrow M i n C o m m o n D i m e n s i o n (μ, ν, d)

;

2: if

k = 1

then

3: return

μ +

“,”

+ ν

;

4: end if

s \leftarrow r e p l a c e (μ, x_{1} x_{2} \dots x_{2^{k - 1}}, y_{2^{k - 1} + 1} y_{2^{k - 1} + 2} \dots y_{2^{k}});

t \leftarrow r e p l a c e (ν, y_{1} y_{2} \dots y_{2^{k - 1}}, x_{2^{k - 1} + 1} x_{2^{k - 1} + 2} \dots x_{2^{k}});

7: if

s \neq μ

then

8: if

t \neq v

then

P \leftarrow Q P (μ, s, k - 1) +

“,”

+ Q P (t, ν, k - 1)

;

10: else

11:

P \leftarrow Q P (μ, s, k - 1) +

“,”

+ t

;

12: end if

13: else

14: if

t \neq v

then

15:

P \leftarrow s +

“,”

+ Q P (t, ν, k - 1)

;

16: else

17:

P \leftarrow s +

“,”

+ t

;

18: end if

19: end if

20: return P;

DOI: 10.7717/peerj-cs.3458/table-5

As shown in Fig. 3, for nodes $μ = 00000000$ and $ν = 10110101$ where $d = 3$ , $μ$ , $ν \in V (F D S C_{8})$ , $μ \in V (F D S C_{4} \cdot 0000)$ and $ν \in V (F D S C_{4} \cdot 0101)$ . In this case, $k = 3$ . Then, we have $s = 01010000$ , $t = 00000101$ and $(s, t)$ is the bridge edge which connects subgraphs $F D S C_{4} \cdot 0000$ and $F D S C_{4} \cdot 0101$ . For nodes $μ = 00000000$ and $ν = 00110000$ where $d = 3$ , $μ$ and $ν$ are in the same $F D S C_{4} \cdot 0000$ . In this case, $k = 2$ . Then, we have $s = 11000000$ and $t = 00110000$ . Subgraphs $F D S C_{2} \cdot 000000$ and $F D S C_{2} \cdot 110000$ are connected by the bridge edge (11000000, 00110000).

For node $μ$ and $s$ , we apply the recursive call of algorithm QP to build the path between $μ$ and $s$ . If $μ = s$ , use node $s$ to represent the path between $μ$ and $s$ . The same method is used to build the path between $ν$ and $t$ . In lines 7–19, we concatenate the path between $μ$ and $s$ , as well as the path between $ν$ and $t$ to obtain the path between $μ$ and $ν$ .

Algorithm QP first determines the minimum common subgraph $F D S C_{2^{k}}$ with $2 \leq k \leq d$ where $μ$ and $ν$ are located, such that $μ$ and $ν$ are in two different modules of $F D S C_{2^{k}}$ , named $D_{0}$ and $D_{1}$ . Then select the connecting edge between $D_{0}$ and $D_{1}$ . Note that the recursive path construction only occurs within the modules $D_{0}$ and $D_{1}$ , and does not involve nodes from other modules of $F D S C_{2^{k}}$ .

Construction of node disjoint paths in $F D S C_{n}$

In this section, we will give some algorithms to construct one-to-one disjoint paths between any two disctinct nodes $μ$ and $ν$ in $F D S C_{n}$ , where $μ$ and $ν$ are in the same embeded subgraph $F D S C_{2^{k}} (1 \leq k \leq d)$ .

Lemma 1. Let $μ$ be any vertex in the embeded $F D S C_{2^{k}}$ of $F D S C_{n}$ with $1 \leq k \leq d - 1$ . Then for each $i$ with $k + 2 \leq i \leq d + 1$ , $μ$ and $μ^{i}$ belong to the same embeded $F D S C_{2^{i - 1}}$ , but in different $F D S C_{2^{i - 2}} s$ .

$μ^{i} = {\begin{matrix} {\bar{s}}_{1} {\bar{s}}_{2} s_{3} = {\bar{x}}_{1} {\bar{x}}_{2} \dots {\bar{x}}_{2^{i - 2}} {\bar{x}}_{2^{i - 2} + 1} {\bar{x}}_{2^{i - 2} + 2} \dots {\bar{x}}_{2^{i - 1}} s_{3} & i f s_{1} = s_{2} \\ s_{2} s_{1} s_{3} = x_{2^{i - 2} + 1} x_{2^{i - 2} + 2} \dots x_{2^{i - 1}} x_{1} x_{2} \dots x_{2^{i - 2}} s_{3} & i f s_{1} \neq s_{2} \end{matrix}$

Obviously, only the leftmost $2^{i - 1}$ -digit binary strings of $μ$ and $μ^{i}$ are different, then $μ$ and $μ^{i}$ belong to the same embeded $F D S C_{2^{i - 1}} \cdot s_{3}$ . Besides, $μ$ belongs to the embeded $F D S C_{2^{i - 2}} \cdot s_{2} s_{3}$ , and $μ^{i}$ belongs to the embeded $F D S C_{2^{i - 2}} \cdot {\bar{s}}_{2} s_{3}$ or $F D S C_{2^{i - 2}} \cdot s_{1} s_{3}$ . Hence, $μ$ and $μ^{i}$ belong to different embeded $F D S C_{2^{i - 2}}$ s of the same embeded $F D S C_{2^{i - 1}} \cdot s_{3}$ .

As seen in Fig. 3, suppose that $μ = 00000000$ which lies in the embeded $F D S C_{2} \cdot 000000$ of $F D S C_{8}$ . Then, $μ^{3} = 11110000$ and $μ^{4} = 11111111$ . We can see that $μ$ lies in $F D S C_{2} \cdot 000000$ , $μ^{3}$ lies in $F D S C_{2} \cdot 110000$ , while $μ$ and $μ^{3}$ belong to the same embeded $F D S C_{4} \cdot 0000$ . Similarly, $μ$ and $μ^{4}$ belong to the same $F D S C_{8}$ , while $μ$ belongs to the embeded $F D S C_{4} \cdot 0000$ and $μ^{4}$ belongs to the embeded $F D S C_{4} \cdot 1111$ .

Lemma 2. Suppose nodes $μ$ and $ν$ are in the same embeded $F D S C_{2^{k}}$ of $F D S C_{n}$ with $1 \leq k \leq d - 1$ , then for each $i$ with $k + 2 \leq i \leq d + 1$ , $μ^{i}$ and $ν^{i}$ are in the same embeded $F D S C_{2^{i - 1}}$ , but in the embeded $F D S C_{2^{i - 2}} s$ in which $μ$ and $ν$ don’t lie.

Proof. Let $μ = x_{1} x_{2} \dots x_{n}$ = $s_{1} s_{2} s_{3}$ , $s_{1} = x_{1} x_{2} \dots x_{2^{i - 2}}$ , $s_{2} = x_{2^{i - 2} + 1} x_{2^{i - 2} + 2} \dots x_{2^{i - 1}}$ and $s_{3} = x_{2^{i - 1} + 1} x_{2^{i - 1} + 2} \dots x_{2^{d}}$ with $k + 2 \leq i \leq d + 1$ . Meanwhile, Let $ν = y_{1} y_{2} \dots y_{n}$ = $t_{1} t_{2} t_{3}$ , $t_{1} = y_{1} y_{2} \dots y_{2^{i - 2}}$ , $t_{2} = y_{2^{i - 2} + 1} y_{2^{i - 2} + 2} \dots y_{2^{i - 1}}$ and $t_{3} = y_{2^{i - 1} + 1} y_{2^{i - 1} + 2} \dots y_{2^{d}}$ . Since $μ$ and $ν$ are in the same embeded $F D S C_{2^{k}}$ , we have $x_{2^{k} + 1} x_{2^{k} + 2} \dots x_{n} = y_{2^{k} + 1} y_{2^{k} + 2} \dots y_{n}$ . Since $i - 1 > k$ , then $s_{3} = t_{3}$ .

By Lemma 1, $μ$ and $μ^{i}$ are in the same embeded $F D S C_{2^{i - 1}} \cdot s_{3}$ for each $i$ with $k + 2 \leq i \leq d + 1$ . For the same reason, $ν$ and $ν^{i}$ are in the same embeded $F D S C_{2^{i - 1}} \cdot t_{3}$ . Hence, $μ^{i}$ and $ν^{i}$ are in the same embeded $F D S C_{2^{i - 1}} \cdot s_{3}$ for each $i$ with $k + 2 \leq i \leq d + 1$ .

Again, by Lemma 1, $μ$ and $μ^{i}$ are in different $F D S C_{2^{i - 2}}$ s of $F D S C_{2^{i - 1}} \cdot s_{3}$ for each $i$ with $k + 2 \leq i \leq d + 1$ . For the same reason, $ν$ and $ν^{i}$ are in different $F D S C_{2^{i - 2}}$ s of $F D S C_{2^{i - 1}} \cdot s_{3}$ . Since $i - 2 \geq k$ , $μ$ and $ν$ are in the same embeded $F D S C_{2^{i - 2}}$ of $F D S C_{2^{i - 1}} \cdot s_{3}$ . Hence, for each $i$ with $k + 2 \leq i \leq d + 1$ , $μ^{i}$ and $ν^{i}$ are in the embeded $F D S C_{2^{i - 2}} s$ in which $μ$ and $ν$ do not lie.

$μ^{i}$ and $ν^{i}$ can lie in the same $F D S C_{2^{i - 2}}$ or in different $F D S C_{2^{i - 2}} s$ . As seen in Fig. 3, we suppose $μ = 00000000$ and $ν = 11000000$ , which lie in the same $F D S C_{2} \cdot 000000$ . Then we have $μ^{3} = 11110000, μ^{4} = 11111111, ν^{3} = 00110000$ , and $ν^{4} = 00001100$ . We can see that $μ^{3}$ and $ν^{3}$ lie in the same $F D S C_{4} \cdot 0000$ , and the same $F D S C_{2} \cdot 110000$ . For $μ^{4}$ and $ν^{4}$ , they lie in the same $F D S C_{8}$ , but in different embeded $F D S C_{4} s$ which are $F D S C_{4} \cdot 1111$ and $F D S C_{4} \cdot 1100$ .

Lemma 3. Suppose nodes $μ$ and $ν$ are in the same embeded $F D S C_{2^{k}}$ of $F D S C_{n}$ with $1 \leq k \leq d - 1$ , then for each $i$ with $k + 2 \leq i \leq d$ , $μ^{i}$ and $ν^{i}$ lie in the same embeded subgraph $F D S C_{2^{i - 1}}$ , which is different from the $F D S C_{2^{i - 1}}$ s where $μ^{i + 1}$ and $ν^{i + 1}$ are located.

Proof. Let $μ = x_{1} x_{2} \dots x_{n}$ . Then $μ$ and $ν$ are in the same embeded $F D S C_{2^{k}} \cdot x_{2^{k} + 1} x_{2^{k} + 2} \dots x_{2^{d}}$ . By Lemma 2, $μ^{i}$ and $ν^{i}$ lie in the same embeded subgraph $F D S C_{2^{i - 1}} \cdot x_{2^{i - 1} + 1} x_{2^{i - 1} + 2} \dots x_{2^{d}}$ , while $μ^{i + 1}$ and $ν^{i + 1}$ lie in the same embeded subgraph $F D S C_{2^{i}} \cdot x_{2^{i} + 1} x_{2^{i} + 2} \dots x_{2^{d}}$ , where $k + 2 \leq i \leq d$ . Since $k + 2 \leq i$ , then $i - 1 > k$ . Hence, $μ$ and $ν$ are in the same embeded subgraph $F D S C_{2^{i - 1}} \cdot x_{2^{i - 1} + 1} x_{2^{i - 1} + 2} \dots x_{2^{d}}$ as $μ^{i}$ and $ν^{i}$ . By Lemma 2, $μ^{i + 1}$ and $ν^{i + 1}$ lie in the embeded $F D S C_{2^{i - 1}} s$ in which $μ$ and $ν$ don’t lie. Hence, $μ^{i}$ and $ν^{i}$ lie in the same embeded subgraph $F D S C_{2^{i - 1}}$ , which is different from the $F D S C_{2^{i - 1}}$ s where $μ^{i + 1}$ and $ν^{i + 1}$ are located.

Let $μ = 00000000$ and $ν = 01000000$ where $μ$ and $ν$ are in the same embeded $F D S C_{2}$ . Then we have $μ^{3} = 11110000, μ^{4} = 11111111, ν^{3} = 00010000$ and $ν^{4} = 00000100$ . We can see that $μ^{3}$ and $ν^{3}$ lie in the same embeded $F D S C_{4} \cdot 0000$ , which is different from $F D S C_{4} \cdot 1111$ and $F D S C_{4} \cdot 0100$ where $μ^{4}$ and $ν^{4}$ are located. Please see Fig. 3.

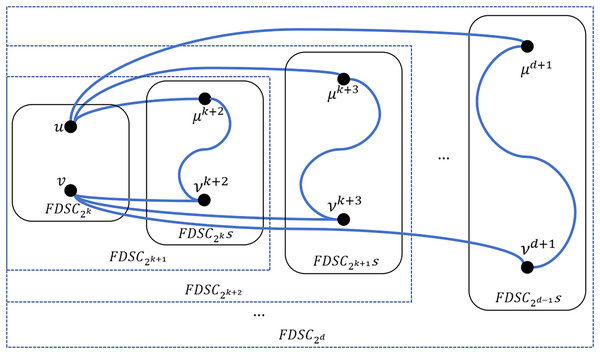
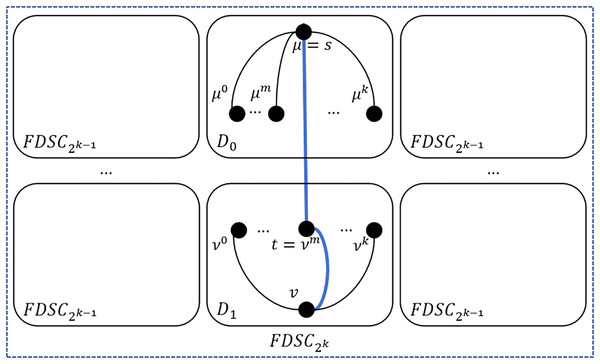
Lemma 4. Let $μ$ and $ν$ be any two distinct nodes in the same embeded $F D S C_{2^{k}}$ of $F D S C_{n}$ , where $n = 2^{d}$ , $d \geq 1$ and $1 \leq k \leq d - 1$ . There exist $d - k$ disjoint paths between $μ$ and $ν$ out of $F D S C_{2^{k}}$ .

Proof. By Lemma 2, $μ$ has an $i$ -neighbor $μ^{i}$ and $ν$ has an $i$ -neighbor $ν^{i}$ , which lie in the same embeded $F D S C_{2^{i - 1}}$ of $F D S C_{n}$ for each $i$ with $k + 2 \leq i \leq d + 1$ . And we can use algorithm QP to construct a path $P_{i} = ⟨ μ, Q P (μ^{i}, ν^{i}, d), ν ⟩$ between $μ$ and $ν$ which traverses $μ^{i}$ and $ν^{i}$ for each $i$ with $k + 2 \leq i \leq d + 1$ . The detailed algorithm is shown as below.

In Algorithm 3, a loop is used to build $d - k$ node disjoint paths between $μ$ and $ν$ out of $F D S C_{2^{k}}$ , where $μ$ and $ν$ are in a certain embeded $F D S C_{2^{k}}$ .The loop will take $d - k$ iterations. Therefore, it takes $O (d - k)$ time. In lines 2–9, we get the $i$ -neighbor $μ^{i}$ of $μ$ . And in lines 10–17, we get the $i$ -neighbor $ν^{i}$ of $ν$ . In line 18, we use algorithm QP to obtain the path between $μ$ and $ν$ which traverses $μ^{i}$ and $ν^{i}$ . In line 20, we return the constructed $d - k$ node disjoint paths between $μ$ and $ν$ out of $F D S C_{2^{k}}$ .

Algorithm 3:

DisjointPathOutFDSCK (

μ, ν, k, d

Input: Nodes

μ = x_{1} x_{2} \dots x_{n}

ν = y_{1} y_{2} \dots y_{n}

d \geq 1

and

1 \leq k \leq d - 1

Output: d − k disjoint paths

{P_{i} | k + 2 \leq i \leq d + 1}

in a FDSC_2^d.

1: for

i = k + 2; i < = d + 1; i + +

s_{1} \leftarrow x_{1} x_{2} \dots x_{2^{i - 2}}

;

s_{2} \leftarrow x_{2^{i - 2} + 1} x_{2^{i - 2} + 2} \dots x_{2^{i - 1}}

;

s_{3} \leftarrow x_{2^{i - 1} + 1} x_{2^{i - 1} + 2} \dots x_{2^{d}}

;

5: if

s_{1} = s_{2}

then

μ^{i} \leftarrow {\bar{s}}_{1} {\bar{s}}_{2} s_{3}

;

7: else

μ^{i} \leftarrow s_{2} s_{1} s_{3}

;

9: end if

10:

t_{1} \leftarrow y_{1} y_{2} \dots y_{2^{i - 2}}

;

11:

t_{2} \leftarrow y_{2^{i - 2} + 1} y_{2^{i - 2} + 2} \dots y_{2^{i - 1}}

;

12:

t_{3} \leftarrow y_{2^{i - 1} + 1} y_{2^{i - 1} + 2} \dots y_{2^{d}}

;

13: if

t_{1} = t_{2}

then

14:

ν^{i} \leftarrow {\bar{t}}_{1} {\bar{t}}_{2} t_{3}

;

15: else

16:

ν^{i} \leftarrow t_{2} t_{1} t_{3}

;

17: end if

18:

P_{i} \leftarrow ⟨ μ, Q P (μ^{i}, ν^{i}, d), ν ⟩

;

19: end for

20: return

{P_{i} | k + 2 \leq i \leq d + 1}

;

DOI: 10.7717/peerj-cs.3458/table-6

According to Lemma 2, nodes $μ^{k + 2}$ and $ν^{k + 2}$ are in the same embeded $F D S C_{2^{k + 1}}$ , but in the embeded $F D S C_{2^{k}} s$ in which $μ$ and $ν$ don’t lie. Hence, algorithm QP $(μ^{k + 2}, ν^{k + 2}, d)$ only occupies the embeded $F D S C_{2^{k}}$ s where $μ^{k + 2}$ and $ν^{k + 2}$ are located and where $μ$ and $ν$ don’t lie. By Lemma 2 and Lemma 3, for each $i$ with $k + 2 \leq i \leq d$ , nodes $μ^{i + 1}$ and $ν^{i + 1}$ are in the same embeded $F D S C_{2^{i}}$ , but in the embeded $F D S C_{2^{i - 1}} s$ in which $μ^{i}$ and $ν^{i}$ don’t lie. Hence, algorithm QP $(μ^{i + 1}, ν^{i + 1}, d)$ only occupies the embeded $F D S C_{2^{i - 1}}$ s where $μ^{i + 1}$ and $ν^{i + 1}$ are located and where $μ^{i}$ and $ν^{i}$ don’t lie. Hence, each path in algorithm DisjointPathOutFDSCK is disjoint. Then, there exist $d - k$ disjoint paths between $μ$ and $ν$ out of $F D S C_{2^{k}}$ . Please see Fig. 4 for an illustration.

An example of one to one node disjoint paths between
$\mu$μ
and
$\nu$ν
out of
$FDS{C_{{2^k}}}$FDSC2k
. — Figure 4: An example of one to one node disjoint paths between $μ$ and $ν$ out of $F D S C_{2^{k}}$ .

Download full-size image

DOI: 10.7717/peerj-cs.3458/fig-4

Each pair of $μ^{i}$ and $ν^{i}$ can lie in different $F D S C_{2^{i - 1}}$ s. In the worst case, $P_{d + 1}$ is the longest path which occupies two embeded $F D S C_{2^{d - 1}}$ s. Since the diameter of $F D S C_{n}$ is $n - 1$ , then in theory, the maximum length of these paths is $L (P_{d + 1}) = n + 1$ .

Lemma 5. Let $μ$ and $ν$ be any two distinct nodes in the same embeded $F D S C_{2}$ of $F D S C_{n}$ ( $n = 2^{d}$ and $d \geq 1$ ). There exist $d + 2$ node disjoint paths between $μ$ and $ν$ in $F D S C_{n}$ .

Proof. Let $μ = x_{1} x_{2} \dots x_{n}$ and $ν = y_{1} y_{2} \dots y_{n}$ . In this case, $x_{3} \dots x_{n} = y_{3} \dots y_{n}$ , then $μ, ν \in V (F D S C_{2} \cdot x_{3} \dots x_{n})$ . Since $F D S C_{2} \cdot x_{3} \dots x_{n}$ is a complete graph, we can construct 3 disjoint paths between $μ$ and $ν$ with algorithm DisjointPathInFDSC2 ( $μ, ν$ ) (Algorithm 4).

Algorithm 4:

DisjointPathInFDSC2

(μ, ν, d

Input: Nodes

μ = x_{1} x_{2} \dots x_{n}

ν = y_{1} y_{2} \dots y_{n}

, and

d \geq 1

Output: 3 disjoint paths

P_{0}, P_{1}, P_{2}

in an embeded FDSC₂.

n o d e s \leftarrow {00 x_{3} \dots x_{n}, 01 x_{3} \dots x_{n}, 10 x_{3} \dots x_{n}, 11 x_{3} \dots x_{n}} - {μ, ν}

2: for

i = 0; i \leq 1; i + +

P_{i} \leftarrow ⟨ μ, n o d e s [i], ν ⟩

;

4: end for

P_{2} \leftarrow ⟨ μ, ν ⟩

;

6: return

{P_{i} | 0 \leq i \leq 2}

;

DOI: 10.7717/peerj-cs.3458/table-7

Then, we use algorithm DisjointPathOutFDSCK to construct disjoint paths out of $F D S C_{2} \cdot x_{3} \dots x_{n}$ .

Algorithm 5 is used to build $d + 2$ node disjoint paths between $μ$ and $ν$ , where $μ$ , $ν \in V (F D S C_{2} \cdot x_{3} \dots x_{n})$ . In line 1, we get three disjoint paths in $F D S C_{2} \cdot x_{3} \dots x_{n}$ , which takes $O (1)$ time. In line 3, we use algorithm DisjointPathOutFDSCK to obtain $d - 1$ disjoint paths between $μ$ and $ν$ out of $F D S C_{2} \cdot x_{3} \dots x_{n}$ . Since algorithm DisjointPathOutFDSCK takes $O (d)$ time, the time complexity of Algorithm 5 is $O (d) + O (1) = O (d)$ . In line 5, we return the constructed $d + 2$ node disjoint paths between $μ$ and $ν$ . The theoretical maximum length of ${P_{i} | 0 \leq i \leq d + 1}$ is $L (P_{d + 1}) = n + 1$ where $d \geq 2$ . If $d = 1$ , then Algorithm 5 only needs to construct three disjoint paths in $F D S C_{2}$ . The theoretical maximum length of these three disjoint paths in $F D S C_{2}$ is 2. Please see Fig. 5 for an illustration.

Algorithm 5:

O2OInFDSC2

(μ, ν, d

Input: Nodes

μ = x_{1} x_{2} \dots x_{n}

ν = y_{1} y_{2} \dots y_{n}

and

d \geq 1

Output:

d + 2

disjoint paths

{P_{0}, P_{1}, \dots, P_{d + 1}}

F D S C_{2^{d}}

{P_{i} | 0 \leq i \leq 2} \leftarrow

DisjointPathInFDSC2(

μ, ν

);

2: if

d \geq 2

then

{P_{i} | 3 \leq i \leq d + 1} \leftarrow

DisjointPathOutFDSCK(

μ, ν, 1, d

);

4: end if

5: return

{P_{i} | 0 \leq i \leq d + 1}

;

DOI: 10.7717/peerj-cs.3458/table-8

An example of one-to-one node disjoint paths between
$\mu$μ
and
$\nu$ν
in the same
$FDS{C_{2}}$FDSC2
. — Figure 5: An example of one-to-one node disjoint paths between $μ$ and $ν$ in the same $F D S C_{2}$ .

Download full-size image

DOI: 10.7717/peerj-cs.3458/fig-5

Lemma 6. Let $μ$ and $ν$ be any two distinct nodes in the same embeded $F D S C_{4}$ of $F D S C_{n}$ ( $n = 2^{d}$ and $d \geq 1$ ). There exist $d + 2$ node disjoint paths between $μ$ and $ν$ in $F D S C_{n}$ .

Proof. Suppose that $μ$ and $ν$ are any two distinct nodes in the same embeded $F D S C_{4}$ named D. First, we will construct four disjoint paths between $μ$ and $ν$ in D. According to the locations of $μ$ and $ν$ , we have the following two cases.

Case 1. $μ$ and $ν$ are in the same $F D S C_{2}$ of D.

We can easily get the four disjoint paths with algorithm O2OInFDSC2( $μ, ν, d$ ).

Case 2. $μ$ and $ν$ are in different $F D S C_{2}$ s of D.

Suppose that $μ$ is in $D_{0}$ and $ν$ is in $D_{1}$ , where $D_{0}$ and $D_{1}$ are two different $F D S C_{2}$ s of D. By Property 1(3), each node has three neighbors in $F D S C_{2}$ . Then, let $U = {μ^{0}, μ^{1}, μ^{2}, μ}$ in $D_{0}$ and $V = {ν^{0}, ν^{1}, ν^{2}, ν}$ in $D_{1}$ . We can build four disjoint paths with the following steps.

Step 1: For each $s$ in U, if $s$ is adjacent with a node $t$ in V, build a path as follows. Then remove $s$ from U and $t$ from V.

(6.1) $P = {\begin{matrix} ⟨ μ, ν ⟩ & i f s = μ a n d t = ν, \\ ⟨ μ, s, ν ⟩ & i f s \neq μ a n d t = ν, \\ ⟨ μ, t, ν ⟩ & i f s = μ a n d t \neq ν, \\ ⟨ μ, s, t, ν ⟩ & i f s \neq μ a n d t \neq ν . \end{matrix} .$

Step 2: For each $s$ in U, if there is a node $t \in V$ such that $s$ and $t$ are connected to the same $F D S C_{2}$ , build a path as follows. Then remove $s$ from U and $t$ from V.

(6.2) $P = {\begin{matrix} ⟨ μ, Q P (μ^{3}, ν^{3}, 2), ν ⟩ & i f s = μ a n d t = ν, \\ ⟨ μ, s, Q P (s^{3}, ν^{3}, 2), ν ⟩ & i f s \neq μ a n d t = ν, \\ ⟨ μ, Q P (μ^{3}, t^{3}, 2), t, ν ⟩ & i f s = μ a n d t \neq ν, \\ ⟨ μ, s, Q P (s^{3}, t^{3}, 2), t, ν ⟩ & i f s \neq μ a n d t \neq ν . \end{matrix} .$

Step 3: For each $s$ in U, if there is a node $t \in V$ such that $s$ and $t$ are connected to different $F D S C_{2}$ s, build a path using the method of Step 2. Then remove $s$ from U and $t$ from V.

By Property 2, there exist one or two edges between $D_{0}$ and $D_{1}$ . Then, we have the following two subcases.

Case 2.1. there exist two edges between $D_{0}$ and $D_{1}$ .

In this case, we can construct two disjoint paths between $μ$ and $ν$ with Step 1, and two disjoint paths between $μ$ and $ν$ with Step 2. Hence, there exist four disjoint paths between $μ$ and $ν$ .

Case 2.2. there exists one edge between $D_{0}$ and $D_{1}$ .

In this case, assume the other two modules of D are named $D_{2}$ and $D_{3}$ . With Step 1, we can construct one disjoint path between $μ$ and $ν$ . In Step 2, for each pair $s \in U$ and $t \in V$ where $s^{3}$ and $t^{3}$ are in the same $D_{i} (2 \leq i \leq 3)$ , we can construct a disjoint path according to Eq. (6.2) where QP $(s^{3}, t^{3}, 2)$ returns $⟨ s^{3}, t^{3} ⟩$ . Hence, there exist two disjoint paths between $μ$ and $ν$ with Step 2. Let $M_{i} (2 \leq i \leq 3)$ be the subgraph of $D_{i}$ , containing the nodes not used in Step 2. Since $D_{i}$ is a complete graph, then $M_{i}$ is a connected graph. Since the bridge edge between $D_{2}$ and $D_{3}$ exists, $M_{2} \cup M_{3}$ is connected. Each node in $U \cup V$ is connected to a different node out of $D_{0} \cup D_{1}$ , then $s \in U$ and $t \in V$ in Step 3 can only connected to $M_{2} \cup M_{3}$ , and there exists one disjoint path between $μ$ and $ν$ with Step 3. Hence, there exist 4 disjoint paths between $μ$ and $ν$ .

For example, in Fig. 2, suppose $μ = 1000, ν = 0010$ , $U = {1100, 0000, 0100, 1000}$ and $V = {0110, 1010, 1110, 0010}$ . With Step 1, we can construct a disjoint path $⟨ 1000, 0010 ⟩$ , then $U = {1100, 0000, 0100}$ and $V = {0110, 1010, 1110}$ . In Step 2, node pairs ${1100, 1110}$ and ${0100, 0110}$ are connected to the same $F D S C_{2}$ , respectively. We can construct two disjoint paths $⟨ 1000, 1100, 0011, 1011, 1110, 0010 ⟩$ and $⟨ 1000, 0100, 0001, 1001, 0110, 0010 ⟩$ , then $U = {0000}$ and $V = {1010}$ . We can see that $M_{2} \cup M_{3}$ is connected where $V (M_{2} \cup M_{3}) = {1111, 0111, 1101, 0101}$ . In Step 3, $0000 \in U$ is connected to $1111 \in V (M_{2} \cup M_{3})$ and $1010 \in V$ is connected to $0101 \in V (M_{2} \cup M_{3})$ . We can build a disjoint path $⟨ 1000, 0000, 1111, 0111, 1101, 0101, 1010, 0010 ⟩$ . Hence, there exist 4 disjoint paths between 1000 and 0010.

After building four disjoint paths in the embeded $F D S C_{4}$ , we can build $d - 2$ disjoint paths out of the embeded $F D S C_{4}$ with algorithm DisjointPathOutFDSCK. Hence, there exist $d + 2$ disjoint paths between any two distinct nodes $μ$ and $ν$ in $F D S C_{n}$ .

Algorithm O2OInFDSC4 is used to build $d + 2$ node disjoint paths between $μ$ and $ν$ , where $μ$ and $ν$ are in the same embeded $F D S C_{4}$ . In lines 1–3, if $μ$ and $ν$ are in the same embeded FDSC₂, we can get $d + 2$ disjoint paths with algorithm O2OInFDSC2. In lines 4–9, we use algorithm DisjointPathInFDSC4 (Algorithm 6) to construct four disjoint paths in the embeded $F D S C_{4}$ , which takes $O (1)$ time. Then use DisjointPathOutFDSCK to obtain $d - 2$ disjoint paths between $μ$ and $ν$ out of the embeded $F D S C_{4}$ , which takes $O (d)$ time. Therefore, the time complexity of Algorithm 7 is $O (1) + O (d) = O (d)$ . In line 10, we return the constructed $d + 2$ node disjoint paths between $μ$ and $ν$ . The theoretical maximum length of ${P_{i} | 0 \leq i \leq d + 1}$ is $L (P_{d + 1}) = n + 1$ where $d \geq 2$ . If $d = 2$ , then Algorithm 7 needs to construct 4 disjoint paths in $F D S C_{4}$ . The theoretical maximum length of 4 disjoint paths in $F D S C_{4}$ is 7, and the path is generated in Step 3.

Algorithm 6:

DisjointPathInFDSC4 (

μ, ν, d

Input: Nodes

μ = x_{1} x_{2} \dots x_{n}

ν = y_{1} y_{2} \dots y_{n}

and

d \geq 2

Output: 4 disjoint paths between μ and ν in an embeded FDSC₄.

1: paths ← [];

U \leftarrow {μ^{0}, μ^{1}, μ^{2}, μ}

;

V \leftarrow {ν^{0}, ν^{1}, ν^{2}, ν}

;

2: for each

s \in U

do Δ Step 1

3: for each

t \in V

4: if isAdjacent(s, t) then

5: build a path P according to Eq. (6.1);

6: paths.append(P);

7: U.remove(s); V.remove(t);

8: end if

9: end for

10: end for

11: for each

s \in U

do Δ Step 2

12: for each

t \in V

13: if s and t are connected to the same FDSC₂ then

14: build a path P according to Eq. (6.2);

15: paths.append(P);

16: U.remove(s); V.remove(t);

17: end if

18: end for

19: end for

20: for each

s \in U

do Δ Step 3

21: for each

t \in V

22: if s and t are connected to different FDSC₂s then

23: build a path P according to Eq. (6.2);

24: paths.append(P);

25: U.remove(s); V.remove(t);

26: end if

27: end for

28: end for

29: return paths;

DOI: 10.7717/peerj-cs.3458/table-9

Algorithm 7:

O2OInFDSC4(

μ, ν, d

Input: Nodes

μ = x_{1} x_{2} \dots x_{n}

ν = y_{1} y_{2} \dots y_{n}

, and

d \geq 2

Output:

d + 2

disjoint paths

{P_{0}, P_{1}, \dots, P_{d + 1}}

F D S C_{2^{d}}

1: if μ and ν are in the same embeded FDSC₂ then

{P_{i} | 0 \leq i \leq d + 1} \leftarrow

O2OInFDSC2

(μ, ν, d

);

3: end if

4: if μ and ν are in different embeded FDSC₂s then

{P_{i} | 0 \leq i \leq 3} \leftarrow

DisjointPathInFDSC4

(μ, ν, d

);

6: if

d > 2

then

{P_{i} | 4 \leq i \leq d + 1} \leftarrow

DisjointPathOutFDSCK(

μ, ν, 2, d

);

8: end if

9: end if

10: return

{P_{i} | 0 \leq i \leq d + 1}

;

DOI: 10.7717/peerj-cs.3458/table-10

Lemma 7. Let $μ$ be any node in the embeded $F D S C_{2^{k}}$ with identifier B in $F D S C_{n}$ ( $n = 2^{d}$ , $d \geq 3$ and $3 \leq k \leq d$ ) and $U = {μ^{0}, μ^{1}, \dots, μ^{k}}$ . Each $μ^{i} (0 \leq i \leq k)$ in U is connected to a different module of $F D S C_{2^{k}} \cdot B$ .

Proof. Suppose that $μ^{i} \in U$ and $μ^{j} \in U$ are in $D_{B_{i}}$ , and they are connected to the same $D_{B_{j}}$ , where $D_{B_{i}}$ and $D_{B_{j}}$ are two modules of $F D S C_{2^{k}} \cdot B$ . By Property 2, we have $μ^{i} = B_{i} B_{i} B$ and $μ^{j} = {\bar{B}}_{i} B_{i} B$ , or vice versa, where $B_{i}$ is a $2^{k - 1}$ -digit binary string. Hence, $μ^{i}$ and $μ^{j}$ are in the same embeded $F D S C_{2^{k - 1}} \cdot B_{i} B$ , but in different embeded $F D S C_{2^{k - 2}}$ s of $F D S C_{2^{k - 1}} \cdot B_{i} B$ . According to the definition of $F D S C_{n}$ , $(μ^{i}, μ^{j}) \in E (F D S C_{2^{k - 1}} \cdot B_{i} B)$ . Then $μ, μ^{i}$ and $μ^{j}$ form a triangle. There is no triangles in $D S C_{n}$ , and for $F D S C_{n}$ , an $e (f)$ -edge is added for each node in the embeded $F D S C_{2}$ s. Hence, there only exist trangles in the embeded $F D S C_{2}$ s in $F D S C_{n}$ . Then, $μ^{i}$ and $μ^{j}$ should be in the same embeded $F D S C_{2}$ , which conflicts with that $μ^{i}$ and $μ^{j}$ are in different embeded $F D S C_{2^{k - 2}}$ s. Hence, each $μ^{i} (0 \leq i \leq k)$ in U is connected to a different module of $F D S C_{2^{k}} \cdot B$ .

Let $μ = 00000000$ in $F D S C_{4} \cdot 0000$ and $U = {μ^{0} = 01000000, μ^{1} = 10000000, μ^{2} = 11000000}$ . We can see that each element in U is connected to a different element in ${F D S C_{2} \cdot 100000, F D S C_{2} \cdot 110000, F D S C_{2} \cdot 010000}$ in Fig. 3.

Lemma 8. Let $μ$ and $ν$ be any two nodes in different embeded $F D S C_{2^{k - 1}}$ s of the same embeded $F D S C_{2^{k}}$ in $F D S C_{n}$ where $n = 2^{d}$ , $d \geq 3$ and $3 \leq k \leq d$ . There exist $d + 2$ node disjoint paths between $μ$ and $ν$ in $F D S C_{n}$ .

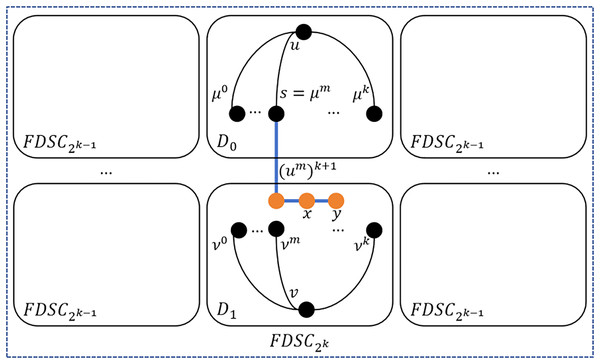
Proof. Suppose D is the embeded $F D S C_{2^{k}}$ , $D_{0}$ and $D_{1}$ are two embeded $F D S C_{2^{k - 1}}$ s of D where $μ \in V (D_{0})$ and $ν \in V (D_{1})$ . By Property 1(2), each node has $k + 1$ neighbors in $F D S C_{2^{k - 1}}$ . Let $U_{I} = {μ^{0}, μ^{1}, \dots, μ^{k}}$ in $D_{0}$ , $U = U_{I} \cup {μ}$ , $V_{I} = {ν^{0}, ν^{1}, \dots, ν^{k}}$ in $D_{1}$ , and $V = V_{I} \cup {ν}$ . First, we construct $k + 2$ disjoint paths between $μ$ and $ν$ in D. Then use algorithm DisjointPathOutFDSCK to obtain the $d - k$ disjoint paths between $μ$ and $ν$ out of D. Considering the locations of $μ$ and $ν$ in $F D S C_{n}$ , we have the following steps to construct $d + 2$ disjoint paths.

Step 1: Identify the vertex pairs $s \in U$ and $t \in V$ such that $s$ and $t$ are directly connected. If such pairs are found, for each pair of $s$ and $t$ , use the following method to construct a path P between $μ$ and $ν$ , and then remove $s$ from U and $t$ from V. Please see Fig. 6 for an illustration. In this case, $s = μ$ is directly connected to $t = ν^{m}$ , then there exists a path $⟨ μ, ν^{m}, ν ⟩$ .

(7.1) $P = {\begin{matrix} ⟨ μ, ν ⟩ & i f s = μ a n d t = ν, \\ ⟨ μ, s, ν ⟩ & i f s \neq μ a n d t = ν, \\ ⟨ μ, t, ν ⟩ & i f s = μ a n d t \neq ν, \\ ⟨ μ, s, t, ν ⟩ & i f s \neq μ a n d t \neq ν . \end{matrix}$

Figure 6: An illustration of step 1.

Download full-size image

DOI: 10.7717/peerj-cs.3458/fig-6

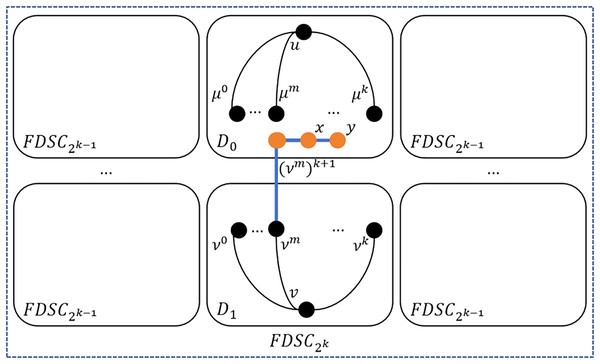
Step 2: Identify the vertex pairs $s \in U$ and $t \in V$ such that the external neighbor $s^{k + 1}$ of $s$ in $D_{1}$ is directly connected to $t$ . If such pairs are found, for each pair of $s$ and $t$ , use the following method to construct a path between $μ$ and $ν$ , and then remove $s$ from U and $t$ from V. Please see Fig. 7 for an illustration. In this case, $s = μ^{m}$ , whose external neighbor $(μ^{m})^{k + 1}$ is directly connected to $t = ν^{m}$ , then there exists a path $⟨ μ, μ^{m}, (μ^{m})^{k + 1}, ν^{m}, ν ⟩$ .

(7.2) $P = {\begin{matrix} ⟨ μ, s^{k + 1}, ν ⟩ & i f s = μ a n d t = ν, \\ ⟨ μ, s, s^{k + 1}, ν ⟩ & i f s \neq μ a n d t = ν, \\ ⟨ μ, s^{k + 1}, t, ν ⟩ & i f s = μ a n d t \neq ν, \\ ⟨ μ, s, s^{k + 1}, t, ν ⟩ & i f s \neq μ a n d t \neq ν . \end{matrix}$

Figure 7: An illustration of step 2.

Download full-size image

DOI: 10.7717/peerj-cs.3458/fig-7

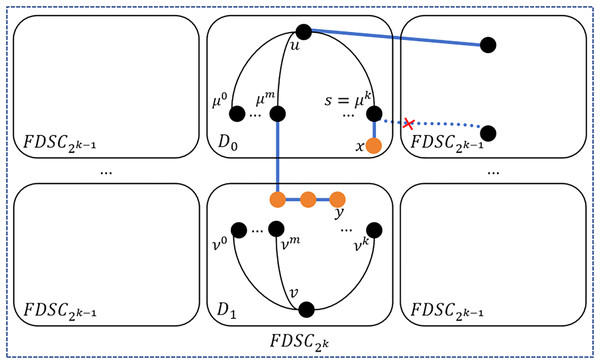
Step 3: Identify the vertex pairs $s \in U$ and $t \in V$ such that the external neighbor $t^{k + 1}$ of $t$ in $D_{0}$ is directly connected to $s$ . If such pairs are found, for each pair of $s$ and $t$ , use the following method to construct a path P between $μ$ and $ν$ , and then remove $s$ from U and $t$ from V. Please see Fig. 8 for an illustration. In this case, $t = ν^{m}$ , whose external neighbor $(ν^{m})^{k + 1}$ is directly connected to $s = μ^{m}$ , then there exists a path $⟨ μ, μ^{m}, (ν^{m})^{k + 1}, ν^{m}, ν ⟩$ .

(7.3) $P = {\begin{matrix} ⟨ μ, t^{k + 1}, ν ⟩ & i f μ = s a n d t = ν, \\ ⟨ μ, s, t^{k + 1}, ν ⟩ & i f μ \neq s a n d t = ν, \\ ⟨ μ, t^{k + 1}, t, ν ⟩ & i f μ = s a n d t \neq ν, \\ ⟨ μ, s, t^{k + 1}, t, ν ⟩ & i f μ \neq s a n d t \neq ν . \end{matrix}$

Figure 8: An illustration of step 3.

Download full-size image

DOI: 10.7717/peerj-cs.3458/fig-8

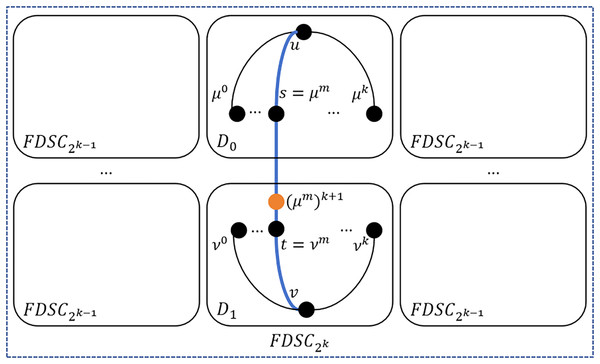
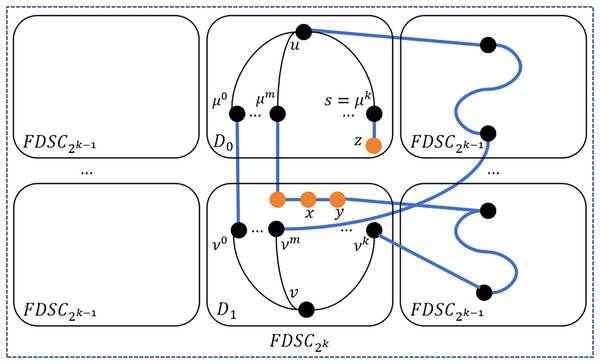
Step 4: Check each vertex $s$ in U. If $s$ is connected to $D_{1}$ and is not adjacent to any of the vertices in V and $N (V)$ , we select an edge $(x, y) \in E (D_{1})$ such that $x \in N (s^{k + 1})$ , $y^{k + 1} \notin V (D_{0})$ and $M_{y} \notin M_{U - {s}}$ . Then put $y$ into U to replace $s$ , and build a partial path from $s$ to $y$ as follows. Since $| M_{U - {s}} | \leq k + 1$ and $| M_{N (s^{k + 1})} | = k + 1$ by Lemma 7, then $M_{U - {s}} = M_{N (s^{k + 1})}$ for the worst case. Hence, we can easily find a node $y$ such that $D_{0} \neq M_{y}$ and $M_{y} \notin M_{U - {s}}$ . Please see Fig. 9 for an illustration. In this case, $s = μ^{m}$ , then there exists a partial path $⟨ μ^{m}, (μ^{m})^{k + 1}, x, y ⟩$ .

(7.4) $P = {\begin{matrix} ⟨ s^{k + 1}, x, y ⟩ & i f s = μ, \\ ⟨ s, s^{k + 1}, x, y ⟩ & i f s \neq μ . \end{matrix}$

Figure 9: An illustration of step 4.

Download full-size image

DOI: 10.7717/peerj-cs.3458/fig-9

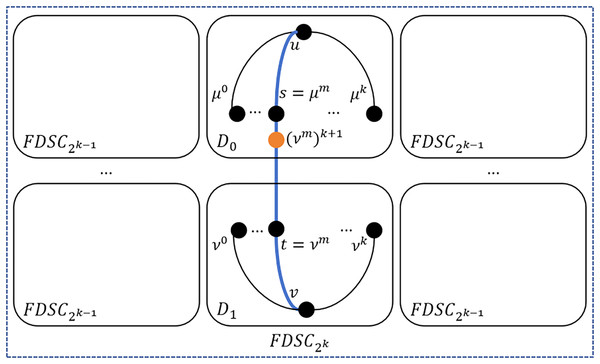
Step 5: Check each vertex $t$ in V. If $t$ is connected to $D_{0}$ and is not adjacent to any of the vertices in U and $N (U)$ , then similiar to Step 4, select an edge $(x, y) \in E (D_{0})$ such that $x \in N (t^{k + 1})$ , $y^{k + 1} \notin V (D_{1})$ and $M_{y} \notin M_{V - {t}}$ . Then put $y$ into V to replace $t$ , and build a partial path from $t$ to $y$ as follows. Please see Fig. 10 for an illustration. In this case, $t = ν^{m}$ , then there exists a partial path $⟨ ν^{m}, (ν^{m})^{k + 1}, x, y ⟩$ .

(7.5) $P = {\begin{matrix} ⟨ t^{k + 1}, x, y ⟩ & i f t = ν, \\ ⟨ t, t^{k + 1}, x, y ⟩ & i f t \neq ν . \end{matrix}$

Figure 10: An illustration of step 5.

Download full-size image

DOI: 10.7717/peerj-cs.3458/fig-10

Step 6: If $μ \in U$ , check each vertex $s$ in $U - {μ}$ . For each $s$ , if $s$ and $μ$ are connected to the same module in D, select a neighbor $z$ of $s$ in $D_{0}$ such that $M_{z} \notin M_{U}$ . Then, put $z$ into U to replace $s$ and construct a partial path from $s$ to $z$ as follows. By Lemma 7, any two different neighbors of $μ$ in $D_{0}$ are connected to different modules in D. Then only $μ$ and one of its neighbor $s$ in $D_{0}$ can be linked to the same module. Since $| N (s) | = k + 1$ and each neighbor of $s$ is connected to a different module, we can easily find a neighbor $z$ of $s$ such that $M_{z} \notin M_{U}$ . Please see Fig. 11 for an illustration. In this case, $s = μ^{k}$ , then there exists a partial path $⟨ μ^{k}, z ⟩$ .

(7.6) $P = ⟨ s, z ⟩ .$

Figure 11: An illustration of step 6.

Download full-size image

DOI: 10.7717/peerj-cs.3458/fig-11

Step 7: If $ν \in V$ , check each vertex $s$ in $V - {ν}$ . Similar to Step 6, for each $s$ , if $s$ and $ν$ are connected to the same module in D, then select a neighbor $z$ of $s$ in $D_{1}$ such that $M_{z} \notin M_{U}$ . Put $z$ into V to replace $s$ and construct a partial path from $s$ to $z$ according to Eq. (7.6).

Step 8: Identify vertex pairs $s \in U$ and $t \in V$ , such that $s$ and $t$ are connected to the same $F D S C_{2^{k - 1}}$ . If found, for each pair of $s$ and $t$ , place $s$ into set $U_{1}$ , $t$ into set $V_{1}$ , and then remove $s$ from U and $t$ from V.

Step 9: For each pair of vertices $s \in U_{1}$ and $t \in V_{1}$ which are connected to the same $F D S C_{2^{k - 1}}$ , use the following method to construct a disjoint path between $μ$ and $ν$ . If $s$ is the replaced node generated in step 4 or step 6, then set S as the partial path generated in step 4 or step 6. Otherwise, set S to an empty string. If $t$ is the replaced node generated in step 5 or step 7, then set T as the partial path generated in step 5 or step 7. Otherwise, set T to an empty string. Afterwards, construct a path P between $s^{k + 1}$ and $t^{k + 1}$ with algorithm QP, and connect P with S and T. Then, we can build a disjoint path between $μ$ and $ν$ . Please see Fig. 12 for an illustration.

(7.7) $P = {\begin{matrix} ⟨ μ, c o n n e c t (S, Q P (s^{k + 1}, t^{k + 1}, k), T), ν ⟩, & i f s = μ a n d t = ν \\ ⟨ μ, s, c o n n e c t (S, Q P (s^{k + 1}, t^{k + 1}, k), T), ν ⟩, & i f s \neq μ a n d t = ν \\ ⟨ μ, c o n n e c t (S, Q P (s^{k + 1}, t^{k + 1}, k), T), t, ν ⟩, & i f s = μ a n d t \neq ν \\ ⟨ μ, s, c o n n e c t (S, Q P (s^{k + 1}, t^{k + 1}, k), T), t, ν ⟩, & i f s \neq μ a n d t \neq ν \end{matrix} .$

Figure 12: An illustration of step 9.

Download full-size image

DOI: 10.7717/peerj-cs.3458/fig-12

We give the detailed algorithm as follows.

Step 10: For each pair of vertices $s \in U$ and $t \in V$ which are connected to the different $F D S C_{2^{k - 1}}$ s, use a method similar to Step 9 to construct a disjoint path between $μ$ and $ν$ . Please see Fig. 13 for an illustration.

Figure 13: An illustration of step 10.

Download full-size image

DOI: 10.7717/peerj-cs.3458/fig-13

Step 11: If $k < d$ , then $μ$ has a neighbor $μ^{i}$ in $F D S C_{2^{i - 1}}$ and $ν$ has a neighbor $ν^{i}$ in $F D S C_{2^{i - 1}}$ for each $i$ with $k + 2 \leq i \leq d + 1$ . We can build $d - k$ disjoint paths between $μ$ and $ν$ with algorithm DisjointPathOutFDSCK.

In lines 3–6, construct a path for each $s \in U$ and $t \in V$ , if $(s, t) \in E (F D S C_{n})$ . In lines 7–16, construct a path for each $s \in U$ and $t \in V$ , if $(s^{k + 1}, t) \in E (F D S C_{n})$ or $(s, t^{k + 1}) \in E (F D S C_{n})$ . In lines 17–23, check each vertex s in U, if $s^{k + 1} \in V (D_{1} - V - N (V))$ , select an edge $(x, y) \in E (D_{1})$ such that $x \in N (s^{k + 1})$ , $y^{k + 1} \notin V (D_{0})$ and $M_{y} \notin M_{U - {s}}$ . In lines 24–30, check each vertex t in V, if $t^{k + 1} \in V (D_{0} - U - N (U))$ , select an edge $(x, y) \in E (D_{0})$ such that $x \in N (t^{k + 1})$ , $y^{k + 1} \notin V (D_{1})$ and $M_{y} \notin M_{V - {t}}$ . In lines 31–39, if $s \in U$ and $μ$ are connected to the same module of D, then select a neighbor $z$ of $s$ in $D_{0}$ such that $M_{z} \notin M_{U}$ . In lines 40–48, if $s \in V$ and $ν$ are connected to the same module of D, then select a neighbor $z$ of $s$ in $D_{1}$ such that $M_{z} \notin M_{U}$ . In lines 49–52, put $s \in U$ and $t \in V$ connected to the same module of D into $U_{1}$ and $V_{1}$ , respectively. In lines 53–56, construct a path for each $s \in U_{1}$ and $t \in V_{1}$ connected to the same module of D between $μ$ and $ν$ with Algorithm 8. In lines 57–60, construct a path for each $s \in U$ and $t \in V$ connected to different modules of D between $μ$ and $ν$ with Algorithm 8. In lines 61–63, construct disjoint paths out of D between $μ$ and $ν$ .

Algorithm 8:

DisjointPathInFDSCK(

μ, ν, s, t, k

Input: Nodes

μ, ν, s

and t in

F D S C_{2^{k}} (k \geq 3)

Output: a disjoint path between μ and ν in

F D S C_{2^{k}}

1: S ← “”; T ← “”;

2: if s was generated in step 4 or step 6 then

3: S ← partial path from step 4 or 6;

4: end if

5: if t was generated in step 5 or step 7 then

6: T ← partial path from step 5 or 7;

7: end if

8: construct a path P according to Eq. (7.7);

9: return P;

DOI: 10.7717/peerj-cs.3458/table-11

From Step 1 to Step 3, for each vertex pair $s \in U$ and $t \in V$ which are adjacent or connected with a common neighbor, we construct a disjoint path between $μ$ and $ν$ which traverses $s$ and $t$ . Each step takes $O (k^{2})$ time. From Step 4 to Step 7, we ensure that the vertices in U and V are connected to different modules of $D - D_{0} - D_{1}$ , respectively. Each step takes $O (k)$ iterations. From Step 8 to Step 10, we first construct disjoint paths between $μ$ and $ν$ which traverses vertex pairs connected to the same module of D, then we construct disjoint paths between $μ$ and $ν$ which traverses vertex pairs connected to different modules of D. Each step has less than or equal to $O (k)$ iterations. Hence, the time complexity from Step 1 to Step 10 is $O (k^{2})$ . In Step 11, we construct disjoint paths between $μ$ and $ν$ out of D. Since the time complexity of algorithm DisjointPathOutFDSCK is $O (d - k)$ , the time complexity of algorithm O2OInFDSCK is $O (m a x (k^{2}, d - k))$ . When $k$ approaches $d$ , $O (k^{2} \leq d^{2})$ dominates the time complexity of algorithm O2OInFDSCK. Hence, $O (d^{2})$ is the time complexity of algorithm O2OInFDSCK in the worst case.

Since $| U | = k + 2$ and $| V | = k + 2$ , then we can build $k + 2$ disjoint paths between $μ$ and $ν$ in $F D S C_{2^{k}}$ from Step 1 to Step 10. In Step 11, we can build $d - k$ disjoint paths between $μ$ and $ν$ out of $F D S C_{2^{k}}$ . Hence, there exist $d + 2$ node disjoint paths between $μ$ and $ν$ in $F D S C_{2^{d}}$ .

In the worst case, $s \in U (s \neq μ)$ is the replaced node in Step 4 and $t \in V (t \neq ν)$ is the replaced node in Step 5, where $s$ and $t$ are connected to different modules of $F D S C_{2^{d}}$ . Set S as the partial path generated in Step 4 where $L (P) = 3$ and set T as the partial path generated in Step 5 where $L (T) = 3$ . Then, $P = ⟨ μ, s, c o n n e c t (S, Q P (s^{k + 1}, t^{k + 1}, k), T), t, ν ⟩$ and the theoretical maximum path length is $L (P) = 1 + L (S) + 1 + (2^{d - 1} - 1) + 1 + (2^{d - 1} - 1) + 1 + L (T) + 1 = n + 9$ for $d \geq 3$ .

Theorem 1. Let $μ$ and $ν$ be any two distinct nodes in the same embeded $F D S C_{2^{k}}$ of $F D S C_{n}$ where $n = 2^{d}$ , $d \geq 1$ and $1 \leq k \leq d$ . There exist $d + 2$ node disjoint paths between $μ$ and $ν$ in $F D S C_{n}$ .

Proof. We have the following three cases.

Case 1. $μ$ and $ν$ are in the same embeded $F D S C_{2}$ .

By Lemma 5, the theorem holds in this case.

Case 2. $μ$ and $ν$ are in the same embeded $F D S C_{4}$ .

By Lemma 6, the theorem holds in this case.

Case 3. $μ$ and $ν$ are in the same embeded $F D S C_{2^{k}}$ where $3 \leq k \leq d$ .

By Lemma 8, the theorem holds in this case.

Hence, there exist $d + 2$ node disjoint paths between $μ$ and $ν$ in $F D S C_{n}$ where $μ$ and $ν$ are any two distinct nodes in the embeded $F D S C_{2^{k}}$ with $1 \leq k \leq d$ .

Based on Algorithms 5, 7 and 9, we define the main algorithm to construct disjoint paths between $μ$ and $ν$ . Algorithm 10 is an implementation of Theorem 1. Since the theoretical maximum path lengths for Algorithms 5, 7 and 9 is $n + 1, n + 1$ and $n + 9$ , Hence, the theoretical maximum path length for Algorithm 10 is $n + 9$ for $d \geq 3$ . For $d = 1$ , the theoretical maximum path length for Algorithm 10 is 2, and for $d = 2$ , the theoretical maximum path length for Algorithm 10 is 7. The time complexity of algorithms O2OInFDSC2, O2OInFDSC4 and O2OInFDSCK are $O (d)$ , $O (d)$ and $O (d^{2})$ , respectively. Therefore, $O (d^{2}) = O ((l o g n)^{2})$ is the time complexity of algorithm O2OMain.

Algorithm 9:

O2OInFDSCK(

μ, v, k, d

Input: Nodes

μ = x_{1} x_{2} \dots x_{n}

ν = y_{1} y_{2} \dots y_{n}

k \geq 3

and

d \geq 3

Output:

d + 2

disjoint paths between μ and ν in

F D S C_{2^{d}}

1: paths ← [];

U \leftarrow {μ^{i} | 0 \leq i \leq k} \cup {μ}

;

V \leftarrow {ν^{i} | 0 \leq i \leq k} \cup {ν}

;

2: for each

s \in U

and

t \in V

where

(s, t) \in E (F D S C_{2^{k}})

doΔ Step 1

3: construct a path P according to Eq. (7.1);

4: paths.append(P);

5: U.remove(s); V.remove(t);

6: end for

7: for each

s \in U

and

t \in V

where

(s^{k + 1}, t) \in E (F D S C_{2^{k}})

do Δ Step 2

8: construct a path P according to Eq. (7.2);

9: paths.append(P);

10: U.remove(s); V.remove(t);

11: end for

12: for each

t \in V

and

s \in U

where

(t^{k + 1}, s) \in E (F D S C_{2^{k}})

do Δ Step 3

13: construct a path P according to Eq. (7.3);

14: paths.append(P);

15: U.remove(s); V.remove(t);

16: end for

17: for each

s \in U

do Δ Step 4

18: if

s^{k + 1} \in V (D_{1})

and

s^{k + 1} \notin V

and

s^{k + 1} \notin N (V)

then

19: select an edge

(x, y) \in E (D_{1})

such that

x \in N (s^{k + 1})

y^{k + 1} \notin V (D_{0})

and

M_{y} \notin M_{U - {s}}

20: U.replace(y, s);

21: build a partial path from s to y according to Eq. (7.4);

22: end if

23: end for

24: for each

t \in V

do Δ Step 5

25: if

t^{k + 1} \in V (D_{0})

and

t^{k + 1} \notin U

and

t^{k + 1} \notin N (U)

then

26: select an edge

(x, y) \in E (D_{0})

such that

x \in N (t^{k + 1})

y^{k + 1} \notin V (D_{1})

and

M_{y} \notin M_{V - {t}}

27: V.replace(y, t);

28: build a partial path from t to y according to Eq. (7.5);

29: end if

30: end for

31: if

μ \in U

then Δ Step 6

32: for each

s \in U - {μ}

33: if s and μ are connected to the same module in D then

34: select a neighbor z of s in D₀ such that

M_{z} \notin M_{U}

35: U.replace(z, s);

36: build a partial path from μ to z according to Eq. (7.6);

37: end if

38: end for

39: end if

40: if

ν \in V

thenΔ Step 7

41: for each

s \in V - {ν}

42: if s and ν are connected to the same module in D then

43: select a neighbor z of s in D₁ such that

M_{z} \notin M_{V}

44: V.replace(z, s);

45: build a partial path from ν to z according to Eq. (7.6);

46: end if

47: end for

48: end if

49: for each

s \in U

and

t \in V

connected to the same module of D do Δ Step 8

50: U₁.add(s); V₁.add(t);

51: U.remove(s); V.remove(t);

52: end for

53: for each

s \in U_{1}

and

t \in V_{1}

connected to the same module of D do Δ Step 9

54:

P \leftarrow

DisjointPathInFDSCK

(μ, ν, s, t, k)

;

55: paths.append(P);

56: end for

57: for each

s \in U

and

t \in V

connected to different modules of D do Δ Step 10

58:

P \leftarrow

DisjointPathInFDSCK

(μ, ν, s, t, k)

;

59: paths.append(P);

60: end for

61: if

k < d

then Δ Step 11

62: paths.append(DisjointPathOutFDSCK(

μ, ν, k, d

));

63: end if

64: return paths;

DOI: 10.7717/peerj-cs.3458/table-12

Algorithm 10:

O2OMain(

μ, ν, d

Input: Nodes

μ = x_{1} x_{2} \dots x_{n}

ν = y_{1} y_{2} \dots y_{n}

, and

d \geq 1

Output:

d + 2

node disjoint paths

{P_{i} | 0 \leq i \leq d + 1}

in FDSC_n.

k \leftarrow M i n C o m m o n D i m e n s i o n (μ, ν, d)

;

2: if

k = 1

then

3: return O2OInFDSC2(

μ, ν, d

);

4: else if

k = 2

then

5: return O2OInFDSC4(

μ, ν, d

);

6: else

7: return O2OInFDSCK(

μ, ν, k, d

);

8: end if

DOI: 10.7717/peerj-cs.3458/table-13

Table 3 compares the number of generated paths, longest path length, time complexity of the disjoint path algorithms for $F D S C_{n}$ and some other hypercube variants. $F D S C_{n}$ has a smaller time complexity because $O ((l o g n)^{2})$ grows far more slowly than $O (n^{2})$ . For large $n$ , this makes $F D S C_{n}$ ’s disjoint path algorithm much more efficient than those of other hypercube variants. For the longest path length, $F D S C_{n}$ has a length of $n + 9$ , which is longer than that of twisted cubes ( $⌈ \frac{n}{2} ⌉ + 1$ ) and folded hypercubes ( $⌈ \frac{n}{2} ⌉ + 2$ ) but comparable to hypercubes ( $n + 1$ ) and better than crossed cubes and m $\ddot{o}$ bius cubes( $3 n - 5$ ).

Table 3:

Comparison of the number of generated paths, longest path length, time complexity of the disjoint path algorithms for

F D S C_{n}

and some other hypercube variants.

Network	Diameter	Number of generated paths	Longest path length	Time complexity
Hypercubes	$n$	$n$	$n + 1$	$O (n^{2})$
Crossed cubes	$⌈ \frac{(n + 1)}{2} ⌉$	$n$	$3 n - 5$	$O (n^{2})$
Twisted cubes	$⌈ \frac{(n + 1)}{2} ⌉$	$n$	$⌈ \frac{n}{2} ⌉ + 1$	$O (n^{2})$
Folded hypercubes	$⌈ \frac{n}{2} ⌉$	$n + 1$	$⌈ \frac{n}{2} ⌉ + 2$	$O (n^{2})$
M $\ddot{o}$ bius cube	$⌈ \frac{(n + 1)}{2} ⌉$ or $⌈ \frac{(n + 2)}{2} ⌉$	$n$	$3 n - 5$	$O (n^{2})$
$F D S C_{n}$	$n - 1$	$l o g n + 2$	$n + 9$	$O ((l o g n)^{2})$

DOI: 10.7717/peerj-cs.3458/table-3

Performance evaluation

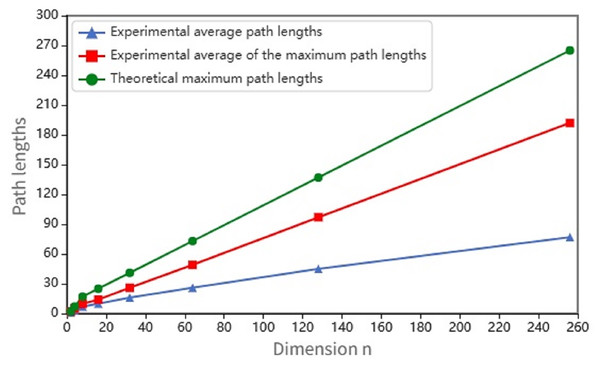
In the section, we conduct a computer experiment to inspect the practical performance of the algorithm O2OMain. We implemented the algorithm using Java programming language, and the target machine is equipped with an Intel Core i5-7200U CPU 2.80 GHz and 12 GB RAM. For $F D S C_{n}$ with various values of $n (n = 2^{d}, 1 \leq d \leq 8)$ , we constructed $d + 2$ node disjoint paths between any two distinct nodes for a certain number of times. Then we evaluated the average path length and the average of the maximum path lengths for each $F D S C_{n}$ . Taking into account the impact of both the parameter $n$ and the positions of the two nodes in $F D S C_{n}$ when constructing disjoint paths, we randomly selected six distinct node pairs for $F D S C_{2}$ , 120 distinct node pairs for $F D S C_{4}$ and 10,000 distinct node pairs for $F D S C_{n} (n = 2^{d}, 3 \leq d \leq 8)$ , respectively.

For each value of $n (n = 2^{d}, 1 \leq d \leq 8)$ , Fig. 14 illustrates the average of maximum and the average lengths of all disjoint paths obtained using algorithm O2OMain compared with theoretical maximum lengths. The theoretical maximum lengths take values of $2$ , 7, $2^{d} + 9$ , corresponding to $F D S C_{2}$ , $F D S C_{4}$ , $F D S C_{n}$ ( $n = 2^{d}, 3 \leq d \leq 8$ ). We can see that the actual average of maximum lengths are very close to the theoretical maximum lengths when $n \leq 16$ . However, when $n \geq 32$ , the gap between them gradually becomes larger.

Figure 14: Results of average of maximum and average path lengths compared with the theoretical maximum path lengths.

Download full-size image

DOI: 10.7717/peerj-cs.3458/fig-14

Conclusion

As a newly proposed hypercube variant, $F D S C_{n}$ has many superior properties over the hypercube. In this work, we investigate the disjoint path problem for $F D S C_{n}$ . The main contributions of this work are that we give an algorithm QP to build a path between any two distinct nodes $μ$ and $ν$ , as well as an algorithm O2OMain for constructing one-to-one disjoint paths in $F D S C_{n}$ . In future work, we can consider the construction of node-to-set disjoint paths (Wang et al., 2022; Kocik, Hirai & Kaneko, 2016; Ling & Chen, 2014) or set-to-set disjoint paths (Zhuang et al., 2024) for $F D S C_{n}$ . In addition, component diagnosticability (Liu et al., 2022) and extra fault diagnosticability (Lin et al., 2021) are also future research directions.

Supplemental Information

Raw Data.

DOI: 10.7717/peerj-cs.3458/supp-1

Download

Source Code.

DOI: 10.7717/peerj-cs.3458/supp-2

Download

[1] Chang Y-H, Pai K-J, Hsu C-C, Yang J-S, Chang J-M. 2021. Constructing dual-cists of folded divide-and-swap cubes. Theoretical Computer Science 856(3):75-87

[2] Chang C-P, Wang J-N, Hsu L-H. 1999. Topological properties of twisted cube. Information Sciences 113(1–2):147-167

[3] Cheng D, Hao R, Feng Y. 2014. Two node-disjoint paths in balanced hypercubes. Applied Mathematics and Computation 242(12):127-142

[4] Fan W, Xiao F, Cai H, Chen X, Yu S. 2023. Disjoint paths construction and fault-tolerant routing in BCube of data center networks. IEEE Transactions on Computers 72(9):2467-2481

[5] Kim J, Kim D, Qiu K, Lee H. 2019. The divide-and-swap cube: a new hypercube variant with small network cost. The Journal of Supercomputing 75(7):3621-3639

[6] Kocik D, Hirai Y, Kaneko K. 2016. Node-to-set disjoint paths problem in a mobius cube. IEICE Transactions on Information and Systems E99D(3):708-713

[7] Kocik D, Kaneko K. 2017. Node-to-node disjoint paths problem in möbius cubes. IEICE Transactions on Information and Systems E100.D(8):1837-1843

[8] Kulasinghe P. 1997. Connectivity of the crossed cube. Information Processing Letters 61(4):221-226

[9] Lai C-N. 2021. Optimal node-disjoint paths in folded hypercubes. Journal of Parallel and Distributed Computing 147(6):100-107

[10] Lin L, Huang Y, Xu L, Hsieh S-Y. 2021. A complete fault tolerant method for extra fault diagnosability of alternating group graphs. IEEE Transactions on Reliability 70(3):957-969

[11] Ling S, Chen W. 2014. Node-to-set disjoint paths in biswapped networks. The Computer Journal 57(7):953-967

[12] Liu H. 2010. The wide diameter of folded hypercube. In: 2010 Third International Joint Conference on Computational Science and Optimization. 2:173-176

[13] Liu S, Wang Y, Fan J, Cheng B. 2024. Node-disjoint paths in balanced hypercubes with application to fault-tolerant routing. In: Algorithms and Architectures for Parallel Processing. Singapore: Springer Nature Singapore. 40-56

[14] Liu J, Zhou S, Wang D, Zhang H. 2022. Component diagnosability in terms of component connectivity of hypercube-based compound networks. Journal of Parallel and Distributed Computing 162(2):17-26

[15] Lv M, Fan J, Cheng B, Yu J, Jia X. 2024. Construction algorithms of fault-tolerant paths and disjoint paths in k-ary n-cube networks. Journal of Parallel and Distributed Computing 183:104761

[16] Ma M, Guo C, Li X. 2022. Disjoint paths in the enhanced hypercube with a faulty subgraph. Journal of Applied Mathematics and Computing 69(2):1343-1354

[17] Saad Y, Schultz M. 1988. Topological properties of hypercubes. IEEE Transactions on Computers 37(7):867-872

[18] Wang X, Fan J, Lin C-K, Jia X. 2016. Vertex-disjoint paths in DCell networks. Journal of Parallel and Distributed Computing 96(12):38-44

[19] Wang X, Fan J, Zhang S, Yu J. 2022. Node-to-set disjoint paths problem in cross-cubes. The Journal of Supercomputing 78(1):1356-1380

[20] Wu S, Fan J, Cheng B, Yu J, Wang Y. 2022. Connectivity and constructive algorithms of disjoint paths in dragonfly networks. Theoretical Computer Science 922(1):257-270