Multilayered digital image encryption approach to resist cryptographic attacks for cybersecurity
- Published
- Accepted
- Received
- Academic Editor
- Markus Endler
- Subject Areas
- Computer Aided Design, Computer Architecture, Emerging Technologies, Optimization Theory and Computation, Neural Networks
- Keywords
- Cryptography, Encryption, Cybersecurity, Digital image
- Copyright
- © 2025 Das et al.
- Licence
- This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, reproduction and adaptation in any medium and for any purpose provided that it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Computer Science) and either DOI or URL of the article must be cited.
- Cite this article
- 2025. Multilayered digital image encryption approach to resist cryptographic attacks for cybersecurity. PeerJ Computer Science 11:e3260 https://doi.org/10.7717/peerj-cs.3260
Abstract
In today’s digital age, protecting sensitive image data is more important than ever, especially with the rise of computing advancements, which threaten traditional encryption methods. This article presents a novel image encryption model designed to enhance security against both conventional and future cyber threats. Our approach combines multiple encryption techniques, including Advanced Encryption Standard (AES), Triple DES (DES3), and Elliptic Curve Cryptography (ECC), along with additional security measures such as pixel shuffling, left circular shifting, and exclusive NOR (XNOR) operations. To ensure secure key exchange, we incorporate Elliptic Curve Diffie-Hellman (ECDH) and a hash-based key derivation function (HKDF) using a Hash-based Message Authentication Code (HMAC). By encapsulating the encrypted image and keys within a secure archive, this method provides a strong and durable solution to safeguard digital images in the evolving landscape of cybersecurity. The proposed cryptosystem achieves the high information entropy, the Number of Pixel Change Rate (NPCR), and the Unified Average Change Intensity (UACI) of 7.9995, 99.59% and 49.96%, respectively. In addition, the proposed model offers a large keyspace and demonstrates an avalanche effect of more than 50% which effectively resists various cryptographic attacks. The achieved results highlight the suitability of the proposed approach for robust encryption and resistance against various attacks. This combination of techniques helps to mitigate the shortcomings of standalone techniques and safeguard sensitive visual data in increasingly hostile digital environments.
Introduction
In this digital age, the use of the Internet has increased multiple times, leading to a wide use of mobile devices and social networks. Various reports from October 2024 state that people using social networks have reached 5.52 billion, which is equal to 63.8% of the total population (Datareportal, 2025). This has resulted in the widespread creation, consumption, and sharing of multimedia, including images. However, this has also made it a lucrative target for cyber adversaries, which can lead to a loss in terms of finance, erodes consumer confidence, etc.
In this current digital landscape, where visual content dominates communication and information sharing, securing sensitive images has become a critical concern over various domains. Cyberattacks targeting image data are becoming more sophisticated. This threatens both personal privacy and organizational integrity (Wall, 2024; Boyer, 1996; Keim et al., 2010). In healthcare and cloud storage, there is a high need for the protection of personal and sensitive images to remain private (Almanasir et al., 2025). Surveillance systems send real-time visual data that can be intercepted. In all of these cases, images are vulnerable to tampering, theft, and misuse. In addition, Table 1 provides an overview of various risks in different domains that make extensive use of images. Some widely known attacks include man-in-the-middle attacks, replay attacks, pixel-level manipulation, and unauthorized decryption. Traditional image security techniques such as watermarking, perceptual hashing, etc., can no longer provide security against evolving attacks. In addition to them, conventional image encryption algorithms such as Rivest Cipher 4 (RC4), Data Encryption Standard (DES), etc., are now largely obsolete or less commonly used alone.
| Domain | Image-specific cybersecurity risks |
|---|---|
| Healthcare systems | Unauthorized access to diagnostic images (e.g., Magnetic Resonance Imaging (MRI), Computed Tomography (CT), X-ray), ransomware attacks on picture archiving and communication systems, and privacy breaches due to weak encryption. |
| Military and defense | Eavesdropping via intercepted reconnaissance or satellite imagery, tampering with mission-critical images, unauthorized decryption of sensitive visual data, etc. |
| Cloud-based image services | Leakage of stored encrypted images, key exposure, insecure transmission channels, cloud misconfigurations, etc. |
| Surveillance and smart cities | Tampering with real-time surveillance images, identity spoofing via image replacement, data injection attacks, etc. |
| E-Governance and digital ID systems | Forgery of ID documents, unauthorized access to facial images, manipulation in official records, etc. |
To overcome the limitations of conventional encryption techniques, algorithms such as Advanced Encryption Standard (AES) and Elliptic Curve Cryptography (ECC) emerged. Although these algorithms offer robust security and scalability, relying solely on a single cryptographic primitive leaves the system vulnerable to targeted attacks that exploit specific algorithmic weaknesses. Furthermore, the rapid advancement of Artificial Intelligence (AI) has introduced new threats to data security. AI-powered systems are capable of analyzing large-scale encrypted data, learning cryptographic patterns, and even developing novel attack strategies that could potentially compromise traditional encryption schemes.
To address these challenges, the proposed encryption methodology integrates multiple layers of cryptographic (using AES and Triple DES (3DES)) and data transformation techniques. Since using these algorithms directly on images could leave potential patterns and risk statistical vulnerabilities, we have integrated pixel-level obfuscation and bitwise exclusive NOR (XNOR) masking as a preprocessing technique to increase confusion. First, both AES and 3DES are applied in a Cipher Block Chaining (CBC) mode. The encryption metadata are further secured using AES in Cipher Feedback (CFB) mode and protected through ECC-based key exchange and AES-Galois/Counter Mode (GCM) encryption. Using AES in CFB or CBC modes significantly improves security over the default Electronic Codebook (ECB) mode, especially for images. CBC and CFB break pattern repetition in the image data and convert a block cipher into a self-synchronizing stream cipher, respectively. This hybrid approach ensures that even if one layer is compromised, the others maintain the integrity and confidentiality of the data. By taking advantage of the strengths of both symmetric and asymmetric encryption, and incorporating advanced key management using Elliptic Curve Diffie-Hellman (ECDH) and Hash-based Message Authentication Code (HMAC)-based Key Derivative Function (HKDF), the proposed scheme is designed to be resilient against both conventional cryptanalysis and emerging AI-driven threats. This work seeks to achieve the following goals:
To propose a robust multilayered image encryption model by integrating AES, 3DES, and ECC, combined with advanced image preprocessing techniques including pixel shuffling and bitwise XNOR masking to ensure high levels of confusion and diffusion.
To strengthen the encryption pipeline through five sequential symmetric encryption layers - three using AES and two using 3DES. Distinct keys, initialization vectors, and two modes are used which improves the resistance against cryptanalytic attacks.
Implement an efficient and secure key exchange mechanism using ECDH and HKDF which makes the system lightweight and suitable for deployment in resource-constrained environments such as Internet of Things (IoT) and mobile platforms.
To introduce a secure packaging and transmission strategy that encrypts the metadata and encryption keys using AES in both CFB and GCM modes, bundling them with the encrypted image in a final archive to prevent unauthorized access or tampering during storage and communication.
Build a forward-secure encryption framework capable of defending against conventional and emerging threats, including man-in-the-middle attacks, replay attacks, and AI-assisted differential cryptanalysis.
The integration of multiple cryptographic layers significantly improves security. For example, AES and DES3 are applied in multiple rounds with varying keys, creating a cascade of encryption that amplifies protection. Although these algorithms are widely popular for text encryption, their underlying mechanisms can be applied to various types of data, including images (Zhang, 2018). The core principles of block-cipher encryption—breaking data into smaller chunks and applying a series of transformations—are agnostic to the type of data. In this context, using block ciphers such as AES and DES3 is essentially converting the image data into a format suitable for encryption using the same techniques applied to text-based data. Finally, the encrypted image and its key information are securely packaged in an archive, providing a fail-safe mechanism for storage and transmission.
This research tackles the dual challenge of securing digital images against present-day threats while adapting to future technological advancements. By combining advanced cryptographic techniques and multilayered defense mechanisms, the proposed model offers a compelling solution to one of the most critical problems in modern cybersecurity. This highlights the vulnerabilities of traditional encryption methods and introduces a reliable methodology to protect digital images, ensuring data integrity in an increasingly uncertain technological landscape. The research contributions of the proposed work are as follows:
Proposed a novel multilayered image encryption framework that combines pixel-level transformations with symmetric encryption algorithms (AES and 3DES) to enhance confusion, diffusion, and cryptographic strength.
Developed a five-stage symmetric encryption pipeline employing three layers of AES and two layers of 3DES, each with unique keys and IVs, to provide deep, sequential encryption and resist differential and statistical attacks.
Designed a secure and lightweight key exchange mechanism using ECDH and HKDF which provides secure key distribution in low-power and constrained environments.
Proposed a secure metadata packaging strategy in which encryption keys, IVs, and parameters are archived and encrypted using a 256-bit AES key (CFB mode), and this AES key is further protected using AES-GCM encryption derived from ECC, ensuring layered security for both data and key material.
Conducted a comprehensive evaluation and comparative analysis of the proposed encryption scheme against existing approaches, demonstrating improved resilience to cryptanalytic attacks and better image reconstruction fidelity through mean squared error (MSE) and peak signal-to-noise ratio (PSNR) metrics.
The structure of the article: ‘Related Works’ provides a brief description of various related architectures in a nutshell. ‘Preliminary Concepts’ and ‘Proposed Cryptosystem’ briefly discuss the preliminary knowledge and details of the proposed cryptosystem. ‘Implementation Details and Experimental Setup’ and ‘Results and Discussions’ provide information on the setup of the experiment and the results obtained, respectively. ‘Conclusion and Future Work’ provides the final remarks.
Related works
Our survey involves the literature in various domains of image encryption. A brief description of various articles is offered below:
The researchers in Alexan, Hosny & Gabr (2025) proposed a color image encryption approach that can concurrently encrypt multiple images. Multiple plain images were combined to form a plain image cube that uses encryption keys generated using the 4D-Hyperchaotic Chen System (4DHCS) and Mersenne Twister (MT). An encryption throughput of 96.4 Mbps is achieved. The keyspace of strengthened the approach. In addition, the model passed all tests of the NIST SP 800-22 suite, proposed by the National Institute of Standards and Technology (NIST). Images from the USC-SIPI database were used for the validation of the results.
The researchers in Gao et al. (2025) proposed a color image encryption algorithm that improves security and computational efficiency. It uses a parallel color image encryption algorithm based on the 2-D logistic-Rulkov neuron map (2D-LRNM). This approach separates three channels of the color image, introduces cross-channel information interaction, and uses block-wise parallel encryption to balance task load. It improves the chaotic unpredictability.
The researchers in Huang, Zhang & Zhao (2025) proposed a color image encryption approach using chaos and layered strategies. Using the proposed Chebyshev–Tent (CT) mapping, an extensive analysis is performed. A chaotic Fisher–Yates (CFY) scrambling technique is also proposed to increase complexity. This algorithm applies multilayered encryption, starting at the pixel level and extending down to the bit level. Various tests including NIST 800-22, Lyapunov exponents, etc., were performed to evaluate the efficacy of the approach.
The researchers in Zhang (2025) proposed a new image encryption method based on the butterfly model and chaos. The author proposed a new method for generating substitution boxes (S-box) with excellent non-linear and avalanche characteristics. A combinatorial chaotic map with a uniform probability density function was introduced for pseudorandom number generation. A butterfly encoding module is introduced based on the butterfly node algorithm. In addition, an enhanced encryption algorithm with ciphertext sensitivity and a unified encryption-decryption process was proposed. The experimentation was conducted using Mathematica on the images from ‘ExampleData,’ having a time complexity and spatial complexity of 3 and 3.03, respectively.
To address the issue of fixed pixel location or lack of randomness in a privacy-preserving environment, the researchers in Soman & Natarajan (2025) proposed a novel approach called ‘CFOPS-BSBEA.’ It highlights the use of Crayfish Optimization (CO) for pixel selection and a block-based encryption method for the cloud computing environment. There is a significant reduction in computation time as well as an increase in complexity. Images from the USC-SIPI database were used for the validation of the results.
Kumar & Sharma (2024) proposed an image encryption scheme that uses chaotic maps, that is, Arnold’s Cat Map (ACM), ECC, and genetic algorithms. ACM introduces chaos in the image, which is proceeded for encryption. The keys used by ECC for encryption are generated by the genetic algorithm, which has the keyspace . In addition, the proposed system also passes the 15 statistical tests of the NIST SP 800. Various analyses, including statistical analysis, key analysis, resistance to various attacks, and robustness analysis, demonstrate the efficacy of the proposed cryptosystem.
The researchers in Wang et al. (2024) discussed various security weaknesses in traditional methods and presented an encryption method for color images to address them. The proposed algorithm uses 3D permutation, global scrambling, 1D diffusion, and DNA coding. Initially, 3D permutation scrambles the image to disrupt pixel correlation. The Rivest-Shamir-Adleman (RSA) and Secure Hash Algorithm 256-bit (SHA-256) algorithms were used to generate a random seed for the chaotic system. After that, global scrambling and 1D diffusion are used to further increase confusion. Then DNA coding for computing ensures security and efficiency in image encryption. Images from the USC-SIPI database were used for the validation of the results.
To secure the transmission of images over devices that are resource-constrained, the researchers in Ali et al. (2024) proposed a lightweight image cryptosystem that uses chaos-based key generation (using a novel chaotic map and a 3D Lorenzo function) and a modified AES algorithm. The study introduces a new method for creating improved S-boxes with enhanced cryptographic properties, including stronger bit independence, reduced periodicity, higher algebraic complexity, and stricter avalanche criteria, replacing the traditional AES algorithm’s mix column function with a circular permutation. In addition, the proposed cryptosystem also passed various tests of the NIST SP 800-22 suite.
Similarly, the researchers in İnce, İnce & Hanbay (2024) proposed a Corner Traversal Algorithm (CTA), an alternative to the pixel scrambling technique. The color image undergoes the scrambling stage using the proposed approach. The process follows the diffusion and encryption of the image data. This lightweight approach is specifically designed for resource-constrained IoT devices. Images from the USC-SIPI database were used for the validation of the results.
To minimize attacks and imply safe storage in the cloud, Mohammed et al. (2024) proposed an image cryptosystem that relies on an optimized AES algorithm for encryption, digital signatures for integrity checks, and a novel approach for image fragmentation. Experiments conducted on an image of size 125 Kb did not show no change in size, and the cryptoprocessing time was 15 s. A better value achieved for the evaluation parameters, including the avalanche test, visual evaluation, correlation and statistical analysis, time complexity, and image histogram, demonstrated the efficacy of the suggested model.
The researchers in Naim & Ali Pacha (2023) proposed a chaotic satellite image encryption technique that uses a pseudo-AES algorithm, a 7D hyperchaotic system, an arrangement permutation for permutation, and a mask matrix to increase randomness. As the name suggests, the pseudo-AES algorithm is a simple and enhanced version of traditional AES, varying the number of rounds. The 7D hyperchaotic system is a chaotic system that operates in a seven-dimensional space, having seven variables that evolve over time, leading to complex, unpredictable behavior that can be harnessed for cryptographic purposes. The proposed cryptosystem has a total keyspace of and passes the 15 tests of the NIST SP 800-22 suite.
From the above-mentioned articles, it could be observed that many researchers are using a single algorithm for a specific purpose. This could lead to its exploitation using its deficiencies. Although an extensive keyspace is used, it is not enough (Oracle Corporation, 2009). The total time required for encryption and decryption could impact the cryptographic latency. To address various gaps, including the above-mentioned ones, the proposed approach uses a combination of algorithms to overcome one’s limitations. A larger keyspace and less computational time make it a suitable approach for a robust approach. Table 2 highlights the key details of various studies in a glance.
| Ref. | Techniques | Key generation | Key contributions | Outcomes |
|---|---|---|---|---|
| Alexan, Hosny & Gabr (2025) | Simultaneous image encryption using 4DHCS on image cubes. | MT for key generation. | Secure and optimized encryption technique; Resistant to cropping and noise attacks. | Throughput rate of 96.4 Mbps with a keyspace of . |
| Gao et al. (2025) | Parallel image encryption using 2D-LRNM. | SHA-256-based key generation function. | Generates enhanced pseudo-random key streams. | Reduction in encryption time of 83% than standalone process. |
| Huang, Zhang & Zhao (2025) | Color image encryption using hybrid chaos methods in different layers. | Using seeds to generate STC chaotic sequence. | Proposing and analyzing CT mapping and STC mapping to enhance security. | Increased encryption depth and complexity. |
| Zhang (2025) | Chaotic maps and butterfly encoding algorithm. | Fusion of piecewise linear map and ACM. | A new method for generating S-boxes; butterfly algorithm. | Low spatial complexity with high speed encryption. |
| Soman & Natarajan (2025) | Image encryption using optimization and block scrambling encryption. | Using Salp Swarm Algorithm (SSA). | Use of CO for steganography and block-based encryption for lightweight encryption. | 15–20% less error in distortions introduced in encryption layers. |
| Kumar & Sharma (2024) | Integration of ACM, ECC, and GA for image encryption. | ECC with GA. | Key generation optimization using GA. | High entropy (7.99); Near zero correlation; less encryption time. |
| Wang et al. (2024) | Multilayer color image encryption using DNA coding and chaotic maps. | SHA-256 and RSA-based key generation function. | Attack-resistant design with a key space of . | Ability to recover image even after a loss of 50% encrypted data. |
| Ali et al. (2024) | Chaos-based key generation and lightweight cryptography. | Combination of chaotic maps with 3D Lorenzo function. | Enhanced AES algorithm and fast S-boxes. | High throughput; Unique key for all the rounds. |
| İnce, İnce & Hanbay (2024) | Chaos-based lightweight pixel scrambling technique for confusion. | Java’s SecureRandom library to generate random seed. | CTA that outperforms various pixel scrambling techniques. | High performance metrics and less time complexity. |
| Mohammed et al. (2024) | Image security for cloud environment. | Using AES. | Defends various attacks including possible leakage, damage, corruption, etc., in cloud. | Optimized AES and a novel fragmentation technique; Integrity using OpenSSL certificates. |
| Naim & Ali Pacha (2023) | AES and Chaotic-based satellite image encryption. | Using 7D hyperchaotic maps. | Use of hyperchaotic maps to dynamically determine the number of last round in conjugation of pseudo-AES. | Highly resistant to noise; Better visuals for decrypted images even at low intensities. |
Preliminary concepts
This section presents an outline of the cryptographic algorithms and techniques used in the proposed approach. Each subsection explains the theoretical basis and specific role of the technique in the encryption pipeline.
Advanced encryption standard
It is a symmetric block cipher widely used for the encryption of data. It operates on fixed 128-bit blocks and supports key lengths of 128, 192, or 256 bits of National Institute of Standards and Technology et al. (2001), Heron (2009). The AES encryption process consists of several transformation steps applied to the data block. First, Key Expansion generates a set of round keys from the original encryption key using a predefined key schedule. Then, the SubBytes step introduces nonlinearity by substituting each byte in the state matrix with a corresponding value from the Rijndael S-box. This is followed by ShiftRows, which performs a cyclic shift of the rows in the state matrix to further diffuse the input. Next, MixColumns transforms each column using a linear mixing function to increase diffusion across the state. Finally, the AddRoundKey step combines the current state with the corresponding round key using a bitwise XOR operation. These steps are repeated over multiple rounds depending on the key size to ensure strong encryption.
The transformation at round is:
(1) In the proposed scheme, AES is employed in three different operating modes to improve security and make it suitable for images. The CBC mode is used to implement layered encryption by introducing chained dependencies between blocks, making each ciphertext block dependent on all preceding blocks. The CFB mode enables the encryption of streaming data, such as files, by converting a block cipher into a self-synchronizing stream cipher. Finally, the GCM is utilized to provide both confidentiality and data authenticity, combining encryption with a built-in authentication mechanism.
Triple data encryption standard
Improves DES security by applying it three times using multiple keys (Sari, Rachmawanto & Haryanto, 2018). Given three keys , , and , encryption is defined as:
(2) where PT is the plaintext and CT is the ciphertext.
In our model, 3DES is used in the CBC mode as an additional encryption layer after AES, reinforcing diffusion and resistance against differential attacks.
Elliptic curve cryptography
ECC is a public key cryptographic method based on elliptic curves in finite fields (Hankerson & Menezes, 2021). Provides strong security with relatively short key sizes, which is ideal for lightweight applications. The general curve is defined as:
(3) where and define the elliptic curve and is a prime modulus.
ECC is employed here using the ECDH key exchange:
(4) where G is a generator point, and are private keys, and , are corresponding public keys.
HMAC-based key derivation function
HKDF is used to derive strong session keys from shared secrets (e.g., ECC-derived keys) using HMAC (Krawczyk & Eronen, 2010). It ensures randomness and context specificity. It operates in two steps:
Extract:
(5) where IKM is the input keying material and is an optional salt.
Expand:
(6) where is optional context-specific information, and OKM is the output key material.
In this system, HKDF derives a symmetric AES key used to encrypt metadata and session parameters.
Pixel shuffling
Pixel shuffling is a spatial transformation that improves confusion by permuting pixel positions using a pseudorandom permutation (Bansal et al., 2017). The mapping is given by:
(7) where F denotes the original image and J represents the shuffled result.
A secure random seed ensures reproducibility for decryption. This step masks spatial features prior to byte-level processing.
XNOR operation
The XNOR operation is a bitwise logical function that enhances diffusion by introducing non-linear transformations at the binary level. It can be calculated as:
(8) where and are bit sequences, represents the XOR operation, and denotes the logical negation.
A binary mask derived from a secure seed is used to XNOR the image byte stream, adding an extra layer of obfuscation prior to encryption.
Proposed cryptosystem
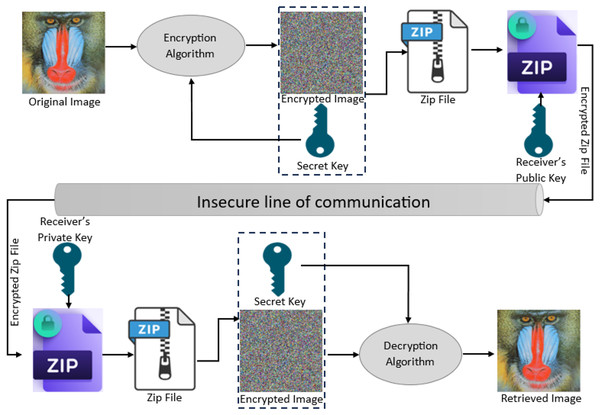
In this section, we present the details of the proposed cryptosystem. Figure 1 provides an overview of the encryption and decryption methodologies, which are discussed in detail later.
Figure 1: Workflow of the proposed cryptosystem.
Encryption steps
The encryption procedure in the proposed scheme involves a series of transformations to ensure a high level of security. It includes, pixel shuffling, bitwise operations, symmetric encryption, and ECC. The Algorithm 1 presents the overall steps in detail. Initially, the input image is loaded, reshaped into a 1D array using NumPy and subjected to pixel shuffling using a pseudorandom seed. It obfuscates the spatial relationship between pixels. This shuffled image is subsequently transformed into a byte stream for further processing.
| Input: Original RGB image I, Receiver’s ECC Public Key PKB |
| Output: Encrypted image, Final encrypted archive final_encrypted_files.zip |
| Step 1: Image Preprocessing |
| Convert I to NumPy array → flatten to 1D vector P |
| Generate random seed s and shuffle P using s to get Pshuffled |
| Convert Pshuffled to byte stream B |
| Step 2: Bitwise XNOR Masking |
| Generate random binary mask M of length |B| |
| XNOR M |
| Step 3: Symmetric Key Generation |
| Generate AES keys: |
| Generate 3DES keys: |
| Step 4: Layered Encryption |
| Step 5: Encrypted Image Conversion and Metadata Storage |
| Convert C5 to 2D grayscale encrypted image Ienc |
| Save Ienc and encryption metadata (keys, IVs, mask, seed) into encryption_info.zip |
| Step 6: Secure Packaging Using ECC and AES-GCM |
| Generate random AES key Kfile |
| Encrypt encryption_info.zip with AES-CFB using Kfile |
| Generate ephemeral ECC key pair |
| Compute shared secret |
| Derive key KECC from S using HKDF |
| Encrypt Kfile using AES-GCM with KECC |
| Package encrypted zip, encrypted Kfile, and PKE into final_encrypted_files.zip |
Next, a bitwise XNOR operation is applied. A binary mask of the same size as the byte stream is generated randomly. Each byte is masked using the XNOR operation. This step significantly increases confusion in the encrypted image data.
After masking, symmetric encryption keys are generated, including three 128-bit keys for AES and two 168-bit keys for 3DES. The byte stream is then encrypted in five sequential layers. The first three layers use AES in CBC mode with each of the three AES keys, followed by two layers of 3DES encryption in CBC mode using the 3DES keys. Each encryption layer employs a unique Initialization Vector (IV), which is saved for decryption.
The output of the final encryption layer is converted into a 2D grayscale image and saved as the encrypted image. All encryption metadata, including AES and 3DES keys, IVs, pixel shuffle indices, XNOR mask, and random seed, are compressed into a secure archive named encryption_info.zip.
To further secure the encryption metadata, a 256-bit AES key is randomly generated and used to encrypt the encryption_info.zip file in the CFB mode of AES. For secure key exchange, an ECC key pair is generated. Using the recipient’s public ECC key, a shared secret is calculated using the ECDH key agreement protocol. A strong symmetric key is derived from this shared secret using the HKDF, which is then used to encrypt the 256-bit AES key using AES in GCM. The final package, named final_encrypted_files.zip, contains the encrypted ZIP archive, the encrypted AES key, and the ephemeral ECC public key.
Decryption steps
The decryption process reverses all the operations performed during encryption to restore the original image. The whole decryption process can be visualized in the Algorithm 2. First, the archive final_encrypted_files.zip is extracted to retrieve the encrypted metadata file (encrypted_my_files.zip), the encrypted AES key, and the ephemeral ECC public key of the sender. Using the private ECC key of the receiver and the public key of the sender, a shared secret is regenerated through the ECDH protocol. This shared secret is passed through HKDF to derive the AES key required to decrypt the encrypted AES file key using AES-GCM.
| Input: final_encrypted_files.zip, Receiver’s ECC Private Key SKB |
| Output: Recovered original image Irec |
| Step 1: Extract Final Archive |
| Extract encrypted_my_files.zip, encrypted_aes_key.bin, PKE |
| Step 2: Recover AES Key using ECC |
| Compute shared secret |
| Derive KECC using HKDF from S |
| Decrypt (encrypted_aes_key.bin, KECC) |
| Step 3: Decrypt Metadata Archive |
| Decrypt encrypted_my_files.zip with AES-CFB using Kfile |
| Extract encryption_info.zip to retrieve keys, IVs, mask, and seed |
| Step 4: Reverse Symmetric Decryption |
| Convert encrypted image Ienc to byte stream C5 |
| Step 5: Reverse XNOR Masking and Pixel Shuffling |
| XNOR M |
| Reshape B into 1D image array Pshuffled |
| Apply inverse shuffle using saved seed to get P |
| Convert P to RGB image Irec |
With the decrypted 256-bit AES key, the system proceeds to decrypt encrypted_my_files.zip using AES in CFB mode, thus obtaining the encryption_info.zip. Once extracted, this archive provides all necessary decryption metadata, including keys, IVs, XNOR mask, and shuffle parameters.
The encrypted grayscale image is then converted back into a byte stream and decrypted through the five symmetric layers in reverse order. Specifically, the data are first decrypted using 3DES with the second key, followed by the first 3DES key, and then using AES with the third, second, and first AES keys, respectively, all in CBC mode. The appropriate IVs are used for each decryption stage accordingly.
After layered decryption, the bitwise XNOR operation is reversed using the saved mask to retrieve the original masked byte stream. This stream is converted back into the RGB image format and inverse pixel shuffling is applied using the previously saved random seed and index order. The reconstructed image is then utilized further.
Implementation details and experimental setup
System specifications
The hardware and software configurations for the implementation of the proposed model are mentioned in Table 3.
| Hardware specifications | |
| Processor | Intel® Core™ i7-10700 CPU 2.90 GHz 16 |
| RAM | 8 GB |
| Architecture type | 64-bit |
| Software specifications | |
| Operating system | Windows 11 |
| Platform | Google colab |
| Dataset | The Signal and Image Processing Institute (SIPI) Image Database (Signal and Image Processing Institute (SIPI), 2025) |
Experimental setup
To evaluate the effectiveness of our proposed method, we performed experiments using the USC-SIPI Image Database. It is a comprehensive collection of digitized images that supports research in image processing and machine vision. Established in 1977 and continuously updated, the database is organized into volumes, with images categorized on the basis of their characteristics. Black-and-white images are stored at 8 bits/pixel, and color images at 24 bits/pixel (Signal and Image Processing Institute (SIPI), 2025). Table 4 summarizes the dataset and sample images from different categories are shown in Fig. 2.
| Category | Volume | Description |
|---|---|---|
| Textures | 155 | Monochrome images, including 130 images with a resolution of and 25 images with a resolution of . |
| Aerials | 38 | Contains 37 color images and one monochrome image. Resolutions include 12 images of , 25 images of , and one image of . |
| Miscellaneous | 44 | Includes 16 color images and 28 monochrome images. Resolutions are 14 images of , 26 images of , and four images of . |
| Sequences | 69 | Comprises four sequences: three sequences include 16, 32, and 11 images of , and one sequence contains 10 images of . |
Figure 2: Samples from the SIPI image database: Row 1 displays textures, Row 2 shows Aerials, Row 3 features miscellaneous images, and Row 4 presents sequences.
Validation metrics
An effective and robust encryption strategy consistently delivers strong performance on various quality assessment metrics. Figure 3 illustrates several metrics widely used to evaluate the security of image encryption techniques (Rout & Mishra, 2024; Pati, Mishra & Rout, 2024; Kaur & Kumar, 2020).
Figure 3: Evaluation metrics for security analysis.
Results and discussions
Keyspace analysis
The keyspace is defined as the total number of possible keys, which directly influences the system’s strength against brute-force attacks. A larger keyspace exponentially increases the computational complexity of key guessing, making unauthorized decryption practically infeasible. The proposed encryption algorithm employs multiple keys derived from symmetric, asymmetric, and chaotic components. The specifications of the key used in the proposed encryption scheme are given in Table 5. Assuming all keys are independently and uniformly distributed, the total keyspace is the product of all individual keyspaces, calculated as:
| S.No. | Key type and description | Key size (bits) |
|---|---|---|
| 1 | AES keys (3 independent keys, each 16 bytes) | |
| 2 | 3DES keys (2 keys, each with 168-bit effective security) | |
| 3 | XNOR mask (random byte sequence equal to image size) | Variable (image-dependent) |
| 4 | ECC private key using SECP384R1 curve | 384 |
| 5 | AES-256 key for compressing/encrypting key information | 256 |
Here, L denotes the length in bytes of the image data subjected to the XNOR masking step. For typical image sizes (for example, a 100 KB image), the term contributes approximately 800,000 bits of entropy, which vastly dominates the total keyspace.
This immense keyspace ensures that exhaustive key search attacks are computationally infeasible, even with state-of-the-art hardware. Thus, the proposed encryption framework provides a robust security guarantee, effectively mitigating brute-force and key-recovery attacks.
Key sensitivity
It refers to the ability of a cryptographic algorithm to produce significantly different ciphertexts when the encryption key is slightly modified, such as by flipping a single bit. This ensures high non-linearity and unpredictability between plaintext, key, and ciphertext, thereby enhancing resistance to cryptanalytic attacks. The Avalanche Effect (AE) quantifies key sensitivity, where an ideal algorithm exhibits an AE value greater than 50%, which means that a one-bit change in the key alters approximately half of the ciphertext bits (Kaur & Kumar, 2022). This property strengthens diffusion, making it infeasible for attackers to infer relationships among plaintext, ciphertext, and key.
To measure AE quantitatively, the Avalanche Criterion (AC) is defined as:
(9) where and are ciphertext pairs generated by encrypting two keys differing by a single bit, denotes their Hamming distance, is the total number of ciphertext pairs and is the length of the ciphertext in bits.
A robust encryption scheme should achieve an AC value close to 50%, indicating that on average half the ciphertext bits change due to a single bit key modification. Figure 4 illustrates this effect in the proposed scheme by demonstrating significant changes in ciphertext caused by minimal alterations in key.
Figure 4: Key sensitivity test: Column 1 displays the original image, Column 2 displays the encrypted image with correct key, Column 3 displays the encrypted image with modified key, and Column 4 displays the difference between Column 2 and Column 3.
Number of pixels change rate (NPCR)
The NPCR measures the percentage of pixels that differ between two cipher images whose corresponding plain images differ by only a single pixel. It evaluates the diffusion capability of an image encryption algorithm, i.e., how effectively a small change in the input propagates throughout the output. NPCR is mathematically defined as:
(10) where is defined as:
(11)
Here, and denote the pixel intensities at position in two cipher images generated from original images differing by only one pixel. L and M represent the height and width of the images, respectively.
Unified average changing intensity (UACI)
UACI measures the average intensity of differences between two cipher images whose corresponding plaintext images differ slightly (e.g., by one pixel). It reflects the confusion property of the algorithm and indicates its ability to obscure the relationship between plaintext and ciphertext. It is defined as:
(12)
For 8-bit grayscale or RGB images, higher NPCR and UACI values indicate strong sensitivity to input changes. Values significantly lower than the standard may suggest weak sensitivity, whereas excessively high values might imply excessive noise or instability in the encrypted output.
Table 6 presents the NPCR and UACI values obtained using the proposed encryption scheme. High NPCR and UACI values indicate that the encryption algorithm exhibits strong sensitivity to small changes in the input image. Specifically, a high NPCR reflects a significant difference in pixel values between two cipher images derived from slightly different plaintexts. A high UACI suggests large average intensity changes at the pixel level. Together, these metrics demonstrate the robustness of the algorithm against differential attacks and its ability to effectively obscure the statistical characteristics of the original image.
| Image name | NPCR | UACI |
|---|---|---|
| Female | 99.35% | 49.97% |
| Baboon | 99.57% | 49.96% |
| Airplane | 99.52% | 49.95% |
| Peppers | 99.55% | 50.02% |
Information entropy (IE)
IE measures the randomness or unpredictability of the intensities of pixels in an image. High entropy indicates that the image data exhibit no discernible patterns. On the other hand, the low entropy suggests that future pixel values can be predicted with greater certainty. IE is a key metric for evaluating the strength of an encryption method, as it helps to assess how well the encryption obscures the original image’s structure (Pizer et al., 1987; Tsai, Lee & Matsuyama, 2008; Gray, 2011; Volkenstein, 2009). The entropy value ranges from 0 to 8, with 8 representing a perfectly random image. In the case of an encrypted image, achieving an entropy value close to 8 indicates strong encryption and resistance to statistical attacks. The entropy of an encrypted image is calculated on the basis of the probability distribution of pixel intensities.
IE for an image can be calculated using the following equation:
(13)
Here, represents the information entropy of the image , S is the total number of possible pixel values (or intensity levels), and denotes the probability that the pixel value occurs in the image.
The results presented in Table 7 shows that the entropy values of the proposed encrypted images are close to 8, confirming their high degree of randomness and robustness against attacks.
| Image name | Original | Encrypted |
|---|---|---|
| Female | 6.9005 | 7.9985 |
| Baboon | 7.7632 | 7.9995 |
| Airplane | 6.6649 | 7.9995 |
| Peppers | 7.6696 | 7.9996 |
Correlation coefficient (CC) analysis
The CC between adjacent pixels in an image indicates the degree of similarity in the intensities of the pixels. In the original image, the correlation between adjacent pixels is often high, as neighboring pixels typically share similar intensity values. To evaluate the effectiveness of an encryption method, we can analyze and compare the correlation coefficients of the original and encrypted (scrambled) images in various directions such as Horizontal (H), Vertical (V), and Diagonal (D) (Li, Du & Liang, 2020; Asuero, Sayago & González, 2006).
For a robust cryptosystem, it is essential that the correlation of an encrypted image in all directions is low, as this ensures that the encryption process has disrupted any predictable patterns. The mathematical computation for the CC between two adjacent pixel positions, which are denoted as R and S, is given by the formula:
(14)
Here, R and S are two adjacent pixel positions, is the covariance between R and S, and and are the standard deviations of R and S, respectively, and W is the total number of pixel pairs analyzed.
The covariance and standard deviations are computed using the following equations:
(15)
(16)
(17)
(18)
(19)
In these equations, and are the mean values of the pixel intensities for the sets R and S, respectively.
In an ideal cryptosystem, the correlation between adjacent pixels in the encrypted image should be minimal or close to zero, indicating that the encryption process has effectively randomized pixel relationships. This disruption of patterns makes it difficult for attackers to exploit the image’s structural information. A low CC indicates that the encrypted image has been successfully randomized, providing better resistance against statistical attacks that rely on the predictability of pixel distributions. In contrast, a high CC suggests that the encryption method may be weak, as the similarity between adjacent pixels could expose valuable information to an adversary.
Figure 5 shows the correlation of adjacent pixels in the H, V, and D directions for both the original and encrypted images. The numerical correlations are given in Table 8. The results clearly indicate that the CC of the encrypted image is significantly reduced compared to the original image, demonstrating the effectiveness of the encryption method in minimizing pixel predictability and improving security.
Figure 5: Correlation coefficient of adjacent pixels in each directions.
Row 1: Baboon (original), Row 2: Baboon (cipher), Row 3: Pepper (original), and Row 4: Pepper (cipher).| Image name | Original | Encrypted | ||||
|---|---|---|---|---|---|---|
| H | V | D | H | V | D | |
| Female | 0.974 | 0.9656 | 0.9514 | 0.0078 | −0.003 | 0.0006 |
| Baboon | 0.8665 | 0.7587 | 0.7261 | 0.0025 | −0.003 | 0.0001 |
| Airplane | 0.9663 | 0.9641 | 0.937 | 0.0017 | 0.0064 | −0.001 |
| Peppers | 0.9767 | 0.9792 | 0.9639 | 0.0018 | 0.0002 | −0.002 |
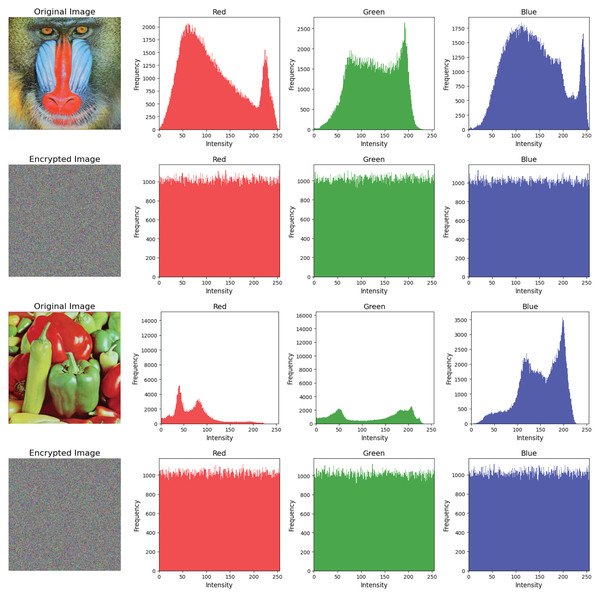
Histogram analysis
It evaluates the distribution of pixel intensities in an encrypted image. For an ideal robust cryptosystem, the histogram of the encrypted image should be uniformly distributed. It prevents any visible patterns or resemblances to the histogram of the original image, as illustrated in Fig. 6. This uniformity ensures that the encryption process effectively conceals the original data, making it highly resistant to statistical attacks (Zhang, 2021; Scott, 2010; Pizer et al., 1987).
Figure 6: Pixel distribution: original baboon image in Row 1 and its corresponding cipher in Row 2.
Original Pepper image in Row 3 and its corresponding cipher in Row 4.Mathematically, the histogram of an image I can be expressed as
(20)
Here, represents the pixel intensity at position , is the pixel intensity level (ranging from 0 to 255 for an 8-bit grayscale image), is the Dirac delta function, which is defined as:
(21)
Peak signal-to-noise ratio (PSNR) and mean squared error (MSE)
The performance of the decryption process in an encryption scheme is evaluated using two important image quality assessment metrics: MSE and PSNR. These metrics quantify the similarity between the decrypted image and the original image. A lower MSE value (close to 0) indicates that the decrypted image is very close to the original, with minimal distortion. A higher PSNR value (typically above 30 dB) suggests that the noise introduced during encryption and decryption is negligible and the visual quality of the image is preserved (Tanchenko, 2014; Joshi, Yadav & Allwadhi, 2016).
The mathematical formulation for MSE is given by the following:
(22)
Here, and represent the pixel values at position in the decrypted and original images, respectively. L and M denote the height and width of the image.
The corresponding PSNR is calculated using the following:
(23)
Table 9 illustrates PSNR values and MSE values close to their ideal values that confirm the effectiveness of the proposed encryption and decryption process. These results also validate that the decryption procedure can successfully reconstruct the original image with minimal loss or degradation.
| Image name | PSNR | MSE | Encryption time | Decryption time |
|---|---|---|---|---|
| Female | 51.0225 | 0.5138 | 0.1264 | 0.4831 |
| Baboon | 51.141 | 0.50001 | 0.5026 | 1.9202 |
| Airplane | 51.145 | 0.4995 | 0.4944 | 1.9548 |
| Peppers | 51.1203 | 0.5023 | 0.5043 | 1.9981 |
Execution time
It is an essential factor to evaluate the feasibility of the model, particularly in scenarios where real-time encryption and decryption are required. A lower execution time indicates that the algorithm is efficient and can handle large image datasets with minimal delay. The execution time is influenced by several factors, including the complexity of the algorithm, the size of the input, and the available computational resources. To assess execution time, we measure the total time taken for both the encryption and decryption processes. The time is calculated in seconds and can be expressed as:
(24)
Here, and represent the time taken to encrypt and decrypt the image, respectively.
The encryption and decryption time of the proposed model are given in Table 9. It could be observed that the whole process is completed faster with a minimal computation time.
Table 10 provides a comprehensive comparison of the proposed image encryption algorithm against several recent methods using the standard Baboon image. The evaluation includes key statistical and cryptographic metrics such as the CC, IE, NPCR, and UACI. The CCs in H, V, and D directions for the proposed method are very close to zero (0.0025, −0.0030, and 0.0001 respectively) which indicates minimal similarity between adjacent pixels in the encrypted image. This reflects a strong level of diffusion, which is important to defend against statistical attacks. Similarly, other methods such as Rout & Mishra (2024) and Pati, Mishra & Rout (2024) exhibit relatively higher correlation values. This indicates weaker encryption effectiveness in breaking pixel relationships. The proposed method also achieves an IE of 7.9995 (close to the ideal value) that demonstrates high randomness and unpredictability in the encrypted image. It is slightly higher than the entropy values reported by other methods, which indicates superiority in resistance to entropy-based analysis. In addition, the proposed scheme shows excellent sensitivity to changes in the input image, as suggested by its NPCR and UACI values of 99.58% and 49.96%, respectively. Although NPCR is comparable to other methods, the UACI of the proposed approach is significantly higher. This indicates a much stronger response to minor changes in the original image and ensures better protection against differential cryptanalysis. Overall, the results clearly show that the proposed encryption technique delivers improved performance and security compared to other existing approaches.
| Method | Correlation coefficient | IE | NPCR (%) | UACI (%) | ||
|---|---|---|---|---|---|---|
| H | V | D | ||||
| Proposed | 0.0025 | −0.0030 | 0.0001 | 7.9995 | 99.58 | 49.96 |
| Kumar & Sharma (2024) | −0.0075 | −0.0071 | 0.0041 | 7.9987 | 99.58 | 33.18 |
| Mohammed et al. (2024) | – | – | – | 7.9973 | 99.58 | 26.32 |
| Rout & Mishra (2024) | 0.0137 | −0.0237 | 0.0089 | 7.9991 | 99.59 | 29.48 |
| Pati, Mishra & Rout (2024) | 0.0024 | −0.0140 | −0.0025 | – | – | – |
The proposed framework strengthens the security posture of image-based systems by integrating multiple cryptographic layers. This strategy improves resistance to various cryptanalytic attacks, such as brute-force, differential, and statistical attacks. The simplicity of the approach makes it eligible for any domain without the need of significant modifications. The practical utilization of the approach is limitless but not confined to:
Healthcare systems: for secure transmission and storage of sensitive medical images.
Military and defense: where encrypted satellite or reconnaissance images must be protected under high-threat conditions.
Cloud storage platforms: to ensure secure image backup and prevent unauthorized access or tampering.
AI-based image analytics: to protect training datasets from reverse engineering or adversarial manipulation.
In addition, the modular, scalable, and adaptable design of the proposed encryption makes it suitable for integration into broader cybersecurity architectures. This study provides a reference framework for future research focused on securing multimedia data in evolving cryptographic threat landscapes.
Conclusion and future work
In this article, we put forward a multilayered image encryption model designed to address the growing threats posed by emerging and unforeseen attack techniques to traditional cryptographic systems. The model combines AES, DES3, and ECC with additional transformations such as pixel shuffling, circular left shifting, and XNOR operations to ensure robust encryption. Key exchange is secured using ECDH and HKDF. The encrypted image and keys are encapsulated within a secure archive for added resilience. The proposed cryptosystem achieves the highest IE, NPCR, and UACI of 7.9995, 99.58%, 49.96%, respectively. In addition, the proposed model offers a large keyspace that demonstrates an avalanche effect of more than 50% and is resistant to various cryptographic attacks. The results demonstrate the strong resistance of the model to various attacks and offer a robust solution to protect sensitive images. Future research could focus on improving computational efficiency for real-time applications and also explore the integration of post-quantum cryptographic algorithms. Another promising area of interest is the extension of the framework to video encryption. Real-world applications, such as secure image transmission, can also be explored, which is particularly relevant in critical domains like healthcare and defense.