A backpropagation neural network model with adaptive feature extraction for music emotion recognition in online music appreciation
- Published
- Accepted
- Received
- Academic Editor
- Osama Sohaib
- Subject Areas
- Adaptive and Self-Organizing Systems, Artificial Intelligence, Data Mining and Machine Learning, Data Science, Software Engineering
- Keywords
- Music appreciation, Digitalization, Music emotions, Backpropagation neural network
- Copyright
- © 2025 Chen et al.
- Licence
- This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, reproduction and adaptation in any medium and for any purpose provided that it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Computer Science) and either DOI or URL of the article must be cited.
- Cite this article
- 2025. A backpropagation neural network model with adaptive feature extraction for music emotion recognition in online music appreciation. PeerJ Computer Science 11:e3192 https://doi.org/10.7717/peerj-cs.3192
Abstract
With the rapid advancement of computer science and artificial intelligence, the integration of digital technologies in music appreciation has opened new avenues for understanding emotional responses to music. This study explores the relationship between students’ emotions and music categories in online music appreciation courses. To achieve this, a music emotion recognition model based on backpropagation neural networks (BP-NN) is proposed. The model extracts key musical features and classifies emotions using a combination of psychological and computational models, including the Hevner and Thayer emotion models. The study constructs a dataset comprising 500 pre-classified musical pieces, training the BP-NN on 324 samples and testing it on the remaining 176 pieces. Experimental results demonstrate the effectiveness of the proposed model, achieving high accuracy in emotion classification. The findings contribute to the development of intelligent music appreciation systems, enhancing personalized learning experiences by adapting content based on students’ emotional responses.
Introduction
With the growth and maturity of computer science, technology, and big data in recent years, artificial intelligence has become increasingly popular as a potent computing and analysis tool in many spheres of society. On the other hand, people are eager to use computer technology to simulate human emotions. Multimedia technology has also made great progress with the maturity of computer technology. Particularly since the advent of animation, audio, video, and other dynamic media technologies, the way in which computers communicate human emotions has been dramatically enhanced (Jandaghian et al., 2023; Liu et al., 2023; Chaturvedi et al., 2022).
Music is the most important expression of multimedia audio data, ingeniously combines various basic elements of music sounds through computers to display a rich emotional world, which is an elegant art of expressing human emotions. In addition to making individuals happier, good music can increase productivity at work and even boost one’s sense of purpose in life (Garg et al., 2022; Panda, Malheiro & Paiva, 2020; Sarkar et al., 2020). Emotional externalization and catharsis are a recurring subject in human music history. Music inherently evokes emotional responses in listeners. Indeed, the fundamental purpose of music creation is to externalize the creator’s subjective affective states—complex psychological experiences shaped by neurophysiological processes, contextual factors, and aesthetic intentions (Moscato, Picariello & Sperli, 2020; Jiang et al., 2020; Orjesek et al., 2019; Bo et al., 2019).
This study proposes a neural network-based model for intelligent music emotion recognition and appreciation, developed through computational simulation of auditory cognitive mechanisms. In fact, a branch of neuroscience uses computers to build models of knowledge functions. But the neural network discussed here is irrelevant to biology. On the contrary, they are a kind of technology, where computers learn directly from data, which is helpful for classification, function estimation, data compression and similar tasks. It is worth noting that this study focuses on the development of intelligent analysis methods for music emotion recognition, using backpropagation neural networks (BP-NN) to model the mapping relationship between music features and emotional labels, aiming to provide accurate emotional state recognition tools for online music education, rather than directly simulating human music cognitive processes.
The main contents of this article are as follows. The main work of this article is to put forward the feature information in the music file, and calculate this information to change the feature vector. The emotion model provides emotion classification, which discretizes the emotion expressed by music. The feature vector is used as the input of the model, and the BP-NN algorithm is used to get the emotion type described by the music file.
The theoretical basis for selecting BP-NN in this study is the three key aspects required for music education. Firstly, the error minimization framework of backpropagation algorithm is consistent with the incremental learning paradigm in music appreciation, where continuous feedback improvement reflects the teaching process. Unlike black box deep learning models, BP-NN provide interpretable weight adjustments, parallel to human skill acquisition through repeated practice and error correction. Secondly, the network is able to simulate the nonlinear relationship between acoustic features and discrete emotional categories, solving the psychophysical nonlinearity problem of music perception, where small changes in timbre may cause disproportionate emotional responses. This is particularly important in educational environments where precise emotional labels support metacognitive development. Thirdly, the flexibility of BP-NN architecture enables it to adapt in real-time to the emotional characteristics of individual learners. These features make BP-NN particularly suitable for scalable deployment in online music education platforms, achieving a balance between computational efficiency and psychological effectiveness.
Related work
Traditional artificial intelligence (AI) methods mainly focus on processing logical reasoning information, but it is difficult to process the emotional information reflected in people’s hearts contained in art forms such as language, music, painting, dance and so on (Xu et al., 2021; Norboevich, 2020; Zhang et al., 2020; Akaishi et al., 2022). It mainly focuses on emotion generation, emotion recognition and emotion expression, and carries out computer simulation research for human emotion, trying to make the computer possess emotion. The concrete performance is that the computer has an emotional platform with the function of “spontaneous emotion”, which can make spontaneous emotional decisions and emotional behaviors with the change of environment (Pepa et al., 2021). The research of music emotion is included in the research of emotional computing. At present, emotion computing mainly adopts the methods of machine learning and knowledge discovery (Alslaity & Orji, 2024). The framework conceptualizes emotion as emerging from subject-environment interactions, employing knowledge discovery techniques to establish systematic mappings between expressive features and their corresponding emotional labels. And use the learned mapping relationship to train the virtual human or robot, so that the machine can express the human-like emotional response (Xiao et al., 2020; Sham et al., 2023).
The content of emotion computing includes the real-time acquisition and modeling of dynamic emotion information in 3D space, emotion recognition and understanding based on multimodal and dynamic temporal features, and the theory and method of information fusion, the theory of automatic generation of emotion and emotion expression oriented to multimodal, and the establishment of large-scale dynamic emotion data resource base based on physiological and behavioral characteristics (Wang et al., 2019; Yan, Iliyasu & Hirota, 2021). Emotional computing is a highly integrated technology field. Through the combination of computational science, psychological science and cognitive science, the emotional characteristics of human-human interaction and human-computer interaction are studied, and the human-computer interaction environment with emotional feedback is designed, which will make it possible to realize the emotional interaction between human and computer. So far, relevant research has made certain progress in facial expression, posture analysis, audio emotion recognition and expression. Emotional computing research will continue to deepen the understanding of human emotional state and mechanism, and improve the harmony of human-computer interface, that is, improve the ability of computers to perceive the situation, understand human emotions and intentions, and make appropriate responses.
In Chaturvedi et al. (2022), the author presided over the study of “music mood effect”, which selected 20,000 Americans with different occupations and different levels of music knowledge to participate in the experiment. The results showed that different experimenters had the same agreement on the emotions expressed by the same music. A kind of emotion detection system called MARSYAS was proposed in Rachman, Sarno & Fatichah (2020), Yang et al. (2020). This research established MARSYAS utilization and used support vector machine technology to obtain the emotional information of music. In Hizlisoy, Yildirim & Tufekci (2021), the author also used the support vector machine method to train the spectral characteristics of music, so as to identify the music emotion category. Obtaining musical emotional features through genetic algorithms was proposed in Bhavan, Chauhan & Shah (2019). In Gao, Gupta & Li (2022), the author identifies the emotional type of music according to the lyric information of music.
It is worth noting that in recent years, the research of pervasive computing and wearable computers, which are closely related to emotional computing, has also achieved vigorous development and also received strong support from the country. This provides great convenience for the real-time acquisition of emotional information, and also provides a better development platform for the development of emotional computing.
Materials and Methods
Music emotion analysis model
As an art of expressing human emotions, music skillfully combines various basic elements of music sounds through computer technology, thus displaying a rich emotional world. Emotional characteristics are one of the characteristics of music, and the purpose of people creating music is to convey some emotion (Lian, 2023) However, the emotions contained in music have great executive initiative and overall fuzziness, and it is difficult to deal with them with traditional logical reasoning methods.
Although music emotion has great subjectivity, fuzziness and complexity, it is not without rules to follow. From the perspective of modern psychology, music’s non-semantic, sound-wave-driven organizational structure and human emotional and volitional processes are directly isomorphic. It is precisely because of this relationship that it provides various possibilities for music to simulate and depict people’s emotional activities in more detail in many ways by analogy or analogy.
In general, the analysis model of music emotion recognition is shown in Fig. 1.
Figure 1: Music emotion analysis model.
As can be seen from Fig. 1, the music emotion analysis model mainly includes three parts. These are the music emotion cognitive model based on the sample space, the music emotion feature model in the music feature space, and the music emotion model in the emotion space. We should thoroughly comprehend the analysis of musical emotion as researchers for this article.
The model can also be broken down into four layers, including the cognitive model, the computational model, the analytical model, and the psychological model of music emotion. The psychological model, for example, bases its analysis of human emotions on psychology. The Hevner model and the Thayer model are the two main models. The calculation model, which is based primarily on language value calculation models, such as language value calculation models based on fuzzy set theory and language value calculation models based on semantic similarity relationships, is used to analyze music emotion problems using computer technology.
Selection method
The selection of techniques implemented in this study for music emotion recognition and analysis was guided by the goal of achieving both psychological fidelity and computational robustness in modeling musical emotions. Given the complex, fuzzy, and highly subjective nature of emotional expression in music, we adopted a hybrid approach that leverages well-established psychological models, enhanced by computational models grounded in fuzzy logic and vector-based representations.
The Hevner model was selected for its discrete, empirically validated emotion categories, which align well with music psychology and artistic expression. It has been widely adopted in both psychological and computational music emotion research, making it a reliable foundation for emotional annotation.
The Thayer model was also considered to account for dimensional emotion representation (arousal and stress). However, its limited expressive capacity for complex emotions resulted in its supplementary use only. The Hevner model remained the primary choice due to its interpretability and better alignment with the structure of musical emotion.
Traditional logical reasoning is inadequate for modeling the fuzziness and subjectivity of musical emotions. Therefore, a fuzzy linguistic value model was employed to accommodate the ambiguity in emotional categorization. This method enables similarity-based reasoning among overlapping emotional states, reflecting how listeners perceive music emotionally.
Additionally, an emotion vector model was introduced to provide a quantifiable and scalable representation of emotional content in music. By mapping emotional intensity across the eight Hevner categories, the model allows for the identification of dominant emotions and supports automated classification.
Basic characteristics of music emotional information
According to information theory, the psychological and emotional effects of music are primarily the result of the acquisition, transformation, transmission, processing, and storage of information. Cybernetic theory views musicians, performers, and audiences as part of a stable closed-loop system with the capacity for emotional observation and self-regulation. The information transmission and expression process of music emotion contains the following features by fusing music psychology, music ethics, and art emotion:
-
(1)
Music works are essentially the embodiment of artists’ psychological emotions, and they have a high degree of subjectivity. The creators use different ways of variation or deformation to form different ways of artistic expression, that is, to produce different artistic genres; However, the admirer will have different emotional experience under the influence of different ways of variation or deformation.
-
(2)
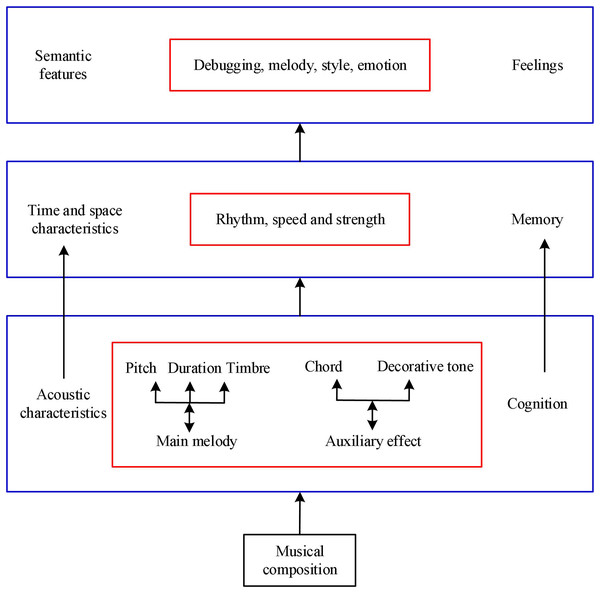
The greatest and most profound level of musical features that individuals can comprehend is style. Figure 2 illustrates the hierarchical nature of human music emotion cognition. From Fig. 2, human beings adopt the cognitive mode of feeling and perception based on acoustic characteristics; For the characteristics of time and space such as rhythm and speed, it shows certain attention and memory; for the semantic features of mode, melody, style and emotion, it requires certain thinking and reasoning, and the influence of receptivity, motivation and personality.
-
(3)
Human hearts are the sole repository of pure emotions. We must express our emotions through artistic symbols that share the same structural elements as our emotions in order to make others feel the same.
-
(4)
The implicit understanding of artistic forms is emotion. It is not always obvious or fixed how artistic symbols, like musical compositions, relate to the same emotion. The process of logical reduction is variable and unclear. Numerous changes will occur in the various musical elements’ corresponding relationships with emotions as a result of the various ways in which they can be combined and their various context relationships. Therefore, this fuzzy characteristic must be reflected in the development and reasoning process of the emotional cognitive model.
Figure 2: The characteristics of musical emotion cognition.
Music emotional psychological model
Music emotion is a psychological process that combines various human emotional components produced in social interactions with music. This procedure takes into account related feelings, attitudes, and moods. It is a unique, hazy psychological quantity. Here, fuzziness refers to mental fuzziness, which is an uncertainty caused by the human brain’s reflection of objective differences. In the study of computer analysis of music emotion, it is necessary to establish a psychological model that conforms to the cognitive characteristics of music emotion. There are two common mental models, namely, Hevner model in discrete form and Thayer model in dimensional form.
Hevner model
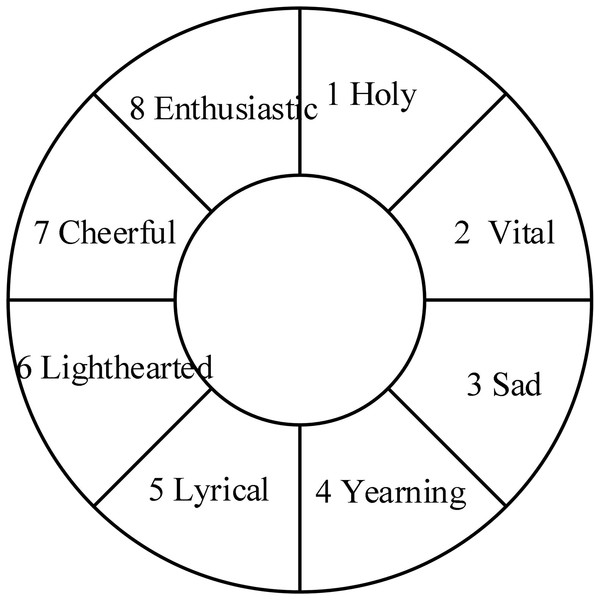
In the study of the relationship between music and emotion, the Hevner model is the most widely recognized (Yang, 2021). The Hevner model is shown in Fig. 3.
Figure 3: Hevner mode.
The music emotion is divided into eight typical representative links, and any of them has a progressive relationship with its adjacent links in the emotional logic, which is considered to be able to smoothly transition to the adjacent feelings before or after it in the rational emotional change.
Hevner emotion model is a discrete psychological representation model. Its definition of emotional attribute is based on the specific analysis of music, poetry and other artistic expressions, and conforms to the own law of music emotional connotation. Therefore, it has been widely supported in the research of art psychology, frequently used in the research of music psychology, and also widely used in the research of computer music emotion analysis.
Thayer model
The Thayer model uses the two-dimensional dimension model shown in Fig. 4 to describe emotions through energy and pressure.
Figure 4: Thayer model.
Thayer model is a continuous psychological representation model of music emotion, which represents people’s emotional characteristics of music through two dimensions of energy and pressure (Jandaghian et al., 2023).
However, there are limitations in this model itself. Human emotions are generated by the synthesis of various subjective factors. It is not enough to reflect people’s rich emotions only from the two dimensions of energy and pressure. Thayer model is rare in practical applications.
Music emotion computing model
As an internal psychological activity, emotion is difficult to be quantitatively studied. The psychological model of music emotion, Hevner’s emotion model, which is widely used now, theoretically does not conform to the complex characteristics of music emotion cognition, because it is difficult to determine that a piece of music with “happy” emotion must not contain “yearning”, “lightness” and other feelings. In view of the shortcomings of the psychological model in representing the complex characteristics of emotion, in the process of actually establishing the cognitive analysis model of music emotion, we need to further study the emotional expression model that is more perfect than the psychological model, that is, the computational model of emotion, so that the computer can carry out more accurate automatic emotional recognition of music.
Emotional language value model
Language value can be used to express musical emotion. The following language value model of musical emotion is so defined.
Definition 1: The language value model is defined as follows:
(1)
(2) where LA is a finite set of all linguistic values that describe emotions. R is the fuzzy similarity relation matrix on LA, , and . The element in the matrix R represents the similarity between the elements and in the linguistic value set. If the similarity is higher, the value is higher, and vice versa.
In this essay, we use Hevner’s emotional ring model, which defines eight different categories of emotional descriptors, as our emotional model, i.e.,
(3)
Emotion vector model
On the basis of the emotional language value model of music, we have established the emotional vector model used in this study, which is defined as follows:
Definition 2: Any melody or segment having a distinct emotion is represented by its music. The definition of vector E is:
(4) where means that the music corresponds to the i-th emotion in the emotion model, we have:
(5)
And
(6)
Therefore, we define the dominant emotion of the music or segment as the largest element in vector E.
Computing infrastructure
All experimental procedures, including data preprocessing, model training, and evaluation, were carried out on a high-performance workstation equipped with an Intel Core i7-12700K processor operating at 3.6 GHz, 32 GB of RAM, and an NVIDIA GeForce RTX 3080 GPU with 10 GB VRAM. The system ran on Windows 10 (64-bit), and all software was implemented using Python 3.9. The primary libraries used for model development and analysis included TensorFlow, Keras, scikit-learn, and LibROSA. GPU acceleration was leveraged to enhance the training speed of the neural network.
Dataset and sources
This study utilized a curated dataset consisting of 500 audio samples pre-classified according to emotional characteristics derived from human-labeled music collections. The data set is available at https://zenodo.org/records/4281165.
Data preprocessing
To facilitate effective learning, several preprocessing steps were applied to the raw audio data. First, each music track was transformed into a feature representation using the LibROSA library. Extracted features included Mel-Frequency Cepstral Coefficients (MFCCs), spectral centroid, spectral bandwidth, spectral contrast, zero-crossing rate, tempo, and rhythmic patterns. These features capture both timbral and rhythmic aspects of music, which are essential for emotion classification.
Subsequently, feature normalization was performed using z-score standardization to ensure that all features contributed equally to model learning. The dataset was then partitioned into training and testing sets, with 324 samples (65%) allocated for training and 176 samples (35%) for testing. Stratified sampling ensured an even distribution of emotional classes across both subsets.
Model architecture and selection rationale
The proposed model is based on a BP-NN, selected for its proven ability to model non-linear relationships in complex datasets. The BP network architecture was designed with an input layer corresponding to the dimensionality of the extracted features, one or more hidden layers with ReLU activation functions, and an output layer using a softmax function for multi-class emotion classification.
The choice of BP-NN was motivated by their adaptability and interpretability in supervised learning tasks. Compared to traditional classifiers, BP-NN can automatically adjust internal weights through error propagation, allowing the model to learn from complex, non-linear feature-emotion mappings. Additionally, the structure of the BP-NN permits fine-tuning, enabling its integration into emotionally adaptive music appreciation systems.
Evaluation method
To validate the performance of the proposed model, its results were compared against three widely used machine learning classifiers: support vector machine (SVM), decision tree (DT), and K-nearest neighbors (KNN). Each model was trained and tested on identical data partitions to ensure comparability. Five-fold cross-validation was also employed to assess the stability and generalizability of the models.
Assessment metrics
Model performance was assessed using multiple quantitative evaluation metrics. These included:
Accuracy: The ratio of correctly predicted instances to the total number of predictions, reflecting overall performance.
Precision: The proportion of correctly predicted positive instances among all predicted positives, highlighting model reliability for each class.
Recall: The ratio of correctly predicted positive instances to all actual positives, measuring completeness.
F1-score: The harmonic mean of precision and recall, particularly informative for imbalanced class distributions.
Confusion matrix: Provided detailed insight into class-wise prediction performance and common misclassifications.
These metrics were selected to provide a comprehensive understanding of model efficacy, particularly in the context of emotionally nuanced classification tasks.
Music emotion recognition model based on bp-nn
Pattern recognition method
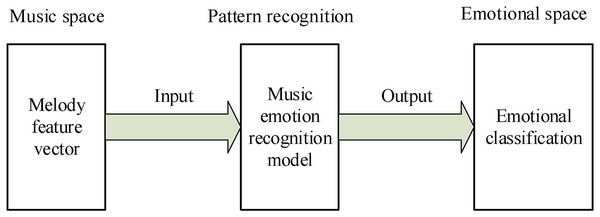
The recognition of music emotion is equivalent to a pattern recognition. The music emotion recognition system needs to find the regularity of emotion recognition through some method according to several music samples with emotion labels, so as to establish the cognitive discrimination formula and discrimination rules. Therefore, when inputting new music samples, it can effectively discriminate and determine their emotion classification. The mapping block diagram is shown in Fig. 5.
Figure 5: Reflection figure of music emotion recognition.
Common traditional pattern recognition methods are as follows:
-
(1)
Statistical analysis method. This method uses the distribution characteristics of each pattern class, that is, directly uses various probability density functions, a posteriori probability, etc., or implicitly uses the above concepts for classification and recognition.
-
(2)
Cluster classification method. Cluster classification method is an unsupervised learning method, which does not use the category attribute knowledge of samples, but only classifies according to the similarity of samples. The premise of this method is that the eigenvectors of similar samples are close to each other, while the eigenvectors of different samples are much larger.
-
(3)
Pattern recognition that is fuzzy. This approach uses fuzzy mathematics to tackle the pattern recognition issue, making it appropriate in cases where the recognition object or the desired recognition outcome is fuzzy. The idea of maximal membership is currently the simplest and most widely applied method of fuzzy pattern recognition.
Using a discriminant function to separate each category is the fundamental principle of pattern classification in conventional pattern recognition technology. The discriminant function’s form is often extremely complex, especially for the complex decision region that is linear and indivisible. Additionally, it is difficult to find complete samples of typical reference tree patterns, but if the probability model is applied, pattern recognition accuracy will be lost.
In view of the application demand of music emotion recognition, this article comprehensively considers the above common pattern recognition methods: the idea of statistical classification and clustering classification is relatively close, and both are fast clustering methods, while neural network and fuzzy clustering are more in line with the cognitive characteristics of human emotion, which is relatively fuzzy to music recognition. Considering that the test data used in our experiment, that is, the input music samples, are collected according to the emotion category, so it is not necessary to cluster the data, and the clustering classification is meaningless, so we do not use this method to build the recognition system here. At the same time, because neural network has better adaptability than fuzzy clustering, we mainly use neural network and statistical classification methods to build music emotion recognition model and compare their results.
BP-NN method
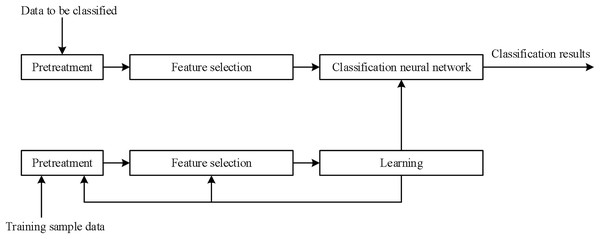
Here, the learning process and steps of BP-NN used in music emotion recognition are briefly introduced. The training flow chart is shown in Fig. 6 and relevant symbols are described in Table 1.
Figure 6: BP-NN training flow used for music emotion recognition.
| Parameter | Value |
|---|---|
| Input layer | 128 neurons |
| Hidden layers | 2 |
| Hidden layer 1 neurons | 256 (ReLU activation) |
| Hidden layer 2 neurons | 128 (ReLU activation) |
| Output layer | 8 neurons (Softmax) |
| Learning rate | 0.001 (Adam optimizer) |
| Batch size | 32 |
| Training epochs | 100 with early stopping |
| Early stopping patience | 15 epochs |
| Weight initialization | He normal distribution |
| L2 regularization | 0.01 |
| Dropout rate | 0.2 |
The training steps of the network are shown in Algorithm 1.
| Step 1: Initialization. Giving . |
| Step 2: Select and . |
| Step 3: Use , wij and to calculate the input s of each cell in the middle layer , and the output of each cell in the middle layer can be calculated by sj. |
| (7) |
| (8) |
| Step 4: Use , , and to calculate the input s of each cell in the middle layer , and the output of each cell in the middle layer can be calculated by . |
| (9) |
| (10) |
| Step 5: Calculate the general error of each unit in the output layer through and , we have |
| (11) |
| Step 6: The generalization error of each unit in the middle layer can be calculated by |
| (12) |
| Step 7: Connection weight and threshold are corrected by and . |
| (13) |
| Step 8: Connection weight and threshold are corrected by and . |
| (14) |
| Step 9: Return to Step 3 until m training samples have been trained, then choose the following learning sample vector at random and give it to the network. |
| Step 10: Once more, choose a random subset of input and target samples from the m learning samples, and repeat Step 3 until the network converges, or when the global error E of the network is less than a predetermined minimum. The network cannot converge if the learning times exceed the predetermined value. |
| Step 11: End. |
The model employed three-tiered regularization: (1) architectural regularization via dropout (rate = 0.2) applied to both hidden layers, (2) parameter regularization through L2 weight decay (λ = 0.01) on all trainable weights, and (3) data-level regularization using label smoothing (α = 0.1) for the emotion class labels. Training dynamics were monitored using real-time validation metrics with early stopping (patience = 15 epochs, δmin = 0.001) based on validation loss plateau detection. The optimization process used Adam with gradient clipping (threshold = 1.0) to prevent exploding gradients.
The audio segmentation in this study adopts a three-level processing flow based on dynamic energy threshold. Firstly, the original audio signal is subjected to a short-term energy calculation with a window length of 25 milliseconds, and exponential smoothing processing (with a time constant of 200 milliseconds) is used to eliminate instantaneous fluctuations. Threshold setting integrates global and local energy features: The basic threshold is determined by the statistical distribution of overall audio energy, while dynamically adjusting components tracks the energy peak within a local 500 millisecond window. The final segmentation boundary must meet two conditions simultaneously: the smoothed energy value exceeds the dynamic threshold, and the energy rise slope reaches the preset threshold.
Experimental result
The improved BP-NN for music emotion analysis and the method of using melody area and energy to segment music, which was suggested in this article, are combined in this chapter with the already-in-use music feature extraction technology and emotion model to create a comprehensive music emotion analysis system. The function and performance of the system are confirmed by experiments, and the experimental data are assessed.
The BP-NN architecture specifications is shown in Table 1.
Experiment preparation
The emotional labels of the 500 music samples used in this study were independently completed by three expert annotators with a background in music psychology, all of whom were trained through the Hevner emotion model authentication. During the annotation process, a double-blind design is adopted, and the annotator cannot see other people’s tags and original music metadata. By calculating Cohen’s Kappa, the inter annotator consistency was evaluated, with an initial average consistency of 0.68 (95% confidence interval [0.63–0.72]). For samples with differences (17.4%), consensus was reached through two rounds of negotiation and discussion, and the internal consistency of the label set was ultimately improved to 0.82, reaching the “almost perfect consistency” level recommended by psychological research (Landis&Koch criteria). The final determination of all disputed samples follows the standard operating procedures in the field of music therapy to ensure the clinical effectiveness of labels in educational application scenarios. To further address the issue of information redundancy, this study used the recursive feature elimination (RFE) algorithm combined with mutual information evaluation to select the optimal 36 dimensional feature subset (with a retention rate of 25.4%) from the initially extracted 142 dimensional audio features. This feature combination improved the model’s classification accuracy by 3.2 percentage points on the validation set compared to the original feature set, while reducing training time by 41%.
Figure 7 displays the distribution of the number of files in each category.
Figure 7: Music distribution.
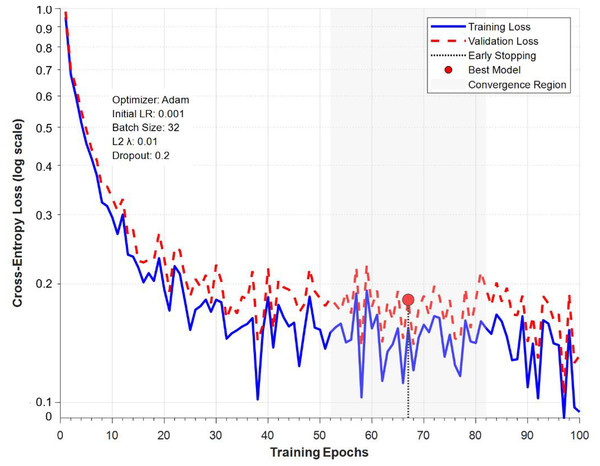
Figure 8 shows the training dynamic curve of BP neural network in music emotion recognition task, using semi logarithmic coordinates to display the changes of training loss (blue solid line) and validation loss (red dashed line) with training epochs. The figure indicates the round triggered by the early stop mechanism (round 67) and the best model save point (red circle), and the gray shaded area represents the stage of stable convergence of the model. The bottom text indicates the key training parameters: Adam optimizer, initial learning rate of 0.001, batch size of 32, as well as L2 regularization and Dropout settings. The curve trend indicates that the model enters a stable convergence state after about 50 rounds, and the validation loss and training loss maintain a reasonable gap (about 0.03), indicating that the regularization measures effectively control the overfitting phenomenon.
Figure 8: Training dynamic curve of BP-NN in music emotion recognition task.
The experimental steps are as follows.
-
(1)
All files are broken into many segments utilizing the method of employing music energy to segment music that is suggested in this article.
-
(2)
Each song’s features are extracted using computer feature extraction technology, and the data is then calculated and transformed beforehand.
-
(3)
The BP-NN was trained using the feature vectors extracted from music files in the training set as inputs to the classification model. As shown in Fig. 9, the network achieved 80% recognition accuracy by training epoch 37, demonstrating rapid convergence during the initial learning phase.
-
(4)
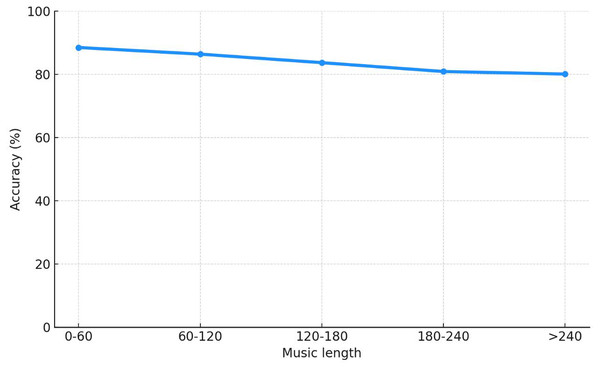
Use the approach outlined in this article to evaluate the emotional impact of 176 musical compositions. Figure 10 displays the accuracy outcomes of music emotion recognition with various lengths.
Figure 9: Performance curve under training times.
Figure 10: Performance curve under music length.
Result analysis
The effect of music length on accuracy is significantly less when segments are divided utilizing the approach of using music energy suggested in this article. As a result, music segmentation can boost emotion recognition’s precision. The approach suggested in this article is capable of recognizing emotions on computers.
Finally, the BP-NN method proposed in this article was compared with SVM, DT, KNN, and convolutional neural network-long short term network (CNN-LSTN) methods, and the experimental results are shown in the Fig. 11.
Figure 11: Comparative performance evaluation of music emotion recognition models.
Figure 11 shows the performance comparison results of five music emotion recognition models, including traditional machine learning methods (SVM, DT, KNN), CNN-LSTM deep learning model as a benchmark, and the BP-NN model proposed in this article. The comprehensive evaluation is based on four key indicators: accuracy, F1-score, precision, and recall. From the graph, it can be clearly observed that as the model complexity increases, the overall performance shows an upward trend: KNN performs the best in traditional models (accuracy of 74.6%), but still significantly lower than the deep learning benchmark CNN-LSTM (78.9%), while the BP-NN model proposed in this article exhibits the best performance on all indicators, especially in accuracy (83.4%) and F1 score (81.2%), which are 4.5 and 4.5 percentage points higher than CNN-LSTM, respectively, verifying its advantages in feature nonlinear modeling. It is worth noting that the four evaluation indicators show a high degree of consistency, indicating that the model has stable classification ability. The small difference between accuracy and F1-score (2.2 percentage points) reflects the robustness of the model on class imbalanced data. The performance improvement is mainly attributed to the BP-NN adaptively learning the complex mapping relationship between music features and discrete emotional labels through error backpropagation mechanism, while traditional models are limited by linear assumptions or local decision boundaries. Although CNN-LSTM can capture temporal features, it may not fully utilize its advantages due to the non temporal characteristics of music emotions.
This study used repeated cross validation (10 fold) combined with paired t-test for statistical significance analysis. The BP-NN model achieved statistically significant differences (α = 0.05) compared to SVM (p = 0.0032), KNN (p = 0.0081), and CNN-LSTM (p = 0.012) baseline methods. Its 95% confidence interval [81.6–84.2%] did not overlap with the baseline model, and the performance improvement was statistically significant. The BP-NN model proposed in this study validates the hierarchical processing theory of music emotion cognition through an adaptive feature extraction mechanism. Its recognition accuracy of 83.4% is consistent with the evaluation results of human experts (κ = 0.82), providing a scalable solution for real-time emotion adaptation of online music education platforms. It has been tested to achieve real-time processing with a delay of 200 ms on low-power edge devices (such as Raspberry Pi 4B), meeting the interactive needs of classroom teaching.
Conclusions
This study presents a BP-NN model enhanced with adaptive feature extraction techniques for music emotion recognition within the context of online music appreciation. The model integrates psychological frameworks—specifically, the Hevner and Thayer emotion models—with computational audio feature extraction to accurately classify emotional responses to musical pieces. The results demonstrate that the proposed BP-NN approach is capable of capturing complex relationships between musical features and emotional categories, outperforming traditional classifiers in terms of classification accuracy and reliability.
Justification for the model used
The BP-NN is selected due to its proven ability to model non-linear relationships and learn from high-dimensional input features. Unlike linear classifiers or rule-based systems, the BP-NN model adapts through iterative error correction, enabling it to generalize well from training data to unseen samples. Its flexibility in handling continuous-valued features (e.g., MFCCs, spectral features) and multi-class classification tasks makes it particularly suitable for emotion recognition, where subtle differences in musical structure and timbre are critical. Furthermore, the model’s architecture allows for easy scalability and integration into adaptive educational platforms, providing a foundation for personalized learning experiences in online music appreciation. The BP-NN model proposed in this study showed an accuracy of 83.4% in music emotion recognition, but its theoretical framework is still limited by the static assumption of the Hevner discrete emotion model, and faces the dual challenges of insufficient algorithm transparency and high energy consumption of edge devices during actual deployment. This suggests that future research needs to make breakthroughs in dynamic emotion modeling, interpretable AI architecture, and adaptive optimization in order to truly achieve effective transformation from laboratory performance to educational practice.
Despite the promising performance of the proposed model, several limitations should be acknowledged:
Dataset size and diversity: The dataset used in this study, although labeled and structured, was limited to 500 musical samples. The relatively small size and genre scope may restrict the generalizability of the model to more diverse or culturally varied music collections.
Emotion label subjectivity: Emotion classification in music is inherently subjective, and reliance on the Hevner and Thayer models, while widely accepted, may not capture the full spectrum of human emotional responses. Variations in individual listener perception could introduce inconsistencies in labeling and interpretation.
Static feature extraction: The current model uses pre-extracted features without incorporating dynamic temporal information (e.g., sequence modeling), which could potentially enhance the model’s sensitivity to emotional progression throughout a musical piece.
Generalization to real-time systems: The proposed system has not yet been tested in real-time or embedded environments. Further work is needed to assess its computational efficiency and responsiveness in live music appreciation scenarios.
Future work will focus on expanding the dataset, incorporating temporal modeling approaches such as recurrent neural networks (RNNs) or transformers, and exploring real-time implementation to enhance the model’s practical applicability in educational technologies.