Research on intelligent registration methods for multidimensional visual communication projection transform images

Image denoising based on wavelet transform optimization

To ensure the accuracy of image registration, an improved adaptive threshold wavelet denoising algorithm is used. To retain fine image details, the image is not processed directly; rather, it is decomposed into the R, G, and B channels, each of which is processed separately (Jozwik-Wabik, Bernacki & Popowicz, 2023). The improved algorithm utilizes the LoG operator, which exhibits specific resistance to noise, to extract edge information. It combines the energy near the wavelet coefficients of the edge part with the correction threshold to obtain an improved threshold function. The enhanced image denoising process is shown in Fig. 1.

Define the noisy image model as:

(1) $$f\left(x,y\right)=g\left(x,y\right)+\chi \left(x,y\right).$$

In the formula, $f\left(x,y\right)$ represents the noisy image, $g\left(x,y\right)$ represents the original image of size $M\times N$ without noise, and $\chi \left(x,y\right)$ represents Gaussian noise.

Decompose the noisy image into gray images of R, G, and B channels, perform edge detection on each channel using the LOG operator to obtain edge images, and then perform wavelet decomposition of the same scale on both the noisy and edge images to obtain two sets of wavelet coefficients $W_{x,y}$ and $W_{x,y1}$. Subtract the two sets of wavelet coefficients obtained to obtain the wavelet coefficient $W_{x,y2}$ of the non-edge image. Afterwards, the wavelet coefficients of the edge image and the non-edge image were processed using different improved threshold functions, resulting in two new sets of wavelet coefficients ${\hat{W}}_{x,y1}$ and ${\hat{W}}_{x,y2}$. Add the two newly obtained sets of wavelet coefficients together to obtain a set of wavelet coefficients ${\hat{W}}_{x,y}$ for the denoised image. To reconstruct the images for the R, G, and B channels, the inverse wavelet transform is performed on the corresponding wavelet coefficients. Finally, the gray reconstructed images of the three channels are synthesized to obtain the denoised image $p\left(x,y\right)$.

Hard threshold function and soft threshold function are the most common threshold functions in wavelet threshold denoising (Al-Khafaji et al., 2022). Among them,

The hard threshold function is:

(2) $${\hat{W}}_{x,y}=\{\begin{array}{c}{W}_{x,y},\left|W_{x,y}\right|\ge \lambda \hfill \\ 0,\left|W_{x,y}\right|<\lambda \hfill \end{array}.$$

The soft threshold function is:

(3) $${\hat{W}}_{x,y}=\{\begin{array}{c}sign\left(W_{x,y}\right)\left(W_{x,y}-\lambda \right),\left|W_{x,y}\right|\ge \lambda \hfill \\ 0,\left|W_{x,y}\right|<\lambda \hfill \end{array}.$$

In the formula, $W_{x,y}$ represents the wavelet coefficients obtained from the noisy image after wavelet transform, ${\hat{W}}_{x,y}$ represents the wavelet coefficients obtained after threshold processing, and $\lambda$ represents the threshold.

Nevertheless, the threshold function described above may mistakenly suppress valuable image details as noise, thereby causing distortion in the reconstructed image. To address this issue, an improved algorithm is adopted to apply new threshold functions to both non-edge and edge parts:

① For non-edge parts of the image, improvements are made based on the soft threshold function. For wavelet coefficients greater than the threshold, the soft threshold function only calculates the difference between the wavelet coefficients and the threshold. While the method is effective in noise removal, it significantly distorts the wavelet coefficients associated with essential image details, resulting in the loss of information and noticeable blurring. Therefore, in improving the threshold function, a threshold error correction coefficient is added to the threshold, and the difference between it and the correction threshold is used for error correction to reduce distortion. Define the improved threshold function as:

(4) $${\hat{W}}_{x,y}=\{\begin{array}{c}{W}_{x,y}\times \left|1-\left(W_{x,y}-\lambda \times s\right)\right|,\left|W_{x,y}\right|\ge \lambda \hfill \\ 0,\left|W_{x,y}\right|<\lambda \hfill \end{array}.$$

In the formula, $s$ represents the threshold error correction coefficient, which is a constant of 0.5–1. For non-edge smooth parts, wavelet coefficients above the threshold are directly corrected, while wavelet coefficients below the threshold are directly set to 0.

② For the edge part of the image, simple error correction of wavelet coefficients cannot guarantee the clarity of the image contour. Therefore, we will continue to improve the threshold function. Because the high-frequency subgraph after wavelet transform contains most of the energy corresponding to the edges and contours of the image, it is necessary to consider the energy $E_{x,y}$ near the wavelet coefficients and compare its relationship with the correction threshold. If its energy is greater than the correction threshold, directly calculate the absolute value of the difference between the energy near the wavelet coefficient and the contraction threshold, then calculate the difference with 1, and multiply it with the wavelet coefficient to obtain a new wavelet coefficient; if the wavelet coefficient is less than the correction threshold, it is directly set to 0.

The improved threshold function is defined as follows:

(5) $${\hat{W}}_{x,y}=\{\begin{array}{c}{W}_{x,y}\times \left|1-\left(E_{x,y}-a\times \lambda \right)\right|,\left|E_{x,y}\right|\ge \lambda \times s\hfill \\ 0,\left|E_{x,y}\right|<\lambda \times s\hfill \end{array}.$$

In the formula, $a$ represents the degree of contraction of the wavelet coefficients, which is controlled by a constant of 0.5–1. $E_{x,y}$ represents the energy near the wavelet coefficients in various directions at the edge of the image, expressed as:

(6) $$E_{x,y}=\sum _{x=1}^X\sum _{y=1}^Y{W}_{x,y}\left(x,y\right).$$

In addition, for the selection of the threshold $\lambda$, a universal threshold is chosen because under the normal Gaussian noise model, for the joint distribution of multidimensional independent normal variables, when the dimensionality tends to infinity, the probability of coefficients greater than this threshold containing noise signals tends to zero:

(7) $$\lambda =\sigma \sqrt{2\log \left(X\times Y\right)}.$$

In the formula, $X$ and $Y$ represents the number of pixels in the horizontal and vertical directions of the image; $\sigma$ represents the standard noise variance.

Extracting image contours based on the LoG operator

As the most essential structural elements of an image, edges benefit significantly from denoising, which improves their clarity and definition (Atal, 2023). The so-called edge refers to the collection of pixels around it that exhibit a step-like or roof-like grayscale change. During the image acquisition process, noise is inevitably introduced due to random disturbances and external influences. The filtering of two-dimensional images aims to suppress noise, enhance image features, improve image quality, and provide a high-quality image with a high signal-to-noise ratio for subsequent processing (Kondo et al., 2022).

This study utilizes the Marr operator to first smooth the image and then perform edge detection to achieve the optimal filtering effect. The Marr operator uses a Gaussian function with a normal distribution as the smoothing function (Beram et al., 2022), that is:

(8) $$G\left(x,y\right)={\displaystyle \frac{\exp \left(-{\displaystyle \frac{x^2+y^2}{2{\delta }^2}}\right)}{2\pi {\delta }^2}.}$$

Firstly, the Gaussian function $G_{\delta }\left(x,y\right)$ is used to convolve the image $f\left(x,y\right)$, resulting in a smoothed image as follows:

(9) $$f_1\left(x,y\right)=G\left(x,y\right)\ast f\left(x,y\right).$$

In the formula, $\ast$ represents the two-dimensional convolution operation of two functions $g$ and $h$.

(10) $$\left(g\ast h\right)\left(x,y\right)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}g\left(x-b,y-c\right)h\left(b,c\right)didj.$$

In the formula, $b$ and $c$ represent two variables.

In the above process, the parameter in Eq. (8) represents the variance of a Gaussian distribution, which can be used as a smoothing factor. The larger the value of $\delta$, the more high-frequency parts are restricted, which can suppress noise. However, the boundaries of the image become blurred. To obtain the Marr operator, the following Laplacian operator must also be used, namely:

(11) $${\mathrm{\nabla }}^2={\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}+{\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{y}^2}.}}$$

In the formula, ${\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}}$ and ${\displaystyle \frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{y}^2}}$ represent the second-order partial derivatives of $x$ and $y$.

As a second-order differential operator, the Laplacian is highly sensitive to image noise, making it challenging to differentiate between noise and true edges. Additionally, its lack of directional sensitivity limits its utility in precise boundary detection.

The second step is to use the Laplacian operator on the smoothed image and obtain the expression of the Marr operator based on the convolution properties:

(12) $$\begin{array}{rl}{f}_2\left(x,y\right)& ={\mathrm{\nabla }}^2{f}_1\left(x,y\right)\\ & ={\mathrm{\nabla }}^2\left(G\left(x,y\right)\ast f\left(x,y\right)\right)\\ & =\left({\mathrm{\nabla }}^{2}G\left(x,y\right)\right)\ast f\left(x,y\right)\end{array}.$$

In the formula:

(13) $${\mathrm{\nabla }}^{2}G\left(x,y\right)={\displaystyle \frac{\left({\displaystyle \frac{x^2+y^2}{2{\delta }^2}-1}\right)\exp \left(-{\displaystyle \frac{x^2+y^2}{2{\delta }^2}}\right)}{\pi {\delta }^2}.}$$

${\mathrm{\nabla }}^{2}G\left(x,y\right)$ is obtained by combining Eqs. (11) and (4), and is called the Gaussian Laplacian operator, abbreviated as the LoG operator. It is an axisymmetric operator, and its one-dimensional function graph is shown in Fig. 2.

The specific steps for using the LoG operator for image contour detection are:

• (1)

  Scan the image in raster order, and when 255 pixels without tracking markers are found, they are considered as the starting point of a boundary, with coordinates denoted as $\left(x,y\right)$;

• (2)

  Starting from the left adjacent 0 pixels of a pixel $\left(x,y\right)$, eight neighboring pixels are arranged in counterclockwise order. If all eight neighborhoods have 0 pixels, they are isolated points. Otherwise, the initial 255 pixels encountered are denoted as $d$;

• (3)

  In the 8-neighborhood of $d$, starting from the next pixel of $d-1$, search for 255 pixels in a counterclockwise direction, and mark the first discovered 255 pixel as $d+1$;

• (4)

  When $d=0$ and $d+1=1$, boundary tracking end. Otherwise, repeat step 3.

Until the search for all pixels in the image is completed, the image contour extraction is finished.

Multi-dimensional image contour matching based on the Fourier descriptor

After extracting the contour of the image using the LoG operator, Fourier descriptors are employed to determine contour matching points based on the image’s contour features.

Fourier descriptors are the Fourier transform coefficients of the shape boundary curve of an object (Jaskólski, Czaplinski & Tomczak, 2024). It is the result of the frequency domain analysis of object boundary curve signals. This method characterizes curves in a manner that is unaffected by shifts or rotations of the origin, ensuring geometric invariance. Take the horizontal axis of the image as the real axis and the vertical axis as the imaginary axis; that is, a point on the plane can correspond to a complex number. By starting at an arbitrary point on the closed boundary of a planar shape and traversing it once in a counterclockwise direction, a one-dimensional complex sequence of boundary points can be obtained:

(14) $$s\left(k\right)=x\left(k\right)+\iota y\left(k\right),k=\left(0,1,2,3,\cdots ,Z-1\right).$$

In the formula, $\iota$ represents the imaginary number. The sequence satisfies the periodic boundary condition, and the sequence is:

(15) $$S\left(u\right)={\displaystyle \frac{\sum _{k=0}^{Z-1}s\left(k\right)\exp \left[{\displaystyle \frac{-\phi 2\pi uk}{Z}}\right]}{Z},u=0,1,2,\cdots ,Z-1.}$$

In the formula, $u$ represents the digital frequency; $S\left(u\right)$ represents the boundary complex sequence, and $s\left(k\right)$ is the spectral coefficient of the boundary complex sequence $S\left(u\right)$. Among these, the high-frequency coefficients correspond to fine contour details, whereas the low-frequency components capture the overall shape of the contour. The DC component corresponds to the geometric center position $\left(x_o,y_o\right)$ of the area surrounded by the boundary, that is:

(16) $$S\left(0\right)={\displaystyle \frac{\sum _{k=0}^{Z-1}\left[x\left(k\right),jy\left(k\right)\right]}{Z}.}$$

In the formula, the real and imaginary parts of the DC component $S\left(0\right)$ are, respectively, the horizontal and vertical coordinates of the geometric center position of the area enclosed by the image boundary. The contour shape of the image boundary curve can be reconstructed by inverse Fourier transform using Fourier transform coefficients $S\left(u\right)$ (Firsov, Khakhulin & Komkov, 2023), that is:

(17) $$s\left(k\right)=\sum _{k=0}^{Z-1}S\left(u\right)\exp \left[{\displaystyle \frac{j2\pi uk}{Z}}\right].$$

If only the first $V$ low-frequency coefficients of $S\left(u\right)$ are taken, and the high-frequency coefficients are filled with zeros, $s\left(k\right)$ can be approximately reconstructed through the inverse Fourier transform, and the approximate contour of the closed boundary can be obtained as follows:

(18) $$\hat{s}\left(k\right)=\sum _{k=0}^{Z-1}S\left(u\right)\exp \left[{\displaystyle \frac{-j2\pi k}{Z}}\right].$$

As a result, the generated curve closely approximates the original image contour, although abrupt changes in the contour are typically smoothed out. The subset of Fourier coefficients in this sense is called a Fourier descriptor.

To identify shapes with rotational, translational, and scaling invariance, Fourier descriptors need to be normalized (Onural, 2024). According to the Fourier transform properties, by translating the starting point position of the shape boundary of an object, with a translation length of $\gamma$, enlarging the object by $r$ times, and rotating it by an angle of $\theta$, the Fourier transform coefficients of the new shape are obtained as follows:

(19) $$s^{\mathrm{\prime }}\left(u\right)=r\cdot \exp \left(j\theta \right)\cdot \exp \left(j{\displaystyle \frac{2\pi }{n}u\gamma }\right)S\left(u\right)+F\left(x_0+\iota y_0\right).$$

From formula, it can be seen that when using Fourier coefficients to describe shape, $\Vert S\left(u\right)\Vert$ has rotation invariance and balance invariance, and is independent of the choice of curve starting point.

When an object is translated, only the value of $F\left(p_0+i{q}_0\right)$ in its $S\left(0\right)$ component is changed. Dividing the amplitude $\Vert S\left(u\right)\Vert$ of each coefficient (except $S\left(0\right)$) by $\Vert S\left(k\right)\Vert$, ${\displaystyle \frac{\Vert S\left(u\right)\Vert }{\Vert S\left(k\right)\Vert }}$ remains invariant to scale changes and has rotation, translation, and scale invariance. It is independent of the starting point position of the curve and is used as a Fourier descriptor. Therefore, the normalized Fourier descriptor $d\left(u\right)$ is defined as:

(20) $$d\left(u\right)={\displaystyle \frac{\Vert S\left(u\right)\Vert }{\Vert S\left(k\right)\Vert }.}$$

In the formula, $\Vert \Vert$ represents modulus taking.

Considering each contour descriptor as a feature vector allows the similarity analysis of image contours to be reformulated as a problem in multidimensional feature space. Determine the similarity between the contours based on the Euclidean distance between them. The calculation method for the Euclidean distance is:

(21) $$Distance=\sqrt{\sum _{k=2}^Z{\Vert d_I\left(k\right)-d_J\left(k\right)\Vert }^2.}$$

In the formula, $d_I\left(k\right)$ and $d_J\left(k\right)$ are Fourier descriptors of two contours. Consider the two contours with the closest Euclidean distance as contour pairs, calculate their centroids, and use them as the mapping point pairs for image registration in the following text.

Image registration based on projection transformation method

The image contours obtained through Fourier feature matching are used as mapping points, and image registration is completed through projection transformation method.

To achieve multidimensional image registration, it is necessary to find the transformation relationship between different images. Therefore, an improved projection transformation is used to complete the mapping of each image (Baum, Hu & Barratt, 2023). Projection transformation is mainly the process of projecting a certain plane onto another plane. Given that multidimensional image registration is intended for three-dimensional data, the approach adopted here involves mapping 2D projection transformations into a restricted form of 3D coordinate transformations (Yang et al., 2022). Consider the projection of points in 3D space onto image planes from different viewpoints, as illustrated in Fig. 3.

For a camera centered at the origin, point $\left(X,Y,L\right)$ in 3D space, and its pixel coordinate is:

(22) $$\mu =V\cdot U.$$

In the formula, $V$ is the camera parameter. Therefore, if $U$ represents the 3D coordinate point corresponding to pixel $\mu$, then the coordinates of point $U$ can be represented as $U=V^{-1}\mu$. The perspective projection relationship between two different image pixels $\mu$ and ${\mu }^{\mathrm{\prime }}$ can be expressed as:

(23) $$\begin{array}{rl}{\mu }^{\mathrm{\prime }}& =V\cdot R\cdot U\\ & =V\cdot R\cdot V^{-1}\cdot \mu \\ & =\mathrm{\Lambda }\cdot \mu \end{array}$$

In the formula, $R$ represents the 3D rotation matrix.

Two-dimensional projection transformation is mainly related to homogeneous three-dimensional vector linear transformation. Under the condition of a homogeneous coordinate system, the non singular matrix of two-dimensional projection transformation is described as:

(24) $$\left[\begin{array}{c}{x}^{\mathrm{\prime }}\hfill \\ y^{\mathrm{\prime }}\hfill \\ {\omega }^{\mathrm{\prime }}\hfill \end{array}\right]=\left[\begin{array}{ccc}{\alpha }_{11}& {\alpha }_{12}& {\alpha }_{13}\\ {\alpha }_{21}& {\alpha }_{22}& {\alpha }_{23}\\ {\alpha }_{31}& {\alpha }_{32}& {\alpha }_{33}\end{array}\right]\left[\begin{array}{c}x\hfill \\ y\hfill \\ \omega \hfill \end{array}\right].$$

Rigid body transformation is a combination of rotation transformation, translation transformation, and scaling transformation. Affine transformation is a general transformation in rigid body transformation. Under homogeneous coordinate conditions, the matrices corresponding to the two transformations in 2D space can be represented as:

(25) $$\begin{array}{rl}& M_{rigid-2D}=\left[\begin{array}{ccc}\cos \theta & -\sin \theta & t_x\\ \sin \theta & \cos \theta & t_y\\ 0& 0& 1\end{array}\right]\\ & M_{affine-2D}=\left[\begin{array}{ccc}{\alpha }_{11}& {\alpha }_{12}& {\alpha }_{13}\\ {\alpha }_{21}& {\alpha }_{22}& {\alpha }_{23}\\ 0& 0& 1\end{array}\right]\end{array}.$$

In the formula, $\theta$ represents the rotation angle during the rotation transformation process, $t_x$ represents the horizontal translation component of the translation transformation, and $t_y$ represents the vertical translation component. In general, affine transformation in Cartesian coordinate system can map pixel coordinate $\left(x,y\right)$ to pixel coordinate $\left(x^{\mathrm{\prime }},y^{\mathrm{\prime }}\right)$ as follows:

(26) $$\left(\begin{array}{c}{x}^{\mathrm{\prime }}\hfill \\ y^{\mathrm{\prime }}\hfill \end{array}\right)=\left(\begin{array}{c}{\alpha }_{13}\hfill \\ {\alpha }_{23}\hfill \end{array}\right)+\left(\begin{array}{cc}{\alpha }_{11}& {\alpha }_{12}\\ {\alpha }_{21}& {\alpha }_{22}\end{array}\right)\left(\begin{array}{c}x\hfill \\ y\hfill \end{array}\right).$$

The projection transformation can map $\left(x,y\right)$ to $\left(x^{\mathrm{\prime }},y^{\mathrm{\prime }}\right)$ using the following formula:

(27) $$\begin{array}{rl}& x^{\mathrm{\prime }}={\displaystyle \frac{{\alpha }_{0}x+{\alpha }_{1}y+{\alpha }_2}{{\alpha }_{6}x+{\alpha }_{7}y+{\alpha }_8}}\\ & y^{\mathrm{\prime }}={\displaystyle \frac{{\alpha }_{3}x+{\alpha }_{4}y+{\alpha }_5}{{\alpha }_{6}x+{\alpha }_{7}y+{\alpha }_8}}\end{array}.$$

After the mapping is completed, the registered image can be obtained.

Experimental subjects

The experimental evaluation was conducted using two datasets: high-resolution landscape photographs of Elephant Trunk Hill and the Potala Palace, each at a resolution of 1,920 × 1,080 shown in Fig. 4. The images vary by capture angle and lighting conditions to simulate real-world projection discrepancies. These datasets were selected for their diverse edge structures and geometric richness, allowing robust testing of contour-based registration methods.

All experiments were conducted on a workstation equipped with an Intel Core i7 CPU, 16 GB of RAM, and without GPU acceleration. The average processing time per image pair was approximately 2.3 s, demonstrating near real-time performance even on standard hardware.

To verify the effectiveness of image registration, the root mean square error index was used for validation. The larger the root mean square error, the greater the distance between the reference image and the registered image, which means that the larger the value, the lower the registration accuracy. The mathematical expression for root mean square error is as follows:

(28) $$E_{rms}\left(f\right)=\sqrt{{\displaystyle \frac{\sum _{i=1}^{N^{\mathrm{\prime }}}{\Vert \left(x_i,y_i\right)-f\left({x^{\mathrm{\prime }}}_i,{y^{\mathrm{\prime }}}_i\right)\Vert }^2}{N^{\mathrm{\prime }}}}}.$$

In the formula, $\left({x^{\mathrm{\prime }}}_i,{y^{\mathrm{\prime }}}_i\right)$ represents the coordinates of the feature points contained in the image to be registered; $\left(x_i,y_i\right)$ represents the coordinates of the feature points contained in the reference image; $f(\cdot )$ represents the transformation model.

Analysis of experimental data

We investigated the impact of key hyperparameters on registration quality. Experiments with different numbers of Fourier descriptors demonstrated that the first 40 low-frequency components are sufficient to capture the primary shape characteristics without introducing sensitivity to noise. For the wavelet threshold correction coefficient, values in the range [0.6–0.8] balanced edge retention with noise suppression. These findings informed our parameter settings. Scalability was assessed by registering image pairs of different resolutions (1,280 × 720 to 3,840 × 2,160). The method retained high accuracy (≥97.5%) across scales, and computation time increased linearly, suggesting good scalability. To determine component-wise contributions, we performed ablation tests by removing each module. Removing wavelet denoising resulted in a rise in RMSE to 0.47, underscoring its significance in maintaining edge integrity. Omitting Fourier normalization reduced rotation-invariant accuracy. Together, these results confirm that the LoG operator and Fourier descriptors are key to robustness and precision.

Figure 5 demonstrates that contour extraction using the LoG operator, combined with Fourier descriptor-based feature matching, resulted in precise and reliable matching performance. The corresponding feature points in the two images are accurately marked with red dots at similar positions, indicating a high degree of consistency in the matching positions. Especially in the hollowed-out part of the Xiangbi Mountain rocks, a relatively large number of contour pairs were matched, reflecting the rich similarity features of the area. These precisely matched contours provide a solid foundation for subsequent projection transformation image registration, ensuring a more accurate and reliable registration process. Therefore, the results in Fig. 5 not only validate the effectiveness of feature extraction and matching algorithms but also provide important guarantees for the successful implementation of the entire image registration process.

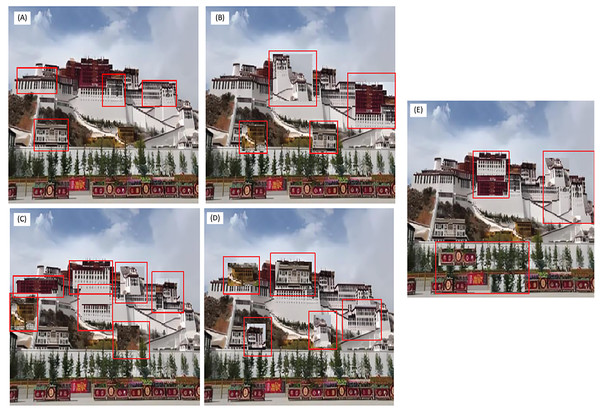
To verify the image registration effect of the method of this article, it was compared with four image registration methods of Arora, Mehta & Ahuja (2023), Mohammadi, Sedaghat & Rad (2022), Hjouj, Jouini & Al-Khaleel (2023), and Liaghat et al. (2023). The image registration results are presented in Fig. 6, while the corresponding root mean square error (RMSE) values are provided in Table 1.

From Fig. 6 and Table 1, it can be seen that when using multiple methods for image registration, the performance of the method of Mohammadi, Sedaghat & Rad (2022) is the worst, with the highest number of registration errors in the image registration results, and the largest root mean square error after registration is completed. Multiple results reflect the registration effect of the reference method (Mohammadi, Sedaghat & Rad, 2022). The registration results obtained by the methods of Arora, Mehta & Ahuja (2023), Hjouj, Jouini & Al-Khaleel (2023), and Liaghat et al. (2023) are relatively similar, with a registration rate of around 94% and a root mean square error of around 0.4. The method introduced in this article proves to be the most effective, attaining a registration accuracy of 99.1% and yielding a RMSE as low as 0.31. It can be considered a complete registration. The approach presented in this study demonstrates effective registration of multidimensional visual projection images, while preserving image integrity and ensuring high registration accuracy.