Identity-based linear homomorphic signature for a restricted combiners’ group for e-commerce
- Published
- Accepted
- Received
- Academic Editor
- Sedat Akleylek
- Subject Areas
- Cryptography, Theory and Formal Methods
- Keywords
- Homomorphic signature, Identity-based linear homomorphic signature, Network coding
- Copyright
- © 2025 Tian et al.
- Licence
- This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, reproduction and adaptation in any medium and for any purpose provided that it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Computer Science) and either DOI or URL of the article must be cited.
- Cite this article
- 2025. Identity-based linear homomorphic signature for a restricted combiners’ group for e-commerce. PeerJ Computer Science 11:e3068 https://doi.org/10.7717/peerj-cs.3068
Abstract
As the volume of electronic transaction data increases and the demand for real-time processing grows, network coding techniques have become popular for improving performance. However, early implementations often overlooked critical data security issues, such as forgery and data leakage. While existing homomorphic signature schemes effectively ensure data integrity, they can unintentionally allow malicious actors to exploit intermediate signatures. This misuse can lead to unnecessary bandwidth consumption and hinder the verification processes for legitimate users. To address the problem of malicious combinations, we apply the Chinese Remainder theorem (CRT) to establish a layer of secret-sharing that restricts access to authorized users in conjunction with homomorphic signatures. Furthermore, we introduce a formal definition for an identity-based linear homomorphic signature for a restricted combiners’ group (IBLHS-RCG). This framework integrates linear homomorphic signatures with the CRT within the context of e-commerce, enabling us to develop a specialized scheme for IBLHS-RCG. We demonstrate that our scheme is unforgeable against adaptive chosen-message attacks. Additionally, simulations conducted using the Python Pairing-based Cryptography Library (PYPBC) show that the signing and verification costs of our approach are low.
Introduction
The security of electronic commerce (Al-Zubaidie, Zhang & Zhang, 2020; Liu et al., 2023) is vital for both individuals and the broader economy. According to the 52nd Statistical Report on China’s Internet Development and data from the National Bureau of Statistics of China, the number of electronic payment users in China reached 943 million by June 2023, marking an increase of 911 million since December 2022. This represents 87.5% of the total number of internet users and 66.9% of the national population. As illustrated in Fig. 1, electronic commerce (Cao, 2023; Al-Zubaidie & Shyaa, 2023) consists of three primary components: service platforms, server clusters, and user groups. The service platform is connected to various servers through a wired network, while each server cluster wirelessly broadcasts to surrounding areas, enabling user access via mobile devices. Different server clusters, such as enterprise and personal transaction databases, store specific data assigned by the service platform and provide validation services for distinct user groups. As the Internet becomes the dominant arena for electronic commerce, ensuring transaction security has emerged as a critical concern. Hackers can exploit network vulnerabilities to compromise systems, resulting in the theft of funds or personal financial information. Moreover, insecure electronic commerce practices can lead to legal challenges and a significant erosion of user trust.
Figure 1: Architecture of electronic services.
Signature schemes that integrate secure multi-party computing (SMPC) are an effective security mechanism for ensuring transaction legitimacy and security. However, mitigating the risk of malicious combinations of intermediate signatures by combiners remains a substantial challenge. To address this issue, we propose a twofold approach: first, designing a signature scheme that incorporates secret segmentation techniques; second, employing homomorphic signature algorithms in place of traditional digital signature algorithms. Homomorphic signatures offer advantageous properties such as secure transmission and verifiable, yet unsolicited, information, effectively mitigating potential information leakage during data transmission. Since e-commerce clients primarily utilize mobile devices, such as cell phones, which have limited capacity and lower computational efficiency, we will implement a linear homomorphic signature algorithm characterized by short signature lengths and high signing and verification efficiency.
In practical electronic commerce (Liu et al., 2023), our scheme is applicable to multiparty signature scenarios, including multiparty account management, transaction authorization, and payment processing. For instance, in a tri-party transaction, one party can generate a signature using their private key while utilizing a shared session key to authorize the inclusion of secondary signers. Additionally, the identity and permissions of each signer can be restricted and managed based on specific needs and roles, thereby ensuring the security and reliability of the transaction.
Our contributions
Our proposed scheme, identity-based linear homomorphic signature for a restricted combiners’ group (IBLHS-RCG), restricts the combiners’ group, proves it is correct and secure in the random oracle model, and operates efficiently under the computer simulation experiments. The specific contributions of this article are as follows:
-
1.
We propose a novel linear homomorphic signature (LHS) scheme that restricts specific authorized intermediate nodes from performing linear combinations of signature vectors according to different tasks. This measure effectively prevents unauthorized nodes from maliciously combining signature vectors.
-
2.
We construct the first linear homomorphic signature scheme that is simultaneously resistant to malicious combinations, based on the original designated single combiner signature scheme (Lin, Xue & Huang, 2021), we expanding its functionality to a linear homomorphic signature scheme that can specify multiple combiners.
-
3.
We compress the time for signature and signature verification to sublinear complexity. Our scheme’s achieved signature length does not change after combination, and it reduces the verification and communication costs during transmission and after the combination signature more than Lin’s designated combiner scheme (Lin, Xue & Huang, 2021).
-
4.
We propose an identity-based linear homomorphic signature scheme for restricted combiner group. we combine this article’s scheme with the identity-based signature scheme, which makes the scheme more compatible with the IP network environment.
Related work
Electronic transactions (Cao, 2023; Al-Zubaidie & Shyaa, 2023) must occur in environments characterized by low latency and well-defined authorization protocols. Various external defense mechanisms and content-based security strategies have been proposed to enhance network protocols. Among these, network coding facilitates efficient content distribution while maximizing transmission throughput. However, a notable drawback is that data packets within network coding are susceptible to corruption, which presents significant challenges for secure data transmission.
To protect data confidentiality, homomorphic encryption can be employed. While encryption prevents attackers from eavesdropping on the original data, it does not inherently verify data integrity and authenticity. This gap can have serious ramifications in financial transactions, as tampered transaction data during transmission can impair recognition by the combiner group, thereby undermining the credibility of electronic transactions and causing substantial harm to electronic finance.
Thus, in addition to securing data content, ensuring data integrity and authenticity is crucial. One effective approach is the use of digital signatures combined with message digest functions to verify both the authenticity and integrity of data packets. Digital signatures provide non-repudiation, ensuring that the sender cannot deny the transmission of a specific message, while message digest functions guarantee that the message remains intact throughout its transmission. The homomorphic signature scheme represents a promising solution that simultaneously addresses these essential criteria.
In the era of big data, with increasing awareness of privacy protection, more attention is being given to securing data during network transmission and ensuring stored data integrity in the cloud. While digital signatures guarantee data integrity and verify data owner identity, their lack of homomorphic properties leads to increased bandwidth consumption during transmission—a major obstacle to their deployment in network environments. Homomorphic signatures aim to preserve the benefits of digital signatures while enabling operations on smaller, homomorphically linked packets. This leverages the aggregation capabilities of intermediate nodes, reducing both the number of packets transmitted and their size, thereby improving efficiency.
Early in 2000, Rivest proposed the basic concept of homomorphic signature schemes (Rivest, 2000). In 2002, the first formal definition of homomorphic signatures was proposed by Johnson et al. (2002). After 2002, research achievements in homomorphic signature schemes emerged in succession, such as linear homomorphic signature (LHS) schemes (Lin, Xue & Huang, 2021; Boneh et al., 2009; Boneh & Freeman, 2011b; Gennaro et al., 2010; Lin et al., 2018; Wang, Hu & Wang, 2013), polynomial homomorphic signature (PHS) schemes (Boneh & Freeman, 2011a), fully homomorphic signature (FHS) schemes (Gentry, 2009; Wang et al., 2015; Wang & Wang, 2020), homomorphic aggregate signature (HAS) schemes (Jing, 2014; Zhang, Yu & Wang, 2012), and multi-key homomorphic signature (MHS) schemes (Aranha & Pagnin, 2019; Fiore et al., 2016; Lai et al., 2018). Among them, LHS schemes (Zhao et al., 2007; Yu et al., 2008; Boneh et al., 2009; Cheng et al., 2016; Li et al., 2018; Chang et al., 2019; SadrHaghighi & Khorsandi, 2016; Zhang et al., 2018; Li, Zhang & Liu, 2022) are particularly useful in preventing pollution attacks in linear network coding.
In 2007, Zhao et al. (2007) proposed a linear homomorphic signature scheme with a network encoding function, which implements a signature scheme in a network encoding environment at a negligible cost; however, its security cannot be guaranteed. In 2008, Yu et al. (2008) proposed an antipollution homomorphic signature scheme based on the RSA difficulty problem, which can achieve improvements in efficiency and security. After 2009, Boneh et al. (2009) proposed the first formal definition of linear homomorphic signatures and proposed more efficient and secure signature schemes in network environments. At this point, research on linear homomorphic signatures began to move in the right direction. Based on Boneh et al. (2009), many linear homomorphic signature schemes based on public key infrastructure (PKI) were designed (Cheng et al., 2016; Li et al., 2018). However, these schemes are unsuitable for electronic transactions with high time requirements because the signature of the data packet needs to be bound with corresponding certificates, resulting in the signature length of the data packet being much longer than the data packet. Subsequently, some identity-based linear homomorphic signature schemes (Chang et al., 2019; Zhang et al., 2018) were proposed to address this issue. These schemes reduce the length of the signature, but the excessive signature generation and verification costs still cannot satisfy the requirements of the Internet environment. It was not until 2022 when Li, Zhang & Liu (2022) proposed a secure and efficient identity-based homomorphic signature, that the cost of signature generation and verification began to level out. For a comprehensive comparison of the various types of linear homomorphic signature schemes, the nature of the underlying hard problems, and other relevant factors, please refer to Table 1.
| Year | Authors | Scheme type | Hard problem |
|---|---|---|---|
| 2007 | Zhao et al. | LHS | (p, k, n)-Diffie-Hellman problem |
| 2008 | Yu et al. | LHS | Integer factorization problem |
| 2009 | Boneh et al. | the formal definition of LHS | Co-computational Diffie-Hellman problem |
| 2016 | Cheng et al. | PKI-based LHS | Integer factorization problem |
| 2018 | Li et al. | PKI-based LHS | Short integers solutions problem |
| 2018 | Zhang et al. | ID-based LHS | Co-computational Diffie-Hellman problem |
| 2019 | Chang et al. | ID-based LHS | Computational Diffie-Hellman problem |
| 2022 | Li et al. | ID-based LHS | Co-computational Diffie-Hellman problem |
However, beyond ensuring transaction verifiability, electronic transactions should also exhibit partial transparency rather than full transparency. This is inherent to the privileged service model of electronic transactions, where only specific, partially privileged intermediate nodes can perform combination and verification at each step. Direct application of homomorphic signatures, however, would render the entire transaction process fully transparent across the network—an outcome we seek to avoid. After combining Li, Zhang & Liu (2022) and Lin, Xue & Huang (2021), we propose an efficient signature scheme that can specify multiple combiners and maintain the generation and verification costs of signatures at a constant level.
Article structure
The rest of this article is structured as follows. In the “Preliminaries and Related Definitions” section, we briefly review some basic concepts in linear homomorphic signature schemes. In the “Concrete Scheme” section, we present the proposed IBLHS-RCG scheme and analyze its correctness. In the “Security Analysis” section, we provide security proof of the scheme. In the “Performance Analysis” section, we provide a performance evaluation of the scheme. Finally, we provide our conclusions in the “Conclusions” section.
Preliminaries and related definitions
This section briefly introduces the proof model used in this scheme, the theoretical basis required for construction, and the formal definition of this scheme.
Preliminaries
Existential unforgeability under adaptive chosen message attacks (EUF-CMA) security model (Boneh & Freeman, 2011a). If an adversary of a probabilistic polynomial time algorithm (PPT) cannot win the challenge response game with advantage within time t after asking for q signatures, then a signature scheme is said to have achieved (t,q, )-security in the EUF-CMA security model. That is, the adversary satisfies the following properties:
-
1.
The adversary can forge the signature for .
-
2.
The forged has not been queried during the interrogation phase.
Asymmetric bilinear mapping (Boneh & Franklin, 2001; Verheul, 2001; Boneh, Lynn & Shacham, 2004; Miller, 2004). Select three cyclic groups , where ( is a prime number), and define a mapping that satisfies the following relationship:
-
1.
Bilinear: , we have .
-
2.
Nondegeneracy: is the identity element of .
-
3.
Computability: can be efficiently calculated.
Co-Computational Diffie-Hellman (co-CDH) problem (Boneh, Lynn & Shacham, 2004; Huang & Wang, 2010; Galbraith & Verheul, 2008). We define two bilinear groups and , where ( is a prime number); we randomly select , give , and the algorithm A can solve . We denote this probability as .
Co-CDH assumption (Huang & Wang, 2010; Ng, Tan & Chin, 2018; Chang et al., 2017). For any PPT adversary, the probability that they can solve the co-CDH problem is negligible; that is, , meaning that the PPT adversary wanting to solve the co-CDH problem will have difficulty.
Chinese Remainder theorem (CRT) (Schindler, 2000; Zheng, Huang & Matthews, 2007; Quisquater, Preneel & Vandewalle, 2002). Suppose that are mutually prime for any two pairs. The equations
(1) have a solution. If are the solutions to these equations, then we have .
ID-based signature
An identity-based signature scheme typically consists of four algorithms: initialization algorithm Setup, key extraction algorithm KeyExt, signing algorithm Sign and verification algorithm Verify. The process involves interaction between the private key generator (PKG) and the user. The main steps are as follows:
: Input security parameter , output public parameters and master secret key , where is kept secret by the PKG.
: Input master secret key and user’s identity ID, PKG computes the user’s private key , and transmits it to the user via a secure channel.
: Input the user’s private key and the message to be signed, output the user’s signature for the message .
: Input the user’s identity ID, the public parameters , the message and its signature , if the verification is passed, output 1; otherwise, output 0.
The formal definition of LHS
A linearly homomorphic signature scheme (LHS) (Boneh et al., 2009) consists of the following four PPT algorithms.
: Input the security parameter and an integer N, generate the bilinear group , choose the generator element of and randomly choose an element on , such that , , output the public key and the private key .
: Input private key SK, file label and vector , output signature .
: Input public key PK, file label , and binary tuple , and then output signature .
: Input public key PK, file label , verification vector , and signature . If is established, the verification passes and outputs 1; otherwise, outputs 0.
Security definitions
In this subsection, we will detail the properties and definitions (Boneh & Freeman, 2011a; Ateniese et al., 2000) related to security analysis as follows.
Unforgeability
Definition 1. The security can be defined using the following game between adversary and challenger . Note that both and cannot know both of user’s private key and the user’s access structure.
-
1.
Initialization phase: The generates public parameters and system master private key , then sends to , and keeps to itself.
-
2.
Random oracle querying phase: obtains favorable information by randomly querying the , thus forging a non-existent message signature pair and passing the verification.
-
3.
Outputs: When receives , needs to use this forged message signature pair to solve the hard problem.
We need to ensure that the probability of solving the hard problem in Outputs is negligible.
Definition 2. A signature scheme is said to be security under the EUF-CMA security model if an adversary of a probabilistic polynomial time (PPT) algorithm is still unable to win the challenge response game with an advantage in time after querying the signature times. That is, the challenge response game can be defined as follows:
-
1.
Setup: Let be a system parameter, where the challenger generates the key pair from . The challenger then sends to the adversary , and retains for answering ’s signature queries.
-
2.
Query: adaptively selects the message for signature lookup, and generates the corresponding to return to .
-
3.
Output: generates the message signature pair , if:
is a legal signature for .
All signatures on not queried.
we assume that won the challenge response game.
Definition 3. If the generated by in Output can make Verify output 1, and if for , . We consider to have won the game.
Confidentiality
Definition 4. This security can be defined as a game between and . In this game, can obtain only the message-signature pair from . If derives information beyond the identity ID by inverse solving , wins the game, and the scheme fails to achieve confidentiality.
Unlinkability
Definition 5. This security can be defined as a game between and . In this game, randomly chooses 0 or 1 from (Here it is assumed that 1 means and come from the same group of combiners, and 0 means and come from a different group of combiners). After n queries, if the probability of guessing correctly is greater than , then the scheme does not have unlinkability.
Traceability
Definition 6. For the receiver Receiver, the receiver is able to verify the legitimacy of the signature by using the signer’s public key , so that we consider the scheme to have Traceability.
Coalition-resistance
Definition 7. Assuming that any combiner without the server’s permission obtains Signer’s message signature pairs and , we consider the scheme is not resistant to a coalition attack if the two combiners can directly generate a new efficient message-signature pair .
Concrete scheme
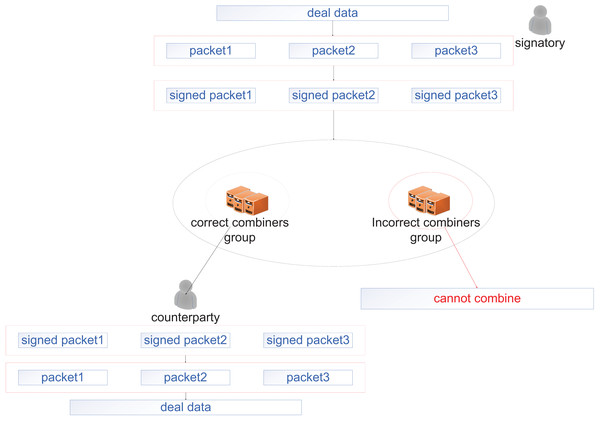
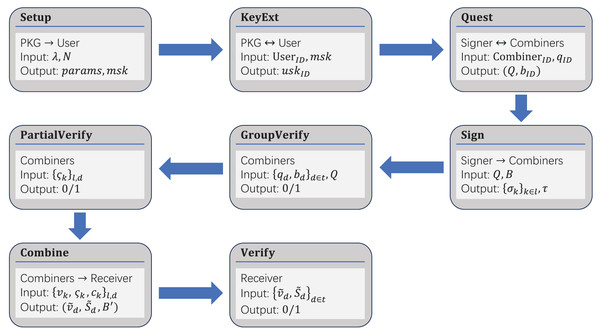
In this section, we provide the details of our scheme. Our scheme introduces an innovative structure—the restricted combiner’s group. The restricted combiner’s group is primarily based on CRT, which converts the single key of Lin’s scheme into a sub-session key derived from a master session key via secret splitting. This enables the structural extension from the single combiner to the restricted combiner’s group. The design improves system flexibility and scalability, providing a robust foundation for subsequent security protocol development. First, our scheme, initialized by private key generation (PKG), generates corresponding public parameters. Second, all users (including signers, combiners, and receivers) need to submit their identity information to PKG to generate their own public keys and private keys. Then, the group of combiners requests the combination rights from the signer. After the signer approves the request, the signatures are distributed. After layer-by-layer verification, the group of combiners composes a signature combination network. Finally, the network provides services to the receiver. Figure 2 shows the process of data transmission and reception between two entities, and Fig. 3 shows the entire workflow of our scheme. In subsection “Correctness”, we demonstrate the correctness of our scheme. The specific details and relevant proof of this scheme are described as follows.
Figure 2: Process of data transmission and reception between two entities.
Figure 3: Entire workflow of our scheme.
The formal definition of IBLHS-RCG
Before presenting the formal definition of this scheme, we give the concrete notation Table 2 for a clearer understanding of our scheme. IBLHS-RCG is a linear homomorphic signature scheme that can only be combined in a specified group of combiners. Based on the original LHS signature, we add four steps KeyExt, Quest, GroupVerify, and PartialVerify, so that the combiners in the scheme cannot take up bandwidth by arbitrarily combining signatures. Our scheme consists of the following eight PPT algorithms. : This step is run by PKG, with the input of security parameter and augmented vector dimension N. The algorithm generates public parameter and broadcasts it to the entire network while secretly preserving the master private key .
| Notation | Meaning |
|---|---|
| Security parameter | |
| N | Augmented vector dimension |
| Master secret key | |
| User’s secret key (associated with ID) | |
| Q | Hierarchical parameter |
| Session sub-key (associated with ID) | |
| Access level parameter (associated with ID) | |
| Vector k | |
| B | Session sub-key |
| Signature corresponding to vector k |
: This step is run by PKG, where the user inputs their own identity ID, PKG inputs , and the algorithm outputs the corresponding user’s private key , which is returned to the user. After receiving , the user can verify the credibility of the PKG.
: This step is run by the signer and the combiners. The applicant combiners submit the identity ID and access level parameter to the signer to apply for the signature combination right of a certain quantum space V. The signer reviews whether the access level of the combiners has reached the security level V. If the access right application has passed, the signer returns to the designated combiners.
: This step is run by the signer, who splits and augments the packet data, signs the basic vectors, and adds the hierarchical parameter Q and session key B. The basic vector-signature pairs are divided into multiple packets and distributed to each designated combiner.
: This step is run by a designated group of combiners, and this group uses the CRT to restore the session master key B. If recovery is correct, the algorithm outputs 1; else, the designated combiners terminate the algorithm and output 0.
: This step is run by a designated group of combiners. In this step, the designated group of combiners can use the session master key B obtained from the algorithm GroupVerify to verify the correctness of the signature, thereby verifying the credibility of the signer.
: This step is completed independently and run by each combiner. Each combiner can combine their received basic vector-signature pairs to generate secondary vector-signature pairs. Then, each combiner sends the pairs to the receiver.
: After receiving the secondary vector-signature pairs sent by the combiners, the receiver can verify the credibility of each combiner through pairing operations.
In our scheme, if any of the first four steps cannot be honestly executed or there are unauthorized combiners in the combiner group, algorithm GroupVerify will output 0, and the dishonest behavior of the signer will result in a return of 0 for the algorithm PartialVerify, while a dishonest operation in any step will make the outputs of algorithm Verify 0. Therefore, our scheme ensures the security of the signature and the designated combination by preventing any malicious behavior of the signer or combiners from passing the verification.
Concrete structure
In our scheme, the combiners need to use the signer’s ID to verify the signature once it has been received. If the received ID is incorrect, the signature cannot pass the verification. Otherwise, each signature scheme will default to make the signer’s ID a part of the signature. Therefore, we can distinguish a specific signer by extracting their ID information from their signature. The overall process of our scheme is shown in Figs. 3 and 4, and the steps are as follows.
Figure 4: Simplified workflow of our scheme.
-
1.
System initialization: Setup
In this step, PKG generates the public parameter params and master private key based on the security parameter and positive integer N (where N is the dimension of the augmented vector). The details are as follows:
-
(a)
PKG generates three cyclic groups with the same prime order , which satisfies an asymmetric bilinear mapping and .
-
(b)
PKG randomly selects generators and then randomly selects a value as , after which PKG calculates and uses the value as the PKG master public key .
-
(c)
PKG selects four collision-resistant hash functions .
-
(d)
PKG broadcasts to the whole network and then secretly remains .
-
-
2.
User registration: KeyExt
This step is composed of two parts. First, the Signer, Combiners, and Receiver request from PKG. Second, users need to check the correctness of their .
-
(a)
The Signer, Combiners, and Receiver send identity ID to PKG, which randomly selects a value . Calculate , , and send as to Signer, Combiners and Receiver through a secure channel.
-
(b)
The Signer, Combiners, and Receiver check if the equation holds. If it holds, save locally, otherwise an error log will be created.
-
-
3.
Combiners apply for permission: Quest
In this step, the signer generates the hierarchical parameter Q corresponding to the data and the session key of the approved combiner. The specific process is as follows:
-
(a)
The signer randomly generates the session master private key and verifies whether meets the confidentiality level of this data. If so, the signer generates the session key of combiners and records the .
-
(b)
When the maximum number of applicants or the deadline for application permission has been reached, the signer calculates and sends to the corresponding approved Combiners. For the convenience of description, it is assumed that the number of approved combinations is and that the dth combination already has .
-
-
4.
Signature generation: Sign
This step is divided into two parts. First, the signer splits and augments the data packet. Then, the signer signs the basic vectors and distributes the basic vector-signature pairs to the approved combiners. The specific process is as follows:
-
(a)
The signer splits the data into m n-dimensional vectors and then augments each to , where holds only in the case of , and the value of is always 0 in other cases. Here, we define the tensor space .
-
(b)
The signer assigns the file identifier for V, binds the signer information to V using , and then signs each basic vector with the signature , as follows:
(2) (3)
Then, the signer sends to the designated combiners, where represents the basic vector signature index received by the combiners. (For example, if Combiner1 receives , then the index is ).
-
-
5.
Validate the combined population: GroupVerify
This step is divided into two parts. First, each approved combiner uses the CRT to jointly solve B. Then, we verify the combination group. The specific process is as follows:
-
(a)
First, each combiner calculates . Second, we calculate . Then, we calculate . Finally, all combiners calculate together.
-
(b)
Each combiner checks whether is true (i.e., determines whether B′ = B is true). If it is true, there are no malicious combiners in the combiner group. Otherwise, the algorithm terminates.
-
-
6.
Partial open verification: PartialVerify
Owing to the hierarchical protection mechanism of data, open verification can only be carried out within the approved group of combiners in this step, the signer can encrypt signature information using a session key, and no arbitrary combiners can be allowed to verify. The workflow is divided into two parts, as follows:
-
(a)
Each combiner calculates .
-
(b)
The signer sends ciphertext to each combiner through broadcasting format. (Only the legal combiners who own the session key can decrypt ciphertext to signature information, others are not able to obtain the user’s information from the ciphertext.) Any combiner can verify whether any is valid. If it is true, the signer is trustworthy; otherwise, the algorithm terminates.
-
-
7.
Signature aggregation: Combine
In this step, the combiners first linearly combine the basic vectors and then add the session key. The specific process is as follows:
-
(a)
Each combiner uses the encoding coefficient to perform the following operation on their respective so that .
-
(b)
The combiners calculate and send to the receiver through intermediate nodes.
-
-
8.
Transaction validation: Verify
After receiving the combiners’ , the receiver first uses B′ to decrypt the signature and then verifies the correctness of the signature. The specific process is as follows:
-
(a)
The receiver uses B′ to solve for and uses the collected to perform a combination calculation to obtain , where is the signature for .
-
(b)
The receiver tests whether is valid. If it is, the verification has passed. Otherwise, the verification has not passed.
-
Correctness
In this section, we assume that all participants faithfully execute the above algorithms and that the correctness of the signature can be checked from the following aspects.
Lemma 1. For pairs generated by Setup, the following conditions must be satisfied:
-
1.
For , is established.
-
2.
For , is established.
-
3.
For , is established.
-
1.
For the sent by the signer, we can conclude that satisfies the relationship mentioned in the previous section. The details are as follows:
(4)
-
2.
For the sent by the above combiners, the receiver first calculates using the CRT, and the expression for the signature of data is as follows: (5) (6)
-
3.
For the signature of the , we can conclude that satisfies the relationship mentioned in the previous section. The details are as follows:
(7)
Security analysis
In this section, we will perform a comprehensive analysis of the security of our scheme, focusing on five key properties: unforgeability, confidentiality, unlinkability, traceability, and coalition-resistance. Detail are as follows.
Unforgeability proof
In this section, we prove that the scheme can achieve adaptive selection under the random oracle model for vector subspace, the existence of which is unforgeable under the attack of messages. Here, we use the challenge response mode to prove this. We define the challenger as , the PPT adversary as , and the number of times interrogates the random oracle as .
Initialization. let , and we define , set the map .
Query the random oracle. The following seven query algorithms are adaptively selected between and .
Create Query. The number of times that asks ’s for the value of is recorded as , and the number of times that creates a user query for ID as a challenger is recorded as . Whenever asks for , performs the following steps:
When , randomly chooses , and we define . Then, returns to Adv and stores into list .
When , randomly chooses , and we define . Then, returns to Adv and stores into list .
Ext Query. Whenever queries ’s for the value of , performs the following steps:
When , queries and returns to .
When , terminates the Ext Query algorithm.
Query. Whenever queries for the value of , performs the following steps:
If , returns as the value of .
If , runs the Create Query algorithm and then returns as the value of .
Query. Whenever queries for the value of for the first time, performs the following steps:
If , randomly chooses , and returns as . Then, stores into list .
If , randomly chooses , calculates , and returns it as . Then, stores into list .
When queries other vectors for the value of , queries whether is on the list . If it is, chal returns . Otherwise, runs the Query algorithm.
Query. Whenever queries for the value of , randomly chooses , , , , and returns as . Then, it stores into list .
When queries other vectors for the value of , queries whether is on the list . If it is, returns . Otherwise, runs the Query algorithm. Q Query. First, randomly chooses , and the number of times asks ’s for the value of is denoted as . When runs the session key query, if the queried ID is equal to the ’s ID, record this query as the query . Whenever asks for , performs the following steps:
If , randomly chooses , and calculates . Then, returns as ’s and stores into list .
If , terminates the Q Query algorithm.
Sign Query. When asks for the signature of ’s basic vectors , performs the following steps:
If , runs the following steps:
-
-
queries whether is in list . If it is, it extracts . Otherwise, runs the Query algorithm before extracting.
-
-
queries whether is in list . If it is, it extracts . Otherwise, runs the Query algorithm before extracting.
-
-
calculates the signature of by the equation:
.
-
-
returns to .
-
If , runs the following steps:
-
-
queries whether is in list . If it is, it extracts . Otherwise, runs the Query algorithm before extracting.
-
-
queries whether is in list . If it is, it extracts . Otherwise, runs the Query algorithm before extracting.
-
-
calculates the signature of , as shown in Eq. (8)
(8)
-
-
returns to .
-
Outputs. We call to win the game in the EUF-CMA security model if forged signature meets the following conditions:
is the legal signature of .
.
The tensor space has not been asked for any signature by .
can pass both Partial open verification and Transaction validation.
First, needs to be able to calculate , and when has sufficient numbers of , it can solve for the corresponding . Below, we prove that can also forge .
That is,
(9)
Then, we let as , so,
(10)
To solve , we must ensure that the following conditions are met:
cannot be orthogonal to .
.
From the above analysis, it can be seen that for to solve the co-CDH problem, the following conditions must be met simultaneously: the probability of attack success cannot be negligible and can be solved. Here are the events where wins the game: is not orthogonal to , is not terminating the query as A, B, C, and the number of times Create Query, Ext Query, Query, Q Query and Sign Query is , , , , and , respectively.
The success probability of chal is denoted as . Next, we first calculate and in Part 1, and is calculated in Part 2.
Part 1. Under the condition that event C occurs, event A occurring means that has won the game without ’s awareness. Assuming that this probability cannot be negligible, this probability is denoted as .
Claim. Event A and event C occur simultaneously, and event B occurs as independent events. Then, .
. Event B is a complementary event of an Event that cannot be orthogonal to , and the probability of the Event that cannot be orthogonal to occurring is the probability of an Event that occurring; that is, , then .
Part 2. The occurrence of event C can be divided into three steps: First, ensure that Ext Query does not terminate the query, then ensure that Q Query does not terminate the query, and finally, ensure that Sign Query does not terminate the query.
The probability of not terminating the query in Ext Query is , the probability of not terminating the query in Sign Query is , and the probability of not terminating the query in Q Query is . Then, .
In sum, means that can solve the co-CDH problem with a non-negligible probability through a PPT algorithm, which contradicts the co-CDH assumption. This proves that there is no such challenger, in turn proving that there is no such adversary. The signature scheme achieves -security in the EUF-CMA model.
Confidentiality proof
In this section, we will prove the confidentiality of the scheme under adaptive chosen message attacks in the random oracle model. We use the challenge-response mode for the proof. Let the challenger be denoted as , the adversary as , and the number of queries to the random oracle as .
Initialization. The challenger initializes the public parameters and master secret key as described in the initialization phase.
Random oracle queries. The adversary adaptively queries the random oracle . The challenger responds to these queries as follows:
For each query , if is already in the query table, return the stored value. Otherwise, randomly select a value from and return it, storing the result in the query table.
For each query to the vector value, if the vector is already in the query table, return the stored value. Otherwise, randomly select a value and return it, storing the result in the query table.
For each query to the session key, if the session key is already in the query table, return the stored value. Otherwise, randomly select a value and return it, storing the result in the query table.
Signature queries. The adversary can request signatures on chosen messages. The challenger responds by generating the signatures as described in the signature phase.
Output phase. The adversary outputs a guess for the ID associated with the message. The challenger checks if the guess is correct. If it is, the adversary wins the game.
The probability of the adversary winning the game is analyzed as follows:
Let A be the event that wins the game.
Let B be the event that the ’s query is orthogonal to the challenge.
The probability of the adversary winning the game is given by:
(11)
Since is negligible, and is also negligible, we can conclude that is negligible. Thus, the scheme is confidential under adaptive chosen message attacks in the random oracle model.
Unlinkability proof
Game definition
-
1.
Setup: The challenger generates and , and registers two users and with private keys and .
-
2.
Challenge phase: The challenger randomly selects , uses to generate a signature , and sends to the adversary.
-
3.
Adversary queries: The adversary can request signatures for other messages or users (excluding and ) and perform verifications.
-
4.
Guess: The adversary outputs a guess . The scheme is unlinkable if .
Key observations
Private key randomness: Each user’s includes a unique random in . Since is fresh per user, is statistically independent across users.
Signature randomization: Signatures depend on both (user-specific) and (session-specific). The term introduces session randomness, preventing linkage across different signatures.
Session key obfuscation: The CRT-based distribution of ensures that partial knowledge of does not reveal B unless combiners collude. This threshold mechanism hides user-specific contributions.
Formal reduction
Assume an adversary can win the unlinkability game with non-negligible advantage . We construct a solver for the CDH problem:
-
1.
embeds a CDH instance into the public parameters and simulates user keys using .
-
2.
When requests a signature, programs the hash oracles to align with the CDH challenge.
-
3.
If successfully links signatures, extracts from the bilinear pairing results, solving CDH.
-
4.
By the CDH assumption, must be negligible, contradicting ’s advantage. Hence, unlinkability holds.
Critical analysis
Leakage prevention: No phase reveals , B, or deterministic relationships between users’ operations. The use of fresh randomness ( , B) in key generation and signing ensures unlinkability.
Verification anonymity: The verification equation depends only on public values ( ) and session-specific terms, avoiding user identity exposure.
Threshold security: The requirement of combiners to recover B ensures that fewer colluders cannot compromise session anonymity.
The scheme achieves unlinkability through:
Randomized private key generation and session-specific parameters.
Threshold-based session key distribution via CRT.
Cryptographic primitives (bilinear maps, collision-resistant hashes) that prevent leakage of user-specific information.
Dynamic binding of signatures to session-specific terms rather than user identities.
Under the challenge-response model, the adversary cannot distinguish signatures from different users beyond random guessing, proving the scheme’s unlinkability.
Traceability proof
Game definition
-
1.
Setup: The challenger generates , , and registers a set of users . Each user receives .
-
2.
Adversary queries: The adversary can:
Request user private keys for any .
Request signatures on messages with specified .
Corrupt combiners to obtain their session keys .
-
3.
Challenge: The adversary outputs a forged signature on a message , claiming it cannot be traced to any registered user.
-
4.
Tracing: The challenger uses the tracing algorithm to extract an identity from . The scheme is traceable if .
Key mechanisms for traceability
Identity binding in private keys: Each user’s is bound to ID via . The term ensures that uniquely encodes ID, and any valid signature must use a valid linked to a registered identity.
Signature structure: Signatures explicitly include ID in . During verification, the challenger can check the consistency of ID with the public parameters and traced keys.
Session key recovery via CRT: The threshold-based recovery of B requires at least honest combiners. If a forged signature uses an invalid B, the tracing algorithm can identify corrupt combiners by analyzing inconsistencies in B′.
Formal reduction
Assume an adversary can forge an untraceable signature with non-negligible probability . We construct a solver for the DLP in :
-
1.
simulates the scheme and embeds a DLP instance into the public parameters.
-
2.
When requests a signature for , programs to align with the DLP challenge.
-
3.
If outputs a forged , extracts from via Eq. (12), (12) since , solves from using the extracted .
-
4.
By the DLP assumption, must be negligible, contradicting ’s success. Hence, traceability holds.
Critical analysis
Non-frameability: Even if the adversary corrupts users, they cannot forge signatures for honest users because depends on (unknown to the adversary).
Threshold security: The CRT-based recovery of B ensures that corrupting fewer than combiners does not compromise B, preventing fake session keys from being accepted.
Public verifiability: The verification equation ensures that only valid ID-bound signatures pass verification.
The scheme achieves traceability through:
Cryptographic binding of user identities to private keys via .
Explicit inclusion of ID in signature components and hash functions.
Threshold mechanisms for session key recovery, limiting collusion impact.
Under the challenge-response model, any forged signature can be traced to a registered user with overwhelming probability, proving the scheme’s traceability.
Coalition-resistance proof
Phase 1: initialization and user registration
Challenger’s operations:
-
-
Generates public parameters and master private key .
-
-
For each user identity requested by the adversary, generates private key , where and .
-
Collusion resistance analysis:
-
-
Even if the adversary obtains multiple users’ private keys , they cannot recover through linear combinations due to the independence of and the secrecy of (relies on the hardness of the discrete logarithm problem).
-
Phase 2: combiner permission application
Challenger’s operations:
-
-
Generates session keys for legitimate combiners and distributes them via CRT.
-
Collusion resistance analysis:
-
-
If the adversary controls combiners with and (threshold), B cannot be recovered (CRT requires at least pairwise coprime ).
-
-
If the adversary forges or , the verification in Phase 4 detects and terminates the protocol.
-
Phase 3: signature generation and distribution
Challenger’s operations:
-
-
Generates signatures for data.
-
Collusion resistance analysis:
-
-
To forge a signature, the adversary must compromise both and B:
is protected by user private keys and bound to .
B is distributed via CRT; partial knowledge of is insufficient for recovery (relies on CRT security).
-
Phase 4: verification and combination
Challenger’s operations:
-
-
Verifies during validation.
-
Collusion resistance analysis:
-
-
If colluders tamper with or , the bilinear pairing check fails (relies on collision resistance of hash functions and properties of bilinear maps).
-
Assume an adversary A can break collusion resistance with non-negligible probability . We construct an algorithm C′ to solve the CDH problem:
-
1.
C′ simulates the scheme using A’s queries and embeds a CDH instance into public parameters.
-
2.
When A forges a signature, C′ extracts the CDH solution from the bilinear map result.
-
3.
By the CDH assumption, is negligible, leading to a contradiction. Hence, collusion resistance holds.
The scheme achieves collusion resistance through:
Master key protection: Distributed generation and verification of and B, preventing single-point leakage.
Session key distribution: Threshold mechanism based on CRT, requiring colluders to exceed the security threshold.
Cryptographic primitives: Bilinear map verification and collision-resistant hash functions ensure tamper detection.
Dynamic binding: Signatures are bound to file identifiers , preventing replay attacks.
Thus, under the challenge-response model, the scheme resists collusion attacks.
Performance analysis
The performance of the proposed scheme is analyzed from both theoretical, experimental simulation and perspectives. The detailed contents are presented in the subsequent sections.
Theoretical analysis
Given that the restricted group of combiners is the first construction proposed in this article and is not directly comparable to other schemes, we focus our analysis on comparing the signature and verification efficiencies of our scheme with those presented in Boneh et al. (2009), Lin et al. (2018), Chang et al. (2019), Lin, Xue & Huang (2021), and Li, Zhang & Liu (2022). In efficiency analysis, the specific parameters are made in Table 3.1 All computational costs are derived directly from the algorithms section of each article, by summing the operations specified in both the signature and verification expressions. The concrete efficiency analysis is shown in Table 4.
| Notation | Meaning |
|---|---|
| Element size on group | |
| Element size on group | |
| Element size on group | |
| Multiplication operations on the group | |
| Multiplication operations on the group | |
| Multiplication operations on the group | |
| Exponential operations on the group | |
| Exponential operations on the group | |
| Exponential operations on the group | |
| Mapping to the hash operation on group | |
| Mapping to the hash operation on group | |
| bilinear pairing operation | |
| Number of vectors | |
| Number of dimensions for each data vector | |
| Number of combined vectors |
| Scheme | Sig.comp | Ver.comp | AS |
|---|---|---|---|
| Boneh et al. (2009) | ✓ | ||
| Lin et al. (2018) | |||
| Chang et al. (2019) | |||
| Lin, Xue & Huang (2021) | ✓ | ||
| Li, Zhang & Liu (2022) | ✓ | ||
| Our scheme | ✓ |
Note:
AS, using asymmetric bilinear pairing operations.
Table 4 shows that the signature overhead of all schemes, except for Lin et al. (2018), Li, Zhang & Liu (2022), and the proposed scheme, increases with the value of . The proposed scheme reduces the number of exponential operations compared to the (Lin et al., 2018) scheme by extending its functionality. In terms of verification overhead, all schemes, except Li, Zhang & Liu (2022) and the proposed scheme, also experience an increase as grows. Although the proposed scheme has operations more than the (Li, Zhang & Liu, 2022) scheme, the performance degradation is minimal. Overall, our analysis indicates that the proposed scheme maintains effective signature and verification efficiency while enhancing the original scheme’s functionality.
Experiment analysis
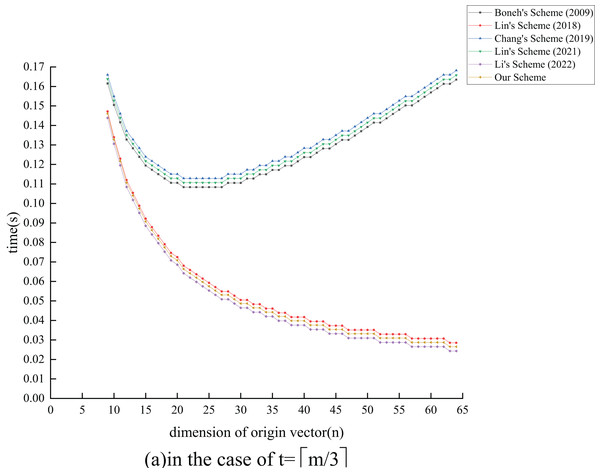
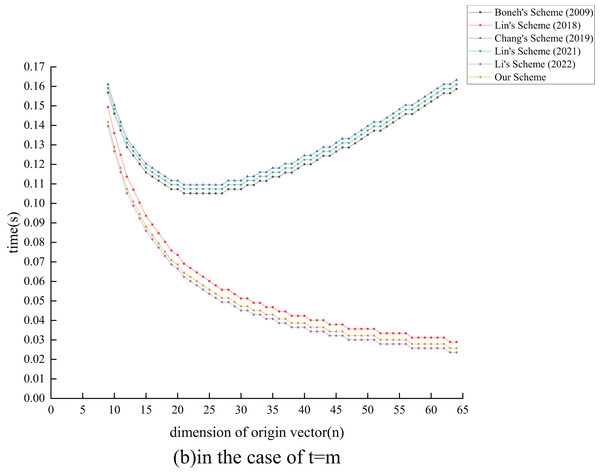
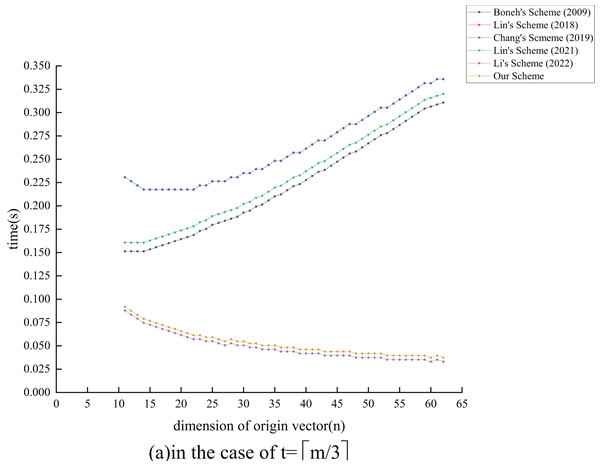
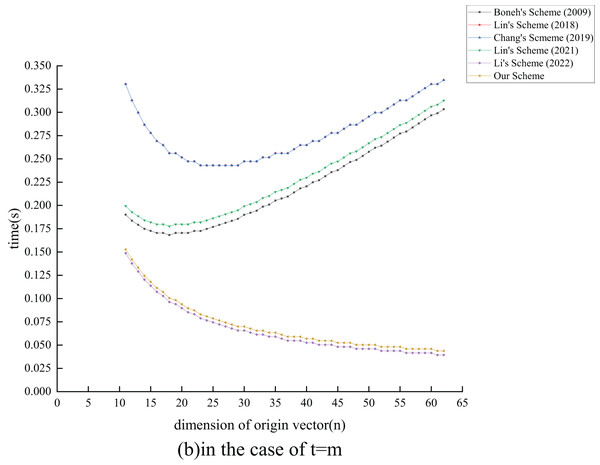
The computational cost of this scheme is calculated through computer simulation. Our simulation uses the Pycharm IDE, with the compiler version being Python 3.8. Our simulation runs on a Linux 5.10.0-8-generic system, using the 11th Gen Intel (R) Core (TM) i7-11800H @ 2.30-GHz processor. The parameters used in the simulation are all standard parameters of the Pypbc library (Duquesne et al., 2006). To design an 80-bit secure2 signature algorithm, the length of any element in the group needs 160 bits (20 bytes), and the length of any element in the group needs 320 bits (40 bytes). The length of each parameter during the experiment is shown in Table 5. In this experiment, we selected a 13-KB file to evaluate the efficiency of each scheme. Each file can be divided into basic vectors, each basic vector can be divided into dimensions, and the augmented vectors’ dimension is . The basic vectors of each dimension are one element of , with a length of 160 bits. For security reasons, the combiners number . Therefore, . For most of the current IP networks, the maximum transmission unit (MTU) payload is 1,460 bytes, so . Following comprehensive consideration, we can conclude that . Our scheme was compared with the aforementioned five schemes under the conditions of and , as detailed in Figs. 5 to 8.
| Parameter | Length |
|---|---|
| The element of | 160 bits |
| The element of | 320 bits |
| The element of | 640 bits |
| The element of | 160 bits |
| The element of | 160 bits |
| The element of | 160 bits |
| The element of | 160 bits |
Figure 5: The time cost of signature generation for a file (t = ).
Figure 6: The time cost of signature generation for a file(t = ).
Figure 7: The time cost of data packet detection(t = ).
Figure 8: The time cost of data packet detection(t = ).
Figures 5 and 6 show our scheme compared to the other five schemes, as well as the signature computing cost of the same file. In all cases, the signature of the generating cost for our scheme and Li, Zhang & Liu (2022) are the smallest, and our proposed scheme also has the ability to limit the scope of combiners. When the basic vectors’ dimension rises, Lin et al. (2018), Li, Zhang & Liu (2022) and our scheme exhibit a gradual drop in the signing time drop, while the signing time of the other three schemes continuously rises. At the maximum transmission efficiency, when the transmission packet size reaches the maximum transmission unit (MTU) with parameters , , the signature cost of our scheme is 27 ms. This is nearly equivalent to the 24 ms reported in Li, Zhang & Liu (2022) and is significantly lower than the costs associated with the other four schemes.
In this simulation experiment, we assume the receiver receives packets. As illustrated in Figs. 7 and 8, when compared with the other five schemes, the time cost of our scheme and that of Li, Zhang & Liu (2022) remains minimal as the dimensionality of the basic vectors increases. When the transmitted data packets reach MTU, the verification cost of our scheme is 44 ms. This is nearly equivalent to the 39 ms reported in Li, Zhang & Liu (2022) and is significantly lower than the costs associated with the other four schemes.
Comprehensive analysis shows that when the file size reaches the MTU, our scheme has equivalent time overhead to Li, Zhang & Liu (2022). We provided a formal description of the definition and security model of IBLHS-RCG and proposed an efficient multiparty supervision scheme suitable for electronic financial transactions. Our scheme can be used to designate combinations to prevent malicious combinations. We demonstrated the security of our scheme. In addition, theoretical analysis and experimental results indicate that our scheme is more efficient and reasonable than comparable schemes.
Conclusion
In this article, we provide a formal definition and security model for the identity-based linear homomorphic signature for a restricted combiners’ group (IBLHS-RCG) and propose an efficient multiparty supervision scheme designed specifically for electronic financial transactions. Our scheme allows for the careful designation of combinations to reduce the risk of malicious collaborations. We establish the security of our approach, and both theoretical analysis and experimental results show that our scheme offers superior efficiency and practicality compared to existing methods.
Supplemental Information
Simulation code.
The computational cost of this scheme is calculated through computer simulation. Our simulation uses the Pycharm IDE, with the compiler version being Python 3.8. Our simulation runs on a Linux 5.10.0-8-generic system, using the 11th Gen Intel (R) Core (TM) i7-11800H @ 2.30-GHz processor. The parameters used in the simulation are all standard parameters of the Pypbc library.