Optimization of multi-objective feature regression models for designing performance assessment methods in college and university educational reform

Target stacking

This section elaborates on the fundamental architecture of the MOFR-LSF model, which combines multi-output feature regression with a stacking framework. The model is designed to capture the unique input-output relationships for each education performance indicator and optimize predictions through target correlation analysis. By introducing target-specific features, the model is able to more accurately model the complex relationships among different indicators, laying a solid foundation for subsequent stacked regression.

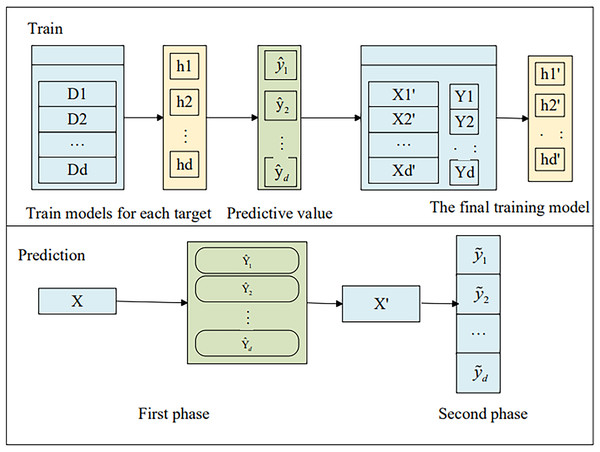
We extend the single-target stacking (SSA) (Fisichella et al., 2015) method to multi-target learning by training d independent regression models using traditional regression techniques, as illustrated in Fig. 1. $h_j:X\to R$. $h_j^i:D_j\mathrm{\backslash }{D}_j^i\to R$.

As shown in Fig. 1, for an unknown sample x, the prediction vector is first obtained through the model in the first stage:

(1) $$\hat{y}=\left({\hat{y}}_1,{\hat{y}}_2,\dots ,{\hat{y}}_d\right).$$

The prediction vector is then expanded into the original feature vector, i.e.,:

(2) $$x^{\mathrm{\prime }}=\left(x_1,\dots ,x_m,{\hat{y}}_1,{\hat{y}}_2,\dots ,{\hat{y}}_d\right).$$

Equation (2) shows a new input for the second stage model prediction and finally the final prediction is made with the second stage model $h_j^{\mathrm{\prime }}$ to get the final prediction:

(3) $$\tilde{y}=\left({\tilde{y}}_1,...,{\tilde{y}}_d\right).$$

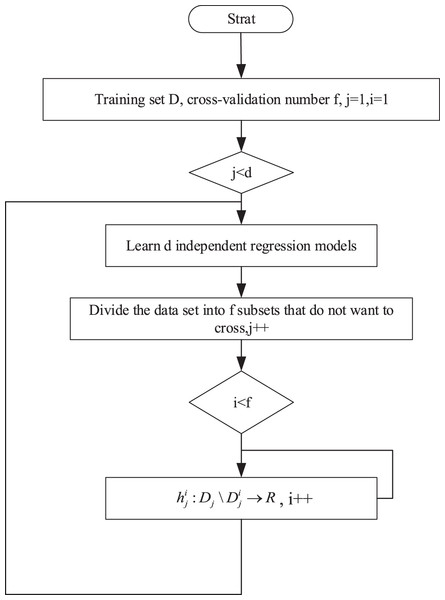
This approach considers the predicted values from the first stage of the remaining targets as the core idea for additional input variables, making it dependent on the estimates of the targets. To further alleviate inter-target dependencies, this article employs the cross-validation method to obtain out-of-sample estimates for the target variables across all training samples. The specific training process is illustrated in Fig. 2.

K-means clustering for binning

Building on the target stacking approach, and to alleviate the challenge of constructing specific features for each target, this article adopts a split-box strategy based on K-means clustering of both targets and features for feature processing. First, the feature matrix X of the training set D undergoes column normalization to obtain $\overline{X}$, the label part $Y$ is unchanged and thus the normalized training set $\overline{D}=\left(\overline{X},Y\right)$ is obtained, K-means clustering is performed on each target with ${\overline{D}}_i=\left(\overline{X},Y_i\right)$ as input and thus binning is done to compute the sum of squares of the intra-cluster errors SSE at each K value:

(4) $$SSE=\sum _{q=1}^k\sum _{p\in C_q}|p-m_q{|}^2$$where $C_q$ is the q-th cluster, p is the sample point in $C_q$, and $m_q$ is the mean of all samples in $C_q$. SSE (Sum of Squared Errors) represents the clustering error for all samples, indicating the quality of the clustering. From this, the SSE for different values of K (ranging from 2 to 20) is calculated for each target. The optimal number of clusters, i.e., the number of bins, for each target is then determined, allowing for the dataset to be partitioned accordingly after binning:

(5) $$D_i=\left\{\left(X_i^1,Y_i^1\right),...,\left(X_i^{B_i},Y_i^{B_i}\right)\right\}$$where $i\in \left\{1,...,m\right\}$. The split-box algorithm is carried out in the following steps.

(1) The feature part of dataset D, $X=\left(X_1,...,X_m\right)$, is normalized by column $\overline{X}=\left({\overline{X}}_1,\dots ,{\overline{X}}_m\right)$ to ensure that all feature values are within the same scale so that subsequent clustering algorithms can work more efficiently. The normalized dataset is recorded as $\overline{D}=\left(\overline{X},Y\right)$. The labeling part remains unchanged and serves as the basis for subsequent evaluation of the model performance.

(2) The dataset $\overline{D}=\left(\overline{X},Y\right)$ was used as input for the subsequent clustering algorithm. For each target variable $i\in \left\{1,...,m\right\}$, perform the following steps for binning.

For each target variable, K-means clustering of $K=B_i$ is performed on the normalized dataset ${\overline{D}}_i=\left(\overline{X},Y_i\right)$ corresponding to the current target variable starting from a preset starting number of clusters s. The number of clusters is denoted as K. The sum of squared intra-cluster errors after clustering is computed using Eq. (4) to evaluate the effectiveness of the clustering process. This calculation continues until the loop reaches the maximum number of clusters, which is set to 20.

After completing the clustering cycle for the current target variable, the number of clusters that minimizes the SSE is selected as the optimal number of clusters based on the trend of the SSE values. Using the records from the normalization process, the normalized dataset after binning is then converted back to the original data scale to obtain the original dataset corresponding to the current target variable after binning.

(3) End the cyclic processing of all target variables and complete the binning of the entire dataset to obtain the binned normalized dataset ${\overline{D}}_i=\left\{\left({\overline{X}}_i^1,Y_i^1\right),\dots ,\left({\overline{X}}_i^{B_i},Y_i^{B_i}\right)\right\}$.

Once the binning process is complete, it becomes possible to apply concepts similar to multi-label taxonomies to identify specific features for each target.

Above, we discussed the K-means clustering strategy employed in the MOFR-LSF model. This strategy is used to identify and group samples with similar characteristics, simplifying model complexity and improving prediction efficiency. By selecting an appropriate number of clusters K, the model can more accurately capture the underlying structure of the dataset, providing strong support for feature selection and weight allocation in subsequent stacked regression.

Multi-objective feature regression model under label-specific features

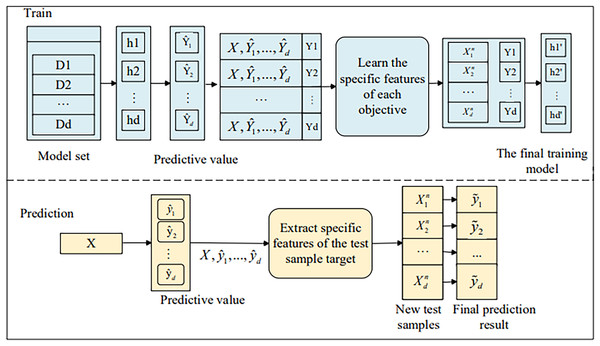
Next, we will introduce the stacked regression component of the MOFR-LSF model. This component further enhances prediction performance by integrating the prediction results of multiple base learners and exploiting the correlations among targets. By introducing a target correlation threshold t, the model is able to screen out and stack prediction values that are highly correlated with the current target, thereby avoiding the interference of noise information. The MOFR-LSF framework, as shown in Fig. 3, is based on the concept of single-target stacking and the split-box technique. The data flow begins with the input features, which first undergo a preprocessing step to extract features specifically relevant to each educational performance indicator (i.e., label). These label-specific features are then used as inputs to the stacked regression framework, where each base learner is trained on a specific performance indicator. At the stacking layer, the model leverages the correlations among targets to generate the final predictions by weightedly combining the predictions of the base learners. In this process, the model not only considers the uniqueness of each label but also fully exploits the correlations between labels, thereby improving the accuracy of the predictions.

In this article, we extend the original feature space by computing initial predicted values before learning the label-specific features for each target. These initial predicted values are subsequently used as additional features.

Then, for each target $Y_j$ find features related to it $X_{TR}^{\mathrm{\prime }}$, and construct label-specific features based on these target-related features. We use the residuals of each iteration to describe the local features as additional features to reflect the local information in the feature space:

(6) $$g_0\left(X_{TR}^{\mathrm{\prime }}\right)=f_q\left(X_{TR}^{\mathrm{\prime }};Y_j\right)$$

(7) $$r_t^j=-{\displaystyle \frac{\delta l\left(Y_j,g_{t-1}\left(X_{TR}^{\mathrm{\prime }}\right)\right)}{\delta g_{t-1}\left(X_{TR}^{\mathrm{\prime }}\right)}}$$

(8) $$g_t\left(X_{TR}^{\mathrm{\prime }}\right)=g_{t-1}\left(X_{TR}^{\mathrm{\prime }}\right)+f_q\left(X_{TR}^{\mathrm{\prime }};r_t^j\right).$$

Equation (6) is mainly used to set the initial condition, which is determined based on the basic learner of linear regression $f_q$. In contrast, the function of Eq. (7) is to calculate the negative gradient value of the current model, which we treat as an estimate of the residuals. During this calculation, the squared error loss function is employed to assess the difference between the predicted and actual values:

(9) $$l\left(Y_j,g_{t-1}\left(X_{TR}^{\mathrm{\prime }}\right)\right)={\displaystyle \frac{1}{2}(Y_j-g_{t-1}\left(X_{TR}^{\mathrm{\prime }}\right){)}^2.}$$

Experimental setting

The experiments in this article are conducted using the following experimental environment: a CPU of Intel^® Core™ i7-11700F @ 2.50 GHz, dual NVIDIA GeForce GTX 1080 Ti GPUs, Python 3.8, PyTorch 1.8.1, Torchvision 0.9.1, CUDA 11.4, and CUDNN 6.0.

To determine the optimal number of clusters K in K-means, we adopted a method based on the sum of squared errors (SSE) within clusters. Specifically, we performed K-means clustering for each target variable, gradually increasing the number of clusters K from 2 to 20, and selected the number of clusters that minimized the SSE as the optimal one. Regarding the threshold t for target correlation, to avoid the model performance being degraded by predictions of targets with low correlation, we set it to a high value of 0.9, ensuring that only predictions highly correlated with the current target are stacked. Such adjustment strategies contribute to enhancing the model’s prediction performance and stability. Additionally, the experiments set the ratio parameter r to control the number of target-specific features. Specifically, a larger value of r leads to a higher value of K for each target’s sub-box, resulting in more centroids and higher-dimensional target-specific features. Based on the LIFT algorithm, the ratio r is set to 0.1 in this article.

A threshold t is used to measure the degree of consideration of target relevance. A higher value of t indicates fewer predicted values for the second-layer target predictions in the model stacking, thereby enhancing the relevance between targets. To prevent the predictions of weakly correlated targets from negatively affecting model performance, the threshold t is set to 0.9 in this study.

Evaluation criteria

Multi-objective regression is typically evaluated using the average relative root mean square error (aRRMSE), where the relative root mean square error (RRMSE) is defined as follows:

(10) $$RRMSE\left(h,D_{test}\right)=\sqrt{{\displaystyle \frac{{\sum }_{\left(X,Y\right)\in D_{test}}{(Y_i-{\hat{Y}}_i)}^2}{{\sum }_{\left(X,Y\right)\in D_{test}}{(Y_i-{\overline{Y}}_i)}^2}}}$$where h is a multi-objective regression model, $D_{test}$ is the test set, $\left(X,Y\right)$ is the test sample, $\hat{Y}$ is the predicted value of the ith objective of the test sample, and $\overline{Y}$ is the mean value of the ith objective of the training set D. The smaller the value of $RRMSE\left(h,D_{test}\right)$ represents the better performance of the model h.

K-fold cross-validation is employed to compute the RRMSE for each fold of the dataset. The final RRMSE value is then obtained as the mean of the RRMSE values across all folds.:

(11) $$aRRMSE\left(h,D\right)={\displaystyle \frac{1}{k}\sum _{i=1}^{k}RRMSE\left(h_i,D_i\right)}$$where D is the training set, and $D_i$ is the i-fold data after k-fold crossover of the training set D, which is used as the test set for the current cross-validation. $h_i$ is the model obtained by utilizing the remaining k-1 fold data as the training set. The smaller value of $aRRMSE\left(h,D\right)$ represents the better performance of the model h.

Comparative analysis

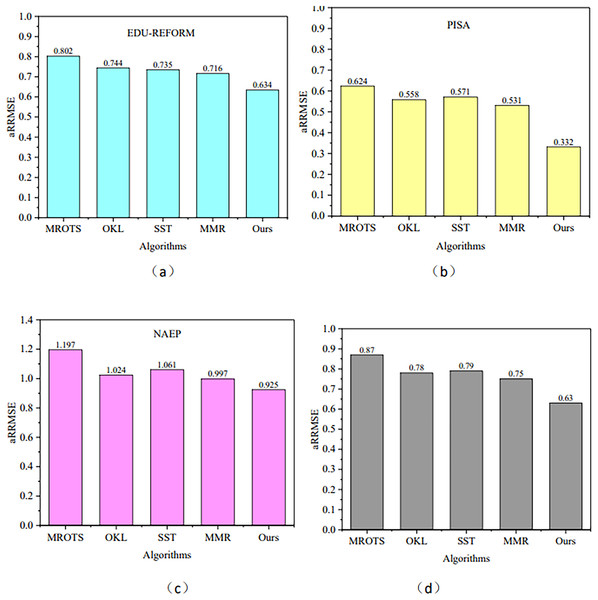
MROTS, a multi-output regression model, leverages the covariance structure of latent model parameters and the conditional covariance structure of the output space, exhibiting certain similarities to MOFR-LSF in addressing multi-target regression problems and thus serving as a benchmark for comparison. Furthermore, methods such as OKL, SST, and MMR are also representative algorithms in the field of multi-target regression. Each of these methods has its unique characteristics: OKL excels in handling nonlinear relationships, SST has a research foundation in the single-target stacking framework, and MMR is capable of modeling both the internal correlations among targets and nonlinear input-output relationships through robust low-rank learning within a single framework. Therefore, this section will use these four models as our comparison models. Figure 4 illustrates the performance of the aRRMSE for the algorithms proposed in this article and for the comparison algorithms MROTS, OKL, SST, and MMR across three datasets. Figure 4D presents the average aRRMSE performance metrics for each algorithm across four datasets. From this, it can be observed that the average aRRMSE values are 0.87 for MROTS, 0.78 for OKL, 0.79 for SST, and 0.75 for MMR. All of these values are higher than the aRRMSE of the MOFR-LSF model presented in this article, indicating that the performance of the proposed model is superior.

When dealing with datasets with complex nonlinear relationships, multilayer perceptrons (MLP) (Almeida, 2020) exhibit strong fitting capabilities. However, in terms of capturing correlations among targets, as shown in Fig. 5, they may not be as refined as the MOFR-LSF model. This is because the MOFR-LSF model, through its stacked regression framework and the construction of label-specific features, may more accurately predict different educational performance indicators. Additionally, the transformer-based model (Shojaee et al., 2023; Li et al., 2025; Huang et al., 2025) has advantages in processing sequential data and capturing long-range dependencies. However, in the context of evaluating the performance of higher education reform, the data does not fully exhibit sequential characteristics. Therefore, the MOFR-LSF model may be more suitable for capturing static correlations among targets.

To highlight the features that contribute most significantly to prediction accuracy, we computed the SHAP values and permutation importance of each feature within the MOFR-LSF model. The results indicate that, across the three datasets—EDU-REFORM, PISA, and NAEP—students’ foundational knowledge and the quality of teaching have notable impacts on predicting academic performance. Conversely, other features such as family background and social environment are more critical in predicting behavioral outcomes. These findings not only validate the effectiveness of our feature selection method but also provide valuable reference information for evaluating the performance of higher education reform initiatives.

The above experiments involve statistical tests of multiple independent trials. However, as the number of comparisons increases, so does the probability of detecting significant differences by chance. The Bonferroni-Dunn test is a post-hoc method for multiple comparisons that mitigates the overall risk of Type I error by adjusting the significance level for each individual comparison. In the context of performance evaluation of educational reforms in higher education, different algorithms may exhibit varying performance across different datasets. The Bonferroni-Dunn test allows for a more precise identification of which algorithmic differences are statistically significant. To present the variability between the compared algorithms more intuitively, this article first calculates the critical difference and then illustrates it graphically. The critical difference is the minimum required difference in average rankings for two methods to be considered significantly different, where k is the number of comparison algorithms and N is the number of datasets.

Therefore, we set k = 9 and N = 18, and the critical value table of the Bonferroni-Dunn test at $a$ = 0.05 is obtained as $q_a=1.506$, at which time CD = 0.7954 can be obtained according to $CD=q_a\sqrt{{\displaystyle \frac{k\left(k+1\right)}{6N}}}$.

According to Fig. 6, the MOFR-LSF algorithm proposed in this article demonstrates a clear performance advantage. Specifically, a significant difference between two algorithms is considered when the difference in their average rankings exceeds 1.12395516. In Fig. 6, by comparing the critical difference (CD) values across the three datasets with the algorithm rankings, it is evident that the MOFR-LSF algorithm is positioned at the far right of the graph, with its average ranking difference being significantly larger than the CD value. This result highlights the superior performance of MOFR-LSF compared to algorithms such as MROTS, OKL, SST, and MMR, offering a more accurate and effective tool for evaluating the performance of educational reforms in universities.

Additionally, from Fig. 6, it is apparent that MOFR-LSF shows only a slight difference in performance compared to MMR but a significant difference when compared to OKL and SST. This suggests that considering target features alone is insufficient. Only by combining both target-specific features and target relevance can the performance of the algorithm be effectively enhanced. This article primarily focuses on enhancing the accuracy and scientific rigor of performance evaluations for higher education reform initiatives. As the size of the dataset increases, the training and prediction time of the model may also grow, necessitating trade-offs and optimizations in practical applications.

Ablation experiments

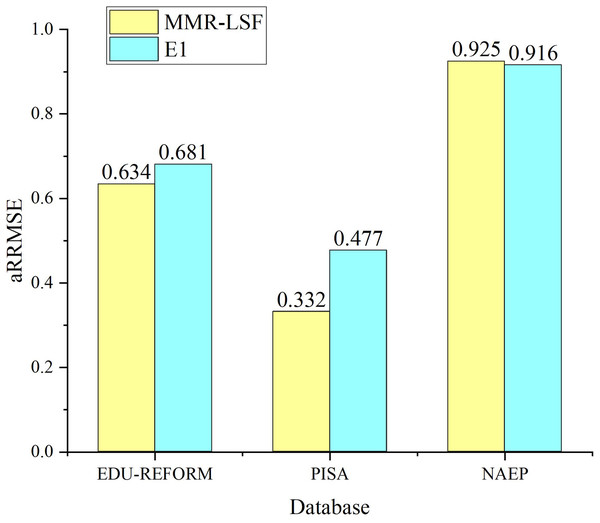
To verify whether label-specific features contribute to improving the prediction performance of the multi-objective feature regression model, ablation experiments are conducted with label-specific features serving as control variables. The experiment that follows the same process as MOFR-LSF but excludes label-specific features is designated as E1. Figure 7 presents the prediction results of MOFR-LSF and E1 using the evaluation metric aRRMSE. As shown in Fig. 6, the prediction performance of MOFR-LSF surpasses that of E1 on both the PISA and NAEP datasets. Label-specific features are capable of capturing the unique input-output relationships for each target, aiding the model in more refined modeling and prediction. Additionally, these features can reveal the correlations among targets, further enhancing the model’s expressive power and generalization ability. Therefore, label-specific features are one of the key factors contributing to the performance improvement of the MOFR-LSF model.

In the MOFR-LSF framework, we introduce the sparse integration method to address the complex associations between input features and output targets. To verify the effectiveness of this sparse integration, we use it as a control variable in ablation experiments. Specifically, this article compares MOFR-LSF with support vector regression (SVR-LSF) (Huang & Lian, 2023) and random forest (RF-LSF) (Mzobe et al., 2020; Jiang et al., 2024; Li & Xing, 2025), both of which do not utilize sparse integration. Figure 7 presents the aRRMSE values of SVR-LSF, RF-LSF, and MOFR-LSF across different datasets. As shown in Fig. 8, the prediction results of MOFR-LSF outperform those of the other two methods on all datasets, demonstrating superior performance. This result further indicates that the introduction of the sparse integration method in this study effectively addresses the complex associations in multi-objective relationships, thereby enhancing the performance evaluation of educational reforms in universities.

Discussion

Traditional performance assessment methods for college education reform often rely on a single indicator or a simple weighted average, a method that is difficult to fully reflect teachers’ multidimensional performance. The MOFR-LSF model, on the other hand, by mining the correlation between targets and constructing target-specific features, is able to capture all aspects of teacher performance in a more comprehensive way, thus providing more accurate assessment results. In addition, the model adopts a split-box method based on K-Means clustering to construct target-specific features, which effectively reduces redundant features and improves the expressive power of the model. The experimental results demonstrate that the MOFR-LSF model is capable of capturing the unique input-output relationships for each educational performance indicator. This implies that it can provide customized predictions and evaluations tailored to different education reform objectives. Such customized predictions furnish decision-makers with more precise information, aiding them in understanding the specific impacts of various reform measures on different performance indicators. Furthermore, the model integrates the predictions of multiple base learners through the stacked regression framework and leverages the correlations among targets to optimize overall prediction performance. This means that decision-makers can obtain a more comprehensive and accurate performance prediction, enabling them to weigh the pros and cons of different reform measures more scientifically and make more informed decisions.

In summary, the MOFR-LSF model has significant application advantages in the performance assessment of educational reform in colleges and universities, which not only improves the comprehensiveness and accuracy of the assessment but also enhances the scientificity and fairness of the assessment. The application of the model helps promote the development of education reform in colleges and universities, promotes the personal growth of teachers, and improves education quality.