Adversarial feature learning for semantic communication in human 3D reconstruction
- Published
- Accepted
- Received
- Academic Editor
- Trang Do
- Subject Areas
- Human-Computer Interaction, Artificial Intelligence, Data Science, Visual Analytics, Neural Networks
- Keywords
- Human 3D reconstruction, Semantic communication, Adversarial feature learning, Dynamic compression, Multilevel semantic feature decoding
- Copyright
- © 2025 Liu et al.
- Licence
- This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits using, remixing, and building upon the work non-commercially, as long as it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Computer Science) and either DOI or URL of the article must be cited.
- Cite this article
- 2025. Adversarial feature learning for semantic communication in human 3D reconstruction. PeerJ Computer Science 11:e2731 https://doi.org/10.7717/peerj-cs.2731
Abstract
With the widespread application of human body 3D reconstruction technology across various fields, the demands for data transmission and processing efficiency continue to rise, particularly in scenarios where network bandwidth is limited and low latency is required. This article introduces an Adversarial Feature Learning-based Semantic Communication method (AFLSC) for human body 3D reconstruction, which focuses on extracting and transmitting semantic information crucial for the 3D reconstruction task, thereby significantly optimizing data flow and alleviating bandwidth pressure. At the sender’s end, we propose a multitask learning-based feature extraction method to capture the spatial layout, keypoints, posture, and depth information from 2D human images, and design a semantic encoding technique based on adversarial feature learning to encode these feature information into semantic data. We also develop a dynamic compression technique to efficiently transmit this semantic data, greatly enhancing transmission efficiency and reducing latency. At the receiver’s end, we design an efficient multi-level semantic feature decoding method to convert semantic data back into key image features. Finally, an improved ViT-diffusion model is employed for 3D reconstruction, producing human body 3D mesh models. Experimental results validate the advantages of our method in terms of data transmission efficiency and reconstruction quality, demonstrating its excellent potential for application in bandwidth-limited environments.
Introduction
With the rapid development of virtual reality (VR), augmented reality (AR), and autonomous driving technology, 3D reconstruction technology has gradually become the focus of scientific research and industrial applications. These technologies have a wide range of application prospects in the fields of digital media, online education, remote sensing monitoring, medical imaging, etc., and can provide a more immersive and interactive user experience (Zhou & Tulsiani, 2023; Anciukevicius et al., 2023). For example, in the field of medical imaging, 3D reconstruction can help doctors analyze and diagnose more accurately (Cai et al., 2013; Wen et al., 2014). In urban planning and disaster assessment, 3D map reconstruction through remote sensing technology can provide more effective decision support. However, 3D reconstruction usually requires processing and transmitting large amounts of data, which is particularly difficult in environments with limited bandwidth or high network latency. In addition, high-quality 3D reconstruction often relies on powerful computational resources, which limits its usefulness in mobile devices or real-time application scenarios (Wu et al., 2023; Melas-Kyriazi, Rupprecht & Vedaldi, 2023).
In order to overcome these limitations, this article proposes a semantic communication approach for 3D reconstruction of the human body. Semantic communication is an innovative communication paradigm (Xu et al., 2023b; Weng et al., 2023; Barbarossa et al., 2023) that focuses on transmitting information that is critical for accomplishing a specific task rather than simply transmitting large amounts of raw data. By transmitting only the most critical semantic information, the method can significantly reduce the amount of data required, thereby increasing transmission efficiency and reducing bandwidth dependency (Nguyen et al., 2011; Zhang et al., 2023; Xu et al., 2023a). The use of semantic communication for human 3D reconstruction not only guarantees the quality of the reconstruction but also significantly reduces the time required for data transmission and processing, which is particularly important for application environments that have restricted network conditions or limited computational resources. Potential applications of this technology include online gaming, telemedicine diagnosis, and holographic projection technology, which all require processing and transmitting large amounts of 3D data while ensuring real-time and high interactivity. By optimizing the data flow, semantic communication brings new development opportunities to these fields, making high-quality 3D reconstruction possible in a wider range of application scenarios.
How to accurately recover detailed human 3D data from limited semantic information and how to design efficient algorithms to achieve stability and reliability under different network and device conditions. In addition, how to balance the efficiency and accuracy between semantic information extraction, transmission, and reconstruction is also a key issue to be addressed in current research (Kang et al., 2023; Yao et al., 2023; Nam et al., 2024). The method in this article accurately extracts the key semantic information that can be used for human 3D reconstruction at the sending end and efficiently transmits it to the receiving end through an adaptive compression algorithm, and then accurately reconstructs the human 3D model at the receiving end by utilizing semantic decoding and 3D reconstruction methods. This strategy not only improves the speed of data processing but also ensures the accuracy and low latency of the reconstruction process. The method in this article can provide a new solution for real-time human 3D reconstruction technology, especially in application environments where bandwidth is limited and real-time response is required, demonstrating its unique advantages and potential prospects for a wide range of applications.
Human 3D reconstruction typically requires processing and transmitting large amounts of data, which is particularly challenging in environments with limited bandwidth or high network latency. In addition, huge computational resources are often required to achieve high-quality reconstruction results, which limits its wide application in mobile devices or application scenarios that require real-time responses. To address the above challenges, our proposed AFLSC method not only optimizes the data flow but also ensures the integrity of the information and the high quality of the reconstruction by accurately extracting the semantic information that is crucial for human 3D reconstruction and efficiently transmitting it through adaptive compression techniques, and the main contributions are summarized as follows:
Innovative semantic encoding mechanism: This study develops a semantic encoding strategy optimized for 3D reconstruction of the human body, which is able to convert 2D images into key semantic data oriented to 3D reconstruction at the sending end. This approach reduces the transmission of irrelevant data and ensures efficient encoding and transmission of key information.
Dynamic compression rate adjustment: this method adaptively adjusts the data compression rate according to the importance of the semantic data and the current network status (bandwidth and latency) by means of dynamic compression technology, which optimizes the data transmission process and significantly reduces the latency while ensuring the integrity of the data and the reconstruction quality.
Efficient semantic decoding and human 3D reconstruction: at the receiver side, our method utilizes the received semantic data, decodes the semantic data into key feature information, and reconstructs the 3D model using these key feature information. Such an approach reduces the computational burden at the receiver side and at the same time ensures the reconstruction quality of the 3D model.
Related work
3D reconstruction of the human body
In recent years, human 3D reconstruction techniques have become a hotspot in computer vision and graphics research, especially in the reconstruction of high resolution and complex scenes, and significant progress has been made. NeRF (Mildenhall et al., 2021) (Neural Radiance Fields for View Synthesis) represents an emerging technique for reconstructing high-quality continuous 3D scenes from sparse views by means of a deep learning framework, which drastically improves the realism of visual effects by optimizing the view synthesis process. PIFuHD (Saito et al., 2020) (Multi-level Pixel-Aligned Implicit Function for High-Resolution 3D Human Digitization) achieves a high-quality 3D scene through a pixel-level Aligned Implicit Function for High-Resolution 3D Human Digitization and achieves a direct conversion from a single image to a high-resolution 3D human model, which significantly improves the detail quality of the reconstruction. The ECON method (Explicit Clothed Humans Optimized via Normal Integration) (Xiu et al., 2023) is employed to optimize the reconstruction process by integrating the displayed human body and garment models. By leveraging normal integration techniques, this approach effectively enhances the reconstruction quality, capturing finer details of both the body and the garments. One-stage 3D Whole-Body Mesh Recovery (Lin et al., 2023) employs the Component Aware Transformer, which directly reconstructs the entire 3D human mesh from a single image, simplifying the reconstruction process and improving the processing speed. In addition, SIFU (Zhang, Yang & Yang, 2024) and GauHuman (Hu, Hu & Liu, 2024) introduced implicit functions under side-view conditions and monocular video-based Gaussian projection techniques, respectively, and these methods have demonstrated great utility and flexibility in real-world application scenarios.
Image semantic communication
Image semantic communication is an emerging cross-cutting area of information and communication technology, focusing on the efficient transmission of image content. Research in this field focuses on reducing the amount of data transmission required while ensuring transmission efficiency and semantic accuracy of images. Huang et al. (2023) demonstrated a deep learning-based image semantic coding method that optimizes the coding and transmission process by extracting the semantic features of an image and significantly improves the transmission efficiency. Wu et al. (2024) improved the semantic accuracy of image transmission by using semantic segmentation techniques. This method reduces the required bandwidth by transmitting only the critical semantic information. Xie et al. (2023) demonstrated a deep learning-based image semantic encoding method that optimizes the coding and transmission processes by extracting semantic features of the image, which significantly enhances transmission efficiency. semantic accuracy, this approach reduces the required bandwidth by transmitting only the critical semantic information. Zhang et al. (2024b) proposed a semantic communication framework for image transfer that presents a multimodal metric called image-to-graph semantic similarity (ISS), which measures the correlation between the extracted semantic information and the original image. Zhang et al. (2024a) proposed a DeepMA approach (end-to-end deep multiple access for wireless image transmission in semantic communication) to implement an end-to-end deep multiple access wireless image transmission system, which demonstrates the potential of deep learning techniques in optimizing complex communication systems. These studies provide theoretical foundations and technical references in image semantic extraction and transmission.
System modeling
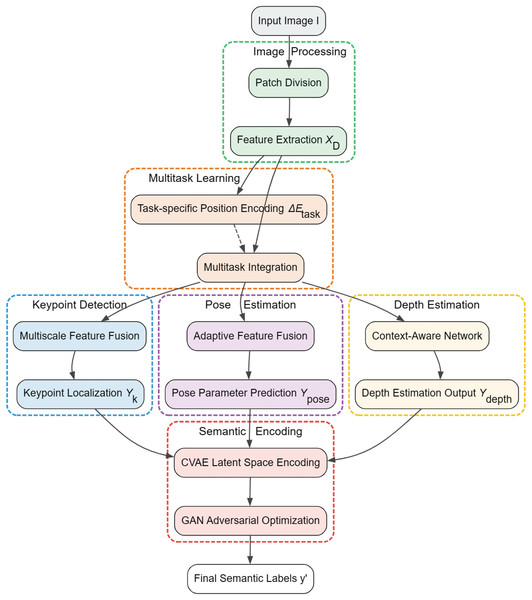
In this study, we design a semantic communication system for 3D reconstruction of the human body to realize the process starting from the input of the original 2D image I at the sender’s end to the final generation of the 3D model at the receiver’s end. The system covers feature extraction and semantic coding of images, compression and transmission of semantic data, and 3D reconstruction based on the received semantic data.
On the sender side, 2D human body images I are used as input and these images are first processed through Vision Transformer (ViT). At this stage, the images are divided into multiple blocks (patches), and each block is processed by ViT to extract key features related to 3D reconstruction of the human body, such as shape, spatial layout, pose, and depth information, to obtain a high-dimensional feature vector X. These features are further semantically encoded by Conditional Variational Auto-Encoders (CVAEs) (Sohn, Lee & Yan, 2015), which, in combination with an adversarial learning approach, generates a labeled dataset with rich semantic information. In order to be transmitted from the sender to the receiver, this semantic data needs to be compressed. We employ a dynamic compression strategy that dynamically adjusts the compression rate based on the current network conditions (e.g., bandwidth and latency) and the importance of the data. This strategy ensures efficient and stable transmission of semantic data in various network environments.
At the receiver side, the system first decodes the received semantic data to obtain potential features and then converts these potential features back to image features through a multi-level decoding process. This process involves multiple decoding layers, each of which gradually reconstructs the detailed features of the image by utilizing the output of the previous layer and the potential state of the current layer. After obtaining the image features, we use a modified ViT-diffusion model to generate a 3D point cloud, a process that progressively refines the point cloud data through a diffusion and inverse diffusion process, and finally converts the point cloud into a fine 3D mesh model using the Marching Cubes algorithm.
The overall system structure is shown in Fig. 1.
Figure 1: System architecture diagram of AFLSC semantic communication approach.
Feature extraction and semantic encoding
In order to enable 3D reconstruction of the human body at the receiver side, it is crucial to efficiently extract and encode the 2D human image features at the transmitter side. These features need to contain not only information about the shape and spatial layout of the object but also capture task-specific details such as the pose and relative depth of the object. Therefore, this chapter aims to explore how to extract key features from complex data and transform them into useful semantic information through advanced deep learning models. We first parse how the ViT model can be adapted and optimized for different visual tasks based on multi-task learning feature extraction techniques. Next, we delve into semantic encoding methods based on adversarial feature learning.
Feature extraction based on multi-task learning
In the traditional ViT model (Han et al., 2023), the image is divided into patches, and each patch is transformed into a D-dimensional feature vector before entering the self-attention mechanism. In order to adapt to multi-task learning, we modify the Transformer structure as follows:
1. Task-related positional coding: to better adapt ViT to keypoint detection and depth estimation tasks, we introduce task-related positional coding increments. The purpose of this design is to enhance the model’s ability to understand spatial information when processing different visual tasks, which is implemented as follows:
(1)
is the original position encoding and is the incremental position encoding adjusted to the type of task, which allows the model to better interpret the spatial relationships in the image when dealing with different visual tasks.
2. Integrated multi-task learning heads: we leverage the capabilities of the ViT model by integrating specialized heads for performing multi-task learning in its architecture. These heads are designed to handle keypoint detection, pose estimation, and depth estimation tasks, respectively. By introducing task-specific branches in the middle layer of the Transformer network, we make it possible for each head to optimize the processing path specifically for its particular task while receiving a shared feature representation.
We introduce three branches on the L-th layer of the Transformer’s output , each of which further processes features through a combination of layer normalization and a task-specific network layer. The specific design of each task header is as follows:
Keypoint detection header. For keypoint detection, we use a multi-scale feature fusion strategy which enhances the localization accuracy of keypoints by combining feature responses at different scales as follows:
(2) where is the sigmoid function, denotes the convolutional layer applied to the -th scale feature, denotes the layer normalization operation, and stands for the -th set of features extracted from the output of the L-th layer when dealing with the keypoint detection task.
Attitude estimation head. In pose estimation, an adaptive feature fusion technique can be defined as the use of a dynamically adjusted weighting system that adapts the network focus according to the dynamic range and spatial distribution of the input features:
(3)
Here, denotes a statistical function, such as mean and variance computation, used to evaluate the activity level of the features. FC is the fully connected layer used to convert the statistics into weights. MLP is the multilayer perceptron used for the final prediction of the pose parameters. stands for the -th set of features extracted from the output of the L-th layer while processing the pose estimation task.
Depth estimation header. In the scheme of this article, the context-aware network for depth estimation can be realized by a hybrid feature extraction network that combines local features and global context information:
(4)
(5) where is the weight generated based on the global context module, which evaluates the importance of different scale features for the task at hand. denotes the inverse convolutional layer, and GC is a network module designed to analyze and integrate the global information from the output of the different layers in order to determine the weight of each feature. stands for processing the depth estimation task by extracting from the output of the L-th layer the of the -th set of features.
While the introduction of task-dependent positional coding and an integrated multi-task learning head can enhance the ViT model’s ability to handle keypoint detection, pose estimation, and depth estimation tasks, in order to further improve the adaptability to the specific needs of 3D reconstruction, especially in dealing with spatial relations and depth perception, we have made the necessary customizations to the self-attention mechanism customization. The self-attention layer is customized to handle spatial relations and depth perception more efficiently for the specific needs of human 3D reconstruction:
(6) where is a mask adjusted based on the task requirements to enhance or suppress the strength of association between certain features, which facilitates the model to focus more on the key features corresponding to the task, e.g., to strengthen the distinction between near and far objects in depth estimation.
In order to optimize all the tasks in the multitask learning model simultaneously, the overall loss function is designed as a weighted sum of the losses of each task, and each task loss corresponds to a weight coefficient, which reflect the importance of each task in the training process. The loss function for multitask optimization is defined as follows:
(7) where is the weight coefficients for each task, these coefficients are used to balance the importance of each task in the training process and to ensure that the model achieves good performance on all the tasks. denotes the predicted outputs of the key point detection task, the pose estimation task, and the depth estimation task, and is the corresponding true label. is the loss function for a specific task. The loss for the keypoint detection task mainly evaluates the difference between the predicted heatmap and the true heatmap, and thus the binary cross-entropy loss is chosen. Posture estimation involves predicting a series of continuous values (e.g., 3D coordinates of joints or rotation angles of body parts), and therefore uses a mean square error loss. The depth estimation task takes into account that depth values are often unevenly distributed, and uses the Structural Similarity Index (SSIM) to more accurately assess visual and structural differences.
Semantic encoding based on adversarial feature learning
For the feature X extracted by our multi-task based learning approach, in order to efficiently encode deep semantic information from X, we propose an adversarial feature learning approach for semantic encoding that integrates a conditional variational auto-encoder (CVAE) and generative adversarial networks (GANs), where the CVAE part is responsible for extracting meaningful latent representations from the input features and the GAN part is used to optimize these representations through adversarial learning to generate more realistic and semantically consistent outputs.
The approach consists of two main components: the CVAE and an auxiliary adversarial discriminator, working together to accurately generate and validate semantic labels. The encoder is designed to capture the joint probability distribution between the input features X and the target semantic labels (used only in the training phase) and efficiently maps this information into a latent space . The process learns the mean and the variance of the input data over the network and is characterized as:
(8) where , represent the centrality and dispersion of potential features, respectively, thus describing the conditional distribution of the latent variable .
The task of the decoder is to reconstruct the input features X from the latent variables and predict as accurately as possible the semantic labels . The decoder combines continuous data reconstruction with discrete label prediction in the expression:
(9) where is a Gaussian distribution that describes the process of reconstructing the input feature X from the latent variable . and define the distribution of the reconstructed data, while provides the probability of generating a specific semantic label from the latent variable . is a categorical distribution for predicting discrete semantic labels based on the latent variable ’s current state. ’s current state to predict the discrete semantic label .
The role of the discriminator is to distinguish the differences between the samples generated by the decoder and the real samples, and to evaluate whether these generated samples are consistent in content with the input features X. The discriminator is a tool that can be used to evaluate the content of the samples generated by the decoder and the real samples. The operation of the discriminator is based on the following equation.
(10) where and are the samples and labels generated by the decoder, respectively, and is the discriminative network.
The training objective of this semantic coding model for adversarial feature learning is optimized through the composition of two main loss functions, a CVAE loss and an adversarial loss, and we combine the CVAE loss and the adversarial loss into a single comprehensive loss function, , which can optimize the model’s reconstruction ability and the realism of the generated samples in a more effective and simultaneous way. This loss function aims to optimize the performance of the entire model by balancing the reconstruction error, scatter, and adversarial evaluation with a single optimization objective. The adversarial loss consists of two parts, one that encourages the discriminator to accurately recognize real samples, and the other that motivates the discriminator to recognize the samples generated by the generator, driving the authenticity and semantic consistency of the generated samples. The integrative loss function is defined as follows:
(11)
Here is used to quantify the accuracy of the reconstruction, while scatter helps to regularize the latent space. and are moderating terms used to balance the influence of the different parts of the loss function to suit specific training needs. controls the influence of scatter, which is typically used to regulate the encoding constraints in the latent space. adjusts the weight of the adversarial loss to ensure that the generated samples are not only true, but also match the expected label semantics.
In the inference phase of the model, we generate the corresponding semantic labels directly from the input features X based on the trained encoder and decoder, without the need for external label input:
(12)
(13)
This adversarial feature learning method effectively integrates the deep data encoding capability of CVAE and the generation quality optimization capability of GAN through its innovative architecture, forming a powerful semantic encoding system. Through the design of the integrated loss function , the model is able to ensure the reconstruction accuracy while further improving the authenticity and semantic consistency of the generated samples through adversarial training.
The schematic diagram of the feature extraction and semantic coding process is shown in Fig. 2, and Algorithm 1 presents the corresponding algorithmic pseudo-code.
Figure 2: System architecture diagram of AFLSC semantic communication approach.
| 1: Input: 2D human image I |
| 2: Output: Semantic labels y′ |
| 3: procedure FEATURE EXTRACTION (I) |
| 4: Divide I into patches |
| 5: Apply ViT on to obtain feature vectors |
| 6: Enhance position encoding: |
| 7: for each task do |
| 8: Integrate task-specific heads into ViT |
| 9: Output from layer L of ViT |
| 10: Apply task-specific normalization and layers |
| 11: end for |
| 12: Compute outputs for each task |
| 13: end procedure |
| 14: procedure SEMANTIC ENCODING ( ) |
| 15: Encode features using CVAE: |
| 16: |
| 17: Decode features and predict labels: |
| 18: |
| 19: Optimize using GAN: |
| 20: Train discriminator D to distinguish between generated and real samples |
| 21: minimize |
| 22: end procedure |
| 23: ▹ Generate semantic labels from features |
Semantic transfer based on dynamic compression rate adjustment
Once the semantically labeled data is extracted from the 2D human body image at the sender, it is particularly important to transmit the data efficiently and reliably to the receiver. Considering the dynamic nature of network environments, especially in mobile or international communication scenarios, transmission efficiency and stability are often challenged by bandwidth fluctuations and delay variations. In order to optimize the transmission of semantic data, this article proposes a dynamic compression rate adjustment method, which is specifically adapted and optimized for semantically tagged data to ensure that high efficiency and data integrity are maintained under different network conditions.
Considering that the semantic label may be closely related to the criminality of a particular task, we define a formula to quantify the importance of each label, with attributes of the label containing type, frequency, and contextual relevance.
Suppose that each tag is associated with an importance weight that reflects its importance in a particular task. We define this weight using the following formula:
(14) where is a task-dependent adjustment factor with respect to the type of the label. denotes the average distance between the label and its contextual label set , and is a normalization factor to adjust for the effect of distance.
We can get instant feedback on current network conditions by periodically sending control packets and measuring their response times. This data helps us evaluate the network congestion level and transmission speed in real time, which provides the basis for the next compression rate adjustment. Based on the real-time monitored bandwidth and latency data, we optimize the compression rate of semantically tagged data using a dynamic tuning method that uses an exponentially weighted moving average (EWMA) approach to smooth the bandwidth and latency measurements, thereby reducing the impact of abrupt changes on the compression rate tuning. The expressions for bandwidth and delay monitored by the method are given below:
(15)
(16) where and represent the packet size and time interval of the -th transmission within the time window, respectively, is the attenuation factor of the bandwidth measurement, and is the weight of the -th response time in the delay measurement. In this way, we are able to obtain smoother and more reliable estimates of the network state, providing accurate inputs for compression rate tuning. Using the importance weights obtained above, we design a dynamic compression rate adjustment formula that is not only based on the importance of labels but also considers the real-time network condition:
(17) where is the importance weight of semantic label and W is the set of importance weights of all labels, and is a network bandwidth and latency based adjustment function defined as follows:
(18) where and are coefficients to balance the effects of bandwidth and delay on the compression rate; , , , denote the maximum and minimum values of bandwidth and delay, respectively, which are used to normalize these measurements.
This dynamic adjustment strategy ensures the flexibility and adaptability of semantic data transmission, which can intelligently optimize the data flow according to the changing network conditions and the importance of the data. With this dynamic compression technique, the transmission of semantically labeled data is more efficient and stable.
3D Reconstruction based on Semantic Data
Semantic transfer allows us to use the semantic data received at the receiver side for 3D human reconstruction. This process involves two key techniques: firstly, multilevel semantic feature decoding, and secondly, improved ViT-diffusion modeling for 3D reconstruction. We will describe in this chapter how to recover image features from semantic tags and utilize these features to guide the generation of 3D models.
Multi-level semantic feature decoding
In the multilevel semantic feature decoding section, we are concerned with accurately reconstructing the complete set of image features from the semantic labels . This process involves extracting the necessary information from a highly parameterized latent space and progressively reconstructing the detailed features of the image through a series of complex decoding layers.
The encoder at the receiver side first maps the received semantic signal to a parameterized potential space. This mapping is realized by a CVAE that employs a hybrid Gaussian model (GMM) (Liu & Zhang, 2012) to express this potential space, thus capturing the complex distribution and intrinsic variability of the input data. The process is represented as:
(19)
(20) where the encoder is still implemented using CVAE, outputting the mean and covariance of the latent variable to provide the required parameters for the subsequent sampling steps. is the mixing weight of the -th Gaussian distribution, which indicates that different regions in the latent space correspond to different semantic features. K is the number of Gaussian distributions. , are the mean and covariance matrix, respectively.
Once the distribution of the latent space has been defined, the next step is to sample from this distribution to generate the latent feature vector that can be used for further decoding. Sampling using the Cholesky decomposition ensures that samples are drawn stably from each component of the Gaussian mixture model by:
(21) where denotes the Cholesky decomposition, which decomposes the covariance matrix into a product of a lower triangular matrix and its transpose, thus allowing us to generate the desired samples from the standard normal distribution by a simple transformation.
After the potential feature vectors are generated, the next task is to reconstruct the original image features by decoding these features layer by layer, with each layer combining the output from the previous layer and the current potential state. During decoding at each level, not only the current potential features are used, but also the information passed from the previous layer is utilized. This integration of information is achieved through recurrent neural networks (Wang et al., 2016), which can process and maintain the flow of information across multiple decoding stages:
(22) where denotes the output of the decoded layer , which is the local features of the image, and is the hidden state of the RNN, which is used to maintain and transfer the dependencies and information between layers. denotes the hidden state of the RNN and feedback is used to handle the complex dependencies between layers. The loss function is designed to balance the accuracy of reconstruction and regularization of the latent space, as well as the adaptability of the model to new semantic information, denoted as follows:
(23) where denotes the final output features of layer , i.e., the features that are integrated and ready to be passed on to the next layer, and is an additional regularization term designed to encourage the diversity of latent variables and to improve the model’s generalization ability and adaptability to new semantic information.
Improved ViT-diffusion model for 3D reconstruction
In this section we explore how to utilize improved and diffused models based on the visual transformer (ViT) in order to achieve 3D human reconstruction based on image features . This process involves not only adapting the structure of the ViT to accommodate multi-scale feature extraction, but also how these features can be effectively applied to the diffusion and inverse diffusion processes, ultimately generating accurate 3D models.
For traditional ViT, the input image is usually divided into blocks (patches) of uniform size. In our improved model, we introduce multiple parallel ViT paths, each processing image chunks of different scales to accommodate multi-level feature capture from local details to global structures, denoted as:
(24) where denotes different scale paths, is a weight that is dynamically adjusted according to the importance of features at each scale, is a function that adjusts the input image to the scale , and is the ViT model parameter of the corresponding scale.
In order to better adapt ViT to the needs of transitioning from images to 3D models, we introduce a dynamic attention adjustment mechanism based on the input feature . This allows ViT to adjust its internal attention allocation according to different regions of the image content:
(25) where is an adjustment matrix dynamically generated based on the input features to adjust the attention weights.
We then incorporate the ViT-extracted feature to guide the diffusion process, an approach that allows us to accurately control the process of generating a 3D point cloud based on the high-dimensional information extracted by deep learning, thus enhancing the representativeness of the model and the accuracy of the generated 3D structure:
(26) where is the noise control coefficient, which is used to adjust the proportion of noise. This noise is not a simple random perturbation, but is regulated by the feature extracted by ViT. The purpose of this is to ensure that the addition of noise reflects the structure and content characteristics of the image itself, so that the generated point cloud is closer to the real 3D structure of the original image.
The noise is then gradually reduced and structured 3D data is recovered through an inverse diffusion process using the same conditionalization strategy. The inverse diffusion formula is:
(27)
A 3D mesh is generated from the final optimized point cloud using the Marching Cubes algorithm: .
The pseudo-code of the 3D reconstruction algorithm based on semantic data is shown in Algorithm 2.
| 1: Input: Semantic labels y′ |
| 2: Output: 3D human model |
| 3: procedure MULTI-LEVEL SEMANTIC FEATURE DECODING (y′) |
| 4: Encode y′ into latent space using CVAE: |
| 5: |
| 6: |
| 7: Sample z′ from using Cholesky decomposition: |
| 8: |
| 9: Decode features from z′ at each layer: |
| 10: for each layer i do |
| 11: |
| 12: |
| 13: end for |
| 14: Optimize loss: |
| 15: |
| 16: end procedure |
| 17: procedure 3D RECONSTRUCTION WITH VIT-DIFFUSION MODEL (si) |
| 18: Adapt ViT to multiple scales and integrate features: |
| 19: |
| 20: Apply diffusion process guided by um: |
| 21: |
| 22: Reverse diffusion to recover structured 3D data: |
| 23: |
| 24: Generate 3D mesh using Marching Cubes: |
| 25: |
| 26: end procedure |
Experiments and results
Experiments
In this study, the training environment comprised a high-performance server equipped with an Intel Xeon CPU, 128 GB of RAM, and an NVIDIA A100 GPU with 80 GB of SGRAM. The dataset used for the experiments was THuman2.0 (Yu et al., 2021), which provides high-quality 3D human body scanning data and is well-suited for evaluating 3D reconstruction algorithms. During the testing phase, both the sender and receiver systems had identical hardware configurations, utilizing Intel i7-11800H CPUs and NVIDIA GTX 3080 GPUs. The experiments were conducted using the PyTorch deep learning framework, with Python as the programming language.
We designed two experimental scenarios to demonstrate the performance of our semantic communication approach in 3D reconstruction applications:
Experimental Scenario A: We define the traditional transmission method as the one that directly performs 3D reconstruction at the sending end, and then sends the 3D model data to be received at the receiving end without employing special data compression or optimization. Then the AFLSC-without SC method (which employs the same 3D reconstruction technique as the AFLSC of this article, but uses the conventional data transmission method) is compared to the AFLSC of this article along with the NeRF (Mildenhall et al., 2021) and PIFuHD (Saito et al., 2020) algorithms, which also employ the conventional transmission method.
Experimental Scenario B: Our approach is compared with other semantic communication techniques using the literature (Zhang et al., 2024b) (referred to as ISS), and literature (Zhang et al., 2024a) (referred to as DeepMA) semantic communication methods to send a 2D image from the sender side, and reconstruct it into a 3D model using NeRF after receiving the semantic image at the receiver side. Through this comparison, we can demonstrate the advantages of this article’s method in terms of data transmission efficiency and reconstruction quality preservation in a bandwidth-constrained environment. In addition, this experiment will validate the effectiveness of the present method in reducing the amount of data required as well as improving the overall 3D model quality.
Evaluation metrics
We used the following metrics in our experiments.
Transmission delay. We will measure the total time required to complete the 3D reconstruction task under the same network conditions, including data transmission and processing time. The data transmission time includes the time from sending at the sending end to successful reception at the receiving end, and the processing time includes the sum of the time for processing the data at the sending and receiving ends. This helps to evaluate the contribution of semantic communication in improving the transmission efficiency.
Reconstruction quality. The quality of models reconstructed by different methods will be compared using 3D model quality assessment criteria using the mean square error (MSE) and the SSIM:
(28)
(29) where represents a point in the original image or model, and is the corresponding point in the reconstructed image or model, with being the total number of points. and are the mean values of the and images, respectively. and are their variances, is their covariance, and and are small constants added to avoid division by zero.
Bandwidth utilization. Record the amount of data required to complete the same task and compare the bandwidth utilization of different methods.
Results and discussion
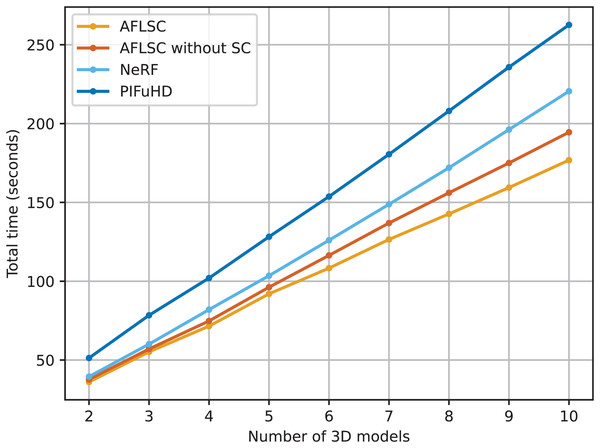
In Experimental Scenario A, we demonstrate the advantages of the AFLSC method in terms of dealing with latency and improving transmission efficiency by comparing the performance of different 3D reconstruction methods in terms of total task time. As can be seen from the experimental data in Fig. 3, the total task time of all methods grows gradually as the number of 3D models increases. However, AFLSC consistently shows lower latency than AFLSC-without SC, NeRF, and PIFuHD. Specifically, AFLSC exhibits lower latency at all model number levels compared to AFLSC without SC, which uses traditional data transfer methods. This advantage suggests that AFLSC is able to process and compress data more efficiently through an optimized semantic transfer approach, thereby reducing the transfer time. In particular, AFLSC shows significantly lower latency in comparison with PIFuHD and NeRF, which is in part due to the fact that PIFuHD and NeRF may need to process more data details, resulting in larger data volumes and longer processing times.
Figure 3: Total task time required to reconstruct the 3D models in experimental scenario A.
The strength of AFLSC stems from its use of a semantic communication strategy that transmits only the most critical information for accomplishing a given task, greatly reducing the size of the data that needs to be transmitted. This strategy is particularly effective in environments with bandwidth constraints or unstable network conditions. In addition, although AFLSC and AFLSC-without SC use the same 3D reconstruction technique, the optimized transmission method makes AFLSC more efficient in the actual data transmission process.
In Experimental Scenario A, we compare the performance of AFLSC with four methods, AFLSC-without SC, NeRF, and PIFuHD, under different network bandwidth conditions. The experimental results in Fig. 4 show that the AFLSC method has the shortest total task time for all bandwidth settings, thus clearly demonstrating its significant advantages in improving data transfer efficiency and reducing latency. The total task time of AFLSC at 1 Mbps bandwidth is 15.7% faster than that of AFLSC-without SC, 21.0% faster than NeRF, and PIFuHD by 31.0%. This significant performance difference indicates that AFLSC significantly improves data processing efficiency through effective semantic compression and transmission optimization. In addition, the total task time decreases for all methods as the bandwidth increases. At the high bandwidth setting of 10 Mbps, AFLSC reduces the time by 3.9%, 22.4% and 28.9% compared to AFLSC-without SC, NeRF and PIFuHD, respectively. This shows that even under the favorable conditions of high bandwidth, the optimized transmission strategy of AFLSC still provides additional performance gains.
Figure 4: Total task time under different network bandwidth conditions.
The superiority of AFLSC is mainly attributed to its ability to efficiently encode 2D image data into the required semantics suitable for 3D reconstruction, and to effectively compress the amount of semantic data, making it possible to rapidly transmit critical data even under low bandwidth conditions, instead of unoptimized transmission of the complete data in traditional approaches. This optimization is particularly suitable for bandwidth-constrained or application scenarios requiring high real-time performance, such as online gaming and telemedicine diagnostics, where reduced latency directly improves user experience and system responsiveness.
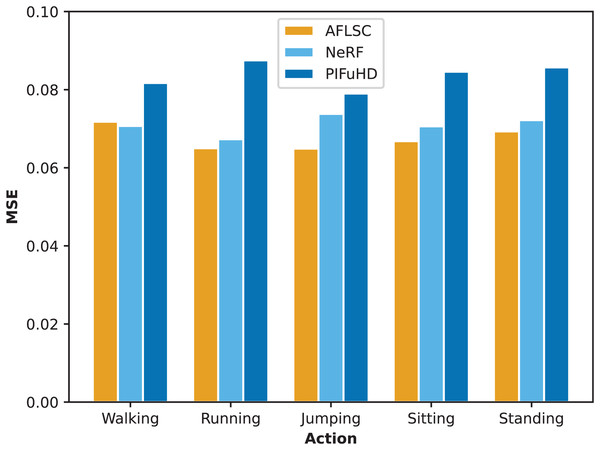
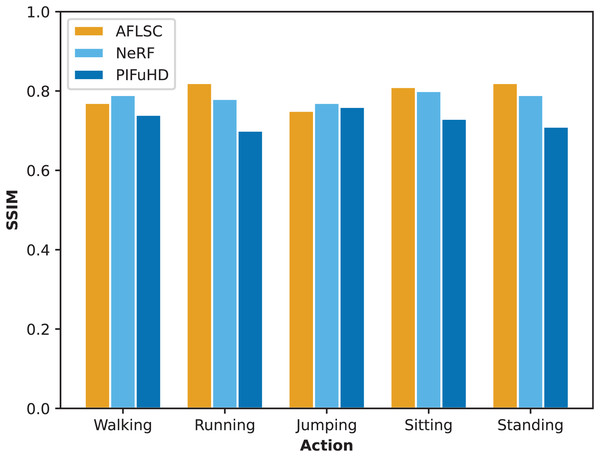
In Experimental Scenario A, we compared the quality metrics, including MSE and SSIM, of AFLSC with AFLSC-without SC, NeRF, and PIFuHD in 3D reconstruction of different human movement types. From the perspective of the MSE data in Fig. 5, AFLSC presents lower error values in the reconstruction of each movement type, especially in the “Running” and “Sitting” movements, with MSE values of 0.0650 and 0.050, respectively, compared with the results of NeRF and PIFuHD, which shows that AFLSC is more capable of accurately capturing important details when dealing with dynamic movements and complex poses. For example, in the “Running” action, AFLSC has about 25.7% lower error than PIFuHD, a difference that emphasizes the efficiency of AFLSC in preserving the dynamic features of the action. In terms of the SSIM data results in Fig. 6, AFLSC also shows high model similarity, especially in the “Running” and “Standing” movements, with SSIM values of 0.82, which are about 17.1% and 17.7% higher than that of PIFuHD, respectively. The SSIM values were 0.82 for the “Running” and “Standing” movements, which were about 17.1% and 15.5% higher than those of PIFuHD. This shows that AFLSC not only can accurately reconstruct the model, but also can be visually closer to the original model, providing a more natural and coherent visual effect. In addition, even when other methods perform better, e.g., the SSIM of NeRF in the “Walking” action is 0.79, the AFLSC’s 0.77 is still competitive, which proves its stable performance in different scenarios.
Figure 5: MSE values during reconstruction of 3D models with different action types.
Figure 6: SSIM values during reconstruction of 3D models with different action types.
The experimental results show that AFLSC demonstrates superior reconstruction quality in most cases, especially in MSE and SSIM. The AFLSC method is able to encode 2D images into key semantic data suitable for 3D reconstruction at the sender’s end, so that the receiver’s end, after receiving this semantic information, is able to use the semantic data that contains the key information of the original image to perform 3D reconstruction, ensuring the quality of 3D reconstruction.
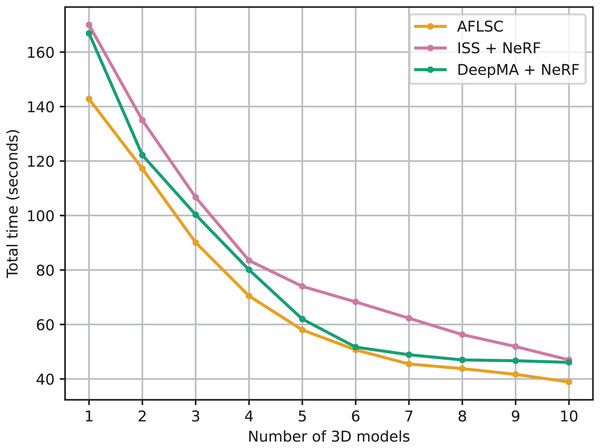
The purpose of Experimental Scenario B is to compare the performance of our AFLSC approach with other semantic communication technologies such as ISS and DeepMA, especially for applications in 3D reconstruction tasks. Through these comparisons, we can demonstrate the advantages of AFLSC in terms of data transfer efficiency and reconstruction quality preservation in bandwidth-constrained environments. As can be seen from the experimental data in Fig. 7, the total task time for all methods grows as the number of 3D model reconstruction tasks increases. However, AFLSC consistently outperforms ISS and DeepMA in task completion time for all model counts, highlighting its efficiency in processing 3D reconstruction semantic data. For example, in the 10-model reconstruction task, AFLSC has a completion time of 176.0 s, while ISS and DeepMA take 194.5 and 190.5 s, respectively. This indicates that AFLSC is 9.5% and 7.6% faster than ISS and DeepMA, respectively, highlighting the superiority of AFLSC in terms of data processing and processing efficiency.
Figure 7: Total task time required to reconstruct the 3D models in experimental scenario B.
A key advantage of AFLSC is its ability to efficiently encode semantic data optimized for 3D reconstruction at the transmitter side, thus allowing the reconstruction process to proceed rapidly at the receiver side. In contrast, ISS and DeepMA, while adept at transmitting compressed image data, do not focus on semantic data optimized specifically for 3D tasks. This leads to the fact that they need to reconstruct the image before reconstructing the 3D model, thus relatively prolonging the reconstruction time.
We compare the total 3D model reconstruction task time of our proposed AFLSC method with two semantic communication techniques, ISS and DeepMA, under different network bandwidth conditions in experimental scenario B conditions. As shown in Fig. 8, the comparison of the experimental data demonstrates the significant advantages of AFLSC in terms of data transmission efficiency and reconstruction quality maintenance in bandwidth-constrained environments. From the experimental data, it can be seen that the task completion time of all methods decreases as the bandwidth increases, but AFLSC consistently outperforms ISS and DeepMA at all bandwidth levels. For example, at a bandwidth of 1 Mbps, AFLSC completes the task in 142.8 s, which is 16.0% faster than ISS and 14.5% faster than DeepMA. At the highest bandwidth of 10 Mbps, AFLSC’s time is 38.9 s, which is 17.4% faster than ISS and 15.6% faster than DeepMA. In addition, AFLSC demonstrates greater performance gains in lower bandwidth settings, suggesting that it is more efficient at compressing and transferring critical semantic information. This is particularly important for application scenarios that require real-time or near real-time 3D reconstruction, such as teleoperation and interactive media.
Figure 8: Total task time under different network bandwidth conditions in experimental scenario B.
The reduction in the total task time also shows the advantages of AFLSC in terms of compression and coding efficiency of semantic data, enabling it to perform the 3D reconstruction task faster in bandwidth-constrained situations. In contrast, ISS and DeepMA are inferior to AFLSC in semantic communication specifically for 3D reconstruction, although they also employ semantic communication strategies.
In Experimental Scenario B, we evaluate the ability of each method in maintaining the quality of 3D model reconstruction by comparing SSIM. From the experimental results in Fig. 9, it is clear that AFLSC outperforms ISS and DeepMA in different movement categories, e.g., in the “Walking” category, the SSIM of AFLSC is 0.80, which is significantly higher than that of ISS (0.66) and DeepMA (0.72), and in the “Jumping” movement, the SSIM of AFLSC is 0.78, compared with that of ISS and DeepMA (0.78). Similarly, in “Jumping”, the SSIM of AFLSC was 0.78, compared to 0.61 for ISS and 0.65 for DeepMA. This advantage is demonstrated across the action types tested. AFLSC achieves its advantage mainly due to its efficient semantic encoding mechanism that accurately captures and transmits the visual and geometric information that is essential for 3D reconstruction. In contrast, ISS and DeepMA, although they also employ semantic transmission of images and are able to reconstruct images at the receiver side and use NeRF for 3D reconstruction, are not as efficient as AFLSC exhibits in terms of data transmission efficiency and reconstruction quality maintenance. In addition, AFLSC outperforms ISS and DeepMA in adapting to different action types and maintaining the reconstruction quality, which is mainly attributed to its fine-grained processing of semantic information during model training and optimization. By precisely controlling the content of the transmitted information, AFLSC not only improves the utilization efficiency of network resources, but also optimizes the detailed performance during the reconstruction process, making the final 3D model more accurate and natural.
Figure 9: SSIM values during reconstruction of 3D models with different action types in experimental scenario B.
Conclusions
In this study, we propose an adversarial feature learning-based semantic communication method for human 3D reconstruction, aiming to address the challenges faced by traditional 3D reconstruction techniques in bandwidth-constrained and high-latency environments. Our approach significantly improves the efficiency of data transmission and the accuracy of the reconstruction process by efficiently extracting and transmitting semantic information critical for 3D reconstruction. We develop an innovative semantic encoding mechanism that converts human 2D images into compressed semantic data containing the necessary 3D reconstruction-oriented data at the sender’s end. This step not only optimizes the data flow, but also reduces bandwidth dependency, enabling high-quality 3D reconstruction even in bandwidth-constrained environments. By introducing a dynamic compression rate adjustment strategy, our system intelligently adjusts the compression rate according to network conditions and data importance, which not only reduces transmission latency but also ensures the integrity of the transmitted data. This feature is lacking in traditional 3D reconstruction methods and provides technical support for efficient and stable remote 3D modeling. In addition, an efficient semantic decoding and reconstruction process at the receiver side enables fast and accurate recovery of detailed 3D models from compressed semantic data. Our method reduces the computational burden at the receiver side while ensuring accurate reconstruction of 3D models, which is particularly suitable for mobile devices or real-time applications with limited computational resources. Through a series of experiments, we demonstrate that our method outperforms the prior art in several aspects. The experimental results show that this study demonstrates significant advantages in both data transfer efficiency and reconstruction quality. The semantic communication strategy and 3D reconstruction method proposed in this article provide a new possibility to realize high-quality 3D reconstruction under various network and device conditions in the future. Future work will focus on further optimizing the performance of the algorithm, extending it to more application scenarios, and solving more kinds of 3D reconstruction tasks. We will also explore applying this approach to other types of data and tasks to validate its generalizability and scalability.