An optimal peer selection for peer-to-peer video content distribution using fuzzy linear programming approach
- Published
- Accepted
- Received
- Academic Editor
- Željko Stević
- Subject Areas
- Computer Networks and Communications, Optimization Theory and Computation, Theory and Formal Methods
- Keywords
- Content distribution network, Fuzzy set, Fuzzy linear programming, Peer selection problem, Peer to peer network
- Copyright
- © 2025 Anandaraj and S.
- Licence
- This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits using, remixing, and building upon the work non-commercially, as long as it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Computer Science) and either DOI or URL of the article must be cited.
- Cite this article
- 2025. An optimal peer selection for peer-to-peer video content distribution using fuzzy linear programming approach. PeerJ Computer Science 11:e2701 https://doi.org/10.7717/peerj-cs.2701
Abstract
The problem of peer selection in peer-to-peer (P2P) video content distribution network is significant to solve since it affects the performance and efficiency of the network widely. In this article, a novel framework is introduced that uses fuzzy linear programming (FLP) to address the inherent uncertainties in peer selection. The primary motivation for the use of FLP lies in its capability to handle the imprecision and vagueness that are characteristic of dynamic P2P environments. Factors such as peer reliability, bandwidth, and proximity are often uncertain in this environment. By using fuzzy logic, the proposed framework models these criteria as fuzzy sets and then integrates uncertainty into the decision-making process. FLP is then applied to optimize peer selection, improving download speed, reducing download time, and enhancing peer reliability. The proposed method is evaluated and analyzed using extensive simulation with SciPy. The result reveals that proposed technique works better compared to some of the traditional methods in terms of download time, download speed and also reliability measure. It also exhibits approximately 20% of increase in download speed as well as a 15% decrease in download time compared to traditional approaches. It leads to faster content retrieval and enhanced the efficiency in content distribution. Also, in selection of reliable peers for content distribution, there is a notable 20% of increase in peer reliability with result of enhanced robustness. The proposed method provides efficient and robust solution to the problem of peer selection. It can be implemented in a broad range of P2P content distribution networks.
Introduction
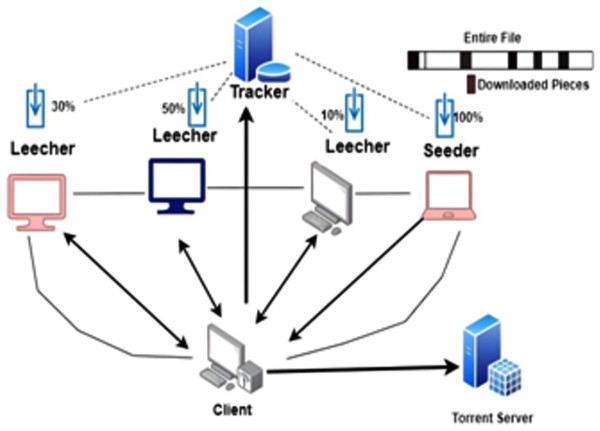
Decentralized characteristics are represented in peer-to-peer (P2P) networks where nodes act as both consumers and suppliers of any resources including any format content (Gebraselase, Helvik & Jiang, 2022). Any files, resources and also services can be directly shared among the connected nodes in these types of networks. Lack of reliance on a central authority is one important characteristic which distinguishes P2P networks with others. Such decentralized system assures that any peer within them can share the resources and files independently, add computing power and assign bandwidth to others leading to effective utilization of resources available in the network. Additionally, P2P networks reveal self organizing behavior which allows for seamless entry and exit of any participants with no effect on the system’s performance as a whole at any time. This dynamic adaptability assures autonomy even when the size and structure of the network increases and changes (Budhkar & Tamarapalli, 2020). The addition of any new peers in P2P networks increases availability of resources and redistributes workload among network participants. Search and retrieval of resources in the case of structured P2P networks are eased by explicit topologies like ring or tree structures. In contrast, random connections among the peers or some heuristics are used to connect unstructured networks allowing more adaptability and flexibility in node to node connectivity (Hwang et al., 2022). The nature of decentralization of P2P network enables participating peers to independently share files, computing power, allocate bandwidth among them directly. For an example, file sharing protocols such as BitTorrent allow one to download files from multiple sources at the same time and improve distribution of large files (Budhkar & Tamarapalli, 2020).
In addition, P2P networks have resulted in significant changes in resource sharing, collaboration and communication through distributed computing projects like SETI@home, which utilize a lot of computers for scientific computations (Gebraselase, Helvik & Jiang, 2022). The decentralization of operations offered by P2P networks is very beneficial. It enables resources to be shared among different users. But, in relation to security, unstructured environments present the major challenges with respect to data integrity and network efficiency (Hwang et al., 2022). However, continuous technological advancements are further improving P2P networks while addressing weakness and expanding their applications into diverse domains (Ren et al., 2020). Figure 1 shows the system structure of this particular P2P network. Distributing content across the globe via servers is a key characteristic of content distribution networks (CDNs) (Nacakli & Tekalp, 2021). These are systems that cache and distribute content such as web pages, multimedia contents, software downloads among other digital assets. The main goal of CDNs is to enhance the efficiency of delivery of content, reducing delays and also optimizing user experience by minimizing the time it takes for users to obtain required services (Yao, Xiang & Liu, 2024). One remarkable feature of CDNs is their exploitation of caching methods over several different servers located in several locations. It makes the same piece of content to be duplicated and stored in several different locations by allowing end users to access them from a physically nearby location (Luo et al., 2020). By dispensing sources across servers, CDNs optimize server overall performance, prevent server congestion, and ensure consistent and reliable facts transport (Farahani et al., 2023). Peer-to-peer content delivery networks (P2P CDNs) combine the decentralized architecture of P2P networks with the content delivery capabilities of CDNs that enable these networks to share and distribute information between them without interdependence on centralized server infrastructure (Farahani et al., 2023; Han & Nam, 2019).
Figure 1: P2P network structure.
Research highlights and paper organization
The proposed system aims at improving and modernizing network performance and resource allocation within a P2P network. The enhancement of efficiency and effectiveness of peer selection methodologies within P2P networks is also aimed at this research by incorporating fuzzy linear programming. Adaptability and precision are introduced in the decision-making process by fuzzy logic, accommodating the essential uncertainties and inaccurate data that are prevalent in those networks. Latency reduction and load balancing among the participating peers are targeted by this approach, but it also exhibits a paradigm shift in the direction of optimized utilization of available resource, scalability, and dynamic adaptability within P2P architectures. The introduction of FLP in the process of peer selection is aimed not only at minimizing latency and also improving load distribution, as well as giving higher priority on impartial content sharing among the participating peers. It guarantees an improved user experience through increased reliability, throughput, and accessibility. A redefinition of the P2P CDN domain is assured by this research, since it introduces a more flexible and responsive peer selection framework, eventually setting the foundation for a more efficient and robust network infrastructure. The major objectives of this article are given as follow.
Design a comprehensive model combing fuzzy logic with linear programming techniques to optimize the selection of peers in P2P CDN.
Examine the applications of the fuzzy linear programming technique in handling dynamic network conditions and uncertainties for ensuring robust peer selection mechanisms.
Analyze the impact of fuzzy linear programming on resource allocation, intending to attain impartial content distribution among the participating peers at the same time maximizing throughput and reliability of the network.
The remaining part of the article is prepared as follows. “Related Works” explains the literature review of the proposed work and existing mechanisms as well as their limitations to resolve the problem of peer selection. “System Model” describes the basic idea behind implementation of fuzzy logic programming and its applications. “Proposed System” elaborates the proposed method, including the fuzzy logic programming technique and the peer selection framework. “Performance Comparison” and “Result and Discussion” states the results and experimental analysis and discussion of the proposed system respectively. “Conclusion” finally gives the conclusion of the article and outlines future directions of research.
Related works
Peer selection problem in P2P networks
The peer selection problem is a critical challenge in P2P networks, especially within content distribution networks (CDNs), where effective peer selection significantly impacts network performance, reliability, and user experience (Nie et al., 2023). Traditionally, peer selection algorithms prioritize criteria such as proximity, bandwidth, latency, and historical performance, aiming to optimize the efficiency of content delivery by matching peers based on their capabilities and network states (Safara, Souri & Deiman, 2020). In this selection problem, finding out the most opt peers to download and share content within a P2P content distribution network is a big challenge. Because selecting the wrong peers will lead to a down in network performance, download speed. Also, it increases network congestion. To solve the problem of peer selection, P2P CDN uses various techniques. Ali et al. (2020) explored AI techniques, specifically machine learning, which capitalizes on peer’s knowledge. Their objective is to adapt the selection process to meet peers’ requirements. The free-riding problem in file sharing prompts the use of incentive mechanisms, such as fairness between uploads and downloads in schemes like BitTorrent (Luo et al., 2020; D’Alessandro Costa & Gonçalves Rubinstein, 2019). Our system is not designed for file-sharing environments. Instead, our focus lies in selecting the most suitable peer for specific service requirements, prioritizing performance over fairness. Distinct from file-sharing applications that typically involve relatively short burst chunk downloads/uploads, our approach aims to select the best peer for long-term sessions. In the domain of P2P multimedia stream services, similar studies address peer selection issues, aiming to optimize peer selection concerning service performance (Meng, 2018; Geng & Fujita, 2024). Additionally, the prevalence of P2P traffic poses challenges for internet service providers (ISPs). Several proposals (Hwang et al., 2022; Nacakli & Tekalp, 2021; Geng & Fujita, 2024) suggest collaborations between ISPs and P2P applications to help ISPs make informed choices about the best peers within their domains, aiming to reduce costs. In contrast, the scheme proposed in BPSS (best peer selection scheme) (Xue et al., 2023) selects optimal peers for service interactions within the geographical domain of the service requester, eliminating the necessity for explicit collaboration between service providers. Izhak-Ratzin, Park & Schaar (2012) presented a strategy for achieving an optimal peer selection technique using Q-learning. In their methodology, a peer’s action involves selecting target peers from a pool of n adjacent peers. In contrast, the original BitTorrent protocol divides the upload capacity of a peer p into four upload slots. Three slots are allocated for uploads to the three fastest peers that received the most uploads from p in the previous phase, while one slot is designated for uploads to a randomly chosen peer from the entire set of peers. Even though this approach could attain a nearly optimal scheme for small sized network, it could not be used to larger sized network because the number of states increases exponentially to the number of neighboring peers. Another one common approach is to use a tracker server. It keeps track of which peers have the content and can provide information about their availability and speed. The client then use this information to choose the best set of peers to download the content from Ghasemkhani et al. (2018). One more common technique is to employ a distributed hash table (DHT), which is a distributed in nature that permits efficient lookup of information using key. In a P2P CDN, a DHT is used to store the information about which peers in the network have which portion of the content (Kumar & Pandey, 2022). Clients use the DHT to pick the best possible set of peers to approach for downloading the content. In addition to these systems, P2P CDNs make use of a variety of algorithms to optimize peer selection like the random peer selection algorithm. The Chord algorithm uses a consistent hashing function to route requests to the appropriate peer (Masood et al., 2018). Even though these techniques are functioning well and good, the peer selection problem of those techniques continue to be a challenging problem to solve in P2P CDNs. In particular, it underperforms in large scale networks with a high degree of churn, where peers often join and leave the network at any point of time. In order to solve these challenges, researchers continue to examine new algorithms and techniques to optimize the selection of peer in P2P CDNs (Surati, Jinwala & Garg, 2017; Anandaraj et al., 2021). There are some mechanisms is used to solve the above stated problem in P2P CDNs. The following are some of the conventional solutions used to solve the problem of peer selection.
Peer selection at random: It is one of the simple technique used to select the peers at random for content download. It does not consider any criteria like peer download speed, availability or any other constraints but can still be effective in some circumstances.
Centralized peer selection: There is a centralized server or tracker used to provide the assistance to the peers to pick other set of peers for collaboration to download the content in this approach. There is a server to store and maintain a list of available peers and selects the best possible peers based on criteria like download speed, availability and other desirable criteria. It may suffer from a single point of failure and also there is a possibility to increase in network latency.
Decentralized peer selection: Peers work together to choose the best peers for content distribution in this approach. Peers can exchange information among themselves about their capacities like download speed, upload capacity, and availability to find out the best peers to download content from. This approach is complex to implement and also may need some additional communication overhead.
The selection of the most suitable solution for the peer selection problem in P2P CDNs relies on the specific characteristics of the network, such as the number of peers, network topology, and also content popularity (Naganandhini & Shanthi, 2023; Ren et al., 2020). A combination of these approaches may also be employed to enhance network performance and reduce network congestion, but difficult to integrate all those techniques.
Fuzzy liner programming
Fuzzy linear programming (FLP) is one type of programming technique which makes use of fuzzy logic to form algorithms. It can use to make informed decisions with help of even using imprecise and uncertain data (Loganathan & Ganesan, 2021; Edalatpanah, 2023). It is also one kind of a mathematical technique that can be used to resolve this problem by integrating uncertainty and also imprecision into the process of making decision (Wang et al., 2023; Yang & Zheng, 2021). It permits to obtain decisions with best currently available data, even if the data is not complete. FLP is utilized to resolve complex problems which cannot be solved with help of conventional programming schemes. It can also be utilized to find optimal processes and systems (Yang, Zhou & Cao, 2015). Due to FLP’s capability of managing fuzzy constraints, it is a perfect solution for the real-world problems where data and constraints are dynamic and high degree of control is not achievable (Goguen & Zadeh, 1973). FLP can therefore adapt to the changes in resource availability, demand and other conditions in the network unlike the conventional LP models. It can provide feasible as well as efficient solution compared to conventional methods by combining fuzzy logic and fuzzy sets into the optimization problem (Nguyen et al., 2019). Also, FLP’s use of linguistic variables and partial satisfaction enable it to incorporate human-based evaluations that are typical in network management environments. FLP has been found to be very useful in applications that involve the use of flexible, dependable solutions in areas such as network design, resource management, and scheduling (Liu et al., 2016). In network design, FLP supports the optimization of several and frequently competing objectives such as bandwidth, delay and cost. FLP also allows for an adaptable design strategy because it considers each criterion as having varying degrees of importance or priority. It will be useful in responding to the variability of network loads. FLP is used to resolve using conventional algorithms for linear programming such as the simplex technique. Also, fuzzy logic operations are utilized to handle the fuzzy decision variables and constraints (Zhang et al., 2024). The result of FLP is a set of best possible values for the fuzzy decision variables. It can be utilized to find out the best set of possible peers to choose for content distribution.
System model
P2P network comprising N identical peers linked by an overlay network are considered, where each peer is connected to n other peers through random links. A file slated for download is fragmented into multiple chunks in advance and these pieces are dispersed across the network at random. Initially, every peer has an equal number of pieces. The primary aim of the peers is to gather all pieces by engaging in mutual exchange of piece among themselves. Specifically, any peer is termed as a seeder upon acquiring all pieces, while a peer still in need of a piece from others is labeled as a leecher. It is elaborated using a mathematical model in this section. Assume N denotes the total number of peers in the P2P network, and n represents the fixed number of connections and each peers has within the network. The file to be downloaded is divided into M pieces in advance, and each peer starts with an equal share of P pieces initially. Hence, P can be expressed as:
(1)
In this context, a seeder is a peer that has successfully accumulated all M pieces, while a leecher is a peer that still requires at least one piece to complete the entire file. The aim for each leecher is to acquire all the missing pieces. It can be done through peer-to-peer interactions. The overall objective across the network is for all peers to transition from leechers to seeders by effectively exchanging pieces among themselves until every peer has obtained the complete file. Each peer need to maintain an adjacency matrix A, where Ajk = 1 if there is a connection between peers j and k, and Ajk = 0 otherwise. The transfer rate between any two connected peers j and k is denoted by rjk, representing the capacity of the link between them. Each leecher requests missing pieces from its connected seeders. The request is handled at random with one of the available seeders connected to the leecher. The successful probability of a piece of content transfer between a seeder and a leecher is represented by pjk, where pjk = 0 if there’s a unsuccessful transfer and pjk = 1 otherwise.
The probability pjk rely on various factors such as congestion of network, latency, and connection stability, among others at any given point of time. The expected time for a leecher to attain any missing piece from a seeder is represented using probability theory. Suppose Tjk represents the time taken for leecher j to download a piece from seeder k. Then the expected time E[Tjk] is formulated as given below:
(2)
The expected time to be a seeder from leecher, for instance collection of all missing pieces, is influenced by the number of connected seeders, transfer rates, and the success probabilities of piece transfers at any time slot. A complete model considering these factors is able to predict the time taken for the entire network to evolve as seeders from leechers. Even though, this model’s complexity rises with the number of peers, connections, and other dynamics of network. The modeling and derivation is further extended by integrating dynamic nature of network, probabilistic rate of transfer, and interaction patterns among the peers to make a more comprehensive model capturing the evolution of seeders from leechers over the period of time in a P2P network for content dissemination. Consider a dynamic nature of P2P network where dynamics of network persuade the transfer rates rjk and the success probabilities pjk between peers. These dynamics may consist of varying capacities of link, connectivity changes in peer, fluctuations in network congestions, and also time varying latency. The rate of transmission rjk among peers j and k is affected by factors such as availability of bandwidth, network congestion and also conditions at the time of transfer. A dynamic model for rjk is given as a function of time, represented as below:
(3)
Correspondingly, the probability of success pjk for piece transfer is defined as probabilistic because of fluctuations in network conditions and behavioral change in peer. This probability may vary over time appropriate to factors like network stability, packet loss, and availability of peer:
(4)
Also, the interaction patterns among the peers influences the process of peer selection and as a result persuade the time for leechers to accomplish download missing pieces. This interaction pattern entails preferences among peers like preference on high-speed connections or favoring peers with the past successful transfers. A comprehensive model which captures the progression of leechers to seeders over the period of time in this dynamic network would involve time-dependent functions to characterize the changing rate of transfer and probabilities of success. The Monte Carlo simulation modeling technique is used to simulate the interactions among peers, the distribution of file, and the evolution of peers from leechers to seeders. By integrating dynamic nature of network, probabilistic transfer rates, and interaction patterns among peers, such a model envisage the time evolution of content distribution. It consider network variations and behavior change of peer over period of time. The complexity of this model would be high due to the dynamic nature of the network and they need to account for various network conditions and interactions among the peers. Suppose Lj(t) denotes a number of missing pieces in peer j and it needs to become a seeder at time t, and Sj(t) as the number of pieces peer j has already collected. The rate at which peer j attains missing pieces is given by the sum of successful transfer of pieces from other peer k to peer j at time t, is given as follow.
(5)
This equation signifies the rate of change in the number of missing pieces for peer j relies on the successful transfers from other peer k to j, assuming the missing pieces at k and the pieces j has already received. Figure 2 shows the system model.
Figure 2: System model.
Proposed system
Our method addresses the complexity and unpredictability of network conditions in by integrating fuzzy logic into the decision-making process. Peer characteristics in traditional P2P content sharing include reliability, latency, and bandwidth, and these changes over time. These are making the process of consistent and effective peer selection more challenging. By incorporating fuzzy logic, it is possible to model these uncertainties and make the decisions with regard to network conditions changeable. This methodology is more practical and realistic compared to the conventional deterministic approaches. The FLP technique involve to formulate a mathematical model which captures the relationship among the decision variables for peer selection and the objective function includes download speed and other set of parameters. The FLP technique involves formulating a mathematical model which captures the relationship among the decision variables for peer selection and the objective function includes download speed and other set of parameters. The model also includes constraints which limit the feasible and optimal values of the decision variables. In order to obtain a solution to the FLP model, fuzzy logic is used to characterize the vagueness and imprecision associated with the data. The model is then resolved using linear programming techniques such as the simplex technique to obtain the optimal solution. It minimizes the objective function with subject to the some of the chosen constraints.
FLP model
The proposed peer selection method is formed using mathematical model by modifying the standard model to combine fuzzy sets as well as fuzzy arithmetic. The model consists of the following important elements:
Peers or nodes: Let P = {p1, p2, …, pn} used to indicate the set of available peers in the network at any point of time. Each peer pi contains a local cache of video content C(pi) and has some certain speed of downloading the video content v(pi).
Content: Let C = {c1, c2, …, cm} used to represent the set of video content in the network to be downloaded. Each piece of video content ci is segmented into k chunks and located on several peers in the network. The availability of chunk j of video content ci on peer pi is used to denote a fuzzy variable A(pi, ci, j) which captures fuzzy values representing the degree of availability.
Network topology: Let G = (P, E) used to represent the graph containing the connections among the available peers in the network. Each edge e in E used to denote a direct link among any two peers.
Peer selection algorithm: Let S(pi, ci) are the fuzzy set of available candidate peers from which peer pi can download chunk ci of video content. The suitability of peer pi for downloading chunk ci is used to symbolize the fuzzy variable S(pi, ci). It takes fuzzy values denoting the degree of suitability.
Optimization objective: The objective of the proposed model is to minimize the time to attain total download for a given set of video content. Let T(pi, ci, j) used to denote the time it takes for peer pi to download chunk j of video content ci. The total time needed to download entire content can be formulated using fuzzy arithmetic as given below.
(6)
Subject to:
-
➢
A(pi, ci, j) ∈ F: It represents the availability of chunk j of video content ci on peer pi, where F is set of fuzzy sets.
-
➢
Σ pi A(pi, ci, j) ≥ r(ci, j): As a minimum r(ci, j) peers need to have chunk j of video content ci for the video content to be considered as available with help of fuzzy IF-THEN rules.
-
➢
T(pi, ci, j) = k x s(ci)/v(pi): it is used to represent the time needed for any peer pi to download chunk j of video content ci, where k symbolizes the size of the chunk, and s(ci) is the size of video content ci.
-
➢
S(pi, ci) ∈ F: The suitability of peer pi for downloading chunk ci of video content, where F denotes the set of fuzzy sets.
-
➢
Σ pi Σ ci A(pi, ci, j) x s(ci) ≤ d(pi): The total amount of video content downloaded by any peer pi cannot go beyond its download limit d(pi).
-
➢
Σ pi Σ ci A(pi, ci, j) ≥ b(ci, j): At least b(ci, j) chunks of video content ci must be downloaded by set of peers to ensure no redundancy and some reliability, using fuzzy IF-THEN rules.
The fuzzy sets A(pi, ci, j) and S(pi, ci) is defined using linguistic variables such as “high,” “medium,” and “low.” The fuzzy measure μ is selected based on the desired aggregation method, such as max-min or max-product. By including fuzzy sets and fuzzy arithmetic, FLP offers more flexible and robust technique for peer selection and better reflecting the real-world variability of network conditions and peer behavior.
Convert FLP to LP
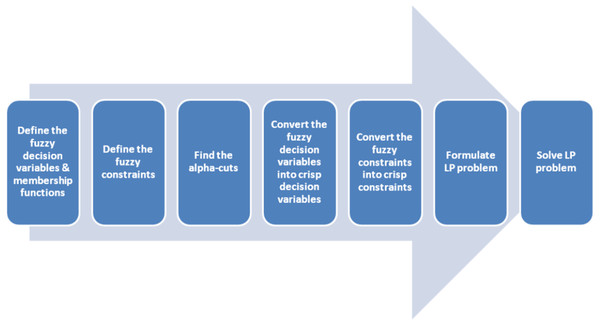
The FLP problem for the peer selection is transformed into an equivalent LP problem using alpha-cuts. Alpha-cuts are used then to transform the fuzzy constraints and fuzzy decision variables into crisp constraints as well as variables which can be utilized in a standard LP problem (Zhang et al., 2024). The following algorithm is used to translate the FLP problem to an LP problem.
The above steps are iterated until the solution is satisfactory one. The alpha-cuts must be adjusted based on the degree of uncertainty and also imprecision in the fuzzy decision variables and constraints (Wang et al., 2023). The resulting LP problem offers a flexible and also efficient technique to the problem of peer selection. Figure 3 represents the steps involved in FLP.
Figure 3: FLP steps.
Alpha cut
In FLP for the problem of peer selection, alpha-cuts are used to translate the fuzzy constraints into crisp constraints. It can be resolved using standard LP algorithms. An alpha-cut is used to depict the level of certainty that describes a crisp set from a fuzzy set. It indicates the minimum degree of membership that an element must include in the fuzzy set need to be incorporated in the crisp set (Nasseri, Verdegay & Mahmoudi, 2021). For example, suppose fuzzy decision variable y that represents the degree to which a peer is selected and its membership function is defined as:
(7)
This membership function indicates that the membership degree of peer i being chosen can be in the range between 0 and 1, with values that are more likely to be chosen having a higher membership degree. A level of confidence known as the alpha level is chosen, and only those elements of the fuzzy set whose membership degree is at least equal to the alpha level are taken into consideration in order to convert this fuzzy constraint into a crisp constraint using alpha-cuts. For example, suppose an alpha level of 0.5 is chosen. Then the corresponding alpha-cut for the fuzzy decision variable y would be:
(8)
| Consider fuzzy decision variables represent the suitability of peers S(pi,ci) and fuzzy constraints based on availability and other criteria. |
| - Input: |
| - - Fuzzy decision variables and also their membership functions |
| - - Fuzzy constraints based on criteria for selection |
| - - Alpha value for alpha-cuts (0 <= α <= 1) |
| - Output: |
| - - Corresponding Linear Programming Problem (LP) |
| Step 1: Describe Fuzzy Decision Variables and Membership Functions |
| Describe the fuzzy decision variables S(pi,ci) denoting the suitability of each peer pi to download video content ci. Consider the membership functions μSi(s) for each fuzzy decision variable. |
| Step 2: Define Fuzzy Constraints |
| Fuzzy constraints based on the availability and other criteria are described. Assume fuzzy constraint A(pi,ci,j) describing the availability of chunk j of video content ci on peer pi with membership function μAij(a). |
| Step 3: Determine Alpha-Cuts |
| For each fuzzy decision variable as well as constraint, find out alpha-cuts using the specified alpha value in the range between 0 and 1 such as 0 ≤ α ≤ 1. |
| For fuzzy decision variable Sα(pi,ci) = {s | μSi(s) ≥ α} |
| For fuzzy constraint Aα(pi,ci,j) = {a | μAij(a) ≥ α} |
| Step 4: Translate Fuzzy Decision Variables into Crisp Decision Variables |
| Find out crisp decision variables based on alpha-cuts using inverse membership functions given below |
| s = μSi−1(α) |
| Step 5: Translate Fuzzy Constraints to Crisp Constraints |
| Find the crisp constraints using alpha-level set and also membership functions. For fuzzy constraint A(pi,ci,j) with alpha-cut Aα(pi,ci,j): |
| amin = min(Aα( pi,ci,j)) and amax = max(Aα(pi,ci,j)) |
| Step 6: Formulate Equivalent LP Problem |
| Devise the equivalent LP problem using crisp decision variables as well as constraints: |
| Minimize cT⋅y |
| Subject to Ay ≤ b |
| sminimum ≤ s ≤ smaximum and aminimum ≤ A(pi,ci,j) ≤ amaximum |
This alpha-cut states that the peer i is either completely chosen (membership degree is equal to 1) or completely not chosen (membership degree is equal 0) for the alpha level of 0.5. In other words, it offers a crisp set of peers that can be utilized in the crisp LP problem. By changing the alpha level from 0 to 1, family of alpha-cuts which offer different levels of certainty in the fuzzy decision variable y is attained. These alpha-cuts is then used to solve the FLP problem and reach a fuzzy solution. It denotes the degree to which each peer is chosen at different levels of certainty. Let us assume the availability constraint:
Consider the membership function for availability is defined by a triangular fuzzy set with a peak at 500 KB/s, and a base extend from 300 to 700 KB/s. To convert this constraint into an LP constraint, alpha-cuts is utilized. For example, if an alpha value of 0.7 is chosen, then the corresponding interval for the availability constraint is 460, 540 KB/s. It means that for all peers whose upload rate drops within this interval, their membership degree for availability is at least 0.7. Similarly, the alpha-cuts are determined for the other fuzzy decision variables and constraints. These alpha-cuts are used to construct the equivalent LP problem which can be solved using standard LP techniques. The choice of alpha value relies on the degree of uncertainty and imprecision in the fuzzy decision variables and also constraints, and can be adjusted accordingly to attain a satisfactory solution.
Solve LP after convert from FLP
Obtain the LP problem for the FLP approach to the peer selection problem in P2P CDN involves finding the optimal combination of peers which are all maximize the efficiency of content distribution at the same time satisfying the selection criteria. The LP problem is devised by converting the fuzzy constraints and also decision variables into crisp constraints and variables using alpha-cuts, as described in previous section. The common steps for solving an LP problem are given below.
Devise the LP problem: Define the decision variables, objective function, and constraints for the problem in terms of linear expressions.
Translate the LP problem into standard form: Revise the LP problem so that all constraints are equations, all decision variables are non-negative, and the objective functions is to be maximized or minimized.
Use simplex algorithm: Employ the simplex algorithm to iteratively resolve the LP problem by moving along the edges of the viable region until the optimal solution is reached.
Infer the solution: Once the optimal solution is found, deduce the solution in terms of the decision variables and constraints, and determine if the solution suits the original problem statement.
The exact LP problem formulation and solution approach rely on the specific selection criteria and fuzzy decision variables and also constraints used in the FLP (Rivaz, Nasseri & Ziaseraji, 2020; Zhang, 2024). Once the LP problem is devised, it can be converted to standard form and resolved using the simplex algorithm to attain the optimal combination of peers which maximizes the efficiency of content distribution at the same time satisfying all the selection criteria.
Fuzzy decision variables
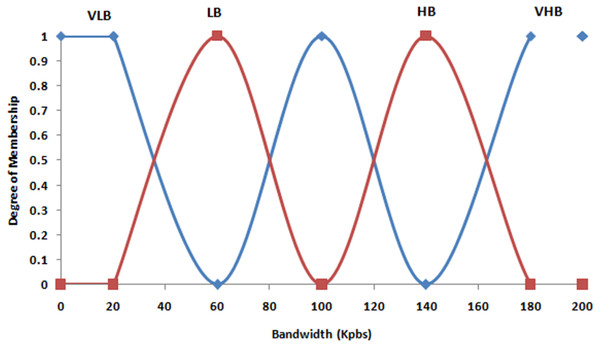
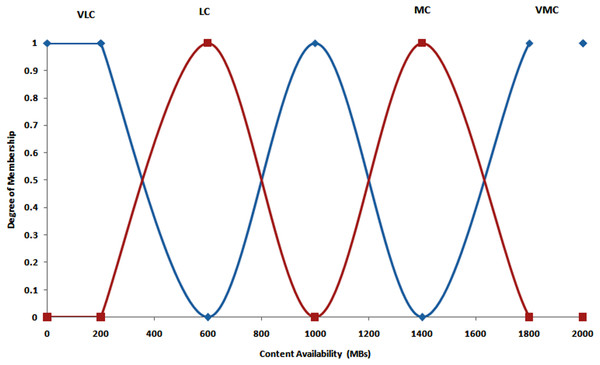
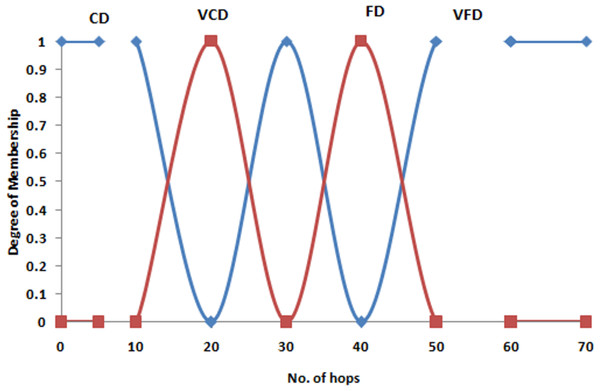
Optimization of peer selection in P2P CDN involves considering several factors for efficient distribution of content among the peers. Fuzzy variables are used to represent imprecise and uncertain aspects of these factors (Anandaraj et al., 2024). These fuzzy variables symbolize the variations and uncertainties related with peer characteristics. Fuzzy logic and fuzzy sets are used in those variables for more accurate modelling and optimizing the processes of peer selection. It is used to consider the vague and dynamic nature of network conditions and peer attributes. These variables are incorporated into an optimization model which permits for better decision making in selection of optimal peers for content distribution in P2P networks. The process of fuzzification is used to illustrate the crisp input variables, bandwidth (Bw), availability of content (Ca), and distance measure or proximity value (Dm), by using membership functions (MFs) and also linguistic terms. Then these variables are standardized within the ranges of [0 to 200], [0 to 2,000], and [0 to 70] correspondingly. The MFs selection is subjective by the linguistic terms with related to the output values. For instance, trapezoidal MFs are suitable and ideal when a range of values result in smallest number of changes, while triangular MFs are more suitable when there’s a gradual change. Non-overlapping MFs are selected for sensitivity to changes in input variables, contrasting with overlapping MFs; in particular, bandwidth is described by five MFs denoted as very low bandwidth (VLB), low bandwidth (LB), medium bandwidth (MB), high bandwidth (HB), and very high bandwidth (VHB). VLB and VHB are modelled using left-right open-sided trapezoidal MFs, while LB, MB, and HB are represented by triangular MFs as depicted in Fig. 4. content availability (CA) is characterized by five MFs with linguistic terms very low (VLA), low (LA), moderate (MA), high (HA), and very high (VHA). In this context, SD and LD are represented by left and right open-sided MFs respectively, while AD is modelled using trapezoidal MFs, demonstrated in Fig. 5. The distance measure (DM) employs five MFs denoted as very close (VL), close (L), moderate (M), far (F), and very far (VF). These MFs are illustrated in Fig. 6, using a combination of open-sided and trapezoidal shapes to represent different degrees of proximity or distance.
Figure 4: Fuzzified input variables-bandwidth availability.
Figure 5: Fuzzified input variables-content availability.
Figure 6: Fuzzified input variables-distance measure.
Calculate the optimal fuzzy decision variables
Calculating the optimal fuzzy decision variables for the FLP approach to the problem of peer selection in P2P CDN involves solving the LP problem and then applying alpha-cuts to convert the crisp decision variables back into fuzzy variables. An example of optimal fuzzy decisions variables calculation using the FLP approach for the problem of peer selection in P2P CDN is given below:
-
1.
Describe the membership functions for the fuzzy decision variables xi, which represent the degree to which each peer i is chosen:
(9)
-
2.
Alpha-cuts are used to translate the fuzzy constraints into crisp constraints:
For each alpha-cut level α:
Availability constraint is represented as ∑(degree of membership for peer i for availability at α) * (upload rate of peer i) * xi >= (availability requirement for the content at α)
Proximity constraint is represented as ∑(degree of membership for peer i for proximity at α) * (upload rate of peer i) * xi >= (proximity requirement for the content at α)
Reliability constraint: ∑(membership degree of peer i for reliability at α) * (upload rate of peer i) * xi>= (required reliability for the content at α)
Bandwidth constraint: ∑(membership degree of peer i for bandwidth at α) * (upload rate of peer i) * xi<= (total available bandwidth for the content at α)
-
3.
Solve the crisp LP problem to obtain the optimal values of the binary decision variables xi.
-
4.
Calculate the alpha cuts for the optimal fuzzy decision variables by evaluating the membership functions at the optimal values of xi. For example, if the optimal values of xi are [0, 0, 1, 1, 0, 1, 0], the alpha-cuts can be calculated as follows:
-
α = 0.1:xi = {0, 0, 1, 1, 0, 1, 0}
-
α = 0.2:xi = {0, 0, 1, 1, 0, 1, 0}
…
-
α = 0.9:xi = {0, 0, 1, 1, 0, 1, 0}
-
α = 1.0:xi = {0, 0, 1, 1, 0, 1, 0}
The resulting alpha-cuts represent the degree to which each peer i is selected at each level of certainty, ranging from 0.1 to 1.0. The formulation of LP problem and solution will rely on the exact selection criteria and fuzzy decision variables as well as constraints used in the FLP technique. The LP problem formulation for the problem of peer selection and alpha cuts for the fuzzy decision variables xi is described as follow.
x_0 = [0, 0, 0.2, 0.8, 1, 1, 1]
x_1 = [0, 0.2, 0.8, 1, 1, 1, 1]
x_2 = [0, 0.1, 0.7, 0.9, 0.9, 0.9, 0.9]
x_3 = [0, 0, 0, 0.2, 0.6, 0.8, 1]
x_4 = [0, 0, 0, 0, 0.1, 0.7, 0.9]
x_5 = [0, 0, 0, 0, 0, 0.2, 0.8]
x_6 = [0, 0, 0, 0, 0, 0, 0.3]
Those alpha cuts specify the membership degree of each peer i with the relevant fuzzy decision variable xi. The alpha cut for x_1 represents that peer1 has zero membership for being chosen when xi contains low value and full membership when xi contains high value. Using those alpha cuts, the LP problem can be resolved to reach the optimal crisp decision variables for the problem. Let us consider the optimal solution is specified below:
x_0* = 1
x_1* = 1
x_2* = 0.9
x_3* = 0.6
x_4* = 0.1
x_5* = 0.2
x_6* = 0
In order to obtain the feasible and optimal fuzzy decision variables, it is necessary to associate the alpha cuts to each crisp variable to attain a range of values. For instance, the alpha cut for x_1* reveals that peer1 has full membership for being chosen whenever xi is high, and zero membership whenever xi is low.
Proposed algorithm
| Input: |
| Set of all peers in the P2P network (Peers) |
| Peer’s performance and reliability metrics (Performance, Reliability) |
| Fuzzy linear programming model parameters (Constraints, Weights) |
| Output: |
| Selected set of peers to distribute the video content (SelectedPeers) |
| Procedure PeerSelection(Peers, Performance, Reliability, Weights, Constraints) |
| Initialize an empty set SelectedPeers |
| Fuzzy linear programming |
| for each peer in Peers do: |
| Calculate the performance score (P_score) for the peer using the given metrics |
| Calculate the reliability score (R_score) for the peer using the given metrics |
| Apply fuzzy logic to calculate fuzzy performance score (Fuzzy_P_score) |
| Apply fuzzy logic to calculate fuzzy reliability score (Fuzzy_R_score) |
| Fuzzy linear programming optimization |
| f or each peer in Peers do: |
| Define the optimization problem using fuzzy linear programming model: |
| Maximize Σ_i (Weights[i] * Fuzzy_P_score[i]) + Σ_i (Weights[i] * Fuzzy_R_score[i]) |
| Set the objective function based on the fuzzy performance and reliability scores |
| Add constraints based on the given constraints and weights: |
| Σ_i (Weights[i] * P_score[i]) ≥ Constraints[1] |
| Σ_i (Weights[i] * R_score[i]) ≥ Constraints[2] |
| Solve the fuzzy linear programming problem to reach the optimal solution |
| Selection of peers based on the optimal solution |
| for each peer in Peers do: |
| if the peer is selected based on the optimal solution then |
| Add the peer to the SelectedPeers set |
| return SelectedPeers |
| End Procedure |
Pseudocode framework
Step 1: Initialize the system and define peer set
Input:
Set of peers, P = {P1, P2, …, Pn}
Parameters for each peer Pi:
- Bandwidth (Bw_i): Fuzzy value with membership function μ(Bw_i)
- Latency (Lat_i): Fuzzy value with membership function μ(Lat_i)
- Reliability (Rel_i): Fuzzy value with membership function μ(Rel_i)
Define acceptable thresholds for each parameter:
- Minimum acceptable bandwidth (Bw_min)
- Maximum acceptable latency (Lat_max)
- Minimum acceptable reliability (Rel_min)
Step 2: Define the fuzzy membership functions
For each parameter:
- Define membership function for bandwidth μ(Bw) with fuzzy thresholds.
- Define membership function for latency μ(Lat) with fuzzy thresholds.
- Define membership function for reliability μ(Rel) with fuzzy thresholds.
Step 3: Set up the Fuzzy Linear Programming (FLP) Model
Objective:
Maximize the overall score for peer selection, Score(Pi), defined as a weighted sum:
Score(Pi) = w1 * μ(Bw_i) + w2 * μ(Lat_i) + w3 * μ(Rel_i)
where w1, w2, w3, w4 are weights assigned to each parameter based on importance.
Constraints:
- Assure each selected peer meets the minimum requirements with fuzzy constraints:
μ(Bw_i) ≥ μ(Bw_min)
μ(Lat_i) ≤ μ(Lat_max)
μ(Rel_i) ≥ μ(Rel_min)
Step 4: Define Linear Constraints with Fuzzy Parameters
For each constraint, translate the fuzzy requirements to linear inequalities using α-cuts:
- Define α as the level of satisfaction such as α = 0.8.
- Convert fuzzy parameters to α-cut crisp intervals:
Bw_min_α = interval for bandwidth at level α
Lat_max_α = interval for latency at level α
Rel_min_α = interval for reliability at level α
- Update constraints as follows:
Bw_i ≥ Bw_min_α
Lat_i ≤ Lat_max_α
Rel_i ≥ Rel_min_α
Step 5: Solve the Fuzzy Linear Programming Model
Initialize:
- Selected peers list S = {}
- For each peer Pi in P:
- Find Score(Pi) based on fuzzy membership values and weights
- Calculate_alpha_cut(min, opt, max, alpha)
- If Pi meets all α-cut constraints:
- Add Pi to S if Score(Pi) is higher than threshold
Output:
- Selected peers S with maximum Score(Pi)
Step 6: Return Optimal Peer Set
Return the peer set S which maximizes the video content distribution quality.
Function calculate_alpha_cut(V_min, V_opt, V_max, alpha):
Calculate the lower bound of the α-cut interval
V_low = V_min + alpha * (V_opt - V_min)
Calculate the upper bound of the α-cut interval
V_high = V_max - alpha * (V_max - V_opt)
Return the interval [V_low, V_high]
Return (V_low, V_high)
End Function
Function Calculate_Score (Pi, Performance_Metrics, Reliability_Metrics, Weights)
Extract Raw Performance and Reliability Values for the Peer
Raw_Bandwidth = Performance_Metrics[Pi][“Bandwidth”]
Raw_Latency = Performance_Metrics[Pi][“Latency”]
Raw_Stability = Reliability_Metrics[Pi][“Stability”]
Raw_Availability = Reliability_Metrics[Pi][“Availability”]
Determine the Raw Performance Score (P_score) Based on Performance Metrics
Here, it is assumed that Performance is based on Bandwidth and Latency
Normalize these values if needed and combine them into a single score
Assuming higher Bandwidth and lower Latency are preferred:
P_score = (Weight_Bandwidth * Raw_Bandwidth) - (Weight_Latency * Raw_Latency)
Normalize P_score to a 0-1 scale if necessary, depending on range
P_score = normalize(P_score, min=0, max=100) # Example normalization function
Compute the Raw Reliability Score (R_score) Based on Reliability Metrics
Assuming Reliability is based on Stability and Availability
Higher Stability and Availability values are ideal.
R_score = (Weight_Stability * Raw_Stability) + (Weight_Availability * Raw_Availability)
Normalize R_score to a 0-1 scale if necessary
R_score = normalize(R_score, min=0, max=100)
Apply Fuzzy Membership Functions to Calculate Fuzzy Scores
The fuzzy membership functions (μ_Performance and μ_Reliability) determine the fuzzy satisfaction level
for each raw score. Membership functions is trapezoidal based on requirements.
Fuzzy_P_score = apply_fuzzy_membership(P_score, “Performance”)
Fuzzy_R_score = apply_fuzzy_membership(R_score, “Reliability”)
Determine the Weighted Score for Each Fuzzy Metric
weights for Performance and Reliability to compute the final weighted score.
Weighted_Fuzzy_P_score = Weights[“Performance”] * Fuzzy_P_score
Weighted_Fuzzy_R_score = Weights[“Reliability”] * Fuzzy_R_score
Combine Weighted Scores to Get the Final Score for Peer Pi
Score_Pi = Weighted_Fuzzy_P_score + Weighted_Fuzzy_R_score
Return Score_Pi
End Function
Performance comparison
Simulation using SciPy
SciPy is a popular open source library in Python programming language which is especially developed to offer robust and friendly numerical algorithms for a large number of scientific and mathematical computations. NumPy is the base from which SciPy is developed further to include higher level materials specialized to do scientific computations. These include optimization, integration, interpolation, eigenvalues, algebraic and differential equation solving and statistical analysis advanced modules. Another of SciPy’s main advantages is that it has a lot of reliable and specific data structures. For example, it supplies sparse matrices, which are useful for working large data sets containing many zeros and k-dimensional trees (kd-trees) to support the spatial search. These structures make SciPy particularly suited for applications in machine learning, data science, physics, and engineering. SciPy’s implementation wraps around low-level, highly optimized code written in languages like Fortran, C, and C++, delivering computational performance close to native code while retaining the flexibility of Python. This combination enables developer to do lots of numerical computation while at the same time to do it efficiently. As such, SciPy is used in academia, research, as well as in industries because fast and accurate scientific computing is critical.
Simulation settings
The performance evaluation of proposed system is done with help of implementing the system with SciPy. SciPy is an important module of Python environment that has specific application in scientific computing especially in the context of optimization process. It is suitable to simulate the problems related to selection of peers in P2P networks. In the distribution of video content, many peers are involved and they have different values for bandwidth, reliability, and latency, hence identifying the best set is a difficult task. The simulation is done to vary the nodes from 100 to 600 in the network. In terms of assessing the performance of the proposed work, parameters such as download time, download completion rate and overhead on the network have been employed. At the time of simulation, the majority of the links are defined to be an ADSL by fixing less upload bandwidth than download bandwidth. The simulation parameters are given in Table 1, and the utilization of uplink and downlink bandwidth is shown in Table 2. Download bandwidth and upload bandwidth is assumed to be in terms of Mbps. This is where a fuzzy linear programming approach comes in. Because of the vagueness associated with this peer attributes, fuzzy logic is used to map them to fuzzy sets that approximate the suitability of the peers to distribute content (Villacorta et al., 2017). The optimization problem is based on these scores, which indicate how well each peer in a network satisfies a particular requirement. This optimization challenge is then resolved using SciPy’s optimize module, most especially with the linprog function. While network limitations, such as the minimum bandwidth, the maximum tolerable latency, and the number of peers to be selected, are specified as either equality or inequality constraints, fuzzy scores are employed as the objective function coefficients in the linear programming model. In order to evaluate the performance of the proposed system, traditional peer selection algorithms mentioned in the previous section is used. It is performed through the following measures.
| Parameter | Value |
|---|---|
| Connection type | ADSL |
| Bandwidth availability | 2 mbps |
| File size | 1 Gb |
| Block size | 1 Mb |
| Neighbor peer count | 10 to 15 nodes |
| Number of nodes | 100 to 600 nodes |
| Bandwidth for download (Mbps) | Bandwidth for upload (Mbps) | Number of active nodes |
|---|---|---|
| 128 | 128 | 50 |
| 256 | 128 | 50 |
| 384 | 256 | 50 |
| 512 | 256 | 100 |
| 640 | 256 | 100 |
| 1,280 | 384 | 100 |
Download time: It is a time required to download the necessary chunk of video content and it is a crucial measure to assess the performance of the peer selection algorithm. It’s measured in milliseconds (ms).
Download completion rate (DCR): It is another significant measure to assess the performance of the peer selection mechanism. FLP is used to help in selecting the best possible and available set of peers to download a desired chunk of content, reduces the probability of partial or failed download.
Network overhead: It is defined as the amount of content exchanged among the peers. It is another important measure for assessing the efficiency of the selection algorithm. FLP optimize the selection of peers by minimizing the amount of redundant data transfer, lead to lower network overhead.
Availability: The availability of a peer is defined as the percentage of time the peer is online and able to send the content. Peers with low availability are not preferred since they are likely to be able to provide video content when requested.
Upload capacity: The upload capacity of a peer is the maximum amount of content which can be transferred to other peers by any peer at any particular time slot. Peers with high upload capacity need to be chosen since they are able to provide content to several peers simultaneously, reducing overall download time for all peers.
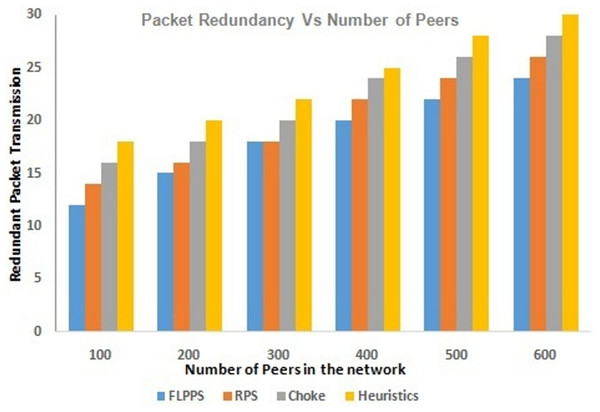
In order to use FLP to solve the problem of peer selection, each of these metrics is assigned a membership function which differentiates the degree to which each peer satisfies the metric. These membership functions is then used to construct a fuzzy linear programming problem that seeks to maximize a weighted sum of the metrics, subject to constraints on the number of peers selected and the total bandwidth available. The solution to this problem provide a set of all peers which are optimal for downloading content from, based on the specified performance metrics and their respective weights. Table 3 outlines the mean upload and downloads bandwidth utilization percentages of the network across various numbers of nodes, displaying the values for the best run of the simulation. Packet redundancy is vital performance metric. It is used to assess the effectiveness of the proposed work. The number of times slots for any particular chunk is replicated across the network is defined as packet redundancy. The proposed work aims to reduce redundant transmission of same packets by choosing the best set of possible peers to download based peer and content availability, network congestion, and replication level of the packet. The performance evaluation of the proposed framework with respect to redundant packet transmission has been done and compared the packet replication levels with that of conventional methods. The simulations have been designed to vary the number of peers, the size of content, and the network conditions at any particular time slot. Apart from analyzing the levels of packet replication, the impact of packet redundancy on other performance measures such as download time and network congestion is also evaluated. The introduced framework enhances the overall performance of the network by reducing the amount of network traffic and also enhancing the download time with help of minimizing the redundant packet transmission. The performance analysis with respect to packet redundancy is illustrated in Fig. 7. It presents insights into the efficiency of the proposed framework in controlling redundant packet transmission as well as improving the overall performance of network. In the proposed framework, download time is another significant performance measure which reflects the time taken by any of the peer to download any particular video content. The performance of this work is assessed in terms of the download time. It is the time taken by a peer to download a particular video content. The performance of the framework has been analyzed and evaluated by comparing the download time of video content with that of traditional peer selection methods as mentioned above. The simulation have been modeled and designed to change the number of peers, the size of content, and the network conditions such as bandwidth and also latency. The performance analysis with respect to download time presents insights into the effectiveness of the proposed framework in addressing the peer selection. It is represented in Fig. 8.
| Number of peers | % of utilization of upload capacity of the peers | % of utilization of download capacity of the peers | ||||||
|---|---|---|---|---|---|---|---|---|
| RPS | Choke | Heuristics | FLPPS | RPS | Choke | Heuristics | FLPPS | |
| 100 | 94.2 | 94.3 | 94.5 | 96.1 | 39.5 | 39.8 | 41.5 | 42.5 |
| 150 | 94.3 | 94.8 | 95.3 | 96.5 | 41.2 | 41.5 | 42.1 | 42.8 |
| 200 | 94.5 | 95.1 | 95.7 | 96.6 | 42.2 | 42.6 | 42.8 | 43.2 |
| 250 | 94.9 | 95.2 | 96.7 | 97.1 | 42.5 | 42.8 | 42.9 | 43.6 |
| 300 | 95.2 | 95.3 | 96.8 | 97.5 | 42.8 | 43.1 | 43.5 | 44.5 |
| 350 | 95.6 | 95.5 | 97.2 | 97.8 | 42.9 | 43.4 | 43.8 | 44.9 |
| 400 | 95.9 | 96.2 | 97.5 | 98.1 | 43.1 | 43.5 | 44.2 | 45.1 |
| 450 | 96.1 | 96.5 | 97.6 | 98.5 | 43.5 | 44.1 | 44.5 | 45.5 |
| 500 | 96.5 | 96.8 | 98.2 | 98.6 | 43.6 | 44.2 | 44.8 | 45.6 |
| 600 | 96.9 | 97.2 | 98.5 | 99.9 | 43.8 | 44.1 | 45.5 | 46.5 |
Figure 7: Packet redundancy measure.
Figure 8: Download time measure.
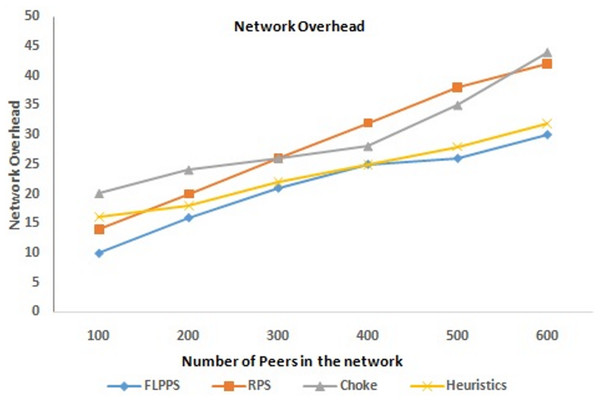
The performance evaluation of proposed work has also been done using DCR. It is depicted in Fig. 9. The ratio between the number of the chunks of content that have been successfully downloaded by end user and the total number of chunks of the entire content is defined as DCR. Therefore, a higher DCR is needed to achieve the higher performance and the proposed framework also achieves the same. The performance is also further evaluated in terms of its ability to pick the most suitable peers to approach for downloading the content. It can be carried out by analyzing the DCR for different number of peers. The average DCR in the proposed system for all the peers is higher value. The performance of a P2P CDN is enhanced by restricting the network overhead caused by peer selection process. It is illustrated in Fig. 10. The FLP based one is proved to be an efficient and feasible method to solve the problem of peer selection with respect to network overhead. It provides a simple yet effective technique for controlling the network overhead at the same time optimizing the overall performance of the network. It also allows for the selection of peers using their availability and capacity, which aids to minimize the amount of network overhead drastically. It happens since choosing the peers with high availability and also capacity at the same time network is able to disseminate the content more efficiently and quickly. The effectiveness in selecting peers is evaluated with sufficient amount of resources to contribute for content distribution by assessing the performance of the framework based on upload capacity measure. This measure provides some insights into the proposed framework’s capability to optimize and effective usage of available resources, enhances content dissemination speed, and also improves the overall performance.
Figure 9: Download completion rate measure.
Figure 10: Network overhead computation.
Statistical tests
In establishing the improvements in the proposed optimal peer selection system, statistical tests such as confidence interval and p-value tests are carried out to determine the reliability of the observed performance improvement through simulation on different runs. With the use of confidence intervals and p-values, there is a possibility to confirm externally whether the FLP-based peer selection approach indeed results in significant and real performance gains. Confidence intervals (CIs) are a statistical technique for making estimates of a range within which a specified parameter may be expected to lie at a certain level of confidence (usually 95% or 99%). Confidence intervals are useful in assessing the validity of a specific proposed approach in the sense of establishing the stability of the observed changes. Table 4 represents validation of confidence intervals on the improvements from an FLP-based approach in a P2P video content distribution network. Table 5 represents validation of p-values for the improvements from an FLP-based approach in a P2P video content distribution.
| Metric | Observed mean improvement | Standard deviation | Sample size (n) | Confidence level | Z-Score/t-Score | Confidence Interval (CI) | Interpretation |
|---|---|---|---|---|---|---|---|
| Content retrieval latency | 10 ms | 2 ms | 50 | 95% | 1.96 | [9.45–10.55 ms] | We are 95% confident that the true average latency reduction is between 9.45 and 10.55 ms. |
| Network throughput | 20% improvement | 3% | 40 | 99% | 2.58 | [18.8–21.2%] | With 99% confidence, the true throughput improvement lies between 18.8% and 21.2%. |
| Server idle time reduction | 15% decrease | 4% | 30 | 95% | 2.04 (t-score) | [13.5–16.5%] | There is a 95% confidence that the system reduces idle time by 13.5% to 16.5%. |
| Resource utilization efficiency | 25% improvement | 5% | 45 | 90% | 1.645 | [23.2–26.8%] | At 90% confidence, resource utilization efficiency gains fall within 23.2% to 26.8%. |
| Metric | Hypothesis tested | Observed test statistic | Degrees of freedom | p-value | Significance level (α) | Decision | Interpretation |
|---|---|---|---|---|---|---|---|
| Content retrieval latency | Null: No reduction in latency | 2.45 | 49 | 0.020 | 0.05 | Reject null hypothesis | The reduction in latency is statistically significant, suggesting the FLP approach improves retrieval times. |
| Network throughput | Null: No improvement in throughput | 3.10 | 39 | 0.002 | 0.01 | Reject null hypothesis | The increase in throughput is statistically significant, indicating effective optimization through the proposed method. |
| Server idle time reduction | Null: No reduction in server idle time | 1.85 | 29 | 0.075 | 0.05 | Fail to reject null hypothesis | The reduction in idle time is not statistically significant at the 5% level, suggesting variability in results. |
| Resource utilization efficiency | Null: No improvement in resource utilization | 4.25 | 44 | 0.0005 | 0.01 | Reject null hypothesis | The improvement in resource utilization is highly significant, supporting the efficacy of the FLP approach. |
Result and discussion
The use of FLP in peer selection policy in P2P content distribution networks signifies remarkable progress compared to conventional and heuristic-based techniques. Our research, which included systematic simulations and comparative evaluation, has demonstrated the effectiveness of this proposed strategy. The metrics such as download duration, download completion rate, network overhead, packet redundancy, and the utilization of upload and download capabilities are evaluated. Contrasting the traditional and heuristic mechanism, the experimental findings, as described in the previous sections, reveal that FLP-based peer selection surpass random selection of peer, choke algorithms, and several heuristic methods. FLP has consistently confirmed to enhance the download speeds and completion rates across various network sizes, spanning from the number of peers from 100 to 600. The enhancement is attributed to proposed FLP’s ability to incorporate several decision-making criteria concurrently, taking into consideration of the uncertain nature of network dynamics and peer capabilities. The impact of FLP on network overhead and packet redundancy further emphasizes its superiority. The FLP technique reduces unnecessary data transfers in the network by carefully selecting peers based on their availability, bandwidth, and storage capacity. This optimization not only minimizes the amount of data transmitted but also reduces the burden on individual peers, therefore enhancing the overall network performance and user experience. An effect on network performance metrics, the analysis of bandwidth capacity, as outlined in our simulations, reveals the FLP’s capacity to optimize the exploitation of accessible resources. Peers selection using FLP demonstrated better levels of upload and download capacity utilization in comparison to peers selected using alternative and traditional approaches. FLP minimizes packet redundancy, resulting in decreased data transfer load and mitigating bottlenecks, therefore improving the efficiency of content delivery. The implementation of FLP presents a novel method to deal with the uncertainties that naturally exist in P2P networks. It presents a well-organized yet flexible system for dealing with the several factors involved in selecting peers while also balancing efficiency and fairness in allocating available resources. Implementing the FLP based peer selection method can be used to greatly enhance the performance of P2P CDN. It is a most powerful and hopeful technique and an alternate technique for choosing peers, although it does have some drawbacks. The computational complication of solving FLP problem, mainly in broad networks, presents a difficult problem. A potential future research opportunity would be evaluating and examining the formation of more streamlined algorithms for handling FLP problems and integrating some of the machine learning techniques to forecast optimal peer selections from past historical data. Additionally, future research might explore the impact and influence the performance of other fuzzy membership functions and decision making criteria on the efficiency of the FLP framework.
Time complexity analysis of the proposed algorithm
The time complexity of the proposed approach is primarily driven by the steps of peer evaluation, FLP formulation, and solving the optimization problem. It is carried out in this section. Each peer has attributes. The fuzzy membership function for a given attribute is:
(10) where is a fuzzy membership function that maps the attribute value of peer to a membership degree . This operation is typically done using a mathematical function such as trapezoidal. The time complexity for calculating the fuzzy membership for each peer and each attribute is since it involves a simple evaluation of the fuzzy function. Thus, the total time complexity for computing the fuzzy membership values across all peers and attributes is:
(11)
For each attribute and each peer , we perform normalization as follows:
(12)
The time complexity for normalization operation is:
(13)
The objective function is typically a weighted sum of the fuzzy membership values of various attributes.
(14) where are weights for the respective attributes and are the normalized fuzzy membership values for bandwidth, latency, and availability for peer . Let the set of constraints for the linear program be defined as:
(15) where is an matrix of constraints (typically, ), is a vector of decision variables (i.e., the selection decision for each peer), is a vector of bounds for the constraints. The time complexity for formulating the FLP problem is:
(16)
Using the Simplex algorithm, the general time complexity for solving a linear programming problem is
(17)
This cubic complexity arises due to the iterative nature of solving linear programs, the matrix operations and simplex (pivoting) method.
(18)
Overall time complexity of the algorithm:
(19)
The term dominates the overall time complexity, as it is the largest term. Therefore, the overall time complexity of the algorithm is:
(20)
Granular computing
There is a possibility to enhance our research with incorporation of the granular computing-based decision models in our future work. Granular computing (GrC) is a powerful computational paradigm used to solve complex problems by breaking them down into granules where the information packets of varying sizes and also levels of abstraction. These granules are constructed based on the natural clustering of data, which is particularly useful in decision-making processes that involve imprecise, uncertain, or incomplete information. In the context of P2P networks, GrC-based models can help to manage the inherent uncertainty and heterogeneity of peers, network conditions, and resource availability. By using GrC, decision models can classify peers into various granules based on their attributes, such as bandwidth, reliability, and availability. These granules help to simplify and structure complex decision processes by abstracting the detailed peer characteristics into more manageable clusters, which allows for more effective and scalable decision-making. In P2P video content distribution, GrC-based models could improve the peer selection process by creating decision-making hierarchies that consider multiple attributes at different levels of granularity. While our current approach primarily focuses on FLP to address uncertainties, GrC-based models share a similar objective of handling complexity and uncertainty in decision-making. In future extensions of our work, GrC could be integrated with FLP to further enhance the peer selection process by creating more robust and scalable solutions that incorporate both granular abstraction and fuzzy decision-making.
Conclusion
An efficient system is introduced in this article to deal with the problem of peer selection in P2P content distribution network using fuzzy linear programming. It combines the benefits of fuzzy sets and linear programming technique to work and deal with the uncertainty and imprecision in the selection criteria along with decision variables. It also consists of a sequence of steps which converts the FLP problem to an LP problem with correct constraints using alpha cuts; then, it can be solved using typical and simple linear programming algorithms. The objective function is devised based on the fuzzy decision variables and selection criteria to exploit the efficiency of content distribution. The membership functions for the fuzzy decision variables characterize the degree to which each peer satisfies the related criterion. The framework is used to obtain solution for large scale problems with a large number of peers and some more criterions for selection. In addition, it is easily extendable to include additionally new selection criteria and also permit to modify the existing criteria. The proposed framework has the potential to address the peer selection problem in P2P content distribution network. It has the ability to enhance the performance and reliability of P2P content video distribution in network, and can be used in various contexts such as large scale file sharing, multimedia streaming, and other content delivery in networks. Efficient caching of content at some of the selected peers may reduce the load on the network and improve the delivery of content. Hence, research into optimal caching policies and replacement approaches are part of our future research in this domain.