A multi-objective path optimization method for plant protection robots based on improved A*-IWOA

Kinematic and energy consumption models of the plant protection robot

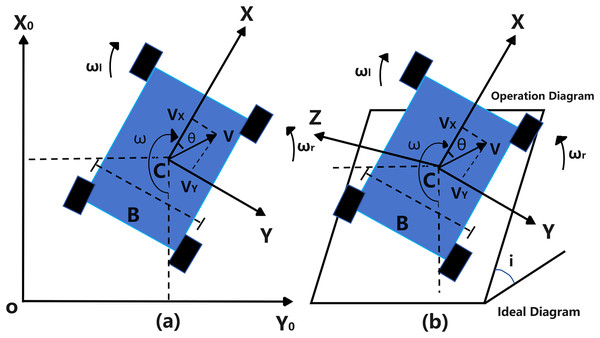
This research subject is a front-wheel differential-driven Ackermann steering plant protection robot operating in unstructured orchard environments. This robot’s coordinate system (XYZ) is defined within the geodetic coordinate system (X₀Y₀Z₀), where the X-axis points directly in front of the robot, the Y-axis points leftward, and the Z-axis is perpendicular to the robot’s moving platform, as shown in Fig. 1. Considering the effects of the robot’s operational status and orchard terrain, this study establishes kinematic state-space equations for movements along the X-axis, Y-axis, and Z-axis, as well as lateral motion around the Z-axis.

Kinematic model

This robot’s motion state variable is defined as $\mathrm{X}=\left[v_x,\mathrm{\omega }\right]$, where $v_x$ is the velocity component along the X-axis and $\mathrm{\omega }$ is the lateral angular velocity around the Z-axis. $\mathrm{U}=\left[{\mathrm{\omega }}_{\mathrm{l}},{\mathrm{\omega }}_{\mathrm{r}}\right]$is defined as control variables, where ${\mathrm{\omega }}_{\mathrm{l}}$ and ${\mathrm{\omega }}_{\mathrm{r}}$ represent the angular velocities of the left and right drive wheels of the robot, respectively. The robot’s motion state equation can be expressed as:

(1) $$\left[\begin{array}{c}{v}_x\\ \omega \end{array}\right]={\displaystyle \frac{\mathrm{r}}{B}\left[\begin{array}{c}{\displaystyle \frac{B}{2}{\displaystyle \frac{B}{2}}}\\ -11\end{array}\right]\left[\begin{array}{c}{\omega }_{\mathrm{l}}\\ {\omega }_{\mathrm{r}}\end{array}\right]}$$

(2) $$\mathrm{z}=\mathrm{\sigma }$$where r is the wheel radius of the robot, B is the track width, z is the Z-axis displacement of the robot, and $\mathrm{\sigma }$ is the road elevation.

The kinematic model of the robot, represented by the unilateral driving wheel motion state, is defined as Zhang et al. (2023):

(3) $$\mathbf{M}\ddot{\text{θ}}+\mathbf{C}(\text{θ},\dot{\text{θ}})+\mathbf{G}(\text{θ})=\mathbf{T}$$where $\text{θ}=\left[{\mathrm{\theta }}_{\mathrm{l}},{\mathrm{\theta }}_{\mathrm{r}}\right],\dot{\text{θ}}=\left[{\mathrm{\omega }}_{\mathrm{l}},{\mathrm{\omega }}_{\mathrm{r}}\right]$, and $\mathbf{T}=\left[{\mathrm{T}}_{\mathrm{l}},{\mathrm{T}}_{\mathrm{r}}\right]$.

Here, M represents the inertia matrix of the robot’s driving wheels, $\mathbf{C}\left(\text{θ},\dot{\text{θ}}\right)$ is the ground rolling resistance moment matrix of the driving wheel, and $\mathbf{G}\left(\text{θ}\right)$ is the gravity matrix of the robot. Also, $\text{θ}$ denotes the angular displacement vector for the left and right driving wheels, $\dot{\text{θ}}$ is the angular velocity vector for the left and right driving wheels, and $\ddot{\text{θ}}$ is the angular acceleration vector for the left and right driving wheels of the robot. $\mathbf{T}$ represents the output torque matrix for the left and right driving wheel motors.

The relationship between the robot’s control variable U and the output torque vector T of the driving wheels can be derived from Eqs. (1) to (3), laying the foundation for developing its energy consumption model.

Energy consumption model

The employed fully electric-driven plant protection robot uses power batteries as the power source, with the motor controller managing motor speed through pulse-width modulation (PWM) (modulation and demodulation) methods. Part of the power output of the driving motor is consumed by the internal resistance of the battery, while the remaining portion powers the robot’s moving platform.

Given the relatively low movement speed of the plant protection robot and the limited tire contact area, air resistance and rolling resistance are negligible. However, the orchard’s uneven terrain and the robot’s considerable mass mean that ramp resistance cannot be ignored (Yin et al., 2019). Therefore, this article defines energy consumption as the sum of battery internal resistance loss and robot ramp resistance loss.

With a constant robot load and motor output torque, and based on the direct proportionality between motor torque and armature current, $I_l$ and $I_r$ are considered constant values. The armature voltages for the left and right drive motors are expressed as:

(4) $$U_l=I_l{R}_B+K_M{i}_0{\omega }_l$$

(5) $$U_r=I_r{R}_B+K_M{i}_0{\omega }_r$$where $I_l$ and $I_r$ are the armature currents of the left and right drive motors, respectively, $R_B$ is the internal resistance of the power batteries, and $U_l$ and $U_r$ denote the armature voltages for the left and right drive motors, respectively. $K_M$ represents the back electromotive force coefficient of the driving motor, and $i_0$ is the transmission ratio of the motor reducer.

The power outputs of the left and right drive motors are expressed by Eqs. (6) and (7), respectively.

(6) $$P_l=U_l{I}_l$$

(7) $$P_r=U_r{I}_r$$

Substituting Eqs. (4) and (5) into Eqs. (6) and (7), the output power expressions become:

(8) $$P_l=I_l^2{R}_B+K_M{i}_0{\omega }_l{I}_l$$

(9) $$P_r=I_r^2{R}_B+K_M{i}_0{\omega }_r{I}_r$$

The internal resistance loss of the battery can thus be expressed as follows:

(10) $$Q_B=\left(I_l^2+I_r^2\right)R_B\sum _{i=1}^N{\displaystyle \frac{d{s}_i}{v_x}}$$where N is the number of state nodes in the path search node space, and $d{s}_i$ is the distance between adjacent state nodes.

Assuming the longitudinal ramp angle of the road surface is $\alpha$, the ramp resistance loss can be expressed by the following equations:

(11) $$F_i=mgtan\mathrm{\alpha }$$

(12) $$tan\mathrm{\alpha }=D\cdot {\displaystyle \frac{z_{i+1}-z_i}{d_0},z_{i+1}\ge z_i}$$where m is the total mass of the robot, ignoring mass changes during operation. The coefficient D in Eq. (12) depends on the search logic, where D = 1 is used for straight line search and D = 0 for diagonal search. $d_0$ denotes the distance between the centers of adjacent cells in a grid map.

Thus, the ramp resistance loss can be further expressed as:

(13) $$Q_i={\displaystyle \frac{mgD}{d_0}\sum _{i=1}^N\left(z_{i+1}-z_i\right){\displaystyle \frac{d{s}_i}{v_x}}}$$

By summing Eqs. (10) and (13), the robot’s energy consumption model is obtained as:

(14) $$Q=\sum _{i=1}^N\left[\mathrm{A}+\mathrm{B}(z_{i+1}-z_i\right)]{\displaystyle \frac{d{s}_i}{v_x}}$$where A and B are constant coefficients related to the robot’s structural parameters and node search logic, respectively.

An improved A^* path searching method based on the constraints of operation conditions

The A* algorithm is a heuristic search method used to find the optimal path in environments with static obstacles, searching within the robot’s motion state space (Min et al., 2021). First, it evaluates the cost at each search position to identify the state node with the lowest cost. Then, it traverses the entire state space until finding the optimal solution, at which point it terminates the search cycle.

In this heuristic search process, evaluating the cost state nodes is crucial, typically expressed by the following cost function:

(15) $$\mathrm{f}\left(\mathrm{n}\right)=\mathrm{g}\left(\mathrm{n}\right)+\mathrm{h}\left(\mathrm{n}\right)$$where f(n) is the cost function from the initial state through state n to the target state, g(n) is the actual cost from the initial state to state n in the state space, and h(n) is the estimated cost of the optimal path from state n to the target state.

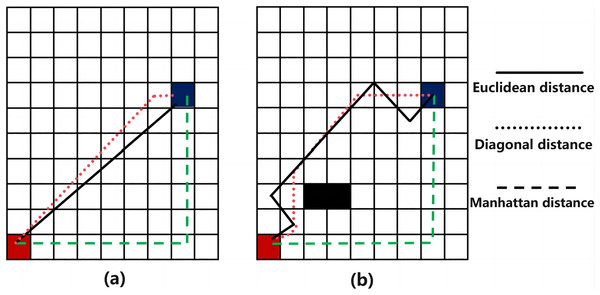
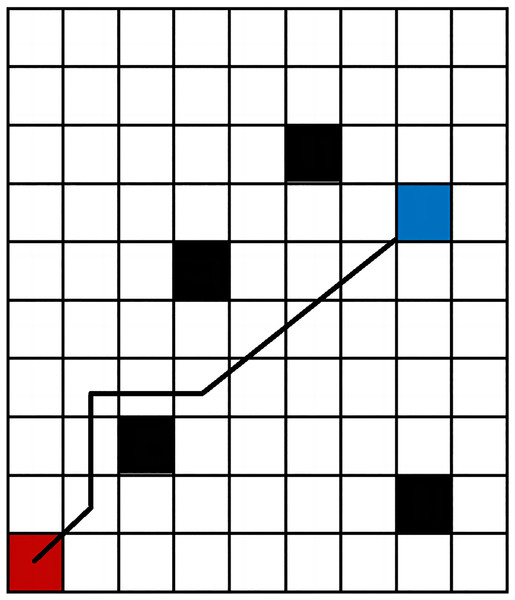
In 2D grid maps, three common h(n) functions are Euclidean distance, Manhattan distance, and diagonal distance, as illustrated in Fig. 2 (Mittelmann & Peng, 2010). While Euclidean distance is the shortest, it may reduce search efficiency in complex environmental maps. Manhattan distance offers simple logic but results in a longer path. In contrast, the diagonal distance method generally performs best in terms of both search path distance and efficiency (Shi et al., 2023), making it a preferred method for optimal path planning.

Enhancement of A^* based on the cost function of vector cross-product winning value

This study addresses the limitations of 2D grid information in describing the working environment and the high demand for computing resources of 3D-occupied grid maps using an octree structure (Wu et al., 2022). Additionally, considering that energy consumption in mountainous areas significantly impacts path selection, this article uses a 2.5D elevation grid map to better capture the robot’s working environment with higher accuracy. This approach adds height information of the grid center point in a 2D map with only horizontal and vertical coordinates, as shown in Fig. 3. Figure 3A displays the terrain conditions of the robot’s passage area with 3D grid node coordinates. Also, Fig. 3B uses hues of different grids to represent the vertical height from the horizontal plane at the grid’s center point, denoted by z_n. Hue differences indicate variations in the vertical coordinates across grid nodes, providing efficient environmental representation with lower maintenance costs and higher real-time performance. In the simulation results, the planned path obtained in a 2.5D elevation grid map differs markedly from the 2D grid environment, where the vertical height of the mountains is disregarded.

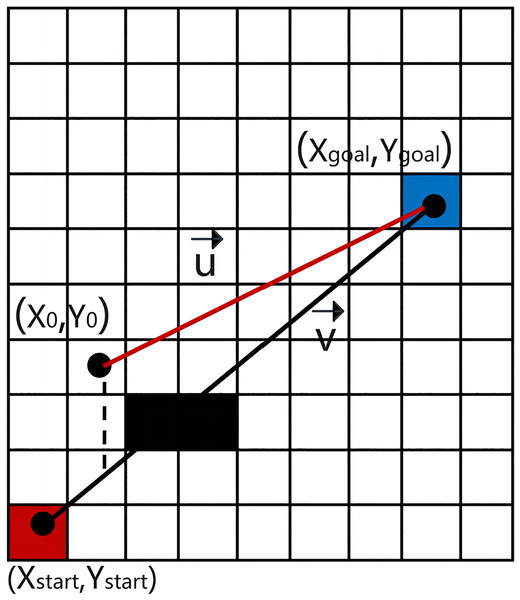
According to the 8-domain diagonal distance search method (Saadatzadeh, Ali Abbaspour & Chehreghan, 2023), a cost function with a cross-product winning value is introduced to bias the planned path toward a straight line from the initial point to the target point (Bays et al., 2024), as illustrated in Fig. 4. The specific definitions are as follows:

(16) $$\mathrm{d}\mathrm{x}1={\mathrm{x}}_{\mathrm{n}}-{\mathrm{x}}_{\mathrm{g}\mathrm{o}\mathrm{a}\mathrm{l}}$$

(17) $$\mathrm{d}\mathrm{y}1={\mathrm{y}}_{\mathrm{n}}-{\mathrm{y}}_{\mathrm{g}\mathrm{o}\mathrm{a}\mathrm{l}}$$

(18) $$\mathrm{d}\mathrm{z}1={\mathrm{z}}_{\mathrm{n}}-{\mathrm{z}}_{\mathrm{g}\mathrm{o}\mathrm{a}\mathrm{l}}$$

(19) $$\mathrm{d}\mathrm{x}2={\mathrm{x}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}-{\mathrm{x}}_{\mathrm{g}\mathrm{o}\mathrm{a}\mathrm{l}}$$

(20) $$\mathrm{d}\mathrm{y}2={\mathrm{y}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}-{\mathrm{y}}_{\mathrm{g}\mathrm{o}\mathrm{a}\mathrm{l}}$$

(21) $$\mathrm{d}\mathrm{z}2={\mathrm{z}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}-{\mathrm{z}}_{\mathrm{g}\mathrm{o}\mathrm{a}\mathrm{l}}$$

In this context, $\mathbf{u}$ and $\mathbf{v}$ represent the vector from the current point to the target point and the vector from the starting point to the target point, respectively, as represented by Eqs. (22) and (23).

(22) $$\mathbf{u}=\left(\mathrm{d}\mathrm{x}1,\mathrm{d}\mathrm{y}1,\mathrm{d}\mathrm{z}1\right)$$

(23) $$\mathbf{v}=\left(\mathrm{d}\mathrm{x}2,\mathrm{d}\mathrm{y}2,\mathrm{d}\mathrm{z}2\right).$$

To measure the deviation of the planned straight path between the current node and the starting and target points, the cross-product vector of $\mathbf{u}$ and $\mathbf{v}$ can be defined as follows:

(24) $$\mathbf{u}\times \mathbf{v}=\left[\begin{array}{ccc}\mathrm{i}& \mathrm{j}& \mathrm{k}\\ \mathrm{d}\mathrm{x}1& \mathrm{d}\mathrm{y}1& \mathrm{d}\mathrm{z}1\\ \mathrm{d}\mathrm{x}2& \mathrm{d}\mathrm{y}2& \mathrm{d}\mathrm{z}2\end{array}\right]=\left(\mathrm{d}\mathrm{y}1\ast \mathrm{d}\mathrm{z}2-\mathrm{d}\mathrm{y}2\ast \mathrm{d}\mathrm{z}1,\mathrm{d}\mathrm{z}1\ast \mathrm{d}\mathrm{x}2-\mathrm{d}\mathrm{x}1\ast \mathrm{d}\mathrm{z}2,\mathrm{d}\mathrm{x}1\ast \mathrm{d}\mathrm{y}2-\mathrm{d}\mathrm{y}1\ast \mathrm{d}\mathrm{x}2\right)$$

On this basis, the vector cross-product winning value is defined by Eq. (25).

(25) $$\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{s}=\sqrt[2]{{\left(\mathrm{d}\mathrm{y}1\ast \mathrm{d}\mathrm{z}2-\mathrm{d}\mathrm{y}2\ast \mathrm{d}\mathrm{z}1\right)}^2+{\left(\mathrm{d}\mathrm{z}1\ast \mathrm{d}\mathrm{x}2-\mathrm{d}\mathrm{x}1\ast \mathrm{d}\mathrm{z}2\right)}^2+{\left(\mathrm{d}\mathrm{x}1\ast \mathrm{d}\mathrm{y}2-\mathrm{d}\mathrm{y}1\ast \mathrm{d}\mathrm{x}2\right)}^2}.$$

The vector cross-product winning value evaluates the positional difference between two vector spaces (Wang, Wang & Liu, 2024). In this regard, the greater the overlap between the two vector spaces, the smaller this value, and conversely, the larger the value.

Thus, by incorporating the vector cross-product winning value, the cost function is redefined as follows:

(26) $$\mathrm{h}\left(\mathrm{n}\right)=1+\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{s}\ast \mathrm{p}$$where (x_n, y_n, z_n), (x_start, y_start, z_start), and (x_goal, y_goal, z_goal) are the coordinates of the current state node, the starting point, and the target point, respectively; p is the vector cross-product weight factor.

In Fig. 4, the parallelogram area formed by $\mathbf{u}$ and $\mathbf{v}$ vectors represent the cross value. It is noted here that the greater the deviation between the current path and the straight path from the start to the target, the larger the cross value becomes. According to the cost function’s tendency, path nodes are chosen in directions closer to the straight path. When the value of p is properly chosen and no obstacles are present, A* can search through fewer state regions while finding efficient paths. However, if a fixed p-value is used in the presence of many obstacles, A* may yield irregular results, as shown in Fig. 5. Therefore, in “Performance testing of the improved IWOA algorithm” below, the intelligent optimization algorithm WOA is employed to optimize the vector cross-product factor p to minimize robot operation energy consumption and path curvature.

Constraints of operation trajectory

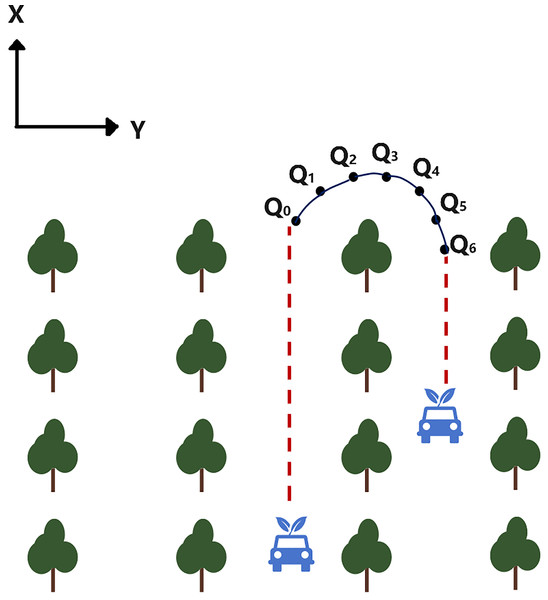
As shown in Fig. 6, the operation trajectory of the plant protection robot is divided into straight and curved segments. The search logic for the straight section is straightforward easily. Points Q₀~Q₆ in the figure represent seven consecutive state nodes within a specific curved trajectory segment, where Q₀ (x₀, y₀) and Q₆ (x₆, y₆) are the start and target points, respectively. It is noted here that Q₁ (x₁, y₁) and Q₅ (x₅, y₅) serve as segmentation points. To simplify the turning logic, the trajectory is symmetrically distributed along the center line. Adjusting the positions of Q₂ (x₂, y₂) and Q₄ (x₄, y₄) can enhance the smoothness of the trajectory. Due to the robot’s unique working environment and structural constraints, the following requirements are established for the motion trajectory in the path planning process:

(1) The curvature of any point on the trajectory is constrained to $\mathrm{\rho }\le {\displaystyle \frac{1}{{\mathrm{R}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}}$, where ${\mathrm{R}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ is the minimum turning radius of the robot.

(2) The front wheel turning angle of the robot is constrained to $\mathrm{\delta }\le {\mathrm{\delta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$, where ${\mathrm{\delta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}{\displaystyle \frac{\mathrm{L}}{{\mathrm{R}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}}$.

(3) The trajectory curvature must be continuous. To avoid situations such as sharp turns and sudden stops, it is essential to maintain a continuous curvature of the trajectory. Thus, point Q₂ should be positioned above the line connecting Q₁ and Q₃; otherwise, excessive curvature change would hinder tracking (Zhai et al., 2024). Ignoring the effects of minor elevation parameters in a 2.5D elevation grid map, the curvature continuity condition can be expressed as:

(27) $$y_2\ge {\displaystyle \frac{y_3-y_1}{x_3-x_1}\left(x_2-x_1\right)+y_1}$$

(4) The angular velocity constraints of the robot front wheel can be given by:

(28) $${\displaystyle \frac{d\delta }{dt}={\displaystyle \frac{d\left(arctan{\displaystyle \frac{2Lsin\phi }{l_d}}\right)}{dt}\le {\omega }_{max}}}$$

This study utilizes cubic B-spline curves to fit trajectories (Ardestani, Safdari & Mallah, 2023). The above trajectory constraints can be summarized as follows:

(29) $$\{\begin{array}{c}\rho \left(t\right)={\displaystyle \frac{y^{\mathrm{\prime }}\left(\mathit{u}\right)x^{\mathrm{\prime }\mathrm{\prime }}\left(\mathit{u}\right)-x^{\mathrm{\prime }}\left(\mathit{u}\right)y^{\mathrm{\prime }\mathrm{\prime }}\left(\mathit{u}\right)}{{\left(x^{\prime 2}\left(\mathit{u}\right)+y^{\prime 2}\left(\mathit{u}\right)+z^{\prime 2}\left(\mathit{u}\right)\right)}^{\frac{3}{2}}}\le {\displaystyle \frac{1}{{\mathrm{R}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}}}\\ y_2\ge {\displaystyle \frac{y_3-y_1}{x_3-x_1}\left(x_2-x_1\right)+y_1}\\ {\displaystyle \frac{d\left(arctan{\displaystyle \frac{2Lsin\phi }{l_d}}\right)}{dt}\le {\omega }_{max}}\end{array}$$where $\mathit{u}$ is the node vector of the cubic B-spline curve, $l_d$ is the robot’s forward viewing distance, and $\phi$ is the heading angle between the robot’s current position and the target point.

Multi-objective optimization of vector cross-product weight factors

Process of multi-objective IWOA based on optimal solution evaluation

The distance between any two adjacent state nodes in the robot path is given by:

(43) $$S_i=\sqrt{{(x_{i+1}-x_i)}^2+{(y_{i+1}-y_i)}^2+{(z_{i+1}-z_i)}^2}$$

During the operation of the plant protection robot, longitudinal speed changes are relatively minor and can be assumed to hold a constant value (Rahimnejad et al., 2023). Therefore, substituting Eq. (43) with Eq. (14) yields the energy consumption of the robot from the starting point to any other point:

(44) $$\mathrm{Q}=\sum _{i=1}^N\left[\mathrm{A}+\mathrm{B}(z_{i+1}-z_i\right)]{\displaystyle \frac{d{s}_i}{v_x}}$$

It is noted here that when ${\mathrm{z}}_{\mathrm{i}+1}\ge {\mathrm{z}}_{\mathrm{i}}$, $\mathrm{B}\ne 0$; otherwise if ${\mathrm{z}}_{\mathrm{i}+1}<{\mathrm{z}}_{\mathrm{i}}$, $\mathrm{B}=0$.

The general parameter equation of the trajectory curve in three-dimensional space can be expressed as:

(45) $$\mathrm{x}=\mathrm{x}\left(\mathrm{t}\right),\mathrm{y}=\mathrm{y}\left(\mathrm{t}\right),\mathrm{z}=\mathrm{z}\left(\mathrm{t}\right)$$

The curvature at any point on the robot’s operation path is expressed as:

(46) $$\mathrm{\rho }\left(\mathrm{t}\right)={\displaystyle \frac{y^{\mathrm{\prime }}\left(t\right)x^{\mathrm{\prime }\mathrm{\prime }}\left(t\right)-x^{\mathrm{\prime }}\left(t\right)y^{\mathrm{\prime }\mathrm{\prime }}\left(t\right)}{{\left(x^{\prime 2}\left(t\right)+y^{\prime 2}\left(t\right)+z^{\prime 2}\left(t\right)\right)}^{\frac{3}{2}}}.}$$

Two fitness functions are therefore established for the IWOA algorithm, as follows:

(47) $$f_1\left(x_i,y_i,z_i\right)=Q,f_2\left(x_i,y_i,z_i\right)=\mathrm{\rho }\left(\mathrm{t}\right).$$

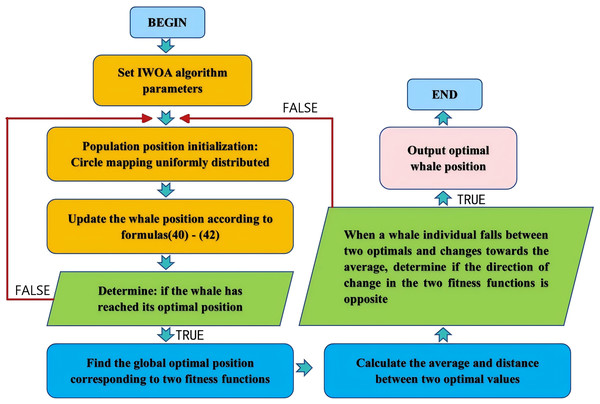
This study uses optimal solution evaluation logic to search for non inferior optimal solutions. In this optimal solution $f_1\left(x_i,y_i,z_i\right)$ and $f_2\left(x_i,y_i,z_i\right)$ change in different directions in updating. Ultimately, the whale’s position is dispersed in a set of non inferior optimal solutions, which can prevent individual fall into the optimal solution region of a certain fitness function, reflecting the constraint relationship between the two fitness functions. The specific process is shown in Fig. 7.

Experiments and analysis

The experimental subject considered in this study is a wheeled plant protection robot independently developed at the author’s university, shown in Fig. 8. As a visual sensor, the robot platform uses an OBI Zhongguang global shutter binocular depth camera with a depth frame rate of 90 fps. The 16-line LiDAR, Raytheon M10P, has a measurement radius of 30 m and a sampling frequency of 20,000 Hz. The processor is NVIDIA’s Orin Nano NX 8 GB, operating on Ubuntu 18.04 LTS, with the overall functional design based on ROS 2. The robot operates at speeds of 2–5 km/h.

To verify the robustness of the proposed algorithm in this study and the improvements in path planning for typical job scenarios, the experiment consists of three parts. First, the improvement effect of the IWOA, which dynamically adjusts a uniformly distributed population position and inertia weight in a simulation environment, was compared to several variations of the WOA: the Lévy flight based on the Whale Optimization Algorithm ((LWOA)) to optimize and update position (Zhao & Peng, 2023), the Whale Optimization Algorithm based on probability selection (MWOA) (Wei, Li & Zhang, 2023), the algorithm that combines the Harmony Search algorithm with the Whale Optimization Algorithm (HSWOA) (Li et al., 2020), the cosine adapted modified whale optimization algorithm (CamWOA) to reduce iteration step sizes (Saha et al., 2022), and the Whale Optimization Algorithm with adaptive weights (WWOA) (Cheng, Wang & Wang, 2022). Additionally, 20 comparative experiments were conducted using six typical benchmark test functions to objectively assess the robustness and effectiveness of the algorithm improvement based on the average convergence curve of the fitness function. Secondly, in a simulation environment, six environmental maps with varying starting points, target points, and obstacles’ numbers and locations were selected as testing scenarios to assess the path improvement of the A*-IWOA algorithm (Wang et al., 2022). The algorithm’s effectiveness was verified by comparing its performance with the traditional A* and RRT algorithms in terms of running time, path length, number of turning points, and energy consumption. Finally, to validate the effectiveness of the A*, RRT, standard A*-IWOA, and improved A*-IWOA algorithms, a physical experiment was conducted in a mountainous orchard in Gansu.

Performance testing of the improved IWOA algorithm

In this experiment, six commonly used benchmark test functions from the IEEE CEC benchmark test set were used, covering unimodal, multimodal, and composite functions, as presented in Table 2. The population size was set to 30, with a maximum number of iterations of 500. Since algorithm dimensionality significantly affects optimization performance, the dimensions of the six test functions in Table 2 vary from 2 to 30, providing a comprehensive test of the algorithm’s solving ability across low to high dimensions.

Figure 9 shows the average convergence curves of the fitness functions, obtained by running each of the six benchmark test functions 20 times. The f₁ and f₅ curves evaluate the algorithm’s development ability (Figs. 9A, 9B), f₈ and f₁₃ assess its search ability (Figs. 9C, 9D), and f₁₅ and f₁₇ reflect its overall optimization ability (Figs. 9E, 9F). Due to the introduction of Circle mapping for uniformly distributed population positions and inertia dynamic adjustment of weights, the algorithm better avoids local optima. The improved IWOA algorithm demonstrates superior convergence speed and accuracy in solving unimodal, multimodal, and composite functions compared to other algorithms, confirming the effectiveness of the improved algorithm.

Table 3 provides performance data summarizing the results of the test functions described above, where the optimal, worst, and average values reflect the algorithm’s optimization ability and effectiveness, while the standard deviation indicates its stability. As shown in Table 3, the improved IWOA achieved theoretical optimal values of 0 with the shortest time when solving the unimodal function f₁. For multimodal function f₁₃, the improved IWOA significantly accelerated convergence by 20% compared to other WOA variants. For composite function f₁₅, the improved IWOA randomly could calculate the changes in dimensions, and its multiple indicators approached a theoretical value of 0.1484, with a slight increase in the time consumption, yet still the fastest among the different algorithms. This indicates that the optimization performance and efficiency of the improved IWOA are significantly enhanced by dynamically adjusting the position and inertia weight of the uniformly distributed population using Circle mapping.

Path planning testing in 2.5D elevation grid map simulation

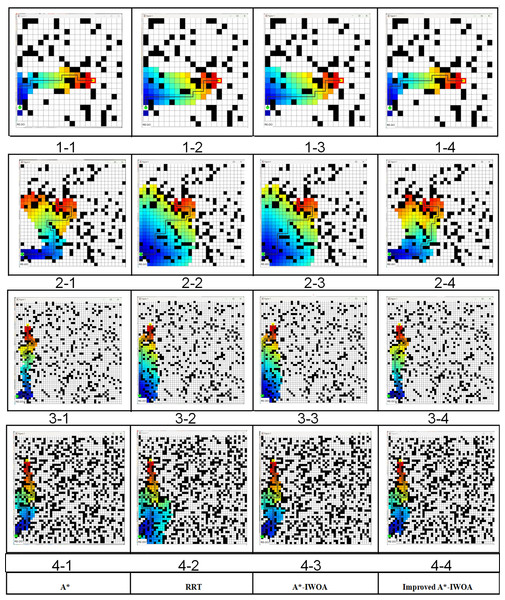
This simulation experiment was conducted on a Windows 10 system with 32 GB of memory, a 2.9 GHz CPU, and a Matlab R2021b programming workstation. The robot’s kinematic parameters and the initial settings of the improved A*-IWOA algorithm are presented in Tables 4 and 5. In this investigation, three grid maps were tested of sizes 20 × 20, 30 × 30, and 50 × 50, where each cell array represents the horizontal, vertical, and elevation values at its center point. In the simulation process, the cell elevation values were represented by the hue H value in the HSV model, where a higher hue H value indicates a greater elevation. For example, in Fig. 3, a purple cell has a higher elevation than a red cell. Following the path search logic described in this article, in the main search area of the path nodes, cell elevation values were distributed randomly for the simulation test (Akay & Karaboga, 2010; Al-Dabbagh et al., 2014). Four scenarios of plant protection robots were constructed, and the A*, RRT, A*-IWOA, and improved A*-IWOA algorithms were applied for path planning simulations, with results shown in Fig. 10.

Figures 10 (1-1)–(1-4) highlight that the occupancy rate of obstacles in the robot passage area is 20% with a grid map of 20 × 20. In Fig. 10 (2-1) to Fig. 10 (2-4), the grid map is 30 × 30 with a 20% obstacle occupancy rate. In Fig. 10 (3-1) to Fig. 10 (3-4), the grid map is 50 × 50 with a 29% obstacle occupancy rate, and in Fig. 10 (4-1) to Fig. 10 (4-4), the grid map is 50 × 50 with a 40% obstacle occupancy rate. The solid black lines represent the planned paths of each algorithm. Differences in path length, number of turning points, and calculation time among the four methods are presented in Table 6. It is noted that the improved A*-IWOA algorithm showed a notable reduction in path length, averaging 5.7%, 9.2%, and 5.1% shorter than the A*, RRT, and A*-IWOA algorithms, respectively. In terms of turning points, the improved A*-IWOA algorithm performed equally well as RRT in larger grids but outperformed other algorithms in smaller grids. In calculation time, the improved A*-IWOA algorithm was 12.2%, 20.2%, and 15.6% faster than A*, RRT, and A*-IWOA, respectively, on average.

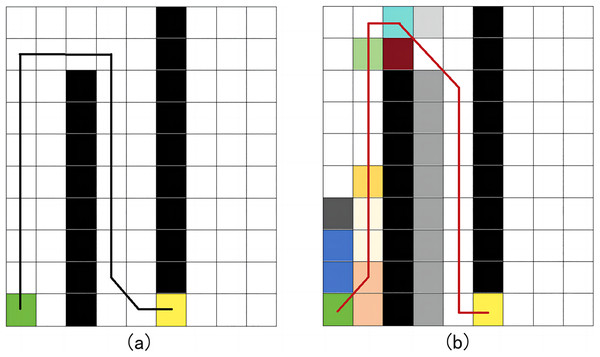
To provide a realistic representation of the inter-row working environment for fruit trees in mountainous environments, a 10 × 10 2.5D elevation grid map was used. Black obstacles represent the inter-row positions of fruit trees, and different grid colors indicate the vertical heights at their positions. The green grid marks the robot’s starting position, while the yellow grid represents the target position. Using Matlab R2021b programming workstation, the path planning effect of the improved A*-IWOA algorithm was tested on both 2D and 2.5D maps. Experimental results are shown in Fig. 11, highlighting notable differences in the planned paths. In Fig. 11B, due to the varying road surface vertical heights, the robot tends to choose and move forward with paths along lower terrain.

Experiment with robot operation path planning in a real orchard

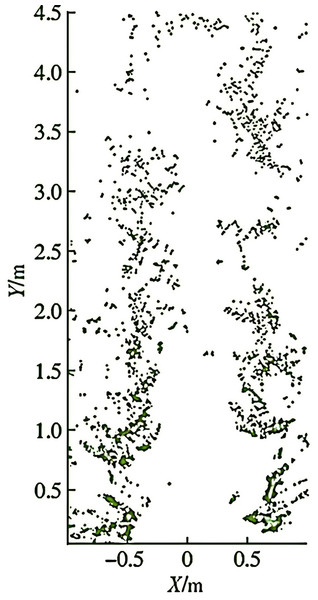
To verify the effectiveness of the improved algorithm, a physical experiment was conducted in a mountainous orchard in Gansu, as shown in Fig. 12. In this orchard, the plant spacing is 20–30 cm, and the row spacing is 70–80 cm. The altitude ranges from 500 to 1,000 m, with a relative height of no more than 200 m, and the slope is relatively gentle. This allows for adjustments to the camera and radar-ranging height of the plant protection robot, ensuring that there are at least five plants within the camera’s field of view at the robot’s speed limit. During the fruit ripening period, the orchard’s visual environment consists of green trees, red fruits, gray-brown ground, and a gray-blue sky, providing clear recognition of the machine’s mission. The K-means clustering method was used to identify the position of the main trunk of the fruit tree (as shown in Fig. 13). Additionally, the navigation line was planned by defining the communicable area through the central area. Variations in width between 70 and 80 cm had minimal impact on recognition error within the central area. In this experiment, the maximum navigation line error was 7.07 cm, the minimum error was 0.5 cm, and the average error was 3.1 cm.

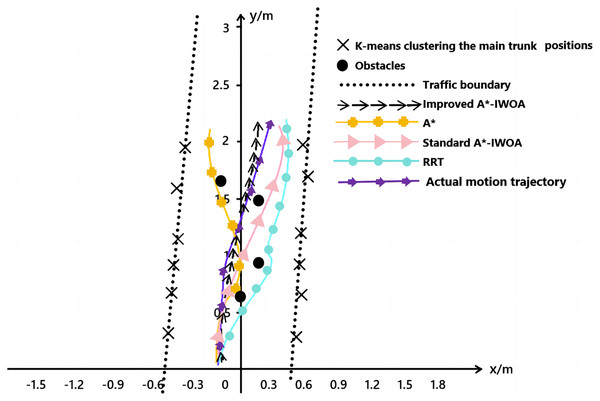
Furthermore, in the physical environment, the A*, RRT, standard A*-IWOA, and improved A*-IWOA algorithms were each loaded onto the robot ROS2 platform, and the path planning effects are shown in Fig. 14. In the figure, the cluster centers of fruit trees were extracted using the K-means clustering algorithm from the LiDAR point cloud data, and the row size of fruit trees was determined based on the least squares method, indicated by the black dotted line in the figure. The obstacle positions, based on point cloud data, are marked by black dots in the figure. It was observed that the improved A*-IWOA algorithm selected a more direct, non-detour path, while the other three algorithms chose a longer, more circuitous route around obstacles. By matching the spatial point cloud position information, the robot’s trajectory information, derived from the improved A*-IWOA algorithm, is overlaid on the image and shown by the purple line. This trajectory closely resembles the path obtained by controlling the robot between rows of fruit trees via the upper computer, demonstrating the high feasibility of the improved A*-IWOA algorithm.