Expectation maximization—vector approximate message passing based generalized linear model for channel estimation in intelligent reflecting surface-assisted millimeter multi-user multiple-input multiple-output systems

Introduction

During the past few years, there have been technological advancements and widespread availability of smart devices at affordable cost. These advancements cause gradual enhancements in the number of users connected to the internet. This trend experienced a significant boost in the aftermath of the pandemic, and it has caused congestion in the internet traffic, especially operating at the lower frequency bands (Han et al., 2015; Raghavan et al., 2016). To overcome such demands in the current scenario and to satisfy the needs of the future, researchers across the globe are exploring the potential of millimeter-wave (mmWave) frequency bands (Gao et al., 2017). However, the mmWave frequency band suffers substantial path loss. Large antenna arrays combined with mmWave technology, or massive multi-input, multi-output (MIMO) systems, are introduced to surmount this issue and ensure a higher data rate (He et al., 2018). Using a large antenna array comes with hardware complexity overhead in the form of dedicated radio frequency (RF) chain requirements and increased power consumption. Numerous studies have demonstrated that these effects can be mitigated using different beamforming techniques and an advanced lens antenna array system (Yang et al., 2018).

Intelligent reflecting surface (IRS) has been explored by many researchers because of its abilities to enhance the effectiveness of wireless communication systems. In fact, the effectiveness of wireless communication systems can further be enhanced, if we opt for the integration of IRS and the existing technologies for tackling various issues, such as channel estimation. In Pan et al. (2022), the authors work on the modelling of channel under different conditions by addressing several research issues.

The both passive IRS-aided systems and active IRS-aided systems is discussed below.

System model

In this article, we consider the uplink scenario for mmWave multi-user MIMO assisted with IRS, as shown in Fig. 1. The number of users, is represented by K. We consider uniform planner array (UPA) with M antennas. IRS is equipped with N reflecting elements, where control of these elements is given to BS (Mishra & Johansson, 2019).

In frequency division duplex (FDD), the reciprocity of channels between the uplink and downlink channels does not hold. In this article, we consider FDD scheme, and the channel between users and BS is computed in a traditional way by switching IRS elements off. The main focus is on getting the CSI of reflecting link.

$\mathbf{G}\in {\mathbf{C}}^{\mathrm{M}\times \mathrm{N}}$ is the channel between IRS and BS, and ${\mathbf{f}}_k\in {\mathbf{C}}^{\mathrm{N}\times 1}$ is the channel from the $k^{th}$ user ( $k=1,2,..,K$) to IRS.

In the uplink transmission signal model, users communicate with the BS. At BS, the received pilot signal can be written as:

(1) $${\mathbf{y}}_k\mathbf{=}{s}_k{\mathbf{w}}_k\mathbf{G}\mathbf{\Phi }{\mathbf{f}}_k+n_k,$$

${\mathbf{y}}_k$ denotes the received signal at the BS, ${\mathbf{w}}_k\in {\mathbf{C}}^{1\times \mathrm{M}}$ is a precoding vector, $s_k\in \mathbf{C}$ is the transmitted signal from the user, and ${\mathbf{n}}_k\in \mathbf{C}$ represents the additive noise. $\mathrm{\Phi }\in {\mathbf{C}}^{\mathrm{N}\times \mathrm{N}}$ represents the reflecting matrix. Assume $\mathrm{\Phi }=diag({\varphi }_1,{\varphi }_2,...,{\varphi }_N)$ representing the diagonal reflecting matrix, and ${\varphi }_n$ is the $n^{th}$ IRS element.

We set ${\varphi }_n={\beta }_n{e}^{j{\psi }_n}$, where ${\beta }_n\in [0,1]$ and ${\psi }_n\in [0,2\pi ]$. The Saleh-Valenzuela channel model is utilized for the computation of $\mathbf{G}$ and ${\mathbf{f}}_k$. $\mathbf{G}$ can be written as:

(2) $$\mathbf{G}\mathbf{=}\sqrt{{\displaystyle \frac{MN}{L_G}}}\sum _{l_1}^{L_G}{\alpha }_{l_1}^G\mathbf{b}({\vartheta }_{l_1}^{G_t},{\psi }_{l_1}^{G_t})\mathbf{a}({\vartheta }_{l_1}^{G_r},{\psi }_{l_1}^{G_r}{)}^T$$

$L_G$ represents the total paths between IRS and BS. Similarly, we can write ${\mathbf{f}}_k$ as:

(3) $${\mathbf{f}}_k=\sqrt{{\displaystyle \frac{N}{L_k}}}\sum _{l_2=1}^{L_k}{\alpha }_{l_2}^k\mathbf{a}({\vartheta }_{l_2}^k,{\psi }_{l_2}^k),$$

$L_k$ represents the total paths between uses and IRS. ${\alpha }_{l_2}^k$ represents the gain, ${\vartheta }_{l_2}^k$ represents the azimuth angle, and ${\psi }_{l_2}^k$ represents the elevation angle. $\mathbf{b}(\vartheta ,\psi )\in {\mathbf{C}}^{\mathrm{M}\times 1}$ and $\mathbf{a}(\vartheta ,\psi )\in {\mathbf{C}}^{\mathrm{N}\times 1}$ are the normalized array steering vector linked with BS and the IRS. For a typical $N1\times N2\left(N=N1\times N2\right)$ UPA, $\mathbf{a}(\vartheta ,\psi )$ is expressed as:

(4) $$\mathbf{a}(\vartheta ,\psi )={\displaystyle \frac{1}{\sqrt{N}}\left[e^{-j2\pi d\cos (\psi ){\mathbf{n}}_{\mathbf{1}}/\lambda }\right]\otimes \left[e^{-j2\pi d\sin (\psi ){\mathbf{n}}_2/\lambda }\right],}$$

${\mathbf{n}}_1=[0,1,...,N_1-1{]}^T$ and ${\mathbf{n}}_2=[0,1,...,N_2-1{]}^T$, λ and d represent the wavelength and spacing between antennas. In this article, we set $d=\frac{\lambda }{2}$.

By setting $\varphi =[{\varphi }_1,{\varphi }_2,...,{\varphi }_N]$, Eq. (1) can be written as:

(5) $${\mathbf{y}}_k=s_k{\mathbf{w}}_k\mathbf{G}diag({\mathbf{f}}_k)\varphi +n_k,$$

(6) $${\mathbf{y}}_k=s_k{\mathbf{w}}_k{\mathbf{H}}_k\varphi +n_k.$$

As mentioned earlier, in this article, we focus mainly on the estimation of cascaded channel by assuming the channel between end users and BS is already known. Where ${\mathbf{H}}_k=\mathbf{G}diag({\mathbf{f}}_k)$ is the uplink cascaded channel for the $k^{th}$ user.

The IRS has limitations in terms of signal processing; therefore, the cascaded channel computation is discussed in Nadeem et al. (2020), Zymnis, Boyd & Candès (2010). If we do channel estimation separately of $\mathbf{G}$ and ${\mathbf{f}}_k$, the computational complexity high. For reducing the computational complexity, we cascade the channel vector ${\mathbf{H}}_k$ and estimated using proposed method. $\mathbf{G}$ is the same for all end users because of having the common IRS between BS and users.

By decomposing ${\mathbf{H}}_k\in {\mathbb{C}}^{M\times N}$ with the help of virtual angular domain, we can write:

(7) $${\mathbf{H}}_k={\mathbf{U}}_M{\tilde{\mathbf{H}}}_k{\mathbf{U}}_N^T,$$where ${\tilde{\mathbf{H}}}_k$ represent the cascaded channel having $\mathrm{M}\times \mathrm{N}$ dimension. The dictionary unitary matrices are expressed as ${\mathbf{U}}_{\mathrm{M}}$ with dimension $\mathrm{M}\times \mathrm{M}$ and ${\mathbf{U}}_{\mathrm{N}}$ with dimension $\mathrm{N}\times \mathrm{N}$ (Mishra & Johansson, 2019).

Dictionary unitary matrix is a complex square matrix, which satisfy the condition ${\mathbf{U}}_{\mathrm{N}}^{\mathrm{T}}{\mathbf{U}}_{\mathrm{N}}=\mathbf{I}$ and ${\mathbf{U}}_{\mathrm{M}}^{\mathrm{T}}{\mathbf{U}}_{\mathrm{M}}=\mathbf{I}$.

The expression for ${\mathbf{U}}_{\mathrm{M}}$ and ${\mathbf{U}}_{\mathrm{N}}$ is given by

$${\mathbf{U}}_{\mathrm{M}}={\displaystyle \frac{\mathbf{1}}{\sqrt{\mathbf{N}}}\left[e^{-j2\pi d\cos (\psi ){\mathbf{n}}_{\mathbf{1}}/\lambda }\right]}$$

$${\mathbf{U}}_{\mathrm{N}}={\displaystyle \frac{\mathbf{1}}{\sqrt{\mathbf{N}}}\left[e^{-j2\pi d\sin (\psi ){\mathbf{n}}_2/\lambda }\right].}$$

In wireless communication systems, particularly those involving IRS and BS, it is crucial for estimation the challenge of channel between them. By dynamically fixing phase shifts, IRS can enhance the efficiency.

In multi-user systems, the channel BS and the IRS remains constant for all users since it depends only on the determined positions.

Since different users communicate with the BS via the common RIS, the channel G from the IRS to the BS is common for all users.

Another solution to reduce the pilot overhead is to directly estimate the corresponding cascaded channels by utilizing the multi-user correlation. Since all users communicate with the BS via the same IRS, the cascaded channels associated with different users have some correlations. Thus, this multi-user correlation can be exploited to reduce the pilot overhead required by the cascaded channel estimation.

It is noted that the reflecting vector at the IRS are the same for all users.

Where ${\overline{\mathbf{H}}}_k$ represent the cascaded channel having $M\times N$ dimension and ${\overline{\mathbf{H}}}_k$ is estimated for all common users.

Apply compressive sensing techniques in ${\overline{\mathbf{H}}}_k$ cascade channel matrix to exploit the sparsity of the IRS-BS channels, reducing the required pilot signals for the estimation of channel.

Exploiting the common IRS-BS channel in a multi-user IRS-assisted communication system is a strategic approach to reducing channel estimation overhead.

Problem formulation

The uplink cascaded channel ${\mathbf{H}}_k$ is calculated with the help of known pilot signals that are sent from users to the BS via IRS over $\mathbf{Q}$ time slots. According to Eq. (5), at the $q_{th}$ $(q=1,2,...,\mathbf{Q})$ time slot, the received pilot signal ${\mathbf{y}}_{k,q}^p\in \mathbf{C}$ at the BS can be expressed as:

(8) $${\mathbf{y}}_{k,q}^p=p_{k,q}{\mathbf{w}}_k{\mathbf{H}}_k{\varphi }_q+n_{k,q},$$where $p_{k,q}$ represents the pilot signals originated from the end users, and ${\varphi }_q$ denotes the reflecting vector of the $q_{th}$ time slot at the IRS, and $n_{k,q}$ is the received noise on $q_{th}$ time slot at the BS that undergoes the complex Gaussian distribution that has a special characteristics of zero mean and the variance as ${\sigma }_n^2$.

Following the transmission of pilots at $\mathbf{Q}$ time slots, the $\mathbf{Q}\times 1$ dimensional expectedoverall received pilot vector ${\mathbf{y}}_k^p={\left[{\mathbf{y}}_{k,1}^p,{\mathbf{y}}_{k,2}^p,...,{\mathbf{y}}_{k,Q}^p\right]}^T$ by assuming $p_{k,q}=1$ can be expressed as:

(9) $${\mathbf{y}}_k^p={\mathbf{w}}_k{\mathbf{H}}_k\mathrm{\Theta }+{\mathbf{n}}_k,$$where $\mathrm{\Theta }={\left[{\varphi }_1^T,{\varphi }_1^T,...,{\varphi }_Q^T\right]}^T$ and ${\mathbf{n}}_k={\left[n_{k,1},n_{k,2},...,n_{k,Q}\right]}^T$.

As $vec(\mathbf{A}\mathbf{B}\mathbf{C})=({\mathbf{C}}^{\mathbf{T}}\otimes \mathbf{A})vec(\mathbf{B})$, Eq. (9) is required to be expressed as:

(10) $${\mathbf{y}}_k^p=({\mathrm{\Theta }}^{\mathbf{T}}\otimes {\mathbf{w}}_k)vec({\mathbf{H}}_k)+{\mathbf{n}}_k$$

The $vec({\mathbf{H}}_k)$ is required to be expressed as $({\mathbf{U}}_{\mathrm{M}}^{\ast }\otimes {\mathbf{U}}_{\mathrm{N}}){\mathbf{h}}_k$, and the Eq. (10) is needed to be re-expressed as:

(11) $${\mathbf{y}}_k^p=({\mathrm{\Theta }}^{\mathbf{T}}\otimes {\mathbf{w}}_k)({\mathbf{U}}_{\mathrm{M}}^{\ast }\otimes {\mathbf{U}}_{\mathrm{N}}){\mathbf{h}}_k+{\mathbf{n}}_k.$$

By denoting ${\mathbf{\Psi }}_k=({\mathbf{\Theta }}^{\mathbf{T}}\otimes {\mathbf{w}}_k)({\mathbf{U}}_{\mathrm{M}}^{\ast }\otimes {\mathbf{U}}_{\mathrm{N}})$ and ${\mathbf{h}}_k\in {\mathbf{C}}^{MN\times 1}$, the received signal is expressed as:

(12) $${\mathbf{y}}_k^p={\mathbf{\Psi }}_k{\mathbf{h}}_k+{\mathbf{n}}_k$$where ${\mathbf{\Theta }}^{\mathrm{T}}\in {\mathbb{C}}^{\mathrm{Q}\times \mathrm{N}}$, ${\mathbf{y}}_k^p=[y_{k,1},y_{k,2},....y_{k,Q}]\in {\mathbf{C}}^{\mathrm{Q}\times 1}$, ${\mathbf{\Psi }}_k=[{\mathrm{\Psi }}_{k,1},{\mathrm{\Psi }}_{k,2},...,{\mathrm{\Psi }}_{k,Q}]\in {\mathbf{C}}^{\mathrm{Q}\times \mathrm{M}\mathrm{N}}$ and ${\mathbf{n}}_k=[n_{k,1},n_{k,2},....n_{k,Q}]\in {\mathbf{C}}^{\mathrm{Q}\times 1}$.

The cascading of ${\mathbf{\Psi }}_k$ and ${\mathbf{h}}_k$ can be re-written as $\mathbf{\Psi }=[{\mathrm{\Psi }}_1,{\mathrm{\Psi }}_2,...,{\mathrm{\Psi }}_k]$ and $\mathbf{h}=[{\mathbf{h}}_1,{\mathbf{h}}_2,...,{\mathbf{h}}_k]$respectively.

Moreover, the pilot vector at the receiving side is required to be re-expressed as:

(13) $${\mathbf{y}}^p=\mathbf{\Psi }\mathbf{h}\mathbf{+}\mathbf{n}.$$

To estimate the channel vector, ${\mathbf{w}}_k\in {\mathbf{C}}^{1\times \mathrm{M}}$ and $\mathbf{\Phi }\in {\mathbf{C}}^{\mathrm{N}\times \mathrm{N}}$ is designed as fixed value.Where $\mathbf{\Theta }={\left[{\varphi }_1^T,{\varphi }_1^T,...,{\varphi }_Q^T\right]}^T\in {\mathbf{C}}^{\mathrm{N}\times \mathrm{Q}}$ denotes the reflecting matrix at the IRS.

Thus, similar to the pilot signals or measurement matrix, the ${\mathbf{\Psi }}_k$ is known for both the user and BS during the channel estimation. The ${\mathbf{h}}_k$ has to estimate based on ${\mathbf{y}}_k^p$ and ${\mathbf{\Psi }}_k$ for the downlink cascaded channel estimation.

Different types of non IID gaussian measurement matrix

For solving problems related to CS, we opt for various kinds of $\mathbf{\Psi }$ matrixes. In these matrixes, the correlation between columns is high. As a result, they do not exhibit satisfactory performance due to the issues linking with the constructing $\mathbf{\Psi }$. For exploring algorithms in terms of robustness, we have the following several kinds of matrixes:

1) Low rank product matrix: With the aim of constructing it, we utilize $\mathbf{\Psi }$ by setting the ratio $MN/N$ for analyzing in terms of robustness.

2) Ill conditioned matrix: With the aim of constructing it, we utilize singular matrix decomposition ( $\mathbf{\Psi }={\mathbf{U}\mathbf{S}\mathbf{V}}^{\mathbf{T}}$).

3) Non-zero mean matrix: All entries in $\mathbf{\Psi }$ follows an IID N(µ,1/M). For measuring the deviation, we utilize mean function.

The approaches like AMP are normally utilized for solving problems related to channel estimation. However, the issue is the minor variations from iid gaussian model leads to the diverge problems (Rangan, Schniter & Fletcher, 2019). Therefore, to tackle this problem, we need various kinds of $\mathbf{\Psi }$ in terms of evaluating robustness.

Proposed channel estimation algorithm

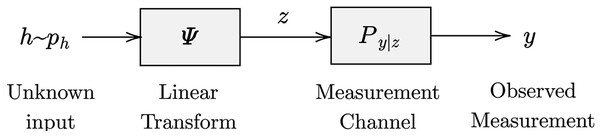
By getting inspiration from the previously outlined channel estimation framework, we can interpret the channel estimation challenge as a variant of noisy quantized compressed sensing. Various strategies have emerged to address this complexity, such as convex relaxation and GAMP (Kamilov, Goyal & Rangan, 2012). However, these approaches heavily rely on the assumed sparsity rate for the channel, which is typically explicitly specified or indirectly inferred through regularization terms or prior distributions. The integration of the generalized linear model (GLM) is illustrated in Fig. 2.

Proposed em-vamp-glm algorithm

Within this section, an extension of EM-VAMP to the GLM framework is presented and mathematically derived for the analysis of the proposed methodology’s performance. In this context, the unidentified random channel vector is represented as $\mathbf{h}\in {\mathbf{C}}^{\mathrm{M}\mathrm{N}\times 1}$, observed from its noisy measurements vector denoted as $\mathbf{y}\in {\mathbf{C}}^{\mathrm{Q}\times 1}$, utilizing a known measurement matrix denoted as $\mathbf{\Psi }\in {\mathbf{C}}^{\mathrm{Q}\times \mathrm{M}\mathrm{N}}$. The expressed output measurements vector is formulated as:

(14) $$\mathbf{y}\mathbf{=}\mathbf{\Psi }\mathbf{h}\mathbf{+}\mathbf{w}.$$

We can recover the channel vector by utilizing VAMP-GLM based technique with the help of the received measurement vector at the output side.

Here, $\mathbf{h}$ undergoes a $\mathrm{p}(\mathit{h}|{\mathrm{\theta }}_{\mathrm{h}1})$ prior density and $\mathbf{w}$ is an additive white Gaussian noise (AWGN) independent of $\mathbf{h}$ with noise variance $\mathit{w}=\mathrm{N}(0,\mathrm{I}/{\mathrm{\theta }}_{h2})$. $\mathit{z}$ undergoes a $\mathrm{p}(\mathit{h}|{\mathrm{\theta }}_{z1})$ prior density and noise variance $\overline{\mathbf{w}}=\mathrm{N}(0,\mathrm{I}/{\mathrm{\theta }}_{\mathrm{z}2})$.

The iterative AMP technique offers a less iterative solution for the aforementioned challenge, particularly when represents a $\mathbf{\Psi }$. However, even slight deviations from the IID sub-Gaussian model can make the AMP algorithm sensitive, leading to divergence. Contrary to AMP-based techniques like GAMP, VAMP’s broader applicability in state evolution includes a wider array of matrices $\mathbf{\Psi }$, specifically those that possesses (RRI). $\mathbf{\Psi }$ can be written as $\mathbf{\Psi }\mathbf{=}{\mathbf{U}}_{\mathrm{A}}{\mathbf{S}}_{\mathrm{A}}{\mathbf{V}}_{\mathrm{A}}^{\mathrm{H}}$ by following SVD, where the elements of ${\mathbf{V}}_{\mathrm{A}}$ should be uniformly drawn. This essential distinction leads the VAMP approach to overcome AMP’s main limitation as well as allows stability, even when dealing with ill-conditioned matrices $\mathbf{\Psi }$. Hence, VAMP is considered in this article.

For exhibiting its applicability to GLM with respect to small changes, we utilized the following relationship:

(15) $$\mathbf{z}\mathbf{=}\mathbf{\Psi }\mathbf{h}\iff 0=\left[\mathbf{\Psi }-\mathbf{I}\right]\left[\begin{array}{c}\mathbf{h}\\ \mathbf{z}\end{array}\right]\iff \overline{\mathbf{y}}=\overline{\mathbf{\Psi }}\overline{\mathbf{h}}+\overline{\mathbf{w}}$$

(16) $$\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\overline{\mathbf{y}}=0,\overline{\mathbf{\Psi }}=\left[\mathbf{\Psi }-\mathbf{I}\right],\overline{\mathbf{h}}=\left[\begin{array}{c}\mathbf{h}\\ \mathbf{z}\end{array}\right],\mathrm{a}\mathrm{n}\mathrm{d}\overline{\mathbf{w}}\sim \mathrm{N}(0,\mathrm{I}/{\gamma }_{\mathrm{e}})\mathrm{a}\mathrm{s}{\gamma }_e\to \mathrm{\infty }.$$

Here, the two sub-vectors ${\hat{\mathbf{h}}}_{\mathrm{i}}\in \mathbb{R}$ and ${\hat{\mathbf{z}}}_{\mathrm{i}}\in \mathbb{R}$ is the output of ${\mathrm{g}}_{\mathrm{i}}$ at iteration $\mathrm{k}$, and the two sub-vectors ${\mathit{r}}_{\mathrm{i}}\in \mathbb{R}$ and ${\mathbf{p}}_{\mathrm{i}}\in \mathbb{R}$ is the input to ${\mathrm{g}}_{\mathrm{i}}$.

${\mathbf{r}}_1=\mathbf{h}+\mathrm{N}(0,\mathbf{I}/{\gamma }_1)$ denotes the pseudo-measurement model and $\mathbf{x}\sim \mathrm{N}({\mathbf{r}}_2,\mathbf{I}/{\gamma }_2)$ denotes the pseudo-prior model is used to estimate the h. Likewise, ${\mathbf{p}}_1=\mathbf{z}+\mathrm{N}(0,\mathbf{I}/{\tau }_1)$) denotes the pseudo-measurements and $\mathbf{z}\sim \mathrm{N}({\mathbf{p}}_2,\mathbf{I}/{\tau }_2)$denotes the pseudo-prior is used to estimate the $\mathbf{z}$.

As we lack information about the parameters ${\mathrm{\theta }}_{\mathrm{h}}=({\mathrm{\theta }}_{\mathrm{h}1},{\mathrm{\theta }}_{\mathrm{h}2})$ and ${\mathrm{\theta }}_{\mathrm{z}}=({\mathrm{\theta }}_{\mathrm{z}1},{\mathrm{\theta }}_{\mathrm{z}2})$ for obtaining precise values of ${\mathrm{p}}_{\mathrm{h}}(\mathbf{h}\mathbf{|}{\mathrm{\theta }}_{\mathrm{h}1})$and $\mathrm{C}\mathrm{N}(\mathbf{y};\mathbf{h},\mathbf{I}/{\mathrm{\theta }}_{\mathrm{h}2})$. Similarly, we lack knowledge of parameters ${\mathrm{\theta }}_{\mathrm{z}}=({\mathrm{\theta }}_{\mathrm{z}1},{\mathrm{\theta }}_{\mathrm{z}2})$ for acquiring accurate values of ${\mathrm{p}}_{\mathrm{z}}(\mathbf{z}|{\mathrm{\theta }}_{\mathrm{z}1})$ and $\mathrm{C}\mathrm{N}(\mathbf{y};\mathbf{\Psi }\mathbf{h},\mathbf{I}/{\mathrm{\theta }}_{\mathrm{z}2})$.

${\mathbf{h}}_1$ is considered as the posterior probability under the prior $\mathrm{p}(\mathbf{h}\mathbf{|}{\mathrm{\theta }}_{\mathrm{h}1}^{\mathrm{t}})$and message $\mathrm{C}\mathrm{N}({\mathbf{h}}_1;{\mathbf{r}}_1^{\mathrm{t}},\mathbf{I}/{\gamma }_1^{\mathrm{t}})$, i.e., $b_{sp}({\mathbf{h}}_1)\alpha p({\mathbf{h}}_1|{\mathrm{\theta }}_{\mathrm{h}1}^t)\mathrm{C}\mathrm{N}({\mathbf{h}}_1;{\mathbf{r}}_1^{\mathrm{t}},\mathbf{I}/{\gamma }_1^{\mathrm{t}})$. Hence, we can write $\mathrm{C}\mathrm{N}({\mathbf{h}}_1,{\hat{\mathbf{h}}}_1,\mathbf{I}/{\mathrm{\eta }}_1^{\mathrm{t}})$ where ${\hat{\mathbf{h}}}_1=\mathbf{E}[{\mathbf{h}}_1|{\mathrm{b}}_{\mathrm{s}\mathrm{p}}({\mathbf{h}}_1)]$ and $1/{\mathrm{\eta }}_{h1}^{\mathrm{t}}=⟨\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(\mathrm{C}\mathrm{o}\mathrm{v}[{\mathbf{h}}_1|{\mathrm{b}}_{\mathrm{s}\mathrm{p}}({\mathbf{h}}_1)])⟩$.

In this context, we determine ${\hat{\mathbf{h}}}_1={\mathrm{g}}_1({\mathbf{r}}_1^{\mathrm{t}},{\gamma }_1)$ and $1/{\mathrm{\eta }}_{\mathrm{h}1}^{\mathrm{t}}=⟨{{\mathrm{g}}^{\mathrm{\prime }}}_1({\mathrm{r}}_1^{\mathrm{t}},{\gamma }_1^{\mathrm{t}})⟩/{\gamma }_1^{\mathrm{t}}$ through the utilization of the denoising function ${\mathrm{g}}_1(.,\gamma )$. These values are written as follows:

(17) $${\mathrm{g}}_{\mathrm{h}1}({\mathbf{r}}_1,{\gamma }_1)={\displaystyle \frac{\int \mathbf{h}{\mathrm{p}}_{\mathrm{h}}(\mathbf{h}|{\mathrm{\theta }}_{\mathrm{h}1})\mathrm{N}(\mathbf{h};{\mathbf{r}}_1,\mathbf{I}/{\gamma }_1)\mathrm{d}\mathbf{h}}{\int {\mathrm{p}}_{\mathrm{h}}(\mathbf{h}|{\mathrm{\theta }}_{\mathrm{h}1})\mathrm{N}(\mathbf{h};{\mathbf{r}}_1,\mathbf{I}/{\gamma }_1)\mathrm{d}\mathbf{h}},}$$

(18) $$⟨{{\mathrm{g}}^{\mathrm{\prime }}}_{\mathrm{h}1}({\mathit{r}}_1^{\mathrm{t}},{\gamma }_1^{\mathrm{t}})⟩={\displaystyle \frac{1}{\mathrm{N}}\mathrm{t}\mathrm{r}\left\{{\displaystyle \frac{\mathrm{\partial }{\mathrm{g}}_{\mathrm{i}}(\mathit{r},\gamma )}{\mathrm{\partial }\mathbf{r}}}\right\},\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{i}=1,2.}$$

Here, $⟨\cdot ⟩$ represents the mean coefficient value, specifically $⟨\mathbf{r}⟩={\displaystyle \frac{1}{\mathrm{N}}{\sum }_{\mathrm{i}=1}^{\mathrm{N}}{\mathit{r}}_{\mathrm{i}}}$. In a general context, the denoising function ${\mathrm{g}}_{\mathrm{h}1}(.,\gamma )$ is employed to remove noise from the pseudo-measurement ${\mathbf{r}}_1=\mathbf{h}+\mathrm{C}\mathrm{N}(0,\mathbf{I}/{\gamma }_1)$ corrupted by AWGN, with prior knowledge of $\mathrm{p}(\mathbf{h}\mathbf{|}{\mathrm{\theta }}_{\mathrm{h}1})$.

${\mathrm{z}}_1$ is considered as the posterior probability under the prior $\mathrm{p}(\mathbf{z}\mathbf{|}{\mathrm{\theta }}_{\mathrm{z}1}^{\mathrm{t}})$ and message $\mathrm{C}\mathrm{N}({\mathbf{z}}_1;{\mathbf{p}}_1^{\mathrm{t}},\mathbf{I}/{\tau }_1^{\mathrm{t}})$, i.e., ${\mathrm{b}}_{\mathrm{s}\mathrm{p}}({\mathbf{z}}_1)\mathrm{\alpha }\mathrm{p}({\mathbf{z}}_1|{\mathrm{\theta }}_{\mathbf{z}1}^{\mathrm{t}})\mathrm{C}\mathrm{N}({\mathbf{z}}_1;{\mathbf{p}}_1^{\mathrm{t}},\mathbf{I}/{\tau }_1^{\mathrm{t}})$. Hence, we can write $\mathrm{C}\mathrm{N}({\mathrm{z}}_1,{\hat{\mathrm{z}}}_1,\mathrm{I}/{\mathrm{\eta }}_1^{\mathrm{t}})$ where ${\hat{\mathrm{z}}}_1=\mathrm{E}[{\mathrm{z}}_1|{\mathrm{b}}_{\mathrm{s}\mathrm{p}}({\mathrm{z}}_1)]$ and $1/{\mathrm{\eta }}_{\mathrm{z}1}^{\mathrm{t}}=⟨\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}(\mathrm{C}\mathrm{o}\mathrm{v}[{\mathbf{z}}_1|{\mathrm{b}}_{\mathrm{s}\mathrm{p}}({\mathbf{z}}_1)])⟩$. Here we have ${\hat{\mathbf{z}}}_1={\mathrm{g}}_1({\mathbf{p}}_1^{\mathrm{t}},{\tau }_1)$ and $1/{\mathrm{\eta }}_{z1}^{\mathrm{t}}⟨{{\mathrm{g}}^{\mathrm{\prime }}}_1({\mathbf{p}}_1^{\mathrm{t}},{\tau }_1^{\mathrm{t}})⟩/{\tau }_1^{\mathrm{t}}$ with the help of noise reducing function ${\mathrm{g}}_{z1}(.,{\tau }_1^{\mathrm{t}})$:

(19) $${\mathrm{g}}_{z1}({\mathbf{p}}_1,{\tau }_1)={\displaystyle \frac{\int \mathbf{z}{\mathbf{p}}_{\mathrm{z}}(\mathbf{z}|{\mathrm{\theta }}_{\mathrm{z}1})\mathrm{N}(\mathbf{z};{\mathbf{p}}_1,\mathbf{I}/{\tau }_1)\mathrm{d}\mathbf{z}}{\int {\mathrm{p}}_{\mathrm{z}}(\mathbf{z}|{\mathrm{\theta }}_{\mathrm{z}1})\mathrm{N}(\mathbf{z};{\mathbf{p}}_1,\mathbf{I}/{\tau }_1)\mathrm{d}\mathbf{z}},}$$

(20) $$⟨{\mathrm{g}}_{z1}^{\mathrm{\prime }}({\mathbf{p}}_1^{\mathrm{t}},{\tau }_1^{\mathrm{t}})⟩={\displaystyle \frac{1}{\mathrm{N}}\mathrm{t}\mathrm{r}\left\{{\displaystyle \frac{\mathrm{\partial }{\mathrm{g}}_{\mathbf{i}}(\mathbf{p},\tau )}{\mathrm{\partial }\mathrm{p}}}\right\},\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{i}=1,2.}$$

Here $⟨\mathbf{p}⟩={\displaystyle \frac{1}{\mathrm{N}}{\sum }_{i=1}^N{\mathbf{p}}_{\mathrm{i}}}$. Lines 16–26 of Algorithm 1 implement LMMSE estimation of $$\overline{h}=\left[\begin{array}{c}h\\ z\end{array}\right]$$ and the pseudo-prior

(21) $$\overline{\mathbf{h}}=\left[\begin{array}{c}\mathbf{h}\\ \mathbf{z}\end{array}\right]=\mathrm{N}\left(\left[\begin{array}{c}{\mathbf{r}}_2\\ {\mathbf{p}}_2\end{array}\right],\left[\begin{array}{cc}\mathbf{I}/{\gamma }_2& \\ & \mathbf{I}/{\tau }_2\end{array}\right]\right).$$

Due to the gaussian nature of prior and likelihood and prior, the estimation of MAP and LMMSE is equivalent:

(22) $$\arg \underset{\overline{\mathrm{h}}}{max}\mathrm{p}(\overline{\mathbf{h}}|\overline{\mathbf{y}})=\arg \underset{\overline{\mathrm{h}}}{min}\{-\ln \mathrm{p}(\overline{\mathbf{y}}|\overline{\mathbf{h}})-\ln \mathrm{p}(\overline{\mathbf{h}})\}$$

(23) $$\arg \underset{\mathbf{h}\mathbf{,}\mathbf{z}}{min}{\gamma }_e{\Vert \mathbf{\Psi }\mathbf{h}\mathbf{-}\mathbf{z}\Vert }_2^2+{\gamma }_2{\Vert {\mathbf{r}}_2-\mathbf{h}\Vert }_2^2+{\tau }_2{\Vert {\mathbf{p}}_2-\mathbf{z}\Vert }_2^2|{\mathrm{\theta }}_{\mathrm{h}2},{\mathrm{\theta }}_{\mathrm{z}2}$$

(24) $${\mathbf{g}}_{\mathrm{h}2}\left({\mathbf{r}}_2,{\mathbf{p}}_2,{\gamma }_2,{\tau }_2,{\mathrm{\theta }}_{\mathrm{h}2}\right)=\mathbf{V}\mathbf{D}({\mathrm{\theta }}_{\mathrm{h}2}{\tau }_2{\mathbf{S}}^{\mathrm{T}}{\mathbf{U}}^{\mathrm{T}}{\mathbf{p}}_2+{\gamma }_2{\mathbf{V}}^{\mathrm{T}}{\mathbf{r}}_2)$$

(25) $${\mathbf{g}}_{\mathrm{z}2}\left({\mathbf{r}}_2,{\mathbf{p}}_2,{\gamma }_2,{\tau }_2,{\mathrm{\theta }}_2\right)=\mathbf{A}{\mathbf{g}}_{\mathrm{h}2}\left({\mathbf{r}}_2,{\mathbf{p}}_2,{\gamma }_2,{\tau }_2\right)$$

(26) $${\left[\mathit{D}\right]}_{\mathrm{n}\mathrm{n}}=({\mathrm{\theta }}_{\mathrm{h}2}{\tau }_2{\mathrm{s}}_{\mathrm{n}}^2+{\gamma }_2{)}^{-1}$$

(27) $${\mathbf{g}}_{\mathrm{h}2}\left({\mathbf{r}}_2,{\mathbf{p}}_2,{\gamma }_2,{\tau }_2,{\mathrm{\theta }}_{h2}\right)={\mathbf{r}}_2+\mathbf{V}{\mathbf{S}}^{\mathrm{T}}{\left({\mathrm{\theta }}_{\mathrm{h}2}{\displaystyle \frac{{\gamma }_2}{{\tau }_2}\mathbf{I}\mathbf{+}\mathbf{S}{\mathbf{S}}^{\mathrm{T}}}\right)}^{-1}({\mathbf{U}}^{\mathrm{T}}{\mathrm{p}}_2-\mathbf{S}{\mathbf{V}}^{\mathrm{T}}{\mathbf{r}}_2)$$

(28) $$\mathrm{\partial }{\mathbf{g}}_{\mathrm{h}2}/\mathrm{\partial }{\mathbf{r}}_2={\gamma }_2\mathbf{V}\mathbf{D}{\mathbf{V}}^{\mathrm{T}}$$

(29) $${\alpha }_2=⟨{{\mathbf{g}}^{\mathrm{\prime }}}_{h2}\left({\mathbf{r}}_2,{\mathbf{p}}_2,{\gamma }_2,{\tau }_2,{\theta }_{h2}\right)⟩={\displaystyle \frac{1}{\mathrm{M}\mathrm{N}}\sum _{n=1}^{\mathrm{M}\mathrm{N}}{\displaystyle \frac{{\gamma }_2}{({\theta }_{h2}{\tau }_2{s}_n^2+{\gamma }_2)}}}$$

(30) $$\mathrm{\partial }{\mathbf{g}}_{z2}/\mathrm{\partial }{\mathbf{p}}_2={\tau }_2\mathbf{S}\mathbf{D}{\mathbf{S}}^{\mathrm{T}}$$

(31) $${\mathrm{\beta }}_2=⟨{{\mathrm{g}}^{\mathrm{\prime }}}_{\mathrm{z}2}\left({\mathbf{r}}_2,{\mathbf{p}}_2,{\gamma }_2,{\tau }_2,{\mathrm{\theta }}_{\mathrm{z}2}\right)⟩={\displaystyle \frac{1}{\mathrm{M}}\sum _{\mathrm{n}=1}^{\mathrm{N}}{\displaystyle \frac{{\tau }_2{s}_{\mathrm{n}}^2}{({\mathrm{\theta }}_{\mathrm{z}2}{\tau }_2{\mathrm{s}}_{\mathrm{n}}^2+{\gamma }_2)}}={\displaystyle \frac{\mathrm{M}}{\mathrm{N}}(1-{\mathrm{\alpha }}_2).}}$$

Choice of prior distribution

To effectively utilize the EM-VAMP in tackling the estimation challenge assisted by IRS, we choose to embrace an approximating prior family. This family presents two viable choices: a BG distribution or GM distribution, each involving unspecified parameters ${\mathrm{\theta }}_{h1}$. This implies ${\mathrm{h}}_{\mathrm{n}}$ of $\mathbf{h}$ is taken out with the help of the subsequent equations:

(32) $$\mathrm{B}\mathrm{G}:p(h_n|{\mathrm{\theta }}_{\mathrm{h}1})={\lambda }_0\mathrm{\delta }(h_n)+(1-{\lambda }_0)CN(h_n;0,\tau )\mathrm{\forall }\mathrm{i}$$

(33) $$\mathrm{B}\mathrm{G}:p(z_n|{\mathrm{\theta }}_{\mathrm{z}1})={\lambda }_0\mathrm{\delta }(z_{\mathrm{n}})+(1-{\lambda }_0)CN(z_n;0,\tau )\mathrm{\forall }\mathrm{i}$$

(34) $$\mathrm{G}\mathrm{M}:p(h_n|{\mathrm{\theta }}_{\mathrm{h}1})={\lambda }_0\mathrm{\delta }(h_n)+\sum _{\mathrm{i}}^{\mathrm{L}}{\lambda }_{\mathrm{i}}CN(h_n;{\mathrm{\mu }}_i,{\tau }_i)\mathrm{\forall }\mathrm{i}$$

(35) $$\mathrm{G}\mathrm{M}:p(z_n|{\mathrm{\theta }}_{\mathrm{z}1})={\lambda }_0\mathrm{\delta }(z_n)+\sum _{\mathrm{i}}^{\mathrm{L}}{\lambda }_{\mathrm{i}}CN(z_n;{\mathrm{\mu }}_{\mathrm{i}},{\tau }_{\mathrm{i}})\mathrm{\forall }\mathrm{i}$$where ${\lambda }_0=\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{b}\{h_n=0\}$ and ${\lambda }_0=\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{b}\{z_n=0\}$, $\mathrm{L}$ is the number of Gaussian distribution mixed in GM; ${\lambda }_{\mathrm{i}}$, ${\mathrm{\mu }}_{\mathrm{i}}$, and ${\tau }_{\mathrm{i}}$ are the weights, means, and variances. The channel coefficient follow the BG distributions for Eqs. (32) and (33), and GM distributions for Eqs. (34) and (35) respectively with unknown parameters ${\mathrm{\theta }}_{\mathrm{h}1}$ and ${\mathrm{\theta }}_{\mathrm{z}1}$ and noise variance ${\mathrm{\theta }}_{\mathrm{h}2}$ and ${\mathrm{\theta }}_{\mathrm{z}2}$, respectively.

The computational complexity and the performance comparison analysis is shown in Table 1.

Results and discussion

The simulation results for the proposed EM-VAMP-GLM is discussed and compared with the existing OMP, GAMP and EM-LAMP. The simulation parameter is shown in Table 2.

The azimuth/elevation angles are uniformly generated from (−π/2, π/2) along the pre-discretized virtual angle grids. Equation (3) is utilized for generating the channel ${\mathbf{f}}_k$. The operating frequency is considered as 28 GHz.

Where the normalized mean square error (NMSE) is defined as $\mathrm{N}\mathrm{M}\mathrm{S}\mathrm{E}={\displaystyle \frac{\mathrm{E}\left\{\sum _{k=1}^K{\Vert {\hat{\mathbf{h}}}_k-{\mathbf{h}}_k\Vert }_2^2\right\}}{\mathrm{E}\left\{\sum _{k=1}^K{\Vert {\mathbf{h}}_k\Vert }_2^2\right\}}}$.

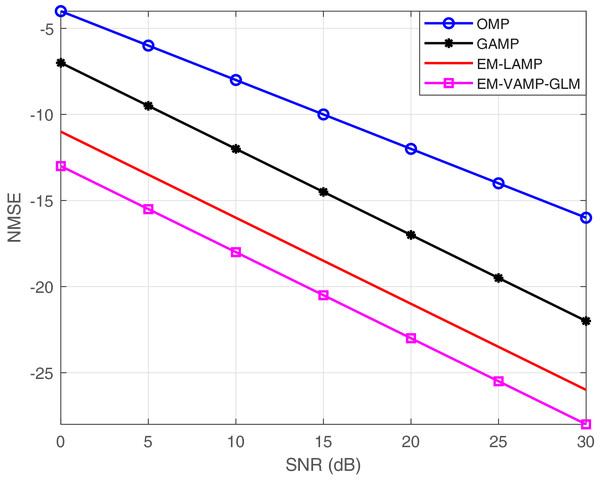
As shown in Fig. 3, the NMSE with respect to SNR is shown between the proposed EM-VAMP-GLM algorithm and alternative approaches including OMP, GAMP, and EM-LAMP. The results show that GAMP and EM-LAMP algorithms exhibit superior performance compared to the OMP algorithm. In the case of an IID Gaussian matrix $\mathbf{\Psi }$, both GAMP and EM-LAMP techniques do not perform well when compared to the proposed EM-VAMP-GLM algorithm.

Figure 4 provides a comprehensive exploration of the NMSE against SNR for various shrinkage function. The performance analysis of various shrinkage functions such as GM, BG, and soft threshold shrinkage function is applied in the proposed EM-VAMP-GLM and EM-LAMP network. The proposed EM-GM-VAMP-GLM, EM-BG-VAMP-GLM and EM-ST-VAMP algorithms, is compared to the existing EM-GM-LAMP, EM-BG-LAMP and EM-ST-LAMP.

LAMP behaves certainly with IID Gaussian matrix $\mathbf{\Psi }$, but less certainly with non-IID-Gaussian $\mathbf{\Psi }$. To address the challenge of non-IID-Gaussian signal estimation, we introduce the EM-GM-VAMP-GLM and EM-BG-VAMP-GLM methodologies. In Fig. 4, the usage of BG or GM shrinkage function for proposed algorithm achieve better performance compared to the soft threshold shrinkage function based EM-VALP-GLM algorithm. Even when $\mathbf{\Psi }$ is not IID Gaussian, EM-GM-VAMP-GLM and EM-BG-VAMP-GLM algorithm perform well compared to the LAMP and GAMP.

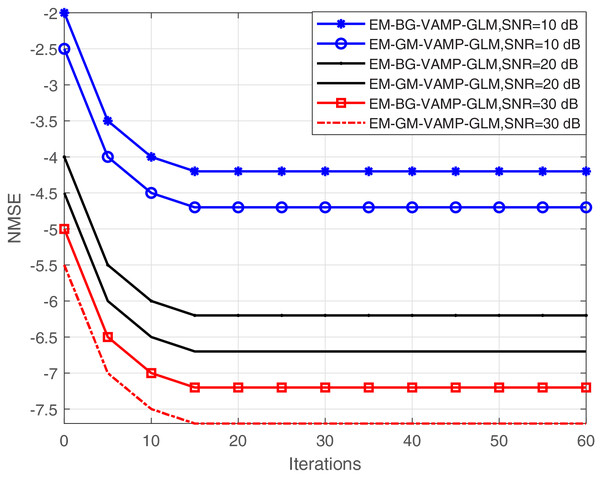
Figure 5 illustrates the relationship between NMSE and the number of iterations for the proposed EM-BG-VAMP-GLM and EM-GM-VAMP-GLM techniques across varying SNRs. Evidently, both the EM-BG-VAMP-GLM and EM-GM-VAMP-GLM algorithms exhibit convergence within a modest span of fewer than 22 iterations. This observation highlights their fast convergence rate, and reduces the computational complexity for BG and GM shrinkage function scenarios. Notably, in both algorithms, an increase in SNR corresponds to an extended the convergence rate with a greater number of iterations, because the BG and GM shrinkage function need additional parameters to be learned in the EM update process of EM-BG-VAMP-GLM and EM-GM-VAMP-GLM algorithms.

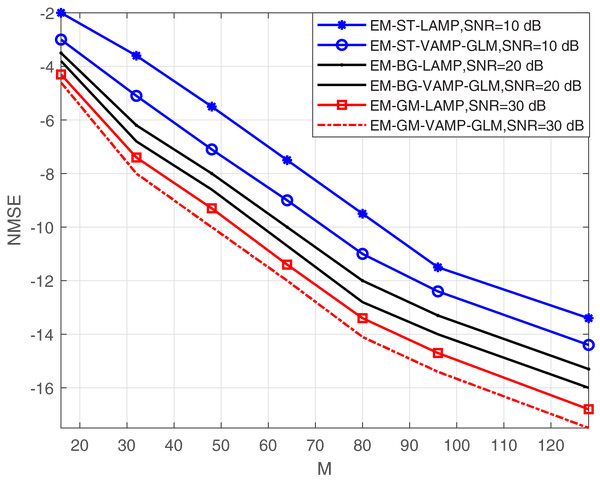
The investigation into NMSE performance vs. the number of BS antennas, denoted as M for both the proposed EM-BG-VAMP-GLM and EM-GM-VAMP-GLM algorithms at different value of SNRs is shown in Fig. 6. For the increased number of antennas M, it is observed that both EM-BG-VAMP-GLM and EM-GM-VAMP-GLM algorithms consistently exhibit reduced NMSE values. The higher SNRs value provide low NMSE value for proposed EM-BG-VAMP-GLM and EM-GM-VAMP-GLM. Under sparser environment, the scattering paths is fixed, so that the number of large non-zero elements is also fixed. The increased number of antennas provide the estimation outcomes are inherently enhanced, under the sparser conditions. Ultimately, these results highlight the practicality and appropriateness of utilizing the suggested EM-BG-VAMP-GLM and EM-GM-VAMP-GLM algorithms for efficient channel estimation with the assistance of IRS in mmWave communication systems. This leverages the benefits derived from angular domain sparsity.

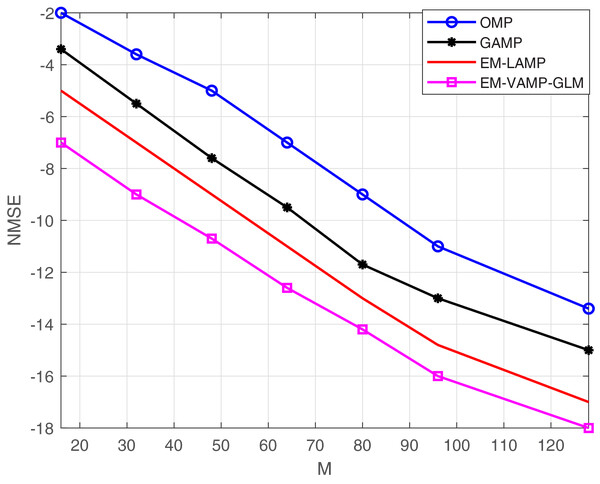
In Fig. 7, we perform the comparison between M and NMSE. As it can be seen in Fig. 7, the proposed approach outscores the existing approaches by exhibiting less NMSE with respect to the increment in the number of antennas.

Figure 8 depicts the NMSE against the number of IRS elements, denoted as N, for the EM-BG-VAMP-GLM and EM-GM-VAMP-GLM algorithms. The quantity of IRS elements, N, increases, with both the EM-BG-VAMP-GLM and EM-GM-VAMP-GLM algorithms consistently demonstrating lower NMSE compared to the other techniques.

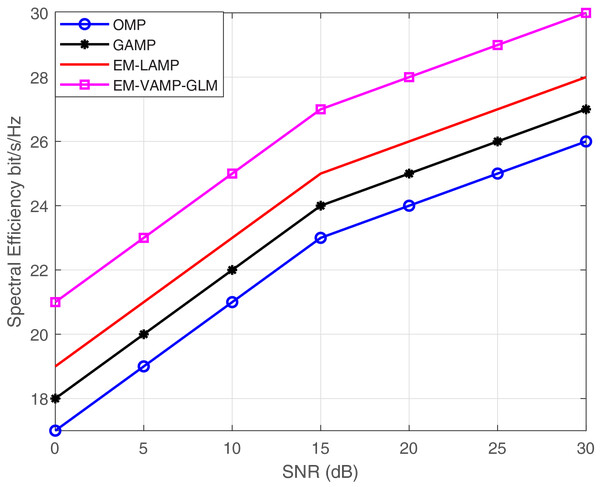
Figure 9 provides the SNR against the Spectral Efficiency for the proposed EM-VAMP-GLM and Existing algorithm such as OMP, GAMP and EM-LAMP algorithm. At 15 dB SNR, the proposed EM-VAMP-GLM algorithm provide 14.8%, 11% and 7%, and 8.5% of enhancement in spectral efficiency compared to OMP, GAMP and EM-LAMP algorithm respectively. The SNRVs Spectral Efficiency is shown in Table 3.

Conclusions

This research focuses on addressing the channel estimation problem within an IRS-assisted mmWave MIMO system. We present the EM-BG-VAMP-GLM and EM-GM-VAMP-GLM techniques for effectively computing channel vector in this scenario. By utilizing EM-VAMP-GLM, we achieve precise channel estimation without the need for crucial parameters like noise variance and prior distribution parameters. The investigation considers two potential distributions–BG and GM distributions–to identify the most suitable model for characterizing the sparse angular domain channel. We perform the comparison between EM-GM-VAMP-GLM and EM-BG-VAMP-GLM techniques against existing methods such as LAMP, GAMP, and OMP. The experimental results indicate that, especially at higher SNRs, the EM-GM-VAMP-GLM demonstrates superior computation accuracy with rapid convergence.

Supplemental Information