Fast binary logistic regression

Introduction

Classification has been extensively investigated in statistical learning as a supervised learning task. As pioneering works, the contributions of Berkson (1944) and Cox (1958) to the field of logistic regression are recognized as foundational. Berkson applied the logistic function to bio-assay, while Cox introduced regression analysis of binary sequences. Different forms of logistic regression are available to handle outputs in binary, multinomial, and ordinal formats, making it a versatile machine learning algorithm capable of addressing a wide range of classification tasks such as marketing, finance, healthcare, and fraud detection. With the rapid development of machine learning, highly flexible models such as extreme gradient boosting (XGBoost), support vector machine (SVM), and neural networks have become prominent (Cioffi et al., 2020). However, studies indicating logistic regression’s superior performance in some scenarios (de Hond et al., 2022; Jiang, Hu & Jia, 2023; Nusinovici et al., 2020; Zabor et al., 2022) and continuous usage of it (Jaskie, Elkan & Spanias, 2019; Lu, 2024) underscore the statistical machine learning community’s continued interest in this method.

Several improvements to the original logistic regression method are proposed (Berkson, 1944), such as weight regularization to obtain a generalized model or adapt the method for large data (Jiang, Hu & Jia, 2023; Bertsimas, Pauphilet & Van Parys, 2021; Tibshirani, 1996; Zaidi et al., 2016). Achieving a generalized model is closely tied to the bias-variance tradeoff where high-bias models risk oversimplification and underfitting, while low-bias models can overfit, exhibiting high variance. The tradeoff involves balancing these extremes to ensure the model generalizes well to unseen data without overfitting or underfitting. The optimal tradeoff is achieved by selecting appropriate model parameters that yield the most effective model complexity for training and validation sets, using techniques such as cross-validation and bootstrapping (Wahba et al., 1998; Gong, 2006; Mohr & van Rijn, 2023). It can be summarized that there must be a match between model complexity and data complexity to ensure that a model trained on training data performs well on unseen test data (Geman, Bienenstock & Doursat, 1992). Identifying optimal model parameters necessitates multiple training iterations with data subsets or random subsamples, a computationally intensive process for various parameter combinations, particularly with large datasets (Mohr & van Rijn, 2023; Emmert-Streib & Dehmer, 2019).

Logistic regression assumes a linear relationship between features and class distributions without demanding a specific statistical distribution. However, it is strictly required that features exhibit no multicollinearity. Regularization emerges as a vital solution to address multicollinearity and effectively manage model complexity. Aside from the intercept term, weight regularization applied to features encourages sparsity in the weight vector, resulting in fewer and more distinct features. This reduces multicollinearity and complexity, improving the model’s generalization abilities (Shi et al., 2010; Zhang et al., 2021; Avalos, Grandvalet & Ambroise, 2003). Additionally, in scenarios with numerous features available but limited training data, the risk of overfitting can arise without an effective regularization technique (Vapnik, 2006). Thus, pursuing a sparse solution is crucial to reduce overfitting and prevent data’s random pattern memorization (Zhang et al., 2021).

$L_2$-norm (also known as Ridge) regularization, first introduced by Tikhonov (1963), penalizes the magnitudes of the weights to enforce smaller values, thereby increasing model robustness. In the literature, other weight regularization techniques (Tikhonov & Arsenin, 1979; Morozov, 2012; Bertero, 1986) also enforce sparsity for better robustness and increased model generalization. Among these techniques, $L_0$-norm¹ , provide most sparse solutions (Wang, Chen & Yang, 2022; Greenwood et al., 2020). Nevertheless, using $L_0$-norm is challenging since it is not convex. Thereby, $L_1$-norm, namely least absolute shrinkage and selection operator (LASSO) (Tibshirani, 1996), is proposed as a convex relaxation of non-convex $L_0$-norm. Each regularization approach imposes different constraints on the model training. For example, $L_2$-norm imposes a squared penalty (Hoerl & Kennard, 1970) and $L_1$-norm imposes an absolute penalty on the model’s parameters (Ozgur, Nar & Erdem, 2018; Wei et al., 2019; Xie et al., 2023) while $L_0$-norm imposes a constant penalty for all non-zero weights (Wang, Chen & Yang, 2022; Greenwood et al., 2020). Note that the Bayesian information criterion (BIC) (Schwarz, 1978) and the Akaike information criterion (AIC) (Akaike, 1998), well-known model selection criteria, are special cases of $L_0$-norm regularization. So, sparse models using $L_0$-norm and $L_1$-norm enforce many coefficients to shrink to exactly zero while $L_2$-norm tends to produce model parameters closer but not precisely zero (Pereyra et al., 2017). Thus, $L_1$-norm and $L_0$-norm are employed in feature selection to avoid overfitting. On the contrary, $L_2$-norm has better computational efficiency than $L_1$-norm and is even more efficient than $L_0$-norm. Thereby, several studies prefer to use $L_1$-norm or $L_2$-norm regularized logistic regression for large scale data (Koh, Kim & Boyd, 2007; Shi et al., 2010; Jovanovich & Lazar, 2012; Su, 2020). Elastic-net combines the $L_1$-norm and $L_2$-norm penalties, so it tends to choose more features than LASSO, but computational efficiency becomes similar to Ridge. Recently, some studies tackled the $L_0$-norm regularization for logistic regression while dealing with challenges of using non-convex $L_0$-norm regularization term (Ming & Yang, 2024; Hazimeh, Mazumder & Nonet, 2023; Knauer & Rodner, 2023; Deza & Atamturk, 2022). Although not proposed for logistic regression, the use of fractional norm as a penalty term was proposed as a flexible and practical approach for enforcing smoothness on the image denoising (Ozcan, Sen & Nar, 2016), where it is also better suited for handling the generalized Gaussian distribution of the variables (Bernigaud et al., 2021).

As already stated in the literature, the maximum likelihood estimation of the logistic regression has some shortcomings:

• It may struggle to handle massive sparse datasets (Holland & Welsch, 1977; Li, Zhu & Wang, 2023) effectively.

• Logistic regression often struggles with imbalanced data, tending to favor the majority class and resulting in poor performance on the minority class (King & Zeng, 2001).

• For the training set where the number of samples is smaller than the number of features, directly solving the logistic regression is an ill-posed problem (Liu, Chen & Ye, 2009).

• It is sensitive to anomalous data and collinearity (Feng et al., 2014; Midi, Sarkar & Rana, 2010).

• Oversampling data instances may decrease estimation performance and increase computational expenses (Wang, 2020).

One strategy to mitigate these challenges involves utilizing the iteratively reweighted least squares method with an appropriate solver to construct binary logistic regression classifiers, particularly for large-scale datasets (Paciorek, 2007; Rouhani-Kalleh, 2007). Employing appropriate numerical solvers can also address these problems. Hence, numerous numerical solvers have been deployed to tackle these challenges, such as gradient descent and its variants, Newton’s method, and quasi-Newton methods. These solvers play a crucial role in training models efficiently by iteratively adjusting parameters to minimize a specified objective function. Although these approaches attempt to eliminate anomalies or collinearity problems in the data, working with many solvers with different regularizers poses a challenging issue for researchers (Liu, Chen & Ye, 2009). The selection of the solver typically depends on the specific characteristics of the data and the nature of the problem under consideration.

Scikit-learn (Pedregosa et al., 2011), a versatile Python library integrating a wide range of state-of-the-art machine learning algorithms, has become one of the most popular choices among many libraries due to its simplicity, comprehensive documentation, and extensive community support. The LogisticRegression class in scikit-learn already incorporates several optimization methods (see Table 1), each tailored for different regularizers, data sizes, and computational needs. Similarly, other open-source libraries, including cuML and Statsmodels, provide their own implementations of logistic regression, each with a variety of solvers and parameter configurations to enhance flexibility and efficiency. In particular, cuML offers graphics processing unit (GPU)-accelerated solvers for large-scale computations and Statsmodels provides robust statistical modeling options for binary response variables.

With increasing dataset sizes, logistic regression needs to improve in terms of efficiency and scalability. In response, advanced versions have emerged, designed to prioritize speed and accuracy. These innovative approaches accelerate learning by leveraging techniques such as dimensionality reduction, parallel processing, and advanced data structures.

Logistic regression training is formulated to solve an optimization problem based on likelihood maximization. However, calculating the gradient with all training data in each iteration for large datasets becomes computationally demanding. Therefore, Song et al. (2021) proposed an adaptive sampling method in which the gradient estimation is divided into several sub-problems according to the data size, and then each sub-problem is solved independently before combining the results of all sub-problems. Shi et al. (2010) suggested a hybrid algorithm that merges two optimization iterations: one that is fast and memory-efficient and another that is slower but yields more precise results.

Various approaches have been proposed to enhance the speed of logistic regression, which can generally be categorized into efficient numerical methods and software-based improvements. Table 1 summarizes the solvers employed in scikit-learn. A notable earlier study by Komarek & Moore (2003) utilizes Cholesky decomposition to accelerate logistic regression. However, since many contemporary methods now incorporate Cholesky decomposition within NumPy or employ more advanced solvers, this study has yet to be considered state-of-the-art. Additionally, some approaches leverage field programmable gate array (FPGA) and GPU (Wienbrandt et al., 2019), stochastic gradient descent, and mini-batch (Yang et al., 2019; Liang et al., 2020; Jurafsky & Martin, 2024) methods to improve the speed of logistic regression. These techniques are often complementary and can be integrated with other methods, representing practical efforts to accelerate logistic regression further.

We introduce a novel numerical approach that remarkably improves the training efficiency of binary logistic regression without relying on dimension reduction or parallel processing and without requiring feature independence. This efficiency is obtained by employing a novel Soft-Plus approximation, which enables reformulation of logistic regression parameter estimation into matrix-vector form. Additionally, unlike the multiple solvers employed in scikit-learn’s logistic regression for different regularization schemas, we present a single flexible $L_f$-norm regularization approach that also provides flexibility to include or exclude penalization of the intercept term. Our regularization approach supports a range of weight penalties through a unified codebase with a specifically designed numerical minimizer. To demonstrate the computational efficiency of our method, we conducted several quantitative experiments, comparing our method against the widely used scikit-learn library. Here, we used benchmark data from OpenML, an open machine learning data repository, and synthetic data designed for controlled experiments. Experiments demonstrate that our method effectively handles collinear features and large data while providing superior efficiency with minimal to no loss in accuracy. Our fast binary logistic regression (FBLR) exclusively utilizes the Python NumPy library. As a result, it benefits from all current capabilities of NumPy and upcoming enhancements while keeping the codebase simple. This streamlined yet powerful approach allows it to surpass the performance of scikit-learn’s logistic regression (LR) implementation in processing speed, which relies on well-established and highly optimized libraries. Our experiments demonstrate that FBLR achieves an average speedup of an order of magnitude faster, with the maximum observed speedup reaching $48.3$ times.

Proposed method

Results

We conducted experiments on a system running Ubuntu Linux 20.04 with an Intel Core i9-10900KF CPU (10 cores) and 64 GB of RAM. Note that NumPy leverages SIMD extensions supported by a CPU to a reasonable extent. For Intel Core i9-10900KF CPU, utilized SIMD extensions by NumPy are SSE, SSE2, SSE3, SSSE3, SSE4.1, SSE4.2, AVX, AVX22, F16C, and FMA3.

For the proposed FBLR method, $\lambda$ and $\gamma$ parameters are set to zero for all experiments unless stated otherwise. Also, fixed default values are used for the parameters $ϵ$, $\xi$, K, and $C_{\mathrm{t}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}}$. The parameter $ϵ$, a small positive constant for the applied $L_f$-norm approximation, is set to ${10}^{-10}$. Also, $\xi$, representing the energy percentile for low-rank approximation, is $99.9999$, excluding zeros or very small eigenvalues. The maximum number of iterations is set to $K=10$, and the convergence tolerance is set to $C_{\mathrm{t}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}}={10}^{-3}$. From this point forward, whenever logistic regression (LR) is mentioned in the text, it refers specifically to the logistic regression within scikit-learn.

Experimental results

For the experiments, we used the real-world data in Table 3 and synthetic data created with make_classification method in the scikit-learn. Real-world data is divided into $70\mathrm{\%}$ training data and $30\mathrm{\%}$ test data.

Experiments on real-world datasets

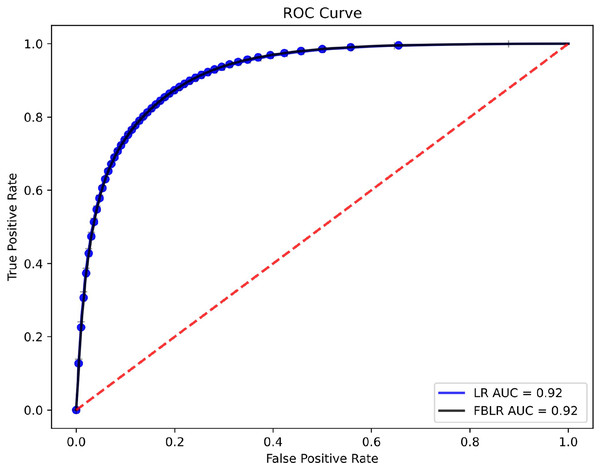
Table 6 presents the performance metrics, while Fig. 1 shows the receiver operating characteristic (ROC) curves for LR and FBLR with default parameters on the HEPMASS dataset. In LR, we used the LIBLINEAR solver for faster execution and set the maximum number of iterations to 250 to ensure high accuracy for a fair comparison. We use a single thread, even though FBLR can run with multiple threads, while LR with LIBLINEAR cannot. Experiments were run 10 times to compare LR and FBLR, showing that all metrics evaluated had an accuracy loss not exceeding 0.005, while $13.56\times$ speedup is obtained.

Table 6:

Multiple performance metrics for LR and FBLR on the HEPMASS dataset.

Metric	Train		Test
	LR	FBLR	LR	FBLR
Accuracy	0.83686	0.83583	0.83646	0.83553
Recall	0.83588	0.83124	0.83562	0.83104
Precision	0.83759	0.83901	0.83708	0.83863
F1-Score	0.83673	0.83511	0.83635	0.83481

DOI: 10.7717/peerj-cs.2579/table-6

LR is powered by LIBLINEAR, a highly efficient C/C++ library designed for large-scale linear classification, among other optimized solvers (see Table 1). On the other hand, the proposed FBLR method relies solely on the NumPy package (with openblas64 as the backbone), a core numerical library of Python. This approach ensures that FBLR takes full advantage of NumPy’s efficient handling of array operations and integration with the basic linear algebra subprograms (BLAS)² .

In Table 7, we give the comparison of LR and FBLR for OpenML datasets in terms of accuracy, time (in seconds), and speedup (LR Time/FBLR Time). No regularization is used in these experiments. In LR, we set LIBLINEAR as a solver parameter and None as a penalty parameter are chosen, while for the other parameters, default values are used. Table 7 gives the significant execution time improvements obtained by comparing FBLR to LR. Our method achieves training times up to $48.3$ times faster, on average, an order of magnitude faster than LR.

Table 7:

Single-run experiment comparing accuracy and execution time (s) of LR and proposed FBLR method without regularization on OpenML datasets.

Filename	LR ACC	FBLR ACC	LR time (s)	FBLR time (s)	Speedup
Kits	0.5700	0.5633	4.5378	0.6795	6.6780
Road-safety	0.6935	0.6956	3.7074	0.1517	24.4337
Creditcard	0.9991	0.9990	3.4729	0.2766	12.5530
Airlines2	0.5965	0.5939	5.0756	0.1051	48.3072
Colon	0.9740	0.9680	10.6571	1.0858	9.8149

DOI: 10.7717/peerj-cs.2579/table-7

In Table 8, we compare regularized LR and regularized FBLR using GridSearchCV. We used the grid search cross-validation in scikit-learn to find the best models (by searching various parameters) to compare LR and our FBLR method. It is worth mentioning that experimenting with a broader range of parameter combinations could improve both methods’ generalization and accuracy. Nonetheless, as our primary objective was to compare the speed of the methods, we maintained an equal number of experiments for consistency. In GridSearchCV, 5-folds are used. It assesses every combination of parameter values to identify the most effective combination, yielding the best classifier. Due to memory limitations in the experimental setup, results for the kits dataset could not be included for the LR algorithm in Table 8 while FBLR is able to process the kits dataset.

Table 8:

GridSearchCV experiment comparing accuracy and execution time (s) of LR and the proposed FBLR method with regularization on OpenML datasets.

Filename	LR ACC	FBLR ACC	LR time (s)	FBLR time (s)	Speedup
Kits	–	0.5667	–	18,761.8684	–
Road-safety	0.6949	0.6951	191.0991	5.8685	32.56
Creditcard	0.9992	0.9990	49.9478	11.1041	4.5
Airlines2	0.5965	0.5956	92.7151	5.9504	15.58
Colon	0.9740	0.9740	145.2604	77.7610	1.87

DOI: 10.7717/peerj-cs.2579/table-8

Table 8 presents the best accuracies and corresponding execution times and speedups for LR and FBLR on 5 OpenML datasets. For LR, we used the solvers (‘lbfgs’, ‘newton-cg’, ‘liblinear’, ‘sag’, ‘saga’) and their penalties (‘l1’, ‘l2’, ‘elasticnet’, None) as GridSearchCV search parameters. As detailed in Table 1, specific solvers may not support certain penalties, so we combine solvers and penalties in GridSearchCV accordingly. To have an equal number of experiments, we limited the FBLR parameters within a specific range and tested 12 combinations. In particular, the parameter settings for FBLR in experiments were set as follows: the norm of $L_f$-norm, $f$, was varied over the values [0, 0.5, 1, 2] and the $L_f$-norm regularization coefficient ( $\lambda$) over the values [0, 1, 2].

The proposed FBLR method is designed to prioritize computational efficiency while maintaining accuracy. We employ SVD for low-rank approximation, and with a high energy percentile (99.9999), it retains significant information. Our novel second-order Soft-Plus approximation provides a good, though not exact, fit, enhancing numerical minimization efficiency and reducing required iterations ( $k$), with minimal potential accuracy loss. If desired, the weight vector from FBLR can be fine-tuned with an efficient Logistic Regression method in just a few iterations for a precise result.

Experiments on synthetic dataset

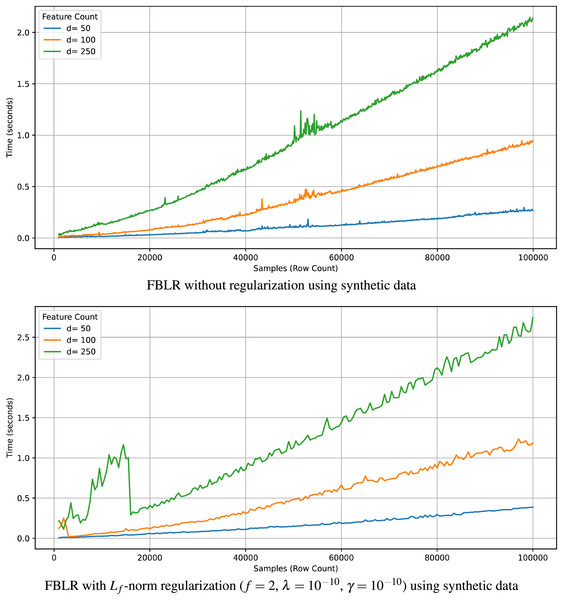
Recall that the computational complexity of the proposed FBLR method is $O(n{d}^{2}k)$ when regularization is applied and $O(ndmax(d,k))$ without regularization. Here, $n$ denotes the number of rows, $d$ denotes the number of features, $k$ denotes the number of iterations, and K denotes the maximum number of iterations. When $d\ge K$, the expression $max(d,k)$ simplifies to $d$, given that $k\le K$, where $k$ iterates up to a maximum of K. Therefore, computational complexity without regularization becomes $O(n{d}^{2}k)$. In accordance, Fig. 2 illustrates that the execution time of FBLR scales linearly with $n$ and exhibits a near-quadratic growth with respect to $d$. Note that we analyzed the theoretical and computational complexity with respect to practical execution times on synthetic datasets since we have more control over synthetic data.

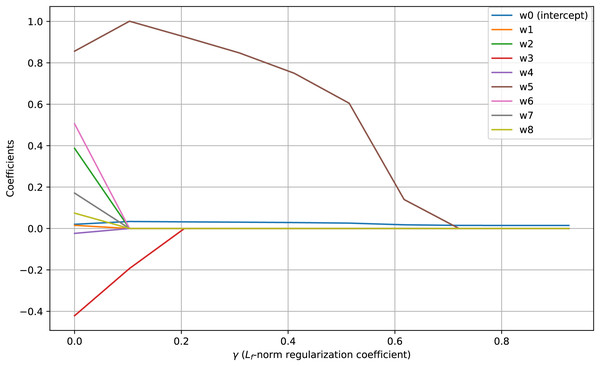
Visualization of regularization paths presents change of feature coefficients as the regularization parameter changes. When coefficients of features drop to zero corresponding feature is removed. Figure 3 shows regularization paths for coefficients of the proposed FBLR method under $L_0$-norm regularization. It illustrates the effect of $L_0$-norm regularization in promoting sparsity within the model’s parameters ( $w_1$ to $w_8$). Sharpness in $L_0$-norm regularization paths and the reduction of weight coefficients to $0$ demonstrate the effectiveness of the proposed $L_f$-norm regularizer in promoting sparsity for $f=0$. Note that, the intercept term, $w_0$, remains unpenalized and almost constant across varying regularization levels determined by the $\gamma$ parameter. Applying regularization without penalizing the intercept is one strong feature of the proposed FBLR method which is not directly supported by LR. In scikit-learn, non-penalizing the intercept requires non-trivial parameter tweaking and also very data dependent.

Conclusion and discussion

This study presents a novel approach, namely fast binary logistic regression (FBLR), to enhance the training efficiency of binary logistic regression. FBLR reduces training times, achieving speeds that are, on average, an order of magnitude faster than those of scikit-learn’s logistic regression, courtesy of the efficient numerical minimizer we developed. Moreover, unlike scikit-learn’s logistic regression, which utilizes multiple solvers, we propose a single, efficient solver that incorporates a second-order accurate Soft-Plus approximation and flexible $L_f$-norm regularizer. This approach supports various weight penalties, thereby enhancing the training process for versatile models. Compared to scikit-learn, our approach relies on a single solver, simplifying the code and improving maintainability.

Furthermore, we have devised a low-rank approximation strategy to address collinearity among features. Our low-rank approach harnesses randomized SVD for high-dimensional feature sets and also a novel SVD with row reduction (SVD-RR) approach, tailored specifically for large datasets containing numerous rows. For smaller to moderate-sized datasets, we just employ truncated SVD. Also, we introduce an innovative strategy to determine the optimal transition from truncated SVD to randomized SVD. To mitigate the dominance of overly large eigenvalues, the logarithm of the eigenvalues was employed to establish the rank, $r$, suitable for low-rank approximation. The achieved computational efficiency is crucial for crafting generalized logistic regression models, enabling iterative parameter tuning to achieve an optimal balance between bias and variance.

In addition to existing computational efficiencies, further acceleration can be achieved by applying stochastic gradient descent or mini-batch methods for faster approximate gradient evaluation. Also, parallel computing frameworks such as CuPy, Numba, PyCUDA, or PyTorch can be utilized. Additionally, deploying a caching strategy for SVD and storing the compact diagonal sparse matrix $\mathbf{S}$ and the dense square matrix $\mathbf{V}$ in a dictionary can enable efficient reuse. Matrix $\mathbf{U}$ can be computed using Eq. (41) once diagonal matrix $\mathbf{S}$ and square matrix $\mathbf{V}$ are retrieved using the hash code of input data $\mathbf{X}$. This is particularly useful for repeated training sessions when performing best-parameter searches in scikit-learn. Originally conceived for binary labels, our method possesses sufficient flexibility to accommodate multinomial classifications using the inherent functions provided by scikit-learn. Nonetheless, our approach offers no advantage over scikit-learn’s logistic regression for handling missing values. Also, similar to scikit-learn’s logistic regression, our method is limited to handling linearly separable data. The matrix-vector form of our cost function, resembling Ridge Regression, allows our method to incorporate kernel methods like Kernel Ridge Regression, enabling nonlinear data handling while supporting linear data in its current form. Such kernel method extension can benefit from techniques such as Random Fourier Features (RFF) (Rahimi & Recht, 2007) to increase execution time performance further.

Appendix

Approximation of soft-plus

The quadratic approximation of $\log (1+e^{\tau })$ at $\hat{\tau }$ is defined as:

(23) $$\log (1+e^{\tau })\approx z{\tau }^2+q\tau +t$$where $\hat{\tau }$ is a proxy constant for $\tau$ and $z$, $q$, and $t$ are all constant coefficients.

First, we determine $t$ by substituting $0$ to $\tau$ as in Eq. (24):

(24) $$\log (1+e^0)\approx z{0}^2+q0+t$$

(25) $$t=\log (2).$$

Then, for $\tau =0$, we have $z=\frac{1}{8}$ and $q=\frac{1}{2}$ using Maclaurin series. Next, for $\tau \ne 0$, to find the value of $q$ and $z$, we compute the equation at $-\hat{\tau }$ and $\hat{\tau }$

(26) $$\log (1+e^{\hat{\tau }})\approx z{\hat{\tau }}^2+q\hat{\tau }+\log 2$$

(27) $$\log (1+e^{-\hat{\tau }})\approx z{\hat{\tau }}^2-q\hat{\tau }+\log 2.$$

By subtracting the Eq. (27) from the Eq. (26) we obtain

(28) $$q=\frac{\log (1+e^{\hat{\tau }})-\log (1+e^{-\hat{\tau }})}{2\hat{\tau }}.$$

Note that,

(29) $$\log (1+e^{-\hat{\tau }})=\log (1+e^{\hat{\tau }})-\hat{\tau }.$$

Then, we obtain $q=\frac{1}{2}$ by plugging Eq. (29) into Eq. (28).

Finally plugging $q$ and $t$ into Eq. (26), we obtain

(30) $$z=\frac{\log (1+e^{\hat{\tau }})-\log 2}{{\hat{\tau }}^2}-\frac{1}{2\hat{\tau }}$$which leads to the below approximation at point $\hat{\tau }$:

(31) $$\log (1+e^{\tau })\approx z{\tau }^2+\frac{1}{2}\tau +\log 2\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{z}=\{\begin{array}{cc}\frac{1}{8}\hfill & \mathrm{f}\mathrm{o}\mathrm{r}\hat{\tau }=0\\ \frac{\log (1+{\mathrm{e}}^{\hat{\tau }})-\log 2}{{\hat{\tau }}^2}-\frac{1}{2\hat{\tau }}& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}$$

Note that our quadratic Soft-Plus approximation is specifically designed for minimizing $-\log l(w)$ and differs from second-order Taylor series-based approximation. Compared to the second-order Taylor approximation, our Soft-Plus approximation more effectively adapts to the shape of the Soft-Plus function, being exact at both the approximation point and the origin. This provides a more accurate quadratic approximation for minimizing the cost function. The second-order Taylor approximation of Eq. (23) at $\hat{\tau }$ is given as below which is different than our approximation:

(32) $$\begin{array}{rl}\log (1+e^{\tau })& \approx \left(\frac{e^{\hat{\tau }}}{2{(1+e^{\hat{\tau }})}^2}\right){\tau }^2\\ & +(\frac{e^{\hat{\tau }}}{1+e^{\hat{\tau }}}-\frac{\hat{\tau }{e}^{\hat{\tau }}}{{(1+e^{\hat{\tau }})}^2})\tau \\ & +(\log (1+e^{\hat{\tau }})-\frac{\hat{\tau }{e}^{\hat{\tau }}}{1+e^{\hat{\tau }}}+\frac{{\hat{\tau }}^2{e}^{\hat{\tau }}}{2{(1+e^{\hat{\tau }})}^2}).\end{array}$$

Empirical quadratic approximation of soft-plus

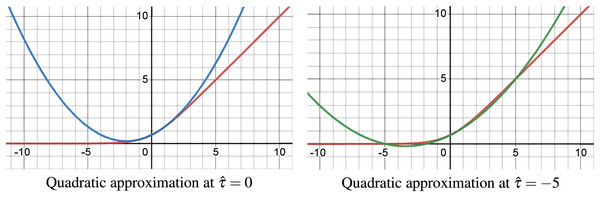
The employed quadratic approximation of the Soft-Plus function given in Eq. (23) at point $\hat{\tau }=0$ and $\hat{\tau }=-5$ are shown in Fig. 4. These approximations are exact at both the approximated point ( $\hat{\tau }$) and the origin ( $\tau =0$), with high accuracy between them, but become less accurate outside this range. In contrast, the second-order Taylor approximation only guarantees exactness at the approximation point $\hat{\tau }$.

Approximation Of $L_f$-norm

We also approximated smooth $L_f(\rho )={\rho }^2(|\rho {|}^{2-f}+ϵ{)}^{-1}$ quadratically at a point $\hat{\rho }$ where $u$ is defined as a constant. Here, $\hat{\rho }$ is a proxy constant for $\rho$. Quadratic approximation of smooth $L_f(\rho )$ function is:

(33) $$L_f(\rho )\approx {\rho }^2(|\hat{\rho }{|}^{2-f}+ϵ{)}^{-1}=u{\rho }^2\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{u}={\left({\left|\hat{\rho }\right|}^{2-\mathrm{f}}+ϵ\right)}^{-1}.$$

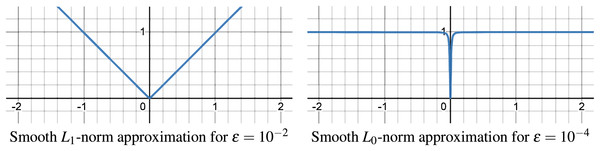
Optimization problems with $L_0$ terms are combinatorial, requiring discrete decisions to minimize non-zero elements, making direct approaches computationally impractical for large-scale issues. Smooth approximations are employed as a solution, substituting the $L_0$ with a continuous, differentiable function that mimics the counting of non-zero elements. Similarly, our $L_f$-norm approximation smoothly mirrors the $L_1$-norm for $f=1$ and $L_0$-norm for $f=0$, as illustrated in Fig. 5. With our smooth approximation, as $ϵ$ gets smaller approximation gets better (default $ϵ={10}^{-10}$).

Despite the $L_1$-norm and $L_0$-norm approximation in Fig. 5 being precise even for relatively large $ϵ$ values ( $ϵ={10}^{-2}$ and $ϵ={10}^{-4}$), its direct use is unsuitable within our cost function, leading us to employ a quadratic approximation over this smooth approximation. The quadratic approximations of the $L_f$-norm for $L_1$-norm ( $f=1$) and for $L_0$-norm ( $f=0$) are depicted in Fig. 6.

SVD with row reduction

In the case of a large data matrix $\mathbf{X}\in {\mathbb{R}}^{n\times d}$, truncated SVD is computationally demanding due to its complexity $O(n{d}^2)$. In scenarios where $d^2$ becomes large, the computational burden of applying SVD is mitigated by utilizing randomized SVD (Halko, Martinsson & Tropp, 2010; Halko et al., 2011; Martinsson et al., 2010). However, this method is less effective in dealing with cases where $n$ is large. In such instances, a large subset of the matrix $\mathbf{X}$ can sufficiently mimic the statistical properties of the full data set. Hence, we sub-sample matrix $\mathbf{X}$ to create $\tilde{\mathbf{X}}$, consisting of $m$ rows. This sub-sampling involves randomly or sequentially selecting $m$ rows from $\mathbf{X}$ where we just sub-sampled the first $m$ rows. Note that one can employ a sampling mechanism proposed in Menon & Elkan (2011), such as the Drineas, Kannan, and Mahoney method, to obtain better statistical guarantees for the sampled subset. We use a simple sampling mechanism where we set $m$ to a sufficiently large value, ${10}^5$, ensuring $\mathbf{X}$’s statistical preservation and reducing computational demands for $n>2m$, thus outperforming direct SVD on the full matrix. However, $\mathbf{U}$ returned by SVD applied on $\tilde{\mathbf{X}}$ is now $m\times d$ instead of $n\times d$ and also $\mathbf{S}$ requires normalization. To address these issues, we define the covariance matrices for the full matrix $\mathbf{X}$ and the subsampled matrix $\tilde{\mathbf{X}}$ as follows:

(34) $$\mathbf{C}=\frac{1}{n-1}{\mathbf{X}}^{\mathrm{\top }}\mathbf{X}$$

(35) $$\tilde{\mathbf{C}}=\frac{1}{m-1}{\tilde{\mathbf{X}}}^{\mathrm{\top }}\tilde{\mathbf{X}}.$$

Assuming $\tilde{\mathbf{X}}$, a large subset of $\mathbf{X}$, reflects the dataset’s statistics, their covariances are nearly equal ( $\mathbf{C}\approx \tilde{\mathbf{C}}$):

(36) $$\frac{1}{n-1}{\mathbf{X}}^{\mathrm{\top }}\mathbf{X}\approx \frac{1}{m-1}{\tilde{\mathbf{X}}}^{\mathrm{\top }}\tilde{\mathbf{X}}.$$

Applying the definition of SVD to both matrices, represented as $\mathbf{X}=\mathbf{U}\mathbf{S}{\mathbf{V}}^{\mathrm{\top }}$ and $\tilde{\mathbf{X}}=\tilde{\mathbf{U}}\tilde{\mathbf{S}}{\tilde{\mathbf{V}}}^{\mathrm{\top }}$ respectively, the aforementioned equation can be reformulated as follows:

(37) $$\frac{1}{n-1}(\mathbf{U}\mathbf{S}{\mathbf{V}}^{\mathrm{\top }}{)}^{\mathrm{\top }}(\mathbf{U}\mathbf{S}{\mathbf{V}}^{\mathrm{\top }})\approx \frac{1}{m-1}(\tilde{\mathbf{U}}\tilde{\mathbf{S}}{\tilde{\mathbf{V}}}^{\mathrm{\top }}{)}^{\mathrm{\top }}(\tilde{\mathbf{U}}\tilde{\mathbf{S}}{\tilde{\mathbf{V}}}^{\mathrm{\top }}).$$