Image based visual servoing with kinematic singularity avoidance for mobile manipulator

Omnidirectional mobile manipulator kinematics

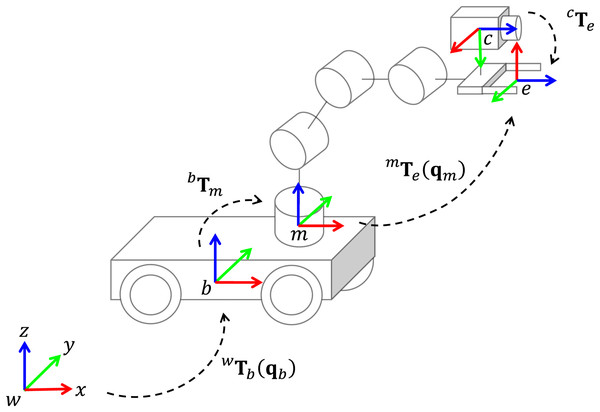
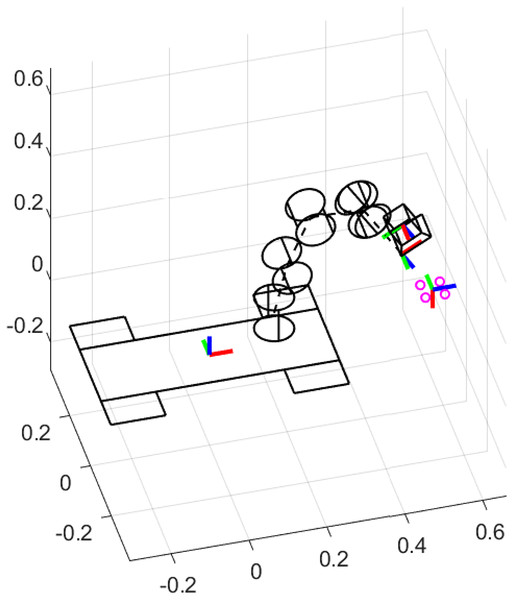
The eye-in-hand system with coordinate frame assignments for robot kinematics is illustrated in Fig. 1. We start defining the following homogeneous matrices: ${}^w{\mathbf{T}}_b$ represents the position and orientation (pose) of the mobile platform, with respect to the world frame, ${}^b{\mathbf{T}}_m$ is a constant transformation between the mobile platform and the manipulator base, ${}^m{\mathbf{T}}_e$ is the transformation from the manipulator base to the end-effector frame. Finally, ${}^c{\mathbf{T}}_e$ is the position and orientation of the end-effector, with respect to the camera frame.

The mobile platform pose ${}^w{\mathbf{T}}_b$ is defined as

(10) $${}^w{\mathbf{T}}_b({\mathbf{q}}_b)=\left[\begin{array}{cccc}\cos \left({\theta }_b\right)& -\sin \left({\theta }_b\right)& 0& x_b\\ \sin \left({\theta }_b\right)& \cos \left({\theta }_b\right)& 0& y_b\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$where ${\mathbf{q}}_{\mathbf{b}}={\left[\begin{array}{ccc}{x}_b& y_b& {\theta }_b\end{array}\right]}^T$ represents the position $(x_b,y_b)$ and orientation ${\theta }_b$ of the omnidirectional platform.

Let ${\mathbf{q}}_{\mathbf{m}}={\left[\begin{array}{cc}{q}_1& q_2\cdots q_n\end{array}\right]}^T$ be the manipulator configuration with $n$ DOF. The manipulator kinematics ${}^m{\mathbf{T}}_e({\mathbf{q}}_m)$ can be computed based on the Denavit-Hartenberg (DH) convention. Then, forward kinematic ${}^0{\mathbf{T}}_n({\mathbf{q}}_m)$ can be defined as

(11) $${}^m{\mathbf{T}}_e({\mathbf{q}}_m)={}^0{\mathbf{T}}_n({\mathbf{q}}_m)={}^0{\mathbf{T}}_1\left(q_1\right){}^1{\mathbf{T}}_2\left(q_2\right)\cdots {}^{n-1}{\mathbf{T}}_n\left(q_n\right)$$where ${}^{i-1}{\mathbf{T}}_i$ transforms the frame attached to the link $i-1$ into the frame link $i$ of the robot manipulator, with $i=0,1,2,\cdots ,n$.

The joint variable for the mobile manipulator is given by $\mathbf{q}=\left[\begin{array}{cc}{\mathbf{q}}_b^T& {\mathbf{q}}_m^T\end{array}\right]$. The forward kinematics ${}^w{\mathbf{T}}_e(\mathbf{q})$ of the mobile manipulator is obtained with

(12) $${}^w{\mathbf{T}}_e(\mathbf{q})={}^w{\mathbf{T}}_b({\mathbf{q}}_b{)}^b{{\mathbf{T}}_m}^m{\mathbf{T}}_e({\mathbf{q}}_m)=\left[\begin{array}{cc}{}^w{\mathbf{R}}_e& {}^w{\mathbf{t}}_e\\ 0& 1\end{array}\right]$$where ${}^w{\mathbf{R}}_e$ is the orientation and ${}^w{\mathbf{t}}_e$ the position of the end-effector, with respect to the world frame $w$.

Inverse kinematics involves calculating the joint variables $\mathbf{q}$ given the desired end-effector pose. This calculation can be achieved by minimizing an error function through an iterative process based on differential kinematics (Sciavicco & Siciliano, 2012). Differential kinematics seeks to establish the relationship between the joint velocities $\dot{\mathbf{q}}$ and the end-effector velocity $\dot{\mathbf{x}}$.

(13) $$\dot{\mathbf{x}}=\mathbf{J}(\mathbf{q})\dot{\mathbf{q}}$$where $\mathbf{J}$ is a Jacobian matrix and $\dot{\mathbf{x}}=(v_e,{\mathit{\omega }}_e)$. $v_e$ and ${\mathit{\omega }}_e$ are instantaneous linear and angular velocities of the end-effector. Moreover, $\dot{\mathbf{q}}=\left[\begin{array}{cc}{\dot{\mathbf{q}}}_b^T& {\dot{\mathbf{q}}}_m^T\end{array}\right]$ where ${\dot{\mathbf{q}}}_b^T$ are the mobile platform velocities $({\dot{x}}_b,{\dot{y}}_b,{\dot{\theta }}_b)$, and ${\dot{\mathbf{q}}}_m^T$ are the manipulator velocities in joint space.

The Jacobian matrix $\mathbf{J}$ can be computed as follows

(14) $$\mathbf{J}\left(\mathbf{q}\right)=\left[\begin{array}{c}{\mathbf{J}}_v\left(\mathbf{q}\right)\\ {\mathbf{J}}_{\omega }\left(\mathbf{q}\right)\end{array}\right]$$where ${\mathbf{J}}_v\left(\mathbf{q}\right)$ matrix relating the contribution of the end-effector linear velocity, and ${\mathbf{J}}_{\omega }\left(\mathbf{q}\right)$ matrix relating the contribution of the end-effector angular velocity.

The matrix ${\mathbf{J}}_v\left(\mathbf{q}\right)$ is defined as

(15) $${\mathbf{J}}_v\left(\mathbf{q}\right)=\left[\begin{array}{ccccccc}{\displaystyle \frac{\mathrm{\partial }{t}_x}{\mathrm{\partial }{x}_b}}& {\displaystyle \frac{\mathrm{\partial }{t}_x}{\mathrm{\partial }{y}_b}}& {\displaystyle \frac{\mathrm{\partial }{t}_x}{\mathrm{\partial }{\theta }_b}}& {\displaystyle \frac{\mathrm{\partial }{t}_x}{\mathrm{\partial }{q}_1}}& {\displaystyle \frac{\mathrm{\partial }{t}_x}{\mathrm{\partial }{q}_2}}& {\displaystyle \cdots }& {\displaystyle \frac{\mathrm{\partial }{t}_x}{\mathrm{\partial }{q}_n}}\\ {\displaystyle \frac{\mathrm{\partial }{t}_y}{\mathrm{\partial }{x}_b}}& {\displaystyle \frac{\mathrm{\partial }{t}_y}{\mathrm{\partial }{y}_b}}& {\displaystyle \frac{\mathrm{\partial }{t}_y}{\mathrm{\partial }{\theta }_b}}& {\displaystyle \frac{\mathrm{\partial }{t}_y}{\mathrm{\partial }{q}_1}}& {\displaystyle \frac{\mathrm{\partial }{t}_y}{\mathrm{\partial }{q}_2}}& {\displaystyle \cdots }& {\displaystyle \frac{\mathrm{\partial }{t}_y}{\mathrm{\partial }{q}_n}}\\ {\displaystyle \frac{\mathrm{\partial }{t}_z}{\mathrm{\partial }{x}_b}}& {\displaystyle \frac{\mathrm{\partial }{t}_z}{\mathrm{\partial }{y}_b}}& {\displaystyle \frac{\mathrm{\partial }{t}_z}{\mathrm{\partial }{\theta }_b}}& {\displaystyle \frac{\mathrm{\partial }{t}_z}{\mathrm{\partial }{q}_1}}& {\displaystyle \frac{\mathrm{\partial }{t}_z}{\mathrm{\partial }{q}_2}}& {\displaystyle \cdots }& {\displaystyle \frac{\mathrm{\partial }{t}_z}{\mathrm{\partial }{q}_n}}\end{array}\right]$$where ${}^w{\mathbf{t}}_e={\left[\begin{array}{ccc}{t}_x& t_y& t_z\end{array}\right]}^T$ is the end-effector position related to the joint variable $\mathbf{q}$. Moreover, the matrix ${\mathbf{J}}_{\omega }\left(\mathbf{q}\right)$ is defined as

(16) $${\mathbf{J}}_{\omega }\left(\mathbf{q}\right)=\left[\begin{array}{cccc}0& 0& {}^w{\mathbf{z}}_0& {}^w{\mathbf{z}}_1\cdots {}^w{\mathbf{z}}_{n-1}\end{array}\right]$$where ${}^w{\mathbf{z}}_m$ and ${}^w{\mathbf{z}}_i$ are the z-axis of the rotation matrices ${}^w{\mathbf{R}}_m$ and ${}^w{\mathbf{R}}_i$, respectively. Notice that the first two rows are set to $\mathbf{0}$ since $x_b$ and $y_b$ displacements do not provoke any end-effector angular velocity.

Rotation matrix ${}^w{\mathbf{R}}_i$ can be found in the homogeneous transformation ${}^w{\mathbf{T}}_i(\mathbf{q})$, which is

(17) $${}^w{\mathbf{T}}_i(\mathbf{q})={}^w{\mathbf{T}}_b({\mathbf{q}}_b{)}^b{\mathbf{T}}_m\prod _{j=1}^{j=i}{}^{j-1}{\mathbf{T}}_j(q_j)=\left[\begin{array}{cc}{}^w{\mathbf{R}}_i& {}^w{\mathbf{t}}_i\\ \mathbf{0}& 1\end{array}\right].$$

Finally, the mapping between the mobile platform ${\dot{\mathbf{q}}}_b^T$ to each wheel velocity is given by the following relationship

(18) $$\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\\ v_4\end{array}\right]=\left[\begin{array}{ccc}\sqrt{2}\sin \left({\theta }_b+\frac{\pi }{4}\right)& -\sqrt{2}\cos \left({\theta }_b+\frac{\pi }{4}\right)& -\left(L+l\right)\\ \sqrt{2}\cos \left({\theta }_b+\frac{\pi }{4}\right)& \sqrt{2}\sin \left({\theta }_b+\frac{\pi }{4}\right)& \left(L+l\right)\\ \sqrt{2}\cos \left({\theta }_b+\frac{\pi }{4}\right)& \sqrt{2}\sin \left({\theta }_b+\frac{\pi }{4}\right)& -\left(L+l\right)\\ \sqrt{2}\sin \left({\theta }_b+\frac{\pi }{4}\right)& -\sqrt{2}\cos \left({\theta }_b+\frac{\pi }{4}\right)& \left(L+l\right)\end{array}\right]\left[\begin{array}{c}{\dot{x}}_b\\ {\dot{y}}_b\\ {\dot{\theta }}_b\end{array}\right]$$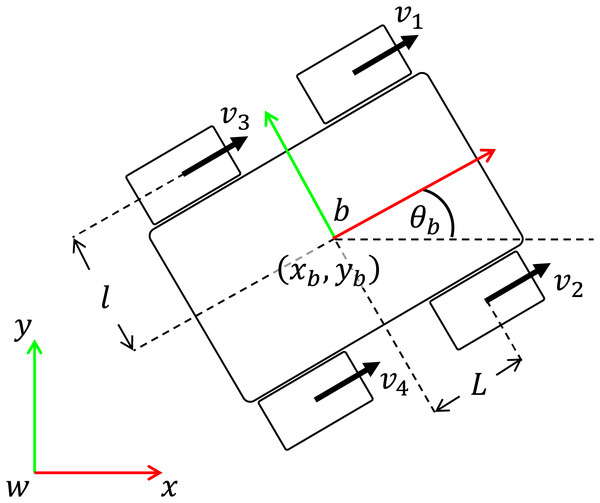where $v_i$ is the linear velocity of wheel $i$, L is half of the distance between the front and the rear wheels, and $l$ is half of the distance between the left and the right wheels, see Fig. 2.

Eye-in-hand scheme with task priority and gravity compensation

To consider an eye-in-hand scheme for mobile manipulator visual servoing, we propose to rewrite (Eq. (9)) to map the camera velocity control to the end-effector velocity expressed in the world frame, which is

(19) $${\mathbf{v}}_w=-\lambda {\left({{\mathbf{L}}_{\mathbf{s}}}^c{\mathbf{V}}_w\right)}^{+}\mathbf{e}$$where ${}^c{\mathbf{V}}_w$ is a spatial motion transform matrix from the camera frame to the world frame, and ${\mathbf{v}}_w=(v_w,{\mathit{\omega }}_w)$ contains the linear $v_w$ and angular ${\mathit{\omega }}_w$ velocity expressed in the world frame. The matrix ${}^c{\mathbf{V}}_w$ is given as

(20) $${}^c{\mathbf{V}}_w=\left[\begin{array}{cc}{}^c{\mathbf{R}}_w& {\left[{}^c{\mathbf{t}}_w\right]}_{\times }\\ \mathbf{0}& {}^c{\mathbf{R}}_w\end{array}\right]$$where ${\left[{}^c{\mathbf{t}}_w\right]}_{\times }$ is the skew-symmetric matrix associated with the vector ${}^c{\mathbf{t}}_w$, and ${}^c{\mathbf{T}}_w{(}^c{\mathbf{R}}_w{,}^c{\mathbf{t}}_w)$ is the transformation matrix from camera to world frame, which is computed as

(21) $${}^c{\mathbf{T}}_w(\mathbf{q})={{}^c{\mathbf{T}}_e}^w{\mathbf{T}}_e(\mathbf{q}{)}^{-1}=\left[\begin{array}{cc}{}^c{\mathbf{R}}_w& {}^c{\mathbf{t}}_w\\ \mathbf{0}& 1\end{array}\right].$$

To map Cartesian velocities ${\mathbf{v}}_w=\dot{\mathbf{x}}$ to joint velocities $\dot{\mathbf{q}}$, using Eq. (13) we have

(22) $$\dot{\mathbf{q}}=\mathbf{J}(\mathbf{q}{)}^{+}{\mathbf{v}}_w$$where $\mathbf{J}(\mathbf{q}{)}^{+}$ is the Moore-Penrose pseudoinverse of $\mathbf{J}(\mathbf{q})$.

To overcome the problem of inverting $\mathbf{J}(\mathbf{q}{)}^{+}$ in the neighborhood of a singularity is provided by the damped least-square (DLS) inverse

(23) $$\mathbf{J}(\mathbf{q}{)}^{+}=\mathbf{J}(\mathbf{q}{)}^T{\left(\mathbf{J}(\mathbf{q})\mathbf{J}{(\mathbf{q})}^T+{\beta }^2\mathbf{I}\right)}^{-1}$$where $\beta$ is a damping factor that improves the conditioning of the inversion from a numerical viewpoint. DLS helps reduce the impact of singular configurations, which occur when $\mathbf{J}{\mathbf{J}}^T$ is not full rank (that is, when its determinant is zero or any of its eigenvalues are zero).

Consider the eigenvalue decomposition $\mathbf{J}{\mathbf{J}}^T=\mathbf{U}\mathrm{\Sigma }{\mathbf{V}}^T$, the matrix $\mathrm{\Sigma }$ is a diagonal matrix containing the eigenvalues $\left\{{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n\right\}$. If we invert the decomposition, we get $(\mathbf{J}{\mathbf{J}}^T{)}^{-1}=\mathbf{V}{\mathrm{\Sigma }}^{+}{\mathbf{U}}^T$, where ${\mathrm{\Sigma }}_{ii}^{+}=\frac{1}{{\sigma }_i}$.

A singularity configuration will have some ${\sigma }_i=0$; we get a stable inversion if we add a positive scalar ${\beta }^2$, as shown in Eq. (24).

(24) $${\mathrm{\Sigma }}_{ii}^{+}=\frac{1}{{\sigma }_i+{\beta }^2}.$$

Then, the stabilized $i$-eigenvalue will be ${\sigma }_i+{\beta }^2$. The final form (Eq. (25)) is the well-known solution of the Thikonov regularization (Nair, Hegland & Anderssen, 1997; Gerth, 2021).

(25) $$\mathbf{U}(\mathrm{\Sigma }+{\beta }^2\mathbf{I}){\mathbf{V}}^T=\mathbf{U}\mathrm{\Sigma }{\mathbf{V}}^T+{\beta }^2\mathbf{U}{\mathbf{V}}^T=\mathbf{J}{\mathbf{J}}^T+{\beta }^2\mathbf{I}.$$

Moreover, this work considers a task priority scheme to deal with feature error convergence of the visual servoing task while maximizing the mobile robot manipulability. The task priority scheme is given by

(26) $$\dot{\mathbf{q}}=\mathbf{J}(\mathbf{q}{)}^{+}{\mathbf{v}}_w+\left(\mathbf{I}-\mathbf{J}{(\mathbf{q})}^{+}\mathbf{J}(\mathbf{q})\right){\dot{\mathbf{q}}}_0$$where ${\mathbf{v}}_w$ is the main task, and $\left(\mathbf{I}-\mathbf{J}{(\mathbf{q})}^{+}\mathbf{J}(\mathbf{q})\right)$ allows the projection of the second task ${\dot{\mathbf{q}}}_0$ into the null space of $\mathbf{J}$.

In this work, we propose a vector ${\dot{\mathbf{q}}}_0$ to avoid singularities based on the manipulability measure $m(\mathbf{q})$ defined as

(27) $$m(\mathbf{q})=\sqrt{det\left(\mathbf{J}\left(\mathbf{q}\right)\mathbf{J}{\left(\mathbf{q}\right)}^T\right)}.$$

The second task ${\dot{\mathbf{q}}}_0$ is calculated with

(28) $${\dot{\mathbf{q}}}_0=k_0\left(\frac{\mathrm{\partial }m(\mathbf{q})}{\mathrm{\partial }\mathbf{q}}\right)$$where $k_0>0$. The robot redundancy is exploited to avoid kinematic singularities by maximizing the manipulability measure. Indeed, ${\dot{\mathbf{q}}}_0$ can be designed for collision avoidance by letting the joints reconfigure to avoid obstacles without affecting the primary task. Moreover, ${\dot{\mathbf{q}}}_0$ can also be designed for joint limit avoidance by guiding the joint configuration towards the middle of their range while simultaneously performing the primary task.

Finally, a gravity compensation term is also considered, which is crucial for real-world implementations. Let us consider the gravitational potential energy as follows

(29) $$\mathbf{u}(\mathbf{q})=g\sum _{i=1}^n{m}_i{h}_i\left(\mathbf{q}\right)$$where $g$ is the gravity acceleration, $m_i$ is the mass of the link $i$ and $h_i$ is the height of the center of mass and it depends on $\mathbf{q}$. For simplicity, we estimate the center of mass at the middle of the link.

The gravity vector $\mathbf{g}(\mathbf{q})$ is calculated with

(30) $$\mathbf{g}(\mathbf{q})=\frac{\mathrm{\partial }}{\mathrm{\partial }\mathbf{q}}\mathbf{u}(\mathbf{q}).$$

Finally, the term $\mathbf{g}(\mathbf{q})$ in Eq. (30) is added to Eq. (26)

(31) $$\dot{\mathbf{q}}=\mathbf{J}(\mathbf{q}{)}^{+}{\mathbf{v}}_w+\left(\mathbf{I}-\mathbf{J}{(\mathbf{q})}^{+}\mathbf{J}(\mathbf{q})\right){\dot{\mathbf{q}}}_0+\mathbf{g}(\mathbf{q}).$$

Equation (31) defines the proposed eye-in-hand scheme with task priority and gravity compensation for a mobile manipulator with an omnidirectional platform.

Simulation results

In simulation tests, four coordinates of interest points in the image were considered, where the desired image features ${\mathbf{s}}_d$ was set as

(35) $${\mathbf{s}}_d={\left[\begin{array}{cccccccc}-0.1302& -0.1492& 0.1302& -0.1492& 0.1302& 0.1113& -0.1302& 0.1113\end{array}\right]}^T$$

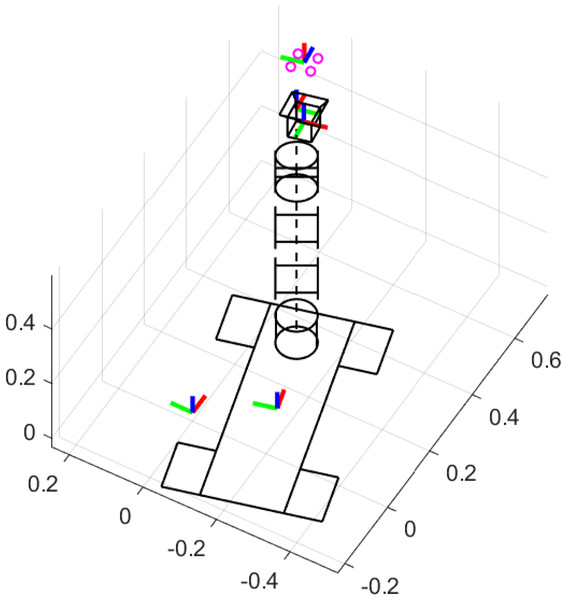
Moreover, the intrinsic parameters of the camera were set as $f=600$, $C_u=320$, $C_v=240$. The simulation scenario of the ideal case is given in Fig. 3.

The ideal simulation aims to show that the second task in Eq. (26) is increasing the manipulability measure while performing the IBVS task with high priority.

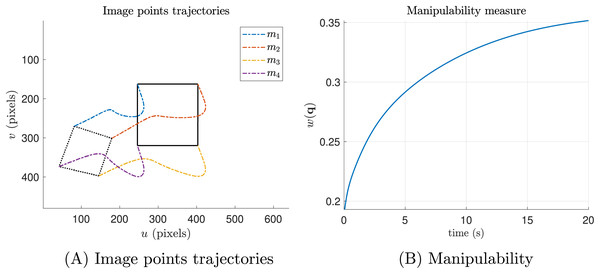
Figure 4 shows the results when the secondary task is not included. Figure 4A the dashed lines represent the starting positions, while the solid lines indicate the desired positions. The colored dashed lines illustrate the trajectories of each keypoint. Although the keypoints reach the desired pose, Fig. 4B shows that, since the secondary task is not included, the manipulability measure does not exceed 0.3.

Conversely, in Fig. 5, we present the results of the same simulation, but with the secondary task included. It is evident that the manipulability measure increases, in contrast to the previous experiment (Fig. 4).

As we can see, Figs. 4A and 5A the image point trajectories (colored dashed lines) confirm that the primary task is being performed successfully.

In addition, in Fig. 6A we show the transition of the image features, where the dashed lines can be seen converging at the desired positions, represented by solid lines. In Fig. 6B we present the joint velocities of the mobile manipulator while performing both the primary and secondary tasks. It can be observed that the velocities converge smoothly to a neighborhood of zero, indicating that the desired positions have been reached.

A singularity test experiment is performed to validate the capacities of the proposed approach to avoid singularities and smooth out discontinuities by inverting the Jacobian matrix based on DLS, see Eq. (23). In this experiment, we also compared the proposal against the classical IBVS

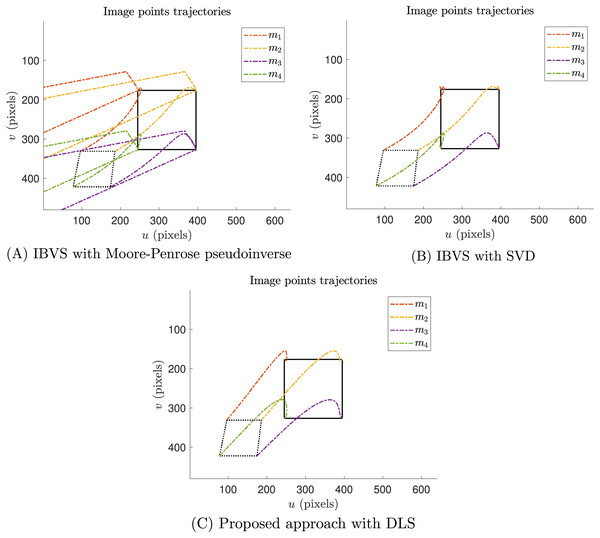
(36) $${\mathbf{v}}_w=-\lambda {\left({{\mathbf{L}}_{\mathbf{s}}}^c{\mathbf{V}}_w\mathbf{J}(\mathbf{q})\right)}^{+}\mathbf{e}$$where the inversion of ${\mathbf{A}}^{+}$ with $\mathbf{A}={{\mathbf{L}}_{\mathbf{s}}}^c{\mathbf{V}}_w\mathbf{J}(\mathbf{q})$ was performed in two ways, using singular value decomposition (SVD) and using the well-known Moore-Penrose pseudoinverse ${\mathbf{A}}^{+}={\mathbf{A}}^T{\left(\mathbf{A}{\mathbf{A}}^T\right)}^{-1}$. SVD in the form $\mathbf{A}=\mathbf{U}\mathrm{\Sigma }\mathbf{V}$ is another method to deal with singularities. To compute the inverse of $\mathbf{A}$, singular values along the diagonal of $\mathrm{\Sigma }$ that are less or equal to a tolerance are treated as zero. Then, all the non-zero values of $\mathrm{\Sigma }$ can be inverted.

Figure 7 illustrates the simulation scenario to perform the singularity test experiment. To identify singularities, Monte Carlo experiments were performed to randomly select numerical joint configurations that provoke the determinant of $\mathbf{J}{\mathbf{J}}^T$ is close to 0. Then, four coordinates of interest points in the 3D world were intentionally placed near the position of the end-effector related to a singular joint configuration.

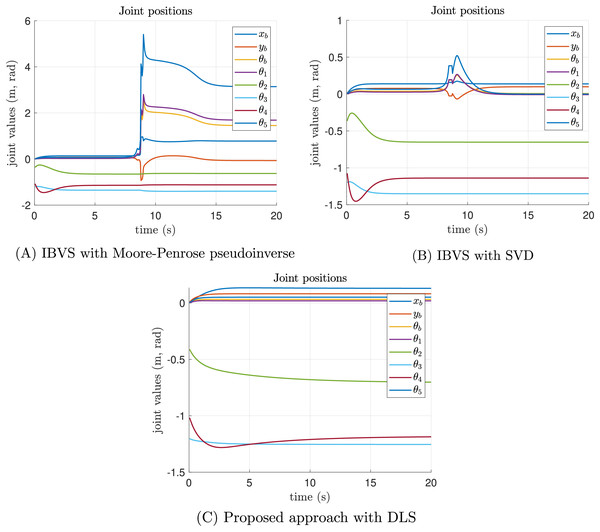
Figure 8 presents the joint positions results along time of the singularity test experiment. As can be seen in Fig. 8A, the Moore-Penrose pseudoinverse suffers from singularities around 9 s of simulation time. Abrupt changes in joint position are presented. Figure 8B shows that SVD reduces the impact of singularities and all joint positions are admissible. However, Fig. 8C demonstrates that the proposed approach significantly reduces the impact of singularities, since joint positions are not perturbed at all.

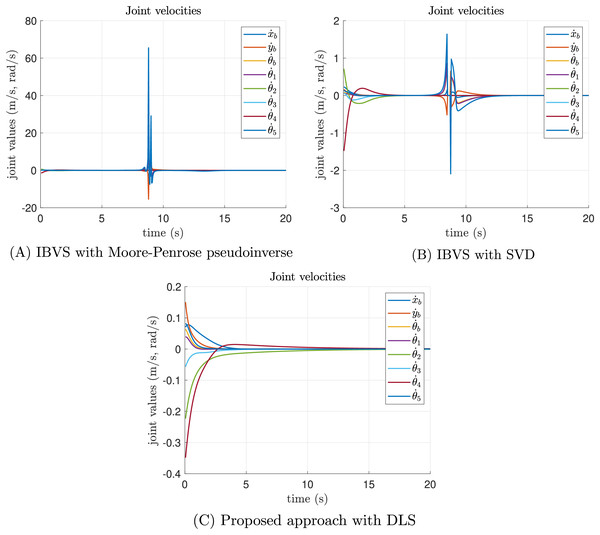
The joint velocity results of the singularity test experiment are reported in Fig. 9. In the case of the Moore-Penrose pseudoinverse, the presence of singularities provokes inadmissible joint velocities as shown in Fig. 9A. Despite the SVD reducing the impact of singularities, discontinuities are presented in some joint velocities which are not recommended for real-world applications, see Fig. 9B. Moreover, the joint velocities reported by the proposed approach are smooth, demonstrating that DLS smooth out discontinuities, see Fig. 9C. All velocities converge to a neighborhood of zero with admissible joint positions.

The image points trajectories of the singularity test experiment are provided in Fig. 10. As expected, Fig. 10A shows that the task of IVBS with Moore-Penrose pseudoinverse failed. In this case, the image points trajectories present abrupt changes that go out of the image boundary. Moreover, Fig. 10B reports that the IVBS with SVD reached the desired image features, despite the velocities discontinuities. Finally, Fig. 10C illustrates that the proposed approach with DLS successfully reached the desired image features.

Now, the proposed approach is tested in the Coppelia simulator. These simulations aim to test the proposed scheme under non-modeled dynamics and gravity compensation. The setup of these simulations is shown in Fig. 11.

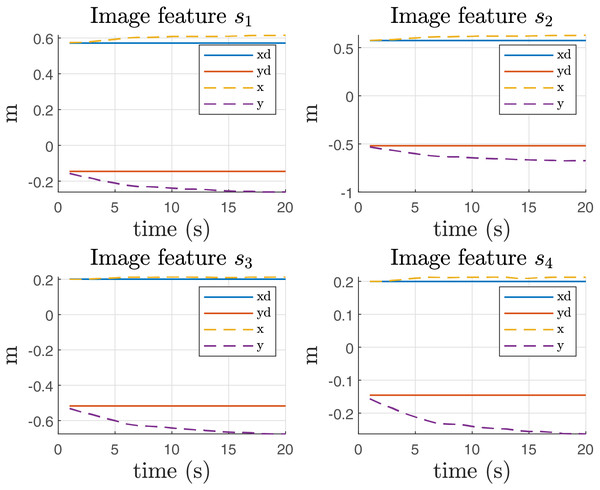
From this experiment, it is important to report the error in the image features, as illustrated in Fig. 12. The figure clearly shows an offset in the $y$ direction, which can be attributed to the influence of gravity on the system. This offset indicates that the image features are not aligning perfectly with the expected positions, likely due to gravitational effects acting on the manipulator during the operation.

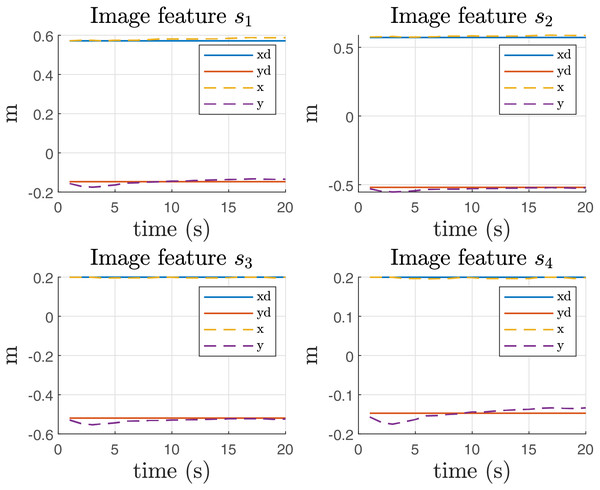
Figure 13 presents the results of implementing gravity compensation. The data clearly demonstrate that the error in the $y$ direction has been significantly reduced as a result of this compensation technique. This improvement indicates that the gravity compensation has effectively minimized the offset previously observed (Fig. 12), leading to better alignment of the image features with their expected positions.

Real-world experimental results

The experiments are conducted using the Kuka Youbot omnidirectional platform, which has an initial pose as shown in Fig. 14. The QR code is placed within the field of view of this initial position. The platform is equipped with encoders which have been used to measure joint positions. Moreover, Encoders have been also used for the wheel odometry to estimate the pose of the mobile platform.

Since the surface where the mobile platform moves is not completely flat, external disturbances by surface imperfections can produce slippages that cause errors in odometry. Even with the lack of accuracy in platform pose estimation, the proposed IBVS succeeds since it does not rely on the internal odometry (Li & Xiong, 2021; Jo & Chwa, 2023), but instead the visual feedback from the QR code.

For this experiment, we measure four image features from a QR code. Figure 14 shows the starting and ending positions in an example of the experimental setup. This experiment was performed over 30 s. In this scenario, the desired image features ${\mathbf{s}}_d$ was set as

(37) $${\mathbf{s}}_d={\left[\begin{array}{cccccccc}0.1459& -0.17507& -0.0865& -0.1705& -0.0929& 0.0595& 0.1491& 0.0611\end{array}\right]}^T$$

Moreover, the intrinsic parameters of the camera were calibrated as $f=623.71$, $C_u=317.97864$, $C_v=257.93234$.

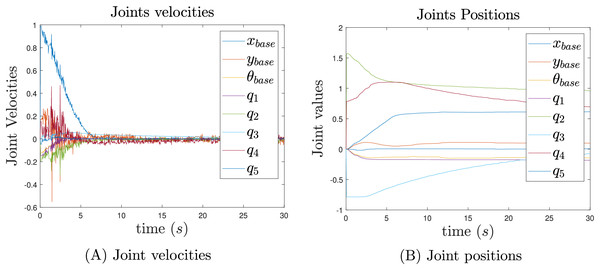
The joint velocities and positions from the experiment are presented in Fig. 15. Although the control signals are not as smooth as those observed in the simulations, Fig. 15A shows that the velocities converge to a neighborhood of zero. Several challenges arose during the real-world implementation, including unmodeled dynamics, external perturbations, robot wear, and surface imperfections. Despite these challenges, the joint positions are still achieved smoothly, as shown in Fig. 15B.

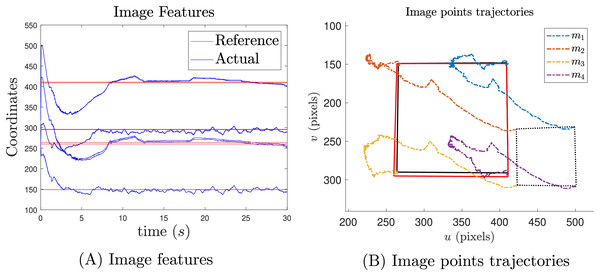
Figure 16A presents the results of the image feature transition and Fig. 16B image point trajectories. The reported results indicate that the reference position is achieved, even in the presence of noisy image features from QR detection. Additionally, Fig. 16A shows that the offset caused by gravity has been mitigated. In Fig. 16B, the black solid square represents the desired position, while the red square indicates the final position.

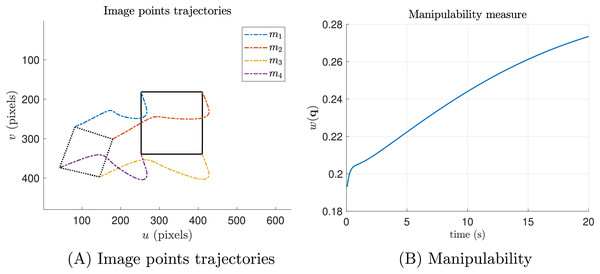
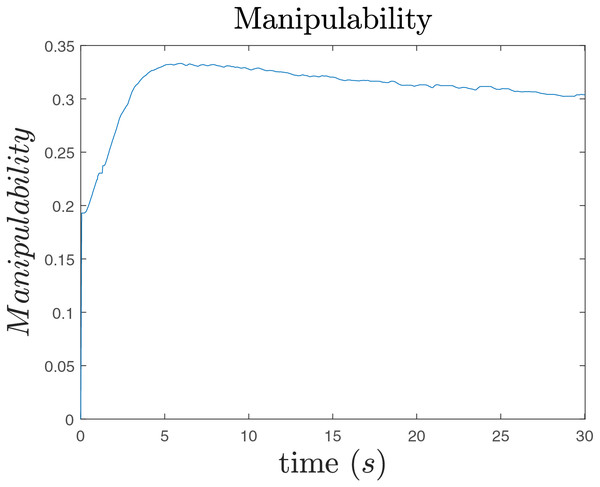
Finally, Fig. 17 shows that the manipulability measure is increased as expected.