Fine-art recognition using convolutional transformers
- Published
- Accepted
- Received
- Academic Editor
- Hoang Nguyen
- Subject Areas
- Artificial Intelligence, Computer Vision, Data Science, Visual Analytics, Neural Networks
- Keywords
- Fine-art, Painting, Deep learning, Recognition, Transfer learning, Transformers
- Copyright
- © 2024 Liu et al.
- Licence
- This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits using, remixing, and building upon the work non-commercially, as long as it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Computer Science) and either DOI or URL of the article must be cited.
- Cite this article
- 2024. Fine-art recognition using convolutional transformers. PeerJ Computer Science 10:e2409 https://doi.org/10.7717/peerj-cs.2409
Abstract
Digital image processing is a constantly evolving field encompassing a wide range of techniques and applications. Researchers worldwide are continually developing various algorithms across multiple fields to achieve accurate image classification. Advanced computer vision algorithms are crucial for architectural and artistic analysis. The digitalization of art has significantly enhanced the accessibility and conservation of fine-art paintings, yet the risk of art theft remains a significant challenge. Improving art security necessitates the precise identification of fine-art paintings. Although current recognition systems have shown potential, there is significant scope for enhancing their efficiency. We developed an improved recognition system for categorizing fine-art paintings using convolutional transformers, specified by an attention mechanism to enhance focused learning on the data. As part of the most advanced architectures in the deep learning family, transformers are empowered by a multi-head attention mechanism, thus improving learning efficiency. To assess the performance of our model, we compared it with those developed using four pre-trained networks: ResNet50, VGG16, AlexNet, and ViT. Each pre-trained network was integrated into a corresponding state-of-the-art model as the first processing blocks. These four state-of-the-art models were constructed under the transfer learning strategy, one of the most commonly used approaches in this field. The experimental results showed that our proposed system outperformed the other models. Our study also highlighted the effectiveness of using convolutional transformers for learning image features.
Introduction
Over the past few decades, numerous archaeological monuments have suffered irreversible damage due to pollution and human activities (Cunliffe, 2014; Ferrara, 2015; Ives, McBride & Waller, 2017). Despite the ongoing discovery of new sites, archaeologists face challenges in accurately determining the historical periods of these structures (King, 1979, 1980; Tapete & Cigna, 2019). Additionally, manual site visits and excavations are often hindered by challenging terrain (Landeschi, Nilsson & Dell’Unto, 2016; Carvajal-Ramírez et al., 2019). In this context, computer vision has emerged as a crucial tool, aiding in the analysis of architectural designs, uncovering hidden patterns, and assigning similarity scores to link structures to specific historical periods (Verhoeven, Taelman & Vermeulen, 2012; Sapirstein, 2021). This technology proves invaluable in classifying the era of newly discovered sites. Furthermore, drones equipped with computer vision modules have significantly advanced the detection of archaeological sites (Barrile, Gelsomino & Bilotta, 2017; Orengo & Garcia-Molsosa, 2019; Khelifi et al., 2021). Computer vision algorithms also play a vital role in creating 3D replicas of damaged monuments, assisting in both their restoration and preservation (Verhoeven, Taelman & Vermeulen, 2012; Sapirstein, 2021). These models are crucial for governments to conduct informed maintenance and reconstruction of historical treasures (Chen & Cheng, 2021; Salcedo, Jaber & Requena Carrión, 2022). Beyond preservation, the global illegal trade in arts and antiquities, valued at over 6 billion dollars, often evades regulatory detection (van Beurden, 2006; Fisman & Wei, 2009; Zubrow, 2016; Chappell & Hufnagel, 2019). Integrating computer vision into monitoring and safeguarding these artifacts offers a promising solution to combat this illicit trade and ensure the protection and preservation of our cultural heritage (Wu et al., 2018; Mademlis et al., 2023). While the United Nations and global governments have enacted various laws to protect artistic works and antiquities, these measures are not always foolproof or fully effective. Recent advancements in analytical methods have revolutionized our ability to gather historical information, providing deeper insights and significantly contributing to the analysis, utilization, preservation, and distribution of art across different eras (Manacorda & Chappell, 2011; Forrest, 2012; Campfens, 2020; Romiti, 2021). Precise categorization of artistic images and antiquities plays a crucial role in reducing their illicit trade (Hatton & MacManamon, 2003; Passas & Proulx, 2011). Moreover, specialized modules integrated into mobile applications offer a novel approach. These apps can provide detailed information about artworks and antiques, helping to verify their origins, history, and authenticity (Godin et al., 2002; Liang, 2011; Chatterjee, Chatterjee & Halder, 2021). They are also effective in confirming whether an item has been reported stolen or is part of an illegal transaction (Sansoni, Trebeschi & Docchio, 2009). This technological intervention aids in safeguarding cultural heritage and supports efforts to reduce the smuggling of precious artifacts, thereby reinforcing global cultural preservation and security.
Fine-art painting, a cornerstone of the visual arts, has evolved significantly over centuries, reflecting the profound shifts in cultural, political, and social landscapes (Arora & Elgammal, 2012). This art form, deeply rooted in human history, encompasses a variety of styles and movements, from the realism of the Renaissance (Rublack, 2013) to the abstract expressions of the 20th century. Researchers have analyzed the evolution of painting styles, finding patterns and influences that transcend time and geography. For instance, Merrill (1987) discusses the impact of socio-political contexts on painting styles, illustrating how artists like Picasso and Monet responded to their environments. The use of color and technique has been another focus, with studies by Brown, Street & Watkins (2013) exploring how color theory has been applied across different art movements. The advent of digital technology has introduced new dimensions to fine-art painting, enabling artists to experiment with digital mediums and techniques (Rani, 2018). Moreover, as highlighted by Richards (2002), Economou (2015), the digitalization of art has allowed for greater accessibility and preservation, democratizing access to fine-art paintings. These developments have not only expanded the boundaries of traditional painting but also opened up new avenues for exploration and appreciation in the art world.
Digital image processing encompasses a wide range of techniques and applications, with researchers worldwide continually developing diverse algorithms across various fields for accurate image classification. Particularly, the realm of architecture and art analysis stands as a dynamic area that extensively utilizes computer vision algorithms. Historically, the art world has embraced advanced imaging techniques since the 19th century, such as X-ray imaging (Pelagotti et al., 2008), infrared photography, and reflectography, employed to identify features related to pigment composition and hidden underdrawings (Barni, Pelagotti & Piva, 2005; Berezhnoy, Postma & van den Herik, 2007). The evolution of soft computing algorithms in this field often reflects enhancements to existing systems, focusing on exploiting features within spatial domains (Yin et al., 2024a, 2024b). Artistic image classification and analysis have primarily concentrated on addressing issues like forgery detection (Li et al., 2012) and identifying painting styles (Johnson et al., 2008; Graham et al., 2010). van den Herik & Postma (2000) made significant strides in extracting color and texture features from artistic images, employing methods such as color histogram analysis, Fourier spectra, Hurst coefficients, and image intensity statistics. This period also witnessed the innovative use of deep neural networks (DNN) for categorizing impressionist paintings, marking a significant milestone (Yelizaveta, Tat-Seng & Ramesh, 2006; Carneiro et al., 2012; Bianco, Mazzini & Schettini, 2017; Sandoval, Pirogova & Lech, 2019; Mohammadi & Rustaee, 2020). Yelizaveta, Tat-Seng & Ramesh (2006) introduced a novel classification approach for artistic images, centered on the unique brushstrokes of artists, opening new avenues for understanding and categorizing art styles. Later, Carneiro et al. (2012) expanded this field by automating the identification of visual classes in artworks, adding a new dimension to the intersection of art and technology. These developments underline the growing complexity and sophistication of digital image processing, particularly in the nuanced world of art and architecture. Bianco, Mazzini & Schettini (2017) utilized multitask learning in multi-branch DNN for painting categorization. Sandoval, Pirogova & Lech (2019) proposed using a two-stage DNN to develop a model for the classification of fine-art paintings. More recently, Mohammadi & Rustaee (2020) developed another DNN-based system for the hierarchical classification of fine-art paintings. Although these existing approaches have achieved promising outcomes, there is a large room for improvement in efficiency for recognizing fine-art paintings.
In our study, we propose a robust recognition system for classifying fine-art paintings using deep learning (DL) enhanced by learned knowledge. To effectively extract image features, we utilize pre-trained networks, including VGG16 (Simonyan & Zisserman, 2014), ResNet50 (He et al., 2015), AlexNet (Krizhevsky, Sutskever & Hinton, 2017), and ViT (Dosovitskiy et al., 2020). Pre-trained deep learning networks in imaging leverage knowledge gained from training on large datasets, like ImageNet, to provide a strong starting point for various tasks including classification, segmentation, and object detection. These networks have learned to recognize general patterns and features in images, which can be fine-tuned for specific applications, greatly enhancing performance and reducing the need for extensive labeled data (Hussain et al., 2020; Xu, Li & Chen, 2022). This approach significantly accelerates the development process and improves accuracy in complex imaging tasks across fields like medical diagnostics and remote sensing (Nguyen et al., 2022; Shi et al., 2023; Jia et al., 2024). In our study, the pre-trained networks are integrated with feed-forward neural networks for fine-tuning, enabling the system to learn specific features of the images. Leveraging the learned knowledge from these pre-trained networks is expected to significantly improve the prediction efficiency of our recognition system.
Data collection
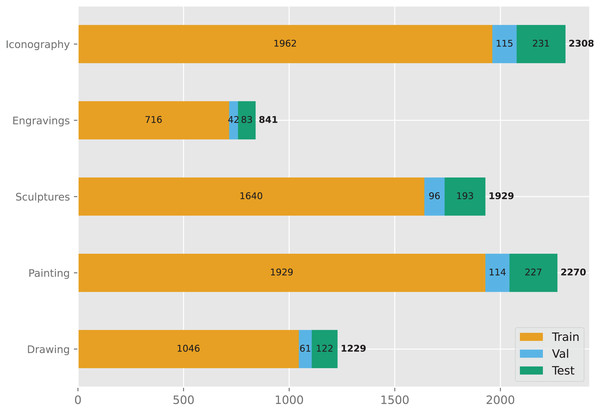
The data used in this study is accessible on Kaggle and is obtained from an openly accessible repository of the Virtual Russian Museum (https://rusmuseumvrm.ru). The dataset consists of 8,577 samples, each categorized into one of five groups (Fig. 1): Drawing, Painting, Sculpture, Engraving, and Iconography. The number of samples in each group is as follows: Drawing (108), Painting (1,229), Sculpture (2,270), Engraving (1,929), and Iconography (2,308). The dataset was divided into three subsets: a training set, a validation set, and a test set, containing 7,293, 428, and 856 samples, respectively (Fig. 2).
Figure 1: An example of different groups of art images in the dataset.
The dataset is available under a creative commons attribution 4.0 International (CC BY 4.0) license and can be accessed at DOI: 10.5281/zenodo.10935164.Figure 2: Overview of the dataset.
Proposed method
Model architecture
To develop our recognition system, we designed a hybrid deep learning architecture combining convolutional neural networks (CNNs) and transformer networks. The model comprises three main blocks (Fig. 3): a convolutional (Conv) block, a max-pooled convolutional (MConv) block, and a transformer block. The Conv block is defined by a two-dimensional convolutional (Conv2D) layer followed by a batch normalization (BatchNorm) layer, which employs a Gaussian error linear unit (GELU) as the activation function. The MConv block includes two Conv2D layers, each succeeded by a BatchNorm layer. The output from the Conv block undergoes max-pooling and is processed through another Conv2D layer to generate residual features, which are subsequently integrated with the main branch’s output to form a new feature vector.
Figure 3: Proposed model architecture for developing our recognition system.
The architecture has three blocks: convolutional (Conv), max-pooled convolutional (MConv), and transformer blocks.The transformer block consists of an attention layer and a feed-forward network (FFN). The output of the MConv block is combined with the attention layer’s output to produce an attention feature vector, which then passes through the FFN layer. This attention feature vector is also added to the FFN’s output, completing this stage of processing. Finally, the transformer block’s output is max-pooled, flattened, and passed through a softmax function to determine the class of the item.
Attention mechanism
In image processing, translation equivariance is a crucial property of a system in which a shift or translation in the input image leads to a corresponding shift in the output feature map. This attribute ensures that the model consistently understands and processes images in different areas, thereby enhancing the reliability and efficiency of detecting features and patterns. To effectively learn image features, the network’s receptive fields must be large enough to cover the entire input, allowing them to capture global context and relationships. Larger contextual information can enhance the model’s learning capacity. While most depth-wise convolutional layers contribute to translation equivariance by capturing spatial interactions, they struggle to capture a global receptive field due to the high computational cost of processing large receptive fields. To address this issue, input-adaptive weighting can be used to dynamically adjust the weights or parameters of a model based on the input data, instead of using fixed weights for all inputs.
The transformer block, which includes an attention layer and a feed-forward network, addresses the high computational cost associated with processing a global receptive field through input-adaptive weighting. A convolutional layer uses a kernel to extract information from a local receptive field:
(1) where denote the input and output at position , respectively, and is the local neighborhood of . The normal self-attention layer enables the receptive field to encompass all spatial locations, calculating the weights through the re-normalized pairwise similarity between each pair .
(2)
(3) where is the global spatial space and is the attention weight. From Eqs. (1)–(3), the pre-normalization version of the attention layer is rewritten as:
(4)
The attention weight is now jointly determined by (representing translation equivariance) and the adaptive input . This combination leverages both the global receptive field and input-adaptive weighting. Crucially, to facilitate a global convolution kernel without excessively increasing the number of parameters, we have redefined as a scalar instead of a vector.
Model benchmarking
To assess our model’s performance, we compared it with other models developed using state-of-the-art methods. Given the success of transfer learning in this domain, we implemented four transfer learning-based recognition systems utilizing well-known pre-trained networks: VGG16 (Simonyan & Zisserman, 2014), ResNet50 (He et al., 2015), AlexNet (Krizhevsky, Sutskever & Hinton, 2017), and Vision Transformers (ViT) (Dosovitskiy et al., 2020). Each model architecture was designed identically, comprising a pre-trained network, three 1-dimensional convolutional (Conv1D) layers, and three fully connected (FC) layers (Fig. 4).
Figure 4: Proposed model architecture for developing our recognition system.
VGG16
VGG16 (Simonyan & Zisserman, 2014), developed by the Visual Graphics Group (VGG) at Oxford University, emerged as one of the prominent networks for image classification tasks. This network is constructed based on convolutional neural networks (CNNs), with a notable advancement in its depth and architectural simplicity. Characterized by its 16 layers, VGG16 employs an arrangement of convolutional layers with small receptive fields, followed by max pooling layers. This design allows the network to capture complex features at various levels of abstraction, making it particularly effective in recognizing and classifying a wide range of images with high accuracy. One of the key strengths of VGG16 is its uniform architecture, which simplifies the training process and enhances feature extraction capabilities. The training process, however, is computationally intensive, resulting in longer training times. It is widely used in transfer learning due to its excellent performance on large-scale image datasets. Its ability to be fine-tuned for specific tasks by adapting the fully connected layers makes it a versatile tool in various applications beyond just image classification, including object detection and image segmentation.
ResNet50
ResNet50, a network in the Residual Network (ResNet) family (He et al., 2015), is designed to tackle the challenges of training DNNs for computer vision. Like other ResNet architectures, ResNet50 also incorporates ‘skip connections’ to effectively address the vanishing gradient problem that hampers the learning process. These skip connections allow data to bypass certain layers while still maintaining the flow of gradients through the network, making it possible to train deeper networks without a loss in performance. This network has proven to be highly effective, achieving impressive results on various image recognition tasks and setting new benchmarks for accuracy. Its development has been a key milestone in DL, paving the way for more complex DNN architectures.
AlexNet
AlexNet (Krizhevsky, Sutskever & Hinton, 2017), a robust DL architecture characterized by CNN, gained prominence for its groundbreaking performance in the 2012 ImageNet Large Scale Visual Recognition Challenge. It is considered one of the most effective networks for image classification tasks. In the context of transfer learning, AlexNet serves as a powerful feature extractor. Its learned features from extensive datasets like ImageNet can be effectively applied to other image classification tasks, particularly in scenarios with limited training data. This adaptability has established AlexNet as a foundational model in DL research, contributing significantly to advancements in computer vision.
ViT
Vision Transformers (ViT) mark a significant innovation in computer vision by adapting the transformer architecture, initially designed for text analysis, to process images (Dosovitskiy et al., 2020). This architecture, introduced by Google in 2020, breaks down images into sequences of patches, treats them as words in a sentence, and analyzes these through transformer layers. This approach enables the model to recognize complex patterns and relationships within the image that extend beyond local areas, differing from the localized processing typical of conventional CNNs. By employing self-attention mechanisms, ViTs assess the relevance of different image parts without being constrained by their spatial proximity. This network has not only improved performance on key computer vision tasks but also prompted further research into the application of transformer models in visual data analysis.
Experiments
Input images have sizes of 224 224 3 is convoluted by the Conv block with 64 feature maps, a kernel size of 3, a stride of 2, and a padding of 1 to create a convoluted vector of size 112 112 64. In the main branch of the MConv block, The first Conv2D layers has 64 feature maps, a kernel size of 3, and a stride of 2 while the second Conv2D and the Conv2D in the residual branch have the same setups of 96 features maps, a kernel size of 1, and a stride of 1. The MConv’s output vector has size of 56 56 96. Our models were trained over 60 epochs with a learning rate of 0.001 and optimized using the Adam optimizer (Kingma & Ba, 2014).
To evaluate our models’ performance, we calculated several metrics at the default threshold of 0.5. These include the area under the receiver operating characteristic curve (AUCROC) and the area under the precision-recall curve (AUCPR), as well as balanced accuracy (BA), Matthews correlation coefficient (MCC), F1-score (F1), recall, and precision. It is worth-noting that all the metrics were weighted values based on the ratio of class samples.
Results and discussion
Model assessment
Table 1 compares the performance of recognition systems developed using our proposed method with those developed using state-of-the-art methods. All comparing models (not including ours) were implemented based on transfer learning in which the pretrained models were used to extract the image’s features. The results indicate that our model outperforms the other deep learning models in all evaluation metrics. In terms of balanced accuracy, our model achieves the highest value, followed by ResNet50-based, VGG16-based, AlexNet-based, and ViT-based models. Our model obtains an MCC of 0.86, higher than the other models, whose MCCs range from 0.81 to 0.84. For F1-score, recall, and precision, our model achieves scores of 0.88, 0.89, and 0.88, respectively. Among these state-of-the-art methods, the VGG16-based model holds the second-best position, followed by the ViT-based, AlexNet-based, and ResNet50-based models.
| Method | AUCROC | AUCPR | BA | MCC | F1 | Recall | Precision |
|---|---|---|---|---|---|---|---|
| VGG16 | 0.9808 | 0.9136 | 0.8069 | 0.8249 | 0.8573 | 0.8640 | 0.8556 |
| ResNet50 | 0.9801 | 0.9124 | 0.8161 | 0.8305 | 0.8624 | 0.8682 | 0.8617 |
| AlexNet | 0.9796 | 0.9148 | 0.8064 | 0.8152 | 0.8493 | 0.8561 | 0.8504 |
| ViT | 0.9807 | 0.9164 | 0.8034 | 0.8195 | 0.8534 | 0.8598 | 0.8521 |
| Our method | 0.9848 | 0.9244 | 0.8363 | 0.8534 | 0.8820 | 0.8862 | 0.8808 |
Table 2 summarizes the performance of the recognition systems developed using our proposed method in comparison with those developed using traditional machine learning methods as baseline models. The image features were extracted from the backbone network (after the Transformer block in our model). The results show that our model achieves better performance than the other machine learning models across all evaluation metrics. Our model achieves the highest accuracy, followed by the RF, -NN, SVM, and XGB models. Additionally, our model obtains a higher MCC compared to the other models, with MCC values ranging from 0.64 to 0.67. In terms of F1-score, recall, and precision, our model also outperforms the baseline models. The results reveal that attention-learned features are less effective when directly used for downstream tasks compared to passing through the subsequent neural network layers for generating prediction outcomes.
| Method | AUCROC | AUCPR | BA | MCC | F1 | Recall | Precision |
|---|---|---|---|---|---|---|---|
| -NN | 0.9585 | 0.8537 | 0.6145 | 0.6689 | 0.6871 | 0.7395 | 0.7295 |
| RF | 0.9626 | 0.8603 | 0.6215 | 0.6782 | 0.6966 | 0.7472 | 0.7282 |
| SVM | 0.9569 | 0.8501 | 0.6090 | 0.6670 | 0.6807 | 0.7374 | 0.7244 |
| XGB | 0.9588 | 0.8545 | 0.5922 | 0.6484 | 0.6594 | 0.7217 | 0.7168 |
| Our method | 0.9848 | 0.9244 | 0.8363 | 0.8534 | 0.8820 | 0.8862 | 0.8808 |
To investigate the contribution of the shortcut connection in our proposed method, we implemented another version of our model in which all shortcut connections were removed. These two models were independently trained under the same conditions to ensure a fair comparison. Table 3 provides information on the differences between the model integrated with shortcut connections and the one with the shortcut connections removed. The results show that the shortcut connections significantly contribute to enhancing the performance of the proposed architecture.
| Method | AUCROC | AUCPR | BA | MCC | F1 | Recall | Precision |
|---|---|---|---|---|---|---|---|
| No shortcut connection | 0.9576 | 0.8525 | 0.6196 | 0.6856 | 0.6966 | 0.7535 | 0.7355 |
| With shortcut connection | 0.9848 | 0.9244 | 0.8363 | 0.8534 | 0.8820 | 0.8862 | 0.8808 |
Model stability
To assess the stability of the proposed method, we conducted experiments 30 times, with the metrics independently measured across these trials. Table 4 presents a summary of these metrics, illustrating minimal variation in the model’s predictive capability, thus indicating its robustness. Specifically, the average AUCROC and AUCPR values for our model were 0.98 and 0.92, respectively, with a very small standard deviation of less than 0.01. The variations in the other metrics, including BA, MCC, F1-score, recall, and precision, ranged from 0.01 to 0.02. These repeated experiments provide substantial evidence of the model’s effectiveness, demonstrating consistent performance across different random data samplings.
| Trial | AUCROC | AUCPR | BA | MCC | F1 | Recall | Precision |
|---|---|---|---|---|---|---|---|
| 1 | 0.9849 | 0.9217 | 0.8432 | 0.8572 | 0.8851 | 0.8890 | 0.8846 |
| 2 | 0.9849 | 0.9235 | 0.8334 | 0.8522 | 0.8823 | 0.8855 | 0.8805 |
| 3 | 0.9850 | 0.9291 | 0.8467 | 0.8602 | 0.8877 | 0.8914 | 0.8872 |
| 4 | 0.9847 | 0.9224 | 0.8308 | 0.8483 | 0.8764 | 0.8820 | 0.8756 |
| 5 | 0.9845 | 0.9252 | 0.8276 | 0.8493 | 0.8783 | 0.8832 | 0.8762 |
| 6 | 0.9845 | 0.9217 | 0.8248 | 0.8442 | 0.8740 | 0.8785 | 0.8756 |
| 7 | 0.9837 | 0.9214 | 0.8437 | 0.8603 | 0.8871 | 0.8914 | 0.8868 |
| 8 | 0.9802 | 0.9081 | 0.7962 | 0.8207 | 0.8531 | 0.8610 | 0.8504 |
| 9 | 0.9810 | 0.9118 | 0.8178 | 0.8347 | 0.8653 | 0.8715 | 0.8644 |
| 10 | 0.9816 | 0.9130 | 0.7940 | 0.8164 | 0.8515 | 0.8575 | 0.8490 |
| 11 | 0.9842 | 0.9222 | 0.8320 | 0.8497 | 0.8780 | 0.8832 | 0.8769 |
| 12 | 0.9813 | 0.9075 | 0.8124 | 0.8317 | 0.8624 | 0.8692 | 0.8611 |
| 13 | 0.9821 | 0.9184 | 0.8106 | 0.8361 | 0.8654 | 0.8727 | 0.8641 |
| 14 | 0.9814 | 0.9080 | 0.8009 | 0.8218 | 0.8529 | 0.8610 | 0.8538 |
| 15 | 0.9802 | 0.9102 | 0.8180 | 0.8411 | 0.8685 | 0.8762 | 0.8700 |
| 16 | 0.9808 | 0.9138 | 0.8168 | 0.8372 | 0.8685 | 0.8738 | 0.8661 |
| 17 | 0.9856 | 0.9286 | 0.8324 | 0.8528 | 0.8793 | 0.8855 | 0.8791 |
| 18 | 0.9849 | 0.9235 | 0.8334 | 0.8522 | 0.8823 | 0.8855 | 0.8805 |
| 19 | 0.9850 | 0.9291 | 0.8467 | 0.8602 | 0.8877 | 0.8914 | 0.8872 |
| 20 | 0.9847 | 0.9224 | 0.8308 | 0.8483 | 0.8764 | 0.8820 | 0.8756 |
| 21 | 0.9862 | 0.9308 | 0.8372 | 0.8560 | 0.8817 | 0.8879 | 0.8824 |
| 22 | 0.9857 | 0.9269 | 0.8385 | 0.8567 | 0.8860 | 0.8890 | 0.8846 |
| 23 | 0.9856 | 0.9313 | 0.8501 | 0.8647 | 0.8914 | 0.8949 | 0.8911 |
| 24 | 0.9854 | 0.9245 | 0.8319 | 0.8498 | 0.8776 | 0.8832 | 0.8770 |
| 25 | 0.9851 | 0.9273 | 0.8276 | 0.8493 | 0.8783 | 0.8832 | 0.8762 |
| 26 | 0.9851 | 0.9242 | 0.8306 | 0.8502 | 0.8791 | 0.8832 | 0.8808 |
| 27 | 0.9845 | 0.9246 | 0.8420 | 0.8588 | 0.8858 | 0.8902 | 0.8857 |
| 28 | 0.9838 | 0.9225 | 0.8191 | 0.8404 | 0.8698 | 0.8762 | 0.8683 |
| 29 | 0.9839 | 0.9214 | 0.8388 | 0.8547 | 0.8797 | 0.8867 | 0.8809 |
| 30 | 0.9846 | 0.9244 | 0.8239 | 0.8381 | 0.8694 | 0.8738 | 0.8701 |
| Average | 0.9838 | 0.9213 | 0.8277 | 0.8464 | 0.8754 | 0.8806 | 0.8747 |
| SD | 0.0018 | 0.0069 | 0.0146 | 0.0124 | 0.0107 | 0.0096 | 0.0110 |
Limitations
Our proposed method is constructed based on CNNs and a Transformer characterized by scaled dot-product attention. While the combination of these components has the potential to enhance model performance across various tasks, it also introduces several limitations, including computational complexity, data inefficiency, challenges in capturing long-range dependencies, overfitting risks, reduced interpretability, and training instability (Vaswani et al., 2017). Therefore, understanding these limitations is crucial for effectively leveraging these models, as well as managing biased modeling in practical applications. Moreover, since this method is designed to adapt to small datasets, it may not perform as well on larger datasets, such as the WikiArt dataset (Tan et al., 2019). Further investigation on datasets of diverse sizes and adjustment of the architecture may help the method work better across different modeling strategies.
Conclusion
In conclusion, the ever-changing landscape of digital image processing offers a wide range of techniques and applications, with researchers from all over the world working to achieve accurate image classification through the development of various algorithms across multiple domains. Advanced computer vision algorithms are especially useful in architectural and artistic analysis. While digitalization of art has significantly improved accessibility and conservation efforts, the ongoing threat of art theft highlights the importance of improving art security through precise identification techniques. Our research presents an improved recognition system for categorizing fine-art paintings that combines convolutional transformers with an attention mechanism to enable focused learning on the data. Transformers, which are part of the deep learning family’s most advanced architectures, show improved learning efficiency thanks to multi-head attention mechanisms. We have integrated our proposed system into cutting-edge models using transfer learning, outperforming established pre-trained networks like ResNet50, VGG16, AlexNet, and ViT. Furthermore, our findings highlight the effectiveness of convolutional transformers in learning image features, indicating promising avenues for future advancements in digital image processing and art security.