A new extension of Poisson distribution for asymmetric count data: theory, classical and Bayesian estimation with application to lifetime data

Introduction

Numerous studies have emphasized the relevance of count data modeling which has aroused significant interest in a range of fields such as medical research, earth science, physics, economics, and insurance. Various lifetime probability distributions have been utilized and investigated in reliability theory. The Poisson distribution is commonly utilized to analyze the “symmetric” and “asymmetric” count datasets, but it cannot describe over-dispersed datasets. As a result, there has been a lot of interest in the discretization of continuous probability distributions. Several techniques may be used to obtain the discrete analog of a continuous probability distribution. The Poisson mixed approach gets great attention from researchers and is most commonly used for generalization or generation of new probability distributions. The Poisson mixed approach is discussed below.

If the Poisson parameter is a random variable with a parameterized distribution (P), then the resulting model is a discrete Poisson mixed model. The distribution P and its parameter vector Θ are referred to as prior distribution and hyperparameter, respectively. The resulting distribution of random variable X is stated as follows:

(1) $$f_X\left(x\right)=\underset{0}{\overset{\mathrm{\infty }}{\int }}{f}_{X|\mathrm{\Lambda }}\left(X|\lambda \right)f_{\mathrm{\Lambda }}^P\left(\lambda \right)d\lambda ,$$where $X|\mathrm{\Lambda }$ is the Poisson distribution with parameter $\lambda$ as

(2) $$f_{X|\mathrm{\Lambda }}\left(X|\lambda \right)=\frac{e^{-\lambda }{\lambda }^x}{x!},x=0,1,2,3,\dots .$$

$f_{\mathrm{\Lambda }}^P\left(\lambda \right)$ is a continuous density function and $\mathrm{\Lambda }$ is a random variable of the Poisson parameter $\lambda$.

In the literature, many authors have compounded the standard Poisson parameter using standard lifetime distributions. The negative binomial distribution was derived by Greenwood & Yule (1920) by combining the Poisson and gamma distributions. Johnson, Kemp & Kotz (1992) combined the Poisson and exponential distributions to get the geometric distribution. Similarly, various authors introduced mixed Poisson distributions, some examples include the Poisson Lindley (Sankaran, 1970), Poisson Pseudo Lindley (Zeghdoudi & Nedjar, 2017), Poisson transmuted exponential (Bhati, Kumawat & Gómez-Déniz, 2017), Poisson Xgamma (Altun, Cordeiro & Ristić, 2021), Poisson Ailamujia (Hassan et al., 2020), Poisson Quasi-Lindley (Altun, 2019), Poisson XLindley (Ahsan-ul-Haq et al., 2022), Poisson moment exponential (Ahsan-ul-Haq, 2022), and Poisson Mirra (Maya et al., 2022).

Al-Nasser, Rawashdeh & Talal (2022) introduced a new weighted exponential distribution. The resulting distribution is named entropy-based weighted exponential distribution (EBWED). Let X be a continuous random variable that follows EBWED with a single parameter $\left(\beta \right)$. The probability density function (pdf) of EBWD will be.

(3) $$f\left(x,\beta \right)={\displaystyle \frac{\beta \left(\beta x-\ln \left(\beta \right)\right)}{1-\ln \left(\beta \right)}{e}^{-\beta x};x>0;\ln \left(\beta \right)\ne 1}$$

The cumulative distribution function (cdf) of the EBWED is

(4) $$F\left(x,\beta \right)=1-{\displaystyle \frac{\left(1+\beta x-\ln \left(\beta \right)\right)}{1-\ln \left(\beta \right)}{e}^{-\beta x}.}$$

The innovation of this study is the derivation of a new Poisson mixed distribution for under, equal, and over-dispersed count datasets to address the above-mentioned issues. This study has the following goals;

• The main objective is to introduce a new flexible Poisson entropy-based weighted exponential distribution. The ensuing distribution is obtained by mixing Poisson with the entropy-based weighted exponential distribution. The moments and associated measures of the new distribution can be calculated analytically when compared to existing discrete distributions, and it has a strong modeling capability. The new model is also incredibly adaptable.

• The model parameter is estimated using the maximum likelihood estimation (MLE) method. A comprehensive simulation is performed to assess the behavior ML estimates.

• The new distribution is used to model “asymmetric” and “right skewed” data in the presence of complete and right-censored data.

• We also take into account censored data with a cure fraction.

• The Bayesian estimation approach is also utilized to estimate the model parameter.

The rest of the document is structured as follows: The derivation of the new discrete probability model is presented in “The PEBWE Distribution”. “Moments and Associated Measures” discusses its underlying mathematical characteristics. “Parameter Estimation” discusses the maximum likelihood estimation for the distribution parameter using complete, censored, and censored data with cure fraction. This section also discusses Bayesian estimation using the MCMC approach. Three examples are given in “Application” to illustrate the adaptability of the new distribution. In the end, concluding remarks and some future directions are given in “Conclusion”.

The pebwe distribution

The following proposition introduces a new mixed-Poisson model by combining the Poisson and Entropy-Based Weighted Exponential distributions.

Proposition 1. Suppose that X follows the compound Poisson-EBWE distribution (PEBWED), which has the following stochastic representation:

$$\left(X|\lambda \right)\sim Poisson\left(\lambda \right)$$

$$\left(\lambda |\beta \right)\sim EBWE\left(\beta \right)$$where $\lambda$ and $\beta >0$. Then, the pmf of X is given by

(5) $$p\left(x;\beta \right)=Pr\left(X=x\right)={\displaystyle \frac{\beta \left(\left(1+\beta \right)\ln \left(\beta \right)-\left(1+x\right)\beta \right)}{{\left(1+\beta \right)}^{2+x}\left(\ln \left(\beta \right)-1\right)},x=0,1,2,}$$

The new model is denoted as $PEBWED(\beta )$, and one can note $X\sim PEBWED(\beta )$ to apprise that X follows that PEBWED with parameter $\beta$.

Proof. The pmf of X can be obtained using the common mixing method shown below.

$$p\left(x;\beta \right)={\int }_0^{\mathrm{\infty }}Pr\left(X=x|\lambda \right)f\left(\lambda |\beta \right)d\lambda ,$$

$$={\int }_0^{\mathrm{\infty }}{\displaystyle \frac{{\lambda }^x{e}^{-\lambda }}{x!}{\displaystyle \frac{\beta \left(\beta \lambda -\ln \left(\beta \right)\right)e^{-\beta \lambda }}{1-\ln \left(\beta \right)}d\lambda ,}}$$

$$={\displaystyle \frac{1}{(1-\ln \left(\beta \right))x!}\left\{{\beta }^2{\int }_0^{\mathrm{\infty }}{\lambda }^{x+1}{e}^{-\lambda }{e}^{-\beta \lambda }d\lambda -\beta \ln \left(\beta \right){\int }_0^{\mathrm{\infty }}{\lambda }^x{e}^{-\lambda }{e}^{-\beta \lambda }d\lambda \right\},}$$

$$={\displaystyle \frac{1}{(1-\ln \left(\beta \right))x!}\left\{{\displaystyle \frac{{\beta }^2\mathrm{\Gamma }\left(x+2\right)}{{\left(\beta +1\right)}^{x+2}}-{\displaystyle \frac{\beta \ln \left(\beta \right)\mathrm{\Gamma }\left(x+1\right)}{{\left(\beta +1\right)}^{x+1}}}}\right\},}$$

$$={\displaystyle \frac{\beta \left(\left(1+\beta \right)\ln \left(\beta \right)-\left(1+x\right)\beta \right)}{{\left(1+\beta \right)}^{2+x}\left(\ln \left(\beta \right)-1\right)},x=0,1,2,\dots }$$

The proof is completed.

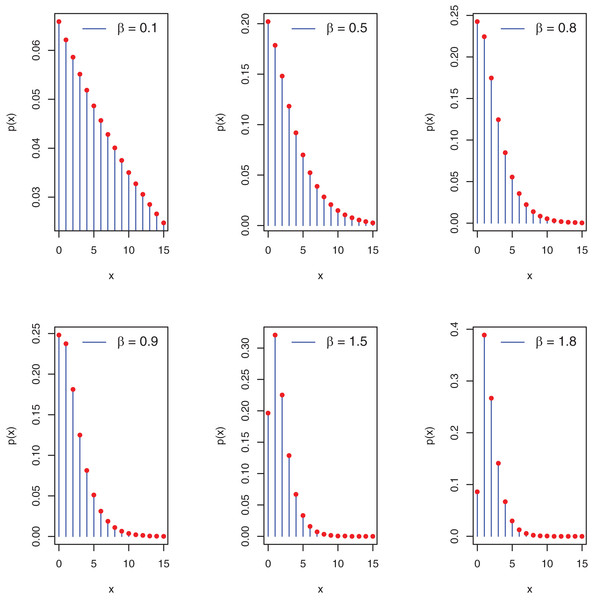
Figure 1 depicts the potential pmf plots of the proposed distribution.

Remark: The first derivative of pmf is

$${\displaystyle \frac{dp\left(x\right)}{dx}=-{\displaystyle \frac{\beta \left(\beta +\left(\left(1+\beta \right)\ln \left(\beta \right)-\left(1+x\right)\beta \right)\ln \left(1+\beta \right)\right)}{{\left(1+\beta \right)}^{2+x}\left(\ln \left(\beta \right)-1\right)},}}$$gives

(6) $$\hat{x}={\displaystyle \frac{\beta -\beta \ln \left(1+\beta \right)+\ln \left(\beta \right)\ln \left(1+\beta \right)+\beta \ln \left(\beta \right)\ln \left(1+\beta \right)}{\beta \ln \left(1+\beta \right)}.}$$

For $\beta >0.6934$ the $\hat{X}$ is a critical point that maximizes the $p(\hat{X};\beta )$ and $0<\beta \le 0.6914$ the pmf is a decreasing function of x.

and

$${\displaystyle \frac{d^{2}p\left(x\right)}{d{x}^2}={\displaystyle \frac{\beta \ln \left(1+\beta \right)\left(2\beta +\left(-\left(1+x\right)\beta +\left(1+\beta \right)\ln \left(\beta \right)\right)\ln \left(1+\beta \right)\right)}{{\left(1+\beta \right)}^{2+x}\left(\ln \left(\beta \right)-1\right)}.}}$$

Therefore, the mode of PEBWED is given by

$$Mode\left(X\right)=\{\begin{array}{c}{\displaystyle \frac{\beta -\beta \ln \left(1+\beta \right)+\ln \left(\beta \right)\ln \left(1+\beta \right)+\beta \ln \left(\beta \right)\ln \left(1+\beta \right)}{\beta \ln \left(1+\beta \right)}for\beta >0.6914}\hfill \\ 0otherwise\hfill \end{array}$$

The cdf and survival function of the PEBWED is given by

(7) $$F\left(x;\beta \right)=Pr\left(X\le x\right)=1-{\displaystyle \frac{\left(1+\beta \left(2+x\right)-\left(1+\beta \right)\ln \left(\beta \right)\right)}{{\left(1+\beta \right)}^{2+x}\left(1-\ln \left(\beta \right)\right)},}$$and

(8) $$S\left(x;\beta \right)={\displaystyle \frac{\left(1+\beta \left(2+x\right)-\left(1+\beta \right)\ln \left(\beta \right)\right)}{{\left(1+\beta \right)}^{2+x}\left(1-\ln \left(\beta \right)\right)}.}$$

The hazard function (hf) of the PEBWED is given by

(9) $$h\left(x;\beta \right)={\displaystyle \frac{p\left(x;\beta \right)}{1-F\left(x;\beta \right)}={\displaystyle \frac{\beta \left(\left(-1-x\right)\beta +\left(1+\beta \right)\ln \left(\beta \right)\right)}{\left(1+\beta \right)\ln \left(\beta \right)-\left(2+x\right)\beta -1}.}}$$

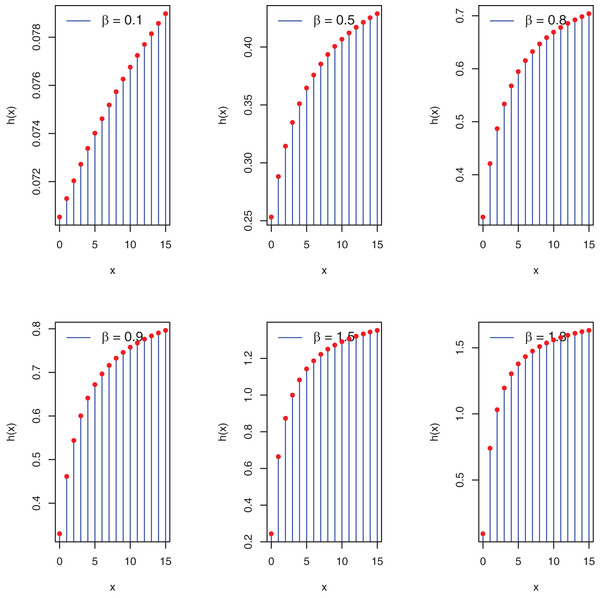
Proposition 2: The PEBWED hf increases as x increases.

Proof: Using the idea of Glaser (1980) and from the pmf of PEBWED

$$\rho \left(x\right)=-{\displaystyle \frac{p^{\mathrm{\prime }}\left(x;\beta \right)}{p\left(x;\beta \right)}}$$

$$=-{\displaystyle \frac{\beta }{\left(1+x\right)\beta -\left(1+\beta \right)\ln \left(\beta \right)}+\ln \left(1+\beta \right)}$$

It follows that

$${\rho }^{\mathrm{\prime }}\left(x\right)={\displaystyle \frac{{\beta }^2}{{\left(\left(1+x\right)\beta -\left(1+\beta \right)\ln \left(\beta \right)\right)}^2}.}$$

As ${\rho }^{\mathrm{\prime }}\left(x\right)>0$, the hf of PEBWED is increasing function.

Furthermore, the graphs in Fig. 2 pertain to the possible shapes of the PEBWED.

Moments and associated measures

In this section, moments, probability generating function, moment generating function, and their associated measures, mean, variance, dispersion index, skewness, and kurtosis are derived and discussed.

Proposition 3: The rth factorial moments of PEBWED are given by

(10) $${\mu }_{\left(r\right)}=E\left(X\left(X-1\right)\dots \left(X-r+1\right)\right)={\displaystyle \frac{\mathrm{\Gamma }\left(1+r\right)\left(\ln \left(\beta \right)-r-1\right)}{{\beta }^r\left(\ln \left(\beta \right)-1\right)}.}$$

Proof: The factorial moment can be calculated using the compound-Poisson theory as follows:

$${\mu }_{\left(r\right)}={\displaystyle \frac{\beta }{1-\ln \left(\beta \right)}{\int }_0^{\mathrm{\infty }}{\lambda }^r\left(\beta \lambda -\ln \left(\beta \right)\right)e^{-\beta \lambda }d\lambda ,}$$

$$\begin{array}{rl}& ={\displaystyle \frac{\beta }{1-\ln \left(\beta \right)}\left\{\beta {\int }_0^{\mathrm{\infty }}{\lambda }^{r+1}{e}^{-\beta \lambda }d\lambda -\ln \left(\beta \right){\int }_0^{\mathrm{\infty }}{\lambda }^r{e}^{-\beta \lambda }d\lambda \right\},}\end{array}$$

$$\begin{array}{rl}& ={\displaystyle \frac{\mathrm{\Gamma }\left(1+r\right)\left(\ln \left(\beta \right)-r-1\right)}{{\beta }^r\left(\ln \left(\beta \right)-1\right)}.}\end{array}$$which complete the proof.

By replacing r = 1, 2, 3, and 4 in Eq. (10), the first four factorial moments of the PEBWED can be derived.

That is,

$${\mu }_{\left(1\right)}={\displaystyle \frac{\ln \left(\beta \right)-2}{\beta \left(\ln \left(\beta \right)-1\right)},}$$

$${\mu }_{\left(2\right)}={\displaystyle \frac{2\left(\ln \left(\beta \right)-3\right)}{{\beta }^2\left(\ln \left(\beta \right)-1\right)},}$$

$${\mu }_{\left(3\right)}={\displaystyle \frac{6\left(\ln \left(\beta \right)-4\right)}{{\beta }^3\left(\ln \left(\beta \right)-1\right)},}$$and

$${\mu }_{\left(4\right)}={\displaystyle \frac{24\left(\ln \left(\beta \right)-5\right)}{{\beta }^4\left(\ln \left(\beta \right)-1\right)}.}$$

Now, using the general connection between factorial moments and moments about the origin, the first four moments about the origin of the PEBWED are obtained. We get

(11) $${\mu }_1^{\mathrm{\prime }}=\mathrm{E}\left(X\right)={\displaystyle \frac{\ln \left(\beta \right)-2}{\beta \left(\ln \left(\beta \right)-1\right)},}$$

$${\mu }_2^{\mathrm{\prime }}=\mathrm{E}\left(X^2\right)={\displaystyle \frac{-2\left(3+\beta \right)+\left(2+\beta \right)\ln \left(\beta \right)}{{\beta }^2\left(\ln \left(\beta \right)-1\right)},}$$

$${\mu }_3^{\mathrm{\prime }}=\mathrm{E}\left(X^3\right)={\displaystyle \frac{-2\left(12+\beta \left(9+\beta \right)\right)+\left(6+\beta \left(6+\beta \right)\right)\ln \left(\beta \right)}{{\beta }^3\left(\ln \left(\beta \right)-1\right)},}$$

$${\mu }_4^{\mathrm{\prime };}=\mathrm{E}\left(X^4\right)={\displaystyle \frac{-2\left(60+\beta \left(72+\beta \left(21+\beta \right)\right)\right)+\left(2+\beta \right)\left(12+\beta \left(12+\beta \right)\right)\ln \left(\beta \right)}{{\beta }^4\left(\ln \left(\beta \right)-1\right)}.}$$

Therefore, the variance of PEBWED is obtained as

(12) $$\mathrm{V}\mathrm{a}\mathrm{r}\left(\mathrm{X}\right)={\displaystyle \frac{2\left(1+\beta \right)+\ln \left(\beta \right)\left(-4-3\beta +\left(1+\beta \right)\ln \left(\beta \right)\right)}{{\beta }^2\left(\ln \left(\beta \right)-1\right)}.}$$

The dispersion Index (DI) of the PEBWED is given by

(13) $$\mathrm{D}\mathrm{I}\left(\mathrm{X}\right)={\displaystyle \frac{2\left(1+\beta \right)+\ln \left(\beta \right)\left(-4-3\beta +\left(1+\beta \right)\ln \left(\beta \right)\right)}{\beta \left(\ln \left(\beta \right)-2\right)\left(\ln \left(\beta \right)-1\right)}.}$$

To obtain explicit formulations for the skewness and kurtosis of the PEBWED, apply the following equations.

$$Skewness\left(X\right)={\displaystyle \frac{\mathrm{E}\left({\mathrm{X}}^3\right)-3\mathrm{E}\left({\mathrm{X}}^2\right)\mathrm{E}\left(\mathrm{X}\right)+2{\left(\mathrm{E}\left(\mathrm{X}\right)\right)}^3}{{\left[Var\left(X\right)\right]}^{\frac{3}{2}}},}$$and

$$Kurtosis\left(X\right)={\displaystyle \frac{\mathrm{E}\left({\mathrm{X}}^4\right)-4\mathrm{E}\left({\mathrm{X}}^3\right)\mathrm{E}\left(\mathrm{X}\right)+6\mathrm{E}\left({\mathrm{X}}^2\right){\left(\mathrm{E}\left(\mathrm{X}\right)\right)}^2-3{\left(\mathrm{E}\left(\mathrm{X}\right)\right)}^4}{{\left[Var\left(X\right)\right]}^2}.}$$

Proposition 4: The probability generating function (pgf) of PEBWED is given by

(14) $$G\left(s\right)=E\left(x^X\right)={\displaystyle \frac{\beta \left(-\beta +\left(1-s+\beta \right)\ln \left(\beta \right)\right)}{{\left(1-s+\beta \right)}^2\left(\ln \left(\beta \right)-1\right)}.}$$for $s\in (-1,1).$

Proof: The pgf of the PEBWED is derived using the well-known compound-Poisson theory in the manner described below

$$G\left(s\right)={\displaystyle \frac{\beta }{1-\ln \left(\beta \right)}{\int }_0^{\mathrm{\infty }}{e}^{\lambda \left(s-1\right)}\left(\beta \lambda -\ln \left(\beta \right)\right)e^{-\beta \lambda }d\lambda ,}$$

$$={\displaystyle \frac{\beta }{1-\ln \left(\beta \right)}\left\{\beta {\int }_0^{\mathrm{\infty }}{e}^{\lambda \left(s-1\right)}\lambda e^{-\beta \lambda }d\lambda -\ln \left(\beta \right){\int }_0^{\mathrm{\infty }}{e}^{\lambda \left(s-1\right)}{e}^{-\beta \lambda }d\lambda \right\},}$$

$$={\displaystyle \frac{\beta }{1-\ln \left(\beta \right)}\left\{{\displaystyle \frac{\beta }{{\left(1-s+\beta \right)}^2}-{\displaystyle \frac{\ln \left(\beta \right)}{\left(1-s+\beta \right)}}}\right\},}$$

$$={\displaystyle \frac{\beta \left(-\beta +\left(1-s+\beta \right)\ln \left(\beta \right)\right)}{{\left(1-s+\beta \right)}^2\left(\ln \left(\beta \right)-1\right)}.}$$which completes the proof.

The moment generating function (mgf) and characteristic function (cf) of the PEBWED are obtained from Eq. (14) when s is substituted by $e^t$ and $e^{it}$ respectively. They are provided, respectively, by

(15) $$M\left(t\right)={\displaystyle \frac{\beta \left(\beta -\ln \left(\beta \right)+{\mathrm{e}}^t\ln \left(\beta \right)-\beta \ln \left(\beta \right)\right)}{{\left(-1+{\mathrm{e}}^t-\beta \right)}^2\left(1-\ln \left(\beta \right)\right)}.}$$for $t\le 0,$ and

(16) $$\varphi \left(t\right)={\displaystyle \frac{\beta \left(\beta -\ln \left(\beta \right)+{\mathrm{e}}^{it}\ln \left(\beta \right)-\beta \ln \left(\beta \right)\right)}{{\left(-1+{\mathrm{e}}^{it}-\beta \right)}^2\left(1-\ln \left(\beta \right)\right)}.}$$for $t\in \mathbb{R}.$

The mean, variance, DI, skewness, and kurtosis for the PEBWED are now shown numerically in Table 1 for various parameter choices.

Parameter estimation

In this section, the model parameter is estimated using the maximum likelihood approach based on complete and censored sampling, censored sampling with cure fraction. This section also covers parameter estimation using the Bayesian approach.

Application

In this section, the new model is applied to three over-dispersed and asymmetric, and right-skewed datasets. We compare the fits of PEBWE distribution with Poisson Ailamujia (PA), discrete Burr Hatke (DBH), discrete inverted Topp-Leone (DITL), discrete moment exponential (DME), and Poisson distributions. Different model selection and goodness-of-fit criteria, log-likelihood (L), Akaike information criteria (AIC), Bayesian information criteria (BIC), and Kolmogorov-Smirnov tests are used to compare the fitted models.

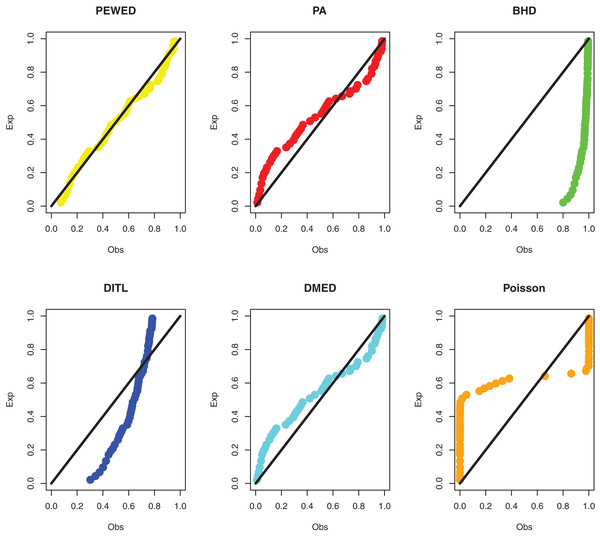
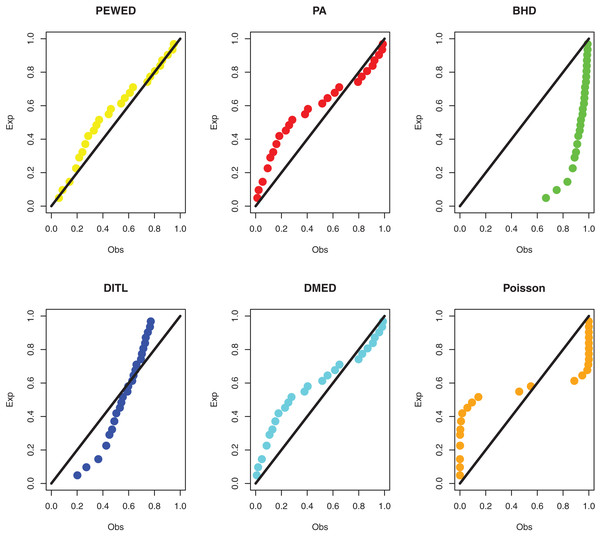
Data I: The first data set is about the number of daily death due to coronavirus in China from 23 January to 28 March 2020. The data set is reported at https://www.worldometers.info/coronavirus/country/china/. The data are: 8, 16, 15, 24, 26, 26, 38, 43, 46, 45, 57, 64, 65, 73, 73, 86, 89, 97, 108, 97, 146, 121, 143, 142, 105, 98, 136, 114, 118, 109, 97, 150, 71, 52, 29, 44, 47, 35, 42, 31, 38, 31, 30, 28, 27, 22, 17, 22, 11, 7, 13, 10, 14, 13, 11, 8, 3, 7, 6, 9, 7, 4, 6, 5, 3 and 5. The MLEs, standard errors, and goodness-of-fit measures are presented in Table 3. PP plots of all considered distributions for the first dataset are given in Fig. 3.

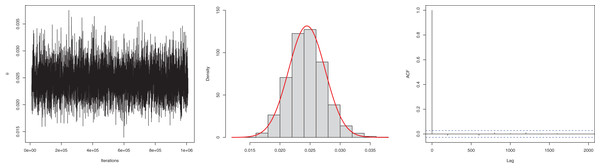
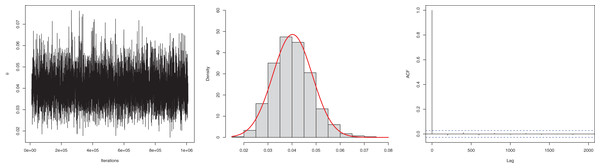
The next goal of this study was to estimate the model parameter using the Bayesian estimation approach presented in “Bayesian Estimation”. The posterior mean for the parameter $\beta$ is 0.0245, and the 95% HPD is 0.0186 to 0.0304. The posterior samples are presented in Fig. 4. The ACF (autocorrelation function) indicates that the posterior samples are independent, and the traceplot demonstrates the appraisal of MCMC samples over the iterations. The Geweke z-score (0.6071) is also indicative of satisfactory convergence of drawn samples to a stable distribution.

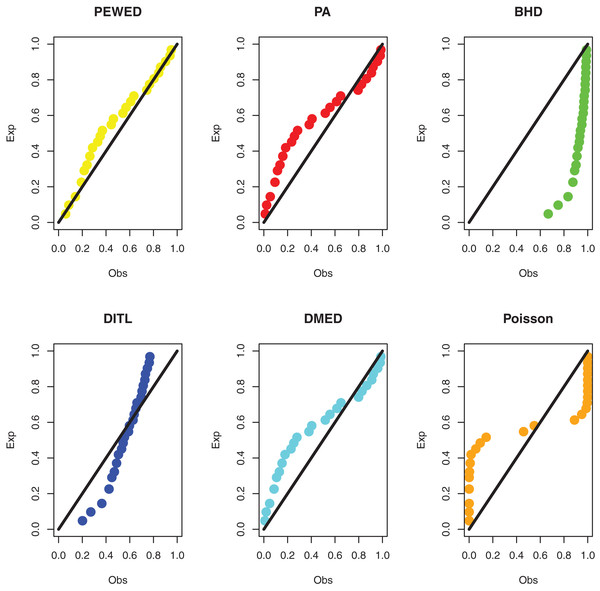
Data II: The second dataset below is remission times (in weeks) for a group of 30 patients with leukemia who received similar treatment (Lawless, 2011). The data observations are; 1, 1, 2, 4, 4, 6, 6, 6, 7, 8, 9, 9, 10, 12, 13, 14, 18, 19, 24, 26, 29, 31+, 42, 45+, 50+, 57, 60, 71+, 85+, 91. The observations with “+” indicate censored times. Using the methodology outlined in “ML estimation based on censored data”, we compute the MLEs. Table 4 shows the ML estimate and goodness of fit metrics. Figure 5 shows a comparison of the PP plots for the model based on the PEBWE distribution and the competitive discrete distributions. The findings presented by models show that the PEBWE distribution efficiently evaluated this data, while the PA distribution is the second-best model. The data was not well fit by models based on the discrete DBH, DITL, and Poisson distributions.

In the Bayesian estimation, similar to the previous example, we utilized gamma as the prior distribution. The mean is 0.0402, and the 95% HPD is 0.02502 to 0.0565. The posterior samples for the parameter are presented in Fig. 6. The ACF (autocorrelation function) indicates that the posterior samples are independent, and the traceplot demonstrates the appraisal of MCMC samples over the iterations. The Geweke z-score (−0.2249) is also indicative of satisfactory convergence of drawn samples to a stable distribution.

Data III: The third dataset is about survival data with a cure fraction. Consider the findings of research done between 2003 and 2013 at the Musculoskeletal Oncology Center of Sun Yat-Sen University’s First Affiliated Hospital in China (Wang et al., 2015). This study’s goal was to assess the efficacy of modular hemipelvis endoprosthesis rebuilding after pelvic tumor resection. Recurrence times for pelvic tumors with marginal or intracapsular margins were 3, 7, 11*, 18, 22*, 25, 28, 32*, 34*, 35, 35*, 36*, 40*, 40*, 41, 54*, 66*, 76*, 84*, 88*, and 92* months, with an asterisk (*) denoting a censored observation. We acquire the ML estimations using the approach described in “ML estimation based on censored data and a cure fraction”. Table 5 shows the ML estimate and goodness of fit metrics. The PP plots based on all competitive distributions are given in Fig. 7. We can see that the results from the PEBWE distribution provide the best fit.

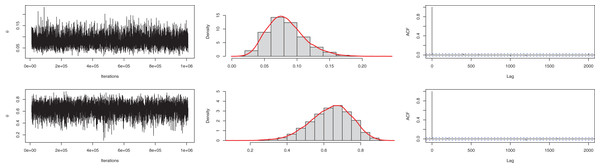
Similar to the previous example, for the Bayesian estimation, we utilized gamma and beta distribution as prior for $\beta$ and $\eta$ parameters. The means of posterior density for the parameters are $\hat{\beta }=0.083$ with a 95% HPD interval (0.0301–0.1401) and $\hat{\alpha }=0.6363$ with a 95% interval (0.4131–0.8434). The posterior samples for the parameter are presented in Fig. 8. The ACF (autocorrelation function) indicates that the posterior samples are independent, and the traceplot demonstrates the appraisal of MCMC samples over the iterations. The Geweke z-score (0.6607) is also indicative of satisfactory convergence of drawn samples to a stable distribution.

Conclusion

Discrete probability models play an important role in the analysis of count datasets. A new one-parameter discrete distribution is proposed by mixing Poisson and entropy-based weighted exponential distributions. Derived some important mathematical properties of the new model. The model parameter is estimated using the maximum likelihood and Bayesian estimation methods. The Bayesian estimation was performed using the MCMC approach using the Metropolis-Hastings algorithm. More importantly, the new probability model is applied to three datasets one is based on the number of deaths due to COVID-19, second leukemia patients, and third pelvic tumors patients. The proposed distribution provides more efficient results than all considered competitive distributions.

Supplemental Information