Exploring Twitter communication dynamics with evolving community analysis
- Published
- Accepted
- Received
- Academic Editor
- Radu Marculescu
- Subject Areas
- Data Mining and Machine Learning, Network Science and Online Social Networks, Social Computing
- Keywords
- Online social networks, Community evolution detection, Community ranking, Data mining
- Copyright
- © 2017 Konstantinidis et al.
- Licence
- This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, reproduction and adaptation in any medium and for any purpose provided that it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Computer Science) and either DOI or URL of the article must be cited.
- Cite this article
- 2017. Exploring Twitter communication dynamics with evolving community analysis. PeerJ Computer Science 3:e107 https://doi.org/10.7717/peerj-cs.107
Abstract
Online Social Networks (OSNs) have been widely adopted as a means of news dissemination, event reporting, opinion expression and discussion. As a result, news and events are being constantly reported and discussed online through OSNs such as Twitter. However, the variety and scale of all the information renders manual analysis extremely cumbersome, and therefore creating a storyline for an event or news story is an effort-intensive task. The main challenge pertains to the magnitude of data to be analyzed. To this end, we propose a framework for ranking the resulting communities and their metadata on the basis of structural, contextual and evolutionary characteristics such as community centrality, textual entropy, persistence and stability. We apply the proposed framework on three Twitter datasets and demonstrate that the analysis that followed enables the extraction of new insights with respect to influential user accounts, topics of discussion and emerging trends. These insights could primarily assist the work of social and political analysis scientists and the work of journalists in their own story telling, but also highlight the limitations of existing analysis methods and pose new research questions. To our knowledge, this study is the first to investigate the ranking of dynamic communities. In addition, our findings suggest future work regarding the determination of the general context of the communities based on structure and evolutionary behavior alone.
Introduction
OSNs have become influential means of disseminating news, reporting events and posting ideas as well as a medium for opinion formation (Topirceanu et al., 2016). Such networks combined with advanced statistical tools are often seen as the best sources of real-time information about global phenomena (Lazer et al., 2009; Aiello et al., 2013). Numerous studies of OSNs in relation to a variety of events have been conducted based on data from Twitter, a micro-blogging service that allows users to rapidly disseminate and receive information within the limit of 140 characters in a direct, grouped or global manner (Williams, Terras & Warwick, 2013; Nikolov et al., 2015). Twitter is currently one of the largest OSN platforms, with 313 million monthly active users1 and as such the vast amounts of information shared through it cannot be accessed or made use of unless this information is somehow organized. Thus, appropriate means of filtering and sorting are necessary to support efficient browsing, influential user discovery, and searching and gaining an overall view of the fluctuating nature of online discussions. Existing information browsing facilities, such as simple text queries typically result in immense amounts of posts rendering the inquirer clueless with respect to the online topics of discussion. Since online social networks exhibit the property of community structure, one of the more implicit manners of grouping information and thus facilitating the browsing process is by detecting the communities formed within the network. Research on community detection on static networks can be found in the Lancichinetti & Fortunato (2009) survey, as well as in the works of Granell et al. (2015), Newman (2006), Leskovec, Lang & Mahoney (2010) and Papadopoulos et al. (2012). Real-world OSNs, however, are definitely not static. The networks formed in services such as Twitter undergo major and rapid changes over time, which places them in the field of dynamic networks (Asur, Parthasarathy & Ucar, 2007; Giatsoglou & Vakali, 2013; Palla, Barabasi & Vicsek, 2007; Takaffoli et al., 2011; Tantipathananandh, Berger-Wolf & Kempe, 2007; Roy Chowdhury & Sukumar, 2014; Gauvin, Panisson & Cattuto, 2014; Greene, Doyle & Cunningham, 2010; Aktunc et al., 2015; Albano, Guillaume & Le Grand, 2014). These changes are manifested as users join in or leave one or more communities, by friends mentioning each other to attract attention or by new users referencing a total stranger. These trivial interactions seem to have a minor effect on the local structure of a social network. However, the network dynamics could lead to a non-trivial transformation of the entire community structure over time, and consequently create a need for reidentification. Particularly in OSNs, the immensely fast and unpredictably fluctuating topological structure of the resulting dynamic networks renders them an extremely complicated and challenging problem. Additionally, important questions related to the origin and spread of online messages posted within these networks, as well as the dynamics of interactions among online users and their corresponding communities remain unanswered.
To this end, we present a framework for analyzing and ranking the community structure, interaction and evolution in graphs. We also define a set of different evolution scenarios, which our method can successfully identify. A community here is essentially a subgraph which represents a set of interacting users as they tweet and mention one another. The edges of the subgraph represent the mentions made between users. A dynamic community is formed by a temporal array of the aforementioned communities with the condition that they share common users (Cazabet & Amblard, 2014; Nguyen et al., 2014). Community evolution detection has been previously used to study the temporal structure of a network (Gauvin, Panisson & Cattuto, 2014; Greene, Doyle & Cunningham, 2010; Palla, Barabasi & Vicsek, 2007; Takaffoli et al., 2011). However, even by establishing only the communities that sustain interest over time, the amount of communities and thus metadata that a user has to scan through is immense. In our previous work (Konstantinidis, Papadopoulos & Kompatsiaris, 2013), we proposed an adaptive approach to discover communities at points in time of increasing interest, but also a size-based varying threshold for use in community evolution detection. Both were introduced in an attempt to discard trivial information and to implicitly reduce the available content. Although the amount of information was somewhat reduced, the extraction of information still remained a tedious task. Hence, to further facilitate the browsing of information that a user has to scan through in order to discover items of interest, we present a sorted version of the data similarly to a search engine. The sorting of the data is performed via the ranking of dynamic communities on the basis of seven distinct features which represent the notions of Time, Importance, Structure, Context and Integrity (TISCI). Nonetheless, the sorting of textual information and thus some kind of summarization is only a side-effect of the dynamic community ranking. The main impact lies in the identification and monitoring of persistent, consistent and diverse groups of people who are bound by a specific matter of discussion.
The closest work to dynamic community ranking was recently presented by Lu & Brelsford (2014) in a behavioral analysis case study and as such it is used here as a baseline for comparison purposes. However, it should be mentioned that the ranking was not the primary aim of their research and that the communities were separately sorted by size thus missing the notions of importance, temporal stability and content diversity which are employed in the proposed framework. To the best of our knowledge, this is the first time that structural, temporal, importance and contextual features are fused in a dynamic community ranking algorithm for a modern online social network application.
Although the overall problem is covered by the more general field of evolving network mining, it actually breaks down in many smaller issues that need to be faced. Table 1 presents the decomposition of the problem into these issues, together with popular available methods which can be used to overcome them, along with the techniques employed by Lu & Brelsford (2014) and the ones proposed by the TISCI framework which is presented here.
| Subproblem | Available methods | Lu & Brelsford (2014) | Proposed framework |
|---|---|---|---|
| Granularity selection | Event-based | Event-based | Time-based |
| Time-based | |||
| Activity-based | |||
| Community detection | Louvain | Infomap | Infomap |
| Infomap | |||
| Modularity Optimization | |||
| Set similarity | Jaccard | Jaccard | Jaccard |
| Sorensen | |||
| Euclidean | |||
| Cosine | |||
| Feature fusion | Reciprocal Rank | None | Reciprocal Rank Fusion |
| Multi-criteria analysis | |||
| Condorcet | |||
| Information ranking | Size | Size | TISCI |
| Centrality | |||
| TISCI |
In this work, we consider the user activity in the form of mentioning posts, the communities to which the users belong, and most importantly, the evolutionary and significance characteristics of these communities and use them in the ranking process. The proposed analysis is carried out in three steps. In the first step, the Twitter API is used to extract mentioning messages that contain interactions between users and a sequence of time periods is determined based on the level of activity. Then, for each of these periods, graph snapshots are created based on user interactions and the communities of highly interacting users are extracted using the Infomap community detection method (Rosvall & Bergstrom, 2008). During the second step, the community evolution detection process inspects whether any communities have persisted in time over a long enough period (eight snapshots). In the last and featured step, the evolution is studied in order to rank the communities and their metadata (i.e., tweeted text, hashtags, URLs, etc.) with respect to the communities’ persistence, stability, centrality, size, diversity and integrity characteristics, thus creating dynamic community containers which provide structured access to information. The temporal (evolutional) and contextual features are also the main reason why a static community detection method was employed instead of a dynamic method which would aggregate the information such as the one proposed by Nguyen et al. (2014).
In order to evaluate the proposed framework it is applied on three datasets extracted from Twitter to demonstrate that it can serve as a means of discovering newsworthy pieces of information and real-world incidents around topics of interest. The first dataset was collected by monitoring discussions around tweets containing vocabulary on the 2014 season of BBC’s Sherlock, the second and third contain discussions on Greece’s 2015 January and September elections, and the last one containing vocabulary regarding the 2012 presidential elections in the US (Aiello et al., 2013). Three community detection methods are also employed to demonstrate that Infomap is the preferable scheme.
Due to the lack of ground truth datasets for the evaluation of the proposed framework, we devised and are proposing a novel, context-based evaluation scheme which could serve as a basis for future work. It is our belief that by studying the contents of discussions being made in groups and the evolution of these groups we can produce a better understanding of the users’ and communities’ behavior and can give deeper insights into unfolding large-scale events. Consequently, our main contributions can be summed up in the following:
-
a novel ranking framework for dynamic communities based on temporal and contextual features;
-
a context-based evaluation scheme aimed to overcome the absence of ground truth datasets for the community discovery analysis;
-
an empirical study on three Twitter datasets demonstrating the merits of the proposed framework.
An additional asset of the TISCI ranking method, which is the main contribution of this paper, is that it was created to work with any kind of community evolution detection method that retains discrete temporal information and that it is independent of the choice of the community detection algorithm applied to the individual timeslots.
Related Work
Mining OSN interactions is a topic that has attracted considerable interest in recent years. Interaction analysis provides insights and solutions to a wide range of problems such as cyber-attacks (Wei et al., 2015), recommendation systems (Kim & Shim, 2014; Gupta et al., 2013), summarization (Schinas et al., 2015; Lin, Sundaram & Kelliher, 2008) and information diffusion (Yang, McAuley & Leskovec, 2013).
One of the most recent attempts comes from McKelvey et al. (2012) who presented the Truthy system for collecting and analyzing political discourse on Twitter, providing real-time, interactive visualizations of information diffusion processes. They created interfaces containing several key analytical components. These elements include an interactive layout of the communication network shared among the most retweeted users of a meme and detailed user-level metrics on activity volume, sentiment, inferred ideology, language, and communication channel choices.
TwitInfo is another system that provides network analysis and visualizations of Twitter data. Its content is collected by automatically identifying “bursts” of tweets (Marcus et al., 2011). After calculating the top tweeted URLs in each burst, it plots each tweet on a map, colored according to sentiment. TwitInfo focuses on specific memes, identified by the researchers, and is thus limited in cases when arbitrary topics are of interest. Both of the aforementioned frameworks present an abundance of statistics for individual users but contrary to our method, they do not take into account the communities created by these users or the evolution of these communities.
Greene, Doyle & Cunningham (2010) presented a method in which they use regular fortnight time intervals to sample a mobile phone network in a two month period and extract the communities created between the users of the network. Although the network selected is quite large and the method is also very fast; the system was created in order to be applied on a mobile phone network which renders it quite different to the networks studied in this paper. The collected data lack the topic of discussion and the content of the messages between users, so there is no way to discover the reason for which a community was transformed or the effect that the transformation really had on the topic of that community. Moreover, although the features of persistence and stability are mentioned in the paper, no effort was made in ranking the communities. Nonetheless, due to its speed and scalability advantages, in this paper we decided to employ and extend their method by introducing a couple of optimization tweaks which render it suitable for large scale applications such as the analysis of an OSN.
Finding the optimal match between communities in different timeslots was proposed in Tantipathananandh, Berger-Wolf & Kempe (2007), where the dynamic community detection approach was framed as a graph-coloring problem. Since the problem is NP-hard, the authors employed a heuristic technique that involved greedily matching pairs of node-sets in between timeslots, in descending order of similarity. Although this technique has shown to perform well on a number of small well-known social network datasets such as the Southern Women dataset, as the authors state in the paper, it does not support the identification of dynamic events such as community merging and splitting thus losing significant information which is of utmost importance in the proposed ranking framework which heavily relies on the content and context of the tweets.
Takaffoli et al. (2011) considered the context of the Enron (250 email addresses in the last year from the original dataset) and DBLP (three conferences from 2004 to 2009) datasets for evaluation purposes, but similar to Greene, Doyle & Cunningham (2010) they also studied the context independently of community evolution. They focused on the changes in community evolution and the average topic continuation with respect to changes in the similarity threshold. The analyzed data presented valuable information as to how to select the similarity threshold but no insight as to important communities, their users or specific topics.
Another dynamic community detection method used to extract trends was introduced by Cazabet et al. (2012). They created an evolving network of terms, which is an abstraction of the complete network, and then applied a dynamic community detection algorithm on this evolving network in order to discover emerging trends. Although the algorithm is very effective for locating trends, it does not consider the interactions made between various users or the evolution of the communities.
The work by Lin, Sundaram & Kelliher (2008) bears some similarities in terms of motivation as they also want to gain insights into large-scale involving networks. They do this via extracting themes (concepts) and associating them with users and activities (e.g., commenting) and then try to study their evolution. However, they provide no way of ranking the extracted themes, which is the focus of our work.
One of the main problems in detecting influential communities in temporal networks is that most of the time they are populated with a large amount of outliers. While tackling the problem of dynamic network summarization, Qu et al. (2014) capture only the few most interesting nodes or edges over time, and they address the summarization problem by finding interestingness-driven diffusion processes.
Ferlez et al. (2008) proposed TimeFall which performs time segmentation using cut-points, community detection and community matching across segments. Despite the fact that they do not rank the communities, the proposed scheme could be employed to extract and detect evolving communities which would in turn be ranked by the TISCI framework.
In Mucha et al. (2010), the concept of multiplex networks is introduced via the extension of the popular modularity function and by adapting its implicit null model to fit a layered network. Here, each layer is represented with a slice. Each slice has an adjacency matrix describing connections between nodes which belong to the previously considered slice. Essentially, they perform community detection on a network of networks. Although these frameworks technically require a network to be node-aligned (all nodes appear in all layers/timeslots), they have been used explicitly to consider relatively small networks in which that is not the case by using zero-padding. However, this creates a huge overhead in OSNs since the majority of users does not appear in every timeslot. In addition, Mucha et al. (2010) do not provide any method for the ranking of the extracted communities, which is the focus of this paper.
A method for ranking communities, specifically quasi-cliques, was proposed by Xiao et al. (2007) in which they rank the respective cliques in respect to their betweeness centrality. However, they also do not take temporal measures into consideration and apply their method on a call graph from a telecom carrier and a collaboration network of co-authors thus excluding the context of the messages.
The most recent work regarding the extraction of information using evolving communities was presented in Lu & Brelsford (2014) which studied the behavior of people discussing the 2011 Japanese earthquake and tsunami. Although they did rank the static communities by size, the evolution regarded only the before and after periods, so no actual dynamic community ranking was performed.
OSN Analysis Framework
OSN applications comprise a large number of users that can be associated to each other through numerous types of interaction. Graphs provide an elegant representation of data, containing the users as their vertices and their interactions (e.g., mentions, citations) as edges. Edges can be of different types, such as simple, weighted, directed and multiway (i.e., connecting more than two entities) depending on the network creation process.
Notation
In this paper, we employ the standard graph notation G = (V, E, w), where G stands for the whole network; V stands for the set of all vertices and E for the set of all edges. In particular, we use lowercase letters (x) to represent scalars, bold lowercase letters (x) to represent vectors, and uppercase letters (X) to represent matrices. A subscript n on a variable (Xn) indicates the value of that variable at discrete time n. We use a snapshot graph to model interactions at a discrete time interval n. In Gn, each node vi ∈ Vn represents a user and each edge eij ∈ En is associated with a directed weight wij corresponding to the frequency of mentions between vi and vj. The interaction history is represented by a sequence of graph snapshots . A community Ci,n which belongs to the set of communities is defined here as a subgraph comprising a subset Vcomm⊆V of nodes such that connections between the nodes are denser than connections with the rest of the network. A dynamic community Ti,n which belongs to the set of time-evolving communities, is defined as a series of subgraphs that consist of subsets of all the nodes in V and the set of interactions among the nodes in these subsets that occur within a set of N timeslots.
Framework description
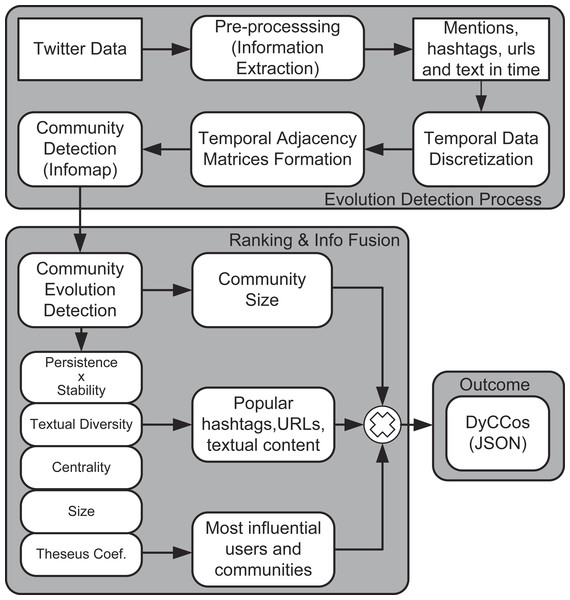
This section describes the proposed framework in three parts: community detection, community evolution detection and ranking. Figure 1 illustrates all the steps of the proposed framework.
Figure 1: Block diagram of the proposed framework.
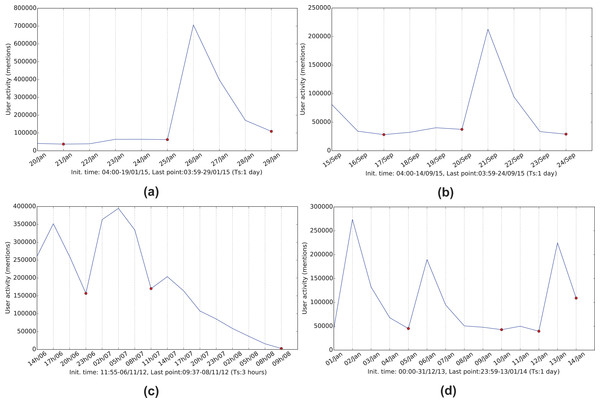
Figure 2: Referencing frequency activity for the four networks.
(A) January 2015 Greek elections, (B) September 2015 Greek elections, (C) 2012 US elections and (D) 2014 BBC’s Sherlock series.Interaction data discretization and graph creation
The tweet timestamp and a corresponding sampling frequency are used to group the interactions into timeslots. The selection of time granularity (inverse sampling frequency) for each network is based on the change in activity. The aim is to create clear sequential graph snapshots of the network as presented in Fig. 2. The sampling time should be meaningful on its own (hours, days) but individually for each case as well. For example, for the Greek election and Sherlock series datasets, a 24-hour period was selected to detect day-by-day changes to the flourishing discussions during the anticipation period of the corresponding events (Election Day, episode broadcasting) and the post-event reactions. The 24-hour period in conjunction with the deep search performed during the evolution detection process, allows the framework to discover persistent communities over a one week time-frame.
Every node in the resulting graphs represents a Twitter user who communicated tweets in the datasets by mentioning or being mentioned. A mention, and thus a directed edge between two users is formed when one of the two creates a reference to the other in his/her posted content via use of the @ symbol. The number of mentions between them forms the edge weight.
Community detection
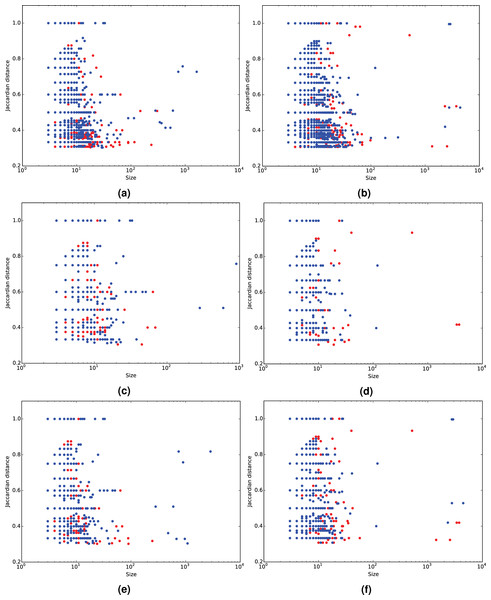
Given a social network, a community can be defined as a subgraph comprising a set of users that are typically associated through a common element of interest. This element can be as varied as a topic, a real-world person, a place, an event, an activity or a cause (Papadopoulos et al., 2012). We expect to discover such communities by analyzing mention networks on Twitter. There is considerable work on the topic and a host of different community detection approaches appear in literature (Fortunato, 2010; Papadopoulos et al., 2012). Due to the nature of Twitter mention networks, notably their sparsity and size, in this paper we apply the Infomap method (Rosvall & Bergstrom, 2008) to detect the underlying community structures. Infomap optimizes the map equation (Rosvall, Axelsson & Bergstrom, 2009), which exploits the information-theoretic duality between the problem of compressing data, and the problem of detecting and extracting significant patterns or structures within those data. The Infomap method is essentially built based on optimizing the minimum description length of the random walk on the network. The Infomap scheme was selected for three reasons; first, according to Lancichinetti & Fortunato (2009) and Granell et al. (2015) and our own preliminary results, Infomap is very fast and outperforms even the most popular of community detection methods such as Louvain (Blondel et al., 2008) and Newman’s modularity optimization technique (Newman, 2006). Further, the low computational complexity of O(m) (m signifies the number of edges in a graph) encourages its use on graphs of large real networks. Last, Lu & Brelsford (2014) used it in their experimental setup and as such it is suitable for comparative purposes. It should be noted that the focus of the framework is to rank the dynamic communities independently from the method used for their detection and not to perform an exhaustive comparison of algorithms able to process dynamic networks. Nonetheless, Fig. 3 as well as Table 2 provide support in favor of Infomap in comparison to the Louvain and Newman methods, as Infomap detects the most communities and significantly more from the middle region. Figures 3, 4C and 4D show the performance of the Louvain and the modularity optimization technique. They both seem to detect either very large or relatively small communities, which are out of the middle section. The middle section poses the most interest for this study as it contains reasonably populated groups for the purposes of a discussion. In the future, it may be interesting to thoroughly investigate the sensitivity of results with respect to the employed community detection method.
Figure 3: Community Jaccard distance (similarity) over community size.
Results using the Infomap (A, B), Newman (C, D) and Louvain (E, F) community detection algorithms for the 2014 BBC’s Sherlock series (A, C, E) and the 2012 US elections (B, D, F). The red dots signify the undetected communities which were missed due to the absence of the time-delay search, whereas the blue-ones signify commonly detected communities.| Louvain | Newman | Infomap | ||
|---|---|---|---|---|
| US election | Delay | 1,696 | 1,021 | 4,422 |
| No delay | 985 | 579 | 2,646 | |
| Sherlock | Delay | 1,369 | 1,175 | 3,374 |
| No delay | 638 | 544 | 1,684 | |
| Greek election January | Delay | 322 | 266 | 1,120 |
| No delay | 235 | 191 | 763 | |
| Greek election September | Delay | 219 | 198 | 639 |
| No delay | 144 | 127 | 403 |
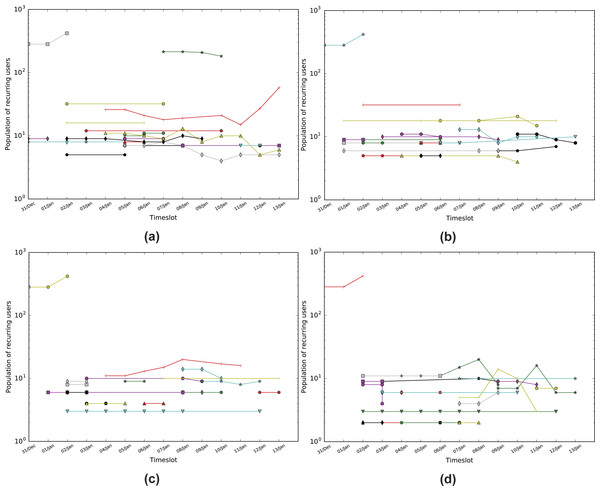
Figure 4: Population of matching nodes per timeslot for the Sherlock dataset.
(A) Infomap with a threshold of 0.3 (TISCI), (B) Infomap with a threshold of 0.5 (Lu & Brelsford, 2014), (C) Louvain with a threshold of 0.3 (Greene, Doyle & Cunningham, 2010) and (D) Newman with a threshold of 0.3. Every line is essentially a dynamic community.Community evolution detection
The problem of finding communities in static graphs has been addressed by researchers for several years (Blondel et al., 2008; Newman, 2006; Giatsoglou, Chatzakou & Vakali, 2013). However, the highly dynamic nature of OSNs has moved the spotlight to the subject of dynamic graph analysis (Nguyen et al., 2014; Asur, Parthasarathy & Ucar, 2007; Giatsoglou & Vakali, 2013; Palla, Barabasi & Vicsek, 2007; Takaffoli et al., 2011; Roy Chowdhury & Sukumar, 2014).
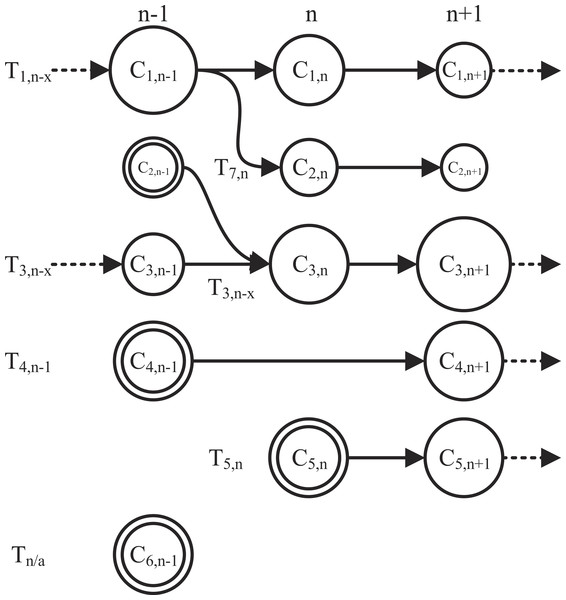
In this paper, we represent a dynamic network as a sequence of graph snapshots . The objective is to detect and extract dynamic communities T by identifying the communities C that are present in the network across a set of N timeslots and create a container which includes a variety of metadata such as popular hashtags and URLs, influential users and the posted text. A dynamic community is represented by the timeline of the communities of users that it comprises. The difference between sets C and T is that the former contains every static community in every available timeslot, whereas the latter contains sequences of communities that evolve through time. In both Ci,n and Ti,n i is a counter of communities and dynamic communities respectively, while particularly in Ti,n n represents the timeslot of birth of the dynamic community. Figure 5 presents an example of the most frequent conditions that communities might experience: birth, death, irregular occurrences, merging and splitting, as well as growth and decay that register when a significant percentage of the community population is affected. In the example of Fig. 5, the behavior of six potential dynamic communities is studied over a period of three timeslots (n − 1, n, n + 1). Dynamic community T1,n−x originated from a previous timeslot n − x which then split up into a fork formation in timeslot n. In T1,n−x, x is an integer valued variable representing the timeslot delay which can acquire a maximum value of D (1 ≤ x ≤ D ≤ N). The split indicates that for some reason the members of C1,n−1 broke up into two separate smaller groups in timeslot n, which also explains the change in size. In our case it could be that a large group of users engaged in conversation during n − 1 but split up and are not cross mentioning each other in n and n + 1. Moreover, although the second group (C2,n) instigated a new dynamic community T7,n, it continued its decaying activity for one more timeslot and then dispersed (community death). Nonetheless, both are obviously important to the evolution of the community and the separation poses a great interest from a content point of view as to the ongoing user discussion and as to why they actually split up. Both can be answered by using the metadata stored in the container corresponding to the dynamic community. A dual example is that of T2,n−1 and T3,n−x in which two communities started up as weak and small but evolved through a merger into one very strong, large community that continues on to n + 2. In this case it could be that two different groups of people witnessed the same event and began conversing on it separately. As time went by, connections were made between the two groups and in the n timeslot they finally merged into one. Actually, the community continued to grow as shown on the n + 1 timeslot. T4,n−1 and Tn∕a were both created (community birth) in n − 1 and both disappeared in n differentiating in that T4,n−1 reappears in n + 1 (irregular occurrence) while Tn∕a does not and thus a dynamic community is not registered. This is the main reason why a timeslot delay is introduced in the system as will be described later; a search strictly between communities of consecutive timeslots would result in missing such re-occurrences.
Figure 5: A study of six potential dynamic communities tracked over three timeslots.
The seven most frequent conditions that communities might experience are birth (concentric circles), death (no exiting arrow), irregular occurrences (skipped timeslot), merging and splitting, as well as growth and decay.To study the various lifecycle stages of a community, the main challenge pertains to the computational process used to identify and follow the evolution of any given community. On the one hand, it should be able to effectively map every community to its corresponding timeline, and on the other hand it should be as less of a computational burden as possible to be applicable to massive networks. However, community matching techniques presume a zero-to-one or one-to-one mapping between users in two communities, thus not supporting the identification of the above conditions in the lifecycle of a dynamic community. In order to overcome this predicament, we employ a heuristic by Greene, Doyle & Cunningham (2010) relying on a user-defined threshold to determine the matching between communities across different timeslots.
The algorithm steps are presented in more detail as follows. Initially, the first set of communities (i.e., the first snapshot) is extracted by applying the Infomap community detection algorithm (Rosvall & Bergstrom, 2008) to the G1 graph. A dynamic community marker Ti,1 (where i = [1, k]) is assigned to each community from this snapshot. Next, the second set of communities is extracted from the G2 graph and a matching process is performed between all the community combinations from the two consecutive snapshots in order to determine any possible evolution from the first snapshot to the next. The dynamic communities are then updated based on that evolution. For example, if Ca1 does not appear in the second snapshot, Ta,1 is not updated; a split is registered if the community appears twice in the new timeslot, and a merger marker is assigned if two or more communities seem to have merged into one.
One of the problems community evolution detection processes face is the lack of consistency in the users’ behavior. The lack of consistent and sequential behavior results in communities being labeled dead when in fact they could just be delayed. In order to avoid potential false positives of community deaths, a trail of several snapshots is retained; meaning that the search covers a wider range of timeslots in total instead of just the immediate previous one. The length of the trail depends on the selected granularity of the discretization process, in a manner that a meaningful period is covered (i.e., if the sampling is performed on a daily basis, the trail will consist of seven timeslots in order to provide a week’s depth). Hence, if the evolution of a community is not detected in the immediate to last timeslot, the system queries the D previous ones in a “last come, first served” order. This means that the search progresses through the trail until a match is found, in which case the search is terminated and the dynamic community is observed to have skipped a timeslot. If no matching community is detected, the community is considered dead. The proof of necessity for such a delay is shown on Table 2. The evolution detection procedure is repeated until all graphs have been processed. It should be noted that the decision for the delay being set to only a few timeslots instead for the whole trail, was made by considering the computational burden of the system in conjunction to the fact that people lose interest. If the users comprising the community do not engage in the discussion for a significant period of time, it would be safe to say, that the community has been dismantled.
In order to determine the matching between communities, the Jaccard coefficient is employed (Jaccard, 1912). Following comparative preliminary results between the Jaccard and the Sorensen index (dice coefficient) (Sørensen, 1948), the former was selected due to its efficiency. In fact, the Jaccard similarity is still one of the most popular similarity measures in community matching (Yang, McAuley & Leskovec, 2013; Alvarez, Sanz-Rodríguez & Cabrera, 2015). The similarity between a pair of consecutive communities Cin and is calculated by use of the following formula, where timeslot delay td ∈ [1, 7]: (1)
If the similarity exceeds a matching threshold ϕ, the pair is matched and Cin is added to the timeline of the Ti,n dynamic community. As in Greene, Doyle & Cunningham (2010), Takaffoli et al. (2011) and Lu & Brelsford (2014), the similarity threshold ϕ is a constant threshold. Following a more extensive analysis on the impact of the threshold selection, Greene suggested the use of 0.3 which concurs with our own results. Figure 4 illustrates that 0.2 allows the creation of many strings of small communities, whereas 0.5 suppresses a lot of communities from the middle region which holds most of the information required for a fuller investigation.
Dynamic community ranking using TISCI
Although the evolution detection algorithm is efficient enough to identify which communities are resilient to the passing of time, it does not provide a measure as to which communities are worth looking into and which are not. A solution to this shortcoming is presented here via the TISCI score that ranks the evolving communities on the basis of seven distinct features which represent the notions of Time, Importance, Structure, Context and Integrity. Specifically, we employ persistence and stability which are temporal measures, normalized-community-centrality which is a relational importance measure, community-size which is a structural measure, mean-textual-entropy and unique-URL average which are contextual measures, and an integrity coefficient inspired by the “ship of Theseus” paradox.
Persistence is defined as the characteristic of a dynamic community to make an appearance in as many timeslots as possible (i.e., overall appearances/total number of timeslots), and stability as the ability to appear in as many consecutive timeslots as possible disregarding the total number of appearances (i.e., overall consecutive appearances/total number of timeslots).
2 3 where δ is the impulse function, m represents the total number of timeslots, x, y are the labels of the oldest community in Tx,y and (4)
We expect consistent dynamic communities to be both persistent and stable as the combination of these features shows either a continuous interest in a subject or its evolution to something new. As such we combine the two features into one via multiplication. Figure 4 shows how stable and how persistent the communities are with respect to the actual number of persistent users. Moreover, it shows the number of people who persist in time within a community in respect with the community’s persistence and stability for the Infomap as well as for the Louvain and Newman methods.
Google’s PageRank (Brin & Page, 1998) is used as the centrality feature which measures the number and quality of links to a community in order to determine an estimate of how important that community is. The same measure is also applied to the users from every dynamic community, ranking them according to their own centrality and thus providing the most influential users per timeslot. There is however a difference between the two in how the final centrality values are extracted, since different timeslots create different populations between the static graphs. Although this does not affect the users’ centralities as they are compared to each other within the timeslot, it does however influence the communities’ centrality measures due to the difference in populations. In order to compare centrality measures from different timeslots, we employ the normalized PageRank solution as proposed in Berberich et al. (2007). The Mean Centrality as it is used here is defined as: (5) where k is the number of communities per timeslot.
One of the measures that provides a sense of popularity is virality which in the case of Twitter datasets translates into multiple bursts of mentions in a short time. This can happen either due to an event or because an influential user (e.g., major newspaper account) posted something of interest. On the other hand, Lu and Berlsford used the lack of increased community size as an indication of disruption in the telecommunication services. For this reason we consider the increased size of a dynamic community as a feature that requires attention. Here, the feature of size is defined as the average size of the static communities that comprise it.
The integrity measure employed is an extension of the ship of Theseus coefficient. The ship of Theseus, also known as Theseus’s paradox, is a thought experiment that raises the question of whether an object which has had all its components replaced remains fundamentally the same object (Rea, 1995). We apply this theory to find out the transformation sustained by the dynamic community by calculating the number of consistent nodes within the communities which represents the integrity and consistency of the dynamic community.
Twitter datasets differ quite a lot to other online social networks since the user is restricted to 140 characters of text. Given this restriction, we assume that it is safe to say that there is a connection between the entropy of tweeted words used in a community (discarding URLs, mentions, hashtags and stopwords), the effort the users put into posting those tweets, and the diversity of its content. Whether there is a discussion between the users or a presentation of different events, high textual entropy implies a broader range of information and therefore more useful results. An added bonus to this feature is that spam and empty tweets containing only hashtags or mentions, as is the case in URL attention seeking tweets, rank even lower than communities containing normal retweets. For the ranking we employ the mean textual diversity of the dynamic community. The textual diversity in a community Ci is measured by Shannon’s entropy H of the text resulting from the tweets that appear in that community as follows: (6) where p(Wm) is the probability of a word Wm appearing in a community containing M words and is computed as follows: (7)
The second contextual feature to be employed regards the references cited by the users via URLs in order for them to point out something they consider important or interesting. In fact, the URLs hold a lot more information than the single tweet and as such we also consider it useful for discovering content-rich communities. The ranking in this case is performed by simply computing the average of unique URLs in each dynamic community over time.
Since we have an array of six features, we have to combine them into a single value in order to rank the dynamic communities. The final ranking measure for every dynamic community is extracted by employing the Reciprocal Rank Fusion (RRF) (Cormack, Clarke & Buettcher, 2009) method; a preference aggregation method which essentially provides the sum of the reciprocals ranks of all extracted aforementioned features Q: (8) where α is a constant which is used to mitigate the impact of high rankings by outlier systems. Cormack, Clarke & Buettcher (2009) set the constant to 60 according to their needs although the choice, as they state, is not critical and thus we prefer a lower score equal to the number of dynamic communities to be considered.
Despite its simplicity, the RRF has proven to perform better than many other methods such as the Condorset Fuse or the well established CombMNZ (Cormack, Clarke & Buettcher, 2009) and is considered one of the best baseline consensus methods (Volkovs, Larochelle & Zemel, 2012). In addition, it requires no special voting algorithm or global information and the ranks may be computed and summed one system at a time, thus avoiding the necessity of keeping all the rankings in memory. However, this preference aggregation method is not without flaws, as it could potentially hide correlations between feature ranks. Although, in other applications this could pose a problem, as shown in Table 3 the lack of correlation between the features’ ranks encourages us to employ this simple but useful method. The correlation was measured using the Spearman rank-order correlation coefficient.
| Centrality | Perstability | Size | Textdiversity | Theseus | Urldiversity | TISCI | |
|---|---|---|---|---|---|---|---|
| Centrality | 1.0 | 0.046 | 0.051 | 0.032 | −0.021 | 0.006 | 0.021 |
| Perstability | 0.046 | 1.0 | 0.032 | 0.154 | 0.015 | 0.047 | 0.029 |
| Size | 0.051 | 0.032 | 1.0 | 0.156 | 0.005 | 0.002 | 0.011 |
| Textdiversity | 0.032 | 0.154 | 0.156 | 1.0 | 0.034 | 0.055 | 0.029 |
| Theseus | −0.021 | 0.015 | 0.005 | 0.034 | 1.0 | −0.008 | 0.016 |
| Urldiversity | 0.006 | 0.047 | 0.002 | 0.055 | −0.008 | 1.0 | −0.01 |
| TISCI | 0.021 | 0.029 | 0.011 | 0.029 | 0.016 | −0.01 | 1.0 |
Complexity and scalability
When it comes to temporal interaction analysis, scalability is always an issue. The cost of the TISCI framework is O(m + k2 + c⋅w) where m are the number of edges for the Infomap method, k is the number of communities of each row in the evolution detection scheme, and c and w are the numbers of dynamic communities and words in each community in the ranking stage. Although currently, the framework would not scale well due to the squared complexity of the evolution detection process, future work will involve the use of Local Sensitivity Hashing to speed up the operation.
Experimental Study
Despite the proliferation of dynamic community detection methods, there is still a lack of benchmark ground truth datasets that could be used for the framework’s testing purposes. Instead, the results presented in this paper were attained by applying our framework on three Twitter interaction network datasets as described in the following section.
Datasets
The tweets related to the US election of 2012 were collected using a set of filter keywords and hashtags chosen by experts (Aiello et al., 2013). Keywords and hashtags in Greek and English containing all the Greek party names as well as their leaders’ were used for the Greek elections of 2015. Last, variations of the names ‘Sherlock’ and ‘Watson’ were used for the Sherlock series dataset. We chose these three datasets as they all share a number of useful features but also have significant differences as one may deduce from the data description and the basic network characteristics which are presented in Table 4. On the one hand all of the datasets regard major events that generate a large volume of communication and are mostly dominated by English-language contributors, making analysis simpler for the majority of researchers. On the other hand, the US election (including voting, vote counting, speculation about results and subsequent analysis) lasted two days, whereas the Greek elections and the Sherlock frenzy lasted 10 days and two weeks, respectively. Similarly, in an event focused discussion such as the US election, almost all the focus is either on specific events/announcements or specific people associated with the events, whereas topics in a general discussion regarding a fictitious character tend to be more spread out over time and to overlap with other topics while becoming more active when specific events take place. These differences help us understand the ways that social networks are used in very different circumstances as well as that the variation in temporal structure depends heavily on the query itself.
| Sherlock | US Election | GR Election Jan | GR Election Sep | |
|---|---|---|---|---|
| # of tweets | 2,904,321 | 4,148,782 | 2,748,613 | 1,084,304 |
| # of tweets with mentions | 1,412,358 | 2,967,779 | 1,836,296 | 622,590 |
| # of hashtags | 643,132 | 4,286,418 | 1,399,109 | 482,376 |
| # of URLs | 139,663 | 675,862 | 581,823 | 215,530 |
| # of unique users | 542,254 | 2,013,301 | 555,859 | 166,807 |
| # of edges | 1,595,435 | 4,190,883 | 2,368,396 | 744,824 |
| # of communities | 186,045 | 416,181 | 108,532 | 31,518 |
| # reduced communities | 37,106 | 73,170 | 32,231 | 11,681 |
| # of evolution steps | 9,211 | 8,843 | 4,336 | 1,610 |
| # of dynamic communities | 3,457 | 3,936 | 1,758 | 639 |
| Sampling time | 24 h | 3 h | 24 h | 24 h |
Sherlock Holmes dataset
This real-world dataset is a collection of mentioning posts acquired by a crawler that collected tweets containing keywords and hashtags which are variations of the names ‘Sherlock’ and ‘Watson.’ The crawler ran over a period of two weeks; from the 31st of December 2013 to the 14th of January 2014, extracting messages containing mentions. The evolution detection process discovered 9,211 dynamic communities comprising 178,361 snapshot communities. The information we sought pertained to the various communities created between people who interact via mentions and are interested in the BBC’s Sherlock series, people who are influenced by these communities and any news that might give us more insight on this world wide phenomenon.
The dynamic community structure resulting from this dataset is totally different from the two election ones in more ways than one. Initially, there are many diverse and smaller communities which persist over time that seem to be fairly detached from the rest. This means that the interest here is widely spread and the groups of people discussing the imminent or last episode of the series are smaller indicating that in most cases we are looking into friends chatting online. Nonetheless, the user can still acquire a variety of information such as the general feeling of the viewers, several spoilers regarding each episode, a reminder about when each episode starts and on what day, and also statistics on the viewership of the series. The latter was extracted from one of the largest communities which informed us that not only was the first episode viewed by an average of 9.2 million viewers but also that Chinese fans relish the series and especially the love theory between the two main characters (http://www.bbc.com/news/blogs-china-blog-25550426). Other typical topics of conversation include the anticipation of the series, commentary regarding the quality of the episode, commentary regarding the character and many more typical lines of discussion. A short list of findings is presented on Table 5. What is interesting enough is that conversations and opinions regarding the bad habits or the sexuality of the character are pretty high in the rankings and that there are plenty of non-English speaking communities. One last remark concerns the DyCCo (ranked #9) which contains a plethora of shopping labels. Usually, consecutive shop labels are an indication of spam as they are usually consistent, stable and contain URLs with the sole purpose to lure a potential customer. However, in this case the shopping labeled communities contain references to books, movies and the original series of Sherlock Holmes sold by major retailers, thus classifying the DyCCo as one that a Sherlock enthusiast would actually be interested in.
| Finding | URL (if available) | |
|---|---|---|
| 1 | Creators reveal they already have series four mapped out | https://goo.gl/5ZDCMt |
| 2 | Cumberbatch’s parents make Sherlock cameo | https://goo.gl/qPgtAj |
| 3 | Chinese fans relish new sherlock gay love theory as fans relish new series | |
| 4 | Episode scores highest timeshifted audience in UK TV history | https://goo.gl/PkfHJs |
| 5 | January 6th is Sherlock’s birthday |
US election dataset
The United States presidential election of 2012 was held on November 6th in 2012. The respective dataset was collected by using a set of filter keywords and hashtags chosen by experts (Aiello et al., 2013). Despite retrieving tweets for specific keywords only, the data collected was still too large for a single user to organize and index in order to extract useful information.
Here, the granularity selection of three hours was made based on the fact that there is a discrete but not wild change in activity. By employing a coarser granularity instead of an hourly one serves to reduce the time zone effect. Moreover, since all four political debates in 2012 lasted for an hour and a half, then twice the span of a debate seemed like a reasonable selection for Twitter users to engage in a political discussion.
Studying the top 20 DyCCos provides a variety of stories which does not only contain mainstream news but other smaller pieces of information that journalists seek out. The first one for example, which is also the most heavily populated, regards a movement of motivating women into voicing their opinion by urging them to post photos of their “best voting looks” but also pleading for Tony Rocha (radio producer) to use his influence for one of the nominees. The first static community alone includes 2,774 people, some of which are @KaliHawk, @lenadunham, @AmmaAsante, @marieclaire and others.
Overall, during Election Day people are mostly trying to collect votes for their candidate of choice by either trying to inspire themselves or ask from a celebrity to do so; whereas after the fact, everyone is either posting victory or hate posts, or commenting on what the election will bring the following day, whether or not the election was falsified/rigged. At all times people are referencing a number of journalists, bloggers and politicians (Herman Cain, Pat Dollard) as well as various newspapers, TV channels and famous blogs. Other examples include comments on racism stopping due to the reelection, a book on President Obama, posts by a number of parishes and many more which unfortunately cannot be illustrated in this manuscript due to space restrictions. However, a short list of non-mainstream findings is presented on Table 6.
| Finding | URL (if available) | |
|---|---|---|
| 1 | Women’s voting motivational movement on Instagram | https://goo.gl/OKs17u |
| 2 | President Obama hoops with S. Pippen on Election Day | https://goo.gl/Ybg83Z |
| 3 | Iran and Russia among countries with messages for Obama | https://goo.gl/hgiaaN |
| 4 | Mainstream media tipped the scales in favor of Obama | foxNews(removed) |
| 5 | Anti-Obama protests escalate at university | WashPost(removed) |
One of the main anticipated characteristics of this particular set is that the news media, political analysts, politicians, even celebrities are heavily mentioned in the event of an election.
Greek election datasets
The two Greek elections of 2015 were held on January 25th and on September 20th and the collection of corresponding tweets was made using Greek and English keywords, hashtags and user accounts of all major running parties and their leaders.
Although participation in the second election was almost cut in half with regard to the first, there are a few similarities in the dynamic communities that are of interest. The top 20 DyCCos of both datasets surfaced groups of an extremely wide and diverse background. Groups from Turkey, Italy, Spain and England anticipated Syriza’s (center-left anti-austerity party) potential wins in both elections and joined in to comment on all matters such as the Grexit, the future of the Greek people, how the Euro hit an 11 year low following the victory of the anti-austerity party but also that the markets managed to shake off the initial tremors created by it. Conspiracy tweets were also posted within a community mentioning operation Gladio; a NATO stay-behind operation during the Cold War that sought to ensure Communism was never able to gain a foothold in Europe, which then evolved into sending warnings to the Syriza party as Greece was supposedly being framed as an emerging hub for terrorists. A short list of non-mainstream findings is presented on Table 7.
| Finding | URL (if available) | |
|---|---|---|
| 1 | Euro hits an 11-year low following the Syriza party victory | (removed) |
| 2 | Candidate slapped pollster over bad numbers announcement | (removed) |
| 3 | Tsipras regains slim lead hours ahead of Greek vote | https://goo.gl/fZA0UX |
| 4 | Vandalisms at Syriza and New Democracy polling centers | https://goo.gl/3YEfRP |
| 5 | Far-right party is the most voted by the unemployed | https://goo.gl/Ydzd8R |
Although there were a lot of interesting international pieces of commentary such as the above, the framework did not miss the local communities where a strong presence was achieved by the far-left supporters, the Independent Greeks supporters, and a slightly milder presence from the right wing and extreme-right wing supporters all of whom were rooting for their party and pointing out the mistakes of the opposing ones.
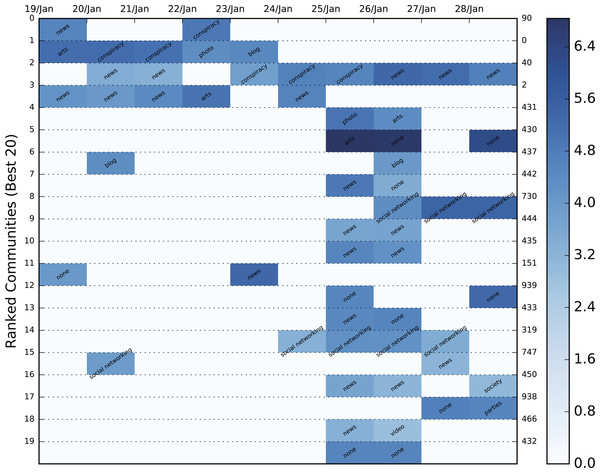
One of the similarities between the two election datasets which is rather impressive lies in the almost identical structure of the two evolutions as shown by the respective heatmaps in the Evaluation section. It is also worth mentioning that many influential users (e.g., @avgerinosx, @freedybruna) and politicians (e.g., @panoskammenos, @niknikolopoulos) who were extremely active in the first election, were also present in the second one.
Data processing
Prior to the framework application, the network data is preprocessed as follows. Initially, all interaction data is filtered by discarding any corrupt messages, tweets which do not contain any interaction information and all self-loops (self-mentions) since they most frequently correspond to accounts who are trying to manipulate their influence score on Twitter. The filtered data is then sampled resulting in a sequence of activity-based snapshots. Figure 2 displays the mentioning activity of the four twitter networks.
The process which puts the greatest computational burden on the framework involves the evolution detection. In order to speed up the searching operation, instead of using strings, the users’ names are hashed resulting in communities comprising sets of hashes. Moreover, we discard all the users’ hashes which appear strictly in a single timeslot since they are considered temporal outliers. However, they are not discarded from the metadata container as they may provide useful information. Two additional acceleration measures are: the discarding of communities with a population of less than three users, and, similarly to the scheme proposed by Arasu, Ganti & Kaushik (2006), a size comparison check prior to the Jaccard similarity calculation (i.e., if the size difference between the communities disallows a threshold overcome, there is no point in measuring their similarity).
Every community in every timeslot is used as a query in a maximum of D older timeslots, essentially searching for similar communities in a D + 1 timeslot window. Whenever a similar community is found the search is halted and two possible scenarios take place. Either a new dynamic community is initiated or the query is added to an already active dynamic community. Each of these dynamic communities contains information such as text, hashtags, URLs, user centralities and edges which are all stored in a Dynamic Community Container (DyCCo).
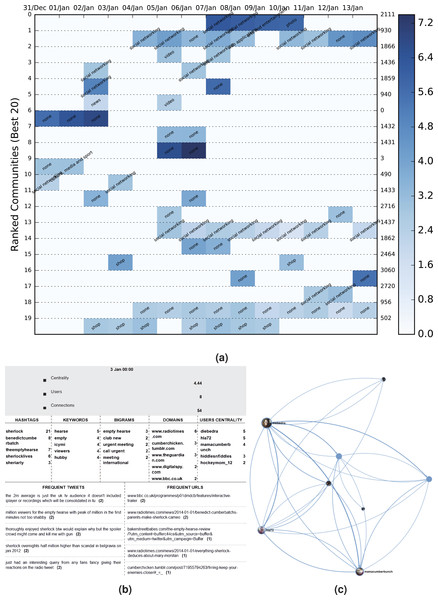
Following the formation of these DyCCos, a TF-IDF procedure is applied in order to extract valuable keywords and bigrams that will pose as a DyCCo guideline for the potential user that might interest him/er more. The corpus of the dataset (IDF) is created by using the unique set of words contained in each timeslot of every available dynamic community and the term frequency is computed by using the unique set of tweets within the community (i.e., only one of the repetitions is used in the case that the sentence was retweeted). For the purposes of better illustration and easier browsing, the products of the framework as seen in Fig. 6 consist of:
Figure 6: DyCCo structure and content illustration for the Sherlock Twitter dataset.
(A) A color heatmap displaying the evolution of the top 20 dynamic communities of BBC’s 2014 Sherlock TV series dataset. Each evolution series contains a characterization of the community based on the contained URLs. The background color varies between shades of blue and is an indication of the logged size of the specific community. The population increases as the shade darkens (the numbers on the right represent the label of each dynamic community). (B) Wordclouds of the most popular keywords, bigrams, hashtags, tweets and URLs acquired from community6, timeslot 3. (C) The corresponding graphical illustration of community6, timeslot 3 under study.-
a word cloud per dynamic community containing the most popular: (a) hashtags, (b) keywords, (c) bigrams, (d) domains and (e) text items;
-
the ten most influential users from each community which could provide the potential journalist/analyst with new users who are worth following
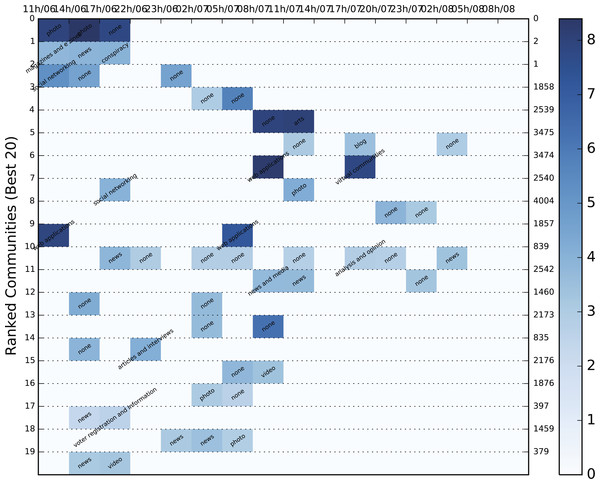
The color heatmap in the figure represents community size but can be adjusted to also give a comparative measure of centrality or density. By using this DyCCo containing framework, the user is provided with a more meaningful view of the most important communities as well as an insight to the evolving reaction of the public with respect to various events. The respective color heatmaps for the US election and the Greek election datasets are presented in Figs. 7–9.
Figure 7: Color heatmap displaying the evolution of the top 20 dynamic communities of the 2012 US election dataset.
Each evolution series contains a characterization of the community based on the contained URLs. The background color varies between shades of blue and is an indication of the logged size of the specific community. The population increases as the shade darkens.Figure 8: Color heatmap displaying the evolution of the top 20 dynamic communities of the January, 2015 Greek election dataset.
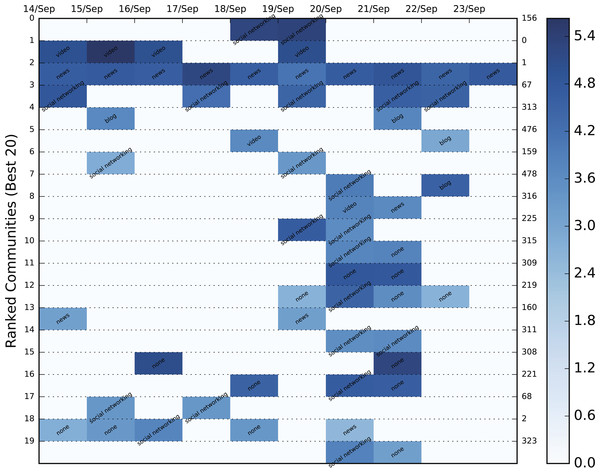
Each evolution series contains a characterization of the community based on the contained URLs. The background color varies between shades of blue and is an indication of the logged size of the specific community. The population increases as the shade darkens.Figure 9: Color heatmap displaying the evolution of the top 20 dynamic communities of the September, 2015 Greek election dataset.
Each evolution series contains a characterization of the community based on the contained URLs. The background color varies between shades of blue and is an indication of the logged size of the specific community. The population increases as the shade darkens.Evaluation
While executing preliminary experiments it was concluded that the framework can undoubtedly provide the user with some useful information whether the query regarded politics, television series, specific events or even specific people/celebrities. Unfortunately, there is no known method to which we can compare the performance of our framework.
Due to this predicament, we took the opportunity to introduce a content-based evaluation scheme through which we may compare the effectiveness of the proposed framework to the size-grounded ranking baseline method used in Lu & Brelsford (2014).
Since it is immensely difficult to evaluate community importance based on the tweets themselves, we employed Amazon’s Alexa service and the contained URLs of each static community to extract the category to which it belonged. Alexa requires a domain as input and returns a string of categories in a variety of languages to which it belongs. In order to avoid duplicates, categories in a language other than English were translated automatically using Google’s translating service. Unfortunately, most of the domains, even popular ones, either returned a vary vague category (e.g., internet) or none at all. Hence, manual domain categorization was also necessary in order to include the most popular of domains. Specifically, the URLs we categorized using the following labels: television, video, photo, news, social networking, blog, conspiracy, personal sites, politics, shop, arts and spam. The dynamic communities of the three Twitter datasets combined contained 78,499 URLs which were reduced to 8,761 unique domains. A mere 2,987 of these domains were categorized either by Alexa or manually, but the overall sample of categorized URLs was significant enough to be used in the categorization process. The result of the most popular category for each community is shown in the color heatmaps displayed in Figs. 6A and 7–9 for each dataset. Besides the labeling, the heatmap also provides information regarding the size of the community. The darker the colors get, the larger the community. By combining the two, the user is provided with a relatively good idea of where to begin his/er search.
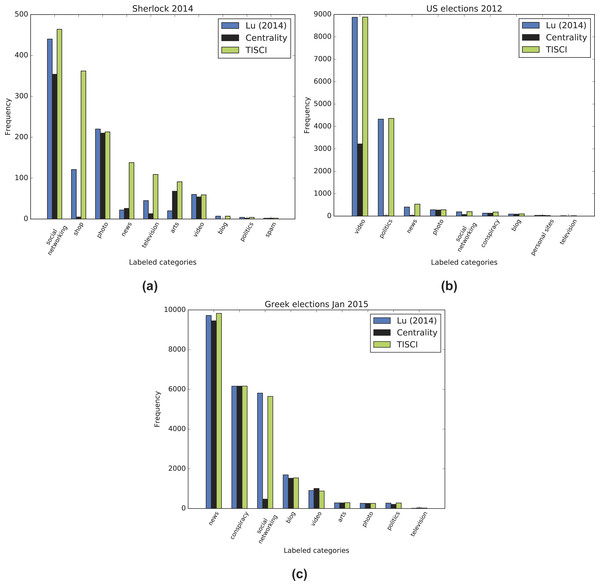
The premise on which the evaluation is based is that the content of the top 10–20 dynamic communities’ content should match the category of the query similarly to a search engine, since most users will not go past these many results. For example, if the queried event concerns an election, the content of the top communities should match that of news, politics, conspiracies, etc. On the other hand, if it concerns a television series, it should contain videos, television and other opinion references (social networks), art (photos), shops where the series is available, etc. The content comparison as represented by the sum of all categories (where available) in the dynamic communities between the proposed and the baseline ranking methods is shown in Fig. 10. The TISCI method seems to either surpass or tie the baseline method in the categories of interest. The single centrality ranking method is used here as an indication to the fact that the proposed method performs well as a whole even when independent features do not.
Figure 10: Content comparison between the proposed and the baseline ranking methods.
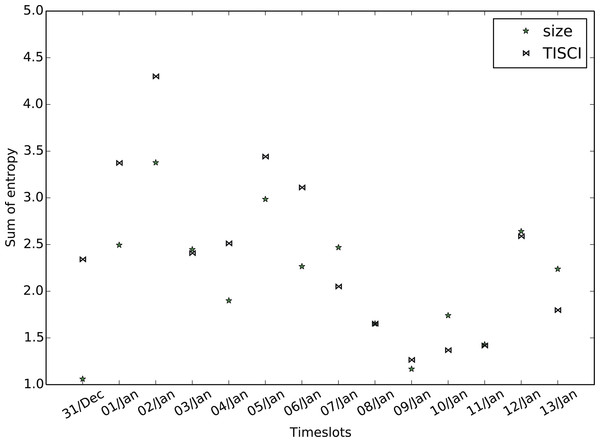
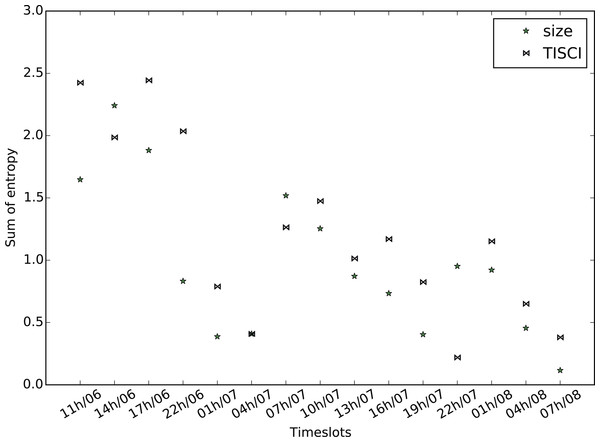
Results for the (A) 2014 Sherlock series, (B) 2012 US election and (C) January 2015 Greek election datasets.The secondary evaluation scheme explores the diversity fluctuation. Greater diversity implies more infomation and therefore more useful results. Employing the entropy feature described in the community ranking section but substituting bigrams for single words in order to increase the sense of diversity, we compute the mean bigram entropy for all timeslots in the top 20 communities and compare the result of the proposed method to that of the baseline. Figures 11–13 show the comparison between the two methods for all three datasets in which the proposed method seems to retrieve more diverse communities in most timeslots. Table 8 presents the total bigram entropy for all the timeslots for each dataset. With the exception of the Greek election dataset in which the difference is quite small, the proposed method performs definitely better compared to the baseline.
Figure 11: Mean bigram entropy.
Comparison between the proposed and the Lu & Brelsford (2014) (size) ranking methods for the Sherlock dataset.Figure 12: Mean bigram entropy.
Comparison between the proposed and the Lu & Brelsford (2014) (size) ranking methods for the US election dataset.Figure 13: Mean bigram entropy.
Comparison between the proposed and the Lu & Brelsford (2014) (size) ranking methods for the Greek election dataset (January 2016).| Sherlock | US election | Greek election | |
|---|---|---|---|
| TISCI | 33.63 | 18.23 | 26.98 |
| Lu and Brelsford | 29.87 | 14.62 | 26.23 |
Conclusions
The paper presented a framework for the extraction of useful information from OSN interactions. The basis of the framework is the study of the temporal structure and the monitoring of the evolution that the OSN communities undergo over time. The contribution of the proposed method lies in the ranking of the detected dynamic communities in respect to structural, evolutionary and importance features. By ranking the communities, the corresponding metadata containers (DyCCos) are also ranked, thus providing the user with popular URLs, tweets and wordclouds of keywords and bigrams. The experimental analysis was based on three evolutionary networks extracted from user interactions in Twitter. When applied on these networks, the framework uncovered a large number of dynamic communities with a variety of evolutionary characteristics. Unfortunately, it also uncovered a lack in a groundtruth evaluation scheme. In order to fill this need, we proposed a content-based evaluation process which hopefully will motivate more research into this direction. The conducted experiments highlighted the potential of the proposed framework for discovering persistent, interesting users, newsworthy pieces of information and real-world incidents around topics of interest as well as a means to follow a story over consecutive, or even non-consecutive, time-lapses. They also revealed the complexity of the analysis and evaluation processes due to the large scale of data to be analyzed and the absence of real ground truth data which the area of dynamic community detection and ranking clearly lacks. Future work will involve fitting the framework with a community detection method that allows overlapping, the implementation of a better means of presentation than wordclouds and heatmaps, the discovery of a non-heuristic way of selecting the sampling time and the employing of local sensitivity hashing to further speed up the evolution detection procedure.