A modular software framework for the design and implementation of ptychography algorithms

State of the art

Iterative algorithms such as ePIE (Maiden & Rodenburg, 2009) or DM (Thibault et al., 2008) are typically employed for the reconstructions. Recently, the rPIE algorithm (Maiden, Johnson & Li, 2017) has been proposed and studied: while being reasonably simple, it provides a fast convergence to a good object estimate (Maiden, Johnson & Li, 2017). Compared to ePIE, we noticed that the rPIE algorithm, at least in our implementation, also provides a large computational FOV, which is comparable to the one seen in more advanced, but also computational eager, optimisation algorithms (Guizar-Sicairos & Fienup, 2008; Thibault & Guizar-Sicairos, 2012; Guzzi et al., 2021b). Indeed, these latter methods are used to refine a previous reconstruction, as they are more prone to stagnation (Thibault & Guizar-Sicairos, 2012). Being new, the rPIE algorithm is currently lacking of: (i) a public implementation; (ii) a model decomposition approach; (iii) a tested position refinement routine. As a whole, a recipe is missing for this kind of algorithm.

Proposed framework - SciComPty

In this article, we describe how these three elements can be combined within the SciComPty GPU framework, a new software released as open-source (Guzzi et al., 2021a), entirely written in the PyTorch (Paszke et al., 2019) Python dialect. Our reconstruction recipe is tested against other solutions and then the results are reported. We designed a fast position refinement technique exploiting Adam (Kingma & Ba, 2015) as a feedback controller. To do so, a fast subpixel registration algorithm (Guizar-Sicairos, Thurman & Fienup, 2008) has also been implemented via a PyTorch GPU code. This latter element has many uses, for example in CT alignment (Guzzi et al., 2021c), or super-resolution imaging (Guarnieri et al., 2021; Guzzi et al., 2018). The details are described in the “method section”. The software and algorithms capabilities are illustrated (“Results section”) with reconstructions from simulated and real soft-X-ray data acquired at TwinMic (Elettra) (Gianoncelli et al., 2016; Gianoncelli et al., 2021). Within the “Discussion section”, we will elaborate more on the features of the reconstructed images. The datasets and the code can be accessed at Guzzi et al. (2021a) and Kourousias et al. (2022).

Background

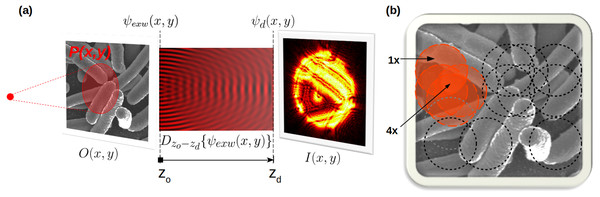
Ptychography aims at recovering the 2D specimen transmission function O(x, y) ∈ ℂ starting solely from a set of diffraction patterns (Williams et al., 2006; Pfeiffer, 2018). In a transmission setup (Fig. 1), a coherent and monochromatic wavefield P(x, y) ∈ ℂ is shined onto the specimen (z = z_O), placed between the source and the detector (z = z_d). In the thin sample approximation (Paganin, 2006), the exit-wave ψ_exw(x, y) transmitted by the object becomes: (1)${\displaystyle {\psi }_{exw}\left(x,y\right)=\psi \left(x,y,z_o\right)=P\left(x,y\right)\cdot \left|O\left(x,y\right)\right|\cdot e^{j\cdot {\varphi }_{O\left(x,y\right)}}.}$

During the path from the sample to the detector, free-space propagation occurs (Paganin, 2006), modelled by the D_z operator (Schmidt, 2010): (2)${\displaystyle {\psi }_d\left(x,y\right)=\psi \left(x,y,z_d\right)=D_{z_d-z_o}\left\{{\psi }_{exw}\left(x,y\right)\right\}=D_{z_d-z_o}\left\{P\left(x,y,z_o\right)\cdot O\left(x,y\right)\right\}.}$

Finally, a 2D photon detector is used to reveal the intensity (magnitude squared) of the incident radiation, producing a real, discrete, and quantised image I(x, y), which is the diffraction pattern. (3)${\displaystyle I\left(x,y\right)={\psi }_d\left(x,y\right)\cdot {\psi }_d^{\ast }\left(x,y\right).}$

Ptychography employs translation diversity to over-condition the problem; a large illumination (probe) is indeed scanned across the sample, by imposing a large overlap on each illuminated region (Fig. 1B); as a result, the object is highly oversampled. A ptychography dataset (real or simulated) is thus composed of multiple diffraction patterns, paired with their corresponding translation coordinates. Geometry and illumination metadata complete the description of a particular instance of the computational forward model.

During the reconstruction process, the model described by Eq. (3) must be inverted to gather back the object transmission function O(x, y). Since this inversion cannot, in general, be done analytically, an iterative procedure is employed. Modern versions of the ptychography reconstruction algorithms (Thibault et al., 2008; Maiden & Rodenburg, 2009) automatically perform the factorisation of the P(x, y) and O(x, y) functions. In a typical imaging-oriented ptychography experiment like ours, the recovery of P(x, y) is just a by-product, though mandatory for the O–P factorisation.

Virtual experiment

Reconstructions apart, SciComPty offers a simple method to perform virtual experiments. To simulate a ptychography dataset, one can implement the general transmission model of Eq. (3), and assign particular values to its setup parameters. In the case of a far-field setup (Schmidt, 2010), by fixing the detector pixel size δ_D, the corresponding pixel size at the sample plane δ_s can be readily calculated (equation 1 in the supplementary material). The recurring parameters in both simulations and reconstructions are W (detector size in pixels), S_d (detector lateral dimension) and z_do (sample-detector distance). In a simulation, δ_s normally defines the basis for the scanning movements, that in the simplest case follows a grid pattern. Random jitter is added to the (x, y) coordinates, to prevent the raster scanning pathology (Thibault et al., 2008; Dierolf et al., 2010; Edo et al., 2013). The overlap factor is defined instead by the maximum step movement. The object function O(x, y) and the illumination function P(x, y) are assembled in magnitude and phase providing two images each. Defining such virtual experiment parameters follows what is actually done during a real experiment (see Listing 1 in the Simulation section of supplementary material).

M-rPIE algorithm

In order to describe partial coherece beams (Chen et al., 2012) the wavefield is decomposed into a set of mutually incoherent probe modes (Thibault & Menzel, 2013; Odstrcil et al., 2016; Li et al., 2016). For each sample position (x_j, y_j), the jth diffraction pattern I_j(x, y) can be modeled by: (4)${\displaystyle I_j\left(x,y\right)=\sum _{p=1}^M|D_z\left\{P_p\left(x,y\right)\cdot O\left(x,y,x_j,y_j\right)\right\}{|}^2=\sum _{p=1}^M|D_z{P}_p\left(x,y\right)\cdot o_j\left(x,y\right){|}^2}$

where P_p with p ∈ {1, …, M} is a particular probe mode; o_j = o_j(x, y) = O(x, y, x_j, y_j) is the cropped region of the object, corresponding to the jth illuminated area in the scan sequence. To reconstruct an object with the model in Eq. (4), we solve for O(x, y) and a set of M mutually incoherent probe functions P_p = P_p(x, y). A public implementation of rPIE is currently missing and its multiprobe variant has not been reported yet. We implemented it in SciComPty, calling it M-rPIE. The procedure to design the method follows what has been done for one of the multimode-ePIE (M-ePIE) versions (Thibault & Menzel, 2013), producing the following new update steps (2D arrays depending on x, y are in bold): (5)${\displaystyle {\mathbf{P}}_{\mathbf{p}}^{\prime }={\mathbf{P}}_{\mathbf{p}}+{\alpha }_P\frac{\left({\psi }_{ex{w}_{p,j}}^{\prime }-{\mathbf{P}}_{\mathbf{p}}\cdot {\mathbf{o}}_{\mathbf{j}}\right)\cdot {\mathbf{o}}_{\mathbf{j}}^{\ast }}{\beta {\left|{\mathbf{o}}_{\mathbf{j}}\right|}_{\max }^2+\left(1-\beta \right){\left|{\mathbf{o}}_{\mathbf{j}}\right|}^2};}$ (6)${\displaystyle {\mathbf{o}}_{\mathbf{j}}^{\prime }={\mathbf{o}}_{\mathbf{j}}+{\alpha }_O\frac{\sum _{p=1}^M\left({\psi }_{ex{w}_{p,j}}^{\prime }-{\mathbf{P}}_{\mathbf{p}}\cdot {\mathbf{o}}_{\mathbf{j}}\right)\cdot {\mathbf{P}}_{\mathbf{p}}^{\ast }}{\gamma {\left(\sum _{p=1}^M|{\mathbf{P}}_{\mathbf{p}}{|}^2\right)}_{\max }+\left(1-\gamma \right)\sum _{p=1}^M|{\mathbf{P}}_{\mathbf{p}}{|}^2}.}$

As usual, ${\mathbf{o}}_{\mathbf{j}}^{\prime }=o_j^{\prime }\left(x,y\right)$ and ${\mathbf{P}}_{\mathbf{p}}^{\prime }=P_p^{\prime }\left(x,y\right)$ represent the updated quantities respectively for the current object box and the current probe, while (7)${\displaystyle {\psi }_{ex{w}_{p,j}}^{\prime }=D_{-z}\left\{\sqrt{{\mathbf{I}}_j}\frac{{\psi }_{ex{w}_{p,j}}}{\sqrt{\sum _{n=1}^N{\left|{\psi }_p\right|}^2}}\right\}}$

is the magnitude-corrected scattering wave produced by the pth illumination mode; α_p and α_o represent the update rates of the probe and object estimates and are typically set to [0.5, 1]. The role of each denominator is to weight the update where the exit wave is not bright (Rodenburg & Faulkner, 2004; Maiden, Johnson & Li, 2017), reducing thus the noise amplification. β and γ are regularisation parameters: when set to 1, M-rPIE simplifies to M-ePIE (Thibault & Menzel, 2013; Maiden, Johnson & Li, 2017). The net effect of the modifications, weighted by β and γ, is to slow down the update, by introducing a loss cost given by o_j(x, y) and P_p(x, y). Increasing the number of modes increases the iteration time by the same factor: that is why it is extremely important the fact that SciComPty is actually working on GPUs.

Adam-based position refinement

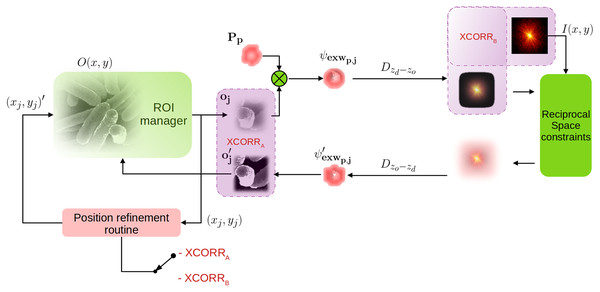
As the resolution increases, the effects of backlash and limited mechanical precision become more and more noticeable. The positions vector is indeed populated by the open-loop commands given to the stage. A correction method must then be introduced a posteriori, increasing the reconstruction time. In Guizar-Sicairos & Fienup (2008); Guzzi et al. (2021b) positions are corrected through an optimisation method, within the gradient-based reconstruction; in Mandula et al. (2016), instead, the authors propose to use a gradient-less method based on Powell (1964) to guide the position refinement procedure. In this work, we consider a fast and reliable way to correct translations. Similarly to Zhang et al. (2013); Tripathi, McNulty & Shpyrko (2014); Loetgering et al. (2015); Dwivedi et al. (2018), it employs a 2D cross correlation signal, calculated at some points in the reconstruction chain. The same principle is used also for CT alignment in Gürsoy et al. (2017); Guzzi et al. (2021c), as the synthesised projection o_j(x, y) are inevitably centred; when confronted with refined estimates ($o_j^{\prime }\left(x,y\right)$, XCORR_A), or measured data (I(x, y), XCORR_B), geometrical shifts can then be measured. Figure 2 shows how such position refinement scheme can be introduced in the canvas of a PIE reconstruction algorithm: 2D weighted phase correlation (Guizar-Sicairos, Thurman & Fienup, 2008) here is used to determine the shift between two different estimates o_j and ${\mathbf{o}}_{\mathbf{j}}^{\prime }$ (switch in position XCORR_A in Fig. 2, more details later) belonging to the same crop-box (x_j, y_j).

In this class of position refinement methods, the error signal (the 2D argmax of the 2D cross-correlation) is extremely small and provides a correction factor that is cumulated at each iteration. A gain factor η_j is indeed used to provide a correction. Here we propose to use a spatially variant and adaptive gain factor, that can change iteration after iteration and is probe-dependent. Our subpixel shift detection is based on the work (Guizar-Sicairos, Thurman & Fienup, 2008) and its implementation in SciPy (Jones et al., 2001). We adapted the same algorithm in PyTorch, allowing for fast GPU computation and avoiding costly move operation between the two memory systems, as the core of the reconstruction (M-rPIE) is already working on the GPU. To speed up the procedure for subpixel scales, the matrix multiplication version of the 2D DFT is employed. An upsampled version of the cross-correlation can then be computed within just a neighbourhood of the coarse peak estimate, without the need for zero-padding. Each probe position is updated at each iteration by the following expressions: (8)${\displaystyle x_j^{\prime }=x_j+{\eta }_{x,j}\cdot \underset{x}{argmax}\left\{XCOR{R}_{i\in \left[A,B\right]}\right\},}$ (9)${\displaystyle y_j^{\prime }=y_j+{\eta }_{y,j}\cdot \underset{y}{argmax}\left\{XCOR{R}_{i\in \left[A,B\right]}\right\},}$

where η_x,j and η_y,j are the gain factors (> > 1). The variable gain is calculated by using the Adam optimization algorithm (Kingma & Ba, 2015): Adam is an extension to stochastic gradient descent, and is nowadays widely used in deep learning (Zhang, 2018). While in Stochastic Gradient Descent (SGD) the same learning rate is kept constant for all the variables, Adam provides a per-parameter factor that is separately adapted as learning unfolds. This is achieved by considering the evolution of each parameter. In our method, the argmax of the 2D cross-correlation takes the place of the gradient in the Adam algorithm, because its value will maximise the position error gradient. The resulting algorithm is then reported in Alg. 1:

 
 
 ------------------------------------------------------------- 
   ----------------------------------------- 
   Data:  The cropped object oj  and its refined estimate o′j 
     Result:  Gain parameters ηx,j  and ηy,j  for the jth  crop-box 
            (the jth  position vector (x,y)j) 
   Initialization as in Alg.  1 of Adam; 
   while reconstruction iteration > 0  do 
        t = t+1; 
  gt = argmax{XCORRi∈[A,B]} ; 
  proceed as from row 3 of Alg.  1 of Adam; 
  [...] 
   end 
    ------------------------------------------------------------- 
   ----------------------------------------- 
 Algorithm 1: The modified Adam algorithm uses the argmax of the 2D phase 
  correlation as the gradient of the error, then the exponentially damped moving 
  averages are updated as in Adam.    

Synchrotron soft-X-ray experiments

Real data have been acquired at the TwinMic beamline of the Elettra Synchrotron facility. We used a 1,020 eV (Fig. 3 and Fig. S1) and 1,495 eV (Fig. 4) soft-X-ray beam obtained from a secondary source of 15 µm. The zone plate has a diameter of 600 µm with a smallest ring width of 50 nm. At those energies the focus length is respectively 36 and 24 mm. The sample was placed at 370 µm from the virtual point source, providing a probe size of roughly 9 µm. The sample-detector distance is set at roughly 75 cm. The Princeton camera is based on a peltier-cooled CCD sensor with a resolution of 1,300 × 1,340 pixels, with a pixel size of 20 µm.

Figure 3 shows a series of phase reconstructions of a group of chemically fixed Mesenchymal-Epithelial Transition (MET) cells, grown in silicon nitride windows and exposed to asbestos fibres (Cammisuli et al., 2018). The reconstruction in Fig. 3A has been produced by the DM algorithm, while the one in Fig. 3B is the output of the ML algorithm (Thibault & Guizar-Sicairos, 2012). In both, the position refinement method (Mandula et al., 2016) is enabled. In the same configuration, similar results can be obtained by the AP method (Marchesini, Tu & Wu, 2016), that can be seen as a parallelised version of the ePIE algorithm, implemented in PyNx. The reconstruction programs for these images are listed in the Supplemental Information. Even if stunning, images in Figs. 3A and 3B appear blurry and full of artefacts. As expected, the ML algorithm provides a better reconstruction than DM; a larger FOV can also be observed. In both, AP was essential to create a meaningful P(x, y), that allowed the object to appear as “reconstructed”. At the end of these reconstructions, it was also required to remove a phase modulation; many details about this post-processing can be found in the supplementary material.

Conversely, Figs. 3C and 3D show the reconstructions obtained with SciComPty, for the same set of parameters and pre-processed data; in either cases, the proposed Adam-based position refinement method is used. Even the simple M-ePIE (Fig. 3C) is able to provide a high quality reconstruction, if paired with the proposed position refinement method. Reconstruction quality can be even increased if the proposed M-rPIE method is engaged (Fig. 3D): the proposed recipe allows to resolve a large FOV, that becomes not only comparable to the one in Fig. 3B, but in some cases (e.g., in the top left corner) even larger: the bottom left fibre can be now observed in its entire length, as well as other cell organelles. No post-processing is required at the end of these reconstructions. The reconstruction for a different region of the MET sample can be found in Fig. S4.

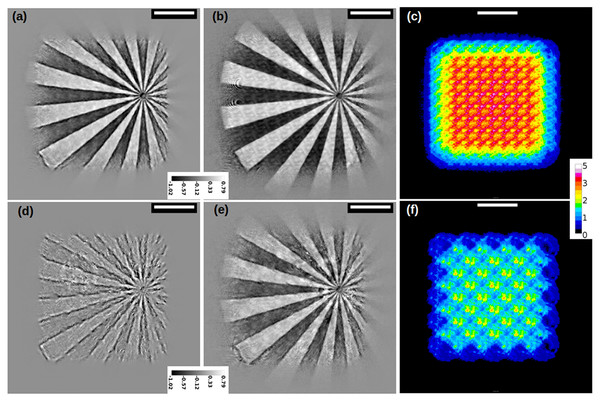
Figure 4 shows the effects of different position correction methods applied on another real dataset, acquired at 1495 eV. Diffraction patterns are acquired following a regular raster grid. Figure 4A shows the reconstruction with the position refinement algorithm in Zhang et al. (2013); in Fig. 4B the algorithm in Mandula et al. (2016) is applied; Fig. 4C is the reconstruction output with no position correction applied at all, while in Fig. 4D the proposed Adam-based position correction is applied. As can be seen, even if with simple features, this dataset is quite challenging to correct. While in Fig. 4A a form of correction can be seen, the reconstruction in Fig. 4B is even worse than the one with no correction at all (Fig. 4C). The proposed method (Fig. 4D) estimates the best correction, while being fast. Note that in Fig. 4D the raster grid pathology is quite absent (actual positions are not regularly spaced).

A large FOV is the most visible feature in any reconstruction employing M-rPIE (Figs. 3D, 5B, 5E and S4). To better analyse this effect, and to disentangle it from the position correction, a sparser dataset has been synthesised from the one of Fig. 4, producing Figs. 5A and 5D which are respectively the reconstructions with M-ePIE with the full and a sparse dataset (half of the probes); the canvas map (Kourousias et al., 2016) in Figs. 5C and 5F shows the two different densities. Figures 5B and 5E show instead the reconstruction with the M-rPIE algorithm: for the same amount of sparsity, the reconstruction is way more resolved in Fig. 5E than in Fig. 5D.

Implementation details

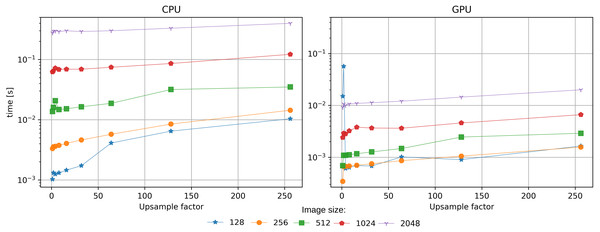
SciComPty software framework leverages GPU-based computing for the entire process. The test configuration is reported in the supplementary material. The performance gain obtained by carrying the reconstruction algorithm from the CPU to the GPU is about 10x (0.1 s vs 1.3 s). The reason for such a large gain is the high number of GPU cores which allow to parallelize array calculations. With no position correction, the performance in terms of speed are comparable to other CUDA based solvers implemented in PyNx, which is currently the fastest alternative. Regarding the position correction, at the best of our knowledge, no implementation of Guizar-Sicairos, Thurman & Fienup (2008) is readily available for GPU computing; consequently, we implemented it in PyTorch GPU. Having part of the algorithm on the GPU(reconstruction) and part on the CPU (registration) would have been detrimental, due to the overhead given by the data transfer. It is indeed extremely important that all the required arrays reside in the same domain, minimising copy operations. Figure 6 shows the computation time measured for the registration algorithm implemented on the two devices: the performance gain is of about an order of magnitude. The acceleration is significant, as during the reconstruction the same operation has to be performed for any position in the dataset.