rtpcr: a package for statistical analysis and graphical presentation of qPCR data in R

Background

Quantitative real-time polymerase chain reaction (qRT-PCR also known as qPCR), is a powerful analytical tool that is able to quantify nucleic acids using reference sequences. The technique’s sensitivity, specificity, and broad quantification range make it the gold standard for the detection and quantification of DNA and RNA sequences. Nowadays, relative quantification using qPCR is primarily used in the field of molecular genetics, genomics and functional transcriptomics to perform gene expression analysis in biological experiments (Harshitha & Arunraj, 2021).

qPCR utilizes the increased fluorescence from a reporter molecule as the template is exponentially amplified. SYBR Green is a commonly used chemical that binds to double-stranded DNA during the primer extension step of the polymerase reaction (Boulter et al., 2016). Specialized oligonucleotide probes like TaqMan hybridization probes are also used as fluorescent reporters for targeted RT-qPCR assays (Navarro et al., 2015).

Reliability of the qPCR results depends on the application of robust mathematical methodologies that ensure accurate data analysis and ouptputs. Various mathematical approaches have been developed for qPCR data analysis (Pabinger et al., 2014; Ritz & Spiess, 2008). The basic method for expression estimation of a gene between conditions relies on the calculation of fold changes (FC) using the PCR amplification efficiency (E) and the threshold cycle (syn. crossing point or C_T). Two basic mathematical methods are commonly used based on FC namely the Livak method and the Pfaffl method. The Livak approach (Livak & Schmittgen, 2001), also known as the 2^−ΔΔCT method, stands out for its simplicity and widespread use where the fold change (FC) expression of a target gene (2^−ΔΔCT) in Treatment condition (Tr) compared to Control condition (Co) is calculated according to the following Eq. (1): (1)${\displaystyle FC=\frac{2^{-{\left(C_{T_{\text{target}}}-C_{T_{\mathrm{ref}}}\right)}_{Tr}}}{2^{-{\left(C_{T_{\text{target}}}-C_{T_{\mathrm{ref}}}\right)}_{Co}}}}$ ${\displaystyle =2^{-\left[{\left(C_{T_{\text{target}}}-C_{T_{\mathrm{ref}}}\right)}_{\mathrm{Tr}}-{\left(C_{T_{\text{target}}}-C_{T_{\mathrm{ref}}}\right)}_{\mathrm{Co}}\right]}}$ ${\displaystyle =2^{-\left(\Delta C{T}_{Tr}-\Delta C{T}_{Co}\right)}.}$

Here, ΔC_T is the difference between two C_T values (e.g., CT_target −CT_ref) in treatment or control condition, and target and ref are target gene and reference genes, respectively. This method assumes that both the target and reference genes are amplified with efficiencies close to 100%, allowing for the relative quantification of gene expression levels (Livak & Schmittgen, 2001).

On the other hand, the Pfaffl method (Pfaffl, Horgan & Dempfle, 2002) offers a more flexible approach by accounting for differences in amplification efficiencies between the target and the reference genes. This method adjusts the calculated expression ratio by incorporating the specific amplification efficiencies, thus provides a more accurate representation of the relative gene expression levels (Pfaffl, Horgan & Dempfle, 2002). The Pfaffl formula can be written as Eq. (2): (2)${\displaystyle \mathrm{FC}=\frac{E^{-{\left(C_{T_{\mathrm{Tr}}}-C_{T_{\mathrm{Co}}}\right)}_{target}}}{E^{-{\left(C_{T_{\mathrm{Tr}}}-C_{T_{\mathrm{Co}}}\right)}_{ref}}}.}$

Many statistical tools and analysis codes have been developed for the statistical analysis of qPCR data in a stand alone format (Yuan et al., 2006), for the R platform (Ahmed & Kim, 2018; Li et al., 2022; Ritz & Spiess, 2008) or SAS software (Yuan et al., 2006). The rtpcr package is a comprehensive tool designed for the analysis of qRT-PCR data in R, providing a set of functions that allow researchers to perform various analyses on their qRT-PCR data using the cycle threshold (C_T) and efficiency values (E) under different experimental conditions.

Implementation

The rtpcr package was developed for the R environment (http://www.r-project.org) in the major operating systems and its source code, binary format, and under-development version are freely available at CRAN (https://cran.r-project.org/web/packages/rtpcr/index.html) and Github (https://github.com/mirzaghaderi/rtpcr). The package functions are mainly based on the calculation of efficiency-weighted ΔC_T (wΔC_T) values from target and reference gene C_T (Eq. (3)). wΔC_T values are weighted for the amplification efficiencies as below. Portions of this text were previously published as part of a preprint (Mirzaghaderi, 2024): (3)${\displaystyle w\Delta C_T=log2\left(E_{target}\right).C{T}_{target}-log2\left(E_{ref}\right).C{T}_{ref}.}$

From the arithmetic mean wΔC_T values over biological replicates, relative expression (RE, ΔC_T method) of a target gene can be calculated for each condition according to Eq. (4): (4)${\displaystyle \mathrm{RE}=2^{-\overline{w\Delta CT}}.}$

The rtpcr package considers efficiency values, thus the results match the Pfaffl method. If all input efficiency values are 2, 2^−ΔΔC_T-based results are returned. The average fold change (FC, ΔΔC_T method) expression statistics and graphs are returned for the target gene based on Eq. (5): (5)${\displaystyle \mathrm{FC}=2^{-\left({\overline{w\Delta CT}}_{\mathrm{Tr}}-{\overline{w\Delta CT}}_{\mathrm{Co}}\right)}.}$

Because both the relative expression and fold change expression follow a lognormal distribution (Derveaux, Vandesompele & Hellemans, 2010; McDavid et al., 2012), a normal distribution is expected for the wΔC_T or wΔΔC_T values making it possible to apply t-tests or analysis of variance to them. wΔC_T values can be statistically compared and standard deviations and confidence intervals are calculated, but the transformation y = 2^−x is applied in the final step to report the results. Here, a brief methodology is presented but details about the mathematical calculations and statistical analyses are available in Ganger, Dietz & Ewing (2017) and Ganger et al. (2020). In the rtpcr package, model creation and analysis of variance is done using the lmer (Bates et al., 2015) function of the lmerTest (Kuznetsova, Brockhoff & Christensen, 2017) package. lmerTest::lmer fits a linear mixed model and provides p-values for fixed effects in the analysis of variance (ANOVA) and summary output. For this, the biological replicate is served as a random effect. Means are compared using the emmeans function (Searle, Speed & Milliken, 1980) from the model. The standard error (standard deviation/sqrt(n)) for average FC or RE is calculated in different ways in literature. This statistic is calculated based on Taylor et al. (2019) by the rtpcr package according to Eq. (6) for average FC. For the standard error of the RE means, RE is used instead of FC.

(6)${\displaystyle Lower.se=2^{log2\left(FC\right)-s{e}_{w\Delta CT}}}$ ${\displaystyle Upper.se=2^{log2\left(FC\right)+s{e}_{w\Delta CT}}.}$

Results

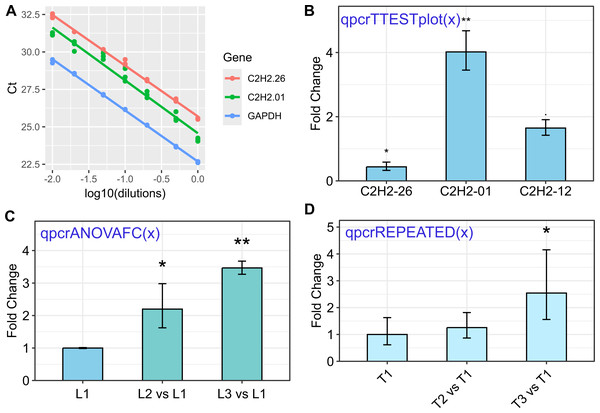
The rtpcr package was developed for amplification efficiency calculation, statistical analysis, and graphical representation of qPCR data in R. It accepts up to two reference genes and amplification efficiency values. Based on the experimental conditions, the functions of the rtpcr package use a t-test, analysis of variance, or covariance (for cases with more than two factors) to calculate the fold change (FC) or relative expression (RE). The functions provide standard errors and confidence intervals for FC or RE means and apply statistical mean comparisons. Different sample data sets were added to the rtpcr package and included in the examples to facilitate the usage of the package functions. The rtpcr package further provides editable ggplots with various editing arguments. Some functionalities of the rtpcr package are presented in Fig. 1 and a more detailed representation of the rtpcr application is shown in Fig. S1.

Input data frame structure

The input data set should be prepared as shown in example data sets of the rtpcr package. The column structure and arrangement of the data frames should follow the format indicated in Tables 1 and 2, as shown in the package help and the vignettes (https://cran.r-project.org/web/packages/rtpcr/vignettes/vignette.html). To see example data sets included in the rtpcr package, you can run the following command in R: data(package = ”rtpcr”). This will display a list of the available example data sets within the rtpcr package. You can then load a specific data set by running its name. Except for the t-test analysis which requires a specific data structure, factor columns should appear first in the data frame followed by blocking factor (if available), biological replicates, target gene efficiencies, C_T values of the target gene, the reference gene efficiencies, and the C_T values of the reference gene, respectively. The data frame can contain one to three factor columns, depending on the experimental design.

Table 1:

Column arrangement of the input data frame for use in the rtpcr package.

To see example data sets, in the rtpcr package rundata (package = ”rtpcr”). Example data sets can be presented by running the name of each data set. targetE and refE: amplification efficiency columns for target and reference genes, respectively. targetCt and refCt: Ct columns for target and reference genes, respectively.

Analysis type	Column arrangement of the input data set	Name of the example data sets
Amplification efficiency	Dilutions - targetCt - refCt	data_efficiency
t-test (accepts multiple genes)	condition (control level first) - gene (ref gene(s) last)- efficiency - Ct	data_ttest
ANOVA or ANCOVA (Up to three factors)	factor1 - rep - targetE - targetCt - refE - refCt	data_1factor
	factor1 - factor2 - rep - targetE - targetCt - refE - refCt	data_2factor
	factor1 - factor2 - factor3 - rep - targetE - targetCt - refE - refCt	data_3factor
ANOVA or ANCOVA with blocking	factor1 - block - rep - targetE - targetCt - refE - refCt
	factor1 - factor2 - block - rep - targetE - targetCt - refE - refCt	data_2factorBlock
	factor1 - factor2 - factor3 - block - rep - targetE - targetCt - refE - refCt
With two reference genes	. . . . . . rep - targetE - targetCt - ref1E - ref1Ct - ref2E - ref2Ct
Calculating biological replicated	. . . . . . biologicalRep - techcicalRep - Etarget - targetCt - Eref - refCt	data_withTechRep
	. . . . . . biolRep - techRep - Etarget - targetCt - ref1E - ref1Ct - ref2E - ref2Ct

DOI: 10.7717/peerj.20185/table-1

Notes:

For ANOVA and ANCOVA analysis, each line in the input data set belongs to a separate individual (reflecting a non-repeated measure experiment).

Table 2:

Repeated measure data structure and column arrangement required for the ‘qpcrREPEATED’ function.

targetE and refE: amplification efficiency columns for target and reference genes, respectively. targetCt and refCt: Ct columns for target and reference genes, respectively. In the “id” column, a unique number is assigned to each individual, e.g. all the three number 1 indicate a single individual.

Column arrangement of the input data set	Name of the example data sets
id - time - targetE - targetCt - ref1E - ref1Ct	data_repeated_measure_1
id - time - targetE - targetCt - ref1E - ref1Ct - ref2E - ref2Ct
id - treatment - time - targetE - targetCt - ref1E - ref1Ct	data_repeated_measure_2
id - treatment - time - targetE - targetCt - ref1E - ref1Ct - ref2E - ref2Ct

DOI: 10.7717/peerj.20185/table-2

Notes:

To see example data sets, in the rtpcr package run data (package = ”rtpcr”). Example data sets can be presented by running the name of each data set.

This recommended column structure ensures compatibility with the various analysis functions provided by the rtpcr package, such as the analysis of variance and analysis of covariance methods, which require the data to be organized in this specific way. For the t-test analysis, the data structure may differ slightly, as it needs to be in a format that allows for the comparison of two experimental conditions. The package documentation and examples will provide guidance on the appropriate data structure for this specific analysis.

Discussion

rtpcr is an open-source R package that covers a lot of aspects of qPCR data analysis including efficiency and fold change analysis, statistical comparisons and graph production from single and multi-factorial experiments with or without a blocking factor. It accepts one or two reference genes, performs post-hoc testing, and provides standard error and confidence limits.

Different R packages have been developed for the analysis of qPCR data with different capabilities (Ahmed & Kim, 2018; Pabinger et al., 2014; Yuan et al., 2006). For example, chipPCR (Rödiger, Burdukiewicz & Schierack, 2015) can handle high throughput qPCR data and qpcR performs sigmoidal model selection for the analysis of the real-time PCR data (Ritz & Spiess, 2008). Some packages such as chipPCR, qpcR and FPK-PCR (Lievens et al., 2012) calculate the C_T values from raw florescence data and some such as ddCT (Zhang, Ruschhaupt & Biczok, 2013), dpcR, EasyqpcR, HTqPCR (Dvinge & Bertone, 2009), NormqPCR (Perkins et al., 2012), qpcrNorm, pcr (Ahmed & Kim, 2018) and qPCRtools (Li et al., 2022) require C_T values for the analysis. These packages also differ in type of quantification and analysis, amplification efficiency handling, post-hoc comparison, error calculation, and graph presentation (Table 6). The main advantages of the rtpcr package over the other R packages are performing expression analysis based on both ΔC_T and ΔΔC_T methods for different experimental conditions and accounting for given amplification efficiencies matching the Pfaffl method. Using the rtpcr package, it is also possible to account for efficiency value for each primer or each reaction which has been recommended to get a more precise quantification result (Ruijter et al., 2021; Ruiz-Villalba, Ruijter & van den Hoff, 2021). The provided sample data frames for all the analysis types and a documentation enables all R users with minimum knowledge of data handling to simply use the rtpcr package. In conclusion, the rtpcr was built based on a general method with both calculational and graphical output capabilities for analyzing qPCR C_T values from the experiments with up to three different factors.

Supplemental Information