Dauer fate in a Caenorhabditis elegans Boolean network model

Constructing the dauer network

We first extracted 85 dauer-involved genes described in the WormBook ‘Dauer’ chapter (Hu, 2005-2018). For each of these genes, we then searched on WormBase (Harris et al., 2019) for genes known to interact with these dauer genes and genes known to act in the same pathways as these dauer genes. We focused on regulatory interactions and included those for which we identified information regarding the direction of the interaction, for example reported relationships between effector proteins and targets. We did not include genetic interactions or genetic masking/enhancing/suppressing effects between genes. Some of our gene pairs may have reported genetic interactions along with regulatory interactions but we focused on regulatory interactions for constructing our model.

We next surveyed the literature for regulatory interactions within this gene and pathway set and created a filtered set of dauer genes and main-effect regulatory interactions (Table S1). For example, of the 40 insulin signaling genes in the C. elegans genome few genes have been reported to act independently in the Insulin/IGF-1 pathway (Girard et al., 2007). We condensed the larger dauer-involved set down to 26 genes, each part of the four dauer-inducing pathways represented as nodes in our Boolean model, and connected by 34 edges. We included the nodes ‘pheromone’ (Golden & Riddle, 1984b) and ‘cmk-1’ (a food receptor Neal et al., 2015) as inputs to the system. These interactions were mainly obtained from the WormBase database (Harris et al., 2019) and verified with the scientific publications cited on WormBase (a full list of nodes, interactions, and citations is given in Table S1).

We used this regulatory interaction information for each gene to formulate Boolean functions (Table S2). We combined literature-reported regulations into a preliminary model and used results obtained from simulations and perturbations to fine-tune the Boolean functions for each node until we were able to mimic the expected behavior of the system. For example, multiple articles reported that daf-16 was activated either when akt was repressed (Henderson & Johnson, 2001; Lin et al., 2001; Lee, Hench & Ruvkun, 2001; Paradis & Ruvkun, 1998) or when daf-12 was activated (Matyash et al., 2004; Dowell et al., 2003). Simulated conditions for normal adult development should therefore result in daf-16 repression and no dauer activation. To achieve this known output for daf-16 we assigned an ‘OR’ operator for these two regulators. In some cases, we were able to extract the relationship between regulatory nodes from the literature. This approach has been similarly demonstrated in previous works to gain qualitative insights using discrete networks (Hopfensitz et al., 2013; Bornholdt, 2008).

Studying system trajectories

The initial conditions used to generate the trajectories of the system’s dynamics were based on well-known environmental cues such as food availability (cmk-1) and dauer pheromone (pher) detected by C. elegans (Jeong et al., 2005; Neal et al., 2015). Favorable conditions allowed the organism to develop into an adult (“no dauer”) and unfavorable conditions into “dauer” (Golden & Riddle, 1984b). We set the initial conditions as cmk-1 = 1 and pher = 0 for normal development (here, dauer = 0) and cmk-1 = 0 and pher = 1 for dauer fate (here, dauer = 1). We monitored the dynamics and convergence of the system based on the state of the ‘dauer’ output node (trajectories for each simulation are shown in Fig. S2). Temperature is another well-known regulator that induces dauer formation. We chose to focus here on dauer as a response to resource availability and our model does not include temperature as an input.

We performed simulations with asynchronous updating using boolean2 software (Albert et al., 2008). In order to explore system dynamics, the Boolean functions for each gene needs to be updated at each timestep to trace out the trajectory of the system. These transitions for the Boolean functions were carried out using an asynchronous scheme that randomly assigned the states of the nodes. Biological events do not occur at the same time and the timescale at which the events occur can be diverse. Here, we represented this with an asynchronous update scenario. In this framework a collector class averaged the states of nodes over multiple runs for simulating a system with a non-deterministic updating scheme. We performed 100 simulations for each set of initial conditions and for every iteration, the collector averaged the state of each node generated for 1,000 steps. In all our simulations, the nodes reached equilibrium after approximately 15 iterations (trajectories are shown in Fig. S2). Nodes with states > 0.5 were considered ‘ON’ (as indicated by Albert et al., 2008) and nodes with states < 0.5 were considered ‘OFF’.

Validating the model

To validate the model, we checked whether the model has the ability to reproduce known experimental outcomes. Mutant phenotypes in C. elegans that lead to either adult or dauer formation are well studied (Hu, 2005-2018). We used published experimental evidence to check whether our model could reproduce similar results. For example, dauer-constitutive (Daf-c) mutants lead to dauer formation in conditions that do not favor dauer while dauer-defective (Daf-d) mutants will not develop into dauer larvae (Vowels & Thomas, 1992; Vowels & Thomas, 1994; Gottlieb & Ruvkun, 1994; Albert & Riddle, 1988). We knocked down known Daf-c and Daf-d genes to validate that our dauer Boolean model captured essential wild type and mutant phenotypes (Fig. S1B).

Our model simulations helped us identify the attractor space and stable motifs. A Boolean model will eventually settle down into a static state where all the nodes are either ‘on’ or ‘off’ and remain in that state through further iterations. This state of the model is called an attractor and in biological modeling attractors depict specific biological phenotypes. Within this, a set of nodes within the network forms cycles which stay in specific states, and these are called stable motifs. We can represent a network as a reduced system using the nodes that are critical for controlling the stable motifs. We can then study the model dynamics using the reduced form and can make predictions using simpler representations of the model.

Attractors of Boolean networks represent biological phenotypes, here the ‘dauer’ and ‘no dauer’ fates. We explored the set of attractors and stable motifs for our model by iterating through all possible combinations of initial conditions and perturbations using pystablemotifs software (Rozum et al., 2021b; Rozum et al., 2021a). A perturbation of a node in our experiments refers to reversing the existing state of a node and specify that along with the initial conditions set. The network diagrams were created using Cytoscape (Shannon et al., 2003). Code, simulations and scripts are available at https://github.com/alekhyaa2/Dauer-Boolean-Model.

Constructing a dauer Boolean network

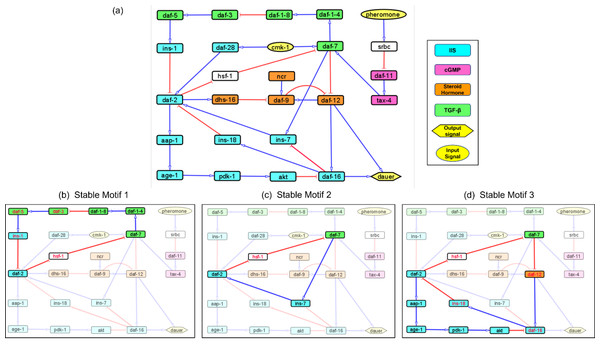
Our exhaustive literature survey identified essential regulatory interactions among dauer pathway genes. From these we constructed a Boolean network with 26 nodes and 34 interactions (Fig. 1A; Table S1). The nodes ‘pheromone’ (Golden & Riddle, 1984b) and ‘cmk-1’ (a food receptor (Neal et al., 2015)) were input signals that allowed the model to converge onto the dauer/no dauer output node.

Validating the model by replicating Daf-c and Daf-d phenotypes

In C. elegans mutant strains can be categorized as dauer-constitutive (Daf-c), genotypes which produce dauer arrest even in the absence of pheromone and presence of food, and Dauer-defective (Daf-d), genotypes which do not enter dauer arrest under typical dauer-favorable conditions (i.e., pheromone present and/or food limited) (Vowels & Thomas, 1992; Vowels & Thomas, 1994; Gottlieb & Ruvkun, 1994; Albert & Riddle, 1988). We validated our model by knocking down known Daf-c genes (daf-2, daf-7, daf-11, and daf-9) separately under initial conditions (cmk-1 = 1 and pher = 0) that do not typically favor dauer and found that these mutants followed the Daf-c phenotype and entered dauer arrest. We also knocked down known Daf-d mutant genes (daf-12 and daf-16) under conditions that typically favor dauer (here, cmk-1 = 0 and pher = 1) and found these replicated the Daf-d phenotype, failing to enter dauer arrest.

Identifying stable motifs

A network attractor is a set of gene states the system can stabilize in  Rozum et al. (2021b). The dauer Boolean network had 10 different attractor states (Fig. S1) with one resulting in developmental progression to adult, eight resulting in the dauer fate and one resulting in either dauer or no dauer depending on system conditions (Rozum et al., 2021a). Although an attractor represents a potential stable point, not all attractors are accessible from all states. To further analyze system stability, we divided the total network into small subgraphs (Zanudo & Albert, 2015; Zanudo & Albert, 2013). We identified three Stable Motifs (SMs) in the developmental progression to adult (Figs. 1B–1D). Each of these encompassed genes from at least two different pathways. Stable Motif 1 (SM1; Fig. 1B) spanned 10 genes across the IGF-1/insulin signaling, TGF-β and Steroid hormone pathways  (Hu, 2005-2018). SM2 and SM3 involved 4 and 8 genes, respectively, across the IGF-1/insulin signaling and TGF-β pathways. daf-2, daf-7 and hsf-1 (heat shock protein) were common between all three stable motifs with hsf-1 acting as a crucial node where different pathways intersect. This result has been shown by previous experimental work (Barna et al., 2012). Each of the SMs involved a different insulin signaling gene, ins-1, ins-7 or ins-18. We did not identify any SMs for dauer formation (the A3 attractor; Fig. S1).

Identifying driver nodes in the SMs

We simulated gene perturbations to identify the driver nodes for each of our identified SMs (Rozum et al., 2021a). Changing the existing state of the critical nodes shared between the stable motifs (i.e., daf-2 or daf-7 downregulation or hsf-1 upregulation) prevented the system from entering into any of the SMs and pushed it to one of the dauer attractors. Perturbation analysis identified the critical causal interactions in the network as SM2, encompassing daf-2, daf-7, ins-7 and hsf-1. Perturbation of daf-2, daf-7 or hsf-1 genes prohibited the system from stabilizing in the SM and the attractors corresponded to each of these nodes. We concluded that daf-2, daf-7 and hsf-1 were the driver nodes for the SMs. When we perturbed the other nodes of these three stable motifs, the system converged onto either dauer or no dauer via different stable motifs. (Table S3). But in case of daf-2, daf-7 and hsf-1 perturbations, the system did not enter into any of the stable motifs, instead settling into the attractors of those corresponding nodes.

Perturbations of daf-2, daf-7 and hsf-1 resembled the Daf-c mutant system. When the model was started with dauer-favorable conditions, the system did not have any stable motifs. The same lack of stable motifs occurred with Daf-c mutant phenotypes. Under both dauer-favorable and Daf-c mutant conditions (here, related gene perturbation and/or favorable initial conditions), the system did not have any cyclic subgraphs facilitating control. Instead, the driver nodes decided the fate of the organism in expressing a wildtype or a Daf-c mutant phenotype.

Analyzing causal interactions in the dauer Boolean network

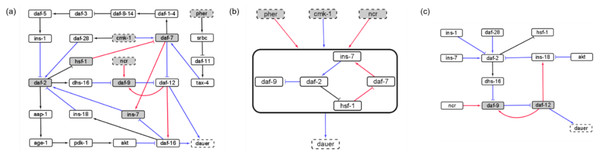
We identified a reduced network representing causal information flow  (Maheshwari & Albert, 2017) from environmental input to dauer fate (Fig. 2A). The reduced network contained a cyclic subgraph (Fig. 2B) similar to SM2, containing daf-2, daf-7, ins-7 and hsf-1. However, it included a necessary inhibitory regulation of daf-9 by daf-2. The dynamics of the entire system can be summarized as input to this subgraph. The full reduced network (Fig. 2C) included 12 nodes and 13 edges.

Insulin signaling drives the binary dauer/no dauer fate

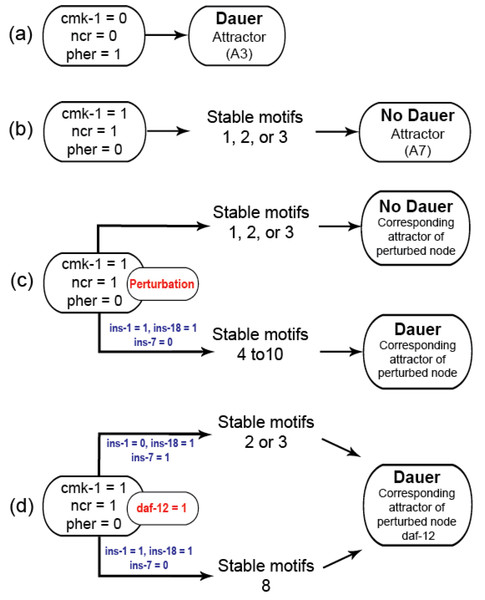
Gene perturbations revealed an additional seven SMs (SM4-10; Table S3). For each of the perturbations performed, the system could end up in one of 10 different attractors but few of these could be reached from stable conditions with active stable motifs. Activating ‘dauer’ conditions including low food and pheromone presence resulted in dauer fate and the A3 attractor (Fig. 3A) and available food with pheromone absence resulted in the system reaching the A7 attractor through SMs 1, 2 or 3 (Fig. 3B).

We identified insulin-dependent dauer arrest attractors across the perturbations. Activation of ins-1 and ins-18 resulted in the dauer fate through SMs 4-10 but inactivation of either pushed the system to normal development (Fig. 3C). Together with ins-7 the activation/inactivation profile of these genes pushed the system to normal development through SMs 1, 2 or 3 (Figs. 1B–1D). Similarly, daf-12 activation resulted in dauer arrest with the insulin profile determining the SM the system entered. When the antagonistic insulins (ins-1 and ins-18) were activated the system stabilized into SM 8 and when ins-1 was turned off the system stabilized in either SM 2 or 3 (Fig. 3D).

We found that the system must travel through SMs 1, 2 or 3 to end up in normal developmental progression and avoid the dauer fate. To enter dauer arrest the system must travel through one of SMs 4-10 with ins-1 and ins-18 activated and ins-7 inactivated. In this model insulin signaling controls the transitions between normal development and dauer in the presence of gene perturbations. The insulin genes act as decision makers for the convergence of these dauer pathways.

Identifying binary states across dauer pathways

For normal development we identified one strongly correlated module, one strongly anticorrelated module and a third set of genes with quantitative relationships across the SMs (Fig. 4). For dauer arrest we identified two strongly correlated modules and two strongly anticorrelated modules. These modules span the four signaling pathways involved in dauer arrest and indicate co-regulation and correlative relationships between distant genes in the network.