Fast computational mutation-response scanning of proteins

Mutations as forces

Point mutations can be modelled by forcing the contacts of the mutated site (Echave, 2008). Let j be the site to mutate, C(j) be the set of contacts of j, and jl the contact between j and l. Then, a mutation is modelled by applying a force

(6) $$\mathbf{f}(j)=\sum _{jl\in C(j)}\mathbf{f}(jl)$$where f(jl) is the force applied to contact jl. Let f(jl) be a scalar and e_jl a unit vector directed from j to l. Then, f(jl) consists of a force f(jl)e_jl applied to l, plus a reaction force −f(jl)e_jl applied to j, and no force applied to other sites.

A random mutation at site j is modelled by picking independent random numbers f(jl) and building f(jl) and f(j) (Eq. (6)). Following previous work (Echave, 2008; Echave & Fernández, 2010; Marcos & Echave, 2020), I use

(7) $$f(jl)\sim N(0,{\sigma }^2)$$Thus, the contact forces are picked from independent identical normal distributions.

Sensitivity matrix, S

What is the effect on a site i of mutating a site j? Consider a random mutation at site j, represented by a force f(j). Then, from (5), the structural deformation due to this mutation is given by

(8) $$\mathrm{\Delta }{\mathbf{r}}^0(j)={\displaystyle \frac{\mathbf{C}}{k_{B}T}\mathbf{f}(j)}$$

Δr⁰(j) can be written:

(9) $$\mathrm{\Delta }{\mathbf{r}}^0(j)=\left(\begin{array}{c}\mathrm{\Delta }{\mathbf{r}}_1^0(j)\\ ⋮\\ \mathrm{\Delta }{\mathbf{r}}_N^0(j)\end{array}\right)$$where Δr⁰_i(j) is the 3 × 1 column vector that contains the change in Cartesian coordinates of site i caused by mutation f(j) applied to site j. Therefore, the magnitude of the effect of the mutation on the structure of site i may be quantified by the Euclidean norm ||Δr⁰_i(j)²||.

The sensitivity matrix S is the matrix with elements

(10) $$S_{ij}=⟨{||\mathrm{\Delta }{\mathbf{r}}_i^0(j)||}^2⟩$$where i is the response site, j the mutated site, and〈⋯〉stands for averaging over mutations. S_ij represents the structural response of site i averaged over mutations at site j. Mutation-response scanning is the calculation of the sensitivity matrix S defined by 10.

Simulation-based mutation-response scanning

The sensitivity matrix S can be obtained using the simulation-based Mutation-Response Scanning method, sMRS. Given a protein’s pdb file, this numerical method proceeds as follows.

1. Set parameters. Set parameters k and R₀ of the ANM model, parameter σ used to generate forces (Eq. (7)), and a desired number of mutations to apply to each site, M.

2. Calculate the covariance matrix. Read protein coordinates from the pdb file, for all pairs of sites calculate C_α − C_α distances, compare them with R₀ to define contacts, then calculate the elastic network’s matrix K using (2) and (3). Finally, invert this matrix to calculate C using (4).

3. Generate mutational forces. For each site j, generate μ = 1 ⋯ M mutational force vectors f(j, μ) using (6) and (7).

4. Calculate mutational deformations. For each mutational force f(j,μ), calculate the resulting response Δr⁰_i(j, μ).

5. Calculate the sensitivity matrix. Average the deformations Δr⁰_i(j, μ) over mutations μ to obtain element S_ij of the sensitivity matrix S, according to (10).

Analytical formula for the sensitivity matrix

In this section, I derive an analytical formula that allows the direct calculation of the sensitivity matrix, S, without performing simulations.

The first step is to consider the deformation caused by forcing a single contact. Let f(jl) be a force applied along contact jl, composed by a force f(jl)e_jl applied to l and a reaction force −f(jl)e_jl applied to j. Replacing f(jl) into (5) and using (9), leads to

(11) $$\mathrm{\Delta }{\mathbf{r}}_i^0(jl)=\left({\mathbf{C}}_{il}-{\mathbf{C}}_{ij}\right){\mathbf{e}}_{jl}f(jl)$$where Δr⁰_i(jl) is the structural shift of site i caused by f(jl) and C_xy is the 3 × 3 block of C corresponding to the covariance between sites x and y.

Second, the deformation resulting from mutating a site is the sum of the deformations caused by forcing its contacts. From (6), (8), and (9), it follows that

(12) $$\mathrm{\Delta }{\mathbf{r}}_i^0(j)=\sum _{jl\in C(j)}\mathrm{\Delta }{\mathbf{r}}_i^0(jl)$$where Δr⁰_i(j) is the shift of i due to mutating j and the sum runs over all contacts of j. Replacing (11) into (12), leads to

(13) $$\mathrm{\Delta }{\mathbf{r}}_i^0(j)=\sum _{jl\in C(j)}\left({\mathbf{C}}_{il}-{\mathbf{C}}_{ij}\right){\mathbf{e}}_{jl}f(jl)$$

Finally, an analytical formula for the direct calculation of the sensitivity matrix may be derived. Replacing (13) into (10), leads to

(14) $$\begin{array}{cc}{S}_{ij}\equiv \hfill & ⟨\parallel \mathrm{\Delta }{\mathbf{r}}_i^0(j){\parallel }^2⟩\hfill \\ =\hfill & \sum _{jl\in C(j)}\sum _{jk\in C(j)}\mathrm{\Delta }{\mathbf{r}}_i{(jk)}^T\mathrm{\Delta }{\mathbf{r}}_i(jl)\hfill \\ =\hfill & \sum _{jk\in C(j)}\sum _{jl\in C(j)}⟨f(jk)f(jl)⟩{\mathbf{e}}_{jk}^T{({\mathbf{C}}_{ik}-{\mathbf{C}}_{ij})}^T({\mathbf{C}}_{il}-{\mathbf{C}}_{ij}){\mathbf{e}}_{jl}\hfill \end{array}$$where〈⋯〉stands for averaging over mutations at j. Since f(jl) ∼ N(0, σ²) are independent identically distributed random variables (“Mutations as forces”), it follows that

(15) $$⟨f(jk)f(jl)⟩={\sigma }^2{\delta }_{jk,jl}$$where δ_xy is the Kronecker delta, which is 1 for x = y and 0 otherwise. Therefore, replacing (15) into (14), leads to

(16) $$S_{ij}={\sigma }^2\sum _{jl\in C(j)}{\mathbf{e}}_{jl}^T({\mathbf{C}}_{il}-{\mathbf{C}}_{ij}{)}^T({\mathbf{C}}_{il}-{\mathbf{C}}_{ij}){\mathbf{e}}_{jl}$$This equation allows the calculation of the sensitivity matrix.

Analytical mutation-response scanning

The analytical Mutation-Response Scanning method, aMRS calculates the sensitivity matrix S using the analytical formula (16). Given a protein’s pdb file, this method proceeds as follows.

1. Set parameters. Set the parameters k and R₀ of the ANM model, and the parameter σ that defines the distribution of forces (Eq. (7)).

2. Calculate the covariance matrix. Read protein coordinates from the pdb file, for all pairs of sites calculate C_α − C_α distances, compare them with R₀ to define contacts, then calculate the elastic network’s matrix K using (2) and (3). Finally, invert this matrix to calculate C using (4).

3. Calculate the sensitivity matrix. Calculate the elements S_ij of the sensitivity matrix S using (16).

Compensation matrix

In this subsection, I define the compensation matrix that DMRS aims to calculate. Let Δr⁰(iμ) be the structural response to a mutation μ at site i, and Δr⁰(jν) be the structural response to a mutation ν at j. The deformation due to introducing both mutations is given by

(17) $$\mathrm{\Delta }{\mathbf{r}}^0(i\mu ,j\nu )=\mathrm{\Delta }{\mathbf{r}}^0(i\mu )+\mathrm{\Delta }{\mathbf{r}}^0(j\nu )$$and the magnitude of this deformation is given by

(18) $$\parallel \mathrm{\Delta }{\mathbf{r}}^0(i\mu ,j\nu ){\parallel }^2=\parallel \mathrm{\Delta }{\mathbf{r}}^0(i\mu ){\parallel }^2+\parallel \mathrm{\Delta }{\mathbf{r}}^0(j\nu ){\parallel }^2+2\mathrm{\Delta }{\mathbf{r}}^0(i\mu {)}^T\mathrm{\Delta }{\mathbf{r}}^0(j\nu )$$

The first two terms are positive, but the third term may be positive or negative. When the third term is negative, the mutations will compensate each other. Given a first mutation iμ, the maximum compensation due to a second mutation at j is obtained when Δr⁰(iμ)^TΔr⁰(jν) is minimum. Therefore, the degree of compensation may be quantified by $\underset{\nu }{min}\mathrm{\Delta }{\mathbf{r}}^0(i\mu {)}^T\mathrm{\Delta }{\mathbf{r}}^0(j\nu )$. For mutations modelled as forces, this is equal to minus the maximum, because if a force maximizes the dot-product, the opposite force, which is as likely, minimizes it. Therefore, to keeps things positive, it is convenient to define the compensating power of j by $\underset{\nu }{max}[\mathrm{\Delta }{\mathbf{r}}^0(i\mu {)}^T\mathrm{\Delta }{\mathbf{r}}^0(j\nu ){]}^2$. With the help of this equation, I define a compensation matrix, D, with elements D_ij given by

(19) $$D_{ij}=⟨{\mathrm{m}\mathrm{a}\mathrm{x}}_{\nu }{[\mathrm{\Delta }{\mathbf{r}}^0(i\mu {)}^T\mathrm{\Delta }{\mathbf{r}}^0(j\nu )]}^2⟩{\mu }^{\frac{1}{2}}$$where〈⋯〉_μ is the average over μ. D_ij is a positive number that quantifies the degree to which mutating j can compensate the structural effect of mutating i.

Forces for double mutation-response scanning

The choice of forces used to model mutations in “Mutations as forces” is not appropriate for calculating the compensation matrix because the maximum involved is ill defined. The value of Δr⁰(iμ)^TΔr⁰(jν) is proportional to the lengths of force vectors f(iμ) and f(jμ). Defined as described in “Mutations as forces”, the lengths of these vectors may become arbitrarily large, making the maximum in (19) infinite. To fix this, I apply the additional constraint

(20) $$\parallel \mathbf{f}(x){\parallel }^2={\sigma }^{2}CN(x)$$where σ² is the parameter used to define contact forces (see Eq. (7)) and CN(x) is the number of contacts of site x. In practice, this is achieved by picking the forces as before, then renormalizing them. The norm of these forces is finite and the maximum of (19) is well defined.

Simulation-based double mutation-response scanning

The compensation matrix may be obtained using the method simulation-based Double Mutation-Response Scanning, sDMRS, which proceeds as follows.

1. Set parameters. Set parameters k and R₀ of the ANM model, parameter σ used to generate forces (Eq. (7)), and a desired number of mutations to apply to each site, M.

2. Calculate the covariance matrix. Read protein coordinates from the pdb file, for all pairs of sites calculate C_α − C_α distances, compare them with R₀ to define contacts, then calculate the elastic network’s matrix K using (2) and (3). Finally, invert this matrix to calculate C using (4).

3. Generate mutational forces. For each site i, generate μ = 1 ⋯ M mutational force vectors f(iμ) using (6), (7), and (20).

4. Calculate mutational deformations. For each mutational force f(iμ), calculate the resulting response Δr⁰(iμ).

5. Calculate the compensation matrix. For each pair (iμ,jν), calculate Δr⁰(iμ)^TΔr⁰(jν), maximize over ν, and average over μ to obtain the elements of the compensation matrix D, according to (19).

Analytical formula for the compensation matrix

In this section, I derive an analytical formula that allows the direct calculation of the compensation matrix, D, without performing simulations.

The first step is to consider the overlap between two deformations, Δr⁰(i)^TΔr⁰(j). Consider two mutations, at sites i and j, represented by forces f(i) and f(j), respectively. From (6) and (8), it follows that

(21) $$\begin{array}{cc}\mathrm{\Delta }{\mathbf{r}}^0(i)=& \sum _{ik\in C(i)}({\mathbf{C}}_k-{\mathbf{C}}_i){\mathbf{e}}_{ik}f(ik)\\ \mathrm{\Delta }{\mathbf{r}}^0(j)=& \sum _{jl\in C(j)}({\mathbf{C}}_l-{\mathbf{C}}_j){\mathbf{e}}_{jl}f(jl)\end{array}$$where Δr⁰(x) is the protein’s deformation due to mutating site x, C_x is the 3 N × 3 block of C with the 3 columns corresponding to site x, and f(xy) is the scalar force applied to contact xy. From (21), the overlap between two deformations is given by

(22) $$\mathrm{\Delta }{\mathbf{r}}^0(i{)}^T\mathrm{\Delta }{\mathbf{r}}^0(j)=\sum _{ik\in C(i)}\sum _{jl\in C(j)}f(ik)f(jl){\mathbf{e}}_{ik}^T({\mathbf{C}}_k-{\mathbf{C}}_i{)}^T({\mathbf{C}}_l-{\mathbf{C}}_j){\mathbf{e}}_{jl}$$

For simplicity of notation, it is convenient to rewrite this equation in matrix form:

(23) $$\mathrm{\Delta }{\mathbf{r}}^0(i{)}^T\mathrm{\Delta }{\mathbf{r}}^0(j)=\mathbf{f}(i{)}^T{\mathbf{A}}_{ij}\mathbf{f}(j)$$where f(i) is a column vector whose elements are the CN(i) contact forces f(ik), f(j) is the column vector with CN(j) elements f(jl), and A_ij is a matrix of size CN(i) × CN(j) with elements

(24) $$A_{ik,jl}\equiv {\mathbf{e}}_{ik}^T({\mathbf{C}}_k-{\mathbf{C}}_i{)}^T({\mathbf{C}}_l-{\mathbf{C}}_j){\mathbf{e}}_{jl}$$

At this point it is easy to derive a formula for the compensation matrix. The maximum of ${\left[\mathrm{\Delta }{\mathbf{r}}^0{(i)}^T\mathrm{\Delta }{\mathbf{r}}^0(j)\right]}^2$, subject to the constraint f(j)² = σ² CN(j) (Eq. (20)) can be shown to be (25) $$max{\left[\mathrm{\Delta }{\mathbf{r}}^0{(i)}^T\mathrm{\Delta }{\mathbf{r}}^0(j)\right]}^2=CN(j)\mathbf{f}(i{)}^T{\mathbf{A}}_{ij}{\mathbf{A}}_{ij}^T\mathbf{f}(i)$$

Then, replacing (25) into (19), and using (15), leads to:

(26) $$D_{ij}={\sigma }^2\sqrt{\mathrm{C}\mathrm{N}(j)\mathrm{T}\mathrm{r}{\mathbf{A}}_{ij}{\mathbf{A}}_{ij}^T}$$where Tr is the trace operator. This equation allows the calculation of the compensation matrix.

Analytical double mutation-response scanning

The analytical Double Mutation-Response Scanning method, aDMRS, calculates the compensation matrix D using the analytical formula (26). Given a protein’s pdb file, this method proceeds as follows.

1. Set parameters. Set the parameters k and R₀ of the ANM model, and the parameter σ that defines the distribution of forces (Eq. (7)).

2. Calculate the covariance matrix. Read protein coordinates from the pdb file, for all pairs of sites calculate C_α − C_α distances, compare them with R₀ to define contacts, then calculate the elastic network’s matrix K using (2) and (3). Finally, invert this matrix to calculate C using (4).

3. Calculate the compensation matrix. Calculate the elements D_ij of the compensation matrix D using (26).

sMRS converges rapidly towards aMRS

I compare aMRS with sMRS for the proteins of Table 1. The point of this work is to assess whether the analytical method is faster than the simulation method. However, since the calculations performed with the simulation method depend on the number of mutations per site, M, before addressing computational cost, I consider the convergence of sMRS calculations.

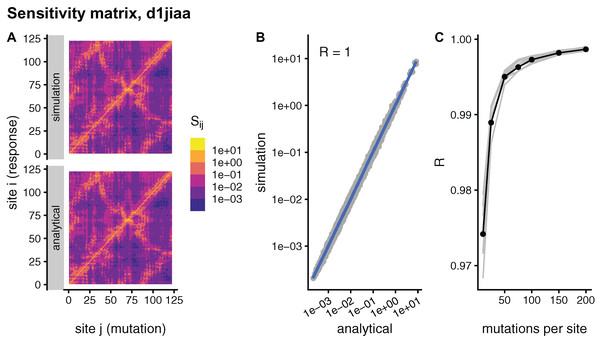
Theoretically, sMRS and aMRS are equivalent ways of calculating the sensitivity matrix S. Specifically, in the limit of an infinite number of mutations per site, $M\to \mathrm{\infty }$, the sMRS S should converge towards the aMRS S. To study this convergence, Fig. 1, compares simulated and analytical matrices for the example case of Phospholipase A2 (SCOP id d1jiaa) (Similar figures for the other proteins studied can be found in Supplemental_info.pdf). For the d1jiaa example, sMRS converges rapidly towards the aMRS matrix as M increases (Fig. 1C), so that the sMRS matrix calculated with M = 200 is very similar to the aMRS matrix (Fig. 1A and Fig. 1B).

For the other proteins the results are similar. Thus, for all cases the sMRS matrix converges rapidly towards the aMRS matrix (see grey lines of Fig. 1C). For M = 200, the correlation coefficient between sMRS and aMRS matrices is 1.00 for all proteins (Table 2). Thus, the sMRS sensitivity matrix converges rapidly with increasing M, so that with M = O(10²) it is very similar to the aMRS matrix.

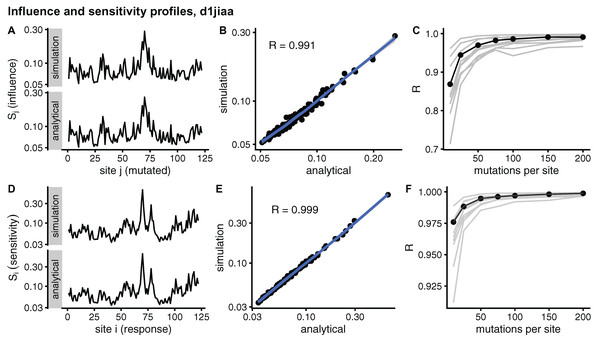
To further assess convergence, I consider sMRS and aMRS profiles. Site-dependent profiles are obtained by averaging the sensitivity matrix over rows or columns. Averaging over rows leads to an influence profile, with elements $S_j\equiv 1N{\sum }_i^N{S}_{ij}$ that measure the average influence of mutating j. Averaging over columns leads to a sensitivity profile, with elements $S_i\equiv 1N{\sum }_j^N{S}_{ij}$ that measure the sensitivity of site i with respect to mutations elsewhere.

Figure 2 compares sMRS and aMRS profiles for Phospholipase A2 (d1jiaa) (Similar figures for the other proteins studied can be found in Supplemental_info.pdf). Comparing influence profiles, we see that sMRS with M = 200 and aMRS profiles are very similar (Fig. 2A and Fig. 2B) and that sMRS influence profiles converge rapidly towards the corresponding aMRS profiles as M increases (Fig. 2C). Similarly, the sensitivity profile estimated by sMRS with M = 200 is also very similar to its aMRS counterpart (Figs. 2D and 2E) and the sMRS profile converges rapidly towards the aMRS profile as M increases (Fig. 2F).

Similar results are found for the other proteins studied. The convergence of influence profiles (grey lines of Fig. 2C) is somewhat slower than that of sensitivity profiles (grey lines of Fig. 2F), but in both cases there is good convergence. For M = 200, Pearson’s correlation between sMRS and aMRS influence profiles is in the range 0.97 ≤ R ≤ 1.00 and the correlation between sensitivity profiles is 1.00 for all proteins (Table 2). In summary, sMRS influence and sensitivity profiles converge rapidly, so that with M = O(10²) they are very similar to their aMRS counterparts.

aMRS is much faster than sMRS

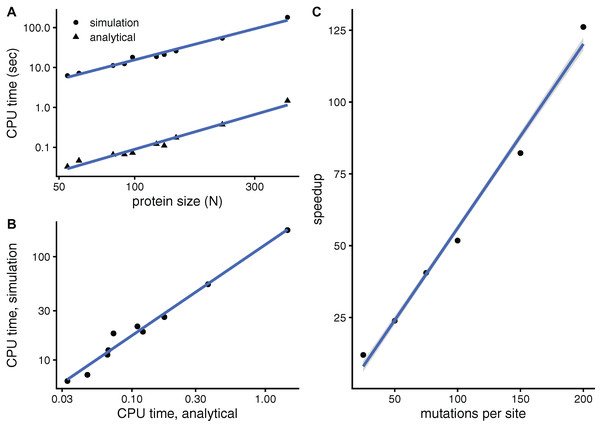
The purpose of this paper is to develop a faster mutation-response scanning method. To see whether aMRS is indeed faster than sMRS, Fig. 3 compares their computational cost. An sMRS calculation using a typical number of M = 200 mutations per site is much slower than an aMRS calculation (Fig. 3A). The computational cost, as measured by CPU time, scales with protein length as N^1.5 for both sMRS and aMRS. As a result, t_sMRS increases linearly with t_aMRS with a slope that is the speedup of aMRS vs. sMRS; For the M = 200 case, this speedup is t_sDMRS/t_aDMRS ≈ 126 (Fig. 3B). Further, the speedup increases linearly with M: t_sMRS/t_aMRS ∝ M (Fig. 3C). Thus, the analytical method provides a speedup of the order of the number of mutations per site, which is typically in the hundreds. In a word, aMRS is much faster than sMRS.

sDMRS converges slowly towards aDMRS

I compare aDMRS with aDMRS for the proteins of Table 1. As in “Mutation-Response Scanning”, before addressing computational cost, I consider the convergence of the simulation method with increasing M.

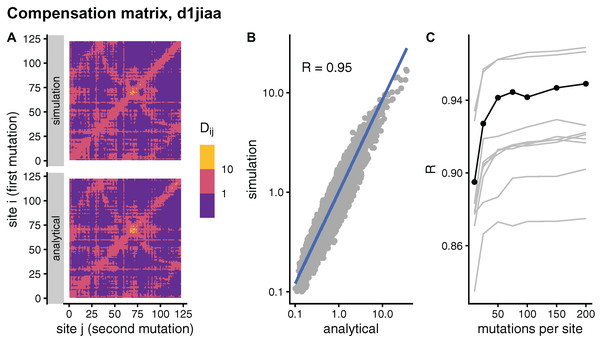
In principle, the simulation and analytical methods are equivalent. The compensation matrix D calculated with sDMRS with $M\to \mathrm{\infty }$ will be identical to the aDMRS matrix. However, in practice the sDMRS matrix depends on M. Figure 4 compares simulated and analytical compensation matrices for the example case of Phospholipase A2 (SCOP id d1jiaa) (Similar figures for the other proteins studied can be found in Supplemental_info.pdf). First, note that the compensation matrix obtained with sDMRS with M = 200 looks similar to the aDMRS matrix (Fig. 4A). More quantitatively, a scatter plot of sDMRS vs. aDMRS matrix elements shows good correlation, but there is a visible scattering of points around the linear fit (Fig. 4C). The similarity between sDMRS and aDMRS matrices can be measured by the correlation coefficient, which in this case is R = 0.95. Figure 4C shows that as M increases, the sDMRS matrix converges rapidly at first towards the aDMRS matrix, but convergence slows down with further increases of M. Thus, for Phospholipase A2, sDMRS with O(10²) mutations per site produces a compensation matrix that is in good agreement with, but not identical to, the aDMRS matrix.

A similar situation is found for the other proteins of the dataset. Convergence quickly slows down as M increases (see grey lines of Fig. 4C ). For M = 200, the correlation between sDMRS and aDMRS matrices falls within the range 0.87 ≤ R ≤ 0.97 (Table 3). Thus, the sDMRS compensation matrix converges slowly towards the aDMRS matrix, so that for M = O(10²) the simulated matrix is in moderate to good agreement with the analytical matrix. The degree of convergence is not clearly related to protein properties such as structural class or protein size, thus convergence should be tested whenever the simulation method is used.

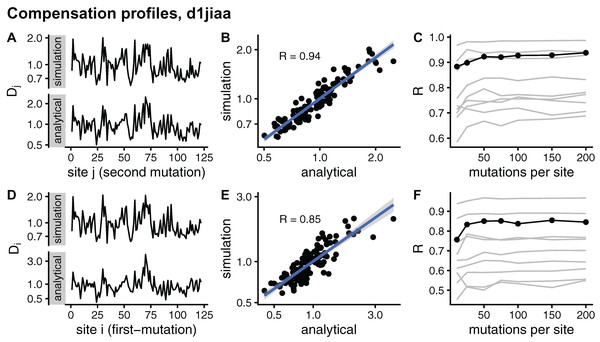
I further assess convergence by considering site-dependent compensation profiles. Averaging D over rows, I obtain a D_j profile that measures the average compensation power of sites j. Averaging over columns, I obtain a D_i profile that measures how likely to be compensated mutations at i are. Figure 5 compares sDMRS and aDMRS profiles for Phospholipase A2 (d1jiaa). The M = 200 sDMRS profiles are visually similar to aDMRS profiles (Fig. 5A and Fig. 5D). The similarity is not very high, however: points are quite scattered around the linear fit in sDMRS vs. aDMRS plots (Fig. 5B and Fig. 5E). The convergence of sDMRS profiles towards their aDMRS counterparts is very slow (Fig. 5C and Fig. 5F).

Similar results are found for the other proteins studied. Profiles generally improve very slowly with increasing M (see grey lines of Fig. 5C and Fig. 5F). For M = 200, the correlation coefficient between sDMRS and aDMRS D_i profiles falls in the range 0.55 ≤ R ≤ 0.97 and between D_j profiles it falls in the range 0.69 ≤ R ≤ 0.99 (Table 3). In summary, sDMRS profiles converge very slowly with increasing M, so that for M = O(10²), they are often poorly converged. In addition, There are no obvious determinants of convergence: R is not clearly determined by either protein size or structural class. Therefore, whenever the simulation method is used, convergence should be tested.

aDMRS is much faster than sDMRS

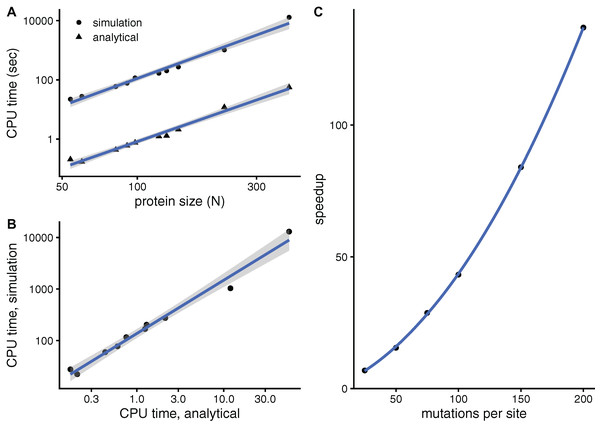
To see whether aDMRS is faster than aDMRS, Fig. 6 compares their computational cost. sDMRS with M = 200 mutations per site is much slower than aDMRS (Fig. 6A). The computational cost, as measured by CPU time, scales with protein length as N³ for both sDMRS and aDMRS. As a result, t_sDMRS increases linearly with t_aDMRS with a slope that is the speedup of aDMRS vs. sDMRS. For the M = 200 case, t_sDMRS/t_aDMRS ≈ 137 (Fig. 6B). The speedup increases non-linearly with M (Fig. 6C). This dependence can be understood from the sDMRS procedure schematised in “Simulation-based Double Mutation-Response Scanning”. The cost of generating the mutations (steps 3 and 4) increases linearly with M, while performing the average and maximization needed to calculate the compensation matrix (steps 5) scales as M². Therefore, for large M the analytical method provides a speedup of O(M²), making aDMRS much faster than sDMRS.