Investigating the effects of intermolecular interactions on nonlinear optical properties of binary mixtures with high repetition rate femtosecond laser pulses
- Published
- Accepted
- Received
- Academic Editor
- Axel Zeitler
- Subject Areas
- Spectroscopy, Physical Chemistry (other)
- Keywords
- High repetition rate (HRR), Nonlinear optical (NLO) properties, Thermo-optical effect, Open-aperture z-scan (OAZS), Close-aperture z-scan (CAZS), Binary mixtures, Cumulative thermal effect, Flowing and non-flowing liquid systems, Intermolecular interactions
- Copyright
- © 2022 Gupta et al.
- Licence
- This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, reproduction and adaptation in any medium and for any purpose provided that it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Physical Chemistry) and either DOI or URL of the article must be cited.
- Cite this article
- 2022. Investigating the effects of intermolecular interactions on nonlinear optical properties of binary mixtures with high repetition rate femtosecond laser pulses. PeerJ Physical Chemistry 4:e23 https://doi.org/10.7717/peerj-pchem.23
Abstract
Measurements of nonlinear optical (NLO) properties of different binary mixtures having carbon disulfide (CS2) as the common component, namely CS2-acetone, CS2-cyclopentanone, CS2-toluene, and CS2-carbon tetrachloride (CCl4), are carried out by using the z-scan technique. Open-aperture z-scan (OAZS) and close-aperture z-scan (CAZS) experiments are performed to determine the nonlinear absorption coefficient (β) and nonlinear refractive index (n2) of all binary liquid mixtures at various compositions of the components by employing a pulsed, high repetition rate (HRR) femtosecond laser. Also, we were able to use the flowing liquid to measure NLO properties in the CS2-acetone binary mixture to remove the cumulative thermal effects produced due to the pulsed HRR laser light. Nonlinear refractive index (n2) values are found to be influenced by the weak dipole-induced dipole intermolecular interactions between the nonpolar CS2 and polar acetone as well as cyclopentanone of the respective binary mixtures. On the contrary n2 values are not found to be affected by the intermolecular interactions in CS2-toluene and CS2-CCl4 binary mixtures. In comparison, the nonlinear absorption coefficient (β) values are not found to be affected by the same in all different sets of binary mixtures.
Introduction
Since NLO materials have major ultrafast applications such as optical switching (Cotter et al., 1999; Almeida et al., 2004), optical data storage (Parthenopoulos & Rentzepis, 1989; Dvornikov, Walker & Rentzepis, 2009), coherent nonlinear optical imaging (Duncan, Reintjes & Manuccia, 1982; Zumbusch, Holtom & Xie, 1999), two-photon fluorescence microscopy (Denk, Strickler & Webb, 1990; Helmche & Denk, 2005), etc., interest in the field of characterizing nonlinear optical materials is growing significantly. The standard basic idea among all these mentioned applications of NLO materials is connected with the change in refractive index when high-intensity light passes through them. There are certain phenomena due to which refractive index change occurs in materials. The first one is due to the Kerr type nonlinearity, wherein the induced electrical polarization and nuclear/molecular reorientation of the material results in anisotropy. The refractive index along the optical field is different from that in other directions. In contrast, another one is due to the temperature-induced changes in the refractive index which arises due to the thermal heating of the sample on interacting with the incident light.
Experimental techniques, like beam distortion measurements (Williams, Soileau & Van Stryl, 1984), have been used to characterize NLO materials. Still, it has been seen that there are difficulties in analysis, and it is quite insensitive to measure the nonlinear optical parameters such as the nonlinear refractive index. The Z-scan technique introduced by Sheik-Bahae et al. (1990) is frequently used as a very sensitive and highly straightforward method for determining the third-order nonlinear optical parameters such as nonlinear refractive index (n2) and nonlinear absorption coefficient (β). One can easily deduce the magnitude and signs of the real and imaginary part of the third-order susceptibility. In this method, the sample being investigated is kept on a translation stage and moved through the focal point in the propagating direction of the laser beam. So, using this technique, we can directly measure the nonlinear absorption coefficient (β) by measuring the change in the intensity of the transmitted light through the sample with a photodetector placed at the far-field position.
Similarly, we can also measure the nonlinear refractive index (n2) by placing a partially closed aperture before the photodetector in the same experimental setup. We can analyze the nature of nonlinear refraction through the analysis of peak and valley positions in the close-aperture z-scan regime, which can directly correspond to self-defocusing (peak followed by dip) and self-focusing (dip followed by peak) (DeSalvo et al., 1992). These effects are highly influenced by various laser properties such as polarization (Vivas et al., 2012), wavelength (Xu & Webb, 1996), pulse width (Shuo et al., 2006), and repetition rate (Falconieri, 1999), which, in turn, modifies the NLO properties of materials. Also, it becomes essential to get fundamental knowledge about the physical source to determine the sign and magnitude of third-order nonlinearity.
Femtosecond high-repetition-rate (HRR) lasers can be used in the Z-scan technique using chopper (‘blanking’) to determine NLO properties of samples, which reduces the thermal effect and linear absorption. Using HRR laser provides high sampling rates due to high frequency (76 MHz). The pulse-to-pulse fluctuation plays a significant role in determining NLO properties, which is excellent for HRR lasers. Optical switches work at a high pulse repetition rate, which is the basis for developing the optical time domain multiplexing transmission systems and optical parallel data processing systems. Thus, operating these at a high pulse repetition rate may become the cause for the occurrence of the interfering cumulative thermal effects. These effects may bring significant changes in the nonlinear behavior of non-resonant materials. In this regime, we have to consider the linear and nonlinear response of the materials in deducing properties of the transmitted light detected through a photodetector, and subsequent possible thermal effects due to single and multi-photon absorption has to be taken into consideration. The occurrence of thermal effects due to the high repetition rate laser source can give rise to erroneous results. It may hamper the nonlinear response of the material under investigation. Despite that, HRR mode-locked lasers are essential in developing NLO materials, which find widespread usefulness in most photonic devices to achieve high sampling rates of signals and more excellent pulse-to-pulse stability. This laser makes it easier to average a large amount of data within a short period to attain high signal-to-noise ratios. In addition, HRR femtosecond lasers are also easier to maintain and can be made available at a low commercial price. Experiments based on nonlinear optical microscopies such as nonlinear absorption microscopy (Yem, Fu & Warren, 2009) and nonlinear pump-probe microscopy (Fischer et al., 2016) employ high repetition rate mode-locked femtosecond or picoseconds laser. High-frequency modulation becomes an essential parameter for achieving high sensitivity. Further laser intensity fluctuation is proportional to (1/f) where ‘f’ is the high-frequency parameter when it occurs at low frequency for megahertz laser can approach quantum shot-noise limit. Here, lock-in-amplifier comes to the rescue as low-intensity fluctuation can be minimized in attaining shot-limited detection sensitivity.
Although a high repetition rate (HRR) laser provides the significant advantage of improved signal-to-noise ratios, it also comes with drawbacks such as pulse-pile-up problems and cumulative photo-thermal effects, which can seriously interfere with the required results. Whenever the time interval between two successive incoming pulses become shorter than the thermal characteristic-time (tc) given by , where w is beam radius, and D (in cm2s−1) is thermal diffusivity, cumulative thermal effects pop up to create difficulties in acquiring pure results. This situation creates problems in attaining equilibrium temperature between two successive pulses, which results in the accumulation of heat in the system under consideration. A steady-state reaches when the rate of heat accumulation in the system becomes equal to the rate of heat generation in the surrounding. This steady-state gives rise to a spatial distribution of temperature, which, in turn, develops a refractive index gradient because the system starts behaving as a lens. Many research papers (Falconieri, 1999; Mian, McGee & Melikechi, 2002; de Nalda et al., 2002) dealt with the thermal lensing effect of the system when z-scan experiments were performed with HRR lasers.
Researchers have developed different methods to eliminate the accumulated heat in the system when HRR lasers are used in the z-scan method (Yang & Song, 2009; Wickremasinghe et al., 2014; Falconieri & Salvetti, 1999; Gnoli, Razzari & Righini, 2005; Abidin et al., 2014; Gomes et al., 2007). Most of these methods employ a mechanical chopper in the laser beam path before the sample by varying the chopping frequency and the chopper opening rise time (Falconieri & Salvetti, 1999; Gnoli, Razzari & Righini, 2005; Abidin et al., 2014). These methods temporally resolved the z-scan signal and worked on the fact that there are no thermo-optical effects at time t = 0, but care must be taken to extrapolate the data to zero time as well as a longer time scale. This sensitivity improved when a thermally managed eclipse z-scan technique was utilized (Gomes et al., 2007). But on the practical ground, none of these methods can be used as there is no possible real-time separation to separate the thermal part.
Our group has already published a paper that deals with managing the cumulative thermal effect in liquid samples where a flowing system is used at different rates. Every time, a fresh sample comes for every shot of laser pulse (Singhal, Dinda & Goswami, 2017). In that work, pure CS2 liquid solvent is used as the sample. A z-scan experiment was performed to determine the nonlinear optical properties like nonlinear absorption coefficient (β) and nonlinear refractive index (n2) at different flow rates. CS2 is used as the standard reference due to its huge nonlinearity to determine these nonlinear optical properties. Thus, this experiment aims to show the effects of intermolecular interaction on the nonlinear optical properties of CS2 when mixed with other well-known liquid solvents, such as acetone, cyclopentanone, toluene, and carbon tetrachloride (CCl4), to make binary mixtures at various composition ratios. All these liquid solvents are highly miscible with CS2 and also do not have two-photon absorption at 780 nm. So, it can provide useful information about the effects of intermolecular interactions on the NLO properties of binary mixtures. Since research in binary mixtures is gaining momentum, it becomes essential to learn about all its possible aspects. Binary mixtures of carbon disulfide and acetone are known to form azeotropes. There are few research papers (Akkermans, 2017; Xiong, Sandler & Burnett, 2014) in CS2-acetone binary mixtures that deal with aspects such as solvation free energy, etc. Still, there are not many studies done on other binary mixtures as mentioned above. Previously, experiments to probe the effects of intermolecular interactions within solvent molecules have been employed using nondegenerate dual-beam z-scan techniques (Long, Swofford & Albrecht, 1976; Ma, Gomes & de Araujo, 1991; Bhattacharyya, Kumar & Goswami, 2011; Ferdinandus et al., 2012). In these experiments, one laser beam acts as a pump beam to excite the sample from the ground excited state. In contrast, another laser beam is used to probe the excited sample. Here excited samples can decay back to the ground state via radiative and non-radiative pathways. Through the non-radiative pathway, there occurs a rise in the temperature of sample molecules, which in turn develops a refractive index gradient in the medium.
Materials & Methods
For this study, we used HPLC grade carbon disulfide (CS2), acetone, cyclopentanone, toluene, and carbon tetrachloride (CCl4). These liquid solvents were purchased from Spectrochem Pvt. Ltd., Mumbai, India, and used without further purification. We prepared CS2-acetone, CS2-cyclopentanone, CS2-toluene, and CS2-CCl4 binary mixtures at various composition ratios.
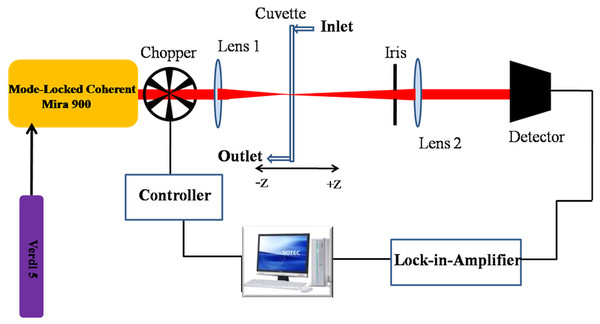
To measure the nonlinear refractive indices and absorption coefficients of binary liquid systems, we used close-aperture and open-aperture z- scan techniques, respectively. Figure 1 shows the schematic diagram of our experimental setup, which was discussed in detail previously (Singhal, Dinda & Goswami, 2017). Data were collected as previously described in Singhal, Dinda & Goswami (2017). Specifically, a mode-locked Ti:Sapphire femtosecond laser (Mira-900F; Coherent, Santa Clara, CA, USA) with a repetition rate of 76 MHz centered at 780 nm wavelength, and pulse width of 140 fs is used as our high-intensity light source. A 5 cm lens is used to focus the laser beam. The beam radius at the focus is measured to be ∼5 µm. The average power of the laser at the sample was 240 mW when measured with a power meter (Coherent, Santa Clara, CA, USA). The binary liquid mixture samples are put in a quartz cuvette of path length 0.1 mm. A peristaltic pump (MasterFlex; Cole-Parmer; Vernon Hills, IL, USA) is used to flow the sample continuously in the sample cuvette at a particular flow rate of 65 ml/min 26. The sample cell is moved along the beam propagation axis near the focus of the laser beam. A computer-controlled motorized translation stage with a 0.1 µm step size resolution (Newport, Irvine, CA, USA) moves the sample cuvette. The transmitted light through the sample is passed through the 50% closed aperture and detected by silicon photodiode (PDA100A-EC; Thorlabs, Newton, NJ, USA). The signal is acquired by a lock-in amplifier controlled by a computer interfaced through a GPIB card. A chopper, running at 800 Hz, is put in the beam path to get a reference signal for the lock-in amplifier (SRS 830 DSP). The lock-in amplifier reduces the random noise in the signal and increases the signal-to-noise ratio.
Figure 1: Schematic of experimental z-scan setup showing inlet and outlet for flowing liquids.
Results
In this study, we probe the effect of intermolecular interaction on the nonlinear optical (NLO) properties of CS2, which has significant two-photon absorption (TPA) at 780 nm wavelength. To prepare binary mixtures with carbon disulfide at varying compositions, we used solvents such as acetone, cyclopentanone, toluene, and carbon tetrachloride. All these co-solvents with CS2 do not have two-photon absorption at 780 nm wavelength, and thus we can acquire information about the intermolecular interactions on the nonlinear optical properties (NLO). Here NLO properties correspond to nonlinear absorption in terms of β and nonlinear refraction in terms of n2. For measuring these properties, we employed a high repetition rate (HRR) pulsed femtosecond laser in both open-aperture z-scan (OAZS) and close-aperture z-scan (CAZS) regimes of the experimental setup.
Further, we used flowing liquid for the CS2-acetone binary mixture system to remove thermal effects using a peristaltic pump at a particular flow rate of 65 ml/min in the experimental setup, as shown in Fig. 1. We took CAZS signals of the binary liquid mixtures system by putting an iris in the path of the transmitted light passing through the sample. Further, for OAZS signals, we removed the iris in an otherwise identical experimental setup. We divided the close-aperture data by the open-aperture one for an accurate CAZS signal devoid of the nonlinear absorption component. We could not get pure signals in flowing systems for other different sets of binary mixtures due to problems of bubble formations and thin sample size, which resulted in too much oscillation in the signals. Since this comparative study aims to find the variations of NLO properties across various sets of binary mixtures, we could use a thick sample size such as one mm path length to enhance the signal-to-noise ratio. Therefore, we took CAZS data for CS2-cyclopentanone, CS2-toluene, and CS2-CCl4 in a one mm path length cuvette to avoid too low signal-to-noise ratios.
Discussion
The OAZS data are fitted with Eq. (1) to obtain the two-photon absorption coefficient (β), and the CAZS signals are fitted with Eq. (2) to evaluate the nonlinear refractive index (n2). These equations were given by Sheik-Bahae et al. (1990) as: (1) (2)
Equation (1) is valid under α0<<1. In Eq. (2), Δ Φ0 is the phase change of the laser beam expressed as: Δ Φ0 = ; where effective sample length, , α0 = linear absorption, L = sample length; x = z/z0 z is the sample position, and z0 is the Rayleigh range of Gaussian beam. These equations also ensure that transmittance is never greater than 1.
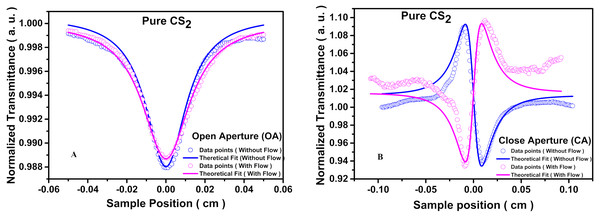
We took OAZS and the CAZS data for all composition ratios of the binary liquid mixtures. Figures 2A–2B shows the same for pure carbon disulfide (CS2), including with-flow and without-flow conditions, respectively.
As shown in Fig. 3A, we are getting the peak-valley kind of trace for the CAZS regime in a non-flowing system. This peak-valley profile occurs because the binary liquid system under consideration is behaving as a self-defocusing lens, whereas for CAZS data using a flowing system, we got the valley followed by the peak trace, which arises because the binary liquid now behaves as a self-focusing one. The peak-valley graph appears due to the thermal-lens behavior of the liquid with a negative value of the thermo-optic coefficient (dn/dt). Further, this occurrence of thermal behavior in liquids is not related to the linear absorption of CS2 because it has negligible linear absorbance at 780 nm. To confirm that heat is not generated by linear absorption, we employed the CW laser having the same average power of 240 mW in precisely the similar z-scan setup. We did not get any z-scan signal with the CW laser, which proved that the thermal behavior of the system arises just because of the nonlinear absorption at 780 nm wavelength.
Figure 2: Plot of open aperture z-scan (OAZS).
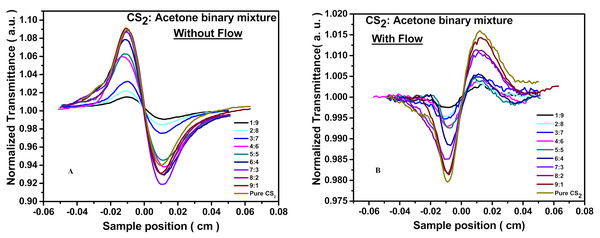
Z-scan data plots of OAZS for the pure carbon disulfide (CS2) liquid under both with-flow and without-flow experimental conditions.Figure 3: CAZS trace for the binary liquid mixture of carbon disulfide with acetone under “without flow” and “with flow” conditions.
We plotted the variation of nonlinear absorption coefficient (β) values with the volume fraction of components of the binary mixture, as shown in Fig. 4 for both flowing and non-flowing liquid systems in the CS2-acetone binary mixture. We noticed the linear increase in β values with the volume fraction of the CS2 in both cases. After fitting to the linear fit for both cases, we found that slope is more in flowing liquid than non-flowing. We note that only CS2 has significant nonlinear absorption at 780 nm light, whereas acetone does not have that in the binary liquid mixture. So, these linear plots for both flowing and non-flowing binary liquid cases in β values show no effect of intermolecular interaction on the nonlinear absorption of CS2 as dilution increases in the binary mixture. This merely means that the higher the dilution with CS2, the higher the nonlinear absorption in the binary liquid mixtures following a linear behavior.
Figure 4: Variations of β with the volume fraction of carbon disulfide in the binary liquid mixture under both without-flow and with-flow experimental conditions.
In Fig. 5 for CS2-acetone binary mixtures, we have the variations of nonlinear refractive index (n2) and change in transmittance between peak and valley (ΔTp−v) with the volume fractions of CS2 in the binary mixtures for both flowing and non-flowing conditions. As we can see in these traces, n2 and ΔTp−v values follow the exact similar trend, which, in turn, shows the direct relationship between these two quantities and supports the Sheik-Bahae et al. (1990) result where ΔTp−v follows the expression ΔTp−v ≈ 0.406kn2I0Leff. Further, variations of n2 and ΔTp−v with volume fractions are much more profound in the non-flowing condition than in the flowing condition. We employed a flowing liquid system to eliminate the excess accumulated heat in the system, which can be seen in the variations of NLO properties under the without-flow condition of binary mixtures. Changes in the values of n2 and ΔTp−v (Fig. 5A) for the binary mixtures in the CAZS regime under without-flow condition is showing nonlinear behavior at higher volume fractions of the CS2.
Figure 5: Variations of n2 and ΔTp-v in CAZS with varying volume fractions of carbon disulfide in binary liquid mixtures of carbon disulfide with acetone for without-flow condition.
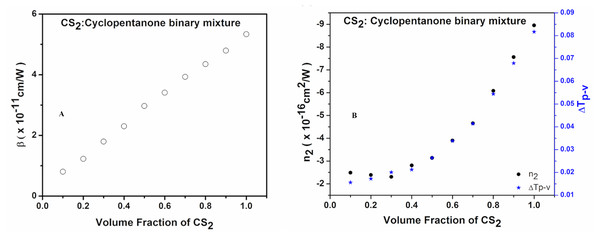
In Figs. 6A–6B for CS2-cyclopentanone binary mixtures, β values are increasing linearly with the volume fraction of CS2, whereas n2 values follow a nonlinear behavior with the same. This nonlinear behavior is directly related to the weak intermolecular interaction amongst the components of the binary mixture. This interaction arises due to the excess thermodynamic properties such as volume, viscosity, refractive index, etc. We also note that CS2 is a nonpolar molecule, while cyclopentanone and acetone molecules are polar. Thus, the dipole and the induced-dipole weak intermolecular interactions between the components of the binary mixtures are bound to occur. This weak intermolecular interaction between CS2 and acetone/cyclopentanone is the sole cause of nonlinear trace in the n2 and ΔTp−v values with respect to the varying volume fractions of components. This nonlinear behavior can also be seen in the flowing condition for CS2-acetone binary mixture as well, although the thermal contribution is removed altogether.
Figure 6: Variations in the respective NLO properties (β) and (n2) with changing volume fraction of carbon disulfide in binary liquid mixtures of carbon disulfide with cyclopentanone in CAZS without-flow experiments.
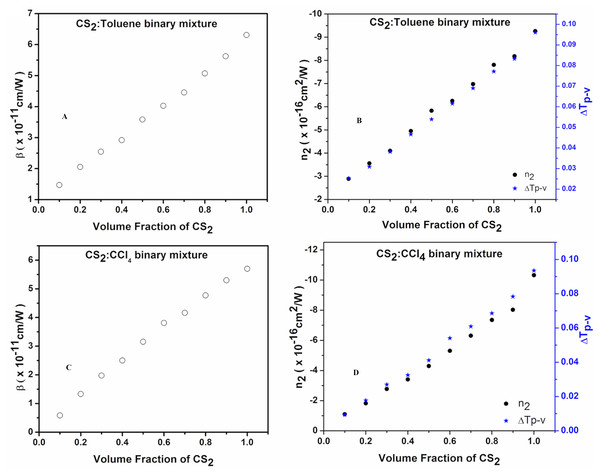
In Figs. 7A–7D for CS2-toluene and CS2-CCl4 binary mixtures, similar linear trends are seen in the β values with the volume fraction of CS2. These trends also support the observation mentioned above that nonlinear absorption is independent of the intermolecular interactions between the components of binary liquid mixtures. But the nonlinear refractive index, n2 values, shows a linear trend with the volume fractions of CS2 for both sets of binary mixtures, contrary to the aforementioned observations. Since all the liquid solvents used are nonpolar, it results in very weak induced dipole-induced dipole intermolecular interactions that do not affect the nonlinear refractive index values of both sets of binary liquid mixtures.
Figure 7: Variations in the respective NLO properties (β) and (n2) with changing volume fraction of carbon disulfide in binary liquid mixtures of carbon disulfide with toluene and carbon disulfide with CCl4 in CAZS without-flow experiments.
Conclusions
This study reveals the effects of intermolecular interaction on the nonlinear optical (NLO) properties of CS2-acetone, CS2-cyclopentanone, CS2-toluene, and CS2-CCl4 binary liquid mixtures at various compositions using the z-scan technique in both open-aperture and close-aperture experimental regimes. We found that the nonlinear refractive index (n2) values are affected due to the dipole-induced dipole intermolecular interactions between the CS2-acetone and CS2-cyclopentanone binary liquid mixture components. This, in turn, directly affects the ΔTp−v values. But n2 values are not found to be affected due to intermolecular interactions in CS2-toluene and CS2-CCl4 binary mixtures because of the nonpolar nature of both the solvents in each set of binary mixtures. However, the nonlinear absorption coefficient (β) varies linearly with the volume fraction of CS2 for all different sets of binary liquid mixtures. This trend shows that (β) values are not affected due to the intermolecular interactions between CS2 and all other liquid solvents. Additional studies can also be done to accurately support these findings, like physicochemical and optical properties such as refractive index, pulse chirp (in the solvents), dielectric constant of solvents, etc., which are pending for future research.
Supplemental Information
Experimental data was collected for various binary liquid samples under flowing versus non-flowing conditions
Each data point indicates the average of 256 laser pulses.