ACO-Kinematic: a hybrid first off the starting block

Initialization phase

The algorithm starts with the creation of archive solution during the initialization of ants. ACOR utilizes Gaussian kernal which has three vectors of parameters: weights, means and standard deviations. The time complexity for this phase is O(n), where n is the number of ants.

Archive population phase

For the archive solution, the means and standard deviations are calculated using Eqs. (1) and (2): (1)${\displaystyle \mu ={\mu }_1,\dots .{\mu }_n=s_1,\dots .,s_n,}$

where μ_i are the means and s_i the archive solutions for i = 1...n, and (2)${\displaystyle s{d}_i=\xi \sum _{n=1}^k\frac{|s_n-s_l|}{k-1},}$

where sd_i is the standard deviation, k is the archive population, ξ is the convergence speed of the algorithm and s_l is the chosen solution. ACOR stores in archive solution the values of the solutions’ n variables and the value of their objective functions. This phase has a time complexity of O(n), where n is the number of ants.

New population creation phase

This phase involves creation of the new population array which is subsequently randomly initialized. This phase has a time complexity of O(1).

Solution construction phase

This phase starts which consists of the Gaussian kernel selection and then generating Gaussian random variable. Gaussian kernel selection is based on roulette wheel selection and probability. The probability is computed based on weights. The weights and probability are given in Eqs. (3) and (4): (3)${\displaystyle w_i=\frac{1}{qk\sqrt{2\ast \Pi }}exp\left(-0.5\frac{{\left(i-1\right)}^2}{{\left(qk\right)}^2}\right),}$ where, w_i is the weight for individual solution, q is the intensification factor and k is the archive population, and (4)${\displaystyle P_i=\frac{w_n}{\sum _{n=1}^k{w}_n},}$

where, P_i is the probability of individual archive solution, k is the archive population and w_n is the weight of individual archive solution.

An ant chooses probabilistically one of the solutions in the archive using Eq. (4).

The position of the new population is the random variable generated using means and standard deviations from the Archive Population Phase and normally distributed random numbers. This phase has a time complexity of O(n), where n is the number of ants.

Evaluation phase

The new constructed solution is then evaluated using a fitness function and merged with the archive population. Finally, the total population is sorted to get the best solution and a new set of archive solution. The time complexity for this phase is O(1).

All phases except the Initialization phase will be repeated until the robot reaches its destination.

Multi-objective path planning problem

The robot path planning problem is formulated as the multi-objective problem. The two objectives are obtaining short path and safe path of the robots.

The following is the definition of a point-mass robot adopted from Prasad et al. (2020a):

Definition 1. A jth point-mass P_j is a disk of radius rp_j ≥ 0 and is positioned at (x_j(t), y_j(t)) ∈ ℝ² at time t ≥ 0. Precisely, the point-mass is the set ${\displaystyle P_j=\left\{\left(z_1,z_2\right)\in {\mathbb{R}}^2:{\left(z_1-x_j\right)}^2+{\left(z_2-y_j\right)}^2\le r{p}_j^2\right\}}$ for j = 1, 2, …, n,

Definition 2. The target for P_j is a disk of center (p_j1, p_j2) and radius rt_j which is described as (5)${\displaystyle T_j=\left\{\left(z_1,z_2\right)\in {\mathbb{R}}^2:{\left(z_1-p_{j1}\right)}^2+{\left(z_2-p_{j2}\right)}^2\le r{t}_j^2\right\}}$ for j = 1, 2, …, n.

Ant representation

The motion of each robot will be guided by a colony of ants which are randomly distributed in the working environment. Since we are considering n point-mass robots, there will be n colonies altogether with each colony having n_j ants. The following is the definition of a moving ant in the jth colony:

Definition 3. The ith ant in the jth colony A_ij is a disk of radius ra_ij ≥ 0 and is positioned at (xa_ij(t), ya_ij(t)) ∈ ℝ² at time t ≥ 0. Precisely, the ith ant in the jth colony is the set ${\displaystyle A_{ij}=\left\{\left(z_1,z_2\right)\in {\mathbb{R}}^2:{\left(z_1-x{a}_{ij}\right)}^2+{\left(z_2-y{a}_{ij}\right)}^2\le r{a}_{ij}^2\right\}}$ for i = 1, 2, …, n and j = 1, 2, …, n.

Problem formulation

The problem is the minimization optimization problem which finds the optimal path for mobile robots in a cluttered environment. The fitness equation is designed by summing all the objective functions defined in this section: (13)${\displaystyle f_{ij}=a.\frac{1}{f{1}_{ij}}+b.\frac{1}{f{2}_{ij}}+c.\frac{1}{f{3}_{ij}}+d.d_{ij}}$ which is the fitness of ith ant for robot j and a, b, c and d are control parameters. The ant having the minimum f_ij will be the fittest ant in the jth colony. It means that the ant is located at a safe distance from obstacles and at a minimum distance from the target. The jth robot will move to the fittest ant of the jth colony and this process will continue until the jth robot reaches its target. The control parameters a, b and c are the fitting parameters that decide path safety. With a high value of parameter a the ants will avoid the stationary circular obstacles from the greater distance. Similarly, a small value of b will mean that the ants will avoid the line segments from a closer distance which can compromise safety. However, when there is a decrease in the value of a, b and c, the chances of collision with obstacles, line segments and other robots are high. Likewise, a higher value of d will minimize the path length and a smaller value will maximize the path length. Therefore, a proper selection of these parameters decides the success of the objective function in planning the next step for a robot.

Motion control

The kinematic equations are used to control the robot to the step location generated ants. The kinematic equations will be used to generate smooth path for the robots in between the nodes.

Case study 1: single point-mass robot and multiple obstacles

The proposed algorithm has been used to navigate the point-mass robot from source to destination in a cluttered environment. The kinematic equations governing the motion of a point-mass robot from its initial position (x₀, y₀) to another point (p₁, p₂) are (14)${\displaystyle \dot{x}={\alpha }_1\left(p_1-x\right),\dot{y}={\alpha }_2\left(p_2-y\right)}$ where α₁ and α₂ are positive real numbers.

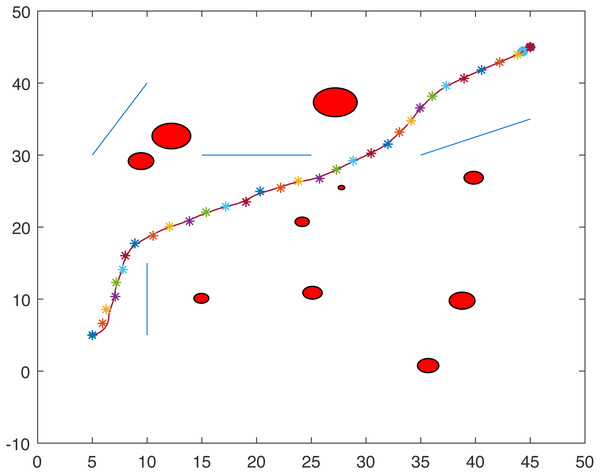
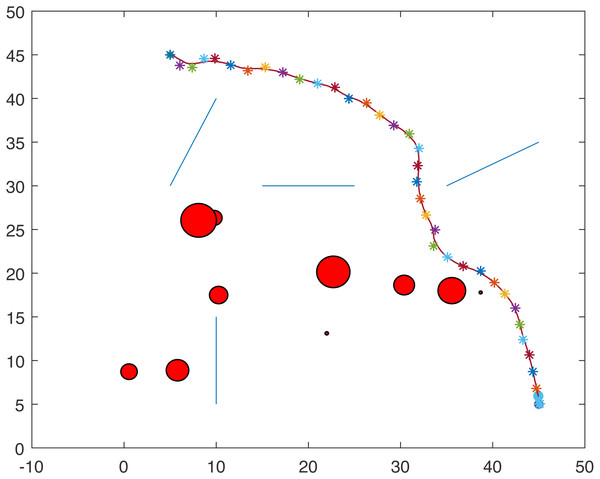
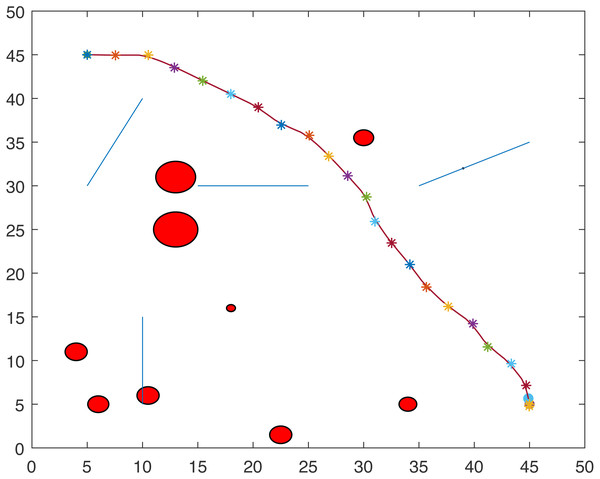
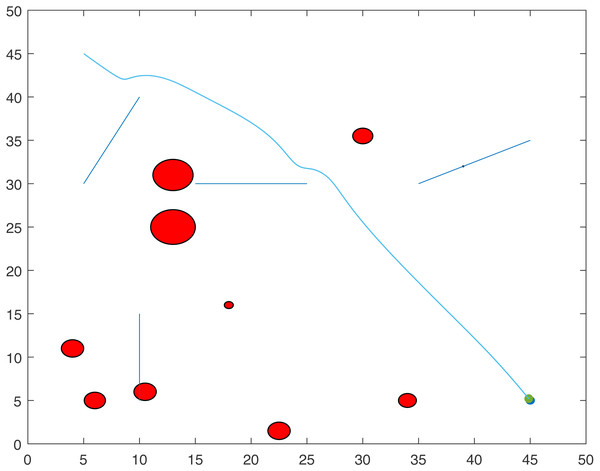
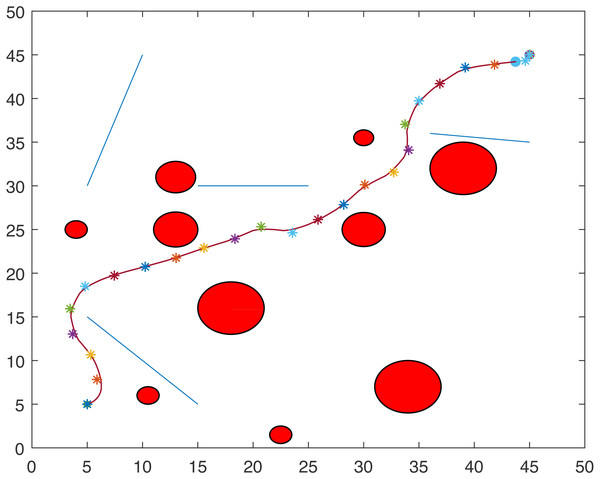
Figures 1 and 2 show two scenarios where the point-mass robot avoids circular and line obstacles to reach its target. The path of the point-mass robot consists of points that have been generated by the ants. The robot moves from one step to another using its kinematic equations.

Case study 2: multiple point-mass robots and multiple obstacles

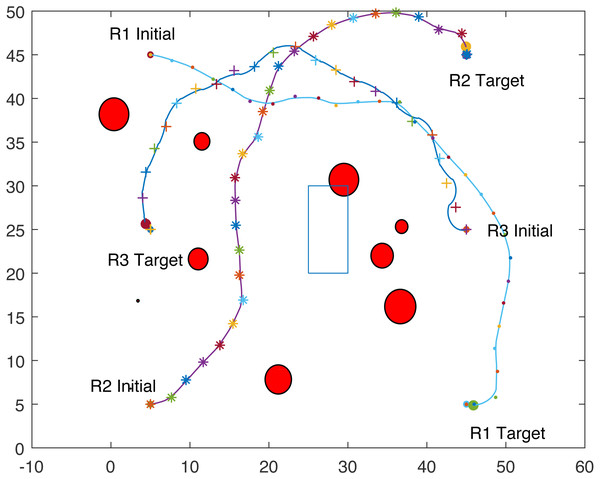
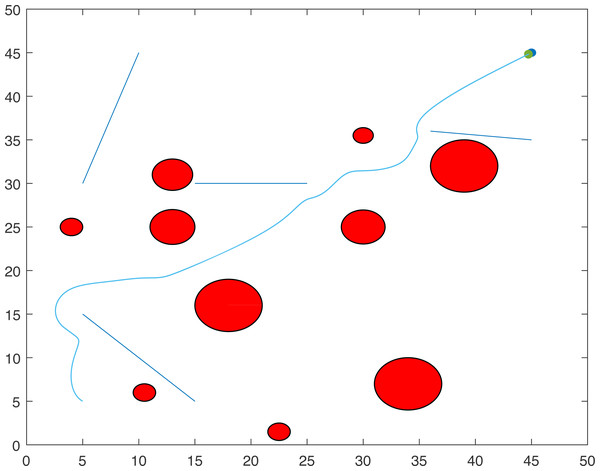
The proposed algorithm has been used to plan and control motion of multiple point-mass robots in a multiple obstacles (circular and rectangular shapes) environment. Figure 3 shows the paths of three point-mass robots. The first robot (R1) has a initial position of (5, 45) and the target placed at (45, 5). The second robot (R2) is placed at the initial position (5, 5) and has to reach the target at (45, 45). The initial and target positions for the third robot (R3) are (45, 25) and (5, 25). The three robots start journey from their initial positions and have a goal to achieve, that is, to reach their target positions safely by taking a shortest route moving from one step to another. The three robots avoid all obstacles in their paths and also avoid colliding with each other. Figure 4 shows the first robot (R1) and the second robot (R2) avoiding each other.

Application: tractor-trailer robot

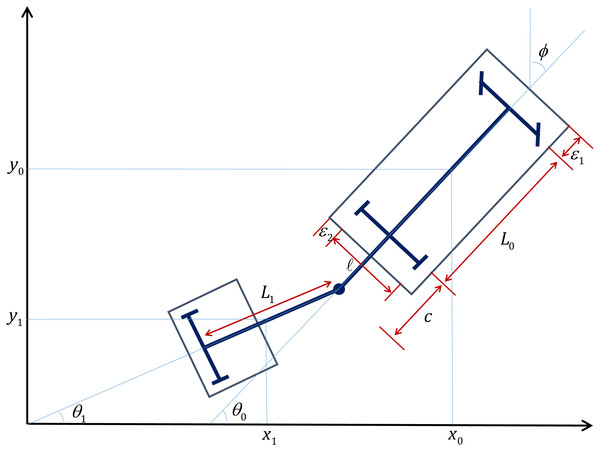
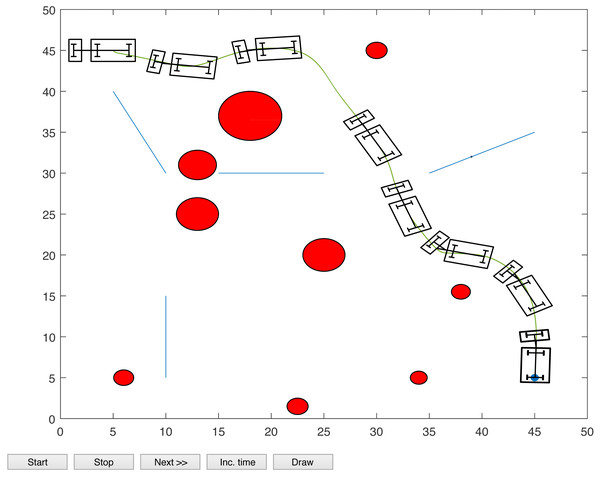
The proposed algorithm has been used for motion planning and control of a tractor-trailer robot system. We consider a non-standard tractor-trailer robot which comprises of a rear wheel driven car-like vehicle and a hitched two-wheeled passive trailer attached to the rear axel of the vehicle (Fig. 5).

Let (x, y) represent the cartesian coordinates of the tractor robot, θ₀ be its orientation with respect to the x-axis, while ϕ gives the steering angle with respect to its longitudinal axis. Similarly, let θ₁ denote the orientation of the trailer with respect to the x-axis. Letting L and L_t be the lengths of the mid-axle of the tractor and trailer, respectively, the motion of the tractor-trailer robot is governed by the following kinematic equations (Prasad et al., 2020b) (15)${\displaystyle \begin{array}{c}\dot{x}=vcos{\theta }_0-\frac{v}{2}tan\varphi sin{\theta }_0,\hfill \\ \dot{y}=vsin{\theta }_0+\frac{v}{2}tan\varphi cos{\theta }_0,\hfill \\ {\dot{\theta }}_0=\frac{v}{L}tan\varphi ,\hfill \\ {\dot{\theta }}_1=\frac{v}{Lt}\left(sin\left({\theta }_0-{\theta }_1\right)-\frac{c}{L}tan\varphi cos\left({\theta }_0-{\theta }_1\right)\right),\hfill \end{array}}$ where v and ϕ which are the translational velocity and the steering angle, respectively, of the tractor robot, given as Prasad et al. (2020b) ${\displaystyle v=\alpha \sqrt{{\left(p_2-y\right)}^2+{\left(p_1-x\right)}^2},}$ ${\displaystyle \varphi =\frac{7}{9}{tan}^{-1}\left(\xi +\frac{\beta }{cos|{\theta }_0-{\theta }_1|}\right)}$ where α is a positive real number and β = max{0, 0.5 − cos|θ₁ − θ₀|}⋅sign(θ₁ − θ₀). Note that (p₁, p₂) is the next step for the robot generated by ant colony optimization and (x, y) is the current position of the robot. ξ is obtained by numerically solving the differential equation ${\displaystyle \dot{\xi }=\frac{\left(p_2-y\right)cos{\theta }_0-\left(p_1-x\right)sin{\theta }_0}{\sqrt{{\left(x-p_1\right)}^2+{\left(y-p_2\right)}^2}+0.01}-\mathrm{atan}2\left(p_2-y,p_1-x\right)+{\theta }_0,\xi \left(0\right)=\mathrm{atan}2\left(p_2-y\left(0\right)\right),\left(p_1-x\left(0\right)\right)-{\theta }_0\left(0\right)}$

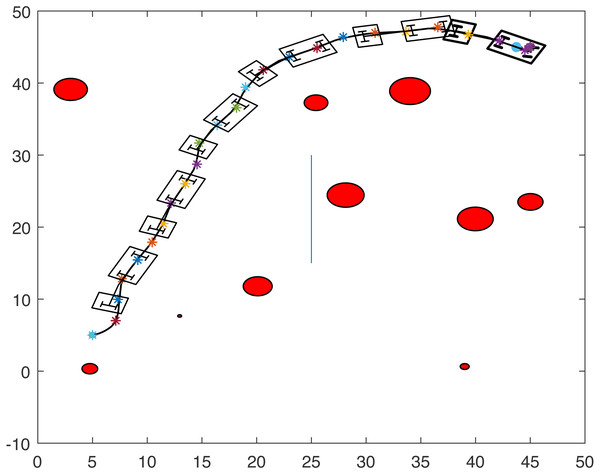
Figsures 6 and 7 show the trajectories of one tractor-trailer robot in two different scenarios.

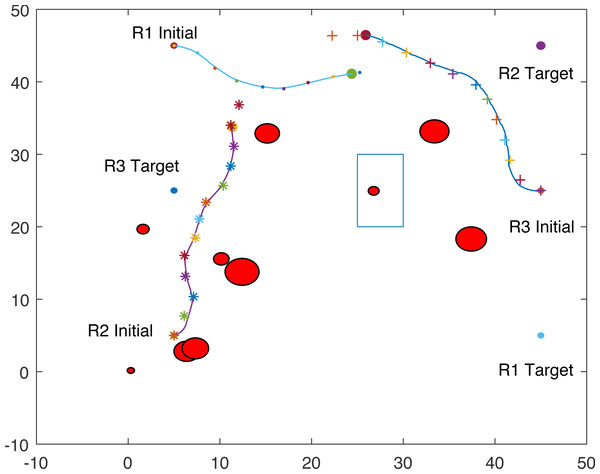
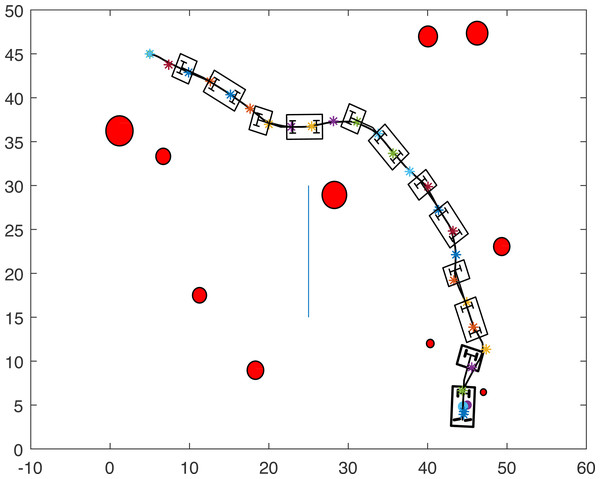
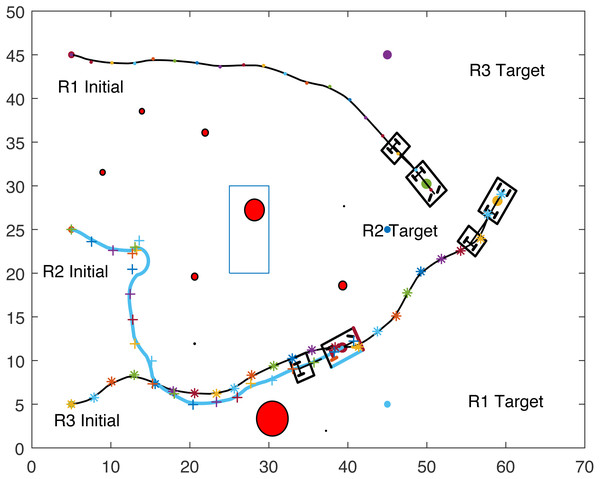
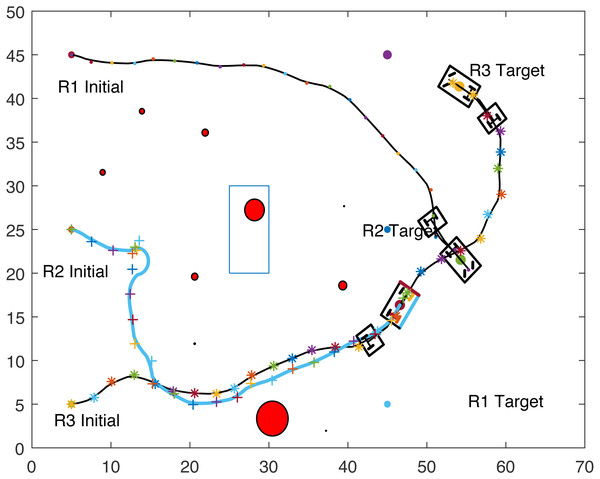
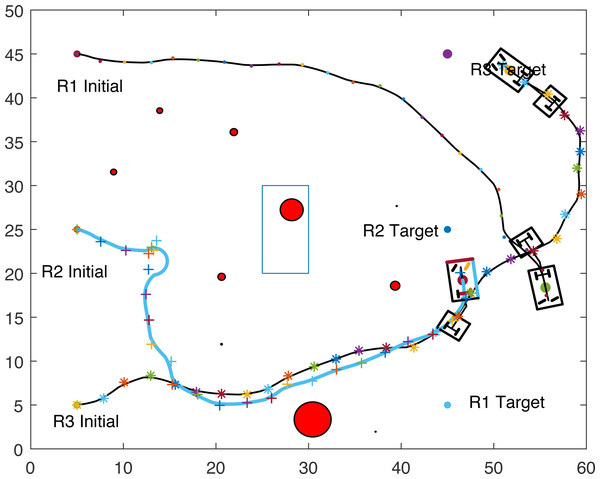
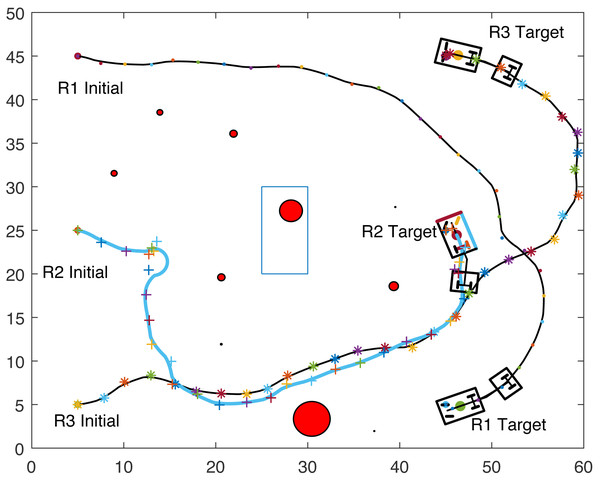
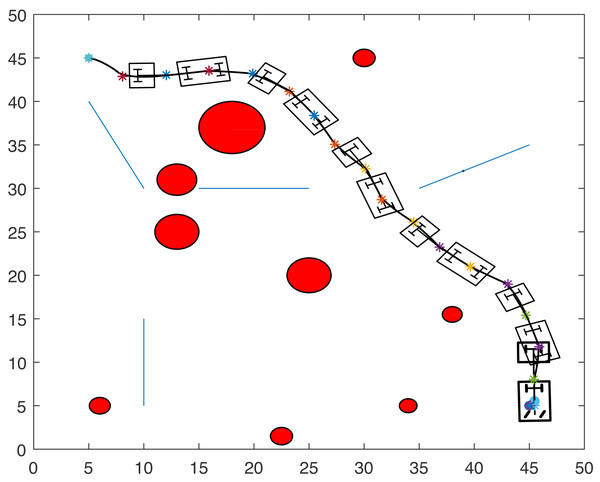
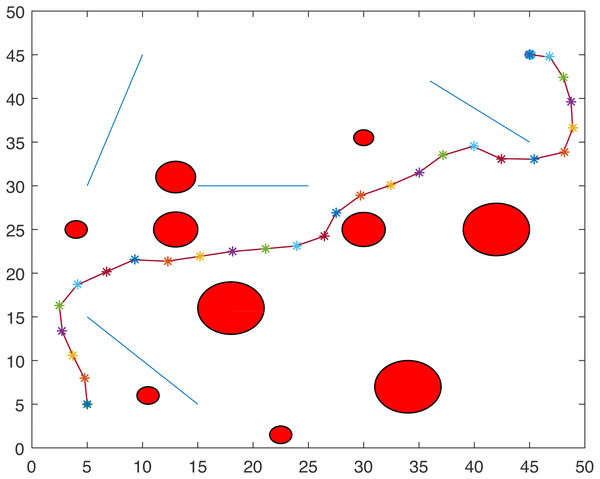
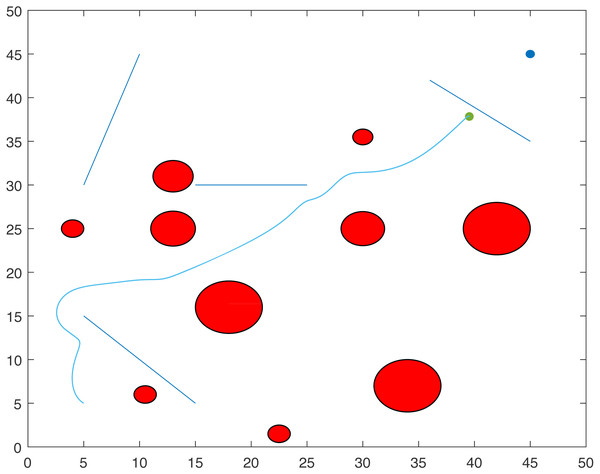
Figures 8, 9, 10 and 11 show the paths of the three tractor-trailer robots. Table 2 shows the initial and target positions for each robot.

Figure 8 shows that R1 is avoiding R3 by stopping and waiting for R3 to pass. R1 has successfully avoided R3 and R1 resumes its journey towards the target, as shown in Fig. 9. Figure 10 shows that R2 and R3 avoid each other. The complete paths for the three robots are shown in Fig. 11. The robots avoid each other using the fitness function given in Eq. (13) which is used in ACO to determine the fittest ant. The robots are then controlled to the location of the fittest ants by the kinematic equations of the robots.